AHP平均随机一致性指标RI取值(上传版)
层次分析法(AHP法)

32
定义一致性比率 : CR CI
RI
一般,当一致性比率 CR CI 0.1 时,认为A
RI
的不一致程度在容许范围之内,有满意的一致性,通 过一致性检验。否则要重新构造成对比较矩阵A,对
aij 加以调整。
一致性检验:利用一致性指标和一致性比率<0.1
及随机一致性指标的数值表,对A进行检验的过程。
实用文档
6
例2 旅游 假期旅游,是去风光秀丽的苏州,还是
去凉爽宜人的北戴河,或者是去山水甲天下 的桂林?通常会依据景色、费用、食宿条件、 旅途等因素选择去哪个地方。
实用文档
7
例3 择业 面临毕业,可能有高校、科研单位、企
业等单位可以去选择,一般依据工作环境、 工资待遇、发展前途、住房条件等因素择业。
实用文档
31
由于λ(A的特征根) 连续的依赖于aij ,则λ比n 大的 越多,A 的不一致性越严重。引起的判断误差越大。 因而可以用 λ-n 数值的大小来衡量 A 的不一致程
度。
定义一致性指标: CI n
n 1
CI=0,有完全的一致性
CI接近于0,有满意的一致性
CI 越大,不一致越严重
实用文档
实用文档
14
2.层次数与问题的复杂程度和所需要分析的详尽 程度有关。每一层次中的元素一般不超过9个,因 一层中包含数目过多的元素会给两两比较判断带 来困难。
实用文档
15
3.一个好的层次结构对于解决问题是极为重 要的。层次结构建立在决策者对所面临的 问题具有全面深入的认识基础上,如果在 层次的划分和确定层次之间的支配关系上 举棋不定,最好重新分析问题,弄清问题 各部分相互之间的关系,以确保建立一个 合理的层次结构。
层次分析法(AHP法.

心理学家认为成对比较的因素不宜超过9个,即 每层不要超过9个因素。
成对比较阵和权向量
比较尺度aij
Saaty等人提出1~9尺度——aij 取值
1,2,… , 9及其互反数1,1/2, … , 1/9
②工作收入较好(待遇好); ③生活环境好(大城市、气候等工作条件等); ④单位名声好(声誉等); ⑤工作环境好(人际关系和谐等) ⑥发展晋升机会多(如新单位或前景好)等。
目标层
工作选择
准则层 方案层
贡收 发 声 工 生 作活 环环
献入 展 誉 境 境
可供选择的单位P1’ P2 , Pn
建立层次结构模型的思维过程的归纳
• 便于定性到定量的转化:
a ij
尺度
1 2 34
Ci
:
C
的重要性
j
相同
稍强
5 6 78 9 强 明显强 绝对强
aij =1,1/2, ,…1/9 ~ Ci :Cj 的重要性与上面相反
• 用1~3,1~5,…1~17,…,1p~9p (p=2,3,4,5), d+0.1~d+0.9 (d=1,2,3,4)等27种比较尺度对若干实例构造成对比较
RI
一般,当一致性比率 CR CI 0.1 时,认为A
RI
的不一致程度在容许范围之内,有满意的一致性,通 过一致性检验。否则要重新构造成对比较矩阵A,对 aij 加以调整。
一致性检验:利用一致性指标和一致性比率<0.1 及随机一致性指标的数值表,对A进行检验的过程。
判断矩阵一致性检验的步骤如下: (1) 计算一致性指标 C.I.:
AHP的一致性问题

AHP的一致性问题第21卷第3期淮北煤师院2000年9月JournalofHuaibeiCoal—Industry.Tea—chersCollegeV0I_21No3Sen2000摘要:本文对AHP的和校正方法,AHP的一致性问题孔宪明赵文才颗学,.致性问题作了较为系统的研究和整理,介绍了几种较为简便且实用的检验关键词:—二塾堡重至查望分类号:0223文献标识码:Af’j~iil,f’¨}文章编号:1000—2227(2000)03—0021—05AHP中判断矩阵的一致性是层次分析法能否使用的关键,许多学者对一致性检验及校正方法作了大量探讨.本文对层次分析法中的一致性问题进行了较为系统的整理,介绍了几种较为简便易行的检验及校正方法.1一致性的概念在层次分析法中,为了形成判断矩哞,引人了l一9比率标度方法,这就使得决策者判断思维数学化.应用层次分析法保持判断思维的一致性是非常重要的. SaatyAL教授将判断矩阵–(.)…的一致性定义为:若对任意k,∈【l,2,…,},总有n=n成立,称判断矩阵A=(蛳)…是一致的.文【l】进一步给出,满足上述条件的判断矩阵称为具有基本一致性.AHP中的一致性除满足基本一致性外,还应满足次序一致性.所谓次序一致性是指,若元素甲比元素乙重要,元素乙比元素丙重要,则元素甲比元素丙重要.由于客观世界的复杂性及人们认识能力的局限性,利用AHP比例标度构造两两比较判断矩阵时,很难保证其具有完全一致性,特别是因素多规模大的问题更是如此.因此,为了保证层次分析法得到的结论基本合理,需要对构造的判断矩阵进行比称为随机一致性比率,记为cR.即cR=莆当CR<..10时,即认为判断矩阵具有满意的一致性.2.2统计检验法若A:(aJ…为n阶判断矩阵,W=(,…,)为其排序向量,c=(c)…为其导出矩阵,其中q1.根据文【2】的结论,判断矩阵为完全一致性矩阵的充要条件是其导出矩阵C中元素全部为1,即C=由人的主观判断偏差造成的判断矩阵不一致,可认为是众多随机干扰联合作用的结果,因而,q可视作以1为均值的正态随机变量.定理设为n阶判断矩阵,c:(c)…为其导出矩阵.c~Ⅳ(1,5),其中8为常数,且各q(,=1,2,一,n)相互独立,则统计量=∑∑(c一1)服从自由度为n的的u‘分布.定理的结论是显然的.且A满足完全一致性当且仅当=0.常数i可根据对判断矩阵的”满意的一致性”的不同要求来选取,通常取吉s5s寺8越小,对判断矩阵一致性的要求越高于是判断矩阵A的一致性检验即为如下的统计假设检验问题::s;对于给定的显着性水平嵋令P(≥)=峨查自由度为的分布表可得临界值瑶.当判断矩阵的观测值<时,即可认为A具有满意的一致性;反之,则认为不具备一致性.2.3次序一致-陛检验保持判断矩阵满足次序一致性是判断矩阵可用的前提条件,因而还需对比较判断矩阵进行次序一致性检验.在1—9比例标度下,判断矩阵:(q)…满足次序一致性的数学描述为: 对任意,,E{1,2,…,n),有(1)若蛳≥1且%>1,则0.±>1(2)若0¨>1且≥1,则o>1(3)若哪≤1且咏<1,则a<1(4)若鲫<1且%≤1,则0.±<1(5)若=l且蛳=1,则m=l第3期孔宪明等AI’Ip的一致性问题由此得次序一致性检验方法如下:(I)给定判断矩阵4=()…(2)令1(3)令=1(4)令=1(5)若满足田≥l且印>1或满足>1且≥1,转步骤(8)(6)若满足q≤l且(1或满足<l且≤1,转步骤(9)(7)若满足哪=1且蛳=1,转步骤(1o)(8)若.≤1,转步骤(11),否则转(14)(9)若.≥1,转步骤(12),否则转(14J(10)若n:1,转步骤(14),否则转(13】(11)输出哪,,∞,指出‰应大于1,转步骤(14)(12)输出,,‰,指出应小于1,转步骤(14)(13)输出%,,,指出口应等于1(14)令=—1(15)若≤n,返回步骤(5)(16)令J=J+1(17)若≤返回步骤(4){18)令i=i+1(19)若≤,返回步骤(3)(20)结束对经检验出现违反次序一致性的判断,应重新予考虑3一致性的校正方法对不满足一致性的判断矩阵,下面介绍两种校正方法3.1向量校正法设4为判断矩阵,将A=()…各列进行规一化后得矩阵=(,m,…),其中为n维列向量(i=1,2,…,n).用和积法求出A的最大特征根所对应的特征向量,得到A的规~他特征向量百=若4完全一致,刚=i=1,2,….n)若A不完全一致,则每个∞与保持一种近似比例关系,而这种近似的比例关系程度可采用向量夹角来度量.记为a与的夹角(i:I,2,….).令p=eosO-黼(其中∞.内积)=s;n=称为∞相对于的一致性系数,为相对于的偏差系数.显然,有性质(1)0≤P.≤1,0≤≤1(i=1.2,…,n)24淮北煤师院2000年(2)当A完全一致时,P.=1,d=O(i=1,2,…,)(3)越小,越大,∞与的一致性程度越好.【4)若p>P/,则<aj,d比∞的一致性好.将所有d按由小到大顺序排列:击l≤d≤…≤dl≤当判断矩阵不满足一致性时,当然需要首先校正偏差最大的列.因而我们选取偏差最大的两个d一.与所对应的两列作为首先调整的对象.假设一.与分别对应原矩阵的第i列与第列,则校正蛳与.为保证新矩阵仍为正互反矩阵,将原嘶=1/校正为n=1/靠.同时,确定n时,应以偏差最小的一对应的㈨列为准,使校正后的两列尽量保持与∞的近似比例关系.对校正后的新矩阵进行一致性检验若仍不满足一致性,则重复上述过程直到满意为止.归纳向量校正法的步骤如下(1)将判断矩阵A=(哪)…各列规一化,得=(d-,--,)(2)计算A的规一化特征向量五(3)计算并按从小到大顺序排列:】≤d&≤…≤d结束由此得到的矩阵A”即为符合满意一致性的判断矩阵,即为其特征向量参考文献:[1]马维野.一种检验判断矩阵次序一致性的实用方法[J】,系统工程理论与实践.1996,I6(11):103—105【2】刘万里,雷治军关于AHP中判断矩阵校正方法的研究.】】系统工程理论与实践.1997,17(6):30—29f3]赵焕臣,许树柏,和金生层次分析法[M]北京:科学出版社.1986. 【4]杜之韩判断矩阵一致性检验的新途径【】]系统工程理论与实践.1998,18(6):102—104.【5】徐泽水判断矩阵一致性改进的一种实用方法【J].系统工程.1998,16(6):61—63.TheProblemofConsistencyinAHPKONGXian-ruingZHAOWen—cai{皿mmMathemag~,Tai∞Educationaltns~e,Taim27/000Abstract:Thispaperpresentsquitesystematicstudyandarrangementofconsi steneyinAHP,also imredueesseveralkindsofeasyandpracticalmethodsofverificationandrecti fication.Keywords:AHP;consistency;rectification旦m。
AHP法的随机一致性(RC)指标
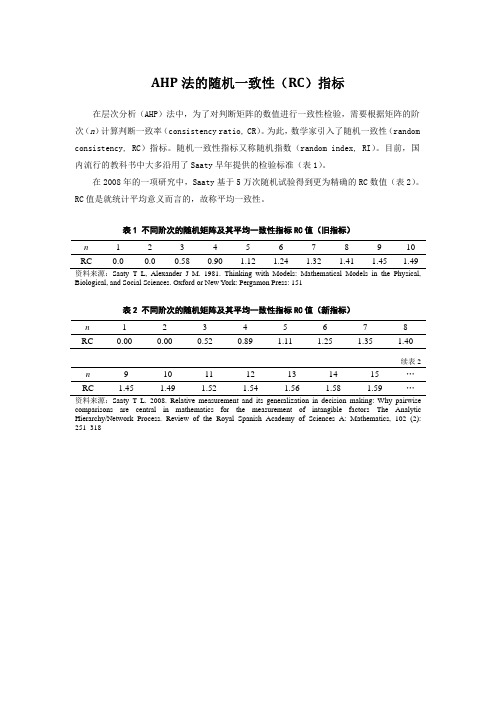
AHP法的随机一致性(RC)指标在层次分析(AHP)法中,为了对判断矩阵的数值进行一致性检验,需要根据矩阵的阶次(n)计算判断一致率(consistency ratio, CR)。
为此,数学家引入了随机一致性(random consistency, RC)指标。
随机一致性指标又称随机指数(random index, RI)。
目前,国内流行的教科书中大多沿用了Saaty早年提供的检验标准(表1)。
在2008年的一项研究中,Saaty基于5万次随机试验得到更为精确的RC数值(表2)。
RC值是就统计平均意义而言的,故称平均一致性。
表1 不同阶次的随机矩阵及其平均一致性指标RC值(旧指标)n 1 2 3 4 5 6 7 8 9 10 RC 0.0 0.0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49资料来源:Saaty T L, Alexander J M. 1981. Thinking with Models: Mathematical Models in the Physical, Biological, and Social Sciences. Oxford or New York: Pergamon Press: 151表2 不同阶次的随机矩阵及其平均一致性指标RC值(新指标)n 1 2 3 4 5 6 7 8 RC 0.00 0.00 0.52 0.89 1.11 1.25 1.35 1.40续表2 n 9 10 11 12 13 14 15 …RC 1.45 1.49 1.52 1.54 1.56 1.58 1.59 …资料来源:Saaty T L. 2008. Relative measurement and its generalization in decision making: Why pairwise comparisons are central in mathematics for the measurement of intangible factors—The Analytic Hierarchy/Network Process. Review of the Royal Spanish Academy of Sciences A: Mathematics, 102 (2):251–318。
层次分析法(AHP法)

(i,j=1,2,….n)
中国最大的资料库下载
B
p1
p2
p1
p2
p3
p4
p5
p6
1
1
1
1
1
2
4
4
1
1
1/2
1/2
p3
p4 p5
1
1/4 1
1/2
1/4 1
1
1/5 1/3
5
1 3
3
1/3 1
1/2
1/3 1
p6
2
6.25
2
5.75
2
6.53
3
20
层次分析法
中国最大的资料库下载
层次分析法(AHP) 美国运筹学家A.L.Saaty于本世 纪 70 年 代 提 出 的 层 次 分 析 法 ( Analytical Hierar-chy Process,简 称AHP方法),是一种定性与定量 相结合的决策分析方法。它是一种 将决策者对复杂系统的决策思维过 程模型化、数量化的过程。
o计算Mi 的n 次方根Wi
Wi =
nM i
(i=1,2,….n)
中国最大的资料库下载
o对向量W=( W1, W2…… Wn)t归 一化处理: Wi= Wi 1nWj
(i =1,2,….n)
W=( W1, W2…… Wn)t
即为所求的特征向量的近似解。
中国最大的资料库下载
C.I
R.I.
中国最大的资料库下载
当 C.R.< 0.10 时,便认为 判断矩阵具有可以接受的一致 性。当C.R. ≥0.10 时,就需要调 整和修正判断矩阵,使其满足 C.R.< 0.10 ,从而具有满意的 一致性。
试论层次分析法_AHP_在公共部门绩效考核指标权重确定中的运用

试论层次分析法(AHP)在公共部门绩效考核指标权重确定中的运用龙朝双 陈志刚董建涛【摘要】公共部门的绩效考核实施起来困难重重,有组织本身的原因,也有方法技术方面的原因。
为应对考核技术的不足,本文试图引入AHP方法来确定考核指标的权重,以增强考核的科学性。
在文章的后面附以层次分析法如何确定公共部门绩效考核指标权重的实例,以资参考。
【关键词】绩效考核 权重 AHP【中文图书分类号】D035 【文献标识号】A1 问题的提出随着全球化的扩张和经济的迅猛发展,传统的官僚制模式之弊端日益凸显,并导致政府面临严重的财政危机、管理危机、信任危机以及合法性危机。
西方各国为了摆脱政府管理的困境,改变过去的政府管理过程导向,加强了对结果的关注。
正是这种转变带来了西方公共部门绩效考核蓬勃发展。
其标志是克莱伦斯·雷德和赫伯特·西蒙的《市政工作衡量:行政管理评估标准的调查》一书。
20世纪70年代初,美国尼克松政府便开始了大规模的公共部门绩效评估,在随后的福特政府、布什政府得到了进一步发展,在国外政府绩效评估热潮的影响和推动下,我国政府和学术界也开始关注和重视政府绩效的评估问题。
2002年厦门思明区政府与厦门大学共同开发了“公共部门绩效评估系统”。
人事部《中国政府绩效评估研究》课题组提出了一套我国地方政府绩效评估指标体系,该评估体系由职能指标、影响指标和潜力指标3个一级指标,11个二级指标以及33个三级指标构成。
在公共部门绩效考核浪潮冲击着传统官僚制政府模式的同时,我们也必须认识到由于公共组织自身的特点以及考核人员方法、技术的不足为考核带来了诸多障碍,其主要包括: 1.1 公共组织特征下的绩效考核困境(1)非市场产出的公共部门的产出大多难以量化政府部门的产品或服务通常是一些非商品性的产出,它们进入市场的交易体系后很难形成一个反映其生产成本的货币价格,从而造成对其进行准确测量的技术上的难度。
政府提供公共物品或服务更具垄断性,这样也不太容易通过横向比较来测度政府部门的绩效。
AHP、TOPSIS、DEA三种方法
南京理工大学泰州科技学院计算机系信管专业10(2)班级专业综合实训姓名:学号:指导老师:职称:设计地点:4306 起讫时间:完成报告书时间:2014 年1 月17 日计算机科学与技术系编印二零一三年一、 AHP 、TOPSIS 、DEA 三种方法的理论基础1 层次分析法(AHP )的概述AHP 的背景层次分析法(Analytic Hierarchy Process,简称AHP)是美国运筹学家、匹兹堡大学T. L. Saaty 教授在20世纪70年代初期提出的,AHP 是对定性问题进行定量分析的一种简便、灵活而又实用的多准则决策方法。
它的特点是把复杂问题中的各种因素通过划分为相互联系的有序层次,使之条理化,根据对一定客观现实的主观判断结构(主要是两两比较)把专家意见和分析者的客观判断结果直接而有效地结合起来,将一层次元素两两比较的重要性进行定量描述。
而后,利用数学方法计算反映每一层次元素的相对重要性次序的权值,通过所有层次之间的总排序计算所有元素的相对权重并进行排序。
该方法自1982年被介绍到我国以来,以其定性分析与定量分析相结合地处理各种决策因素的特点,以及其系统灵活简洁的优点,迅速地在我国社会经济各个领域内,如能源系统分析、城市规划、经济管理、科研评价等,得到了广泛的重视和应用。
AHP 的理论基础 1、层次结构模型:(1) 最高层:只包含一个元素,表示决策分析的总目标,因此也称为总目标层。
(2) 中间层:包含若干层元素,表示实现总目标所涉及的各子目标,包括各种准则、约束、策略等,因此也成为目标层。
(3) 最低层:表示实现各决策目标的可行方案、措施等,也称为方案层。
在层次结构模型中,相邻两层次元素之间的关系用直线标明,称为作用线;元素之间不存在关系,就没有作用线。
在实际操作中,模型的层次数由系统的复杂程度和决策的实际需要而定,一般每一层次的元素个数不超过9个,过多的元素会给确定各指标权重带来困难。
基于AHP法的乡村景观质量评价体系构建——以川西林盘为例
基于AHP法的乡村景观质量评价体系构建——以川西林盘为例李宇奇;罗奕爽;黎燕琼;彭培好;郑绍伟【摘要】为了更好地开展乡村景观保护,明确乡村景观质量的各项影响因子之间的关系,以川西林盘为例,运用层次分析法(AHP)建立乡村景观质量评价体系.通过对103个林盘样地的分析,从美学价值、生态价值和社会价值3个方面,选取民居乡土特色、水体质量、维护碳氧平衡功能、巴蜀文化等17个评价指标;通过构建判断矩阵,计算出各指标的权重.结果表明,川西林盘生态价值(0.466)>美学价值(0.275)>社会价值(0.259).生态价值中最重要的因子为净化功能,美学价值中最重要的因子为民居乡土特色,社会价值中最重要的因子为巴蜀文化.提出川西林盘景观质量评价的综合模型,为乡村景观质量的研究作理论参考.%In order to better protect landscape in rural area,and to clearly understand the relationship between the factors which affect the quality of rural landscape,this paper took Linpan of Western Sichuan as an example to establish assessment system for rural landscape quality by using analytic hierarchy process (AHP) method.Through the analysis of 103 sampling plots,17 assessment indixes were selected from the aspects of aesthetics,ecology,and society,including residential local characteristics,water quality,the function of maintenance,the carbon and oxygen balance,local culture,etc.The weight of each hierarchy index was calculated by assessment matrix analysis.The results indicated that the ecological value (0.466) > aesthetic value (0.275) > social value (0.259).The most important factor in the ecological value was the purification function.The most important factor of the aestheticvalue was the residential and local characteristics.The most important factor of the social value was the green culture of sustainable development.Based on the results,a model for the assessment of the landscape quality of Linpan was established to provide theoretical references for the future rural landscape quality studies.【期刊名称】《西北林学院学报》【年(卷),期】2018(033)002【总页数】6页(P263-268)【关键词】川西林盘;景观质量;评价体系;AHP法【作者】李宇奇;罗奕爽;黎燕琼;彭培好;郑绍伟【作者单位】成都理工大学旅游与城乡规划学院,四川成都610059;四川省林业科学研究院,四川成都610081;成都理工大学旅游与城乡规划学院,四川成都610059;四川省林业科学研究院,四川成都610081;四川省林业科学研究院,四川成都610081;成都理工大学旅游与城乡规划学院,四川成都610059;四川省林业科学研究院,四川成都610081【正文语种】中文【中图分类】S731.7在我国“大力推进生态文明建设”[1]的背景下,新农村的建设更加快速推动着我国乡村景观的发展[2],乡村景观逐渐被重视和保护。
港口综合能源系统的AHP
港口综合能源系统的AHP随着我国经济的飞速发展,环境污染和能源短缺等问题变得日益严重。
港口作为货物转运的重要枢纽,在经济发展中发挥着重要作用的同时,其高耗能、高污染特点也凸显出来。
随着“一带一路”倡议的实施,港口发展进一步加速,其节能环保问题引起了社会各界人士的高度重视[1-2]。
近年来,融合了风能、太阳能和天然气等各种可再生和清洁能源的综合能源系统(integrated energy system,IES)受到了能源领域的广泛关注。
随着我国港口电力能源消耗比例的逐年攀升,为节约电能,提高港口周边的环境质量,港口企业也在努力开发适用于港口的港口综合能源系统(port integrated energy system,PIES)[3-7]。
为经济科学地建设和利用PIES,需要建立一个有效的PIES评价方法。
虽然IES的概念近几年才提出,但目前在IES的评价方法的研究上,国内外均有一些进展。
文献用互相独立的矩阵来评价冷热电联产系统的节能潜力,文献[9-12]对IES的运行进行了分析和研究,在整个系统的规划设计和能效评估方面取得了不少进展。
文献基于信息熵法构建了IES的评价方法。
现阶段IES的评价方法研究主要是针对一个城市、城镇和地区的,关于PIES的评价方法研究还处于起步阶段。
本文根据PIES的特点,建立PIES评价指标体系,利用层次分析法(analytic hierarchy process,AHP)-模糊综合评价法对PIES的发展水平进行评估。
1 PIES1.1 PIES简介PIES指以港口的配电网为核心,综合冷热电三联供系统、新能源发电系统、港口岸电系统等供能和用能系统,并与储能技术相结合,联合“源-网-荷-储”同时运行,将前沿的能源综合管理系统、人工智能、大数据等技术应用于港口多元能源的生产、存储、转换、传输和使用,通过对整个系统的优化控制实现多元能源安全可靠地服务于整个港口的生产运行的系统。
ahp设施选址步骤ahp层次分析法步骤
ahp设施选址步骤ahp层次分析法步骤如何确定城市物流节点体系、规模及分布选址的问题,对优化整个物流网络起着重要作用。
下面就为大家解开ahp设施选址步骤,希望能帮到你。
(1)通过对系统的深刻认识,确定该系统的总目标,弄清规划决策所涉及的范围、所要采取的措施方案和政策、实现目标的准则、策略和各种约束条件等,广泛地收集信息。
(2)建立一个多层次的递阶结构,按目标的不同、实现功能的差异,将系统分为几个等级层次。
(3)确定以上递阶结构中相邻层次元素间相关程度。
通过构造两比较判断矩阵及矩阵运算的数学方法,确定对于上一层次的某个元素而言,本层次中与其相关元素的重要性排序--相对权值。
(4)计算各层元素对系统目标的合成权重,进行总排序,以确定递阶结构图中最底层各个元素的总目标中的重要程度。
(5)根据分析计算结果,考虑相应的决策。
1、建立国民素质评价系统的递阶层次结构;2、构造两两比较判断矩阵;根据层次分析模型示意图所示,每位问卷评分者就可以依据个人对评价指标的主观评价,进行综合分析,对各指标之间进行两两对比之后,然后按9分位比率排定各评价指标的相对优劣顺序,依次构造出评价指标的判断矩阵。
3、针对某一个标准,计算各备选元素的权重; 关于判断矩阵权重计算的方法有两种,即几何平均法(根法)和规范列平均法(和法)。
(1)几何平均法(根法) 计算判断矩阵a各行各个元素mi的乘积; 计算mi的n次方根; 对向量进行归一化处理; 该向量即为所求权重向量。
(2)规范列平均法(和法) 计算判断矩阵a各行各个元素mi的和; 将a的各行元素的和进行归一化; 该向量即为所求权重向量。
(3)计算矩阵a的最大特征值?max 对于任意的i=1,2,…,n, 式中为向量aw的第i个元素一致性检验构造好判断矩阵后,需要根据判断矩阵计算针对某一准则层各元素的相对权重,并进行一致性检验。
虽然在构造判断矩阵a时并不要求判断具有一致性,但判断偏离一致性过大也是不允许的。
