层次分析法中高阶平均随机一致性指标_RI_的计算
层次分析法在汽车零件供应商评估中的应用

层次分析法在汽车零件供应商评估中的应用本文以某大型汽车制造企业零件供应商选择为例,设计了在汽车零件供应商选择过程中甄选最优者的指标体系,在评估方法上,采取定性与定量相结合的方法,运用层次分析法(AHP)确定了指标权重系数,并通过一致性检验,证明所建立的供应商甄选评估体系是实际可操作的。
标签:层次分析法供应商评价一、汽车零件供应商评价指标设计利用AHP法对汽车零件供应商评估进行分析,可建立三个层次的结构模型,即评估内容层、评估目标层、评估指标层。
评估内容层是指评估所指向的具体对象与范围,它具有相对性。
对于不同的零件供应商评估内容存在差异。
评估内容层中的元素是对汽车零件供应商进行评估的内容。
笔者设计的汽车零件供应商测评内容主要包括:质量、价格、技术、服务、创新。
评估项目层是根据评估内容的要求给出的,是对评估内容的具体规定。
如技术内容,要通过以下评估项目:通用化、模块化、电子及职能化、环保化、轻量化来体现。
而技术只是对评估项目的一个综合说明。
测评项目的选择要通过一定的定量分析方法来实现,不能任意的指定。
一般采用德尔菲咨询、问卷调查与层次分析法、多元分析法进行选择。
评估指标层是评估项目层的可操作化的表现形式。
对于每一个测评指标都必须认真分析研究,给予清楚、准确的表述,使评估各方均能明确评估指标的涵义,不会因对测评指标的不同理解而导致标准不一产生评估结果误差。
选择评估指标时不但要求要具有实际价值,还要是切实可行的,最好是能够量化的。
二、分别构造判断矩阵本文只针对项目层进行讨论,根据表2,对各指标进行两两比较,采用层次分析法,确定其权重,构造出判断矩阵。
(表3~表4)注:(确定价格、技术、服务、创新等指标评估的判断矩阵及权重方法同上,不再列举)三、确定各指标权重1.首先将判断矩阵的每一列元素作归一化处理,其元素的一般项为:2.将各列归一化后的判断矩阵按行相加3.再将向量归一化,得到得到的W=[W1,W2,…,Wn]T即为所求特征向量。
层次分析法判断矩阵求权值以及一致性检验程序

function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性检验。
其中A为判断矩阵,不同的标度和评定A将不同。
m为A的维数RI为判断矩阵的平均随机一致性指标:根据m的不同值不同。
当CR<0.1时符合一致性检验,判断矩阵构造合理。
下面是层次分析法的简介,以及判断矩阵构造方法。
一.层次分析法的含义层次分析法(The analytic hierarchy process)简称AHP,在20世纪70年代中期由美国运筹学家托马斯·塞蒂(T.L.Saaty)正式提出。
它是一种定性和定量相结合的、系统化、层次化的分析方法。
由于它在处理复杂的决策问题上的实用性和有效性,很快在世界范围得到重视。
它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。
二.层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。
(1)层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构,然后得用求解判断矩阵特征向量的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后再加权和的方法递阶归并各备择方案对总目标的最终权重,此最终权重最大者即为最优方案。
这里所谓“优先权重”是一种相对的量度,它表明各备择方案在某一特点的评价准则或子目标,标下优越程度的相对量度,以及各子目标对上一层目标而言重要程度的相对量度。
层次分析法比较适合于具有分层交错评价指标的目标系统,而且目标值又难于定量描述的决策问题。
层次分析法的计算
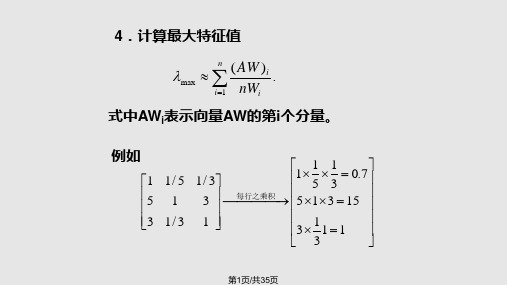
0.467 0.155
e2
e '2 e '2
1 3.014
0.565 1.991
0.184 0.661
第8页/共35页
1 1 1/ 5 0.155 0.471 e '3 Ae2 1 1 1/ 3 0.184 0.559 , e '3 0.471 0.559 1.988 3.018
表三
S1 A
B
A1
1/4
B4
1
C 1/2 1/8
CW
2 0.1818 8 0.7272 1 0.0910
第27页/共35页
0.1818
1 1/ 4 2 0.1818
W
0.7272
.AW
4
1
8
0.7272
0.0910
1/ 2 1/ 8 1 0.0910
1 0.1818+0.72721/4+2 0.0910 0.5456
5 3 1 0.659 1.994
0.473 0.156
e4
e '4 e '4
1 3.028
0.561 1.994
0.185 0.659
第10页/共35页
由于e4=e3,迭代经过4次中止,权系数是
1 0.156,2 0.185,3 0.659.
相应的综合评价公式是
y 0.156x1 0.185x2 0.659x3
G S1 S2 S3 S1 1 5 3 S2 1/5 1 1/3 S3 1/3 3 1
第17页/共35页
4、层次单排序及其一致性检验(用方 根法计算这三个准则关于目标的排序权值)
层次分析法确定评价指标权重及Excel计算

江苏科技信息February 2012表2判断矩阵摘要:文章介绍了层次分析法确定评价指标权重的过程和计算方法,建立的Excel 计算模板操作简单,方便推广,具有较强的实用性。
关键词:决策分析法;层次分析法;权重;Excel ;计算模板作者简介:曹茂林,扬州市环境监测中心站,高级工程师;研究方向:环境监测技术与环境科技管理。
■曹茂林层次分析法确定评价指标权重及Excel 计算层次分析法(Analytic hierarchy process ,简称AHP 法)是美国运筹学家T.L.Saaty 等人在20世纪70年代中期提出了一种定性和定量相结合的,系统性、层次化的多目标决策分析方法。
在环境科研实践中,AHP 法广泛应用于生态安全[1]、环境规划[2]、区域承载力[3]、化学品环境性能评价[4]等众多领域。
AHP 法的核心是将决策者的经验判断定量化,增强了决策依据的准确性,在目标结构较为复杂且缺乏统计数据的情况下更为实用。
应用AHP 法确定评价指标的权重,就是在建立有序递阶的指标体系的基础上,通过比较同一层次各指标的相对重要性来综合计算指标的权重系数。
具体步骤如下:1.构造判断矩阵同一层次内n 个指标相对重要性的判断由若干位专家完成。
依据心理学研究得出的“人区分信息等级的极限能力为7±2”的结论,AHP 法在对指标的相对重要性进行评判时,引入了九分位的比例标度,见表1。
判断矩阵A 中各元素a ij 为i 行指标相对j 列指标进行重要性两两比较的值。
显然,在判断矩阵A 中,a ij >0,a ii =1,a ij =1/a ji (其中i ,j=1,2,…,n )。
因此,判断矩阵A 是一个正交矩阵,左上至右下对角线位置上的元素为1,其两侧对称位置上的元素互为倒数。
每次判断时,只需要作n(n-1)/2次比较即可。
表2是一个7阶判断矩阵,本文以此为例介绍应用Excel 计算指标权重并进行一致性检验的方法。
层次分析法判断矩阵求权值以及一致性检验程序

function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性检验。
其中A为判断矩阵,不同的标度和评定A将不同。
m为A的维数RI为判断矩阵的平均随机一致性指标:根据m的不同值不同。
当CR<0.1时符合一致性检验,判断矩阵构造合理。
下面是层次分析法的简介,以及判断矩阵构造方法。
一.层次分析法的含义层次分析法(The analytic hierarchy process)简称AHP,在20世纪70年代中期由美国运筹学家托马斯·塞蒂(T.L.Saaty)正式提出。
它是一种定性和定量相结合的、系统化、层次化的分析方法。
由于它在处理复杂的决策问题上的实用性和有效性,很快在世界范围得到重视。
它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。
二.层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。
(1)层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构,然后得用求解判断矩阵特征向量的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后再加权和的方法递阶归并各备择方案对总目标的最终权重,此最终权重最大者即为最优方案。
这里所谓“优先权重”是一种相对的量度,它表明各备择方案在某一特点的评价准则或子目标,标下优越程度的相对量度,以及各子目标对上一层目标而言重要程度的相对量度。
层次分析法比较适合于具有分层交错评价指标的目标系统,而且目标值又难于定量描述的决策问题。
AHP法在确定绩效考核指标权重的应用

AHP法在确定绩效考核指标权重的应用摘要:人力资源绩效评价的选择关键在于权重的确定,如何确定绩效考核指标的权重是建立绩效考核体系过程中一个非常重要的环节。
本文通过介绍绩效考核指标权重以及针对具体实例采用层次分析法确定绩效考核指标的步骤,以期达到运用AHP法来提高绩效考核指标权重确定的科学性和准确性的目的。
关键词:绩效考核;考核指标;权重;层次分析法1.引言现实的员工绩效评价工作中存在许多应当改进的方面,如指标怎样确立才更公平、怎样做到合理量化、权重如何分配更准确等。
本文建立相对完善的评价指标体系,以层次分析法为基础构建矩阵,解决排序问题即权重问题,并通过一致性检验,建立员工绩效综合评价模型以解决实际工作中的难题。
国内企业普遍存在基础管理薄弱,缺乏历史资料的问题,尤其是在非财务指标方面,以前大多没有进行过这些方面的考核,也就没有数据的积累,不具备应用客观赋权法的基础条件。
再者,从心理学角度看,人们对自己承诺的事情会加倍努力去做。
因此,让有代表性的管理者和员工参与到指标权重的制定中来,会比通过复杂的计算而大家根本不了解它是怎么来的要有意义,更能激发员工贯彻绩效考核标准的主动性。
有鉴于此,选择主观赋权法更为合理实用、有效。
本文为提高考评结果的可比性与客观性,针对具体的实例,采用了集定量与定性于一身的层次分析法(AHP法)来确定绩效考核指标权重系数,以期达到提高科学性、客观性和可比性等的目的。
2.绩效考核指标权重及其设置的意义确定完整、合理的绩效考核指标是绩效考核的重要前提,但真正的难点是确定每个指标的权重。
如何确定绩效考核指标的权重是建立绩效考核体系过程中一个非常重要而又值得研究的环节。
权重是绩效指标体系的重要组成部分,通过对每个被评估者职位性质、工作特点及对经营业务的控制和影响等因素的分析,确定每类及每项指标、工作目标设定整体及其中各项在整个指标体系中的重要程度,赋予相应的权重,以达到考核的科学合理。
层次分析法
层次分析法(AHP)求解流程图
建立 层次 结构 分析 模型 构造 判断 矩阵
层次单 排序及 其一致 性检验
层次 总排 序 层次总 排序的 一致性 检验
层次分析法的基本步骤
一、建立层次结构分析模型
二、构造判断矩阵 三、层次单排序及其一致性检验 四、层次总排序 五、层次总排序的一致性检验
(2) 相对于调动职工劳动积极性准则,各方案之间 的重要性比较 (判断矩阵B1—S):
(3)相对于提高企业技术水平准则,各方案之间的重 要性比较 (判断矩阵B2—S):
(4)相对于改善职工物质文化生活准则, 各方案之间的重要性比较 (判断矩阵B3—S):
层次分析法的基本步骤
一、建立层次结构分析模型 二、构造判断矩阵 三、层次单排序及其一致性检验 四、层次总排序 五、层次总排序的一致性检验
一、建立层次结构分析模型 二、构造判断矩阵 三、层次单排序及其一致性检验 四、层次总排序 五、层次总排序的一致性检验
二、构造判断矩阵 AHP的信息基础主要是人们对每一层次各因 素的相对重要性给出判断,这些判断用数值表示 出来,写成矩阵形式就是判断矩阵。判断矩阵表 示针对上一层次某因素,本层次与之有关的各因 素之间的相对重要性。假定A层中因素Ak与下层 中因素B1,B2,……,Bn有关系,则判断矩阵如下: Ak B1 B2 …… Bn B1 b11 b12 …… b1n B2 b21 b22 …… b2n …… …… …… …… …… Bn bn1 bn2 …… bnn
根据上面的例子,我们假定厂长或职工代表大会 根据实际情况构造的数值判断矩阵如下: (1)相对于合理使用企业利润,促进企业发展的 总目标,各考虑准则之间的相对重要性比较 (判断 矩阵A—B):
层次分析法
bn1
bn2 ……
bnn
bij是对于Ak而言,Bi对Bj的相对重要性的数值表示。
Bij通常取1、3、5、7、9及其他们的倒数,其含义为:
尺度
1 3 5 7 9
含义
第i个因素与第j个因素的影响相同 第i个因素比第j个因素的影响稍强 第i个因素比第j个因素的影响强 第i个因素比第j个因素的影响明强 第i个因素比第j个因素的影响绝对地强
层次分析法
一 问题的提出
例1 购物 买钢笔,一般要依据质量、颜色、实用性、价格、
外形等方面的因素选择某一支钢笔。 下馆子,则要依据馆子的饭菜质量、区位条件、档
次、饭菜价格、服务质量等方面因素来选择。
例2 旅游 假期旅游,是去风光秀丽的苏州,还是去迷人的
北戴河,或者是去山水甲天下的桂林,一般会依据景 色、费用、食宿条件、旅途等因素选择去哪个地方。
课题D2
课题可行性B3
难
研财
易
究政
程
周支
度
期持
c3
c4
c5
课题D3
层次分解时注意事项:
如果所选的要素不合理,其含义混淆不清,或 要素间的关系不正确,都会降低AHP法的结果质量, 甚至导致AHP法决策失败。 为保证递阶层次结构的合理性,需注意以下问题: 1、要对问题的影响因素有充分的理解,必要的时 候可以咨询相关的专家; 2、分解简化问题时把握主要因素,不漏不多 3、注意相比较元素之间的强度关系,相差太悬殊 的要素不能在同一层次比较。 4、以上均为完全层次
层次总排序的一致性检验
(1)
(2)
(3)
在(1)式中,CI为层次总排序的一致性指标,CIj为与aj对应 的B层次中判断矩阵的一致性指标;在(2)式中,RI为层次总排 序的随机一致性指标,RIj为与aj对应的B层次中判断矩阵的随 机一致性指标;在(3)式中,CR为层次总排序的随机一致性比例。
层次分析法中高阶平均随机一致性指标(RI)的计算
层次分析法中高阶平均随机一致性指标(RI)的计算
洪志国;李焱;范植华;王勇
【期刊名称】《计算机工程与应用》
【年(卷),期】2002(038)012
【摘要】利用层次分析法分析和解决问题时,要对通过两两比较判断出的矩阵一致性进行检验[1].高阶平均随机一致性指标的值一般无法直接通过查表而得,这一难点阻碍着层次分析法大面积的推广应用[2].文章在深刻剖析层次分析法的基础上,给出根据平均随机一致性指标的定义计算高阶平均随机一致性指标值的算法,并且基于windows环境在delphi6.0下予以程序实现.该算法已成功运用于中国科学院知识创新工程某智能决策系统中.
【总页数】4页(P45-47,150)
【作者】洪志国;李焱;范植华;王勇
【作者单位】中国科学院软件所GSL实验室,北京,100080;中国科学技术大学计算机系,合肥,230027;中国科学院软件所GSL实验室,北京,100080;中国科学院软件所GSL实验室,北京,100080
【正文语种】中文
【中图分类】TP18
【相关文献】
1.关于平均随机一致性指标的新定义方法 [J], 孙水玲
2.层次分析法中平均随机一致性指标的数学软件实现 [J], 陈晓江
3.AHP法中平均随机一致性指标的算法及MATLAB实现 [J], 焦树锋
4.马氏环境中树指标马氏链随机转移概率调和平均的强极限性质 [J], 石志岩;鲍丹;吴佰慧
5.等距数列平均指标计算方法研究——兼评“中位数总是介于算术平均数和众数之间吗?”一文中的一个错误结论 [J], 朱(鱼它)华
因版权原因,仅展示原文概要,查看原文内容请购买。
试论层次分析法_AHP_在公共部门绩效考核指标权重确定中的运用
试论层次分析法(AHP)在公共部门绩效考核指标权重确定中的运用龙朝双 陈志刚董建涛【摘要】公共部门的绩效考核实施起来困难重重,有组织本身的原因,也有方法技术方面的原因。
为应对考核技术的不足,本文试图引入AHP方法来确定考核指标的权重,以增强考核的科学性。
在文章的后面附以层次分析法如何确定公共部门绩效考核指标权重的实例,以资参考。
【关键词】绩效考核 权重 AHP【中文图书分类号】D035 【文献标识号】A1 问题的提出随着全球化的扩张和经济的迅猛发展,传统的官僚制模式之弊端日益凸显,并导致政府面临严重的财政危机、管理危机、信任危机以及合法性危机。
西方各国为了摆脱政府管理的困境,改变过去的政府管理过程导向,加强了对结果的关注。
正是这种转变带来了西方公共部门绩效考核蓬勃发展。
其标志是克莱伦斯·雷德和赫伯特·西蒙的《市政工作衡量:行政管理评估标准的调查》一书。
20世纪70年代初,美国尼克松政府便开始了大规模的公共部门绩效评估,在随后的福特政府、布什政府得到了进一步发展,在国外政府绩效评估热潮的影响和推动下,我国政府和学术界也开始关注和重视政府绩效的评估问题。
2002年厦门思明区政府与厦门大学共同开发了“公共部门绩效评估系统”。
人事部《中国政府绩效评估研究》课题组提出了一套我国地方政府绩效评估指标体系,该评估体系由职能指标、影响指标和潜力指标3个一级指标,11个二级指标以及33个三级指标构成。
在公共部门绩效考核浪潮冲击着传统官僚制政府模式的同时,我们也必须认识到由于公共组织自身的特点以及考核人员方法、技术的不足为考核带来了诸多障碍,其主要包括: 1.1 公共组织特征下的绩效考核困境(1)非市场产出的公共部门的产出大多难以量化政府部门的产品或服务通常是一些非商品性的产出,它们进入市场的交易体系后很难形成一个反映其生产成本的货币价格,从而造成对其进行准确测量的技术上的难度。
政府提供公共物品或服务更具垄断性,这样也不太容易通过横向比较来测度政府部门的绩效。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
$ #!$9"#!*’):"#&!%(9"#$!$"! $ #!!9"#!*’):"#!!)"9"#"(&*’ $ #!%9"#!*’):"#!!)"9"#"(&*’ $ #!&9"#!*’):"#$!!&9"#"%&+) $ #%$9"#$&!+:"#(%)"9"#"+$"% $ #%!9"#$&!+:"#$"&)9"#"$&+( $ #%%9"#$&!+:"#!’*%9"#"%(+!
求得 !7389’#" , /,9" ; 对于 "! 有:
.! /!$ /!! /!% /!& /!$ $ "#’ "#’ $1% /!! ! $ $ "#’ /!% ! $ $ "#’ /!& % ! ! $ 0 "#&!%( "#!!)" "#!!)" "#$!!&
求得 !7389&#"$"% , /,9"#""%+ ; 对于 "% 有:
#%!、 #%%。
%
判断矩阵
在 6;< 解题手续中, 判断矩阵的构造及其相关的计算, 是
6;< 问题求解的关键 =+>。
图$
首先,构造两两比较 矩 阵 。 在 比 较 矩 阵 ! 中 元 素 的 取 值 ( 一个因素对另一个矩阵的比值) 采用如下的标度:
经过专家问卷调查, 两两比较判断矩阵及单一准则下的权 值 $ 如下: 第一层次下:
$
引言
层次分析法( 简 称 %-1) 是 !" %&’()*+, -+./’/,0) 1/2,.33,
比未能穷尽的不足, 对判断矩阵做一致性检验, 成为不可或缺 的环节 8=:。 在对判断矩阵进行一致性检验时, 要使用平均随机一致性 参与计算 84:。一般而言, 对于低阶判断矩阵( 阶数 @! 指标( >?) , 其平均随机一致性指标可以查表得到; 但对于高阶判断矩 $< ) , 平均随机一致性指标的值就无法直接获取了 8B:。 阵( 阶数 @A$<) 该文提出的算法, 正是解决了两两比较判断矩阵中高阶平均随 的计算问题。 机一致性指标( >?)
对于高阶( 比 在笔者的课题里, 阶数超过 $’ 。那么, &@$’ ) 较判断矩阵而言, 为了进行一致性检验, 相应的值从何得到呢? 只能根据平均随机一致性指标的定义进行计算。 该算法步骤如 下: 构造随机判断矩阵, 设 地取 $?+ 标度下的可能值。对于固定的 ’ ( 较矩阵中的阶数) , 随 机 地 构 造 出 正 互 反 矩 阵 ! A, 其 中 (A)* ( 由 随机地取自 $ , 于正互反性, 规定 )+* ) !, %, &, ’, (, ), *, +, $ 1 !, $1
5@8(0$%(: 52 ’&’()I. ’&M 32(V. N/2O(.63 L+*0 %&’()*+, -+./’/,0) 1/2,.33 &..M3 ’ ,0.,W 2& *0. ,2&3+3*.&,) 2G ’ 6’X */+Y ,26+&S G/26 ’ *L2 F*L2 ,26N’/+32& 8$:#U3J’(() N.2N(. ,’& 0’/M() S.* *0. V’(J. 2G -+S0 F>’&W.M >#?#+66.M+’*.() *0/2JS0 ,2&3J(*+&S /.(’*.M *’O(.3, ’&M ’3 ’ /.3J(*, +* 0+&M./3 ’ 6’33 2G ’NN(+,’*+2&3 2G %&’()*+, -+./’/,0) 1/2,.33 8!:#Z& *0. O’3+3 2G ’ *02/2JS0 ’&’()3+3 2G %&’()*+, -+./’/,0) 1/2,.33, *0. ’(S2/+*06 *2 ,’(,J(’*. 2J* *0. V’(J. 2G -+S0F>’&W.M > ? ’,,2/M+&S *2 *0. M.G+&+*+2& 2G > ? +3 2GG./.M +& *0. N’N./#50. N/2S/’6 2G *0. ’(S2/+*06 J&M./ L+&M2L3 J3+&S M.(N0+ =#" +3 N/2V+M.M ’3 L.((#50. ’(S2/+*06 0’3 O..& 3J,,.33GJ(() ’NN(+.M *2 ’ N/2R.,* 2G *0. +&*.((+S.&* M.,+3+2& 3)3*.6 +& *0. W&2L(.MS. +&&2V’*+2& 2G P0+&.3. %,’M.6) 2G 7,+.&,.3# A26B*038: T+S+*’(+I’*+2& 2& &2&FM+S+*’(+I.M N/2O(.63, %&’()*+, -+./’/,0) 1/2,.33, -+S0F/’&W.M /’&M26+I.M 6’*/+Y , %V./X ’S. >’&M26 P2&3+3*.&,) ?&M.Y , 12L./ ’(S2/+*06
6 .$ .! .% .$ $ "#’ "#!’ .! ! $ "#’ .% & ! $ 0 "#’)$& "#!*’) "#$&!+
23345 标度 $ % ’ ) + !, &, (, *
相应上述数的倒数
含义 表示待比较的两个因素有相同的重要性 一个因素比另一个因素稍微重要 一个因素比另一个因素明显重要 一个因素比另一个因素强烈重要 一个因素比另一个因素极端重要 因素之间重要性比较在上述描述之间 一个因素比另一个因素不重要的上述描述
.% /%$ /%! /%% /%$ $ "#! $1% /%! ’ $ % /%% % $1% $ 0 "#(%)" "#$"&) "#!’*%
%, $ 1 &, $ 1 ’, $ 1 (, $ 1 ), $ 1 *, $ 1 + 共 $) 个 数 值 中 的 某 一 个 , 用 充 得 到 ! A的 最 大 特 征 值 的 平 均 值 分大的子样( 如 $""" 个 子 样 ) 定义随机性指标 %,9( 用比值 #%.#, - %, 来 !A738, !738?& ) -( &?$ )
! %-1 的基本步骤
运用 %-1 方法解决问题, 大体可按如下步骤进行: ( 将问题分解, 建立层次结构; $) 构造两两比较判断矩阵; ( !) ( 由判断矩阵计算比较元素的相对权重; 9) 计算各层元素的组合权重。 ( ;) 现举例说明上述过程。
%-1 对人们的主观判断 加 以 形 式 化 地 表 达 和 处 理 , 逐 步
计算机工程与应用 !""!#$!
;<
例 $: 对 ! 进行评价, 其层次结构如图 $ 所示。 待评目标 ! , 其辖有一级评价要 素 "$、 同样地, 对 "! 和 "%; 辖 有 二 级 评 价 要 素 #$$、 对 于 "!, 辖有 于 "$ , #$!、 #$%、 #$& 和 #$’; 二 级 评 价 要 素 #!$、 对 于 "%, 辖 有 二 级 评 价 要 素 #%$、 #!!、 #!%、 #!&;
关键词 定性问题定量化 层次分析法 高阶随机判断矩阵 文献标识码 % 平均随机一致性指标 中图分类号 51$B 乘幂法
文章编号 $""!FB99$F( !""! ) $!F"";<F"9
#$%&’$()*+ *+ ,)-./0$+123 ! " *4 5+$’6()% ,)20$0%.6 70*%288
求得 !7389%#" , /,9" ; 第二层次下, 对于 "$ 有:
.$ /$$ /$! /$% /$& /$’ /$$ $ $ $ $ "#! /$! $ $ $ $ "#! /$% $ $ $ $ "#! /$& $ $ $ $ "#! /$’ ’ ’ ’ ’ $ 0 "#!%*$ "#!%*$ "#!%*$ "#!%*$ "#"&)(
