八年级数学知识网络结构图
最新八年级 数学(下册)各单元知识结构图
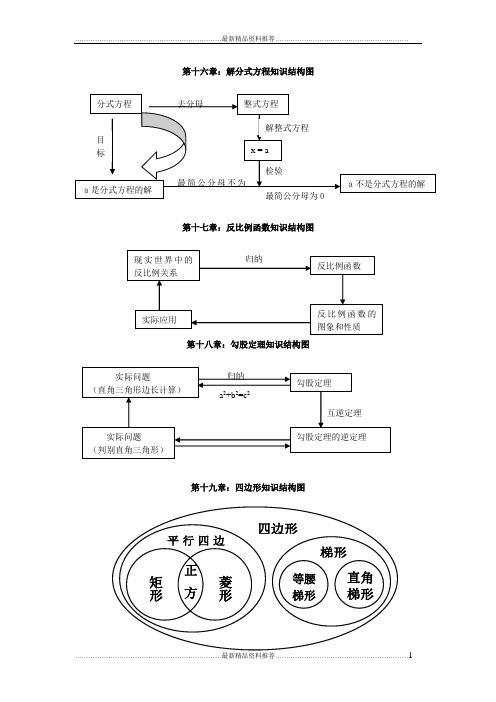
第十六章:解分式方程知识结构图第十七章:反比例函数知识结构图第十八章:勾股定理知识结构图第十九章:四边形知识结构图四边形梯形等腰 梯形直角 梯形平行四边矩形菱形正方形第二十章:数据的分析知识结构图中国的河流 第一课时 外流区为主 1.最终没有流入海洋的河流为 ,该种河流所在的区域为 ;最终流入海洋的河流为 ,该种河流所在的区域为 。
2.中国外流河的水文特征深受 气候的影响。
以秦岭——淮河为界,以南地区的河流主要流经湿润地区,水量 ,汛期 ,含沙量 ,冬季河流 ;以北地区的河流主要流经半湿润或半干旱地区,水量 ,汛期较 ,且冬季河流有 。
3.内流河的河水主要来自 。
河流大部分属于 河流。
活动一:探究“外流区(河)和内流区(河)”概念读课本“我国的内流区和外流区图”,完成下列活动。
1.小组探究(1)读“我国的内流区和外流区图”可知,我国内、外流区的大致分界线与 mm 等降水量线相近,并在图上用彩笔描出它们的分界线。
(2)观察图中该线东西两侧,可以看出,以东属于 区,多 河;以西属于 区,多 河。
2.探究结论我国西北多内流河,东南多外流河的原因:(1)地形、地势因素: 。
(2)气候因素: 。
活动二:探究河流的水文特征1.小组探究(1)读“我国东部主要河流年变化曲线图”,比较图中四条河流水文特征,完成下表。
一个角是直角两腰相等梯形另一组对边不平一组对边平行 四边形 直角梯形等腰梯形一个角是直角一个角是直角一组邻边相等一组邻边相等两组对边分别平平行四边形矩形菱形 正方形数据的代表 数据的波动 平均数 中位数 众 数极差 方差 用样本估计总用样本平均数估计总体平均数用样本方差估计总体方差河流松花江黄河长江西江流量汛期结冰期(有或无)季节变化(2)我国南北河流水文特征存在着较大的差异,通过比较完成下表。
河流水文要素流量汛期含沙量有无结冰期秦岭-淮河(以北)秦岭-淮河(以南)2.探究结论(1)河流的水文特征主要包括的要素有。
八年级各章知识结构图

知识结构图
第二十五章概率初步
知识结构图
第二十六章二次函数
知识结构图
第二十七章相似
知识结构图
第二十八章锐角三角函数
知识结构图
第二十九章投影与视图
知识结构图
第一章有理数
知识结构图
第二章整式的加减
知识结构图
知识结构图
第四章图形的认识初步
知识结构图
第五章相交线与平行线
知识结构图
第六章平面直角坐标系
知识结构图
第七章三角形
知识结构图
第八章二元一次方程组
知识结构图
第九章不等式与不等式组
知识结构图
第十章数据的收集、描述与整理
知识结构图
第十一章全等三角形
知识结构图
第十二章轴对称
知识结构图
等十三章实数
知识构图
第十四章一次函数
知识结构图
第十五章整式的乘除与因式分解
知识结构图
第十六章分式
知识结构图
第十七章反比例函数
知识结构图
第十八章勾股定理
知识结构图
第十九章四边形
知识结构图
第二十章数据的分析
知识结构图
第二十一章二次根式
知识结构图
第二十二章一元二次方程
知识结构图
第二十三章旋转
知识结构图
人教版八年级各章知识结构图
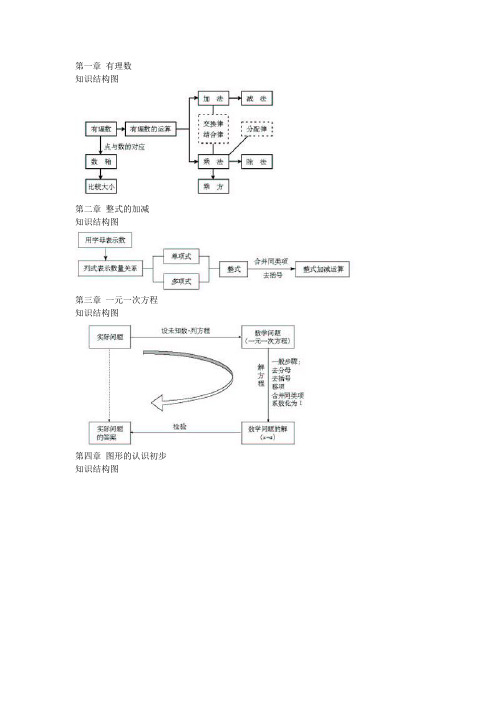
第一章有理数
知识结构图
第二章整式的加减
知识结构图
第三章一元一次方程知识结构图
第四章图形的认识初步知识结构图
第五章相交线与平行线知识结构图
第六章平面直角坐标系知识结构图
第七章三角形
知识结构图
第八章二元一次方程组
知识结构图
第九章不等式与不等式组
知识结构图
第十章数据的收集、描述与整理知识结构图
第十一章全等三角形知识结构图
第十二章轴对称
知识结构图
等十三章实数
知识结构图
第十四章一次函数知识结构图
第十五章整式的乘除与因式分解知识结构图
第十六章分式
知识结构图
第十七章反比例函数
知识结构图
第十八章勾股定理知识结构图
第十九章四边形
知识结构图
第二十章数据的分析知识结构图
第二十一章二次根式
知识结构图
第二十二章一元二次方程知识结构图
第二十三章旋转
知识结构图
第二十四章圆
知识结构图
第二十五章概率初步知识结构图
第二十六章二次函数知识结构图
第二十七章相似
知识结构图
第二十八章锐角三角函数知识结构图
第二十九章投影与视图知识结构图。
人教版 八年级上册数学 章节思维导图集 图片版
你现在的努力要对得起别人对你的好!
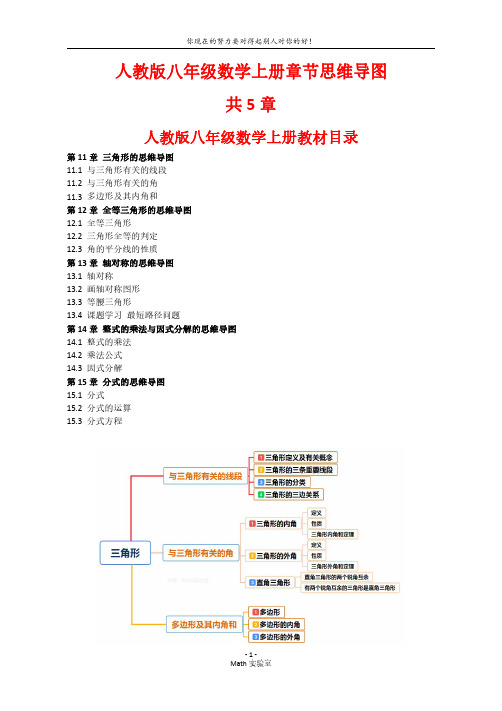
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。
八年级数学知识网络结构图

正方形
①③
菱形
对角 线相 等
同一底 边上的 两个角 相等
性质 判定
③
②④
平行四边形
等腰
直 角
梯形
四边形
辅助线
作 延 平 平 利用腰中点
高长移 线两两
移 对
割补成--全等三角形、
腰 腰 角 平行四边形
线
5
四边形 平行四边形
矩
正
菱
方
形
形
形
等腰 梯形 梯
形
直角 梯形
6
一般 在平面内,四条线段首 四边形 尾顺次相接组成的图形
A.ba
1 2
a 5a 2aB.b
0 2
a 2 C. b 1
a 1 D. b 1
考点二、整式的加减
例2 : 化简: 5a 2a .
例3: 化简: m n (m n的) 结果为(
A.2m
B. 2n
C.2n
)
D.2m
31
考点三、幂的运算性质
例4 在下列运算中,计算正确的是( )
A. a3 a2 a 6
勾
股
定
理
27
内容
勾股定理
验证
勾
原
股
命
应用
定 理
题
命
互逆 互逆
题 逆 命题 定理
命
题
内容
勾股定理 的逆定理
验证
应用
毕达哥拉斯 赵爽 茄菲尔德
已知直角三角形的两边求第三边
在数轴上表示无理数 实际问题
构造全等的直角三角形
已知三边判断形状
实际问题
28
积的乘方 幂的乘方 同底数幂的乘法
人教版八年级数学上册知识点汇总(框架图)

人教版八年级数学上册知识点汇总(框架图)人民教育版,八年级,第一册,数学知识点总结第11章全等三角形同构:两个完全重合的图形称为同构全等三角形:两个完全重合的三角形称为全等三角形基本上定义相应的顶点:在全等三角形中互相重合的顶点称为相应的顶点对应边:全等三角形中的重叠边称为对应边对应角:在全等三角形中彼此重合的角称为对应角三角形的稳定性:当三角形的三条边的长度被确定时,三角形的形状和大小都被确定在。
这个性质叫做三角形的稳定性。
全等三角形的性质:全等三角形的对应边相等,对应角相等边和边:三条边对应于两个三角形的等价角边:两条边和夹角相等的三角形是全等的判断定理转角(ASA):两个三角形,其两个角和它们的夹紧边对应于相等的同余角边:两个角的对边相等的两个三角形,其中一个角是全等的斜边和直角边:斜边和直角边对应于两个相等的直角三角形的同余。
绘画:教科书第19页角平分线的性质定理:角平分线上的点到角两边的距离相等性质定理的逆定理:从角的内侧到角的两侧距离相等的点在角的平分线上1、明确已知命题并验证基本方法2,根据问题的含义画一个图形,并用数字符号来表示已知的和经过验证的3、经过分析,从已知中找出证明的方法,写出证明过程全等三角形第12章轴对称轴对称图形:如果一个图形是沿直线折叠的,则直线两侧的部分相互之间的重量为,该图形称为轴对称图形两个图形形成轴对称:一个图形沿某一条直线折叠,如果它能与另一个图形重合,那么这两个图形就称为关于直线对称基本概念线段的垂直平分线:穿过线段中点并垂直于线段的直线称为线段的垂直平分线等腰三角形:两条边相等的三角形称为等腰三角形两条相等的边叫做腰,另一边叫做底边,两条腰之间的角叫做顶角,底边和腰之间的角叫做底角等边三角形:三条边相等的三角形称为等边三角形1.无论是轴对称图形还是两个图形关于一条直线对称,的对称性质是轴是由任何一对对应点连接的线段的垂直平分线轴对2的基本性质,对称图相等轴对称1。
八年级上册数学思维导图第一至五章

八年级上册数学思维导图第一至五章
八年级上册数学思维导图第一至五章:
第一章《三角形》
三角形这章的主要考点有5个:(1)三角形三边的关系,主要能判断三条线段能否构成三角形,能求线段的取值范围或证明线段的不等关系;(2)三角形的高、角平分线和中线的应用;(3)有关三角形内角与外角的计算;(4)多边形的内角和与外角和;(5)数学思想的应用,这章主要有方程思想、分类讨论思想和化归思想的应用。
难点是数学思想的应用。
第二章《三角形全等》
全等三角形的主要考点主要有2个:(1)全等三角形的判定和性质;(2)角平分线的性质。
难点是三角形种常需要添加辅助线构造全等三角形。
第三章《轴对称》
本章考点有6个:(1)判断轴对称图形;(2)画轴对称图形;(3)坐标系内点的对称问题;(4)等腰三角形“三线合一”定理;(5)利用轴对称解决最短距离问题;(6)直角三角形中30度角性质。
这章的难点是解决最短距离问题,我们数学称为将军饮马数学模型,也就是建模思想的应用。
第四章《整式乘除与因式分解》
这章考点有5个:(1)幂的运算法则与逆运用;(2)整式乘除法运算;(3)乘法公式的应用;(4)0指数和负整指数幂;(5)因式分解。
本章难点是幂运算法则的逆运用和整体代换思想的运用。
第五章《分式及分式方程》
分式这章的考点有4个:(1)分式的化简求值;(2)解分式方程;(3)分式应用题。
这章的难点是分式应用题,在解题应用题我们要注意应用题的基本等量关系及每份量×份数=总量,若每份量和份数都未知,可以确定为分数应用题;易错点是分式化简求值时,代入的值要保证原分式的分母和除数都不为零,解分式方程要记得验根。
初中数学知识结构图思维导图

圆 上
圆 外
外心:是三边垂直平 分线的交点. 到三顶点的距离相等锐—形内;直—斜边上;钝—形外
相交
相切
相离
切线的 性质.判定
切线长 定理
内心:是三角平分线的交点. 到三边的距离相等在三角形内
外 离
内 含
外 切
内 切
相 交
等分圆周
正多边形
弧等
性质
平行线
相交线
对邻 顶补 角角
垂 直
性质
判定
相等
和 为1800
点到直线 的距离
性质
定义
画法
条件
平行公理.推论
一“放”二“靠” 三“推”四“画”
同位角相等
内错角相等
同旁内角互补
同位角相等
同旁内角互补
内错角相等
分类
结构
命题
关系
借助角研究平面内两条直线的位置关系
三角形
有关线段
多边形 及其 内角和
解决几何中的 极值问题
利用轴对称制作图案
对称轴
全等 三角形 与 相似 三角形
定义
性质
条件
角平分线
表示方法
完全重合 两个三角形
对应边、角、周长 面积、中线、高线、 角平分线相等
两个三角形 用符号≌连接
SSS
AAS
ASA
HL
SAS
适合判定所有三角形 全等
适用于 直角三角形
会画统计图
集中趋势
离散程度
平均数
中位数
众数
极 差
方 差
反映数据向其中心值聚集的程度
反映数据分布的离散程度
借助抽样做决策
比例线段
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题 逆 命题 定理
命
题
内容
勾股定理 的逆定理
验证
应用
毕达哥拉斯 赵爽 茄菲尔德
已知直角三角形的两边求第三边
在数轴上表示无理数 实际问题
构造全等的直角三角形 已知三边判断形状 实际问题
积的乘方 幂的乘方 同底数幂的乘法
平方差、完全平方
多项式除以 单项式
单项式除以 单项式
除法
同底数 幂相除
乘法 运算
加减
o
x
的
y
y
增 b=0,图象在
大
一三象限 o 注意x:过原点o
而
增
y
y
大 b<0,图象在
o
x
o
一三四象限
一条直线
b>0,图象在 x 一二四象限
b=0,图象在 x 二四象限
b<0,图象在 x 二三四象限
Y
随
Y
x
随
的
每x
增
一的
大
象增
而
限大
减
内而
小
减
K同号时, 小
图象在
图象在
Y
一三象限 二四象限
随
每x
y
y
一的
提公因式法 公式法
因式分解
十字相乘法
分类
多项式
单项式
整
式
分组分解法
分母不为零
有意义
分母不为零 分子为零
通分
公因式
分 式
子积为子 母积为母
注:分子、 分母为多 项式时先 分解因式
化除法为 乘法
a b
n
an bn
n为整数
an
1 an
n为整数
解法 整式方程
应用 是 解
解方程
X=a 检验
0≠最简公分母=0
增根
实 列式 分式
类比分
类比分
数性质 分式基本性质 数运算
分式运算
际
问 列方程 题
分式方程
去分母
整式方程
目 标
实际 问题 的解
目 标
解整式方程
分式方程的解 检验 整式方程的解
数反相 轴数 分类
法数计学科
值对绝
近似数与 有与数轴关系 无理数
整式的乘 除与因式 分解
分式
一次 函数
反比例 函数 课题学习
数学 活动
全等三 角形 四边形
实数
数与
代数
概率与
实践与 运用
空间与 图形
轴对称
勾股 定理
统计
数据的 分析
八年级
数学
第十一章:
全等三角 形
第十二章:
轴对 称
第十五章:
整式的乘除 与因式分解
第十四章: 一次函数
第十三 章: 实数
八年级数学 (上)
菱形
同一
对角 线相 等
底边 上的 两个 角相
性质等 判定
③
②④
平行四边 形
直 角
梯形
四边形
辅助线
作 延 平 平 利用腰中点 高 长 移 移 割补成--线 两 两 对 全等三角形、
腰 腰 角 平行四边形 线
四边形 平行四边形
正
菱
矩 形
方
形
形
等腰 梯形 梯
形
直角 梯形
一般 在平面内,四条线段首 四边形 尾顺次相接组成的图形
翻折后与
另一图形 重合
基本图形 对称轴
判定 应用 性质
垂直平分线
对称点 特征
定义
利用轴对称 要素 用
成轴对称 制作图案
坐标
表示
一
条 直
对称轴
线
轴对称图形
静
轴对称变换
轴对 称
静
动
翻折后与 另一部分
重合
定义
轴对称
作关于 x轴、 y轴 的对 称点
两 边 相 等
定义
等
三
边
线
对
合
等
一
角
性质
等 角 对 等 边
ox
o
x
象 限
增 大
双曲线
内而 增
k>0
k<0
大
k>0
k<0
有两交点。 K异号时,
图象
性质
最优方案
应用
形如y=kx+b (k.b为常数,k≠0)
图象
有两个、一个
关系 或无交点
性质
一次函数
反比例函数
柱形储应藏用室轮船卸货 力学
一次
解析式
当b=0时,是 正比例函数
待定函与系数反数法 比例
解析式 形如y k 实际问题,图象在第一象限
四边形
有一个角 是直角
矩形 有一组
邻边相等
四 特殊
两组对边 分别平行
平行四边形
有一组邻边相等有一个角是直角
有一组 邻边相等
菱 有一个角 形 是直角
边
四边 形
形
重心
一组对边平 行、另一组
对边不平行
梯形
规则的几何图形重心 不规则的几何图形重心
两条腰相等
等腰梯形
有一个角是直角
几何中心
直角 梯形
悬线法
中点 四边形
HL
适合 判定 所有 三角 形全 等
AAS ASA SAS SSS
对应边相等、 对应角相等.
两个三角形全等 用符号≌连接
性质 条件
表示方法 定义
角平分线
全等 三角形
应用 判定
到角两 边距离 相等的
点
性质
点到角
两边的
距离相
等
对应边相等 对应角相等
全等形
全等形三角形
解决问题
SSS,SAS,ASA, AAS,HL
x
函数
(k为常数,k 0)
建立数
变
学模型
化
函数
中
的
世
界
一次函数
再
认
识
应
用
一元一次方程
一元一次不等式
二元一次方程组
图像 性质
课题学习 选择方案
现实
世界
中的
归纳
反比
例函
数
反比 例函
数
实际应 用
反比 例函 数图 象和 性质
概率与统计
第十六章: 分式
第二十章: 数据的分析
第十八章: 勾股定理
第十七章:
反比例函 数
第十九 章: 四边形
八年级数学 (下)
形状:取决 于原四边形
对角线的 相等或垂直
中点 四边形
④ ②
矩形
对边平行 性质
且相等 判定 边 对角相 性质
等邻角 互补
判定 性质
角 对角线
对角线 判定
互相平
分
正方形
①③
判定
等 边 三 角 形
特例
等腰三角形
等腰三角形
生
活
中
的 轴
轴对称
对
称
等边三角形 作轴对称图形的对称轴 作轴对称图形 用坐标表示轴对称
互逆命题 互逆定理
定理的证明
已知两边 求第三边
应用
三角形全等
定理的证明
应用
面积法
勾股定理
勾股定理的逆定理
勾 股 定 理
内容
勾股定理
验证
勾
原
股
命
应用
定 理
题
命
互逆 互逆
对角线相等的四边形的中点四边形是菱形 对角线互相垂直的四边形的中点四边形是矩形
正方形
梯形辅助线作法(以等腰梯形为例)
A
D
A
D
O
A
D
BE
FC
(作高线)
A
D
B
E
C
(平移一腰)
A
B
C
(延长两腰)
D
B
C
(平移对角线)
A
D
中点
B
C
(割补成三角形)
B
C
(补全平行四边形)
A
D
中点
(B割补成平行四边形C )
适用于 直角三角形
性质与 运算
平方根与立方根
实数和数轴
重要 概念
实 数
乘方
互为逆运算
开方
开平方 开立方
平方根 立方根
知识展开顺序
算术平方根
平方根
立方根
无理数
实数
唯一确 定性
解 析 式 法
列 表 法
图 象 法
变量与函数 一次函数
基本概念
图像 反比例函数
描点法 数形结合
函 数
y
y
b>0,图象在
Y 随
一二三象限 o
x
