第2章 运算器和运算方法-习题
第2章运算方法和运算器74181

第2位向第3位的进位公式为: P=X0X1X2X3
Cn +3 =Y2 + X2 Cn +2 =Y2 +Y 1 X1 +Y0 X1 X2 +X 0 X1 X2 Cn
第3位的进位输出(即整个4位运算进位输出)公式为: C n + 4 = Y 3 + X 3 C n + 3 = Y 3 + Y 2 X 3 + Y 1 X 2 X 3 + Y 0 X 1 X 2 X 3 + X 0 X 1X 2 X 3 C n
i
Y3+Y2X3+Y1X2X3+Y0X1X2X3 =G
2.5.2多功能算术/逻辑运算单元(ALU)续8
3.算术逻辑运算的实现
除了S0-S3四个控制端外,还有一个控制端 M,它使用来控制ALU是进行算术运算还是进行逻 辑运算的。
当M=0时,进行算术操作。M对进位信号没 有任何影响。此时F不仅与本位的被操作数Y和操 作数X有关,而且与本位的进位输出,即C有关。 当M=1时,进行逻辑操作。封锁了各位的进 位输出,即C =0,各位的运算结果F仅与Y和X有关。
定点运算器的组成
4位之间采用先行进位公式,根据式(2.36),每一
位的进位公式可递推如下: 第0位向第1位的进位公式为:
Cn +1 =Y0 +X0 Cn 其中Cn是向第0位(末位)的进位。
第1位向第2位的进位公式为:
Cn + + X1 C Y1 + Y0 X1 +X X X1Cn+Y X X X 设: = Y Y Y 2=Y1G n+ 1= 3+ 2X3+ 1 02X 3 0 1 2 3
将Xi 和Yi代入前面的进位表达式,可简化为: Cn+i+1=Yi+Xi Cn+ i
1 1
0
1 1
Ai
定点运算器的组成
计算机组成原理白中英(第5版)课后习题-运算方法和运算器(圣才出品)

第2章 运算方法和运算器1.写出下列各整数的原码、反码、补码表示(用8位二进制数)。
其中MSB 是最高位(符号位),LSB 是最低位。
(1)-35(2)128(3)-127(4)-1答:(1)[-35]原=1010 0011[-35]反=1101 1100[-35]补=1101 1101(2)[127]原=0111 1111[127]反=0111 1111[127]补=0111 1111(3)[-127]原=1111 1111[-127]反=1000 0000[-127]补=1000 0001(4)[-1]原=1000 0001[-1]反=1111 1110[-1]补=1111 11112.设[x]补=7650....a a a a ,其中i a 取0或1,若要x>-0.5,求0126,,,...a a a a 的取值。
答:[x]补=a7. a6 a5…a0①若a7=0,则x>0,满足x>-0.5,此时a0→a6可任意;②若a7=1,则x<=0,要满足x>-0.5,需a6=1。
即a7=1,a6=1,a0→a5有一个不为0。
3.有一个字长为32位的浮点数,符号位1位;阶码8位,用移码表示;尾数23位,用补码表示;基数为2。
请写出:(1)最大数的二进制表示;(2)最小数的二进制表示;(3)规格化数所能表示的数的范围。
答:IEEE 754格式(E的取值范围:1~254,全0和全1分别表示0和无穷大)如下。
(1)最大数的二进制:阶码取最大的正数,尾数取最大的正数,表示为0 11111111 11111111111111111111111即2127×(1-2-23)(2)最小数的二进制:阶码取最大的正数,尾数取最大的负数,表示为1 11111110 11111111111111111111111即-2127×2-23(3)规格化数所能表示数的范围:最小的正数:阶码取最小的负数,尾数取最小的正数0 00000001 00000000000000000000001 即2-127×(2-1+2-23)最大的正数:阶码取最大的正数,尾数取最大的正数0 10000000 11111111111111111111111 即2127×(1+2-1-2-23)最大的负数:阶码取最大的正数,尾数取最大的负数1 10000000 11111111111111111111111 即-2127×(2-1+2-23)最小的负数:阶码取最小的负数,尾数取最小的负数1 00000001 00000000000000000000000 即-2-127所以范围是:-2127至-2-127×(2-1+2-23),2-127×(2-1+2-23)至2127×(1+2-1-2-23)4.将下列十讲制数表示成IEEE754标准的32位浮点规格化数。
计算机组成原理第二章课后习题答案

第二章运算方法和运算器练习一、填空题1. 补码加减法中,(符号位)作为数的一部分参加运算,(符号位产生的进位)要丢掉。
2. 为判断溢出,可采用双符号位补码,此时正数的符号用(00)表示,负数的符号用(11)表示。
3. 采用双符号位的方法进行溢出检测时,若运算结果中两个符号位(不相同),则表明发生了溢出。
若结果的符号位为(01),表示发生正溢出;若为(10),表示发生负溢出。
4. 采用单符号位进行溢出检测时,若加数与被加数符号相同,而运算结果的符号与操作数的符号(不一致),则表示溢出;当加数与被加数符号不同时,相加运算的结果(不会产生溢出)。
5. 利用数据的数值位最高位进位C和符号位进位Cf的状况来判断溢出,则其表达式为over=(C⊕Cf)。
6. 在减法运算中,正数减(负数)可能产生溢出,此时的溢出为(正)溢出;负数减(正数)可能产生溢出,此时的溢出为(负)溢出。
7. 补码一位乘法运算法则通过判断乘数最末位Yi和Yi-1的值决定下步操作,当YiYi-1=(10)时,执行部分积加【-x】补,再右移一位;当YiYi-1=(01)时,执行部分积加【x】补,再右移一位。
8. 浮点加减运算在(阶码运算溢出)情况下会发生溢出。
9. 原码一位乘法中,符号位与数值位(分开运算),运算结果的符号位等于(两操作数符号的异或值)。
10. 一个浮点数,当其补码尾数右移一位时,为使其值不变,阶码应该(加1)。
11. 左规的规则为:尾数(左移一位),阶码(减1)。
12. 右规的规则是:尾数(右移一位),阶码(加1)。
13. 影响进位加法器速度的关键因素是(进位信号的传递问题)。
14. 当运算结果的补码尾数部分不是(11.0×××××或00.1×××××)的形式时,则应进行规格化处理。
当尾数符号位为(01)或(10)时,需要右规。
计算机组成原理.各章例题
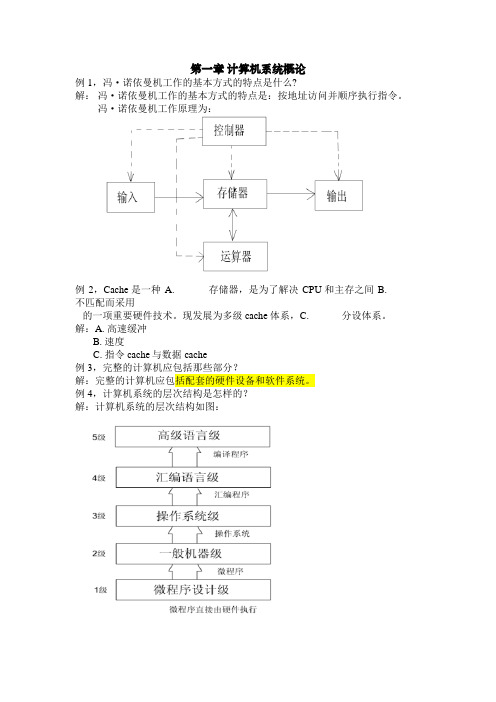
第一章计算机系统概论例1,冯·诺依曼机工作的基本方式的特点是什么?解:冯·诺依曼机工作的基本方式的特点是:按地址访问并顺序执行指令。
冯·诺依曼机工作原理为:例2,Cache是一种A. ______存储器,是为了解决CPU和主存之间B. ______不匹配而采用的一项重要硬件技术。
现发展为多级cache体系,C. ______分设体系。
解:A. 高速缓冲B. 速度C. 指令cache与数据cache例3,完整的计算机应包括那些部分?解:完整的计算机应包括配套的硬件设备和软件系统。
例4,计算机系统的层次结构是怎样的?解:计算机系统的层次结构如图:第二章 运算方法和运算器例 1.设机器字长32位,定点表示,尾数31位,数符1位,问:(1)定点原码整数表示时,最大正数是多少?最大负数是多少? (2)定点原码小数表示时,最大正数是多少?最大负数是多少? 解:(1最大正数:数值 = (231 – 1)10最大负数: 数值 = -(231 – 1)10 (2)定点原码小数表示: 最大正数值 = (1 – 231 )10最大负数值 = -(1–231 )10例2.已知 x = - 0.01111 ,y = +0.11001, 求 [ x ]补 ,[ -x ]补 ,[ y ]补 ,[ -y ]补,x + y = ? ,x – y = ?解:[ x ]原 = 1.01111 [ x ]补 = 1.10001 所以 :[ -x ]补 = 0.01111[ y ]原 = 0.11001 [ y ]补 = 0.11001 所以 :[ -y ]补 = 1.00111 [ x ]补 11.10001 [ x ]补 11.10001 + [ y ]补 00.11001 + [ -y ]补 11.00111 [ x + y ]补 00.01010 [ x - y ]补 10.11000所以: x + y = +0.01010 因为符号位相异,结果发生溢出例3.设有两个浮点数 N 1 = 2j1 × S 1 , N 2 = 2j2 × S 2 ,其中阶码2位,阶符1位,尾数四位,数符一位。
计组课后习题及作业

A.高速芯片 B.两套相互独立的读写电路 C.流水技术 D.新型器件
总 线 系 统
理 学 院电技教研室
首页
5
A. 运算器 B.控制器 C.运算器和控制器 D.运算器、控制器和主存储器 2、在CPU中跟踪指令后继地址的寄存器是_____ B 。 A. 主存地址寄存器 B.程序计数器 C.指令寄存器 D.状态条件寄存器 D 。 3、操作控制器的功能是____ A. 产生时序信号 B.从主存取出一条指令 C.完成指令操作码译码 D. 产生有关的操作控制信号 4、由于CPU内部的操作速度较快,而CPU访问一次主存所花的时间较长, 因此机器周期通常用____ A 来规定。 6章 A.主存中读取一个指令字的最短时间 B.主存中读取一个数据字的最长时间 C.主存中写入一个数据字的平均时间 D.主存中读取一个数据字的平均时间 B 。 5、微程序控制器中,机器指令与微指令的关系是____ 总 A.每一条机器指令由一条微指令来执行 B.每一条机器指令由一段用微指令 C.一段机器指令组成的程序可由一条微指令来执 线 编成的微程序来解释执行 行 D.一条微指令由若干条机器指令组成 系 6、为了确定下一条微指令的地址,通常采用断定方式,其基本思想____ C 。 统 A.程序计数器PC B.微程序计数器uPC C.通过微指令控制字段由设计者指 定或者由设计者指定的判别字段控制 D.通过指令中指定一个专门字段
计 算 机负数 11.正数补码算术移位时,符号位_____ 补码算术左移时,符号位不变 ____,低位补____ 0 。负数补码算术 不变 舍去。 右移时,符号位 ____,高位补____ 1 ,低位____
线 系 统
理 学 院电技教研室
首页
统
理 学 院电技教研室
【5A版】计算机组成原理习题解答

△E =-1,应修改x
△E=Ex-Ey=[Ex]补+[-Ey]补=11 101 +00 010=11 111
修改后的x表示为:
[x]浮= 11 110,0.010010(1)
② 尾数求和 Mx+My =1 . 1 1 0 1 0 0 (1)
存储容量
存储器所能保存二进制数据的总数,常用单位为KB、MB等。
单元地址 用于识别存储器中每个存储单元的编号,即单元地址。 数据字 表示计算机所要处理数据的计算机字,称为数据字。 指令字 表示一条指令的计算机字,称为指令字。
5
1.6 什么是指令?什么是程序?
指令:
1
计算机组成原理习题解答
河南大学计算机与信息工程学院
2
第一章 计算机系统概论
3
1.4 冯诺依曼型计算机的主要设计思想是什么? 它包括哪些主要组成部分?
冯诺依曼计算机的主要设计思想是: 存储程序并按地址顺序执行。
冯诺依曼计算机主要包括:
存储器、运算器、控制器、输入和输出五部分组成。
4
1.5 什么是存储容量?什么是单元地址? 什么是数据字?什么是指令字?
15
2.7 用原码阵列乘法器、补码阵列乘法器分别计算x×y。 (1) x=11011 y=-11111 (2) x=-11111 y=-11011 (1) 输入数据的原码: [x]原=0 11011
16
[y]原=1 11111
符号位单独运算: 0⊕1=1 算前求补器输出: |x|=11011 |y|=10011 乘法阵列: |x| ×|y| = 1 1 0 1 0 0 0 1 0 1
计算机组成原理前3章课后习题参考答案-

白中英第五版计算机组成原理课后习题参考答案第一章计算机系统概述4、冯•诺依曼型计算机的主要设计思想是什么它包括哪些主要组成部分答:冯•诺依曼型计算机的主要设计思想是存储程序和程序控制,其中存储程序是指将程序和数据事先存放到存储器中,而程序控制是指控制器依据存储的程序来控制全机协调地完成计算任务。
总体来讲,存储程序并按地址顺序执行,这就是冯•诺依曼型计算机的主要设计思想。
5、什么是存储容量什么是单元地址什么是数据字什么是指令字答:见教材P8和P10。
7、指令和数据均存放在内存中,计算机如何区分它们是指令还是数据答:见教材P10。
第二章运算方法和运算器】1、写出下列各整数的原码、反码、补码表示(用8位二进制数)。
3、有一个字长为32位的浮点数,符号位1位,阶码8位,用移码表示,尾数23位,用补码表示,基数为2,请写出:(1)最大数的二进制表示阶码用移码表示,题中并未说明具体偏移量,故此处按照移码的定义,即采用偏移量为27=128,则此时阶码E的表示范围为0000 0000~1111 1111,即0~255,则在上述条件下,浮点数为最大数的条件如下:所以最大数的二进制表示为:0 1111 1111 1111 1111 1111 1111 1111 1111 111对应十进制真值为:+(1-2-23)×2127(2)最小数的二进制表示浮点数为最小数的条件如下:所以最小数的二进制表示为:1 1111 1111 0000 0000 0000 0000 0000 000对应十进制真值为:-1×2127(3)规格化数所表示数的范围规格化要求尾数若为补码表示,则符号位和最高有效位符号必须不同。
(A)浮点数为最大正数的条件如下:所以最大正数的二进制表示为:0 1111 1111 1111 1111 1111 1111 1111 1111 111 对应十进制真值为:+(1-2-23)×2127(B)浮点数为最小正数的条件如下:所以最小正数的二进制表示为:0 0000 0000 1000 0000 0000 0000 0000 000对应十进制真值为:+2-1×2-128=+2-129(C)浮点数为最大负数的条件如下:所以最大负数的二进制表示为:0 0000 0000 0111 1111 1111 1111 1111 111对应十进制真值为:-(2-1+2-23)×2-128(D)浮点数为最小负数的条件如下:所以最小负数的二进制表示为:0 0000 0000 0000 0000 0000 0000 0000 000对应十进制真值为:-1×2127所以,规格化数所表示数的范围如下:正数+2-129~+(1-2-23)×2127负数-2127 ~-(2-1+2-23)×2-1284、将下列十进制数表示成IEEE754标准的32位浮点规格化数。
计算机组成原理第一,二章经典习题整理

经典习题整理第一章计算机系统概论一.填空题。
1.存储______并按______顺序执行,这是______型计算机的工作原理。
解析:计算机的硬件系统是根据冯.诺依曼计算机体系结构的思想设计的,采用了存取程序的设计思想,存储程序并按地址顺序执行,是冯.诺依曼型计算机的工作原理。
2.计算机中有在流动:一股是,即操作命令,其发源地是,它分散流向各个部件;另一股是,它受的控制,从一个部件流向另一个部件,边流动边加工处理。
解析:计算机中有两股信息在流动:一股是控制信息,即操作命令,其发源地是控制器,它分散流向各个部件;另一股是数据信息,它受控制信息的控制,从一个部件流向另一个部件,边流动边加工处理。
3.程序设计语言一般可分为三类:,,。
解析:程序设计语言一般可分为三类:机器语言,汇编语言,高级语言。
4.操作系统最早出现在第代计算机。
解析:第三代计算机的主要特点:用集成电路代替了分立元件,用半导体存储器取代了磁芯存储器;在软件方面,操作系统日益成熟。
5.多媒体CPU是带有技术的处理器,它是一种技术,特别适用于处理。
解析:多媒体PC机是指具有多媒体功能的PC机。
其CPU 带有MMX技术的处理器,它是一种多媒体拓展结构技术,特别适用于图像数据处理,它以新一代奔腾CPU为代表,极大地提高了在多媒体和通信应用方面的功能。
二.选择题。
( D )1.完整的计算机应包括______。
A 运算器、存储器、控制器。
B 外部设备和主机。
C 主机和实用程序。
D 配套的硬件设备和软件系统。
( C )2.至今为止,计算机中的所有信息仍以二进制方式表示的理由是______。
A.节约元件 B 运算速度快C 物理器件的性能决定D 信息处理方便( D )3.我国在______年研制成功了第一台电子数字计算机,第一台晶体管数字计算机于______年完成。
A 1946,1958B 1950,1968C 1958,1961D 1959,1965(C )4.主机中能对指令进行译码的部件是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
真
0 1 0 0 0
1 0 0 1 0 1 1 0 0 0
=-0.11011+0.0000011011 =-0.1101000101
0.(1)(1) (0) (1) (1) 1 1 0 1 1
18
8、用原码阵列除法器计算x÷y 用原码阵列除法器计算x (1) x=0.11000 y=-0.11111 y=解:[|x|]原=0.11000 [|x [|x|]补=00.11000 00000 [|x [|y|]原=0.11111 [|y [|y|]补=00.11111 [|y [-|y|]补=11.00001 |x |÷|y|=0.11000 余数为余数为-0.00000 00110 S=Sx⊕Sy=0⊕1=1 =0⊕
13
(2)x=0.11011 y= -0.10101
解: [x]变补=00.11011 [y]变补=11.01011 [x+y]变补=00.00110 由于两个符号位相同,所以未发生溢出。 由于两个符号位相同,所以未发生溢出。
14
6、已知x和y,用变形补码计算x - y,同时指出 已知x 用变形补码计算x 结果是否溢出。 结果是否溢出。
(1)-35/64
解: x = −35 / 64 = (−100011× 2 −110 ) 2 = (−0.100011) 2 [ x]原 = 11000110
[ x]反 = 10111001 [ x]补 = 10111010
3
(2)23/128
解:
x = 23 / 128 = (10111 × 2 −111 ) 2 = (0.0010111) 2 [ x]原 = 00010111 [ x]反 = 00010111 [ x]补 = 00010111
(2)-27/64
解: x=x=-11011*2-110=-1.1011*2-2 S=1 M=1011 规格化表示: 1 011 1110 1101 1000 0000 0000 0000 0000=(BED80000)16
11
4、将下列十进制数表示成浮点规格化数,阶码3位, 将下列十进制数表示成浮点规格化数,阶码3 用补码表示;尾数9 用补码表示。 用补码表示;尾数9位,用补码表示。
(1)27/64
解:
x=11011*2-110=0.11011*2-1 浮点规格化表示: 浮点规格化表示:0 11011000 111=(6C7)16
(2)-27/64
解:
x=x=-11011*2-110=-0.11011*2-1 浮点规格化表示: 浮点规格化表示:1 00101000 111=(847)16
符号位(1) 阶码(8) 尾数(23) 符号位(1) 阶码(8) 尾数(23) 1 2 3 正数,尾数最大, 0 正数,尾数最大, 阶码最大 负数,尾数(负) 负数,尾数( 最小, 最小,阶码最大 正最大数 正最小数 负最大数 负最小数 1 0 0 1 1 11…1 11… 11…1 11… 11…1 11… 00… 00…0 00… 00…0 11…1 11… 11…1 11… 00… 00…0 11…1 11… 100… 100…0 011…1 011… 00… 00…0 二进制表示 7FFFFFFF FF800000 7FFF FFFF 0040 0000 803F FFFF FF80 0000 真值 (1-2-23)*2127 (1-1*2127 (1-2-23)*2127 (10.5*2-128 -(0.5+2-23)*2-128 -1*2127
最少用几位二进制数即可表示任一 最少用几位二进制数即可表示任一5位长的十 用几位二进制数即可表示任一5 进制正整数? 进制正整数? 解:
最大的5 最大的5位正整数是 99999 由于2 由于216<99999<217 故最少要用17位二进制数 故最少要用17位二进制数
1
习题2 习题2
写出下列各数的原码、反码、补码表示(用8 写出下列各数的原码、反码、补码表示(用8位二进 制数)。其中MSB是最高位(又是符号位),LSB 制数)。其中MSB是最高位(又是符号位),LSB 是最低位。如果是小数,小数点在MSB之后;如果 是最低位。如果是小数,小数点在MSB之后;如果 是整数,小数点在LSB之后。 是整数,小数点在LSB之后。 (1)-35/64 (2)23/128 (3)-127 (4)用小数表示-1 )用小数表示(5)用整数表示-1 )用整数表示2
10
4、将下列十进制数表示成IEEE754标准的32位浮点规格化数 将下列十进制数表示成IEEE754标准的 位浮点规格化数 标准的32
(1)27/64
解: x=11011*2-110=1.1011*2-2 S=0 M=1011 E=-2+127=125 浮点规格化表示: 浮点规格化表示: 0 011 1110 1101 1000 0000 0000 0000 0000=(3ED80000)16
7、用原码阵列乘法器、补码阵列乘法器分别 用原码阵列乘法器、 计算x 计算x×y
(1)x=0.11011 y=-0.11111 y=解:用原码阵列乘法器
Sx=0 [|Mx|]原=0.11011 [|M Sy=1 [|My|]原=0.11111 [|M S=Sx⊕Sy=0⊕1=1 =0⊕ M= |Mx | × |My|=0.1101000101 |M [x×y]原=1. 1101000101 0.1 1 0 1 1 × 0.1 1 1 1 1 0.1 1 0 1 1 0.1 1 0 1 1 0.1 1 0 1 1 0.1 1 0 1 1 0.1 1 0 1 1 0.1 1 0 1 0 0 0 1 0 1
6
(5)用整数表示-1 用整数表示解:
x = −1 = (−1) 2 [ x]原 = 10000001 [ x]反 = 11111110 [ x]补 = 11111111
7
2、设[x]补=a0.a1a2…a6,其中ai取0或1,若要x>-0.5,求a0,a1, 其中a 若要x>-0.5, a2,…, a6的取值。 的取值。
17
7、用原码阵列乘法器、补码阵列乘法器分别 用原码阵列乘法器、 计算x 计算x×y (0).1 1 0 1
× (1).0 (1)x=0.11011 y=-0.11111 y=(0). 1 (0). 0 0 解:用补码阵列乘法器 (0). 0 0 0 [x]补=(0).11011 (0). 0 0 0 0 [y]补=(1).00001 (0). 0 0 0 0 0 [x×y] =0.(1)(1)(0)(1)(1)11011 0.(1)(1) (0)(1) (1)
19
8、用原码阵列除法器计算x÷y 用原码阵列除法器计算x
(1) x=0.11000 y=-0.11111 y=解: [|x [|x|]原=0.11000 [|x [|x|]补=0.11000 00000 [|y [|y|]原=0.11111 [|y [|y|]补=0.11111 [-|y|]补=1.00001 |x |÷|y|=0.11000 余数为余数为-0.00000 00110 S=Sx⊕Sy=0⊕1=1 =0⊕
解:
Q [ − 0 . 5 ] 补 = 1 . 100000 ∴ 当 x ≥ 0时, a 0 = 0, a1 ~ a 6 任意 当 − 0 . 5 < x < 0时, a 0 = 1, a1 = 1, a 2 ~ a 6 不全 为 0
8
思考题1 思考题1:
1.
已知x=0.a 已知x=0.a1a2a3a4a5a6(ai为0或1),讨论下列几种情况时ai ),讨论下列几种情况时 讨论下列几种情况时a 各取何值。 各取何值。 (1)x>1/2 (2)x≥1/8 (3)1/4 ≥ x>1/16
(2)x=0.10111 y= 0.11011
解: [x]变补=00.10111 [y]变补=00.11011 [-y]变补=11.00101 [[x-y]变补= [x]变补+[-y]变补= 11.11100 [x +[由于两个符号位相同,所以未发生溢出。 由于两个符号位相同,所以未发生溢出。
16
4.
设x为真值,x*为绝对值,说明[-x*]补=[-x]补能否成立。 为真值, 为绝对值,说明[ =[能否成立。
9
3. 有一个字长为32位的浮点数,符号为1位,阶码8位,用移码表示;尾数23 有一个字长为32位的浮点数 符号为1 位的浮点数, 阶码8 用移码表示;尾数23 用补码表示;基数为2 请写出: 位,用补码表示;基数为2。请写出: 最大数的二进制表示, (1)最大数的二进制表示, 最小数的二进制表示, (2)最小数的二进制表示, 规格化数所能表示的数的范围, (3)规格化数所能表示的数的范围, 最接近于零的正规格化数与负规格化数。 (4)最接近于零的正规格化数与负规格化数。 解:
(1)x=0.11011 y= -0.11111
解: [x]变补=00.11011 [y]变补=11.00001 [-y]变补=00.11111 [[x-y]变补= [x]变补+[-y]变补= 01.11010 [x +[由于两个符号位不相同,所以结果溢出。 由于两个符号位不相同,所以结果溢出。
