数的整除单元知识点总结
小学整除知识点总结

小学整除知识点总结一、整除的概念整除就是某个数,除尽了另一个数,即余数为0。
例如8 ÷ 4 = 2,9 ÷ 3 = 3,都是整除的情况。
其中8被4整除,9被3整除。
二、整除的特点1. 被除数是整除数的整倍数;2. 如果一个数能被2整除,那么它一定是偶数;3. 如果一个数能被3整除,那它的各位数字之和也是3的倍数;4. 如果一个数能被5整除,那么它的末尾数字必须是0或5;5. 如果一个数能被6整除,那么它既能被2整除,也能被3整除;6. 如果一个数能被9整除,那么它的各位数字之和也是9的倍数。
三、整除的判断方法整除的判断方法有多种,根据题目要求选择不同的方法来进行计算。
下面列举一些常见的整除判断方法:1. 除数能否整除的判断方法:可以直接将被除数÷除数得到商,如果商为整数,则被除数能被除数整除;2. 末尾数字的规律判断:对于末尾为0、2、4、6、8的数,能被2整除;对于末尾为0、5的数,能被5整除;3. 各位数字之和判断:对于各位数字之和能被3、6、9整除的数,能被3、6、9整除。
四、整除的应用整除运用非常广泛,不仅在数学中应用广泛,也涉及到日常生活中的计算。
下面列举一些整除在日常生活中的应用:1. 购物找零:购物时,有时需要进行找零,这就需要进行整除的运算。
2. 时间计算:小时和分钟的计算也需要进行整除运算,如几点钟开始上课,几点钟下课等。
3. 数学题中的应用:解决数学题中的知识点,有时需要用到整除的运算方式。
总结:小学整除作为数学学习的重要知识点之一,在日常生活中也有着广泛的应用。
掌握整除的相关知识和技巧,除了能够帮助孩子们更好地学习数学知识外,也能够帮助他们在日常生活中更好地解决实际问题。
因此,家长和老师应该引导孩子们认真学习整除知识,并能够帮助他们将整除知识与日常生活相结合,更好地掌握和应用整除的相关知识。
整除知识点总结与练习

整除知识点总结与练习一、整除的定义整除是指对于两个整数a和b,如果a能够被b整除,即a除以b的结果是一个整数,则称a能够被b整除,记作b|a。
其中a称为被除数,b称为除数,整数的除法结果称为商。
例如,6÷3=2,6除以3的结果是2,因此6能够被3整除,即3|6。
整除的定义表明了整除的两个基本特点:1. 整数a能够被整数b整除的定义是a÷b的结果是一个整数。
2. 整除的概念是具有传递性的,即如果a能够被b整除,b能够被c整除,则a能够被c整除。
二、整除的判定在计算整除时,通常需要用到整除的判定方法。
整除的判定方法主要有以下几种:1. 除法判定法:即直接计算被除数除以除数的结果是否为整数。
2. 因数判定法:利用被除数和除数的因数来判断整除关系。
3. 余数判定法:如果a能够被b整除,那么a÷b的余数为0。
4. 分解质因数判定法:将被除数和除数分解质因数,如果被除数分解后能够完全包含除数分解质因数的情况,那么a能够被b整除。
下面通过一些实例来说明整除的判定方法:例1:判断24能否被6整除?方法一:除法判定法,直接计算24÷6=4,结果为整数,因此24能够被6整除。
方法二:因数判定法,24的因数包括1、2、3、4、6、8、12,其中6是24的因数,因此24能够被6整除。
方法三:余数判定法,24÷6=4余0,余数为0,因此24能够被6整除。
方法四:分解质因数判定法,24=2³×3,6=2×3,24的分解质因数包含6的分解质因数,因此24能够被6整除。
综上所述,24能够被6整除。
例2:判断35能否被5整除?方法一:除法判定法,35÷5=7,结果为整数,因此35能够被5整除。
方法二:因数判定法,35的因数包括1、5、7、35,其中5是35的因数,因此35能够被5整除。
方法三:余数判定法,35÷5=7余0,余数为0,因此35能够被5整除。
数的整除知识点总结

数的整除知识点总结数的整除是数论中的一个基本概念,也是初等数学中的重要内容。
它与因数、倍数和约数等概念密切相关,对于解题和推理都有着重要的作用。
下面将对数的整除进行详细总结。
一、定义:如果整数a能够被整数b整除,即a/b是整数,那么称a是b的倍数,b是a的因数。
可以用数学表达式a=b*k来表示,其中k是整数。
二、性质:1.任何一个整数都是它自身的倍数,也是它自身的因数,即a是a的倍数,a是a的因数。
2.任何一个正整数都是1的倍数,即对于任何整数a,都有a是1的倍数。
3.任何一个整数都是它自身的因数,即对于任何整数a,都有a是a的因数。
4.如果a是b的倍数,b是c的倍数,那么a也是c的倍数,即若a是b的倍数且b是c的倍数,则a是c的倍数。
5.如果a是b的倍数,b是a的倍数,那么a和b是互为倍数,即a是b的倍数且b是a的倍数,则a和b互为倍数。
6.如果a是b的因数,b是c的因数,那么a也是c的因数,即若a是b的因数且b是c的因数,则a是c的因数。
三、判断一个数能否整除另一个数的方法:1.因式分解法:将被除数和除数都分解成质因数的乘积形式,然后进行比较。
如果被除数的质因数包含除数的质因数,并且对应质因数的指数均大于等于相应的质因数的指数,则被除数能够整除除数。
2.试商法:用除数去除被除数,如果商是整数且余数为0,则被除数能够整除除数,否则不能整除。
四、整除的性质:1.整除关系具有传递性,即如果a能够整除b,b能够整除c,则a 能够整除c。
2.整除关系具有反对称性,即如果a能够整除b,b能够整除a,则a 和b相等或互为相反数。
3.整除关系具有自反性,即任何一个数都能整除它本身。
4.整除关系具有非传递性,即如果a能够整除b,b能够整除c,但a 不能整除c。
例如:2能整除4,4能整除8,但2不能整除8五、整数的混合运算与整除的关系:1.若a整除b,b整除c,则a整除c。
2. 若a整除b,b整除c,则a整除bc。
数的整除知识点总结
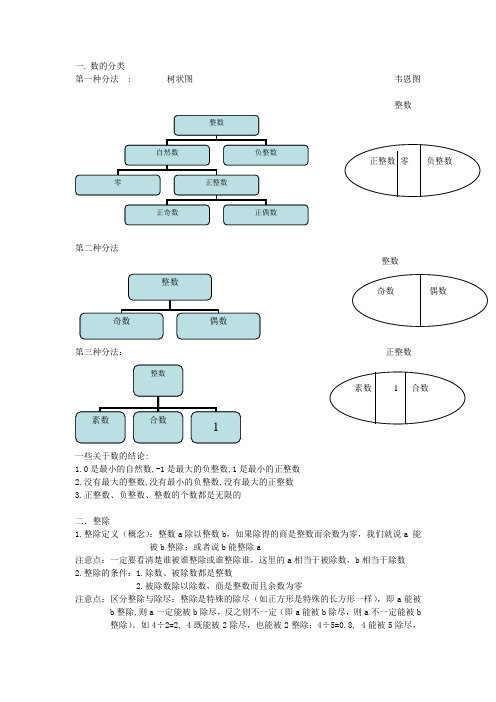
一. 数的分类第一种分法 : 树状图 韦恩图整数第二种分法 整数第三种分法: 正整数一些关于数的结论:1.0是最小的自然数,-1是最大的负整数,1是最小的正整数2.没有最大的整数,没有最小的负整数,没有最大的正整数3.正整数、负整数、整数的个数都是无限的二.整除1.整除定义(概念):整数a 除以整数b ,如果除得的商是整数而余数为零,我们就说a 能被b 整除;或者说b 能整除a注意点:一定要看清楚谁被谁整除或谁整除谁,这里的a 相当于被除数,b 相当于除数2.整除的条件:1.除数、被除数都是整数2.被除数除以除数,商是整数而且余数为零注意点:区分整除与除尽:整除是特殊的除尽(如正方形是特殊的长方形一样),即a 能被b 整除,则a 一定能被b 除尽,反之则不一定(即a 能被b 除尽,则a 不一定能被b 整除)。
如4÷2=2, 4既能被2除尽,也能被2整除;4÷5=0.8, 4能被5除尽,却不能说4能被5整除三.因数与倍数1.因数与倍数的定义:整数a能被整数b整除,a 就叫做b的倍数,b就叫做a的因数(约数)。
注意点:1.因数和倍数是相互依存的,不能简单的说某个数是因数,某个数是倍数。
如: 6÷3=2,不能说6是倍数,3是因数;要说6是3的倍数,3是6的因数。
2.因数与倍数是建立在整除的基础上的,所以如4÷0.2=20,一般是不说4是0.2的倍数,0.2是4的因数。
2.因数与倍数的特点:一个整数的因数中最小的因数是1,最大的因数是它本身。
一个数的倍数中最小的倍数是这个数本身,没有最大的倍数。
因数的个数是有限的,都能一一列举出来,倍数的个数是无限的。
3.求一个数因数的方法:利用积与因数的关系一对一对找,找出哪两个数的乘积等于这个数,那么这两个数就是这个数的因数。
如16=1×16=2×8=4×4,那么16的因数就有1、2、4、8、16,计算时一定不要忘了1和这个数本身都是它的因数,注意按照一定的顺序以防遗漏。
数的整除性与最大公约数知识点总结

数的整除性与最大公约数知识点总结在数学中,数的整除性与最大公约数是一个重要的概念。
了解和掌握这些知识点对于学习和解决数学问题至关重要。
本文将对数的整除性和最大公约数进行总结和讲解。
一、数的整除性数的整除性是指一个数能够被另一个数整除。
在数学中,我们常用符号“|”来表示整除。
例如,如果一个整数 a 能够被一个整数 b 整除,我们可以写作 a | b。
下面是数的整除性的一些基本性质:1. 如果 a | b 且 b | c,则 a | c。
这意味着如果一个数能整除另外两个数,那么它也能整除这两个数的和、差、积和商。
2. 如果 a | b 且 a | c,则 a | (xb + yc)。
这意味着如果一个数能整除另外两个数,那么它也能整除这两个数的任意整数线性组合。
3. 如果 a | b,则 -a | b。
这意味着如果一个数能整除另一个数,那么它的负数也能整除同样的数。
4. 0 | a,其中 a 是任意整数。
这意味着 0 能整除任意整数。
但要注意,0 不能被任何数整除,因为除以 0 是没有意义的。
二、最大公约数最大公约数,简称为最大公因数,是指两个或者多个数中最大的能够同时整除这些数的正整数。
最大公约数有多种求解方法,下面简单介绍两种常用的方法:1. 穷举法:列举出两个数的所有因数,然后找出它们的公共因数中的最大值。
这种方法适用于较小的数。
例如,求解 24 和 36 的最大公约数,列举它们的因数如下:24 的因数为 1、2、3、4、6、8、12、24;36 的因数为 1、2、3、4、6、9、12、18、36。
我们发现它们的公共因数有 1、2、3、4、6 和 12,其中最大的是12,因此最大公约数是 12。
2. 辗转相除法:辗转相除法是一种快速求解最大公约数的方法。
它的基本思想是利用两个数的除法运算,将较大数除以较小数,然后再将余数除以除数,一直重复这个过程,直到余数为 0。
最后一个非零余数即为最大公约数。
数的整除知识点总结数的整除知识整理

数的整除知识点总结数的整除知识整理数的整除知识点总结如下:1. 除数和被除数:一个数被另一个数整除时,被除数称为整数,除数称为除数。
2. 整除关系:如果一个数a能被另一个数b整除,即a ÷ b = c,则称a能被b整除,或者说b能整除a,记作b|a。
3. 余数:当一个数a被另一个数b整除时,如果除完后还有剩余部分,即a ÷ b = c 余 r(0 ≤ r < |b|),则r称为数a除以b的余数。
4. 因数:对于一个数a,如果存在一个数b,使得b能整除a,即a = b × c,则称b 是a的因数,c是a的倍数。
a的因数包括1和a本身。
5.倍数:对于一个数a,如果存在一个数b,使得a能整除b,即b = a × c,则称b 是a的倍数,c是a的因数。
a的倍数包括0和任意正负整数。
6.公约数:对于两个数a和b,如果存在一个数c,既能整除a又能整除b,即c|a 且c|b,则称c是a和b的公约数。
7.最大公约数:对于两个数a和b的公约数中,最大的一个公约数称为a和b的最大公约数,记作gcd(a, b)。
8.最小公倍数:对于两个数a和b的公倍数中,最小的一个公倍数称为a和b的最小公倍数,记作lcm(a, b)。
9.质数:一个大于1的自然数,除了1和它本身外,无法被其他自然数整除的数称为质数。
质数只有两个因数,即1和该数本身。
10.合数:一个自然数,除了1和它本身外,还有其他因数的数称为合数。
合数有多个因数。
11.互质:两个数的最大公约数为1时,称这两个数互质。
12.互质数性质:互质数的乘积等于它们的最小公倍数。
13.素数分解:将一个合数分解成质数的乘积的过程,这个过程叫做素数分解。
这些是数的整除的基本知识点。
数的整除知识点

数的整除知识点数的整除问题,容丰富,思维技巧性强。
它是小学数学中的重要课题,也是小学数学竞赛命题的容之一。
数的整除1.整除——因数和倍数例如:15÷3=5,63÷7=9一般地,如a、b、c为整数,b≠0,且a÷b=c,即整数a除以整除b(b不等于0),除得的商c正好是整数而没有余数(或者说余数是0),我们就说,a能被b整除(或者说b能整除a)。
记作b|a.如果整数a能被整数b整除,a就叫做b的倍数,b就叫做a 的因数。
例如:在上面算式中,15是3的倍数,3是15的因数;63是7的倍数,7是63的因数。
2.数的整除性质性质1:如果a、b都能被c整除,那么它们的和与差也能被c 整除。
即:如果c|a,c|b,那么c|(a±b)。
例如:如果2|10,2|6,那么2|(10+6),并且2|(10—6)。
性质2:如果b与c的积能整除a,那么b与c都能整除a.即:如果bc|a,那么b|a,c|a。
性质3:如果b、c都能整除a,且b和c互质,那么b与c 的积能整除a。
即:如果b|a,c|a,且(b,c)=1,那么bc|a。
例如:如果2|28,7|28,且(2,7)=1,那么(2×7)|28。
性质4:如果c能整除b,b能整除a,那么c能整除a。
即:如果c|b,b|a,那么c|a。
例如:如果3|9,9|27,那么3|27。
3.数的整除特征①能被2整除的数的特征:个位数字是0、2、4、6、8的整数.“特征”包含两方面的意义:一方面,个位数字是偶数(包括0)的整数,必能被2整除;另一方面,能被2整除的数,其个位数字只能是偶数(包括0).下面“特征”含义相似。
②能被5整除的数的特征:个位是0或5。
③能被3(或9)整除的数的特征:各个数位数字之和能被3(或9)整除。
④能被4(或25)整除的数的特征:末两位数能被4(或25)整除。
例如:1864=1800+64,因为100是4与25的倍数,所以1800是4与25的倍数.又因为4|64,所以1864能被4整除.但因为2564,所以1864不能被25整除.⑤能被8(或125)整除的数的特征:末三位数能被8(或125)整除。
数的整除知识点整理

数的整除知识点整理
一、基本概念和符号:
1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号“|”,不能整除符号“ ”;因为符号“∵”,所以的符号“∴”;
二、整除判断方法:
1.能被2、5整除:末位上的数字能被2、5整除。
2.能被4、25整除:末两位的数字所组成的数能被4、25整除。
3.能被8、125整除:末三位的数字所组成的数能被8、125整除。
4.能被3、9整除:各个数位上数字的和能被3、9整除。
5.能被7整除:
①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6.能被11整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7.能被13整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:
1.如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2.如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3.如果a能被b整除,b又能被c整除,那么a也能被c整除。
4.如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数的整除单元练习
一. 学习重点和难点:
系统梳理本单元基本概念
二. 教学过程
1. 梳理本单元基本概念,并请独立写出每一个概念的意义。
2. 运用基本概念回答下面各题。
(1)填空。
①6和12,(12)能被(6)整除,6是12的(约数),12是6的(倍数)。
②12和15的公约数有(1,3),最大公约数是(3)。
③(2)既是偶数,又是质数。
(1)既不是质数,又不是合数。
④在7、21、111三个数中,(7)和(111)是互质。
⑤把435分解质因数。
(435=3×5×29)
⑥在1~100中,能同时被3,5整除的最小两位偶数是(30)。
能同时被2,3,5整除的最大数是(90)。
⑦一个非零自然数,除以4,除以7,除以8都得整数而没有余数,这个数最小是(56)。
⑧如果a=2×3×5,b=3×5×7
(a,b)=15 [a,b]=210
(2)判断,对的在()里画“√”,错的画“×”。
①一个自然数,不是奇数就是偶数。
(√)
②如果甲数除以乙数,商7。
那么乙数一定是甲数的约数。
(√)
③能同时被2,3整除的最小三位数是120。
(×)
④在1—20的自然数中,合数有12个。
(×)
(3)选择题。
把正确答案的序号填在()里。
①11乘以一个质数,积一定是(B)
A. 质数
B. 合数
C. 奇数
D. 偶数
②已知A=2×2×3×7,B=2×3×3×5×7,那么A和B的最大公约数是(C)
A. 7
B. 21
C. 42
(4)直接写出各组数的最大公约数。
(5,7)=1 (9,10)=1(9,18)=9
(4,6)=2(6,9)=3(14,28)=14
(5)直接写出各组数的最小公倍数。
[6,8]=24 [4,8,32]=32 [4,6,24]=24
[11,33]=33 [5,2,7]=70 [3,4,5]=60
(6)用短除法计算。
①求24和36的最大公约数和最小公倍数。
(24,36)=12 [24,36]=72
②求18,24和42的最小公倍数。
[18,24,42]=504
(7)用本单元所学知识,解释下面的算式。
21÷7=3
①21能被7整除②7能整除21 ③21是7的倍数④7是21的约数
(8)“五一”时学校搞联欢,用36朵红花和48朵黄花扎成花束。
如果每个花束的红花朵数相同,黄花的朵数也相同,那么最多可以扎成(12)束花。
(36,48)=2×2×3=12
【模拟试题】(答题时间:40分钟)
一、填空。
1. 在5、46、2、15、51、24、47、30、210中
(1)能被2整除的有();
(2)能被3整除的有();
(3)能被5整除的有();
(4)能同时被3、5整除的有();
(5)能同时被2、3、5整除的有()。
2. 28的约数有()。
3. 把70分解质因数(70=)。
4. 1.4÷0.7=2,我们就说1.4能被0.7()。
5. 写出一组一个是质数一个是合数的互质数()。
6. 最小的自然数除以最小的质数商是()。
7. 一个数的最小倍数是17,这个数的最大约数是()。
8. 一个数除以3、4、6都余2,这个数最小是()。
二、判断,对的在括号里画“√”,错的画“×”。
1. 所有自然数的公约数是1。
()
2. 自然数不是质数就是合数。
()
3. 6是倍数,2是约数。
()
4. 一个数的最小的倍数除以它的最大的约数商是1。
()
三、选择正确答案填在括号里。
1. 下面各式中,第二个数能整除第一个数的是()
A. 15÷4
B. 1.8÷3
C. 42÷7
D. 4÷0.2
2. 2是最小的()
A. 自然数
B. 质数
C. 合数
3. 把36分解质因数是()
A. 4×9=36
B. 36=2×2×3×3×1
C. 36=2×2×3×3
D. 36=2×2×9
四、把下面各数分解质因数。
1. 56
2. 102
3. 225
4. 105
五、直接写出下面各组数的最大公约数和最小公倍数。
1. (3,5)= (4,8)= (6,7)=
[3,5]= [4,8]= [6,7]=
2. (1,13)= (4,6)= (8,9)=
[1,13]= [4,6]= [8,9]=
六、直接写出下面各组数的最小公倍数。
1. [4,3,5]= [2,9,7]= [6,5,7]=
2. [18,9,3]= [5,30,10]= [14,56,28]=
七、求下面各组数的最大公约数和最小公倍数。
1. 72和24
2. 36和48
八、求下面各组数的最小公倍数。
1. 26、39和52
2. 18,20和15
九、学生参加跳绳比赛,进行分组。
按每组6人,每组8人或每组10人分组,都余3人,参加跳绳比赛的一共有多少人?
【试题答案】
一、填空。
1. 在5、46、2、15、51、24、47、30、210中
(1)能被2整除的有(46,2,24,30,210);
(2)能被3整除的有(15,51,24,30,210);
(3)能被5整除的有(15,30,210);
(4)能同时被3、5整除的有(15,30,210);
(5)能同时被2、3、5整除的有(30,210)。
2. 28的约数有(1,2,4,7,14,28)。
3. 把70分解质因数(70=2×5×7)。
4. 1.4÷0.7=2,我们就说1.4能被0.7(除尽)。
5. 写出一组一个是质数一个是合数的互质数(3,4)。
6. 最小的自然数除以最小的质数商是(0)。
7. 一个数的最小倍数是17,这个数的最大约数是(17)。
8. 一个数除以3、4、6都余2,这个数最小是(14)。
二、判断,对的在括号里画“√”,错的画“×”。
1. 所有自然数的公约数是1。
(√)
2. 自然数不是质数就是合数。
(×)
3. 6是倍数,2是约数。
(×)
4. 一个数的最小的倍数除以它的最大的约数商是1。
(√)
三、选择正确答案填在括号里。
1. 下面各式中,第二个数能整除第一个数的是(C)
A. 15÷4
B. 1.8÷3
C. 42÷7
D. 4÷0.2
2. 2是最小的(B)
A. 自然数
B. 质数
C. 合数
3. 把36分解质因数是(C)
A. 4×9=36
B. 36=2×2×3×3×1
C. 36=2×2×3×3
D. 36=2×2×9
四、把下面各数分解质因数。
1. 56=2×2×2×7
2. 102=2×3×17
3. 225=3×3×5×5
4. 105=3×5×7
五、直接写出下面各组数的最大公约数和最小公倍数。
1. (3,5)=1 (4,8)=4 (6,7)=1
[3,5]=15 [4,8]=8 [6,7]=42
2. (1,13)=1 (4,6)=2 (8,9)=1
[1,13]=13 [4,6]=12 [8,9]=72
六、直接写出下面各组数的最小公倍数。
1. [4,3,5]=60 [2,9,7]=126 [6,5,7]=210
2. [18,9,3]=18 [5,30,10]=30 [14,56,28]=56
七、求下面各组数的最大公约数和最小公倍数。
1. 72和24
(72,24)=24
[72,24]=72
2. 36和48
(36,48)=12
[36,48]=144
八、求下面各组数的最小公倍数。
1. 26、39和52
2. 18,20和15
[26,39,52]=156 [18,20,15]=180
九、学生参加跳绳比赛,进行分组。
按每组6人,每组8人或每组10人分组,都余3人,参加跳绳比赛的一共有多少人?
[6,8,10]=120
120+3=123(人)
答:参加跳绳比赛的一共有123人。
