计算物理作业 2
物理计算题精选

物理计算题精选(二)1、小明在户外检到一颗漂亮的小石头,回家后利用一把刻度尺,一条细线,一个厚底薄壁圆柱形的长杯子(杯壁厚度不计)和一桶水来测这颗小石头的密度。
做法是:将装有适量水的长杯子放入桶内的水中,使杯子竖直漂浮在水面上,如图甲所示,用刻度尺测得杯底到桶中水面的高度h1为6cm,杯底到杯内水面高度h2为4cm;然后把小石头没入杯内水中,杯子继续竖直漂浮在水面上,如图乙所示,用刻度尺测得杯底到桶中水面的h3为9cm,杯底到杯内水面高度h4为5.5cm,小明还测得杯子底面积S为20cm2。
已知水的密度是1.0×103kg/m3。
求:(1)甲图中,杯底受到桶中的压强;(2)小石头的体积;(3)小石头的密度。
2、在我市江北区的开发过程中,推土机发挥了重要的作用。
推土机发动机的额定功率为120kW,质量为2.0×104kg,履带与地面的总接触面积为2.5m2,(g取10N/kg)。
求:(1)推土机静止时对水平地面的压强;(2)若推土机在平直场地上以额定功率作业,在其以1.5m/s的速度匀速前进10m的过程中,它受到的阻力及阻力所做的功。
3、“龙门吊”是港口、货场中常见的起重设备,其滑轮组部分如图所示。
现用此装置将地面上一个重为3×104N,与地面的接触面积为1.2m2的重物匀速吊到3m的高处;重为1×104N。
请解答以下问题:(1)重物被吊起前对地面的压强是多大?(2)提升重物过程中滑轮组的机械效率是多少?(3)若再用此装置提升2×104N的重物时,它对机械效率将(填“变大”、或“或不变”)。
09陕西4、某班科技小组的同学设计了一种简易的电子拉力计,图甲是其原理图。
放在水平地面上的物体A通过硬质弹簧与拉环相连,弹簧上端和金属滑片P固定在一起(弹簧的电阻不计,P与R2接触良好且不计摩擦)。
已知物体A的质量这100kg,定值电阻R1=6Ω,R2是一根长为6cm的均匀电阻线(阻值与其长度成正比),其最大阻值为24Ω,电源电压为6V,电流表的量程为0~0.6A。
大学物理习题详解No.2波动方程

《大学物理》作业 No.2波动方程班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、判断题[ F ] 1. 解:电磁波就可以在真空中传播。
[ F ] 2. 解:波动是振动的传播,沿着波的传播方向,振动相位依次落后。
[ F ] 3. 解:质元的振动速度和波速是两个概念,质元的振动速度是质元振动的真实运动速度,而波速是相位的传播速度,其大小取决于介质的性质。
[ F ] 4. 解:振动曲线描述的是一个质点离开平衡位置的位移随时间的变化关系;波形曲线是某一时刻,波线上各个质点离开平衡位置的情况。
[ F ] 5. 解:对于波动的介质元而言,其动能和势能同相变化,它们时时刻刻都有相同的数值。
二、选择题:1. 一平面简谐波表达式为)2(sin 05.0x t y --=π (SI) ,则该波的频率v (Hz)、波速u (m ⋅s -1)及波线上各点振动的振幅A (m)依次为:(A) 2/1,2/1,05.0- (B) 2/1,1,05.0-(C) 2/1,2/1,05.0 (D) 2 ,2,05.0[ C ]解:平面简谐波表达式可改写为(SI))22cos(05.0)2(sin 05.0ππππ+-=--=x t x t y与标准形式的波动方程 ])(2[cos ϕπ+-=u xt v A y 比较,可得 )s (m 21,(Hz)21,(m)05.01-⋅===u v A 。
故选C2. 一平面简谐波的波动方程为)3cos(1.0πππ+-=x t y (SI),t = 0时的波形曲线如图所示。
则:(A) O 点的振幅为-0.1 m(B) 波长为3 m (C) a 、b 两点位相差 π21(D) 波速为9 m ⋅s -1解:由波动方程可知(Hz),23(m),1.0==νA (m)2=λ,)s (m 32231-⋅=⨯==νλua 、b 两点间相位差为:2422πλλπλπϕ===∆ab故选C3. 一平面简谐波沿x 轴正向传播,t = T/4时的波形曲线如图所示。
《大学物理AII》作业 No.02 波动方程 参考答案

2、一平面简谐波,波长为 12m,沿 Ox 负向传播。如图所示为原点处质点的振 动曲线,求: (1)原点处质点的振动方程, (2)此波的波函数。
解:由题意得:振幅 A=0.4m,初始位置 y0 0.2 相为
2 , 其对应旋转矢量如上图所示。 从图还可以看出 5s 后, 矢量转动的角度: 3 5 2 t 5 12 s ; ,则 , T 3 2 6 6 2 ) m) 所以其振动方程为 y 0.4 cos( t ( 6 3 2 12 s ,波速 u 1( m / s ) ,又因传播方向为负, (2)由题意 12m , T T 2 ( ] m) 所以波函数为: y 0.4 cos[ (t x) 6 3
答:振动是波动的基础,振动在空间的传播就形成波动。平面简谐波动方程是关 于时间和空间的函数, 而简谐振动方程只是关于时间函数;当平面简谐波动方程 中的空间变量 x 确定时,波动方程成为表述该点运动的振动方程。振动曲线是以 位移为纵坐标, 时间为横坐标做的曲线,描述质点在不同时刻离开平衡位置的位 移;波形曲线是位移为纵坐标,介质元空间位置为横坐标做的曲线,用来描述某 一时刻,波线上各个质元离开平衡位置的距离。 2、平面简谐行波波函数的表达式与哪些因素有关?总结求波函数的基本步骤。 答:平面简谐行波波函数与波的特征量:振幅、周期、频率、波速及其传播方向 有关, 此外与坐标原点、 计时起点的选择有关。 求波函数的基本步骤可以概况为: (1)选择一个参考点,根据已知条件确定出该参考点的振动方程; (2)选定坐标原点,选定正方向,建立坐标;
《大学物理 AII》作业
No.02 波动方程
班级 ________ 学号 ________ 姓名 _________ 成绩 _______
物理作业 第二章 典型习题答案与解析

【第二章典型习题】1.教室门框的高度最接近于()A 1米B 2米C 5米D 8米2.小明同学用刻度尺测出一个物体的长度为,下面物体中最接近这个数值的是( )A、物理课本的厚度B、一根粉笔的长度C、黑板的长度D、饮水杯的高度3.章天同学用一把刻度尺4次测量物理课本的宽度,下列记录数据中错误的是()A.B.C.D.4.以相同速度同方向飞行的加油机和受油机,选地面为参照物,它们是的;选其中的任何一个为参照物,另一个是的。
5.小船在河里顺流而下,船上坐着一个人,河岸上有树,那么相对于船来说,人是_____的,树是_______的(填“运动”或“静止”)6.诗人曾写下这样的诗句:“人在桥上走,桥流水不流”。
其中“桥流水不流”,诗人选择的参照物是( )A、桥B、河岸C、水D、岸上的树7.小明骑自行车在沱江河堤上沿河岸向下游行驶,感觉无风,但堤上柳树的枝叶却在随风飘动,此时的风向是( )A、向下游B、向上游C、向河对岸D、从对岸吹过来8.坐在逆水驶向上游的船中的乘客,我们说他静止是以下列哪个物体为参照物的?( )A.河岸上的树B.船舱C.迎面驶来的船D.河水9.临沂是一座历史文化名城,今天的临沂更是美丽壮观。
位于临沂市中心处的某大酒店建有观光电梯,乘客在竖直上下的过程中便可欣赏到临沂城的美丽景色。
在这一过程中,下列说法正确的是 ( )A.以电梯内的某一乘客为参照物,其他乘客是运动的B.以电梯为参照物,所有乘客都是运动的C.以地面上的树为参照物,乘客是运动的D.以路面上行驶的汽车为参照物,乘客是静止的10.谁也没有我跑得快!我是()A.高速奔驰的磁悬浮列车B.高空翱翔的超音速战机C.让万物生长的阳光D.把“神六"送上天的“长征”运载火箭11.即将开工建设的京沪高速列车运行速度可达350㎞/h,这个速度相当于m/s,两地之间的铁路线长为1400㎞,那么列车从北京到上海至少需要h.12.飞机在10min内飞行了180km,它的速度是_________km/h,合_____m/s。
吉林大学大学物理作业答案综合练习题(下)(二)
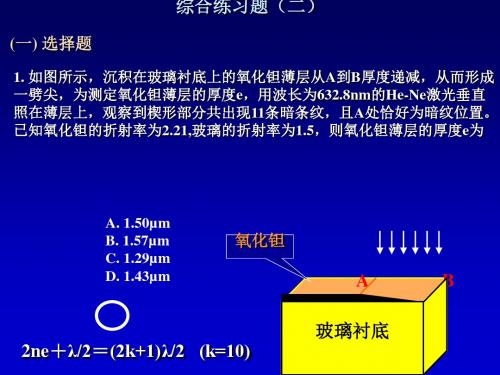
(一) 选择题
1. 如图所示,沉积在玻璃衬底上的氧化钽薄层从A到B厚度递减,从而形成 一劈尖,为测定氧化钽薄层的厚度e,用波长为632.8nm的He-Ne激光垂直 照在薄层上,观察到楔形部分共出现11条暗条纹,且A处恰好为暗纹位置。 已知氧化钽的折射率为2.21,玻璃的折射率为1.5,则氧化钽薄层的厚度e为
2 a b 10 2 4 0 0 n m s i n 3 0
1
4.一平面透射光栅,当用白光垂直照射时,能在30°衍射方向上观察到600nm的第 二级干涉主极大,并能在该处分辨△λ=0.05nm的两条光谱线,但在此30°方向上却 测不到400nm的第三级主极大,计算此光栅的缝宽a和缝距b以及总缝数N 。
6.氢原子中核外电子所处状态的角量子数是l=2,其绕核运动的角动量的 大小 ;该角动量的空间取向可能有 5 种。 一级明
6
a sin 3 ;
a sin k; 2
k1 .5
9.一电磁波在空气中通过某点时,该点某一时刻的电场强度 为E,则同时刻的磁场强度H= ,能流密度S= 。
光栅对第k级主极大的分辨本领为
对于 =600nm的第二级主极大有
0 . 0 5 n m
所以,光栅总缝数
R kN
6 0 0 N 6 0 0 0 k 2 0 . 0 5
5. 在惯性系K中观测到相距 的两地点相隔 8 发生两事 x 9 1 0m 件,而在相对于K系沿x轴正向以匀速度运动的 系中发现此两事件 恰好发生在同一地点,试求在 系中此两事件的时间间隔。 t 5s
m向下拉x时,
kx a J m 2 R k 2 J m 2 R
T2 k ( x x 0 ) mg T 1 ma T R T R J 2 1 a R
马文淦_计算物理_习题

3、投针法计算圆周率数值,画出流程图,编写程序 方法 1 投针 10^1 次,pi 的蒙卡模拟值为 2.500000000000000 投针 10^2 次,pi 的蒙卡模拟值为 2.777777777777778 投针 10^3 次,pi 的蒙卡模拟值为 2.985074626865672 投针 10^4 次,pi 的蒙卡模拟值为 3.133813851457223 投针 10^5 次,pi 的蒙卡模拟值为 3.142875102143441 投针 10^6 次,pi 的蒙卡模拟值为 3.143418467583497 投针 10^7 次,pi 的蒙卡模拟值为 3.142216400044368 //本程序在 Visual C++ 6.0 下编译通过 #include<stdio.h> #include<math.h> #include<windows.h> void main() { int xi10, xi20; double delta1,delta2; double I; double pi; int n; double N; FILE *fp; fp = fopen("3.txt","w"); for (n = 1; n <= 7; n++) { I = 0; srand(time(0)); for (N = pow(10, n); N > 0 ; N--) { xi10 = rand(); xi20 = rand(); delta1 = (double)(xi10 % 32767) / 32767.0 / 2.0; delta2 = (double)(xi20 % 32767) / 32767.0 / 2.0 * 3.1415926; if (delta1 < (sin(delta2) / 2.0)) { I = I + 1; }
大学物理作业题2

M dm dx l
x
dx
f
M dt L L f 2 1 0 L 0
2 m ( v1 v 2 ) t Mg
1 Mglt ml (v1 v 2 ) 2
17、空心圆环可绕竖直轴AC自由转动,如图所示,其转动惯量 为I0,环半径为R,初始角速度为0.质量为m的小球,原来静 置于A点,由于微小的干扰,小球向下滑动.设圆环内壁是光滑 的,问小球滑到B点与C点时,小球相对于环的速率各为多少?
L y v2 L x 1 2 c
v2 0.5 1 2 0.866 c
把 = 45°及Lx ',Ly '代入,得
v 0.816 c
(2)在S系中测得米尺长度为
L
Ly sin 45
0.707 m
3、在惯性系S中,有两事件发生于同一地点,且第二事件比第 一事件晚发生t =2s;而在另一惯性系S'中,观测第二事件比 第一事件晚发生t'=3s.那么在S'系中发生两事件的地点之 间的距离是多少? 解: 令S'系与S系的相对速度为v,有
2
1 1 ( v / c )2
1)
代入题干中的具体数值,解得 平均寿命为
v = 0.91c
t
t0
1 (v / c)
2
5.31 10 8
9、一正负电子对撞机可以把电子加速到动能=2.8×109eV.这 种电子速率比光速差多少? 这样的一个电子动量是多大?(与电子 静止质量相应的能量为=0.511×106eV ) 解:
解 : ( 1)
t
t 0 v2 1 2 c
t 0 2 10 6 s
d vt 9470 m
因d>6000m,故该介子能到达地球
高一物理假期作业2 (2)

2022-2023学年期中物理试卷学校:___________姓名:___________班级:___________考号:___________1. 建立物理模型时,需要突出问题的主要因素,忽略次要因素,以下说法正确的是( )A. 研究跳水运动员全红婵的翻转动作时,可将其看作质点B. “香蕉球”是足球在空中旋转、整体运动径迹为类似香蕉型弧线的一种运动,在研究如何才能踢出“香蕉球”时,可以把足球看作质点C. 用GPS定位系统确定正在南极冰盖考察的某科考队员的位置时,该队员可看成质点D. 列车在平直轨道上行驶时,研究它的传动机构及车轮的运动,可以将列车整体视为一个质点2. 如图所示,底端置于粗糙水平地面上的杆,其顶端被一根细线用手拉住,杆处于静止状态,细线水平。
下列说法正确的是( )A. 杆对细线的弹力方向为水平向右B. 细线对杆的弹力方向垂直杆向左C. 杆受到地面的弹力是由杆的形变产生的D. 地面受到杆的弹力沿杆向左下方3. 如图所示,物体的运动分三段,第0∼2s为第Ⅰ段,第2∼4s为第Ⅱ段,第4∼5s为第Ⅲ段,则下述说法中正确的是( )A. 第Ⅰ段与第Ⅲ段的平均速度相等B. 第Ⅰ段与第Ⅲ段的加速度与速度的方向都相同C. 第1s与第5s的速度方向相反D. 第1s的加速度大于第5s的加速度4. 某同学骑自行车由静止开始沿直线向前运动,他在第1s内、第2s内、第3s内、第4s内通过的位移分别为1m、2 m、3m、4m。
下列关于此4秒内的运动性质的描述正确的是( ) A. 可能做匀速直线运动 B. 一定做匀加速直线运动C. 可能做匀加速直线运动D. 一定做加速度变化的变速直线运动5. 甲、乙两汽车在同一条平直公路上同向运动,其速度-时间图像分别为如图所示的甲、乙两条图线。
下列对甲、乙运动的描述正确的是( )A. 0∼t 0时间内甲的加速度逐渐增大B. 0∼t 0时间内乙的加速度逐渐减小C. 0∼t 0时间内甲的加速度始终小于乙的加速度D. t 0时刻两车相遇6. 如图甲所示,火箭发射时,速度能在10s 内由0增加到100m/s ;如图乙所示,汽车以72km/ℎ的速度行驶,急刹车时能在2.5s 内停下来,下列说法中正确的是( )A. 10s 内,火箭的速度改变量为10m/sB. 2.5s 内,汽车的速度改变量为20m/sC. 火箭的速度变化比汽车的速度变化快D. 火箭的加速度比汽车的加速度小7. 图中各物体均处于静止状态.图中画出了小球A 所受弹力的情况,其中正确的是( ) A. B. C. D.8. 质点做直线运动的位移x 与时间t 的关系为x =6t +3t 2(各物理量均采用国际单位制单位),下列不正确的是( )A. 初速度为6m/sB. 3s 末的速度为24m/sC. 前2s 内的平均速度是12m/sD. 任意1s 内的速度增量都是3m/s9. 以下关于物理学研究方法的叙述中不正确的是( )A. 伽利略在研究自由落体运动时采用了抽象思维、数学推导和科学实验相结合的方法B. 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法是假设法C. 根据速度定义式v =Δx Δt ,当Δt →0时,ΔxΔt 就可以表示物体在t 时刻的瞬时速度,该定义运用了极限思维法D. 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,再把各小段位移相加,这里运用了理想模型法10. 如图所示为在研究汽车速度变化时所画出的示意图,若汽车原来的速度是v1,经过一小段时间Δt之后速度变为v2,在图中以原来的速度v的箭头端为起点,以后来的速度v的箭头端为终点,作出一个新的箭头,用它表示速度的变化量Δv,则以下说法中正确的是( )A. 图甲中的汽车正在做加速运动,图乙中的汽车正在做减速运动B. 用速度的变化量Δv和发生这一变化所用时间Δt的比值可以表示速度的变化快慢,即加速度C. 速度较小的汽车其加速度也较小,速度较大的汽车,其加速度也较大D. 汽车加速时,其加速度方向与速度方向相同,汽车减速时,其加速度方向与速度方向相反11. 做自由落体运动的甲乙两物体所受的重力之比为2:1,下落高度之比为1:2,则( )A. 下落过程中的加速度之比是2:1B. 落地速度之比是1:1C. 落地速度之比是1:√2D. 下落时间之比是1:√212. 利用图像法研究物理量之间的关系是常用的一种数学物理方法,如图所示为四个物体做直线运动时各物理量之间的关系图像(x、v、a、t分别表示物体的位移、速度、加速度和时间),则下列说法中正确的是( )A. 由图可求出甲物体的加速度大小为1m/s2B. 由图可求出乙物体的加速度大小为5m/s2C. 由图可求出丙物体的加速度大小为2m/s2D. 由图可求出丁物体在前2s内的速度变化量大小为3m/s13. 根据《机动车驾驶证申领和使用规定》,司机闯红灯要扣6分,并处罚金200元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算物理作业第一题:a.用最小二乘法拟合下面的一组数据0 1 2 3 4 5 6 7 7.82 7.93 7.98 7.59 7.92 7.91 7.80 7.71 寻求经验公式,并拟合以上数据。
答:matlab程序如下:n=7; % n表示拟合的精度,在此取7x=0:1:7;y=[7.82 7.93 7.98 7.59 7.92 7.91 7.80 7.71];a1=polyfit(x,y,n);x1=0:0.1:7;y1=polyval(a1,x1);plot(x,y,'*',x1,y1,'-r'); %作出x-y的散点图和x1-y1的拟合曲线程序运行之后:a1 -0.0024 0.0610 -0.6073 3.0190 -7.7576 9.4799 -4.0827 7.8200所以该组数据的经验公式就是:用matlab拟合的曲线蓝色的散点图是x-y图,红色的多项式曲线就是拟合后的曲线。
当n取6或者更小时,拟合效果并没有上面的好,如下n=6时的拟合曲线所示:b.在某次实验中需要观察水分的渗透速度,测得时间t与水重量w的数据t 1 2 4 8 16 32 64w 4.22 4.02 3.85 4.59 3.44 3.02 2.59 已知t与w关系,试用最小二乘法确定A、S。
答:先对式子两边取对数,化为一阶,然后使用上题的一阶拟合的程序,取n=1 t=[1 2 4 8 16 32 64];w=[4.22 4.02 3.85 4.59 3.44 3.02 2.59];x=log(t);y=log(w);a1=polyfit(x,y,1);A=exp(a1(2));S=a1(1);x1=1:0.1:64;y1=A*x1.^S;plot(t,w,'*',x1,y1,'-r');程序运行结果:a1 -0.1107 1.5153因此,A=S=-0.1107拟合曲线:第二题:复化梯形计算定积分:要求:递交算法说明过程,源程序及实际结果。
答:复化梯形的迭代公式为:在这里,a=0,b=π,。
算法如下:x=zeros(1,100);y=zeros(1,100);%x、y是两个一维零矩阵,用来存储不同的n和与之对应的梯形公式的定积分% t=0;j=1;for n=1:1:100;for i=1:n-1;t=t+2*sin(i*pi/n); %每个n对应的的值赋值给t%end;t1=(pi/(2*n))*t;y(1,j)=t1;x(1,j)=n; %每个n(存储在x矩阵)对应的定积分值存储在y矩阵% j=j+1;t=0; %n值递增,t归零,j递增来将不同n对应的值y矩阵的不同位置% end;plot(x,y); %作图x-y%图梯形算法在计算精度n不同时的取值可以从matlab中读出y矩阵中的不同元素,比如n=10时,y=1.9835;n=10时,y=1.9959。
n=2~100,1.57079632679490 1.81379936423422 1.89611889793704 1.933765598092811.95409723331371 1.96631667876589 1.974231601945551.97965081121648 1.98352353750945 1.986386986581661.98856377658432 1.99025717534777 1.991600427355071.99268383153077 1.99357034377234 1.994304944309461.99492046358345 1.99544131832019 1.995885972708721.99626859873946 1.99660022026927 1.996889516466771.99714339580395 1.99736741254563 1.997566073264041.99774306535854 1.99790142946568 1.998043690970561.99817196134365 1.99828801696417 1.998393360970141.99848927218760 1.99857684413418 1.998657016333451.99873059962485 1.99879829674997 1.998860719196551.99891840105786 1.99897181049707 1.999021359278081.99906741072689 1.99911028641187 1.999150271773441.99918762088765 1.99922256051286 1.999255293540041.99928600194513 1.99931484932406 1.999341983076261.99936753629151 1.99939162938520 1.999414371519651.99943586184290 1.99945619057124 1.999475439937671.99949368502489 1.99951099449860 1.999527431254561.99954305299081 1.99955791271468 1.999572059193141.99958553735338 1.99959838864004 1.999610651334151.99962236083861 1.99963354993397 1.999644249008121.99965448626288 1.99966428789999 1.999673678288961.99968268011871 1.99969131453476 1.999699601263501.99970755872496 1.99971520413531 1.999722553600021.99972962219876 1.99973642406284 1.999742972445841.99974927978828 1.99975535777672 1.999761217397971.99976686898870 1.99977232228115 1.999777586445001.99978267012597 1.99978758148133 1.999792328212631.99979691759594 1.99980135650976 1.999805651460761.99980980860766 1.99981383378336 1.999817732515361.99982151004476 1.99982517134390 1.999828721132731.99983216389399 1.99983550388744可以看到当n取较小值时,梯形公式计算定积分的值逐渐接近精确值2而且是迅速的上升;在n比较大时,值接近平缓,也无限接近理论值2。
第三题:使用Romberg算法计算定积分要求算法说明,源程序,最后结果,并与理论值比较。
答:Romberg迭代公式为:在Matlab中设计实现积分功能的M函数,然后在matlab对话框中输入要计算的函数,给出区间和精度即可。
新建function文件,如下:function [y] = romberg( f,n,a,b )z=zeros(n,n);h=b-a;z(1,1)=(h/2)*(f(a)+f(b));f1=0;for i=2:nfor k=1:2^(i-2)f1=f1+f(a+(k-0.5)*h);endh=h/2;z(i,1)=0.5*z(i-1,1)+0.5*h*f1;for j=2:iz(i,j)=z(i,j-1)+(z(i,j-1)-z(i-1,j-1))/(4^(j-1)-1);endendy=z(n,n);zend在matlab的命令窗口输入以下程序:>> clear>> f=inline('sin(x)');>> I=romberg(f,10,0,pi)z =Columns 1 through 70.0000 0 0 0 0 0 00.7854 1.0472 0 0 0 0 01.3408 1.5259 1.5578 0 0 0 01.6575 1.7631 1.7789 1.7824 0 0 01.8255 1.8815 1.8894 1.8912 1.8916 0 01.9120 1.9408 1.9447 1.9456 1.9458 1.9459 01.9558 1.9704 1.9724 1.9728 1.9729 1.9729 1.97291.9778 1.9852 1.9862 1.9864 1.9865 1.9865 1.98651.9889 1.9926 1.9931 1.9932 1.9932 1.9932 1.99321.9945 1.9963 1.9965 1.9966 1.9966 1.9966 1.9966 Columns 8 through 100 0 00 0 00 0 00 0 0 0 0 0 0 0 0 0 0 0 1.9865 0 0 1.9932 1.9932 0 1.9966 1.9966 1.9966 I =1.9966 >>第四题:用改进的欧拉公式,求解常微分方程初值问题答:()_1_111,(,)(,)2n n n n n n n n n n y y hf x y h y y f x y f x y ++++=+⎛⎫=++ ⎪⎝⎭程序:x=[0.1 0.12 0.14 0.16 0.18 0.2 0.22 0.24 0.26 0.28 0.3 0.32 0.34 0.36 0.38 0.4];%取h=0.02,代入梯形公式%f=zeros(1,16);%f为1*16维矩阵,用来存储y(x)的值%ya=1;f(1,1)=ya;for i=2:16;yb=ya+0.02*ya^2;ya=ya+0.01*(ya^2+yb^2);f(1,i)= ya;endplot(x,f,'r+'); %作出x-f的散点图,用红色+点表示% hold on;z=dsolve('Dy=y^2','y(0.1)=1','x'); %解出y=f(x)的方程% ezplot(z,[0.1,0.4]); %作出z曲线% ylabel('y');legend('\it caculate','\it theory');hold off; %将散点图和曲线图组合到一个图表输出%由图可知计算值能很好的逼近理论值第五题:用四阶龙格-库塔法求解微分方程答:)3,(4)25.0,5.0(3)15.0,5.0(2),(1)432221(611k y h t hf k k y h t hf k k y h t hf k y t hf k k k k k y y i i i i i i i i i i ++=++=++==++++=+程序:x=[2 2.05 2.1 2.15 2.20 2.25 2.3 2.35 2.4 2.45 2.5 2.55 2.6]; %步长=0.05%f=zeros(1,13);%1*13矩阵,用以存储y 值% f(1,1)=1; for i=2:13;k1=x(1,i-1)/f(1,i-1);k2=(x(1,i-1)+0.025)/(f(1,i-1)+0.025*k1); k3=(x(1,i-1)+0.025)/(f(1,i-1)+0.025*k2); k4=(x(1,i-1)+0.05)/(f(1,i-1)+0.05*k3); f(1,i)=f(1,i-1)+(0.05/6)*(k1+2*k2+2*k3+k4); endplot(x,f,'r+'); % 作出x-f 的散点图,用红色+点表示% hold on ;z=dsolve('Dy=x/y','y(2)=1','x'); %解出y=f (x )的方程% ezplot(z,[2,3]); %作出z 曲线% ylabel('f');legend('\it caculate','\it theory');hold off ; %将散点图和曲线图组合到一个图表输出%第六题:计算3重积分:120=⎰⎰⎰I xzdxdydz积分区间:平面x=0、平面y=0、平面z=0、平面x+y+z=1所围区域 要求:要有源程序及结果及不同投点数的比较 答:设D=(x,y,z)是在V 中均匀分布的随机变量,则(,,)((,,)|(,,))*V f x y z dV E f x y z x y z V V =∈⎰⎰⎰其中,E(f)为函数f 在指定区间内的数学期望。
