工程力学静力学某市科大东北大学版版四.pdf
工程力学材料力学第四版(北京科技大学与东北大学)习题答案

(北京科技大学与东 北大学)
第 一意轴向拉伸和压缩
, 1-1 lfJ截 Illi法 求 下列各轩指 定的 lii fl'J 内 )J
2
f
2
F 2k N
I
(a 1
2
f
(bl
3P
11
(d 1
2kN P
2
2
(e 1
题 1 ) [fI
解
P
({)
P rlp|p
iE
『
e-
I Iz Il
F
5,
为 20 俐 , 许用应力 I δ]=50 Mpa . 试
根据吊钩螺纹部分的强主确定吊钩的阵 111 起重盐 1 解 P= 119kN
P
3m
B
P
E
题1-1 8 固
lIlí l - l ~ 罔
1 - 1 9 如入所示结构的 ABH 为钢轩,其帧故而积 -4.:::6 cm2 • 咛用阻力 ( σ 1=140 MPa ; BC
<.l
(bl
题 1-3 归
且ø 1 -4 因
1-4 : 桩杆起lli:机如 l 国所示,起lli:忏 AB 为钢管 , J[外径 。=2ûrnm , 内径 d= 1 8mrn;制绳
CB 的棋极而而积为 01cnEZe 己知l起重证
P=2脱lO N ,
试计fI起重机轩;归 钢丝绳的应 )J.
解 受力分析得
解
E = GPa . v = 0.3 17
1- 10: i主杆端部与的如1I相迹 , 其构应如罔 ,谊作用在连杆的轴向 jJ P=l28KN , 蝉挟处的内
径 d = 3.7cm , 螺栓材料的冉川剧
工程力学材料力学第四版(北京科技大学和东北大学)习题答案解析

工程力学材料力学(科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力 解:(a):N 1=0,N 2=N 3=P (b):N 1=N 2=2kN(c):N 1=P,N 2=2P,N 3= -P (d):N 1=-2P,N 2=P(e):N 1= -50N,N 2= -90N (f):N 1=0.896P,N 2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a 所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b 所示;拉杆上端螺纹的内径d=175mm 。
以知作用于拉杆上的静拉力P=850kN ,试计算大钟拉杆的最大静应力。
解:σ1= 2118504P kN S d π==35.3Mpaσ2=2228504P kNS d π==30.4MPa∴σmax =35.3Mpa1-3:试计算图a 所示钢水包吊杆的最大应力。
以知钢水包与其所盛钢水共重90kN ,吊杆的尺寸如图b 所示。
解:下端螺孔截面:σ1=19020.065*0.045P S ==15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa上端双螺孔截面:σ3=3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB 为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm 2。
已知起重量P=2000N ,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F 1*sin15=F 2*sin45 F 1*cos15=P+F 2*sin45∴σAB = 11F S =-47.7MPa σBC =22F S =103.5 MPa1-5:图a 所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c 所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力. 解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S=38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形. (2)AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm (2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:AC AC ACLNL EA EA σε===1.59*104,CB CB CBLNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧 制压力.压头材料的弹性模量E=200Gpa. 解:1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
工程力学(1997修订版)北京科技大学 东北大学-静力学习题解答供参习

第一章 静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑故: 161.2R F N==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有故:3R F KN== 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0.577AB F W =(拉力) 1.155AC F W =(压力) (b ) 由平衡方程有:1.064AB F W =(拉力)0.364AC F W =(压力) (c ) 由平衡方程有:0.5AB F W = (拉力)0.866AC F W =(压力)(d ) 由平衡方程有:0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解:(a )受力分析如图所示:由x =∑cos 450RA F P -=由Y =∑sin 450RA RB F F P -=(b)解:受力分析如图所示:由 联立上二式,得:2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN = (压力) 5RB F KN =(与X 轴正向夹150度) 2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑ cos 0AC r F F α-=由0Y =∑ sin 0AC N F F W α+-=2-7解:受力分析如图所示,取左半部分为研究对象由x =∑ cos45cos450RA CB P F F --=联立后,解得: 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑ cos60cos300AC AB F F W ⋅--=联立上二式,解得: 7.32AB F KN =-(受压)27.3AC F KN =(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程 (1)取D 点,列平衡方程由x =∑ sin cos 0DB T W αα-=(2)取B 点列平衡方程:由0Y =∑ sin cos 0BD T T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑ cos sin sin 0BC DC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BC BC F F '= 解得: 取E 为研究对象:由0Y =∑ cos 0NH CE F F α'-=CECE F F '= 故有:2-11解:取A 点平衡:联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:由对称性及 AD AD F F '=2-12解:整体受力交于O 点,列O 点平衡由x =∑ cos cos300RA DC F F P α+-=联立上二式得: 2.92RA F KN =1.33DC F KN =(压力) 列C 点平衡联立上二式得: 1.67AC F KN =(拉力)1.0BC F KN =-(压力) 2-13解:(1)取DEH 部分,对H 点列平衡联立方程后解得: RD F = (2)取ABCE 部分,对C 点列平衡且 RE RE F F '=联立上面各式得: RA F =(3)取BCE 部分。
工程力学材料力学第四版(北京科技大学与东北大学)习题答案
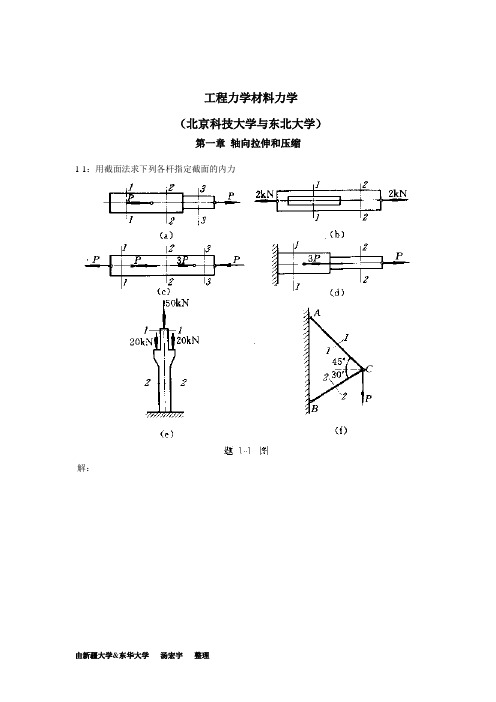
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N 1=0,N 2=N 3=P(b):N 1=N 2=2kN(c):N 1=P,N 2=2P,N 3= -P(d):N 1=-2P,N 2=P(e):N 1= -50N,N 2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa 上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104, CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
工程力学--静力学(北京科大、东北大学版)第4版 第五章习题答案

第五章习题5-1 重为W=100N,与水平面间的摩擦因数f=0.3,(a)问当水平力P=10N时,物体受多大的摩擦力,(b)当P=30N时,物体受多大的摩擦力?(c)当P=50N时,物体受多大的摩擦力?5-2 判断下列图中两物体能否平衡?并问这两个物体所受的摩擦力的大小和方向。
已知:(a)物体重W=1000N,拉力P=200N,f=0.3;(b)物体重W=200N,拉力P=500N,f=0.3。
5-3 重为W的物体放在倾角为α的斜面上,物体与斜面间的摩擦角为ρ,且α>ρ。
如在物体上作用一力Q,此力与斜面平行。
试求能使物体保持平衡的力Qde 最大值和最小值。
5-4 在轴上作用一力偶,其力偶矩为m=-1000N.m,有一半径为r=25cm的制动轮装在轴上,制动轮与制动块间的摩擦因数f=0.25。
试问制动时,制动块对制动轮的压力N至少应为多大?5-5 两物块A和B重叠放在粗糙的水平面上,在上面的物块A的顶上作用一斜向的力P。
已知:A重1000N,B重2000N,A与B之间的摩擦因数f1=0.5,B与地面之间的摩擦因数f2=0.2。
问当P=600N时,是物块A相对物块B运动呢?还是A、B物块一起相对地面C运动?5-6 一夹板锤重500N,靠两滚轮与锤杆间的摩擦力提起。
已知摩擦因数f=0.4,试问当锤匀速上升时,每边应加正应力(或法向反力)为若干?5-7 尖劈顶重装置如图所示,重块与尖劈间的摩擦因数f(其他有滚珠处表示光滑)。
求:(1)顶住重物所需Q之值(P、α已知);(2)使重物不向上滑动所需Q。
注:在地质上按板块理论,太平洋板块向亚洲大陆斜插下去,在计算太平洋板块所需的力时,可取图示模型。
解:取整体∑Fy =0 FNA-P=0∴FNA=P当F<Q1时锲块A向右运动,图(b)力三角形如图(d)当F>Q2时锲块A向左运动,图(c)力三角形如图(e)5-8 图示为轧机的两个压辊,其直径均为d=50cm,两棍间的间隙a=0.5cm,两轧辊转动方向相反,如图上箭头所示。
东北大学版工程力学第四版静力学第四章

合力 合力偶
§4-3 平面一般力系向作用面内一点简化 主矢与主矩
二、主矢与主矩的定义
力线平移定理将平面一般力系分解为两个力系: 平面汇交力系,平面力偶系。
主矢 FR Fi
主矩 M O M O ( Fi )
主矢与简化中心无关,而主矩一般与简化中心有关。
§4-3 平面一般力系向作用面内一点简化 主矢与主矩
对同一点的矩代数和。
F2 y
x2
MO1 x1F1y y1F1x y1 F1 y1F1
y2
y1
F2 x
MO2 x2 F2 y y2 F2 x
M
o
( Fi ) ( xi Fiy yi Fix )
§4-3 平面一般力系向作用面内一点简化 主矢与主矩
主矢、主矩的计算 FRx Fix Fix Fx FRy Fiy Fiy Fy
M O M O ( Fi )
§4-5 平面一般力系的平衡条件与平衡方程
一、平面一般力系的平衡条件 因为
FR ( Fx ) 2 ( Fy ) 2
M O M O ( Fi )
Fx 0 Fy 0 M o 0
平面任意力系的平衡方程
X A T cos 0 l T sin l P Qa 0 A 2 l Q l a P YA l 0 2 l T sin l P Qa 0 y 2 l X A YA Q l a P YA l 0 2 A l X A tan l P Q a 0 2
§4-4 简化结果的分析 合力矩定理
工程力学--材料力学(北京科大、东北大学版)第4版习题问题详解
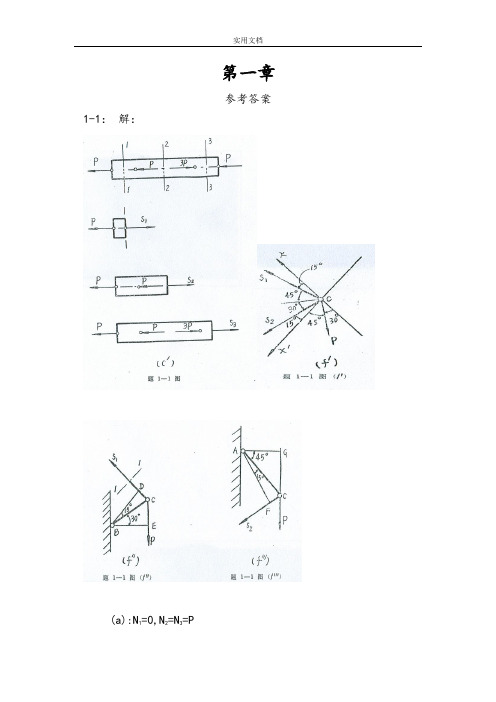
第一章参考答案1-1:解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa ∴σmax=35.3Mpa1-3:解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2PS =8.72MPa上端双螺孔截面:σ3= 3PS =9.15Mpa∴σmax =15.4Mpa1-4:解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2FS =38.1MPa1-6:解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ==== AC AC AC L NL EA EA σε===1.59*104,CB CB CB L NL EA EA σε===6.36*104 1-8:解:Nll EAl l ε∆=∆= ∴NEA ε=62.54*10N EA N ε∴==1-9:解:208,0.317E GPa ν==1-10:解:[][]max 59.5MPa σσ=<1-11:解:(1)当45oα=,[]11.2σσ=>强度不够 (2)当60oα=,[]9.17σσ=< 强度够 1-12:解:[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13:解:[]max 200213MPa MPa σ=<1-14:解:1.78, 1.26d cm d cm ==拉杆链环1-15 解:BC F ==70.7 kN70.70.505140F S FS σσ=∴=== 查表得: 45*45*31-16解:(1)[]2401601.5s s n σσ===MPa[][]24P SP dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPa S d σπ===≤⎛⎫⎪⎝⎭1-17 解:(1)2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭ 78.4AC F MPa S σ== 300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F S F S Nσσ===='61544014.521542390F n F ===≈1-18 解:P=119kN1-19 解:::3:4:535()44AB BC AB BC S P S S P S P =∴==拉,[][][]112841123484AB AB S A kN S P kN P kN σ=====同理所以最大载荷 84kN1-20 解: P=33.3 kN1-21 解:71,,12123A B C P F F P F P ===1-22 解:10MAX MPa σ=-1-23 解:A B X R R R =∴==∑t r l l ∆=∆ t AB l l t α∆=21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1 一螺栓连接如图所示,已知P=200 kN , =2 cm ,螺栓材料的许用切应力[τ]=80Mpa ,试求螺栓的直径。
工程力学材料力学(北京科大、东北大学版)第4版习题答案第二到九节

第二章习题2-1 一螺栓连接如图所示,已知P=200 kN, =2 cm,螺栓材料的许用切应力[τ]=80Mpa,试求螺栓的直径。
2-2 销钉式安全离合器如图所示,允许传递的外力偶距 m=10kN·cm,销钉材料的剪切强度极限=360 Mpa,轴的直径D=30mm,为保证m>30000 N·cm 时销钉被剪切断,求销钉的直径 d。
2-3 冲床的最大冲力为400 kN,冲头材料的许用应力[σ]=440 Mpa,被冲剪钢板的剪切强度极限=360 Mpa。
求在最大冲力作用下所能冲剪圆孔的最小直径D和钢板的最大厚度。
2-4 已知图示铆接钢板的厚度=10 mm,铆钉的直径为[τ]=140 Mpa,许用挤压应力[]=320 Mpa,P=24 kN,试做强度校核。
2-5 图示为测定剪切强度极限的试验装置。
若已经低碳钢试件的直径D=1 cm,剪断试件的外力P=50.2Kn,问材料的剪切强度极限为多少?2-6一减速机上齿轮与轴通过平键连接。
已知键受外力P=12 kN,所用平键的尺寸为b=28 mm,h=16 mm,l=60 mm,键的许用应力[τ]=87 Mpa,[]=100 Mpa。
试校核键的强度。
2-7图示连轴器,用四个螺栓连接,螺栓对称的安排在直径D=480 mm的圆周上。
这个连轴结传递的力偶矩m=24 kN·m,求螺栓的直径d需要多大?材料的许用切应力[τ]=80 Mpa。
(提示:由于对称,可假设个螺栓所受的剪力相等)2-8 图示夹剪,销子C的之间直径为0.6 cm,剪直径与销子直径相同的铜丝时,若力P=200 N,a=3 cm,b=15 cm,求铜丝与销子横截面上的平均切应力。
2-9 一冶炼厂使用的高压泵安全阀如图所示,要求当活塞下高压液体的压强达到p=3.4 Mpa时,使安全销沿1-1和2-2两截面剪断,从而使高压液体流出,以保证泵的安全。
已知活塞直径D=5.2cm,安全销采用15号钢,其剪切强度极限=320 Mpa,试确定安全销的直径d。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{教育管理}工程力学静力学某市科大东北大学版版四
4-3试求下列各梁或刚架的支座反力。
解:
(a)受力如图
由∑M=0F•3a-Psin30°•2a-Q•a=0
∴FRB=(P+Q)/3
由∑x=0F-Pcos30°=0
Ax
∴F=P
Ax
由∑Y=0F+F-Q-Psin30°=0
Ay RB
∴F=(4Q+P)/6
Ay
4-4高炉上料的斜桥,其支承情况可简化为如图所示,设A和B为固定铰,D为中间铰,料车对斜桥的
总压力为Q,斜桥(连同轨道)重为W,立柱BD质量不计,几何尺寸如图示,试求A和B的支座反力。
4-5齿轮减速箱重W=500N,输入轴受一力偶作用,其
力偶矩m=600N.m,输出轴受另一力偶作用,其力偶1
矩m=900N.m,转向如图所示。
试计算齿轮减速箱A 2
和B两端螺栓和地面所受的力。
4-6试求下列各梁的支座反力。
(a)(b)
4-7各刚架的载荷和尺寸如图所示,图c中m>m,
21
试求刚架的各支座反力。
4-8图示热风炉高h=40m,重W=4000kN,所受风压力可以简化为梯形分布力,如图所示,q=500kN/m,
1
q=2.5kN/m。
可将地基抽象化为固顶端约束,试求地2
基对热风炉的反力。
4-9起重机简图如图所示,已知P、Q、a、b及c,求
向心轴承A及向心推力轴承B的反力。
4-10构架几何尺寸如图所示,R=0.2m,P=1kN。
E为中间铰,求向心轴承A的反力、向心推力轴承B的反力及销钉C对杆ECD的反力。
4-11图示为连续铸锭装置中的钢坯矫直辊。
钢坯对矫直辊的作用力为一沿辊长分布的均布力q,已知
q=1kN/mm,坯宽1.25m。
试求轴承A和B的反力。
4-12立式压缩机曲轴的曲柄EH转到垂直向上的位置时,连杆作用于曲柄上的力P最大。
现已知P=40kN,飞轮重W=4kN。
求这时轴承A和B的反力。
4-13汽车式起重机中,车重W=26kN,起重臂CDE
1
重G=4.5kN,起重机旋转及固定部分重W=31
2
kN,作用线通过B点,几何尺寸如图所示。
这时起重
臂在该起重机对称面内。
求最大起重量P。
max
4-14平炉的送料机由跑车A及走动的桥B所组成,跑车装有轮子,可沿桥移动。
跑车下部装有一倾覆操纵
柱D,其上装有料桶C。
料箱中的载荷Q=15kN,力Q
与跑车轴线OA的距离为5m,几何尺寸
如图所示。
如欲保证跑车不致翻倒,试问小车连同操纵柱的重量W最小应为多少?
4-15两根位于垂直平面内的均质杆的底端彼此相靠地搁在光滑地板上,其上端则靠在两垂直且光滑的墙上,质量分别为P1与P2。
求平衡时两杆的水平倾角α与α的关系。
12
4-16均质细杆AB重P,两端与滑块相连,滑块A和B可在光滑槽内滑动,两滑块又通过滑轮C用绳索相互连接,物体系处于平衡。
(a)用P和θ表示绳中张力T;
(b)当张力T=2P时的θ值。
4-17已知a,q和m,不计梁重。
试求图示各连续梁
在A、B和C处的约束反力。
4-18各刚架的载荷和尺寸如图所示,不计刚架质量,
试求刚架上各支座反力。
4-19起重机在连续梁上,已知P=10kN,Q=50kN,不计梁质量,求支座A、B和D的反力。
4-20箱式电炉炉体结构如图a所示。
D为炉壳,E为炉顶拱,H为绝热材料,I为边墙,J为搁架。
在实际
炉子设计中,考虑到炉子在高温情况下拱顶常产生裂缝,可将炉拱简化成三铰拱,如图b所示。
已知拱顶
是圆弧形,跨距l=1.15m,拱高h=0.173m,炉顶重
G=2kN。
试求拱脚A和B处反力。
4-21图示厂房房架是由两个刚架AC和BC用铰链连接组成,A与B两铰链固结于地基,吊车梁宰房架突出
部分D和E上,已知刚架重G
=G=60kN,吊车桥重Q=10kN,风力F=10kN,几何12
尺寸如图
所示。
D和E两点分别在力G和G的作用线上。
求
12
铰链A、B和C的反力。
4-22图示构架由滑轮D、杆AB和CBD组成,一钢丝绳绕过滑轮,绳的一端挂一重物,重量为G,另一端系
在杆AB的E处,尺寸如图所示,试求铰链A、B、C
和D处反力。
4-23桥由两部分组成,重W1=W2=40kN,桥上有载荷P=20kN,尺寸如图所示,试求出铰链A、B和C的反力。
4-24图示结构,在C、D、E、F、H处均为铰接。
已知
P=60kN,P=40kN,P=70kN,几何尺寸如图所示。
试求123
各杆所受的力。
4-25构架的载荷和尺寸如图所示,已知P=24kN,求铰链A和辊轴B的反力及销钉B对杆ADB的反力。
4-26构架的载荷和尺寸如图所示,已知P=40kN,R=
0.3m,求铰链 A 和 B 的反力及销钉 C 对杆 ADC 的反力。
4-27 图示破碎机传动机构,活动夹板 AB 长为 600mm,假设破碎时矿石对活动夹板作用力沿垂直于 AB 方向的分力 P=1kN,BC=CD=600mm,AH=400mm,OE=100mm,图示位置时,机构平衡。
试求电机对杆 OE 作用的力偶的
力偶矩 m 。
04-28 曲柄滑道机构如图所示,已知 m=600N.m,OA=0.6m,BC=0.75m 。
机构在图示位置处于平衡,α=30°,β=60°。
求平衡时的 P 值及铰链 O 和 B 反力。
4-29 插 床 机 构 如 图 所 示 , 已 知 OA=310mm ,O B=AB=BC=665mm,CD=600mm,OO
=545mm,P=25kN 。
11在图示位置:OO A 在铅锤位置;O C 在水平位置,机
11构处于平衡,试求作用在曲柄 OA 上的主动力偶的力偶矩 m 。
4-30 在图示机构中,OB 线水平,当 B 、D 、F 在同一铅垂线上时,DE 垂直于 EF,曲柄OA正好在铅锤位置。
已知 OA=100mm,BD=BC=DE=100mm,EF=100mm,不计杆重和摩擦,求图示位置平衡时 m/P 的值。
4-31 图 示 屋 架 为 锯 齿 形 桁 架 。
G =G =20kN ,12
W =W =10kN,
几何尺寸如图所示,试求各杆内力。
124-32 图 示 屋 架 桁 架 。
已 知 F =F =F =F =30kN ,
1245。
