第四章 图形的初步认识基础知识及测试题
七年级上第四章《图形的初步认识》复习测试题含答案
北
B
A 西
东
54
北
D
西 B东
第 7题
第 8题
8. 如图所示 , 若 AB∥ CD,则∠ A+∠ M+∠ N+∠C=( C.540° )
第 9题
9. 如图所示 , 由 B 测 A 的方向是 (A. 北偏西 54° ) 10. 如图甲，用一块边长 10cm 的正方形 ABCD厚纸板，做了一套七巧板．将七巧板拼成一座桥（如图
七年级上第四章《图形的初步认识》复习测试题
（时间 120 分钟，满分 120 分） 一、选择题（ 每题 3 分，满分 30 分） 1. 下列图形中 ,( A 2)(4)(5)) 不是多面体一
1
.
2
3
2. 如图所示 , 哪个图形不能折成一个正方体表面
4
.( b )
5
6
A
C
D
3. 下列语句中，正确的个数是（ B.2 ）个 ①两条直线相交 , 只有一个交点 . ②在∠ ABC的边 BC的延长线上取一点 D . ③若∠ 1+∠ 2+∠ 3=90° , 则∠ 1、∠ 2、∠ 3 互余 . ④一个角的余角比这个角的补角小 . 4. 在图中，不同的线段的条数是（ C.10 ）
∴AD∥ BC(同位角相等 , 两直线平行 )
A
B
25. （本题 12 分） 如图， ∠ 1=80°，∠ 2=100°，∠ BAD=60
（1）直线 AB与 CD是什么关系？请说明理由 .
（ 2）求∠ D的度数 .
解 :(1)AB 与 CD平行 . ∵∠ 1=80°（已知）∴∠ ABE=80°（对顶角相等）
3
22
2
3
第四章--图形的初步认识知识点及评价测试题(含答案)
⎧⎨⎩⎧⎨⎩第四章 图形的初步认识知识点及评价测试题一、立体图形与平面图形立体图形：棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形 平面图形：三角形、四边形、圆等。
主（正）视图---------从正面看 2、几何体的三视图 侧（左、右）视图-----从左（右）边看俯视图---------------从上面看（1）会判断简单物体（直棱柱、圆柱、圆锥、球）的三视图。
（2）能根据三视图描述基本几何体或实物原型。
3、立体图形的平面展开图（1）同一个立体图形按不同的方式展开，得到的平现图形不一样的。
（2）了解直棱柱、圆柱、圆锥、的平面展开图，能根据展开图判断和制作立体模型。
4、点、线、面、体（1）几何图形的组成点：线和线相交的地方是点，它是几何图形最基本的图形。
线：面和面相交的地方是线，分为直线和曲线。
面：包围着体的是面，分为平面和曲面。
体：几何体也简称体。
（2）点动成线，线动成面，面动成体。
二、直线、射线、线段（一）.直线、射线、线段的区别与联系： 基本概念（二）.直线、线段性质：经过两点有一条直线，并且只有一条直线；或者说两点确定一条直线；1、线段的性质 两点的所有连线中，线段最短。
简单地：两点之间，线段最短。
2.画线段的方法（1）度量法（2）用尺规作图法3、线段的大小比较方法（1）度量法（2）叠合法4、点与直线的位置关系二、角（一）.角的意义：1、角：由公共端点的两条射线所组成的图形叫做角。
2、角的表示法（四种）：3、角的度量单位及换算4、角的分类有公共端点的两条射线组成的图形叫做角，公共端点是角的顶点，这两条射线是角的两条边，角也可以看做由一条射线绕着它的端点旋转而形成的图。
注意：表示角时，一定要对照几何图形，注意不能漏掉角的符号，切记用三个大写字母表示一个角时，顶点字母一定要写在中间；同一顶点处有多个角时，切不可用顶点字母来表示。
（二）.角的度量：1°=60′ 1′=60″1直角=90° 1平角=180 ° 1周角=360°（三）.角的大小的比较：（1）叠合法，使两个角的顶点及一边重合，另一边在重合边的同旁进行比较；（2）度量法。
七年级数学第四章图形的初步认识(知识点归纳+达标检测)
第四章图形的初步认识（知识点归纳+达标检测）4.1.1认识几何图形几何图形我们见过的长方体、圆柱、圆锥、球、圆、线段、点，以及小学学过的三角形、四边形等，都是从形形色色的物体外形中得出的。
我们把这些图形称为几何图形。
1）立体图形长方体、正方体、球、圆柱、圆锥等。
2）平面图形平面图形的概念线段、角、三角形、长方形、圆等它们的各部分都在同一平面内，它们是平面图形。
注：立体图形与平面图形是两类不同的几何图形，它们的区别和联系：立体图形的各部分不都在同一平面内，而平面图形的各部分都在同一平面内；立体图形中某些部分是平面图形。
【达标提升】下列几种图形：①长方形；②梯形；③正方体；④圆柱；⑤圆锥；⑥球.其中属于立体图形的是（）A.①②③；B.③④⑤；C.①③⑤；D.③④⑤⑥总结：1、2、平面图形与立体图形的关系：立体图形的各部分不都在同一平面内，而平面图形的各部分都在同一平面内；立体图形中某些部分是平面图形。
4.1.2几何图形立体图形转化平面图形1：从正面、左面、上面观察得到的平面图形你能画出来吗？【达标提升】1.如图是由七个相同的小正方体堆成的物体，从上面看这个物体的图是（）A．B．C．D．2．右图是由几个小立方块所搭几何体的俯视图，请画出这个几何体的主视图和左视图。
现实物体几何图形平面图形立体图形看外形4.1.3几何图形（一）、立体图形的展开1、试一试：在你想象的基础上，请将准备好的长方体、圆柱、圆锥和三棱柱的纸盒剪开展平，看看与下面的展开图一样吗？圆柱圆锥三棱柱长方体思考：请你指出上面展开图各部分与几何体的哪一部分相对应？2、剪一剪、画一画：动手把一个立方体的包装盒沿一边剪开，铺平，看看它的展开图由哪些平面图形组成；再把展开的纸板复原，你有什么体会?再将所有的展开图画出来，以上画出了部分了展开图，除此之外还有5种，共有11种,请你画出其余5种。
（二）、立体图形的折叠探究：下图是一些立体图形的展开图，用它们能围成怎样的立体图形？做一做：下面是一些常见几何体的展开图，你能正确说出这些几何体的名字么？【达标提升】1.下列图形中，不是正方体的表面展开图的是（）A．B．C．D．12122.一个正方体的平面展开图如图所示，将它折成正方体后“建”字对面是（）A．和B．谐C．沾D．益4.2.1点、线、面、体1．几何体的概念（1）长方体是一个几何体，我们还学过哪些几何体？_______________________________________________________________________；（2）观察长方体和圆柱体，说出围成这两个几何体的面有哪些？这些面有什么区别？2．面的分类通过对上面问题的解决，得出面的分类：____面和___面。
第四章图形认识初步练习题及答案初一数学
图形认识初步一、选择题1、小华从正面察看以下图所示的两个物体，看到的是（）正面 A 、 B 、C、D、2、假如用□表示 1 个立方体，用表示两个立方体叠加，用■表示三个立方体叠加，那么下边右图由 6 个立方体叠成的几何体，从正前面察看，可画出的平面图形是（）3、指出图中几何体截面的形状（）4、以下语句正确的选项是 ( )A. 假如 PA=PB,那么 P 是线段 AB的中点B. 作∠ AOB的均分线 CDC. 连结 A、B 两点得直线 ABD. 反向延伸射线 OP(O为端点 )5、假如线段 AB＝2cm，BC＝ 5cm，那么 A、C 两点的距离是（）A．3cm B、 7cm C、 3cm或 7cm D、以上答案都不对6、（ 2008 浙江省绍兴市， 4 分）如图，量角器外缘边上有A， P， Q 三点，它们所表示的读数分别是1800， 700， 300，则∠ PAQ 的大小为（）A ．10oB ．20o C．30o D ．40o7、两个角 , 它们的比是 6:4, 其差为 36° , 则这两个角的关系是( )A. 互余B. 互补C. 既不互余也不互补D. 不确立8、如图，已知直线AB、 CD订交于点 O，OA 均分∠ EOC，∠ EOC=70°，则∠BOD的度数等于（）A、30°B、35°C、20°D、 40°9、假如∠α =3∠β ,∠α =2∠θ ,则必有()E D A B OC1123A A 4A. ∠β = 2∠θ ;B. ∠β = 3∠θ ;C. ∠β = 3∠θ ;D. ∠β =4A 3A 2∠θ ;A 110. 如下图 , 已知∠ AOB=64°,OA 1 均分∠ AOB,OA 2均分∠ AOA 1, OA 3 均分∠ AOA 2,OA 4 均分∠ AOA 3, 则∠ AOA 4的大小为 ( )A.1 °B.2°C.4°D.8°O(5)B二、填空题我1、分别是“我”、“喜”、萍萍同学在一个正方体盒子的每个面都写上一个字，“欢”、“数”、“学”、“课”，其平面睁开图如下图，那么在该正方体盒子喜 欢 数学 课中，和“我”相对的面上的字是.2、圆柱侧面睁开图是 ________, 圆锥侧面睁开图是 ________.图 43、已知线段 AB=acm,点 A 1 均分 AB,A 2 均分 AA 1,A 3 均分 AA 2,, A n 均分 AA n-1 , 则AA n =_______________cm. 4、∠ 1+∠2=180°,∠ 2+∠3=180°,依据 ________,得∠ 1=∠3. 5、如图， OA 的方向是北偏东 15°,OB 的方向是 西偏北 50°。
第四章《图形认识初步》综合复习检测卷(四)及答案
第四章《图形认识初步》综合复习检测卷(四)一、选择题（每小题3分，共30分）1.下列关于棱柱的说法：①棱柱的所有面都是平面；②棱柱的所有棱长都相等；③棱柱的所以侧面都是长方形或正方形；④棱柱的侧面个数与底面边数相等；⑤棱柱的上、下底面形状、大小相等其中正确的有 （ ）.（A ）2个 （B ）3个 （C ）4个 （D ）5个2．下列图形中是正方体的表面展开图的是 （ ）.(A) (B) (C) (D)3.如图1，点C 是线段AB 的中点，点D 线段BC 的中点，下列等式不正确的是（ ）.（A ）CD=AC-DB （B ）CD=AD-BC （C ）CD=21AB-BD （D ）CD=31AB图14.一个物体的从正面、左面、上面三个方向看是下面三个图形，则该物体形状的名称为 （ ）(A) 圆柱 (B) 棱柱(C) 圆锥 (D) 球 正面 左面 上面5．下列判断正确的是 （ ）． 图2（A ）平角是一条直线 （B ）凡是直角都相等（C ）两个锐角的和一定是锐角 （D ）角的大小与两条边的长短有关6．如图3，∠AOB ＝∠COD ＝90°，那么∠AOC=∠BOD ，这是根据 （ ）.(A)直角都相等 (B) 同角的余角相等(C)同角的补角相等 (D)互为余角的两个角相等图37. 点M 、O 、N 顺次在同一直线上，射线0C 、0D 在直线MN 同侧，且∠MOC=64°，∠DON=46°，北则∠MOC 的平分线与∠DON 的平分线夹角的度数是 （ ）.（A ）85° （B ）105° （C ）125° （D ）145°8. 某测绘装置上一枚指针原来指向南偏西50°（如图4）， 把这枚指针按逆时针方向旋转41周，则结果指针的指向 （ ）． （A ）南偏东50º （B ）西偏北50º（C ）南偏东40º （D ）南偏东45° 图49．如图5，每个长方体的六个面上分别写着1～6这六个数，并且任意两个相对的面上所写的两个数之和所写的两个数之和都等于7，靠在一起的长方体中，相连接两个面的数字之和等于8，图中打“？”的面上所写的数字是 （ ）.（A ）3 （B ）5 （C ）2 （D ）110．计算180°-48°39′40″-67°41′35″的值是 （ ）. 图5（A ）63°38′45″ （B ）58°39′40″ （C ）64°39′40″ （D ）63°78′65″二、填空题（每小题2分，共20分）11．如图6所示的图形绕虚线旋转一周,所围成的几何体是_____.图6 图7 12.如图7是一个正方体纸盒的展开图,在其中的四个正方形内有数字1、2、3和-3，要在其余正方形内分别填上-1、-2，使得按虚线折成正方体后，相对面上的两个数互为相反数，则A 处应填_____.13.植树时,只要定出_______个树坑的位置,就能确定同一行树坑所在直线,根据是_______.14.如图8是三个几何体的展开图,请写出这三个立体图形_________ __________ ________图815.某工程队在修筑高速公路时,有时需要将弯曲的道路改直,以缩短路程,这样作的理论依据是________.16.如图9,点C是∠AOB的边OA上一点,D、E是OB上两点，则图中共有_____条线段,_____条射线,_____个小于平角的角.图9 图1017.如果一个角的补角是150°,那么这个角的余角是________.18.乘火车从A站出发,沿途经过3个车站可到达B站,那么在A、B两站之间共有____种不同的票价.19.如图10,将一副三角板叠放在一起,使直角的定顶点重合于点0,则∠AOC+∠DOB=_____.20.在直线l上取A、B、C三点，使得AB=4cm，BC=3cm，如果0是线段AC的中点，则线段OB的长度为_________.三、解答题(1-6每小题6分,7-8分每小题7分)21．观察图11中的几何体，画出从正面、左面、上面三个方向看，得到的平面图形。
第4章《图形的初步认识》整章水平测试(C)及答案
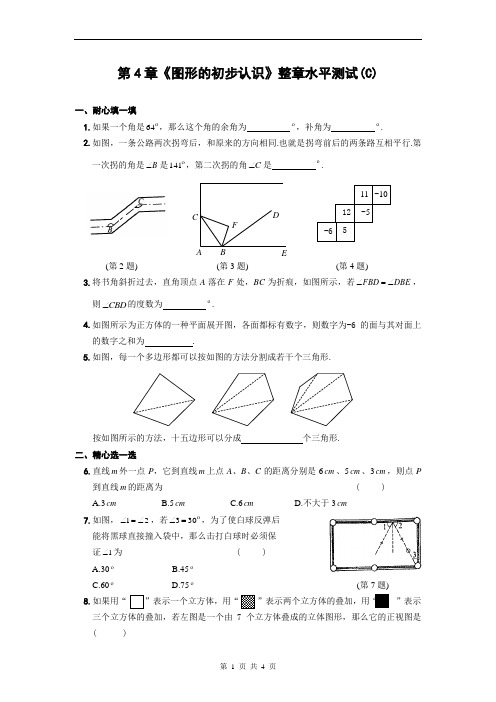
9.如图，A、B、C分别表示学校、电影院、公园所在的位置，且电影院位在学校的正东方向上，公园在学校的南偏西 方向上，那么平面图上的 等于( )
A.115 B.155 C.25 D.65
(第9题) (第10题)
10.如图所示，已知A、O、B在同一条直线上，且 ，则 的余角有( )
A.3 B.5 C.6 D.不大于3
7.如图， ，若 ，为了使白球反弹后
能将黑球直接撞入袋中，那么击打白球时必须保
证 为( )
A.30 B.45
C.60 D.75 (第7题)
8.如果用“”表示一个立方体，用“”表示两个立方体的叠加，用“”表示三个立方体的叠加，若左图是一个由7个立方体叠成的立体图形，那么它的正视图是( )
(4)从(1)、(2)、(3)题的结论中你得出了什么结论?
(5)根据这一规律你能编一道类似的关于线段的题目吗?
13.小芳给自己家的小狗乐乐做了一个小木屋，其侧面如图所示.若她已测出 ，由于受条件影响，屋顶的
的度数无法测出.哥哥看到后说，不用测量，
他也能算出 的度数，你知道小芳的哥哥是怎
样做的吗?试着说出他的方案，并计算出 的度数.
第4章《图形的初步认识》整章水平测试(C)
一、耐心填一填
1.如果一个角是 ，那么这个角的余角为 ，补角为 .
2.如图，一条公路两次拐弯后，和原来的方向相同.也就是拐弯前后的两条路互相平行.第一次拐的角是 是 ，第二次拐的角 是 .
(第2题)(第3题)(第4题)
3.将书角斜折过去，直角顶点A落在F处，BC为折痕，如图所示，若 ，则 的度数为 .
A.1个B.2个C.பைடு நூலகம்个D.4个
三、细心解答下列问题
图形认识初步检测题及答案
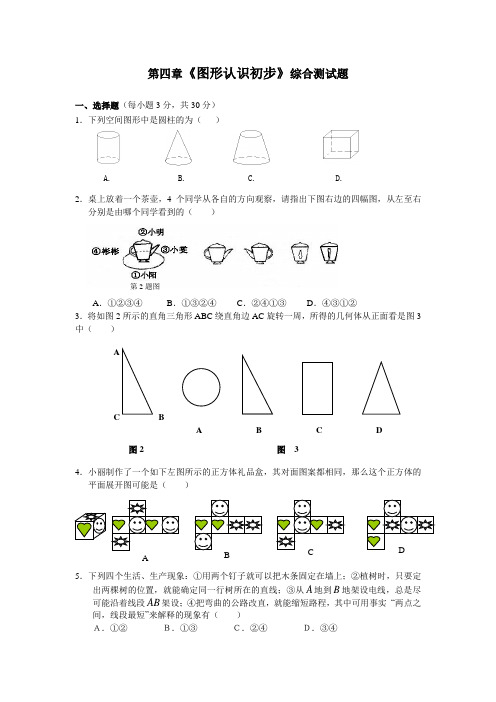
第四章《图形认识初步》综合测试题一、选择题（每小题3分，共30分）1．下列空间图形中是圆柱的为（）2．桌上放着一个茶壶，4个同学从各自的方向观察，请指出下图右边的四幅图，从左至右分别是由哪个同学看到的（）A．①②③④B．①③②④C．②④①③D．④③①②3．将如图2所示的直角三角形ABC绕直角边AC旋转一周，所得的几何体从正面看是图3中（）4．小丽制作了一个如下左图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是（）5．下列四个生活、生产现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路改直，就能缩短路程，其中可用事实“两点之间，线段最短”来解释的现象有（）Ａ．①②Ｂ．①③Ｃ．②④Ｄ．③④AC D第2题图A. B. C. D.BAC图2A B C D图 36．已知∠α＝35°19′，则∠α的余角等于（ ）A ．144°41′B ．144°81′C ． 54°41′D ． 54°81′7．线段12AB cm =，点C 在AB 上，且13AC BC =，M 为BC 的中点，则AM的长为（）A.4.5cmB. 6.5cmC. 7.5cmD. 8cm8．如图，下列说法中错误的是（ ）Ａ．OA 方向是北偏东30o Ｂ．OB 方向是北偏西15o Ｃ．OC 方向是南偏西25o Ｄ．OD 方向是东南方向二、填空题（每小题2分，共20分）1．长方体由 个面， 条棱， 个顶点.2．下列图形是一些立体图形的平面展开图，请将这些立体图形的名称填在对应的横线上.3．如图，在射线CD 上取三点D 、E 、F ，则图中共有射线_________条。
4．（1）=048.32 度 分 秒。
（2）///422372= 度。
5．如图，OB 平分∠AOC ，∠AOD=78°，∠BOC=20°，则∠COD 的度数为_______.6．把一张长方形纸条按图的方式折叠后，量得∠AOB ＇=110°，则∠B ＇OC=______. 7．下图是由一些相同的小正方体构成的几何体从不同方向看得到的平面图形，这些相同的小正方体的个数是_______.O ABCD北东南西︒75︒30︒45︒25第10题图8．如图所示的几何体是由棱长为1的小立方体按一定规律在地面上摆成的，若将露出的表面都涂上颜色（底面不涂色），则第n 个几何体中只有两个面．．．涂色的小立方体共有 个．三、解答题 1.计算：（1）22°18′×5；（2）90°-57°23′27″.2.已知∠α与∠β互余，且∠α比∠β小25°，求2∠α-31∠β的值3. 一个角的补角加上010后等于这个角的余角的3倍，求这个角.4．⑴已知如图，点C 在线段AB 上，线段AC ＝10，BC ＝6，点M 、N 分别是AC 、BC 的中点，求MN 的长度。
第4章 图形的初步认识 华东师大版七年级上册数学单元测试(含答案)
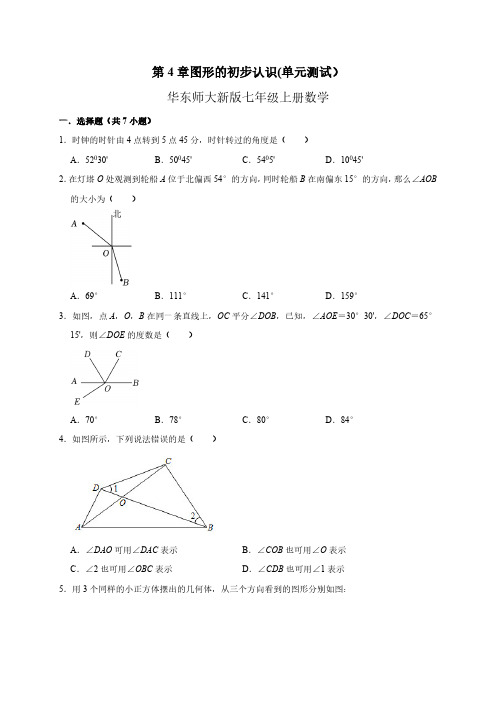
第4章图形的初步认识(单元测试）华东师大新版七年级上册数学一．选择题（共7小题）1．时钟的时针由4点转到5点45分，时针转过的角度是（ ）A．52030'B．50045'C．5405'D．10045'2．在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB 的大小为（ ）A．69°B．111°C．141°D．159°3．如图，点A，O，B在同一条直线上，OC平分∠DOB，已知，∠AOE＝30°30'，∠DOC＝65°15'，则∠DOE的度数是（ ）A．70°B．78°C．80°D．84°4．如图所示，下列说法错误的是（ ）A．∠DAO可用∠DAC表示B．∠COB也可用∠O表示C．∠2也可用∠OBC表示D．∠CDB也可用∠1表示5．用3个同样的小正方体摆出的几何体，从三个方向看到的图形分别如图：．．．．＝∠A．∠AOC＝∠BOCB．∠AOC＜∠AOBC．∠AOC＝∠BOC或∠．如图所示，图（表面上），请根据要求回答问题：，求的值；运动秒后都停止运动，此时恰有＝BD第4章图形的初步认识(单元测试）华东师大新版七年级上册数学参考答案与试题解析一．选择题（共7小题）1．时钟的时针由4点转到5点45分，时针转过的角度是（ ）A．52030'B．50045'C．5405'D．10045'【答案】A【解答】解：钟表12个数字，每相邻两个数字之间的夹角为30°，每相邻两个数字之间有5个格，每格之间的度数为6°，时钟的时针由4点转到5点45分，时针转过的5+5×格，时针转过的度数＝6°×（5+5×）＝52°30′．故选：A．2．在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB 的大小为（ ）A．69°B．111°C．141°D．159°【答案】C【解答】解：由题意得：∠1＝54°，∠2＝15°，∠3＝90°﹣54°＝36°，∠AOB＝36°+90°+15°＝141°，故选：C．3．如图，点A，O，B在同一条直线上，OC平分∠DOB，已知，∠AOE＝30°30'，∠DOC＝65°15'，则∠DOE的度数是（ ）A．70°B．78°C．80°D．84°【答案】C【解答】解：∵OC平分∠DOB，∠DOC＝65°15'，∴∠BOD＝2∠DOC＝130°30′，∴∠AOD＝180°﹣130°30′＝49°30′，∴∠DOE＝∠AOD+∠AOE＝49°30′+30°30′＝80°．故选：C．4．如图所示，下列说法错误的是（ ）A．∠DAO可用∠DAC表示B．∠COB也可用∠O表示C．∠2也可用∠OBC表示D．∠CDB也可用∠1表示【答案】B【解答】解：A、∠DAO可用∠DAC表示，本选项说法正确；B、∠COB不能用∠O表示，本选项说法错误；C、∠2也可用∠OBC表示，本选项说法正确；D、∠CDB也可用∠1表示，本选项说法正确；故选：B．5．用3个同样的小正方体摆出的几何体，从三个方向看到的图形分别如图：这个几何体是（ ）A．B．C．D．【答案】B【解答】解：由俯视图可知，小正方体摆出的几何体为：，故选：B．6．如图是由几个相同的小正方体组成的几何体，则下列说法正确的是（ ）A．左视图面积最大B．俯视图面积最小C．左视图面积和正视图面积相等D．俯视图面积和正视图面积相等【答案】D【解答】解：观察图形可知，几何体的主视图由4个正方形组成，俯视图由4个正方形组成，左视图由3个正方形组成，所以左视图的面积最小，俯视图面积和正视图面积相等．故选：D．＝∠A．∠AOC＝∠BOCB．∠AOC＜∠AOBC．∠AOC＝∠BOC或∠＝∠＝∠＝＝＝×【答案】（1（2）图形见解答．【解答】解：的距离为×∴△ABM的面积＝×10×5＝25．或△ABM′的面积＝×10×21＝105．19．如图甲，点O是线段AB上一点，C、D两点分别从O、B同时出发，以2cm/s、4cm/s的速度在直线AB上运动，点C在线段OA之间，点D在线段OB之间．（1）设C、D两点同时沿直线AB向左运动t秒时，AC：OD＝1：2，求的值；（2）在（1）的条件下，若C、D运动秒后都停止运动，此时恰有OD﹣AC＝BD，求CD的长；（3）在（2）的条件下，将线段CD在线段AB上左右滑动如图乙（点C在OA之间，点D在OB 之间），若M、N分别为AC、BD的中点，试说明线段MN的长度总不发生变化．【答案】见试题解答内容【解答】解：（1）设AC＝x，则OD＝2x，又∵OC＝2t，DB＝4t∴OA＝x+2t，OB＝2x+4t，∴；（2）设AC＝x，OD＝2x，又OC＝×2＝5（cm），BD＝×4＝10（cm），由OD﹣AC＝BD，得2x﹣x＝×10，x＝5，OD＝2x＝2×5＝10（cm），＝AC＝×＝BC＝×＝acm＝AC＝BC＝AC+BC＝AB＝acm＝AC＝BC＝AC﹣BC＝（）＝bcm（2）数轴上表示a和﹣5的两点A和B之间的距离是 |a+5| ；（3）若数轴上三个有理数a、b、c满足|a﹣b|＝1，|a﹣c|＝7，则|b﹣c|的值为 6或8 ；（4）当a＝ 1 时，|a+3|+|a﹣1|+|a﹣4|的值最小，最小值是 7 ．【答案】见试题解答内容【解答】解：（1）2﹣（﹣3）＝5，故答案为：5；（2）|AB|＝|a﹣（﹣5）|＝|a+5|，故答案为：|a+5|；（3）当a＞b＞c时，|b﹣c|＝|a﹣c|﹣|a﹣b|＝7﹣1＝6；当b＞a＞c时，|b﹣c|＝|a﹣c|+|a﹣b|＝7+1＝8；C点在A，B两点之间时不符合题意，综上|b﹣c|的值为6或8，故答案为：6或8；（4）∵当﹣3≤a≤4时，|a+3|+|a﹣4|的最小值为7，∴只需要|a﹣1|的值最小即可，此时a＝1，|a﹣1|＝0，∴当a＝1时，|a+3|+|a﹣1|+|a﹣4|的值最小，最小值是7．故答案为：1；7．。
第四章 图形认识初步单元检测题及答案
第四章 图形认识初步单元检测题班级 .姓名 .学号 .一、选择题（每题4分，共40分）1.圆锥的侧面展开图是（ ）A ．圆形B ．长方形C ．扇形D ．半圆形2. 下列说法错误的是（ ）A ．线段AB 和线段BA 是同一条线段; B ．射线AB 和射线BA 是同一条射线C ．直线AB 和直线BA 是同一条直线;D ．线段AB 是直线AB 的一部分3.下面图形经过折叠可以围成一个棱柱的是（ ）A B C D4.下列图形中是正方体的展开图的为（ ）A .B . C. D.5. 如果点C 是线段AB 上的一点，M 、N 分别是AC 、BC 的中点，则下列结论正确的是（ ）A ．MN=21AB B ．NC=21ABC ．MC=21ABD ．AM=21AB 6.直线上不同的四个点，能够得到不同的线段条数共有（ ）A ．四条B ．五条C ．六条D ．七条7. 2000年5月12日，在四川省汶川县发生8.0级特大地震，能够准确表示汶川这个地点位置的是（ ）A ．北纬31oB ．东径103.5oC ．金华的西北方向上D ．北纬31o ，东径103.5o8.在时刻8：30，时钟上的时针和分针之间的夹角为（ ）A ．85°B ．75°C ．70°D ．60°9. 从点A 看B 的方向是北偏东35°，那么从B 到A 的方向是（ ）A ．南偏东55°B ．南偏西55°C ．南偏东35°D ．南偏西35°10. 一个画家有14个边长为1cm 的正方体，他在地面上把它们摆成如图所示的形式，然后他把露出的表面都涂上颜色，那么被涂上颜色的总面积是（ ）A ．19cm 2B ．21cm 2C ．33cm 2D ．34cm 2二、填空题（每题4分，共20分）11.将下列几何体分类，柱体有：，锥体有（填序号）.12.植树时只要先定两个树坑的位置，•就能确定一行树所在的位置，其根据是___________．13. ∠1和∠2互补，且∠2+∠3=180°，则∠1=_______.14. 已知：∠A=60°，那么∠A的补角是．15.如图所示，将一副三角板叠放在一起，使直角的顶点重合于点O，则∠AOC+∠DOB的度数为_______．三、解答题（共40分）16.（共10分）（1）175°16′30″-47°30′÷6+4°12′50″×3；（2）一个角的补角加上10°等于这个角的余角的3倍，求这个角.17.（共10分）已知：如图所示，从点O 引四条射线OA 、OB 、OC 、OD ，如果OA ⊥OC ，OB⊥OD ．（1）若∠BOC ＝35°，求∠AOB 与∠COD 的大小；（2）若∠BOC ＝50°，求∠AOB 与∠COD 的大小；（3）你发现∠AOB 与∠COD 的大小有什么关系？18.（共10分）如果一个锐角的补角比这个角的余角的2倍还多40°，那么这个角的余角是多少度？A C O D B19.（共10分）（1）如下图，已知点C 在线段AB 上，6cm AC =且，4cm BC =，点M N ，分别是AC ，BC 的中点，求线段MN 的的长度．（2）在（1）中，如果cm AC a =，cm BC b =，其它条件不变，你能猜出MN 的长度吗？请你用一句简洁的话表述你发现的规律．（3）对于（1）题，如果我们这样叙述它：“已知线段6cm AC =，4cm BC =，点C 在直线AB 上，点M N ，分别是AC BC ，的中点，求MN 的长度．”结果会有变化吗？如果有，求出结果．参考答案一、选择题1.C2.B3.C4.A5.A6.C7.D8.B•9.D 10.C二、填空题11.1、2、3 5、6 12.两点确定一条直线13.∠3， 14.120° 15. 180°三、解答题16.（1）180°（2）40°17.（1）∵OA⊥OC∴∠AOB+∠BOC＝90°∵∠BOC＝35°∴∠AOB+35°＝90°∴∠AOB=55°∵OB⊥OD∴∠COD+∠BOC＝90°∵∠BOC＝35°∴∠COD+35°＝90°∴∠COD=55°（2）∵OA⊥OC∴∠AOB+∠BOC＝90°∵∠BOC＝50°∴∠AOB+50°＝90°∴∠AOB=40°∵OB⊥OD∴∠COD+∠BOC＝90°∵∠BOC＝50°∴∠COD+50°＝90°∴∠COD=40°（3）从（1）、（2）的运算知道：∠AOB=∠COD18.解法一：设这个角为x°，则其余角为（90-x）°，补角为（180-x）°∴180-x=2（90-x）+40，∴x=40∴90-x=50°答：这个角的余角是50度．解法二：设这个角的余角为x°，则其补角为（90+x）°∴90+x=2x+40，∴x=50答：这个角的余角是50度．19.（1）5㎝（2）MN =（a㎝+b㎝）÷2 MN的长度为线段AC，BC长度的二分之一（3）解：有变化已知AC=6㎝，BC=4㎝当AB在点C左侧时CN=3㎝，CM=2㎝MN=1㎝所以，点C在直线AB上，点M，N分别是AC，BC的中点，MN的长度有变化。
图形的初步认识单元测试题
54西东北北西东AB第4章 图形的初步认识单元测试题一、选择题:(每小题4分,共48分)1.如图所示哪个图形不能折成一个正方体表面?( )A B CD2.下图中所示的三视图是什么立体图形?( )正视图左视图俯视图GOAE D B(第8题) A.棱锥 B.圆柱 C.圆锥 D.圆柱与圆锥组合体3.如上图所示,OE ⊥AB 于O.OC 、OD 分别是∠AOE 、∠BOE 的平分线,图中互余的角共有( )A.3对B.4对C.5对D.6对4.如果两个角两条边对应平行,其中一个角为34度,则另一个角为______度. A.34° B.56° C.34°或56° D.34°或146°5.下列4种说法中,正确的说法有( )(1)相等且互补的两个角都是直角; (2)两个角互补,则它们的角平分线互相垂直(3)两个角互为邻补角,则它们的角平分线互相垂直; (4)一个角的两个邻补角是对顶角. A.1个 B.2个 C.3个 D.4个6.∠A 与∠B 互为补角,且∠A>∠B,那么∠B 的余角等于( )A. 12(∠A-∠B)B. 12(∠A+∠B)C. 12∠AD. 12∠B7.如图所示的立方体,如果把它展开的图形是( )8.如图,由B 测A 的方向是( )A.北偏西36°B.北偏西54°C.南偏东36°D.南偏东54° 9.平行于同一直线的两条直线( )3题O C A D BA.平行B.垂直C.相交D.平行或重合10.将线段AB 延长至C,再将AB 反向延长至D,则图中共有( )条线段. A.3 B.4 C.5 D.611.已知∠AMB=45°,∠BMC=30°,则∠AMC=( )A.45°B.15°或30°C.75°D.15°或75° 二、填空题:(每小题3分,共12分)12.若一个角的补角相等于这个角的余角的6倍,则这个角为______度.第12题O CADB13.如图所示,已知∠AOB=160°,∠AOC=∠BOD=90°,则∠COD=_____度.14.如图所示,已知直线AB 、CD 相交于O,OE 平分∠AOC,∠AOE=25°,则∠BOD= ____度. 15. 计算:180°－23°13′6″=__________. 三、解答题:16,如图，OC 平分∠AOB,∠AOB=60°,∠AOD=50°,求∠COD 的度数.17. 若线段AB=16cm,在直线AB 上有一点C,且BC=8cm,M 是线段AC 的中点,求AM 的长.第13题 OCA E DB13题 114题。
第四章 图形的初步认识单元测试卷(含答案)-
第四章图形的初步认识单元测试卷（总分：120分，时间：120分钟）一、填空题（每题3分，共30分）1．经过直线外一点P，有______条直线与这条直线平行．2．将线段AB延长到C，使BC=2AB，AB=_______AC．3．如果一个角是10°，用10倍放大镜观察这个角是______度．4．已知∠A=30°，则∠A的补角的度数为_______．5．如图1所示，两条直线a，b被第三条直线c所截，如果a∥b，∠1=70°，•那么∠2=_______．图1 图2 图3 图46．如图2，∠AOB=∠COD=90°，∠AOD=146°，则∠BOC=_______．7．把图3折叠成一个正方体，如果相对面的值相等，则一组x，y的值是______．8．如图4，BC=4cm，BD=7cm，D是AC的中点，则AC=_____cm，AB=_____cm．9．如图5，直线AB∥CD，EF交AB于点M，MN⊥EF于点M，MN交CD于点N，若∠BME=•125°，则∠MND=________．图5 图610．如图6，从方框外的图形中挑选合适的图形，将该图形的序号填在方框内的横线上．二、选择题（每题3分，共24分）11．如图测7，能表示点到直线（或线段）的距离的线段有（）A．2条 B．3条 C．4条 D．5条图7 图812．如图8所示，从A地到C地，可供选择的方案是走水路、走陆路、走空中，从A地到B地有两条水路、两条陆路，从B地到C地有3条陆路可供选择，走空中，从A地不经B地直线到C地，则从A地到C地可供选择的方案有（）A．20种 B．8种 C．5种 D．13种13．如图9，下列能拼成左边的正方体的是_______（•立体图形看不见的面都是白面）14．在时钟上8：30时，时钟上的时针和分针之间的夹角是（）A．85° B．75° C．70° D．60°15．如图10将五角星沿着虚线折叠，使得A，B，C，D，E五个点重合，得到的立体图形是（）A．棱柱 B．圆锥 C．圆柱 D．棱锥图10 图11 图1216．如图11所示，已知AB∥CD，直线EF分别交AB，CD于点E，F，EG平分∠BEF，若∠1=50°，则∠2的度数为（）A．50° B．60° C．65° D．70°17．如图12，是一个3×3的正方形，则图中∠1+∠2+∠3+…+∠9等于（）A．270° B．315° C．360° D．405°18．如图13，是一个小立方块所搭建的几何体的俯视图，•正方形中的数字表示该位置小立方块的个数，则它的正视图是（）三、解答下列各题（共37分）19．（10分）如图，CD∥AB，CD∥EF，∠A=105°，∠ACE=51°，求∠E的度数．20．（8分）中学生运动会上在比赛跳远，如图所示，是一名运动员的一次跳远示意图，A，B两点为该名运动员的脚印落点，起跳线为EF，请画图说明如何计算该运动员的跳远成绩，并说明理由．21．（10分）如图，B，C两点把线段MN分成三部分，其比为MB：BC：CN=2：3：•4，P是MN的中点，PC=2cm，求MN的长．22．（9分）如图测4-17所示，已知∠B=∠C，AD∥BC，试说明：AD平分∠CAE．四、探究题（9分）23．如图，照样子把图剪下来，先分别量出图中的角度，并记录∠1=_____，∠2=______，∠3=_______．（1）计算∠1+∠2+∠3=_______;（2）由此猜想出一个结论：________________；（3）设法验证这一结论．五、新情景题（10分）24．如图，有一只蚂蚁从点A出发，按顺时针方向沿图所示的方向爬行，•最后又爬回到A 点，那么蚂蚁在此过程中共转了多少度的角？（为了帮助同学们分析，我们在图中作出线段PQ）六、应用题（10分）25．如图，平原上有A，B，C，D四个村庄，为解决当地缺水问题，•政府准备投资修建一个蓄水池．（1）不考虑其他因素，请你画图确定蓄水池H点的位置，使它到四个村庄距离之和最小；（2）计划把河水引入蓄水池H中，怎样开渠最短？并说明根据．答案:1．且只有一 2．133．10 4．150° 5．110° 6．34°7．x=2，y=3或x=3，y=2 8．6 10 9．35° 10．（3）11．D 12．D 13．B 14．B 15．D 16．C 17．D 18．C19．∠E=24°（点拨：因为CD∥AB，所以∠A+∠ACD=180°，又因为CD∥EF，•所以∠E=∠ECD=∠ACD-∠ACE=75°-51°=24°）20．如图所示，过B点作EF的垂线段BO，测量BO的长度即可．理由：由直线外一点向这条直线所做垂线段的长度叫做点到直线的距离．21．MN=36cm．22．∵AD∥BC，∴∠2=∠B，∠1=∠C又∵∠B=∠C，∴∠1=∠2．23．略（1）∠1+∠2+∠3=180°（2）三角形内角和等于180°（3）把三个角剪下拼成一个平角．24．蚂蚁旋转三个圆圈，转了1080°．25．（1）连AD，BC交于H，则H为蓄水池位置．（2）过H作HG⊥EF垂足为G．“两点之间线段最短是确定H位置的根据”，•“过直线外一点与直线上各点的连线中，垂线段最短”是把河水引入蓄水池H中开渠最短的根据．。
第四章 图形认识初步单元测试卷(含答案)-
第四章图形认识初步单元测试卷（总分：120分时间：120分钟）一、填空题（每题3分，共30分）1．写出三个常见的几何体名称_____，_______，_______．2．小明用一个钉子把木条钉在墙上时，发现木条会转动，然后再钉一个钉子时，•木条就被固定了，这是根据___________原理．3．8点整，时针与分针的夹角为_______度．4．已知角α为28°15°21″，则它的补角为_______．5．如图所示，O是直线AB上一点，∠AOD=∠BOF=120°，∠AOC=90°，OE•平分∠BOD，则图中与∠COD相等的角有_______个．6．从七边形的某一顶点出发，连接其余各顶点，•可以把这个七边形分割成_____个三角形．7．若∠AOB=40°，∠BOC=60°，则∠AOC=_______．8．如图点M是线段AB的三等分点，E是AB的中点，如果AM=2，那么ME=______．9．如图各几何体中，三棱柱是_______．(1) (2) (3) (4)10．如图所示，要把角钢（1）弯成120°的钢架（2），则在角钢（1）上截去的缺口是____________度．(1) (2)二、选择题（每题3分，共30分） 11．下列语句中，正确的是（ ）A ．直线比射线长B ．射线比线段长C ．无数条直线不可能相交于一点D ．两条直线相交，只有一个交点 12．已知线段AB ，延长AB 到C ，使BC=13AB ，D 为AC 的中点，若DC=4cm ，则AB 的长是（ ） A ．3cm B ．6cm C ．8cm D ．10cm 13．如图图形中不可以拼成正方体的图形是（ ）14．如图平面展开图是下面名称几何体的展形图，•立体图形与平面展开图不相符的是（ ）15．平面上有三点A ，B ，C 如果AB=8，AC=5，BC=3，则（ ） A ．点C 在线段AB 上 B ．点B 在线段AB 的延长线上C ．点C 在直线AB 外D ．点C 可能在直线AB 上，也可能在直线AB 外 16．若∠α和∠β互为余角，∠α和∠γ互为补角，∠β与∠γ的和等于周角的13，则这三个角分别为（ ）A ．75°，15°，105°B ．60°，30°，120°C ．50°，40°，130°D ．70°，20°，110°17．某物体从不同方向看得到图4-7所示的三个图形，那么该物体形状是（ ）A ．长方形B ．圆锥形C ．正方体D ．圆柱体 18．如图所示，以A ，B ，C ，D ，E 为线段的端点，图中共有线段（ ）A ．8条B ．10条C ．12条D ．14条19．（经典题）如图所示，B ，C 是线段AD 上任意两点，M 是AB 的中点，N 是CD 的中点，若BC=a ，MN=b ，则AD 的长度是（ ）A ．b-aB ．a+bC ．2b-aD ．以上都不对20．如图所示，下列说法正确的是（ ）A ．CA 为东偏北30°B ．OB 为东偏南20°C ．OC 为北偏西50°D ．以上都不正确三、解答题（共60分）21．（8分）已知∠α和∠β互余，且∠α比∠β小25°，求∠α-15∠β的度数．22．（8分）如图，B ，C 两点把线段AD 分成2：3：4三部分，M 是AD 中点，CD=8cm ，求MC 的长．23．（8分）如图所示，已知点C在线段AB上，且AC=6cm，BC=23AC，点M，N分别是AC，BC的中点，求线段MN+BN的长度．24．（8分）如图所示，已知∠AOB=120°，∠AOC是直角，OD平分∠BOC，OE•平分∠AOC，求∠DOE的度数．25．（8分）画出线段AB．（1）如图（1）所示，在线段AB上画出1个点，这时图中共有几条线段？（2）如图（2）所示，在线段AB上画出2个点，这时图中共有几条线段？（3）如图（3）所示，在线段AB上画出3个点，这时图中共有几条线段？（4）当在线段AB上画出n个点时，则共有几条线段？26．（10分）（探索题）如图所示，已知方格纸中的每个小方格是边长为1•的正方形，A，B两点在小方格的顶点上，位置如图所示，请在小方格的顶点上确定一点C，连接AB，AC，BC，使三角形ABC面积为2个平方单位，画出所有可能的图形．27．（10分）（应用题）如图所示，A，B，C是一条公路上的三个村庄，A，B•间路程为100km，A，C间路程为40km，现在A，B之间建一个车站，设P，C之间的路程为xkm．（1）用含x的代数式表示车站到三个村庄的路程之和；（2）若路程之和为102km，则车站应设在何处？（3）使路程和最小，车站应建在何处？答案:1．圆柱，正方体，棱柱 2．两点确定一条直线3．120° 4．151°44′39″ 5．3 6．57．100°或20° 8．1（点拨：AB=6，AE=12AB=3，3-2=1）9．（4） 10．60° 11．D 12．B 13．C 14．A 15．A 16．A 17．D 18．B19．C（点拨：BM+CN=b-a，AB+CD=2b-2a）20．C21．∠α=32.5°，∠β=57.5°，结果为21°22．1cm23．MN=102=5cm，BN=12×4=2cm，∴MN+BN=7cm．24．∠DOE=12∠BOC+45°=12（120°-90°）+45°=15°+45°=60°25．（1）三条线段（2）六条线段（3）十条线段（4）n+1+n+n-1+…+1或12（n+1）（n+2）条线段．26．如图所示．27．（1）路程之和为PA+PC+PB=（100+x）km．（2）100+x=102，x=2，车站在C两侧2km处．（3）当x=0时，x+100=100，小站建在C处路程和最小，路程和为100km．。
(新版人教版)七年级上第四章《图形认识初步》单元测试卷及解析答案
第四章《图形认识初步》 综合测试题（满分120 分时间90 分钟）一、选择题（每题 3 分，共 30 分）1． ①平角是一条直线；②射线是直线的一半；③射线一个扩大 2 倍的放大镜去看一个角， 这个角会扩大= 120 °50. ?AB 与射线 BA 表示同一条射线；④用2 倍；⑤两点之间，线段最短； ⑥ 120.5 °以上说法正确的有 (A.0 个B.12．以下四个图中，能用∠)个 C.2 个 D.3 个1、∠ AOB 、∠ O 三种方法表示同一个角的是（）3．以下表达正确的选项是（） A ． 180°是补角B 120°和 60°互为补角 C 120 °和 60°是补角 D 60°是 30°的补角4. 如图 1 表示一个用于防震的 L 形的包装用泡沫塑料，当从上边看这一物体时看到的图形形状是（）A ．B ．C ．D ．(图 1)5．以下图形中，哪一个是正方体的睁开图（）6．甲看乙的方向为南偏西25°，那么乙看甲的方向是 （）A ．北偏东 75° B．南偏东 75° C．北偏东 25° D ．北偏西 25°7．若∠ A 的余角是 70°，则∠ A 的补角是（）A ． 70°B ．110°C ． 20°D ． 160°8．如图，AOC和BOD都是直角，假如D CAOB150 ，那么 COD（）AA 、30B 、40C 、50D 、60BO9.经过随意三点中的两点共可画出（）A ．1 条直线B ． 2 条直线C ．1 条或 3 条直线D ． 3 条直线10. 如下图，从O点出发的五条射线，能够构成角的个数是（）．A．10个B．9个C．8个D．4个二、填空题（每题 3 分，共 30 分）11．橙子近似 ______ 体，菠萝近似 _______ 体，角柜近似 _______ 体，金字塔近似 _______体，粉笔盒近似 _______体。
第四章图形认识的初步——知识总结+考点分析+典型例题(含答案)
第四章 图形认识初步【知识要点】4．1多姿多彩的图形1.⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧平面图形球体椎体（棱锥、圆锥）柱体（棱柱、圆柱）立体图形几何图形 2.研究立体图形的方法（1）平面展开图：有些立体图形是由一些平面图形围成的，将它们的表面适当剪开，可以展开成平面图形。
这样的平面图形称为相应立体图形的展开图。
（2）从不同的方向看（“三视图”）3.几何图形的形成：点动成线，线动成面，面动成体。
4.几何图形的结构：点、线、面、体组成几何图形。
点是构成图形的基本元素。
4．2直线、射线、线段1.点：表示一个物体的位置，通常用一个大写字母表示，如点A 、点B 。
2.直线（1）直线的表示方法：①可以用这条直线上任意两点的字母（大写）来表示；②用一个小写字母来表示。
（2）直线的基本性质：经过两点有一条直线，并且只有一条直线。
简述为，两点确定一条直线。
（3）直线的特征：①直线没有端点，不可量度，向两方无限延伸； ②直线没有粗细； ③两点确定一条直线；④两条直线相交有唯一一个交点。
（4）点与直线的位置关系：①点在直线上（也可以说这条直线经过这个点）； ②点在直线外（也可以说直线不经过这个点）。
（5）两条直线的位置关系有两种——相交、平行 3.射线：直线上一点和它一旁的部分叫做射线。
(1)射线的表示方法：①用两个大写字母表示，表示端点的字母写在前面，在两个字母前加上“射线”； ②用一个小写字母表示。
(2)射线的性质：①射线是直线的一部分；②射线只向一方无限延伸，有一个端点，不能度量、不能比较长短； ③射线上有无穷多个点；④两条射线的公共点可能没有，可能只有一个，可能有无穷多个。
4.线段：直线上两点和它们之间的部分叫做线段。
（1）线段的特点：线段是直的，它有两个端点，它的长度是有限的，可以度量，可以比较长短。
（2）线段的表示方法：①用两个端点的大写字母表示； ②用一个小写字母表示。
（3）线段的基本性质：两点的所有连线中，线段最短。
初一数学第四单元图形初步认识及测试题
一、选择题 1、下图中几何体的左视图为（ ）
2、一个立体图形的三视图如图所示，则它是 （ ） A．圆锥 B．圆柱 C．三棱锥 D．四棱锥
第二题
3、下图，把左边的图形绕着给定直线旋转一周后可能形成的几何体是．．．．．．．( )
4、下图是由一些相同的小正方体搭成的几何体的 三视图，则搭成这个几何体的小正方体的个数是 （ ）
初一数学第四单元图形初步认识及测试题
知识网络：概念、定义： 1、 我们把实物中抽象的各种图形统称为几何图形（geometric figure）。2、有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一平面内，它们是立体图形（solidfigure）。3、有些几何图形（如线段、角、三角形、长方形、圆等）的各部分都在同一平面内，它们是平面图形（planefigure）。4、将由平面图形围成的立体图形表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图（net）。5、几何体简称为体（solid）。6、包围着体的是面（surface），面有平的面和曲的面两种。7、面与面相交的地方形成线（line），线和线相交的地方是点（point） 8、点动成面，面动成线，线动成体。
第9题
9、如图是某几何体的展开图，则该几何体是＿＿＿＿＿。
10、一个角等于它的余角，则这个角是_______ 。
11、如图是一个正方体的平面展开图，若图中的“进”表示正方体的前面，“步”表示右面，“习”表示下面，则“祝”、“你”、“学”分别表示正方体的_____、_________、______。
主视图
左视图
俯视图
5、在海上，灯塔位于一艘船的北偏东40°方向， 则这艘船位于灯塔的（ ） A、南偏西40° B、南偏西50 ° C、北偏东40° D、北偏东50°
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 图形的初步认识基础知识【一】
一、几何图形 1、常见几何图形：
平面图形
—
几何图形 柱体
立体图形 球体
锥体
2、从不同方向看：
3、立体图形展开图：
圆柱
棱柱
圆锥
棱锥
4、点、线、面、体
组成图形的最基本元素是。
（1）动态：点动成，线动成，面动成。
举例：
（2）静态：线与线相交成，
面与面相交成，
面与面围成。
二、直线、射线、线段
1、基本概念：
2、直线公理：
（1）经过两点，有一条直线并且只有一条直线。
简述：（2）应用举例：
（3）两条直线相交，有且只有一个交点。
3、线段公理
（1）两点之间最短。
（2）应用举例： （3）两点间距离定义： 4、线段的中点：
线段中点的定义：
注：类比线段的三、四…等分点 5、线段的比较：
（1）已知线段a ，画一条线段等于线段a
（2）线段比较方法：
三、角
1、角的有关概念：
角的定义： 2、角的比较方法：
3、角的度量：
1°= ′ 1′= ″ 1°= ″
M AB M AB AM =BM
1AM ==AB AM =
AB 2
AB=AM =2 M AB ∴∴ （1）点是线段的中点 （2）点在线段上，（ ）（ ）（或， ）
（ ）（ ）点是线段的中点a
a b
4、如图，在下面的横线上填上适当的角； （1）∠AOC=∠ +∠ ； （2）∠AOB=∠ －∠ ；
或∠AOB=∠ －∠ ；
（3）若∠AOC=∠BOD ，则∠AOB ∠COD （填“>”、“<”或“=”）； （4）若∠AOB=∠COD ，则∠AOC ∠BOD
）。
5、角的平分线：
角平分线的定义：
6、余角和补角：
（1）余角定义：
（2）补角定义： （3）等角的余角相等；等角的补角相等。
如图：∠AOC=∠BOD=90°， 试说明∠AOB 和∠COD 的关系。
如图：直线AB 、CD 相较于点O ，
试说明∠AOC 和∠BOD 的关系。
O
O C AO B AO C =BO C AO C ==AO B AO B=AO C =2 O C AO B ∠∠∠∴∠∠∠∠∴∠ （1）
射线是的平分线 （2）（ ）（ ）（或 ）（ ）（ ）射线是的平分线
第四章【图形的认识初步】复习过关检测
检测时间：45分钟，满分：100分
班级姓名得分
一、填空题：
1．正方体有______条棱，_____个顶点，个面.
2．请同学们手拿一枚硬币，将其立在桌面上用力一转，它形成的是一个体,由此说明________________.
3．已知线段AB＝6cm，在直线AB上画线段AC＝2cm，则BC的长是_________cm．
4．讲台上放着一个圆锥和一个正方体（如图）请说明下面的三幅图分别是从哪个方向看到的。
（1）从面看到的平面图形；（2）从面看到的平面图形；（3）从面看到的平面图形。
5．已知，如图，∠1＝∠2，∠3＝∠4，∠AOF＝︒
=
∠90
2
1
AOB.
（1）射线OD是∠AOC的_______；（2）∠AOC的补角是____________；（3）________是∠AOC的余角；（4）∠DOC的余角是____________；（5）∠COF的补角____________.
6．已知一个角的补角比这个角的余角3倍大10°，则这个角的度数是．
(第6题)
(第7题)
7.当10kg的菜放在称上时，指示盘上的指针转了180°，当1.5kg的菜放称上时，指针转过度，若指针转了36°，这些菜有___kg．8．北京时间2点30分，钟面上的时针和分针的夹角为度。
9．用一副三角板可以画的角共有______个锐角______个钝角. 10．如图，折叠围成一个正方体时，数字会
在与数字2所在的平面相对的平面上。
二、选择题：
11．平面上有五个点，经过这些点最多可以作直线的条数（）A．6条 B.8条 C.10条 D.12条
12．下列图形中，图中共有8个角的是 ( )
A． B. C. D.
13．把一张报纸的一角斜折过去，使A点落在E点处，BC为折痕，BD是∠EBM的平分线，则∠CBD＝（）
A.85°
B.80°
C.75°
D.90°
14．如图，AB=16 cm，C是AB上一点，且AC=10 cm，D是AC的中点，E是BC的中点，则线段DE的长度为( )
A．6 cm B.8 cm C.10 cm D.12cm
15．如图，能用∠1，∠ACB，∠C三种方法表示同一个角的是( )
16.下图中是正方体的展开图的共有（ ） A ．1个 B.2个 C.3个 D.4个
三、解答题： 17．如图，12B C
A B
=，D 为AC 的中点，2D C
cm
=，求AB 的长．
18. 已知：如图，点C 是线段AB 上一点，且3AC =2AB ．D 是AB 的中点，E 是CB 的中点，DE =6，求：（1）AB 的长 ；（2）求AD ：CB ．
19. 已知2αβ
∠=∠，α∠的余角的3倍等于β∠的补角，求α∠、β∠的
度数．
20．如图，有一个几何体，请画出从不同方向看它的平面图形
(1)从正面看；(2)从左面看；(3)从上面看
21．如图，直线AB与CD相交于点O，OE⊥CD，OF⊥AB，∠DOF=65°。
求：（1）∠BOE的度数；
（2）∠AOC的度数。
22、灯塔A在灯塔B的南偏东60°方向上，A、B相距30海里，轮船C在B的正南方向，在灯塔A的南偏西60°方向上，通过画图（用1个单位代表10海里）确定轮船C的位置，求∠BAC和∠ACB的度数，并求出轮船C与灯塔B的距离．
23、如图，（1）已知∠AOB为直角，∠AOC为锐角，OE平分∠BOC，
OF平分∠AOC，求∠EOF的度数；（2）若将（1）中的
条件“∠AOB为直角”改为“∠AOB为任意一个角”，
则∠AOB与∠EOF的大小关系如何？发现结论并说明
理由．。