图形的初步认识测试题
七年级上册数学单元测试卷-第二章 几何图形的初步认识-冀教版(含答案)

七年级上册数学单元测试卷-第二章几何图形的初步认识-冀教版(含答案)一、单选题(共15题,共计45分)1、将一副三角尺按不同位置摆放,摆放方式中∠α与∠β互余的是()A. B. C. D.2、如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为()A. B. C. D.33、把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A-45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为()A. B.5 C.4 D.4、下列语句错误的有①近似数0.010精确到千分位②如果两个角互补,那么一个是锐角,一个是钝角③若线段,则P一定是AB中点④A与B两点间的距离是指连接A、B两点间的线段A.4个B.3个C.2个D.1个5、如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后向下平移2个单位,则A 点的对应点的坐标为( )A. B. C. D.6、如图,在△ABC中,∠B=90°,AB=4,BC=3,将△ABC绕点A逆时针旋转,使点B落在线段AC上的点D处,点C落在点E处,则C、E两点间的距离为()A. B.2 C.3 D.27、若∠A=30°18′,∠B=30°15′30″,∠C=30.25°,则这三个角的大小关系正确的是()A.∠C>∠A>∠BB.∠C>∠B>∠AC.∠A>∠C>∠B D.∠A>∠B>∠C8、如图,在△ABC 中,∠ABC=40°,在同一平面内,将△ABC 绕点 B 逆时针旋转 100°到△A′BC′的位置,则∠ABC′=()A.40°B.60°C.80°D.100°9、北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,過极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道在点O南偏东70°的方向上,则这条跑道所在射线与正北方向所成角的度数为()A.160°B.110°C.70°D.20°10、下列说法中正确的有( )(1)过两点有且只有一条直线(2)连接两点的线段叫两点的距离(3)两点之间线段最短(4)如果AB=BC,则点B是线段AC的中点A.1B.2C.3D.411、如图,将绕点C顺时针旋转得到,使点A的对应点D恰好落在边上,点B的对应点为E,连接.下列结论一定正确的是()A. B. C. D.12、如图,在△ABC中,∠ACB=90°,将△ABC绕着点A逆时针旋转得到△ADE,点C落在边AD上,连接BD.若∠DAE=α,则用含α的式子表示∠CBD的大小是()A.αB.90°﹣αC.D.13、如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是()A.70°B.35°C.40°D.50°14、如图1,在矩形ABCD中,AB=1,BC=.将射线AC绕着点A顺时针旋转α(0°<α≤180°)得到射线AE,点M与点D关于直线AE对称.若x=,图中某点到点M的距离为y,表示y与x的函数关系的图象如图2所示,则这个点为图1中的()A.点AB.点BC.点CD.点D15、下图是几种汽车轮毂的图案,图案绕中心旋转90°后能与原来的图案重合的是()A. B. C. D.二、填空题(共10题,共计30分)16、40°的补角等于________;40°18′的余角等于________.17、如图中的图形绕着中心至少旋转________度能与自身重合.18、计算:=________度.19、如图所示的圆柱体中底面圆的半径是,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是________.(结果保留根号).20、如图,平分,平分,,,则的度数为________.21、一个角的余角比它的补角的还少20°,则这个角是________.22、如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是________.23、如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结AA′,若∠1=20°,则∠B=________度.24、如图,将Rt△ABC的斜边AC绕点C顺时针旋转()得到CD,直角边BC绕点C逆时针旋转()得到CE,若AC=5,BC=4,且,则DE=________.25、一个角的补角加上14°,等于这个角的余角的5倍,这个角的度数是________°.三、解答题(共5题,共计25分)26、已知有一个长为5cm,宽为3cm的长方形,若以这个长方形的一边所在的直线为轴,将它旋转一周,你能求出所得的几何体的表面积吗?27、如图1是三个直立于水面上的形状完全相同的几何体(下底面为圆面,单位:厘米),将它们拼成如图2的新几何体,求该新几何体的体积(结果保留π).28、已知:如图,线段MN=m,延长MN到点C,使NC=n,点A为MC的中点,点B为NC的中点,求线段AB的长.29、已知线段AB=12,点D、E是线段AB的三等分点,求线段BD的长.30、如图,已知是的余角,是的补角,且,求、的度数.参考答案一、单选题(共15题,共计45分)1、C2、B3、B4、B5、B6、A7、D8、B9、B10、B11、D12、A13、C14、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
七年级数学上学期第四单元几何图形初步测试卷5套带答案
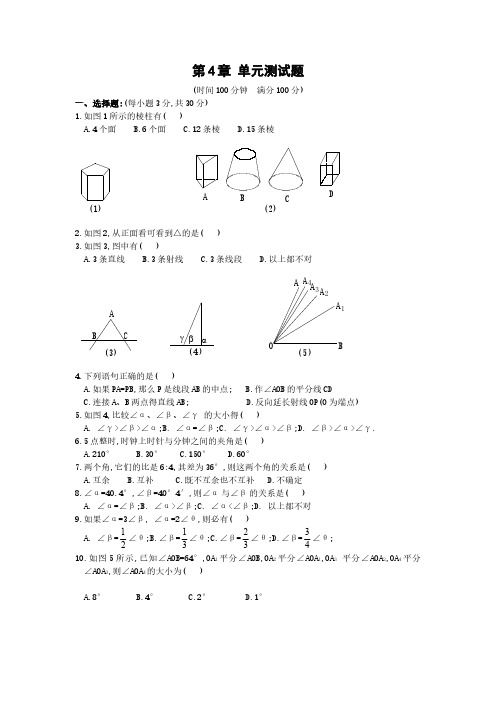
第4章 单元测试题(时间100分钟 满分100分)一、选择题:(每小题3分,共30分)1.如图1所示的棱柱有( )A.4个面B.6个面C.12条棱D.15条棱C(2)A DB2.如图2,从正面看可看到△的是( )3.如图3,图中有( )A.3条直线B.3条射线C.3条线段 D.以上都不对4.下列语句正确的是( )A.如果PA=PB,那么P是线段AB的中点;B.作∠AOB的平分线CDC.连接A、B两点得直线AB;D.反向延长射线OP(O为端点)5.如图4,比较∠α、∠β、∠γ 的大小得( )A. ∠γ>∠β>∠α;B. ∠α=∠β;C. ∠γ>∠α>∠β;D. ∠β>∠α>∠γ.6.5点整时,时钟上时针与分钟之间的夹角是( )A.210°B.30°C.150°D.60°7.两个角,它们的比是6:4,其差为36°,则这两个角的关系是( )A.互余B.互补C.既不互余也不互补D.不确定8.∠α=40.4°,∠β=40°4′,则∠α与∠β的关系是( )A. ∠α=∠β;B. ∠α>∠β;C. ∠α<∠β;D. 以上都不对9.如果∠α=3∠β, ∠α=2∠θ,则必有( )2310.如图5所示,已知∠AOB=64°,OA1平分∠AOB,OA2平分∠AOA1,OA3平分∠AOA2,OA4平分∠AOA3,则∠AOA4的大小为( )A.8°B.4°C.2°D.1°二、填空题:(每小题3分,共30分)11.已知线段AB=8cm,延长AB 至C,使AC=2AB,D 是AB 中点,则线段CD=______.12.如图,从城市A 到城市B 有三种不同的交通工作:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为___________.13.57.32°=_______°_______′_______″;27°14′24″=_____°.14.已知∠a=36°42′15″,那么∠a 的余角等于________.15.∠1+∠2=180°,∠2+∠3=180°,根据________,得∠1=∠3.16.表示O 点南偏东15°方向和北偏东25°方向的两条射线组成的角等于____17.如图,∠AOC=90°,∠AOB=∠COD,则∠BOD=______°.航线铁路公路(6)A B18.102°43′32″+77°16′28″=________;98°12′25″÷5=_____.19.已知线段AB=acm,点A 1平分AB,A 2平分AA 1,A 3平分AA 2,……,____________cm.20.在平面上有任意四点,过其中任意两点画直线,能画_______条直线.三、解答题:(21、24、25、26每题6分,22、23题每题8分)21.根据下列语句画图:(1)画∠AOB=120°;(2)画∠AOB 的角平分线OC;(3)反向延长OC 得射线OD;(4)分别在射线OA、OB、OD 上画线段OE=OF=OG=2cm;(5)连接EF、EG、FG;(6)你能发现EF、EG、FG 有什么关系?∠EFG、∠EGF、∠GEF 有什么关系?22.已知线段AB=10cm,直线AB 上有一点C ,且BC=4cm,M 是线段AC 的中点,求AM 的长.23.如图,直线AB、CD 交于O 点,且∠BOC=80°,OE 平分∠BOC,OF 为OE 的反向延长线.(1)求∠2和∠3的度数.(2)OF平分∠AOD吗?为什么?24.一个角的补角与它的余角的度数之比是3:1,求这个角的度数.25.测量员沿着一块地的周围测绘.从A向东走600米到B,再从B向东南(∠ABC= 135°)走500米到C,再从C向西南(∠BCD=90°)走800米到D.用1厘米代表100米画图, 求DA的长(精确到10米)和DA的方向(精确到1°).北D CA B26.利用线段、角、三角形、圆等图形为你的学校设计一个校标,并简述你的设计思路.参考答案一、选择题1.D2.C3.C4.D5.C6.C7.B8.B9.C 10.B二、填空题11.12cm 12.两点之间,线段最短 13.57、19、12;27.2414. 53°17′45″ 15.同角的补角相等16.140° 17.90 18.180°;19°38′29″. 19. 20.1或4或6三、解答题21.(6)EF=EG=FG,∠EFG=∠EGF=∠FEG=60°22.AM=7cm或3cm23.(1)∠2=100°,∠3=40°;(2)∠AOF=40°,OF平分∠AOD24.设这个角为x0,( 180-x):(90-x)=3:1,x=45.第4章 单元测试题2检测时间:45分钟,满分:100分班级 学号 姓名 得分一、填空题:(每空2分,共46分)1.正方体有______条棱,_____个顶点, 个面.2.圆柱的侧面展开图是一个 ,圆锥的侧面展开图是一个 ,棱柱的侧面展开图是一个 。
“图形认识初步”综合测试题

南
王 晓平
_
一
一一 一
、
选 择题
一
1
.
图 1 是
个用 纸 板 做 的空 正 方体盒 子
.
,
夜 间老 鼠在 盒 子上 面 啃出
一
个洞钻 了进去
。
然后顺 利地 在盒子前边 又 啃出
)
.
个 洞 爬 了 出来 把 这 个 盒
.
子展开
其平 面 展 开 图可 能是 (
画
图 I
2
.
鼻音币 加 导口 中 扭
A
一
A
.
0 个
B
.
1
个
C
.
2 个
D
.
3 个
—— I= i 壤 塞 怒
6
.
有
一
个 正 方 体
.
在 它 的 各个 面 上 分 别 标 有 字母A
、
B
,
、
C
、
D
、
E
、
F
甲
、
乙
.
、
丙 三 位 同学 分 别从 三 个 不 同的方 向观 察这 个 正 方 体
,
观 察结 果 如
图 5 那 么
这 个 正 方 体上 标 有 字母 A
.
:
(1 )连 接 两 点 间 的 线 段
一
,
叫做这 两 点 间 的距 离
;
(2 )
两 个 角互 补
其 中
;
一
定有
个 锐角
;
(3 )把
一
个 角分成两 部 分的射线 是 这
一
个 角 的平 分线
(4 )过 3 个 点 中 的 每 两 个 点 画 )
《图形的认识初步》测试题

《图形的认识初步》测试题学号姓名成绩一、选择题(每小题3分,共24分)1、下列说法正确的是()A、直线AB和直线BA是两条直线B、射线AB和射线BA是两条射线C、线段AB和线段BA是两条线段D、直线AB和直线a不能是同一条直线2、下列图中角的表示方法正确的个数有()A、1个B、2个C、3个D、4个3、下面图形经过折叠可以围成一个棱柱的是()4、经过任意三点中的两点可以画出()A、一条直线B、两条直线C、一条或三条直线D、三条直线5、如图,每个图片都是6个相同的正方形组成的,不能折成正方形的是()6、若∠A=20 o 18′,∠B=20 o 15′30〞,∠C=20.25 o,则()A、∠A>∠B>∠CB、∠B>∠A>∠CC、∠A>∠C >∠BD、∠C >∠A >∠B7、如左图所示的正方体沿某些棱展开后,能得到的图形是()8、下列语句正确的是()A、钝角与锐角的差不可能是钝角;B、两个锐角的和不可能是锐角;C、钝角的补角一定是锐角;D、∠α和∠β互补(∠α>∠β),则∠α是钝角或直角。
二、填空题(每空2分,共36分)1、有公共顶点的两条射线分别表示南偏东15o与北偏东25o,则这两条射线组成的角的度数为;2、如图,若CB = 4 cm,DB = 7 cm,且D是AC的中点,则AC = ;3、8:30时,时针与分针的夹角是;4、如图所示,小于平角的角有个;5、如图,从学校A到书店B最近的路线是号路线,其中的道理用数学知识解释应是;6、48 o 15′的余角是 ,补角是 ;7、一个长方体有 个顶点, 条棱, 个面。
8、一周角= 平角= 直角= o9、经过一点有 条直线,经过两点有 条直线;10、n 条直线两两相交,最少有 个交点,最多有 个交点。
三、解答题(每小题6分,共30分)1、如图,∠AOB 是直角,OD 平分∠BOC ,OE 平分∠AOC ,求∠EOD 的度数。
第4章图形的初步认识单元测试卷20212022学年华东师大版七年级上册数学.docx

2021-2022学年华东师大新版七年级上册数学《第4章图形的初步认识》单元测试卷一. 选择题1.有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中A, B, C,。
中的()位置接正方形.2.下列几何体中,是圆锥的为(4.如图所示的物体是一个几何体,从正面看到的图形是(B. C. D.5.如图是一个由4个相同的正方体组成的立体图形,则它的主视图为(A.天空划过一道流星B.汽车雨刷在挡风玻璃上刷出的痕迹C.抛出一块小石子,石子在空中飞行的路线D.旋转一扇门,门在空中运动的痕迹9.把14个棱长为1的正方体在地面上堆叠如图所示的立体,然后将露出的表面部分涂成红色,那么红色部分的面积为()A. 21B. 24C. 33D. 3710.如图所示是一个三棱柱,画出它的主视图和左视图均正确的是()主视图左视图二. 填空题11 •如果一个六棱柱的一条侧棱长为5cm,那么所有侧棱之和为12.已知圆柱按如图所示方式放置,其左视图的面积为48,则该圆柱的侧面积为主视方向13.请你写出一种几何体,使得它的主视图、左视图和俯视图都一样,它是.14.若一个棱柱有30条棱,那么该棱柱有个面.15.在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是(填上序号即可).16.墙角处有若干大小相同的小正方体堆成如图所示的立体图形,如果你打算搬走其中部分小正方体(不考虑操作技术的限制),但希望搬完后从正面、从上面、从右面用平行光线照射时,在墙面及地面上的影子不变,那么你最多可以搬走个小正方体.I上面7正面17.如图所示,在直角三角形中,以其中一条直角边所在的直线为轴旋转一周,得到几何体的体积为.(结果保留TT)18.长方体是一个立体图形,它有个面,条棱,个顶点.19.一个正〃棱柱共有15条棱,一条侧棱的长为5cm, 一条底面边长为3cm,则这个棱柱的侧面积为cnr.20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体.三. 解答题21.画出如图图形的三视图.23.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为8cm.宽为4cm的长方形,绕它的一条边所在的直线旋转一周,求得到的圆柱体的体积是多少?24.已知一个直棱柱有8个面,它的底面边长都是5ce侧棱长都是4cm.(1)它是几棱柱?它有多少个顶点?多少条棱?(2)这个棱柱的所有侧面的面积之和是多少?25.由7个相同的小立方块搭成的几何体如图所示,(1)请画出它的三视图?(2)请计算它的表面积?(棱长为1)IF而26.如图,如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.图①图②(1) 第1个几何体中只有2个面涂色的小立方体共有 个.第3个几何体中只有2个面涂色的小立方体共有 个.(2) 求出第100个几何体中只有2个面涂色的小立方体的块数.(3) 求出前100个几何体中只有2个面涂色的小立方体的块数的和.27. 如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱, 6个顶点,观察图形,填写下面的空. (1)四棱柱有——个面,_ ___ 条棱,_ __ 个顶点; (2)六棱柱有— —个面,_ ___ 条棱,— __ 个顶点;(3) 由此猜想”棱柱有 个面,条棱,个顶点.三棱柱四棱柱五棱柱六棱柱参考答案与试题解析一.选择题1.解:如图所示:根据立方体的展开图可知,不能选择图中A的位置接正方形.故选:A.2.解:观察可知,C选项图形是圆锥.故选:C.3.解:A、该几何体为四棱柱,不符合题意;3、该几何体为圆锥,不符合题意;C、该几何体为三棱柱,符合题意;D、该几何体为圆柱,不符合题意.故选:C.4.解:该几何体是一个圆台,从正面看到的图形是一个等腰梯形,故选C.5.解:根据题干分析可得,从正面看到的图形是| | ..故选:A.6.解:A、圆柱的主视图和左视图都是长方形,俯视图是圆,故此选项错误;3、长方体的三视图不相同,故此选项错误;。
《图形认识初步》综合测试题(A)

, ,/
不论什么时候 . 只要 你 有 一个 目标 , 就 得 牺 牲 一 定 的 自由去 实 现 它 。—— W.. 姆 你 S毛
, , /
,
4 7
2 . 案 不 唯一 . 如 6答 例 问 : 车 相 向 而行 . 时相 遇 ? 两 何 解: 设 小 时 后 相 遇 , 由题意 , ( 5+4 =4 , 得 3 5 0
Go l e em i asd t r newha o r ongt e t u’eg i b . y o
一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一 一
1
2 . 七年 级 共 有 名 学 生 。 3设 则根 据 题 意 有 +2 = . 得 =3 0 解 6.
60 45
解 得 = .
2
答 : 年 级 共 有 30名 学 生 . 七 6
答: 相向 两车 而行, ÷小时后 相遇.
二
2改 : 一) (一 )7 4 为2 2 3x导 :, . ( 一2
1 . 图中几 何体 , 正 面看 能得 到 ( 2下 从
) .
日] ]
第 l 2题 图 A D
1. 3 同时 经过 平 面 内的三 点可 以作 直线 ( A 一条 . B j条 .
) .
) . C 0条 . D 0条 或一 条 .
1. 图 , 4如 它需 再 添 …个 面 , 叠 后 才能 围成 一个 正 方 体 , 图 中 的黑 色小 正 方形 分 别 由四名 同 折 下
第三单元《图形的初步认识法(一)》--一年级数学上册单元检测卷(苏教版2024秋)(学生版)

第三单元《图形的初步认识(一)》时间:90分钟满分:100分难度系数:0.50(较难)班级:姓名:学号:一、慎重选择(每题1分,共6分)1.(本题1分)(24-25一年级上·江苏·课后作业)元元想画一个〇,他可以使用下面的()号物品来画。
A.B.C.(本题1分)(23-24一年级上·湖北黄石·期末)要将下图的图形拼成一个大正方体,至少还需要()2.个小正方体。
A.5 B.7 C.83.(本题1分)(23-24一年级上·山东滨州·期末)下面能站稳的图形是()。
A.B.C.4.(本题1分)(23-24三年级上·陕西宝鸡·期末)观察同一个立体图形,奇思看到的形状是○,妙想看到的形状是。
这个立体图形是()。
A.球B.圆柱C.长方体5.(本题1分)(23-24一年级下·江西宜春·期末)从下面物体()的表面不能找到长方形。
A.B.C.6.(本题1分)(23-24一年级下·湖北襄阳·期末)用下图做一个,的对面是()。
A.B.C.二、仔细想,认真填(共26分)7.(本题3分)(23-24一年级上·河南周口·期末)(1)一共有( )个图形。
(2)从左边数,排第( );从右边数,排第( )。
8.(本题4分)(23-24一年级上·浙江温州·期末)数一数,填一填。
长方体有( )个,正方体有个,圆柱有( )个,球有( )个。
9.(本题4分)(23-24一年级上·浙江温州·期末)我们来数一数吧!有( )个,有( )个,有( )个,有( )个。
10.(本题6分)(23-24一年级上·江苏盐城·期中)看图填空。
(1)一共有( )个图形,其中有( )个。
(2)的左边有( )个图形,右边有( )个图形。
(3)从右数第( )个和第( )个是。
《图形认识初步》综合测试题(A)

所示 , B平分 厶4 , C平分 LB D, LB C=2 。则 O O OC O O 且 O 5, D=
/ D
1
/
C
A产
。
.
|B /
第 6题 图 第 8题 图
.
…
第 5题 图
果两个 角互补 , 并且 它们 的差是 3 。那 么较 大的角 等于 0,
,
从 地到 曰地有三条路 ① 、 、 可走 , ② ③ 每条路长分别为 z n 图中“广 、 J , ( m, ”“ -
体 块.
c
。
日日
’
— ] I — ] _ 1 J l 图 题
ffII JI l lf
知两 根木 条 , 一根 长 6 0厘米 , 根 长 10厘米 , 它们 的一 端 重合 , 在 同一 条 直 一 0 将 放 两根木条 中点 的距离是 厘米.
\
西 5。 0
E1 / 、 。 \
/
D
南
第 2 图 9题
3 0
分) 1 图 是棱 长 为 口的小 正 方体 , 2 图 3是 由这样 的小 正 方体摆 放 而 的 图形 . 照这 图 、 戈 按
拘方法 继续 摆放 , 自上 而下 分别 叫 做第 l 、 2层 、 … 、 n层 , n层的小 正方 体 的 层 第 … 第 第 毁记做 5 请解 答下列 问题 . 。 I 按要 求填 表 :
4 4
、 一 一一 .、 一 一
人 生 的奋 斗 目标 决 定你 将 成 为 什 么样 的人 。— — 华 盛 顿 ・ 文 欧
tr a ho em a e r a e t p k sge tme n.
.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章 《图形的初步认识》单元检测(1)
得分:______
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题意要求的)
1.下列几何体是三棱柱的是( ).
2.将如图所示的直角三角形绕直线l 旋转一周,得到的立体图形是( ).
3.如图,已知几何体由5个相同的小正方体组成,那么它的左视图是( ).
4.将如图所示表面带有三个图案的正方体沿某些棱展开后,得到的图形是( ).
5.如图,C ,D 是线段AB 上两点,若CB =4 cm ,DB =7 cm ,且D 是AC 的中点,则AC 的长等于( ).
A .3 cm
B .6 cm
C .11 cm
D .14 cm 6.下午2点30分时(如图),时钟的分针与时针所成角的度数为( ).
A .90°
B .105°
C .120°
D .135° 7.若∠A =20°18′,∠B =20°15′30″,∠C
=20.25°,则(
).
A .∠A
>∠B >∠C
B .∠B >∠A >∠
C C .∠A >∠C >∠B
D .∠C >∠A >∠B 8.一个角的余角比它的补角的
1
2
少20°,则这个角为( ). A .30° B .40° C .60° D .75°
9.如图,长方形ABCD 沿AE 折叠,使D 点落在BC 边上的F 点处,如果∠BAF =60°,则∠DAE 等于( ).
A .10°
B .15°
C .20°
D .30° 10.如图∠AOD -∠AOC =( )
A 、∠ADC
B 、∠BO
C C 、∠BO
D D 、∠COD
二、填空题(本大题共8小题,每小题3分,共24分.把答案填在题中横线上) 11.如图,该多面体是__________,它有__________个顶点,有__________条棱,有__________个面.
12.如图,线段AD 上有两点B 、C ,图中共有__________条线段.
13.工人师傅在用方砖铺地时,常常打两个木桩,然后沿着拉紧的线铺砖,这样地砖就铺得整齐,这个事实说明的原理是__________. 14.92.76°=__________度__________分__________秒;22°32′24″=__________度. 15.如图所示,由点A 测得点B 的方向为__________. 16.如图,点A 、O 、B 在一条直线上,且∠AOC =48°32′,OD 平分∠AOC ,则图中∠BOD =__________.
17.如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数是__________个.
18.如图所示,将一副三角板叠放在一起,使直角的顶点重合于
点O ,则∠AOC +∠DOB 的度数为__________.
第4章《图形的初步认识》单元检测(2)
三、解答题(本大题共6小题,共66分.解答应写出文字说明、证明过程或演算步骤) 19.(本题满分8分)A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由.
20.作图题:(不写作法,但要保留作图痕迹)(8分)
已知:如图,线段a、b.
求作:线段AB,使AB=a+2b;
21.如图,线段AB=14cm,C是AB上一点,且AC=9cm,O是AB的中点,求线段OC的长度。
(10分)
22.(本题满分10分)如图是一个几何体的三视图.
(1) 写出这个几何体的名称;
(2) 求此几何体表面展开图的面积.
23.(本题满分10分)如图,已知线段AB,延长AB到C,使BC=
1
2
AB,D为AC的中点,已知DC=3 cm,求线段BD的长.
24.(本题满分10分)如图所示,∠ABC=80°,∠CBD=30°,BE平分∠ABD,求∠CBE的度数.
25.(本题满分10分)如图①,已知线段AB=12 cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB中点,则DE=__________ cm;
(2)若AC=4 cm,求DE的长;
(3)试利用“字母代替数”的方法,说明不论点C运动到什么位置时,DE的长不变;
(4)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE=60°与射线OC的位置无关.
参考答案
1答案:C
2答案:B
3答案:A点拨:左视图是从左面看几何体得到的平面图形.
4答案:C
5答案:B点拨:因为CB=4 cm,DB=7 cm,
所以CD=7-4=3(cm).
因为D是AC的中点,
所以AC=2DC=2×3=6(cm).
6答案:B
7答案:A点拨:因为∠A=20°18′,∠B=20°15′30″,∠C=20.25°=20°15′,所以∠A>∠B>∠C.
8答案:B点拨:设这个角为x°,
根据题意,得
1
(180)
2
x
--(90-x)=20,解得x=40,即这个角为40°.
9答案:B点拨:因为∠BAF=60°,
所以∠F AD=90°-60°=30°.
因为∠DAE=∠F AE,
所以∠DAE=
1
2
×30°=15°.
10答案:B点拨:观察图1和图2可知P代表圆、M代表正方形、N代表三角形,从而可知Q代表线段,故P&Q应为圆与线段组合而成的图形.
11答案:五棱柱10157
12答案:6点拨:图中有线段AB、AC、AD、BC、BD、CD共6条.
13答案:经过两点有且只有一条直线或两点确定一条直线
14答案:92453622.54点拨:因为0.76°=60′×0.76=45.6′,0.6′=60″×0.6=36″,
所以92.76°=92度45分36秒.
因为24″=
24
60
'
⎛⎫
⎪
⎝⎭
=0.4′,32.4′=
32.4
60
⎛⎫
︒
⎪
⎝⎭
=0.54°,
所以22°32′24″=22.54度.
15答案:南偏东58°
16答案:155°44′点拨:∵∠AOC=48°32′,OD平分∠AOC,
∴∠AOD=48°32′÷2=24°16′.
∴∠BOD=180°-∠AOD=155°44′.
17 答案:4或5点拨:如图,该几何体有以下三种情况,其中图①和图②都是由4个小正方体组成的,图③是由5个小正方体组成.
图①图②图③
18答案:180°点拨:∠AOC+∠DOB=∠AOD+∠DOC+∠DOB=∠DOC+∠AOB=90°+90°=180°.
19解:如图,连结AB,交l于点P,点P即为所求.
理由:两点之间,线段最短.
20解:(1)①如图,作射线AM ;②在射线AM 上顺次截取线段AC =a ,CD =DB =b ,则线段AB =a +2b ;
(2)①如图,作∠BOC =∠α;(2)以OC 为一边,在∠BOC 内部作∠AOC =∠β,则∠AOB =∠α-∠β.
21解:(1)圆柱;
(2)此几何体表面展开图的面积为:20π×40+2×π×102=1 000π. 22解:∵D 为AC 的中点,DC =3 cm , ∴AC =2DC =6 cm.
∵BC =
1
2AB , ∴BC =1
3
AC =2 cm.
∴BD =CD -BC =1 cm. 23解:∵∠ABC =80°,∠CBD =30°, ∴∠ABD =110°.
∵BE 平分∠ABD ,∴∠ABE =55°. ∴∠CBE =∠ABC -∠ABE =80°-55°=25°. 24解:(1)6;
(2)∵AB =12 cm ,AC =4 cm , ∴BC =8 cm.
∵点D 、E 分别是AC 和BC 的中点, ∴CD =2 cm ,CE =4 cm. ∴DE =6 cm.
(3)设AC =a cm , ∵AB =12 cm , ∴BC =(12-a ) cm.
∵点D ,E 分别是AC 和BC 的中点,
∴CD =
1 cm 2a ,CE =1
(12)2
a - cm. ∴DE =CD +CE =1111
(12)62222
a a a a +-=+-=6(cm).
∴不论点C 运动到什么位置时,DE 的长不变.
(4)∵OD ,OE 分别平分∠AOC 和∠BOC , ∴∠DOE =∠DOC +∠COE =
12(∠AOC +∠COB )=1
2
∠AOB . ∵∠AOB =120°,∴∠DOE =60°.
∴∠DOE 的度数与射线OC 的位置无关.。
