四边形动点问题(一)
四边形动点问题
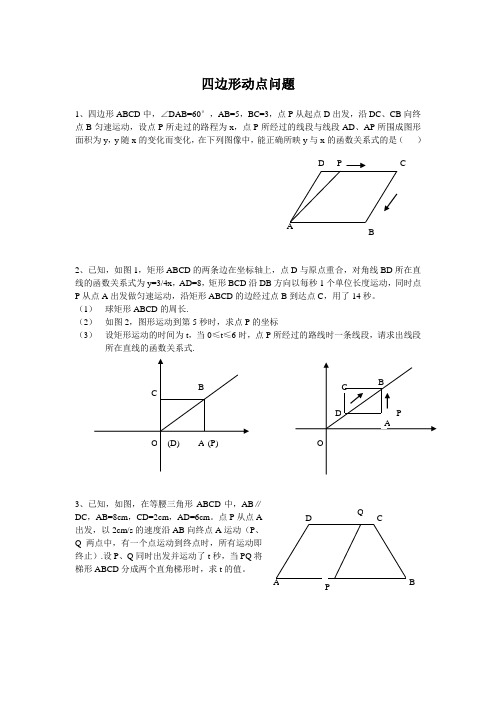
四边形动点问题1、四边形ABCD 中,∠DAB=60°,AB=5,BC=3,点P 从起点D 出发,沿DC 、CB 向终点B 匀速运动,设点P 所走过的路程为x ,点P 所经过的线段与线段AD 、AP 所围成图形面积为y ,y 随x 的变化而变化,在下列图像中,能正确所映y 与x 的函数关系式的是( )2、已知,如图1,矩形ABCD 的两条边在坐标轴上,点D 与原点重合,对角线BD 所在直线的函数关系式为y=3/4x ,AD=8,矩形BCD 沿DB 方向以每秒1个单位长度运动,同时点P 从点A 出发做匀速运动,沿矩形ABCD 的边经过点B 到达点C ,用了14秒。
(1) 球矩形ABCD 的周长.(2) 如图2,图形运动到第5秒时,求点P 的坐标(3) 设矩形运动的时间为t ,当0≤t ≤6时,点P 所经过的路线时一条线段,请求出线段所在直线的函数关系式.3、已知,如图,在等腰三角形ABCD 中,AB ∥DC ,AB=8cm ,CD=2cm ,AD=6cm 。
点P 从点A 出发,以2cm/s 的速度沿AB 向终点A 运动(P 、Q 两点中,有一个点运动到终点时,所有运动即终止).设P 、Q 同时出发并运动了t 秒,当PQ 将梯形ABCD 分成两个直角梯形时,求t 的值。
4.如图,在平面直角坐标系中,O 时原点,A 、B 、C 三点的坐标分别为A (18,0)、B (18,6)、C (8,6),四边形OABC 时梯形,点P 、Q 同时从原点出发,分别作匀速运动,其中点P 沿OA 向终点A 运动,速度为每秒1个单位长度,点Q 沿OC 。
CB 向终点运动,当着两点中有一点到达自己的终点时,另一点也停止运动。
设从出发起运动了运动了t 秒,如果点Q 的速度为每秒2个单位长度,试写出点Q 的坐标,并写出此时t 的取值范围 .5.已知,如图,在矩形ABCD 中,AB=1/3AD=3cm ,点Q 从A 点出发,以1cm/s 的速度沿AD 向终点D 运动,点P 从点C 出发,以1cm/s 的速度沿CB 向终点运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t 秒。
四边形动点问题解题技巧

四边形动点问题解题技巧引言四边形动点问题是数学中常见的一个问题,也称为四边形运动几何问题。
它涉及到一个四边形,其中三个顶点是固定不动的,而第四个顶点在运动当中。
本文将介绍四边形动点问题的基本概念和解题技巧,以帮助读者更好地理解和解决这类问题。
基本概念在开始讨论四边形动点问题之前,我们先来了解一些基本概念:1.四边形:四边形是由四个线段连接在一起形成的几何图形。
它有四个顶点和四条边。
2.动点:动点是指在一定时间内位置发生改变的点。
在四边形动点问题中,通常涉及到一个顶点作为动点,其位置会随着时间的变化而变化。
解题技巧解决四边形动点问题的关键是要能够分析和利用几何图形的性质。
以下是一些常用的解题技巧:折线法折线法是解决四边形动点问题的常用方法之一。
具体步骤如下:1.根据题目所给条件,确定四边形的固定顶点和动点。
2.假设动点在某一时刻位于四边形的某个位置,通过分析几何性质,确定其他顶点和边的位置。
3.根据动点随时间的变化,得出四边形其他顶点和边的变化规律。
4.利用求解几何图形的方法,求出动点的运动轨迹。
5.根据题目要求,确定动点的最终位置或特性。
共线关系在解决四边形动点问题时,有时可以利用共线关系来简化求解过程。
当四边形的三个固定顶点及其对应的边共线时,可以利用相似三角形的性质来求解动点的位置。
各种特殊情况的考虑在解决四边形动点问题时,有时需要考虑一些特殊情况,如四边形退化为三角形的情况、四边形退化为直线的情况等。
针对不同的特殊情况,需要采取相应的分析方法和解题技巧。
解题示例下面通过一个具体的例子来演示如何应用解题技巧解决四边形动点问题。
例题:一个矩形的两个对角线交于点O,其中一个顶点A固定不动,另一个顶点B在矩形的一侧边上以一定速度向下移动。
求矩形的另外两个顶点C和D的运动轨迹。
解答: 1. 设矩形的高为h,宽为w,动点B的初始位置为(0, h)。
2.假设动点B的坐标为(x, y),根据矩形的性质,可以确定顶点C和D的坐标:–顶点C的坐标为(x+w, y);–顶点D的坐标为(x+w, y-h)。
动点点问题专题训练参考答案

动点问题专题训练参考答案 1.(1)相等理由是:因为四边形ABCD 、EFGH 是矩形, 所以,,EGH EGF ECN ECP CGQ CGM S S S S S S ∆∆∆∆∆∆===所以,EGH ECP CGM EGF ECN CGQ S S S S S S ∆∆∆∆∆∆--=-- 即:S S '= ………… (2)AB =3,BC =4,AC =5,设AE =x ,则EC =5-x ,34(5),,55PC x MC x =-=所以12(5)25S PC MC x x ==- ,即21212(05)255S x x x =-+≤≤ 配方得:2125()3252S x =--+,所以当52x =时, S 有最大值3(3)当AE =AB =3或AE =BE =52或AE =3.6时,ABE ∆是等腰三角形.……(每种情况得1分)2.解:(1)点 M ···························· 1分(2)经过t 秒时,NB t =,2OM t = 则3CN t =-,42AM t =- ∵BCA ∠=MAQ ∠=45∴ 3QN CN t ==- ∴ 1 PQ t =+ ·················· 2分 ∴11(42)(1)22AMQ S AM PQ t t ==-+ △ 22t t =-++ ······························ 3分∴2219224S t t t ⎛⎫=-++=--+ ⎪⎝⎭ ····················· 5分∵02t ≤≤∴当12t =时,S 的值最大. ················· 6分 (3)存在. ····························· 7分 设经过t 秒时,NB =t ,OM=2t 则3CN t =-,42AM t =-∴BCA ∠=MAQ ∠=45······················ 8分①若90AQM ∠= ,则PQ 是等腰Rt △MQA 底边MA 上的高 ∴PQ 是底边MA 的中线 ∴12PQ AP MA == ∴11(42)2t t +=- ∴12t =∴点M 的坐标为(1,0) ······················· 10分②若90QMA ∠= ,此时QM 与QP 重合 ∴QM QP MA ==∴142t t +=- ∴1t =∴点M 的坐标为(2,0) ······················· 12分3.(1)设动点出发t 秒后,点P 到达点A 且点Q 正好到达点C 时,BC BA t ==,则1630,102BPQ S t t ∆=⨯⨯=∴=(秒)则()()10,2BA cm AD cm ==; (2)可得坐标为()()10,30,12,30M N (3)当点P 在BA 上时,()213sin 010210y t t B t t =⨯⨯⨯=≤<; 当点P 在DC 上时,()()1101859012182y t t t =⨯⨯-=-+<≤ 图象略4.解:(1)t =(50+75+50)÷5=35(秒)时,点P 到达终点C .……………(1分)此时,QC =35×3=105,∴BQ 的长为135-105=30. ………………(2分) (2)如图8,若PQ ∥DC ,又AD ∥BC ,则四边形PQCD 为平行四边形,从而PD =QC ,由QC =3t ,BA +AP =5t 得50+75-5t =3t ,解得t =1258.经检验,当t =1258时,有PQ ∥DC .………(4分)(3)①当点E 在CD 上运动时,如图9.分别过点A 、D 作AF ⊥BC 于点F ,DH ⊥BC 于点H ,则四边形 ADHF 为矩形,且△ABF ≌△DCH ,从而FH = AD =75,于是BF =CH =30.∴DH =AF =40.图9H图8又QC =3t ,从而QE =QC ·tan C =3t ·CHDH =4t .(注:用相似三角形求解亦可) ∴S =S ⊿QCE =12QE ·QC =6t 2;………………………………………………………(6分)②当点E 在DA 上运动时,如图8.过点D 作DH ⊥BC 于点H ,由①知DH =40,CH =30,又QC =3t ,从而ED =QH =QC -CH =3t -30.∴S = S 梯形QCDE =12(ED +QC )DH =120 t -600.…………………………(8分)(4)△PQE 能成为直角三角形. ……………………………………………………(9分) 当△PQE 为直角三角形时,t 的取值范围是0<t ≤25且t ≠1558或t =35. …(12分)(注:(4)问中没有答出t ≠1558或t =35者各扣1分,其余写法酌情给分) 下面是第(4)问的解法,仅供教师参考:①当点P 在BA (包括点A )上,即0<t ≤10时,如图9.过点P 作PG ⊥BC 于点G ,则PG =PB ·sin B =4t ,又有QE =4t = PG ,易得四边形PGQE 为矩形,此时△PQE 总能成为直角三角形.②当点P 、E 都在AD (不包括点A 但包括点D )上,即10<t ≤25时,如图8. 由QK ⊥BC 和AD ∥BC 可知,此时,△PQE 为直角三角形,但点P 、E 不能重合,即 5t -50+3t -30≠75,解得t ≠1558. ③当点P 在DC 上(不包括点D 但包括点C ), 即25<t ≤35时,如图10.由ED >25×3-30=45, 可知,点P 在以QE =40为直径的圆的外部,故 ∠EPQ 不会是直角.由∠PEQ <∠DEQ ,可知∠PEQ 一定是锐角. 对于∠PQE ,∠PQE ≤∠CQE ,只有当点P 与C 重合,即t =35时,如图11,∠PQE =90°,△PQE 为直角三角形.综上所述,当△PQE 为直角三角形时,t 的取值范围是0<t ≤25且t ≠1558或t =35. 5.解:(1)在矩形OABC 中, 60OA =,80OC =,100OB AC ∴===.……………………1分PT OB ⊥ ,Rt Rt OPT OBC ∴△∽△. PT OP BC OB ∴=,即560100PT t =,3y PT t ∴==.……3分 当点P 运动到C 点时即停止运动,此时t 的最大值为80165=. 图10(P )图11所以,t 的取值范围是016t ≤≤. ··················· 4分 (2)当O 点关于直线AP 的对称点O '恰好在对角线OB 上时,A T P ,,三点应在一条直线上(如答图2).……………………5分 AP OB ∴⊥,12∠=∠.Rt Rt AOP OCB ∴△∽△,OP AO CB OC ∴=. 45OP ∴=.∴点P 的坐标为(450),.…………6分设直线AP 的函数解析式为y kx b =+.将点(060)A ,和点(450)P ,代入解析式,得60045.a b k b =+⎧⎨=+⎩,解这个方程组,得4360.k b ⎧=-⎪⎨⎪=⎩,∴此时直线AP 的函数解析式是4603y x =-+.·············· 8分 (3)由(2)知,当4595t ==时,A T P ,,三点在一条直线上,此时点A T P ,, 不构成三角形.故分两种情况:(i )当09t <<时,点T 位于AOP △的内部(如答图3).过A 点作AE OB ⊥,垂足为点E ,由AO AB OB AE = 可得48AE =.APT AOP ATO OTP S S S S ∴=--△△△△211160544843654222t t t t t t =⨯⨯-⨯⨯-⨯⨯=-+. ············ 10分 若14APT OABC S S =△矩形,则应有26541200t t -+=,即292000t t -+=.此时,2(9)412000--⨯⨯<,所以该方程无实数根.所以,当09t <<时,以A P T ,,为顶点的APT △的面积不能达到矩形OABC 面积的14. ······························ 11分(ii )当916t <≤时,点T 位于AOP △的外部.(如答图4)此时2654APT ATO OTP AOP S S S S t t =+-=-△△△△. ············· 12分 若14APT OABC S S =△矩形,则应有26541200t t -=,即292000t t --=.解这个方程,得192t +=,2902t =<(舍去).(第28题答图3)(第28题答图2)由于288162525>=,991722t +∴=>=.而此时916t <≤,所以t =所以,当916t <≤时,以A P T ,,为顶点的APT △的面积也不能达到矩形OABC 面积的14. 综上所述,以A PT ,,为顶点的APT △的面积不能达到矩形O A B C 面积的14.--------14分6.解:(1)AB y ∥轴. ························· 1分理由: Rt OAB △中,tan :ABO OA OB ∠==30ABO ∴∠=. ···· 2分 设AB 交OP 于点Q ,交x 轴于点S , 矩形的对角线互相平分且相等,则QO QB =,30QOB ∴∠= ,过点M 作MT x ⊥轴于T ,则t a n M O T ∠=,30MOT ∴∠= ,60BOS ∴∠= ,90BSO ∴∠= ,AB y ∴∥轴.······· 3分(2)设l 在运动过程中与射线OM 交于点C ,过点A 且垂直于射线OM 的直线交OM 于点D ,过点B 且垂直于射线OM 的直线交OM 于点E ,则OC t =.2OP t =+ ,)OB t ∴=+,3(2)4OE t =+,1(2)2OA t =+,1(2)4OD t =+.····································· 4分①当10(2)4t t <+≤,即203t <≤时,23S =. ············· 6分 ②当13(2)(2)44t t t +<+≤,即263t <≤时,设直线l 交OB 于F ,交PA 于G ,则OF t =,PG ==,AG PA ∴==,211(2)22322426S t ⎛⎫=-++=+- ⎪ ⎪⎝⎭. ·········· 8分 ③当3(2)4t t >+,即6t >时,2CP = ,114)(2)22S S t t∴=-⨯=+⨯+矩22)t=+=+-………………………………………………10分7.(1)34PM=,(2)2t=,使PNB PAD△∽△,相似比为3:2(3)PM AB CB AB AMP ABC∠=∠⊥,⊥,,AMP ABC△∽△,PM AMBN AB∴=即()PM a t t a tPMt a a--==,,(1)3t aQMa-=-当梯形PMBN与梯形PQDA的面积相等,即()()22QP AD DQ MP BN BM++=()33(1)()22t a t ta a t t ta a-⎛⎫⎛⎫-+--+⎪ ⎪⎝⎭⎝⎭==化简得66ata=+,3t≤,636aa∴+≤,则636a a∴<≤,≤,(4)36a<≤时,梯形PMBN与梯形PQDA的面积相等∴梯形PQCN的面积与梯形PMBN的面积相等即可,则CN PM=()3ta t ta∴-=-,把66ata=+代入,解之得a=±a=所以,存在a,当a=PMBN与梯形PQDA的面积、梯形PQCN的面积相等.8.(1)因为四边形ABCD是平行四边形,所以AB DG········· 1分所以,B GCE G BFE∠=∠∠=∠所以BEF CEG△∽△························· 3分(2)BEF CEG△与△的周长之和为定值.················· 4分理由一:过点C作FG的平行线交直线AB于H,因为GF⊥AB,所以四边形FHCG为矩形.所以FH=CG,FG=CH因此,BEF CEG△与△的周长之和等于BC+CH+BH由BC=10,AB=5,AM=4,可得CH=8,BH=6,所以BC +CH +BH =24 ·························· 6分 理由二:由AB =5,AM =4,可知在Rt△BEF 与Rt△GCE 中,有:4343,,,5555EF BE BF BE GE EC GC CE ====,所以,△BEF 的周长是125BE , △ECG 的周长是125CE 又BE +CE =10,因此BEF CEG 与的周长之和是24. ··········· 6分(3)设BE =x ,则43,(10)55EF x GC x ==- 所以21143622[(10)5]2255255y EF DG x x x x ==-+=-- ········· 8分 配方得:2655121()2566y x =--+. 所以,当556x =时,y 有最大值. ····················· 9分最大值为1216. ······························ 10分9.(1)证明:设11()E x y ,,22()F x y ,,AOE △与FOB △的面积分别为1S ,2S ,由题意得11ky x =,22k y x =.1111122S x y k ∴==,2221122S x y k ==. 12S S ∴=,即AOE △与FOB △的面积相等.(2)由题意知:E F ,两点坐标分别为33k E ⎛⎫⎪⎝⎭,,44k F ⎛⎫ ⎪⎝⎭,,1111432234ECF S EC CF k k ⎛⎫⎛⎫∴==-- ⎪⎪⎝⎭⎝⎭△, 11121222EOF AOE BOF ECF ECF ECF AOBC S S S S S k k S k S ∴=---=---=--△△△△△△矩形11112212243234OEF ECF ECF S S S k S k k k ⎛⎫⎛⎫∴=-=--=--⨯-- ⎪⎪⎝⎭⎝⎭△△△2112S k k ∴=-+. A M xH GFED CB当161212k =-=⎛⎫⨯- ⎪⎝⎭时,S 有最大值.131412S -==⎛⎫⨯- ⎪⎝⎭最大值.(3)解:设存在这样的点F ,将CEF △沿EF 对折后,C 点恰好落在OB 边上的M 点,过点E 作EN OB ⊥,垂足为N . 由题意得:3EN AO ==,143EM EC k ==-,134MF CF k ==-, 90EMN FMB FMB MFB ∠+∠=∠+∠= ,EMN MFB ∴∠=∠.又90ENM MBF ∠=∠=,ENM MBF ∴△∽△.EN EM MB MF ∴=,11414312311331412k k MB k k ⎛⎫-- ⎪⎝⎭∴==⎛⎫-- ⎪⎝⎭, 94MB ∴=. 222MB BF MF += ,222913444k k ⎛⎫⎛⎫⎛⎫∴+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得218k =.21432k BF ∴==. ∴存在符合条件的点F ,它的坐标为21432⎛⎫⎪⎝⎭,.10.1)证明:在正方形ABCD 中,无论点P 运动到AB 上何处时,都有AD =AB ∠DAQ =∠BAQ AQ =AQ∴△ADQ ≌△ABQ ············ 2分(2)解法一:△ADQ 的面积恰好是正方形ABCD 面积的61时, 过点Q 作Q E ⊥AD 于E ,QF ⊥AB 于F ,则QE = QF21QE AD ⨯=ABCD 正方形S 61=38 ∴QE =34····························· 4分由△DEQ ∽△DAP 得 DADEAP QE = 解得2=AP ∴2=AP 时,△ADQ 的面积是正方形ABCD 面积的61········ 6分解法二:以A 为原点建立如图所示的直角坐标系,过点Q 作QE ⊥y 轴于点E ,QF ⊥x 轴于点F .21QE AD ⨯=ABCD 正方形S 61=38 ∴QE =34 ∵点Q 在正方形对角线AC 上 ∴Q 点的坐标为44()33,∴ 过点D (0,4),Q ()34,34两点的函数关系式为:42+-=x y 当0=y 时,2=x ∴P 点的坐标为(2,0) ∴2=AP 时,△ADQ 的面积是正方形ABCD 面积的61. ········ 6分 (3)若△ADQ 是等腰三角形,则有 QD =QA 或DA =DQ 或AQ =AD ①当点P 运动到与点B 重合时,由四边形ABCD 是正方形知 QD =QA 此时△ADQ 是等腰三角形②当点P 与点C 重合时,点Q 与点C 也重合,此时DA =DQ , △ADQ 是等腰三角形 ········ 8分 ③解法一:如图,设点P 在BC 边上运动到x CP =时,有AD =AQ∵ AD ∥BC ∴∠ADQ =∠CPQ 又∵∠AQD =∠CQP ∠ADQ =∠AQD ∴∠CQP =∠CPQ ∴ CQ =CP =x∵AC =24 AQ = AD =4∴424-=-==AQ AC CQ x即当424-=CP 时,△ADQ 是等腰三角形 ·········· 10分11.(1)解法一:如图25-1过A 作AE ⊥CD ,垂足为E .依题意,DE =25249=-. …………………………2分在Rt △ADE 中,AD =522560=⨯=︒cos DE . ………5分 解法二:如图25-2过点A 作AE ∥BC交CD 于点E ,则CE =AB =4 . …2分 ∠AED =∠C =60°. 又∵∠D =∠C =60°,∴△AED 是等边三角形 .∴AD =DE =9-4=5 . …………………………………5分 (2)解:如图25-1∵CP =x ,h 为PD 边上的高,依题意,△PD Q 的面积S 可表示为: S=21PD ·h ………………………………………6分 =21(9-x )·x ·sin60° =43(9x -x 2) =-43(x -29)2+16381. (8)分由题意,知0≤x ≤5 . ……………………………………………………… 9分 当x =29时(满足0≤x ≤5),S 最大值=16381. …………………………… 10分 (3)证法一:如图25-3假设存在满足条件的点M ,则PD 必须等于D Q . ………………………… 11分于是9-x =x ,x =29. 此时,点P 、Q 的位置如图25-3所示,连Q P .△PD Q 恰为等边三角形 .过点Q 作Q M ∥DC ,交BC 于M ,点M 即为所求.连结MP ,以下证明四边形PD Q M 是菱形 .易证△MCP ≌△Q DP ,∴∠D=∠3 . MP =PD图25-1图25-2 图25-3。
四边形中的动点问题

四边形中的动点问题动点问题是初中数学中常见的问题之一。
这种问题涉及到一些物体或点在平面或空间中的运动轨迹,从而引发一系列有趣的问题。
本文将重点讨论四边形中的动点问题。
一、定义四边形是一个拥有四个端点并且每个端点有两条相邻的边相连的图形。
在四边形中,如果一些点在边界或内部移动,我们称这些点是动点。
二、基本问题四边形中的动点问题主要有三个基本问题:1. 四边形内任取一个动点,这个点的移动轨迹是什么?2. 四边形内任取两个动点,它们的运动是否有任何联系?3. 四边形内任取三个动点,它们是否存在特殊的位置关系?三、解决方法1. 关于第一个问题,我们可以采用向量法、坐标法、三角函数法等不同的方式来解决。
其中最常用的方法是向量法,即用向量表示动点在平面内的位置,并利用向量的加减法来求得动点的移动轨迹。
比如,对于任意一边AB,在边AB上取一点C,设动点P的向量表示为向量a,向量AC表示为向量b,则P点在AC向量上的投影可以表示为向量b’。
而向量a’可以表示为由向量b’平移而来的向量,其中平移的大小和方向取决于向量b和a之间的夹角。
2. 第二个问题比较复杂,需要利用向量叉乘、双曲线函数等高深的数学知识来解决。
一般来说,我们需要找到两个动点之间的代数关系式,再根据这个关系式来判断它们是否有联系。
比如,如果我们发现两个动点在一条直线上运动,则它们存在一定的约束条件,这个约束条件可以用向量叉乘来表达。
3. 第三个问题则是考验计算几何能力的问题。
一般来说,我们需要找到一种不变量来描述三个动点之间的特殊位置关系。
比如,如果我们发现这三个动点共线,则我们可以通过向量叉乘或线性方程组来计算它们的位置关系。
如果我们发现这三个点可以构成一个三角形,则我们可以通过三角形的几何性质来判断它们的位置关系。
如果我们发现这三个动点可以构成一个正方形或者矩形,则我们可以通过它们的对角线、边长、面积等几何参数来计算它们的位置关系。
四、典型例题1. 在正方形ABCD中,点E、F分别在边AB、CD上,且AE=CF。
特殊四边形动点问题专题训练及解析精编版

2015特殊四边形动点问题专题训练及答案解析(一)已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,(1)求证:四边形ADCE是平行四边形;(2)当△ABC满足什么条件时,平行四边形ADCE是矩形?证明:(1)因为四边形BCED是平行四边形,所以BD=CE且BD∥CE,又因为D是△ABC的边AB的中点,所以AD=BD,即DA=CE,又因为CE∥BD,所以四边形ADCE是平行四边形.(2)当△ABC为等腰三角形且AC=BC时,四边形ADCE是矩形理由:∵AC=BC,D是△ABC的边AB的中点∴CD⊥AD,即∠ADC=90°,由(1)可知,四边形ADCE是平行四边形∴四边形ADCE是矩形.(二)如图,已知E是▱ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.(1)求证:△ABE≌△FCE.(2)连接AC、BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.(三)如图,O为△ABC的边AC上一动点,过点O的直线MN∥BC,设MN分别交∠ACB的内、外角平分线于点E、F。
(1)求证:OE=OF(2)若CE=12,CF=5,求OC的长(3)当点O在AC边上运动到何处时,四边形AECF是矩形?证明你的结论(4)在(3)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并说明你的理由。
(1)证明:∵CE平分∠ACB∴∠ACE=∠BCE∵MN∥BC∴∠OEC=∠BCE,∴∠ACE=∠OEC,∴OE=OC,同理:OF=OC∴OE=OF(2)∵CE平分∠ACB∴∠ACE=∠ACB/2∵CF平分∠ACD∴∠ACF=∠ACD/2∴∠ECF=∠ACE+∠ACF=∠ACB/2+∠ACD/2=(∠ACB+∠ACD)/2=180/2=900在Rt△ECF中,EF2= CE2+ CF2= 122+ 52=169∴EF=13由(1)可知OE=OF∴OC=EF/2=13/2(3)、当O运动到AC的中点时,AECF是矩形证明:∵O是AC的中点∴AO=CO∵OE=OF∴四边形AECF是平行四边形由(2)可知∠ECF=900∴四边形AECF是矩形3、△ABC为直角三角形,且∠ACB=90时,四边形AECF是正方形证明:∵∠ACB=900,MN∥BC∴∠AOM=∠ACB=900,由(3)知四边形AECF是矩形∴四边形AECF 是矩形(四)如图,已知平行四边形ABCD 的对角线AC 、BD 相交于点O ,AC=20cm 、BD=12cm ,两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动.(1)求证:当E 、F 运动过程中不与点O 重合时,四边形BEDF 一定为平行四边形; (2)当E 、F 运动时间t 为何值时,四边形BEDF 为矩形?(1)解:连接DE ,EB ,BF ,FD∵两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动. ∴AE=CF在平行四边形ABCD 中,OD=OB ,OA=OC ∴OA-AE=OC-CF 或AE-OA=CF-OC 即OE=OF∴四边形BEDF 为平行四边形.(2)当点E 在OA 上,点F 在OC 上时EF=BD=12cm , 四边形BEDF 为矩形 ∵运动时间为t∴AE=CF=2t ∴EF=20-4t=12 ∴t=2(s )当点E 在OC 上,点F 在OA 上时,EF=BD=12cm EF=4t-20=12 ∴t=8(s )因此当E 、F 运动时间2s 或8s 时,四边形BEDF 为矩形.(五)如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,BD=12cm ,AC=6cm ,点E 在线段BO 上从点B 以1cm/s 的速度运动,点F 在线段OD 上从点O 以2cm/s 的速度运动.(1)若点E 、F 同时运动,设运动时间为t 秒,当t 为何值时,四边形AECF 是平行四边形. (2)在(1)的条件下,①当AB 为何值时,四边形AECF 是菱形;②四边形AECF 可以是矩形吗?为什么?解:(1)连接DE ,EB ,BF ,FD∵两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动. ∴AE=CFOCDBAEF∵平行四边形ABCD的对角线AC、BD相交于点O,∴OD=OB,OA=OC(平行四边形的对角线互相平分)∴OA-AE=OC-CF或AE-OA=CF-OC即OE=OF∴四边形AECF为平行四边形.(对角线互相平分的四边形是平行四边形)(2)当点E在OA上,点F在OC上时EF=BD=12cm,四边形BEDF为矩形∵运动时间为t∴AE=CF=2t∴EF=20-4t=12∴t=2(s)当点E在OC上,点F在OA上时,EF=BD=12cmEF=4t-20=12∴t=8(s)因此当E、F运动时间2s或8s时,四边形AECF为矩形.(六)如图,已知在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm ,AB=8cm,BC=26cm,动点P从A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t 秒.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形ABQP为矩形?(七)(1)设经过xs的时间,四边形PQCD是平行四边形因为四边形PQCD是平行四边形所以DP=CQ由已知得:DP=AD-AP=24-xCQ=3x所以24-x=3xx=6答:经过6s的时间,四边形PQCD是平行四边形(2)设经过xs的时间,四边形PQBA是矩形因为四边形PQBA是矩形所以AP=BQ由已知得:AP=XBQ=BC-CQ=26-3x所以x=26-3xx=13/2答:经过13/2s的时间,四边形PQBA是矩形。
四边形中的动点问题(带答案)

四边形中的动点问题(带答案)四边形中的动点问题1、如图,把矩形ABCD沿 EF翻折,点B恰好落在AD边的B'处,若AE= 2, DE= 6,Z EFB= 60°, 则矩形ABCD勺面积是 _____________________2、如图,在四边形ABCD中对角线ACL BD 垂足为0,点E, F, G, H分别为边AD AB, BC CD 的中点•若AC= 8, BD= 6,则四边形EFGH的面积为3、如图,正方形ABCD勺边长为4,点P在DC 边上,且DP= 1,点Q是AC上一动点,则D® PQ 的最小值为 _____________________4、如图,在Rt△ ABC中,/ B= 90°,AC= 60 cm Z A= 60°,点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D, E 运动的时间是t s(0 < t < 15) •过点D作DF 丄BC于点F,连接DE EF.(1)求证:AE= DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)当t为何值时,△ DEF为直角三角形?请说明理由5、如图,在等边三角形ABC中,BC=6cm射线AG// BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t. (1)连接EF当EF经过AC边的中点D时,(1)求证:△ ADE^A CDF:6、在菱形ABCD中,/ B=60°,点E在射线BC上运动,/ EAF=60,点F在射线CD上(1)当点E在线段BC上时(如图1)( 1)求证:EC+CF=A; (2) 当点E在BC的延长线上时(如图2),线段EC CFAB有怎样的相等关系?写出你的猜想,不需证明图1 027、如图,在菱形ABC[中, AB=2 / DAB=60 , 点E 是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N 连接MD AN(1)求证:四边形AMDI是平行四边形;(2)填空:①当AM的值为时,四边形AMD是矩形;②当AM的值为时,四边形AMD是菱形.D8 如图,△ ABC中,点0是边AC上一个动点,过0作直线MN BC 设MN交/ BCA的平分线于点E, 交/ BCA 的外角平分线于点F.(1)探究:线段0E与OF的数量关系并加以证明;(2)当点0运动到何处,且△ ABC满足什么条件时,四边形AECF是正方形?(3)当点0在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,则说明理由.9、如图,已知菱形ABC[中, / ABC=60 , AB=8 过线段BD上的一个动点P (不与B、D重合)分别向直线AB AD作垂线,垂足分别为E、F.(1)BD的长是______ ;(2)连接PC当PE+PF+P(取得最小值时,此时PB的长是_______10、如图,/ MON=9°,矩形ABCD勺顶点A B 分别在边OM ON上,当B在边ON上运动时,A随之在OMk运动,矩形ABCD勺形状保持不变,其中AB=2 BC=1运动过程中,点D到点O的最大距离为 __________________ .11、如图,已知矩形ABCD AD=4 CD=10 P是AB上一动点,M N E分别是PD PC CD的中点.(1)求证:四边形PMEI是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN 是菱形;(3)四边形PMEf有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.12、如图,在平行四边形ABCD中,对角线BD=12cm AC=16cm AC BD相交于点0,若E, F 是AC上两动点,分别从A, C两点以相同的速度向C、A 运动,其速度为0.5cm/s。
四边形中的动点问题(带答案)
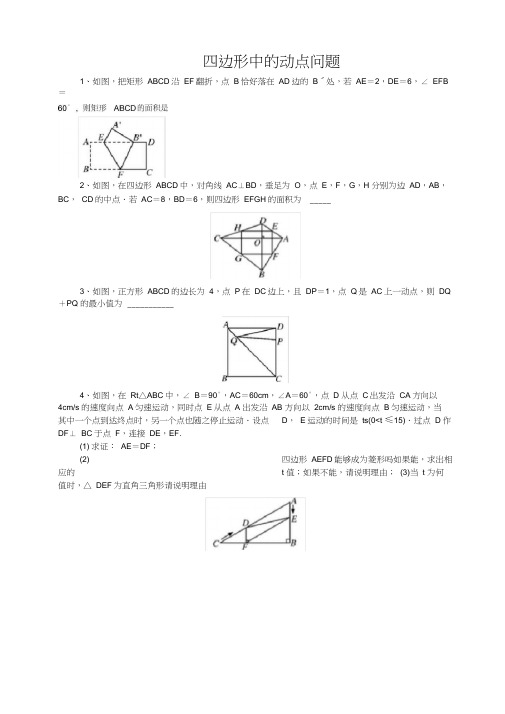
四边形中的动点问题1、如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠ EFB =2、如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H 分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 _____3、如图,正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ +PQ 的最小值为___________4、如图,在Rt△ABC中,∠ B=90°,AC=60cm,∠A=60°,点 D 从点C出发沿CA方向以4cm/s 的速度向点A匀速运动,同时点E从点 A 出发沿AB 方向以2cm/s 的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t ≤15).过点 D 作DF⊥ BC于点F,连接DE,EF.(1) 求证:AE=DF;(2) 四边形AEFD能够成为菱形吗如果能,求出相应的t 值;如果不能,请说明理由;(3)当t 为何值时,△ DEF为直角三角形请说明理由5、如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点 A 出发沿射线AG以1cm/s 的速度运动,同时点 F 从点 B 出发沿射线BC以2cm/s 的速度运动,设运动时间为t.(1)连接EF,当EF经过AC边的中点 D 时,(1)求证:△ ADE≌△ CDF;:(2)当t 为____ s 时,四边形ACFE是菱形;6、在菱形ABCD中,∠ B=60°,点E在射线BC上运动,∠ EAF=60°,点 F 在射线CD上(1)当点E在线段BC上时(如图1),(1)求证:EC+CF=AB;(2)当点 E 在BC的延长线上时(如图2),线段EC、CF、AB 有怎样的相等关系写出你的猜想,不需证明7、如图,在菱形ABCD中,AB=2,∠ DAB=60°,点E是AD边的中点.点M 是AB边上一动点不与点 A 重合),延长ME交射线CD于点N,连接MD、AN.(1)求证:四边形AMDN 是平行四边形;(2)填空:①当AM 的值为____ 时,四边形AMDN 是矩形;②当AM 的值为____ 时,四边形AMDN 是菱形.8、如图,△ ABC中,点O 是边AC上一个动点,过O 作直线MN ∥BC,设MN 交∠ BCA的平分线于点E,交∠ BCA 的外角平分线于点F.(1)探究:线段OE与OF 的数量关系并加以证明;(2)当点O 运动到何处,且△ ABC满足什么条件时,四边形AECF是正方形(3)当点O 在边AC上运动时,四边形BCFE会是菱形吗若是,请证明,若不是,则说明理由.9、如图,已知菱形ABCD中,∠ ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D 重合)分别向直线AB、AD 作垂线,垂足分别为E、F.(1)BD的长是___ ;(2)连接PC,当PE+PF+PC取得最小值时,此时PB 的长是__10、如图,∠ MON=90°,矩形ABCD的顶点A、B分别在边OM,ON 上,当B在边ON 上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O 的最大距离为_____ .11、如图,已知矩形ABCD,AD=4,CD=10,P 是AB上一动点,M、N、E分别是PD、PC、CD的中点.(1)求证:四边形PMEN 是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN 是菱形;(3)四边形PMEN有可能是矩形吗若有可能,求出AP 的长;若不可能,请说明理由.12、如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F 是AC上两动点,分别从A,C两点以相同的速度向C、A 运动,其速度为/s。
动点问题1

• 6、如图, 射线MB上,MB=9,A是射线MB外一 点,AB=5且A到射线MB的距离为3,动点P从M沿射 线MB方向以1个单位/秒的速度移动,设P的运动 时间为t. • 求(1)△ PAB为等腰三角形的t值;(2)△ PAB为直角三角形的t值; • (3) 若AB=5且∠ABM=45 °,其他条件不变, 直接写出△ PAB为直角三角形的t值
.
如图,在四边形ABCD中,AD∥BC,且AD>BC, BC=6cm,P、Q分别从A,C同时出发,P以1cm/s 的速度由A向D运动,Q以2cm/s的速度由C向B运 动,几秒后四边形ABQP是平行四边形?
A
P
D
B
Q
C
如图:已知正方形ABCD的边长为8,M在 DC上,且DM=2,N是AC上的一动点,求 DN+MN的最小值。
• 如图1,四边形ABCD是正方形,点E是边BC的中点., 且EF交正方形外角的平行线CF于点F,求证:AE=EF. • 小明展示了一种正确的解题思路:取AB的中点M,连接 ME,则AM=EC,易证,所以. • 在此基础上,同学们作了进一步的研究: • (1)小颖提出:如图2,如果把“点E是边BC的中点”改 为“点E是边BC上(除B,C外)的任意一点”,其它条 件不变,那么结论“AE=EF”仍然成立,你认为小颖的观 点正确吗?如果正确,写出证明过程;如果不正确,请说 明理由; • (2)小华提出:如图3,点E是BC的延长线上(除C点 外)的任意一点,其他条件不变,结论“AE=EF”仍然成 立.你认为小华的观点正确吗?如果正确,写出证明过程; 如果不正确,请说明理由.ADFCGEB图1 • 解:(1)正确.
2、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1, N为对角线AC上任意一点,则DN+MN的最小值为 5 3、如图,在中,,.点是的中点,过点的直线从与重合的位置 开始,绕点作逆时针旋转,交边于点.过点作交直线于点,设 直线的旋转角为.(1)①当 度时,四边形是等腰梯形, 此时的长为 ;OECBDAlOCBA(备用图) ②当 度时,四边形是直角梯形,此时的长为 ; (2)当时,判断四边形是否为菱形,并说明理由.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四边形动点问题(一)
1. 如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN 交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?证明你的结论.
2.已知等腰△ABC中,AB=AC,AD平分∠BAC交BC于D点,在线段AD上任取一点P(A点除外),过P点作EF∥AB,分别交AC,BC于E,F点,作PM∥AC,交AB于M点,连接ME.
(1)求证:四边形AEPM为菱形;
(2)当P点在何处时,菱形AEPM的面积为四边形EFBM面积的一半?
3. 如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为时,以点P、A、D、E为顶点的四边形为平行四边形;(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
4. 如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=,∠B=45°.直角三角板
含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则求CF的长
5.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M从点A开始,沿边AD向点D运动,速度为1cm/s;点N从点C开始,沿
边CB向点B运动,速度为2cm/s、点M、N分别从点A、C出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒.
(1)当t= 时,四边形MNCD是平行四边形.
(2)当t= 时,四边形MNCD是等腰梯形
6.如图,在ΔABC中,D是BC的中点,BC=10㎝,AD=7㎝,从点A沿着A→D的方向运动,速度是每秒2㎝,连结CE,BE,过点B作BF∥CE,交射线AD于点F,设运动时间为t秒(0<t<3.5)
(1)求证:ΔBDF≌ΔCDE
(2)当t为何值时,四边形BFCE是矩形,说明理由
(3)若四边形BFCE是矩形,当AB和CA满足什么条件时,四边形BFCE是正方形。
7.如图,在梯形ABCD中,AD∥BC, ∠B=90°,AD=16㎝,AB=12㎝,BC=21㎝,动点P沿射线BC的方向以每秒2㎝的速度运动 ,动点Q从点A出发,在线段AD上以
每秒1㎝的速度向点D运动,点P、Q分别从点B、A同时出发,当点Q 运动到点D时,点P也随之停止运动,设运动时间 t(秒)
(1)若四边形PQDC是平行四边形时,求此时t的值;
(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60㎝²?
(3)当ΔPQD是以PQ为腰的等腰三角形时,直接写出所有满足要求的t的值。
8 .如图梯形ABCD中AD∥BC,AD=CD,DE⊥BC于点E,且DE=1,AD=4, ∠B=45°. (1)直接写出BC的长;
(2)直线AB以每秒0.5个单位的速度向右平移,交AD于点Q,则当直线AB的移动时间为多少秒,形成的四边形ABQPQ恰好为菱形?
(3)AB移动的方向、速度如同第(2)题,移动时间为t秒,AB扫过梯形ABCD 的面积S(用t的代数式表示,直接写出答案即可)。
