2010学年第一学期高三数学区期末统测试卷(文科)

合集下载

浙江省宁波市2010届高三数学上学期期末试题(文) 新人教版

宁波市2009学年度第一学期期末试卷高三数学(文科)说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分．考试时间120分钟．请考生将所有题目都做在答题卷上．参考公式：球的表面积公式棱柱的体积公式24S R π= V Sh =球的体积公式其中S 表示棱柱的底面积，h 表示棱柱的高343V R π= 棱台的体积公式其中R 表示球的半径 121()3V h S S =棱锥的体积公式其中12,S S 分别表示棱台的上、下底面积，13V Sh = h 表示棱台的高其中S 表示棱锥的底面积，h 表示棱锥的高如果事件,A B 互斥，那么()()()P A B P A P B +=+第Ⅰ卷（共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若i 为虚数单位，则11ii+=- （A ）i （B ）i - （C ） 1- （D ）12．已知集合2{|230}A x x x =--<，{}1|>=x x B ，则AB =（A ）{|1}x x > （B ）{|3}x x < （C ）{|13}x x << （D ）{|11}x x -<<3．设函数3y x =与21()2x y -=的交点横坐标为0x ，则0x 所在的区间是（A ）(0,1) （B ）(1,2) （C ）(2,3) （D ）(3,4) 4．在公比1q <的等比数列{}n a 中，28466,5a a a a =+=，则57a a = （A ）56 （B ）65 （C ）23 （D ）325．P 在曲线x y ln =上移动，则在点P 处曲线的切线斜率取值范围是 ()(,0)(0,)()(,)()(0,)()(,0)A B C D -∞⋃+∞-∞+∞+∞-∞6．在ABC ∆中，7,5,6AB BC CA ===，则AB BC ⋅= （A ）19 （B ）19- （C ）38 （D ）38- 7．执行如图的程序框图，若9p =，则输出的S =（A ）910 （B ）718 （C ）89 （D ）258．设n m ,是平面α内的两条不同直线，21,l l 是平面β内两条相交直线，则βα⊥的一个充分不必要条件是n l m l B l m l m A ⊥⊥⊥⊥1121,)(,)(n l n m D l n l m C ⊥⊥⊥121,//)(,)(9．函数()sin()3f x x π=-，则要得到函数2cos()3y x π=+的图象，只需将函数()y f x =的图象（A ）向左平移23π个单位（B ）向左平移2π个单位（C ）向右平移23π个单位（D ）向右平移2π个单位10．已知函数)(x f 是周期为4的函数,当40≤≤x 时,1|2|)(--=x x f ，若)(x f 的图象与射线)0(21≥=x y 交点的横坐标由小到大依次组成数列{}n a ,则2219||a a -=()4 ()5 ()7 ()8A B C D二、填空题：本大题共7小题，每小题4分，共28分．11．某校高三有1000个学生，高二有1200个学生，高一有1500个学生，现按年级分层抽样，调查学生的视力情况，若高一抽取了75人，则全校共抽取了 ▲ 人．12．已知椭圆)0(12222>>=+b a by a x 的离心率23=e ，其中{}10,9,8,7,6,5,4,3,2,1,∈b a ，在这些椭圆中，事件=A “2>-b a ”的概率为 ▲ ．13．如图是一个正三棱柱的三视图，若三棱柱的体积是38，则=a ▲ ．14．以双曲线22:145x y C -=的右焦点为圆心，且与双曲线C 的渐近线相切的圆的方程是 ▲ ．15．在平面几何里，有：“若ABC ∆的三边长分别为,,,c b a 内切圆半径为r ，则三角形面积为r c b a S ABC )(21++=∆”，拓展到空间，类比上述结论，“若四面体BCD A -的四个面的面积分别为,,,,4321S S S S 内切球的半径为r ，则四面体的体积为 ▲ ”．16．在直角坐标系中，若不等式组⎪⎩⎪⎨⎧-≤≤≥)1(30x k y x y y 表示的一个三角形区域的面积为43，则实数k 的值是 ▲ ． 17．设,1,1,,>>∈b a R y x 若,22,4=+==b a b a yx 则yx 11+的最大值为 ▲ ．三、解答题：本大题共5小题，共72分．解答应写出文字说明、证明过程或演算步骤．18．（14分）已知函数2()2cos cos f x x x x =+．求（1）函数()f x 的周期；（2）函数()f x 的单调递减区间；（3）函数()f x 在区间[0,]2π上的最值．19．（14分）若数列{}n a 满足：11=a ，且nnn a a a +=+11 （1）证明：数列⎭⎬⎫⎩⎨⎧n a 1为等差数列，并求出数列{}n a 的通项公式；（2）设数列{}n b 的前n 项和记为n S , 且n n b S -=2，n N *∈，求数列⎭⎬⎫⎩⎨⎧n n a b 的前n 项和n T ． 20．（15分）AB 为圆O 的直径，点F E ,在圆上，EF AB //，矩形ABCD 所在平面与圆O 所在平面互相垂直，已知,2=AB 1=EF ．（1）求证：⊥BF 平面DAF ；（2）求BF 与平面ABCD 所成的角；（3）若AC 与BD 相交于点M ，求证：ME //平面DAF21．（14分）已知直线l ：b kx y +=交抛物线C ：221x y =于),(11y x A ，),(22y x B 两点，交y 轴于点P ，若02>x ，且121-=x x ，记PB t AP =．（1）求证：直线l 过抛物线的焦点；（2）当23=t 时，求以原点为中心，以P 为一个焦点，且过点B 的椭圆方程．22．（15分）设x a ax x x f )1(2131)(23-+-=)(R a ∈．（1）若1=x 是函数)(x f 的极大值点，求a 的取值范围；（2）若在]3,1[∈x 上至少存在一个0x ，使2)(0≥x f 成立，求a 的取值范围．宁波市2009学年度第一学期期末答题卷高三数学（文科）一. 选择题（本大题共10小题，每小题5分,满分50在每小题给出的四个选项中只有一项是正确的．）二．填空题（本大题共4小题，每小题7分，满分28分. 11、 12、 13、 14 、 15、 16、 17、三. 解答题（本大题共5小题，满分72分．解题应写出文字说明，证明过程或演算步骤.） 18、（14分）19．（14分）20 ．（15分）得分评卷人21．（14分）22．（15分）宁波市2009学年度第一学期期末参考答案及评分标准高三数学(文科)一．选择题（本大题共10个小题，每小题5分，共50分。

山东省淄博市2010届高三上学期期末考试(数学文)

保密★启用前淄博市2010届高三上学期期末考试文科数学试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分，共4页，满分150分，考试时间120分钟.考试结束后，将本试卷和答题卡一并交回. 注意事项：1. 答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上，并将准考证号条形码粘贴在答题卡上指定位置.2. 第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔在答题卡各题的答题区域内作答；不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效.4. 填空题请直接填写答案，解答题应写出文字说明，证明过程或演算步骤.第Ⅰ卷(共60分)一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设全集I 是实数集R ， 3{|2}{|0}1x M x x N x x -=>=≤-与都是I 的子集（如图所示），则阴影部分所表示的集合为A ．{}2x x <B ．{}21x x -≤<C ．{}12x x <≤D ．{}22x x -≤≤2．下列函数中既不是奇函数，又不是偶函数的是A ．2xy = B ． (lg y x =+C ． 22xxy -=+ D ． 1lg1y x =+ 3．若曲线x x x f -=4)(在点P 处的切线平行于直线03=-y x ，则点P 的坐标为A ．（1，0）B ．（1，5）C ．（1，－3）D ．（－1，2）4．在ABC ∆中，a b 、分别是角A B 、所对的边，条件“a b <”是使 “cos cos A B >”成立的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5. 若抛物线1262222=+=y x px y 的焦点与椭圆的右焦点重合，则p 的值为 A ．－4 B ．4 C ．－2 D ．26. 已知函数),6cos()6sin()(ππ++=x x x f 则下列判断正确的是A ．)(x f 的最小正周期为2π，其图象的一条对称轴为12π=xB ．)(x f 的最小正周期为2π，其图象的一条对称轴为6π=xC ．)(x f 的最小正周期为π，其图象的一条对称轴为12π=xD ．)(x f 的最小正周期为π，其图象的一条对称轴为6π=x7. 一空间几何体的三视图如图所示，则该几何体的表面积为 A．2π+ B．42π+ C．6π+ D．62π+ 8. 若直线:10 l ax by ++=始终平分圆M ：224210x y x y ++++=的周长，则()()2222a b -+-的最小值为AB ．5C．D ．109. 设b c 、表示两条直线，αβ、表示两个平面，下列命题中真命题是A ．若c ∥α，c ⊥β，则αβ⊥B ．若b α⊂，b ∥c ，则c ∥αC ．若b α⊂，c ∥α，则b ∥cD ．若c ∥α，αβ⊥，则c β⊥10. 已知数列{}n x 满足3n n x x +=，21||()n n n x x x n N *++=-∈，若11x =，2 (1,0)x a a a =≤≠，则数列{}n x 的前2010项的和2010S 为A ．669B ．670C ．1338D ．134011. 在平面直角坐标系中，O 为坐标原点，设向量).3,1(),1,3(,,====b a b OB a OA 其中若10,≤≤≤+=μλμλ且b a OC ，C 点所有可能的位置区域用阴影表示正确的是俯视图正视图侧视图（第7题图）12．已知点F 是双曲线)0,0(12222>>=-b a by a x 的左焦点，点E 是该双曲线的右顶点，过F且垂直于x 轴的直线与双曲线交于A B 、两点，若ABE ∆是锐角三角形，则该双曲线的离心率e 的取值范围是A ． ()1,+∞B ．()1,2C．(1,1+D．(2,1第Ⅱ卷（共90分）二、填空题：本大题共4小题，每小题4分，共16分. 13. 对任意非零实数a b 、，若a b ⊗的运算原理如图所示，则()221log 82-⎛⎫⊗= ⎪⎝⎭______．14．在ABC ∆中，已知41AB AC ==，， ABC S AB AC ∆⋅则的值为．15. 设n S 表示等差数列{}n a 的前n 项和，且918S =，240n S =，若()4309n a n -=>，则n = ．16. 已知两个不相等的实数a b 、满足以下关系式：204a sin a cos πθθ⋅+⋅-=，204b sin b cos πθθ⋅+⋅-=，则连接A ()2a ,a 、 B ()2b ,b 两点的直线与圆心在原点的单位圆的位置关系是．三、解答题：本大题共6个小题，共74分. 17．（本小题满分12分）已知函数2()sin cos f x x x x =+．（Ⅰ）求()f x 的最小正周期；A ．B ．C ．D ．（第13题图）（Ⅱ）求()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值． 18．本小题满分12分）如图，已知AB ⊥平面ACD ，DE ∥AB ，ACD ∆是正三角形，2AD DE AB ==，且F 是CD 的中点．（Ⅰ）求证：AF ∥平面BCE ；（Ⅱ）求证：平面BCE ⊥平面CDE ． 19．（本小题满分12分）已知数列{}n a 的首项15a =，前n 项和为n S ，且125n n S S n +=++()n N *∈．（Ⅰ）设1n n b a =+，求数列{}n b 的通项公式；（Ⅱ）求数列{}n a 的前n 项和n S ． 20．（本小题满分12分）如图所示，将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ，要求B 点在AM 上，D 点在AN 上，且对角线MN 过C 点，已知3=AB 米，2=AD 米．（I ）要使矩形AMPN 的面积大于32平方米，则DN 的长应在什么范围内？（II ）当DN 的长度是多少时，矩形花坛AMPN 的面积最小？并求出最小值． 21．（本小题满分12分）已知函数22()ln ()f x x a x ax a R =-+∈．（Ⅰ）当1a =时，证明函数()f x 只有一个零点；（Ⅱ）若函数()f x 在区间()1,+∞上是减函数，求实数a 的取值范围． 22．（本小题满分14分）已知椭圆C ：()222210x y a b a b +=>>过点3(1,)2A ，且离心率12e =．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）若直线l ：()0y kx m k =+≠与椭圆交于不同的两点M N 、，且线段MN 的(第20题图)ABCDEF(第18题图)垂直平分线过定点1(,0)8G ，求k 的取值范围．保密★启用前文科数学试卷参考答案及评分标准本试卷分第Ⅰ卷和第Ⅱ卷两部分，共11页，满分150分，考试时间120分钟.考试结束后，将本试卷和答题卡一并交回. 注意事项：1. 答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上，并将准考证号条形码粘贴在答题卡上指定位置.2. 第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔在答题卡各题的答题区域内作答；不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效.4. 填空题请直接填写答案，解答题应写出文字说明，证明过程或演算步骤.第Ⅰ卷(共60分)一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设全集I 是实数集R ， 3{|2}{|0}1x M x x N x x -=>=≤-与都是I 的子集（如图所示），则阴影部分所表示的集合为A ．{}2x x <B ．{}21x x -≤<C ．{}12x x <≤D ．{}22x x -≤≤2．下列函数中既不是奇函数，又不是偶函数的是A ．2xy = B ． (lg y x =+C ． 22xxy -=+ D ． 1lg1y x =+ 3．若曲线x x x f -=4)(在点P 处的切线平行于直线03=-y x ，则点P 的坐标为A ．（1，0）B ．（1，5）C ．（1，－3）D ．（－1，2）4．在ABC ∆中，a b 、分别是角A B 、所对的边，条件“a b <”是使 “cos cos A B >”成立的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5. 若抛物线1262222=+=y x px y 的焦点与椭圆的右焦点重合，则p 的值为 A ．－4 B ．4 C ．－2 D ．26. 已知函数),6cos()6sin()(ππ++=x x x f 则下列判断正确的是A ．)(x f 的最小正周期为2π，其图象的一条对称轴为12π=xB ．)(x f 的最小正周期为2π，其图象的一条对称轴为6π=xC ．)(x f 的最小正周期为π，其图象的一条对称轴为12π=xD ．)(x f 的最小正周期为π，其图象的一条对称轴为6π=x7. 一空间几何体的三视图如图所示，则该几何体的表面积为 A．2π+ B．42π+ C．6π+ D．62π+ 8. 若直线:10 l ax by ++=始终平分圆M ：224210x y x y ++++=的周长，则()()2222a b -+-的最小值为AB ．5C．D ．109. 设b c 、表示两条直线，αβ、表示两个平面，下列命题中真命题是A ．若c ∥α，c ⊥β，则αβ⊥B ．若b α⊂，b ∥c ，则c ∥αC ．若b α⊂，c ∥α，则b ∥cD ．若c ∥α，αβ⊥，则c β⊥10. 已知数列{}n x 满足3n n x x +=，21||()n n n x x x n N *++=-∈，若11x =，2 (1,0)x a a a =≤≠，则数列{}n x 的前2010项的和2010S 为A ．669B ．670C ．1338D ．134011. 在平面直角坐标系中，O 为坐标原点，设向量).3,1(),1,3(,,====其中若10,≤≤≤+=μλμλ且b a OC ，C 点所有可能的位置区域用阴影表示正确的是俯视图正视图侧视图（第7题图）12．已知点F 是双曲线)0,0(12222>>=-b a by a x 的左焦点，点E 是该双曲线的右顶点，过F且垂直于x 轴的直线与双曲线交于A B 、两点，若ABE ∆是锐角三角形，则该双曲线的离心率e 的取值范围是A ． ()1,+∞B ．()1,2C．(1,1+D．(2,1第Ⅱ卷（共90分）二、填空题：本大题共4小题，每小题4分，共16分. 13. 对任意非零实数a b 、，若a b ⊗的运算原理如图所示，则()221log 82-⎛⎫⊗= ⎪⎝⎭___1___．14．在ABC ∆中，已知41AB AC ==，， ABC S AB AC ∆⋅则的值为 ±2 ．15. 设n S 表示等差数列{}n a 的前n 项和，且918S =，240n S =，若()4309n a n -=>，则n = 15 ．16. 已知两个不相等的实数a b 、满足以下关系式：204a sin a cos πθθ⋅+⋅-=，204b sin b cos πθθ⋅+⋅-=，则连接A ()2a ,a 、 B ()2b ,b 两点的直线与圆心在原点的单位圆的位置关系是相交．三、解答题：本大题共6个小题，共74分. 17．（本小题满分12分）已知函数2()sin cos f x x x x =+．（Ⅰ）求()f x 的最小正周期；A ．B ．C ．D ．（第13题图）（Ⅱ）求()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值．解：（Ⅰ）∵ 2()sin cos f x x x x =+)12sin cos cos 212x x x =⋅+ 1sin 222x x =+ ……………3分 sin 232x π⎛⎫=++ ⎪⎝⎭ ……………5分 ∴ 函数()f x 的最小正周期22T ππ==． ……………6分（Ⅱ）∵ 62x ππ-≤≤，40233x ππ≤+≤∴ sin 2123x π⎛⎫-≤+≤ ⎪⎝⎭， ……………9分 ∴ 20sin 213222x π⎛⎫≤++≤+= ⎪⎝⎭， ∴ ()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值为22+，最小值为0．……………12分18．（本小题满分12分）如图，已知AB ⊥平面ACD ，DE ∥AB ，ACD ∆是正三角形，2AD DE AB ==，且F 是CD 的中点．（Ⅰ）求证：AF ∥平面BCE ；（Ⅱ）求证：平面BCE ⊥平面CDE ．解：（Ⅰ）取CE 中点P ，连结FP 、BP ，∵F 为CD 的中点，∴FP ∥DE ，且FP =.21DE 又AB ∥DE ，且AB =.21DE∴AB ∥FP ，且AB =FP ，∴ABPF 为平行四边形，∴AF ∥BP ．…………4分ABCDEF(第18题图)BE又∵AF ⊄平面BCE ，BP ⊂平面BCE ， ∴AF ∥平面BCE …………6分（Ⅱ）∵△ACD 为正三角形，∴AF ⊥CD∵AB ⊥平面ACD ，DE //AB∴DE ⊥平面ACD 又AF ⊂平面ACD ∴DE ⊥AF又AF ⊥CD ，CD ∩DE=D∴AF ⊥平面CDE …………10分又BP ∥AF ∴BP ⊥平面CDE 又∵BP ⊂平面BCE∴平面BCE ⊥平面CDE …………12分 19．（本小题满分12分）已知数列{}n a 的首项15a =，前n 项和为n S ，且125n n S S n +=++()n N *∈．（Ⅰ）设1n n b a =+，求数列{}n b 的通项公式；（Ⅱ）求数列{}n a 的前n 项和n S ．解：（Ⅰ）由125n n S S n +=++()n N *∈得 ()1215n n S S n -=+-+(,2)n N n *∈≥两式相减得 121n n a a +=+ ……………………………… 3分 ∴ ()1121n n a a ++=+即 n n b b 21=+(,2)n N n*∈≥ …………………………………… 4分又1165111122=+=++=-=a S S S a ∴ 12122=+=a b ，6111=+=a b∴ 122b b = …………………………………… 6分 ∴ 数列{}n b 是首项为6，公比为2的等比数列∴ nn n b 23261⋅=⋅=- ………………………………… 8分（Ⅱ）法一由（Ⅰ）知321nn a =⋅- ……………………………… 9分∴ 12n n S a a a =++⋅⋅⋅+2323232nn =⨯+⨯+⋅⋅⋅+⋅-()221321n n -=⨯--1626326n n n n +=⋅--=⋅--． ……………………… 12分（Ⅱ）法二由已知125n n S S n +=++()n N *∈ ① 设()()112n n S c n d S cn d ++++=++ 整理得 12n n S S cn d c +=++- ②对照① 、②，得 1,6c d == ……………………………………8分即①等价于 ()()11626n n S n S n ++++=++∴ 数列{}6n S n ++是等比数列，首项为11161612S a ++=++=，公比为2q =∴ 11612232n n n S n -+++=⋅=⋅∴ 1326n n S n +=⋅--． …………………………………… 12分20．（本小题满分12分）如图所示，将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ，要求B 点在AM 上，D 点在AN 上，且对角线MN 过C 点，已知3=AB 米，2=AD 米．（I ）要使矩形AMPN 的面积大于32平方米，则DN 的长应在什么范围内？（II ）当DN 的长度是多少时，矩形花坛AMPN 的面积最小？并求出最小值．解：（I ）设DN 的长为x （0x >）米，则2AN x =+米∵AMDC ANDN =，∴()32x AM x+=， ……………………2分 (第20题图)∴ ()232AMPN x S AN AM x+=⋅= 由32>AMPNS 得 ()23232x x +> ，又0x >，得 2320120x x -+>，解得：2063x x <<> 或即DN 长的取值范围是2(0)(6)3∞，，+ ……………………7分（II ）矩形花坛AMPN 的面积为()22323121212312x x x y x x x x+++===++1224≥= ……………………10分当且仅当1232x x ,x==即时矩形花坛AMPN 的面积取得最小值24．故，DN 的长度是2米时，矩形AMPN 的面积最小，最小值为24平方米．…12分21．（本小题满分12分）已知函数22()ln ()f x x a x ax a R =-+∈．（Ⅰ）当1a =时，证明函数()f x 只有一个零点；（Ⅱ）若函数()f x 在区间()1,+∞上是减函数，求实数a 的取值范围．解：（Ⅰ）当1a =时，2()ln f x x x x =-+，其定义域是(0,)+∞ ∴ 2121()21x x f x x x x--'∴=-+=- …………2分令()0f x '=，即2210x x x ---=，解得12x =-或1x =． 0x >Q ，∴ 12x ∴=-舍去．当01x <<时，()0f x '>；当1x >时，()0f x '<．∴ 函数()f x 在区间()01,上单调递增，在区间()1,+∞上单调递减∴ 当x =1时，函数()f x 取得最大值，其值为2(1)ln1110f =-+=．当1x ≠时，()(1)f x f <，即()0f x <．∴ 函数()f x 只有一个零点． ……………………6分（Ⅱ）显然函数22()ln f x x a x ax =-+的定义域为(0,)+∞ ∴ 222121(21)(1)()2a x ax ax ax f x a x a x x x-++-+-'=-+== ………7分 ① 当0a =时，1()0,()f x f x x'=>∴在区间()1,+∞上为增函数，不合题意……8分 ② 当0a >时，()()00f x x '≤>等价于()()()21100ax ax x +-≥>，即1x a ≥ 此时()f x 的单调递减区间为1,a ⎡⎫+∞⎪⎢⎣⎭．依题意，得11,0.a a ⎧≤⎪⎨⎪>⎩解之得1a ≥．………10分 ③ 当0a <时，()()00f x x '≤>等价于()()()21100ax ax x +-≥>，即12x a ≥- 此时()f x 的单调递减区间为12,a ⎡⎫-+∞⎪⎢⎣⎭， ∴1120a a ⎧-≤⎪⎨⎪<⎩ 得12a ≤- 综上，实数a 的取值范围是1(,][1,)2-∞-+∞U …………12分法二：①当0a =时，1()0,()f x f x x'=>∴在区间()1,+∞上为增函数，不合题意……8分 ②当0a ≠时，要使函数()f x 在区间()1,+∞上是减函数，只需()0f x '≤在区间()1,+∞上恒成立，0x >∴只要22210a x ax --≥恒成立，2214210a a a a ⎧≤⎪∴⎨⎪--≥⎩解得1a ≥或12a ≤- 综上，实数a 的取值范围是1(,][1,)2-∞-+∞U …………12分22．（本小题满分14分）已知椭圆C ：()222210x y a b a b +=>>过点3(1,)2A ，且离心率12e =．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）若直线l ：()0y kx m k =+≠与椭圆交于不同的两点M N 、，且线段MN 的垂直平分线过定点1(,0)8G ，求k 的取值范围．解：（Ⅰ）由题意12e =，即12c e a ==，2a c =， ∴ ()22222223b a c c c c =-=-= ∴ 椭圆C 的方程可设为2222143x y c c+=………………………………… 3分代入3(1,)2A ，得222312143c c ⎛⎫ ⎪⎝⎭+= 解得21c = ∴ 所求椭圆C 的方程是22143x y +=． ……………………………………… 6分（Ⅱ）法一由方程组22143x y y kx m⎧⎪+=⎨⎪=+⎩ 消去y ，得()2223484120k x k m x m +++-= ……… 4分由题意，△()()()22284344120km km =-+-> 整理得：22340k m +->① …… 7分设()()1122,,M x y N x y 、，MN 的中点为00(,)P x y ，则12024234x x km x k +==-+， 002334m y kx m k=+=+ ………………… 8分由已知，MN GP ⊥ 即1MN GP k k ⋅=-即 223034141348m k k km k -+⋅=---+ 整理得：2348k m k+=- ……………………… 10分代入①式，并整理得：2120k >，即||k >………………………12分∴,,k ∈-∞+∞ ⎪ ⎪⎝⎭⎝⎭……………… 14分（Ⅱ）法二由方程组221,43x y y kx m⎧⎪+=⎨⎪=+⎩ 消去y ，得()2223484120k x k m x m +++-= ……… 4分由题意，△()()()22284344120km km =-+-> 整理得：22340k m +-> ① …… 7分设()()1122,,M x y N x y 、，MN 的中点为00(,)P x y ，则22112222143143x y x y ⎧+=⎪⎨⎪+=⎩ 整理得： 00314y x k =-⋅ ② 又MN GP ⊥ ∴ 00118y k x =-- ③ …………9分由②、③解得 001238x y k ⎧=⎪⎨⎪=-⎩代入()0y kx m k =+≠，得 2348k m k+=- ……………………… 12分代入①式，并整理得： 2120k >，即 ||10k > ∴ 5,,k ⎛⎛⎫∈-∞+∞ ⎪ ⎪⎝⎭⎝⎭……………… 14分法三：由00(,)P x y 在椭圆内部，得：221328143k ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭+< 整理得： 2120k >，即 ||k >∴ ,,k ∈-∞+∞ ⎪ ⎪⎝⎭⎝⎭……………… 14分。

2010学年第一学期十校联合体高三期末联(文)答案

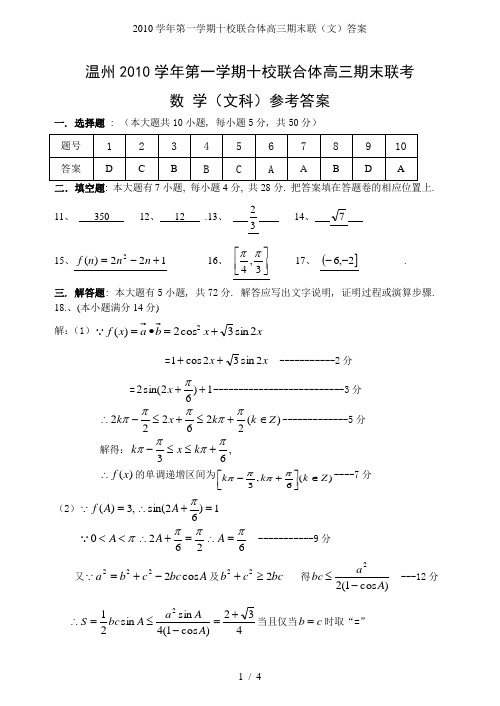
温州2010学年第一学期十校联合体高三期末联考数学（文科）参考答案一. 选择题 : （本大题共10小题, 每小题5分, 共50分）二．填空题: 本大题有 7小题, 每小题4分, 共28分. 把答案填在答题卷的相应位置上.11、 350 12、 12 .13、321415、122)(2+-=n n n f 16、 ⎥⎦⎤⎢⎣⎡3,4ππ 17、 (]2,6-- .三. 解答题: 本大题有5小题, 共72分. 解答应写出文字说明, 证明过程或演算步骤. 18.、(本小题满分14分)解：（1）x x b a x f 2sin 3cos 2)(2+=•==x x 2sin 32cos 1++ -----------2分 =1)62sin(2++πx --------------------------3分 )(226222Z k k x k ∈+≤+≤-∴πππππ-------------5分解得：,63ππππ+≤≤-k x k)(x f ∴的单调递增区间为)(6,3Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ----7分（2）,3)(=A f 1)62sin(=+∴πA π<<A 0 262ππ=+∴A 6π=∴A -----------9分又A bc c b a cos 2222-+= 及bc c b 222≥+ 得)cos 1(22A a bc -≤ ---12分432)cos 1(4sin sin 212+=-≤=∴A A a A bc S 当且仅当c b =时取“=”∴S 的最大值为432+----------------------------14分 19、(本小题满分14分)(1)设等差数列{}n a 的首项为1a ，公差为d,则⎪⎩⎪⎨⎧=⨯+=⨯+325665212211d a d a ————2分 ⎩⎨⎧-==131d a 解得 ———4分 n d n a a n -=-+=∴4)1(1 ————6分（2）)(,22)4(*∈⋅=⋅-=N n n a b n n n n ————7分2222121nn n S ⋅++⋅+⋅= ①13222)1(2221 2+⋅+⋅-++⋅+⋅=n n n n n S ②①-②，得1212222+⋅-++=-n nn n S —11分 1221)21(2+⋅---=n n n —13分 22)1(1+⋅-=∴+n n n S -------------14分20、(本小题满分14分)(1)由题意，⊥PA 面ABC ，BC PA ⊥∴，又A AB PA AB BC =⋂⊥,,⊥∴BC 面PAB又⊂BC 面PBC ，∴面⊥PAB 面PBC ———6分(2),,BC AB BC PA AB PA A ⊥⊥⋂=,BC PAB PB PAB ∴⊥⊂面又面,//BC PB MN BC MN PB ∴⊥∴⊥又,Rt PAB PA AB M ∆=在中，为中点,AM PB ∴⊥ ,AM MN M PB AMN ⋂=∴⊥面PNM ∴∠即为所求角或其补角————————10分设2PA =，则PB PM AC PC PN =====36sin ==∠∴PN PM PNM ,即所求角的正弦值为36.———14分21.（本题满分15分）(1)2()()x f x x x e '=- —————2分令()0f x '≥，则1x ≥或0x ≤,()f x ∴在(,0],[1,)-∞+∞上单调递增，在[0,1]上单调递减———5分20t ∴-<≤ —————7分(2)①若20t -<≤，则()f x 在[2,]t -上单调递增，()(2)f t f ∴>-，即n m >——————9分②若01t <≤，则()f x 在[2,0]-上单调递增，在[0,]t 上单调递减又213(2),(1)f f e e-==，()(1)(2)f t f f ∴≥>-，即n m >——11分 ③若1t >，则()f x 在(,0],[1,]t -∞上单调递增，在[0,1]上单调递减()(1)(2)f t f f ∴>>-，即n m >——13分综上，n m > ———15分22.（本题满分15分）(1)由题意，220028x y +=，即220028y x =-……①由220028184x y x x y y ⎧+=⎪⎨+=⎪⎩，则22220000(2)1664160y x x x x y +-+-=———4分代入①式，得220020x x x x -+=，则0∆=，∴直线为椭圆的切线——6分(2)设00(,)P x y ，则0040x y +-=，即004x y =-设1122(,),(,)M x y N x y ，则由(1)知，,PM PN 切线方程为1122184184x xy yx x y y⎧+=⎪⎪⎨⎪+=⎪⎩且过00(,)P x y ，则10102020184184x x y y x x y y ⎧+=⎪⎪⎨⎪+=⎪⎩， MN ∴所在直线方程为00184x x y y+=，即00280x x y y +-=———10分设所求距离为d ，且(2,0)F ，则|28||2|x y d -====∴当04y =时，max d =1 ————————————————15分(2)另解：(2)设00(,)P x y ，则0040x y +-=，即004x y =-设1122(,),(,)M x y N x y ，则由(1)知，,PM PN 切线方程为1122184184x xy yx x y y⎧+=⎪⎪⎨⎪+=⎪⎩ 且过00(,)P x y ，则10102020184184x x y y x x y y ⎧+=⎪⎪⎨⎪+=⎪⎩，MN ∴所在直线方程为00184x x y y+=，即00280x x y y +-= 082)4(00=-+-∴y y x y 过定点A(2,1)，又(2,0)F∴当直线AF MN ⊥时，即MN 所在直线方程为1=y ,点F 到直线MN 的距离最大为1.命题人：温州八中厉彩霞 138********（681991）审核人：乐清市第三中学谢丽俏（672508）陈林德（677527）。

2010年高三数学文科试卷及答案

{}02010年普通高等学校招生全国统一考试数学（文科）本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：1.答卷时，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室、座位号填写在答题卡上。

用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4.作答选作题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答。

5.考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

参考公式：锥体的体积公式Sh V 31=，其中S 是锥体的底面积，h 是锥体的高. 一、选择题：本大题共10小题，每小题5分，满分50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合{}3,2,1,0=A ，{}4,2,1=B 则集合=⋃B AA. {}4,3,2,1,0B. {}4,3,2,1C. {}2,1D. 解：并集，选A.2.函数)1lg()(-=x x f 的定义域是A.),2(+∞B. ),1(+∞C. ),1[+∞D. ),2[+∞ 解：01>-x ，得1>x ，选B.3.若函数xxx f -+=33)(与xxx g --=33)(的定义域均为R ，则A. )(x f 与)(x g 与均为偶函数B.)(x f 为奇函数，)(x g 为偶函数C. )(x f 与)(x g 与均为奇函数D.)(x f 为偶函数，)(x g 为奇函数解:由于)(33)()(x f x f x x=+=----,故)(x f 是偶函数,同理，g （x ）为奇函数，选D7.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是 A.54 B.53 C. 52 D. 5110.在集合{}d c b a ,,,上定义两种运算○+和○*如下那么d ○*a (○+=)cA.aB.bC.cD.d解：由上表可知：a (○+c c =),故d ○*a (○+=)c d ○*a c =，选A二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分。

高三文科数学试卷(含答案)经典题

高三文科数学试卷一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}24M x x =<，{}2230N x x x =--<，且M N =IA ．{}2x x <-B ．{}3x x >C ．{}12x x -<<D ．{}23x x << 2．若函数2()log f x x =，则下面必在()f x 反函数图像上的点是A ．(2)a a ，B ．1(2)2-， C ．(2a a ， D ．1(2)2-，3．右图为某几何体三视图，按图中所给数据，该几何体的体积为 A ．64+163 B ． 16+334 C ．163 D ． 164．在各项都为正数的等比数列}{n a 中，首项为3，前3项和为 21，则=++543a a a （）A ．33B ．72C ．84D ．189 5. 将函数)32sin(π+=x y 的图像向右平移12π=x 个单位后所得的图像的一个对称轴是：A. 6π=x B. 4π=x C. 3π=x D. 2π=x6．若以连续抛掷两次骰子分别得到的点数m ，n 作为点P 的坐标，则点P 落在圆1022=+y x 内（含边界）的概率为A ．61 B ．41 C ．92 D ．3677．下列有关命题的说法正确的是A ．“21x =”是“1-=x ”的充分不必要条件B ．“2=x ”是“0652=+-x x ”的必要不充分条件．C ．命题“x R ∃∈，使得210x x ++<”的否定是：“x R ∀∈，均有210x x ++<”． D ．命题“若x y =，则sin sin x y =”的逆否命题为真命题．P TMAOA B C D8．在约束条件⎧⎪⎪≤⎨⎪≤⎪⎩x>0y 12x-2y+10下，目标函数y x z +=2的值 A ．有最大值2，无最小值 B ．有最小值2，无最大值 C ．有最小值21，最大值2 D ．既无最小值，也无最大值 9．已知复数12z i =+，21z i =-，则12z z z =在复平面上对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限10．将n 个连续自然数按规律排成右表，根据规律，从2008到2010，箭头方向依次是第二卷非选择题(共110分)二、填空题：本大题共5小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．11．若Ａ（－２，３），Ｂ（３，－２），Ｃ（21，ｍ）三点共线，则ｍ的值为．12．程序框图（即算法流程图）如图所示，其输出结果是．13. 已知|a |=|b |=|b a -|=1,则|a +b 2|的值为．14．（坐标系与参数方程选做题）在极坐标系中，曲线3=ρ截直线1)4cos(=+πθρ所得的弦长为．15．（几何证明选讲选做题）如图PT 为圆O 的切线，T 为切点，3ATM π∠=，圆O 的面积为2π，则PA = ．开始a =1 a =3a +1 a >100?结束是否a =a +1输出a三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分12分）已知31cos 32cos sin 2)(2--+=x x x x f ，]2,0[π∈x⑴ 求)(x f 的最大值及此时x 的值； ⑵ 求)(x f 在定义域上的单调递增区间。

2010届高三数学文上学期期末质量调考新人教版

绝密★启用前2009—2010学年度揭阳市高中毕业班期末质量测试数学试题(文科)本试卷共4页，21小题，满分150分．考试用时l20分钟．注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上．3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁,考试结束后，将试卷和答题卡一并交回．参考公式：锥体的体积公式13V Sh =,其中S 表示底面积，h 表示高．一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．定义集合运算：{|,,}A B z z xy x A y B ⊗==∈∈．设2{0,2},{|320}A B x x x ==-+=，则A B ⊗＝A.{0,2,4}--B. {0,2,4}-C.{0,2,4}D.{0,1,2} 2．若复数2sin cos cos z i ααα=-+是纯虚数，则tan α的值为A ．2B ．31 C ．41 D ．213．已知向量(1,2),(0,1)=a b =，设,2k +u =a +b v =a b ，若//u v ，则实数k 的值为 A .－1 B.12-C. 12D. 1 4．已知α、β表示两个不同的平面，直线m α⊂，则“//m β”是“//αβ”的DC B A A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件5．已知函数()cos (0)f x x x ωωω=->的图象与直线2=y 的两个相邻交点的距离等于π，则为得到函数()y f x =的图象可以把函数2sin y x ω=的图象上所有的点 A. 向右平移12π B. 向右平移6π C. 向左平移12π D. 向左平移6π 6．某校高三（1）班共有60人，现需从中抽取所有座位号能被3整除的同学参加某项测试，7．若函数ln y x =与2y x=的图象的交点为00()x y ，，则0x 所在的区间是 A ．（1，2） B ．（2，3） C ．（e,3） D ． (),e +∞ 8．在等差数列{}n a 中，18153100a a a ++=，则9102a a -的值为A ．24B ．22C ．20D ．－89．椭圆的焦点为F 1、F 2，过点F 1作直线与椭圆相交，被椭圆截得的最短的线段MN 长为83，N MF 2∆的周长为12，则椭圆的离心率为A ．522 BCD．310．在矩形ABCD 中，AB=4,AD=6,在该矩形内任取一点P ,则使2APB π∠≥的概率为A.6πB.16π-C. 112π-D. 12π二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（11－13题）OP CA睡眠时间频率/组距(单位:小时)11．已知函数23,0() 1.0x x f x x x -⎧>⎪=⎨-≤⎪⎩，则[(2)]f f -= .12．如果圆22222240x y ax ay a +--+-=与圆224x y +=总相交，则实数a 的取值范围是．13．飞机的航线和山顶C 在同一个铅锤平面内，已知飞机的高度保持在海拔h （km ），飞行员先在点A 处看到山顶的俯角为α，继续飞行a （km ）后在点B 处看到山顶的俯角为β, 试用h 、a 、α、β表示山顶的海拔高度为（km ）．（二）选做题（14、15题，考生只能从中选做一题）14．(坐标系与参数方程选做题) 已知抛物线C ：222x t y t ⎧=⎨=⎩，（t 为参数）设O 为坐标原点，点M 在C 上,且点M 的纵坐标为2，则点M 到抛物线焦点的距离为． 15．（几何证明选讲选做题）如图，AC 为⊙O 的直径，弦BD ⊥于点P ，2PC =，8PA =，则tan ACD ∠的值为 __________.三．解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本题满分12分）已知：△ABC 中角A 、B 、C 所对的边分别为a 、b 、c 且sin cos sin cos sin 2A B B A C ⋅+⋅=. (1)求角C 的大小；(2)若,,a c b 成等差数列，且18CA CB ⋅=，求c 边的长. 17．（本题满分12分）某单位为了解职工的睡眠情况，从中抽取40名职工作为样本进行调查.调查的数据整理分组如下表示：（1）将以上表格补充完整，（2）在给定的坐标系内画出样本的频率分布直方图；（3）若按下面的方法在样本中从睡眠不足6小时的职工中抽取一人：把睡眠不足6小时的8人从2到 9进行编号，先后两次抛掷一枚均匀的骰子，出现的睡眠时间（单位：小时）[4,5) [5,6) [6,7) [7,8) [8,9) [9,10]频数 26128频率0．20D 1ABCDE点数之和为被抽取人的序号.试求抽到5或8号的概率.18．（本题满分14分）如图，已知ABCD 为矩形，1D D ⊥平面ABCD ， 11AD DD ==，2AB=，点E 是AB 的中点．(1)右图中指定的方框内已给出了该几何体的俯视图，请在方框内画出该几何体的正视图和侧视图；(2)求三棱锥C －1DED 的体积； (3)求证：平面1DED ⊥平面1D EC .19．（本题满分14分）已知数列{}n a 的前n 项和为n S ，且点n P (,)n n S a (n N *∈)总在直线310x y --=上.（1）求数列}{n a 的通项公式；（2）设n T 为数列1{}n a 的前n 项和，若对*n N ∀∈总有12n m T ->成立，其中*m N ∈ ，求m 的最小值． 20．（本题满分14分）已知椭圆的中心在坐标原点，短轴的长为12e =. （1）求椭圆的标准方程；（2）设O 为坐标原点，F 是椭圆的右焦点，点M 是直线4x =上的动点，过点F 作OM 的垂线与以OM 为直径的圆交于点N ，试探究线段ON 的长是否为定值？并说明理由.21．（本题满分14分）已知函数2(),()1f x bx g x ax ==+，()ln h x x =.（,a b R ∈）（1）若{|()()0}M x f x g x =+≥,1,2M M -∈∈，3z a b =-，求z 的取值范围；（2）设()()()h x F x f x =，且0b <，试判断函数()F x 的单调性；（3）试证明：对n N *∀∈，不等式11ln()e n nn n++<恒成立．2009—2010学年度年揭阳市高中毕业班期末质量测试数学试题(文科)参考答案及评分说明一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二、对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数，选择题和填空题不给中间分数．一．选择题：CDCBA CBCBD解析：1. {0,2},{1,2}A B ==,则{0,2,4}A B ⊗=, ,故选C.2．依题意，12sin cos 0,cos 0,tan 2αααα-=≠=，故选D. 3．∵(1,2),(2,5)k =+=u v 且//u v ∴211,522k k +==，选C. 5．依题意知函数()y f x =的周期为π，∴2ω=，∴()2sin(2)2sin 2()612f x x x ππ=-=-，故选A.PD 7. 因0x 是函数()2ln f x x x=-的零点，而()()20,30,f f <> ∴0x 所在的区间是(2,3），选B. 8.法1:18158831005100,20,a a a a a ++=∴==910810108220a a a a a a -=+-==，法2：由18153100a a a ++=得1720a d +=，9102a a -=112(8)(9)a d a d +-+=1720a d +=,故选C.9．由椭圆的定义知412,3a a ==，又2222285,4,5,3b c b c a b e a a ===-===，故选B. 10．如图：以AB 为直径作半圆，则当点P 落在半圆的内部（包括边界）时2APB π∠≥，故24612APB ABCD S P S ππ===⨯半圆.故选D ．二．填空题：11.127；12. 220a -<或022a <<； 13.sin sin sin()a h αββα-- （或tan tan tan tan a h αββα--）； 14. 52；15.2 .解析：12．圆22222240x y ax ay a +--+-=即22()()4x a y a -+-=，其圆心为(,)a a ，半径2r =，根据两圆相交的充要条件得2202408022a a a <<⇒<<⇒<<220a -<<13．如图在△ABC 中，由正弦定理得sin()sin a BCβαα=-， ∴sin sin()a BC αβα=-，在Rt BDC ∆中sin sin sin sin()a CD BC αβββα==-∴sin sin sin()a CE h CD h αββα=-=--（km ）. 〔或tan ()tan CD AD a BD αα==+，tan BD CD β=⇒tan tan tan tan a CD αβαβ=-∴tan tan tan tan a CE h CD h αββα=-=--.〕14. 抛物线的普通方程为22y x =，则其准线的方程为12x =-，由点M 的纵坐标为2得其横0.050.100.20:小时)坐标2x =，由抛物线的定义得15||2()22MF =--=. 15．由相交弦定理和垂径定理得: 216,4BP PC PA BP =⋅==∵ACD ABP ∠=∠ ∴8tan tan 24AP ACD ABP BP ∠=∠===. 三．解答题：16．解：(1) ∵sin cos sin cos sin 2A B B A C ⋅+⋅=∴sin()sin 2A B C +=，------------------------------------2分 ∵,sin()sin A B C A B C π+=-∴+=∴sin sin 22sin cos C C C C ==，-----------------------------4分 ∵0C π<< ∴sin 0C > ∴1cos 2C =∴.3C π= --------------------------------6分 (2)由,,a c b 成等差数列，得.2b a c +=----------------------------7分∵18CA CB ⋅=，即.36,18cos ==ab C ab ----------------------------------------9分由余弦弦定理ab b a C ab b a c 3)(cos 22222-+=-+=，36,3634222=⨯-=∴c c c ，.6=∴c ---------------------------12分17．解：（1）见下表：-------------------------------------------3分(2) 样本的频率分布直方图如右图示-------------------------------------8分（3）设“抽到5或8号”为事件A ，先后两次抛掷一枚均匀的骰子，出现的点数为（x ，y ）. 所有的基本事件有（1，1）、（1，2）、（1，3）、 ……、（6，6），共36个.事件A 包含的基本事件有：（1，4）、（2，3）、（3，2）、（4，1）、（2，6）、（3，5）、（4，4）、（5，3）、（6，2）共9个91()364P A ∴==----------------------12分18．解：(1)该几何体的正视图和侧视图如右图示：(准确反映三视图的图形特征)-------4分（2）∵1D D ⊥平面ABCD∴11311C-DED D DEC DEC V V S DD -∆==⋅⋅--- 6分而1121122DEC ABCD S S ∆==⨯⨯=∴1111133C DED V -=⨯⨯=---------------7分(3) ∵ E 为AB 的中点，∴△DAE 与△EBC 都是等腰直角三角形∴45AED BEC ∠=∠=∴CE DE,⊥------10分又∵1D D ⊥平面ABCD ，EC ⊂平面ABCD ∴11CE DD ,DE DD D ⊥⋂=∴CE ⊥平面1D ED --------------------------------------------------------12分 ∵EC ⊂平面1D EC∴平面1DED ⊥平面1D EC ----------------------------14分19．解：（1）∵点n P (,)n n S a (n N *∈)总在直线310x y --=上.∴3 1.n n S a =+ ---------------------------------------------------------1分当1n =时，1131,a a =+ ∴112a =-------------------------------------2分当2n ≥时，1133n n n n n a S S a a --=-=-113232n n n n a a a a --=⇒=（2n ≥）即数列}{n a 是首项112a =-，公比32q =的等比数列. --------------------------5分∴11113()22n n n a a q--==-⨯.---------------------------------------6分（2）∵113()22n n a -=-⨯，∴1122()3n n a -=-⨯，------------------------------------------------7分 ∴n n a a a T 11121+++=＝212222[1()()()]333n --++++-----------------------9分＝2[1()]2326[1()]2313n n --⨯=-⨯--6>--------------------------------------------11分 ∵对*n ∀∈N 总有12n m T ->成立 ∴必须并且只需162m -≤-即13m ≥.∴m 的最小值为13.------------------------------------------------------14分20．解：（1）由2b =b =12e =得2a c =------------------------------------2分 ∵222222433b a c c c c =-=-== ∴1c =，2a =-----------------------------4分∴所求的椭圆的标准方程为：22143x y +=或22134x y +=---------------------------------6分（2）解法1：设点(4,)M t 、以OM 为直径的圆上任一点Q 的坐标为(,)x y 则由QO QM⊥得14y y tx x -⋅=-- ()(4)0y y t x x -+-=--------------------------------------------------------------------------8分若0t =，则以OM 为直径的圆方程为2240x y x +-=，即22(2)4x y -+=，设圆心为A,易知△ONA 为等边三角形，∴||2ON =------------------------------------------------------10分若0t ≠ ∵FN OM ⊥ ∴14FN OMk k t=-=-∴直线FN 的方程为4(1)y x t=----------------------------------------11分设点N 的坐标为00(,)x y则0000()(4)0y y t x x -+-=---------------------------①a-b+1=0004(1)y x t=-------------------------------②由②得004(1)x t y -=代入①得0000004(1)[](4)0x y y x x y --+-= 22004x y+=∴||2ON ==即线段ON 的长为定值.--------------------------------------------------------------------------14分[解法2：设点(4,)M t ,若0t =，由相交弦定理得：2||||||ON OF OM =⋅∵||1,||4OF OM == ∴||2ON =------------------------------------7分若0t ≠,则直线OM 的方程为4ty x =--------------------------① ∵FN OM ⊥ ∴14FN OMk k t=-=-∵(1,0)F ∴直线FN 的方程为4(1)y x t=------------------②-----------9分解由①②联立组成的方程组得221616416x t t y t ⎧=⎪⎪+⎨⎪=⎪+⎩,即直线OM 与FN 的交点P 的坐标为22164(,)1616tt t ++---------------------------------------------------11分∴22222221616||(16)(16)t OP t t =+++,22||16OM t =+ ∴22222222161616(16)||||16161616t t OP OM t t t +⋅=+==+++ ----------------13分 ∴||||4OP OM ⋅=由相交弦定理得2||||||4ON OP OM =⋅= ∴||2ON =即线段ON 的长为定值.---------------------------------------------------------------------14分] 21．解：（1）解法1：不等式()()0f x g x +≥即210ax bx ++≥由1,2M M -∈∈得104210a b a b -+≥⎧⎨++≥⎩----------------2分画出不等式组所确定的可行域如右图示：作平行线族3b a z =-可见当0.5,0.5a b =-=时z 有最小值，min 2z =-∴z 的取值范围为2z ≥-.----------------------------------------4分[解法2：令()()()h x f x g x =+由1,2M M -∈∈得(1)0,(2)0h h -≥≥由1(1)421(2)a b h a b h -+=-⎧⎨++=⎩得(2)2(1)36(2)4(1)36h h a h h b +--⎧=⎪⎪⎨--+⎪=⎪⎩-------------------------2分 ∴153(2)(1)233a b h h -=+-- ∵(1)0,(2)0h h -≥≥ ∴32a b -≥-，即z 的取值范围为2z ≥-.------------4分]（2）∵ln ()x F x bx =∴21ln '()x F x bx-= -----------------------------------6分令'()0F x =得1ln 0x -=∴x e = ------------------------------------------------------------7分∵当0x e <<时21ln '()0x F x bx-=<，当x e >时'()0F x > ∴函数()F x 在(0,]e 上单调递减，在[,)e +∞上单调递增--------------------------9分（３）证法1：由（2）知当x e =时函数有最小值min 1()()F x F e be ==∴在(0,)+∞上恒有ln 1()x F x bx be =≥，------------------------------------------------11分 ∵0b < ∴ln 1x x e≤当且仅当x e =时“＝”成立 ∴对任意的(0,)x ∈+∞恒有1ln x x e≤--------------------------------------------------12分 ∵10n n +>且1n e n +≠∴111ln n n n e n ++<⋅11ln()e n n n n++⇒< 即对n N *∀∈，不等式11ln()e n n n n++<恒成立．-----------------------------------------14分〔证法2：构造函数()ln x p x x e=-，(0,)x ∈+∞----------------------------------------10分令11'()p x x e=-0= 得x e = ∵当0x e <<时'()0p x >，当x e >时'()0p x <∴函数()p x 在(0,]e 上单调递增，在[,)e +∞上单调递减----------------------12分当x e =时函数()p x 有最大值max ()()0p x p e ==∴对任意的(0,)x ∈+∞恒有1ln 0x x e -≤，即1ln x x e≤ ∵10n n +>且1n e n +≠∴111ln n n n e n ++<⋅11ln()e n n n n++⇒< 即对n N *∀∈，不等式11ln()e n n n n ++<恒成立．-----------------------------------------14分〕。

宁波市201011学年高三期末考试数学(文)试题及答案

宁波市2010学年第一学期期末试题高三数学（文科）试卷说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分．考试时间120分钟．注意：本卷考试时间120分钟，请考生将所有题目都做在答题卷上．参考公式：球的表面积公式 S = 4πR 2 球的体积公式334R V π=其中R 表示球的半径锥体的体积公式 V =31Sh 其中S 表示锥体的底面积，h 表示锥体的高柱体的体积公式 V = Sh其中S 表示柱体的底面积，h 表示柱体的高台体的体积公式)(312211S S S S h V ++=其中S 1，S 2分别表示台体的上、下底面积， h 表示台体的高如果事件A ，B 互斥，那么P (A +B ) = P (A ) + P (B )第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．（1）如果集合B A ,满足A B ⊆，则下列式子中正确的是BA B C D A B B C C A B A B B B A A A A ==== ))(()()()()(（2）已知i a ibi+=+-212（b a ,∈R ），其中i 为虚数单位，则=b 9)(1)(9)( 1)(D C B A --（3）某中学共有高中学生1800人，其中高一、高二、高三年级的人数之比为8:9:7，要用分层抽样的方法从所有高中学生中抽取一个容量为120的样本，则应抽取高三年级的学生人数为50)(45)(40)(35)(D C B A（4）若向量),2(y =（∈y R ），则“5=y ”是“3||=”的(A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件 (5) 若某几何体的三视图 (单位：cm) 如图所示，则此几何体的体积等于(A) 2123πcm 3 (B) 70πcm 3正视图侧视图(C)3263πcm 3(D) 100πcm 3（6）已知0>b ，直线02)1(2=+++ay x b 与直线012=--y b x 互相垂直，则ab 的最小值为32)(22)(2)(1)(D C B A（7）定义在R 上的偶函数)(x f ，当0≥x 时有)()2(x f x f =+，且)2,0[∈x 时，12)(-=x x f ，则=-+)2011()2010(f f1)(0)(1)(2)(D C B A --（8）设n m ,是两不同的直线，βα,是两不同的平面，则下列命题正确的是(A) 若α⊥β，n =βα ，m ⊥n ，则m ⊥α (B) 若m ⊂α，n ⊂β，m ∥n ，则α∥β (C) 若m ∥α，n ∥β，m ⊥n ，则α⊥β (D) 若n ⊥α，n ⊥β，m ⊥β，则m ⊥α（9）椭圆)320(112222<<=+b b y x 与渐近线为02=±y x 的双曲线有相同的焦点21,F F ,P 为它们的一个公共点,且9021=∠PF F ,则椭圆的离心率为615)(630)(621)(66)(D C A A（10）定义在R 上的奇函数)(x f ，当0≥x 时，⎪⎩⎪⎨⎧+∞∈--∈+=).,1[|,3|1)1,0[),1(log )(21x x x x x f ，则关于x 的函数)10()()(<<-=a a x f x F 的所有零点之和为aa a a D C B A 21)(21)(12)(12)(------第II 卷（非选择题共100分）二、填空题：本大题共7小题，每小题4分，共28分．（11）已知31)22sin(=+θπ，则=θcos ▲ ．（12）在R 上定义运算)1(y x y x -=⊗⊗：，则不等式 2)2()2(<+⊗-x x 的解集为 ▲ ．（13）某程序框图如图所示，则该程序运行后输出的x 的值为 ▲ ．（14）已知等比数列{}n a 的公比为q ，前n 项和为n S ，若201220102011,,S S S 成等差数列，且11=S ，则=n a ▲ ．（15）如图AB 是半圆O 的直径，D C ,是弧AB 的三等分点，N M ,是线段AB 的三等分点，若6=OA ，则=⋅ND MC ▲ ．（16）过点(0,0)O作直线与圆22((8)169x y -+-=相交，在弦长均为整数的所有直线中，等可能的任取一条直线，则长度不超过14的概率为 ▲ ．（17）若实数y x ,满足不等式组⎪⎪⎩⎪⎪⎨⎧≥≥-≥-≤-00263y x y x y x ，且目标函数by ax z += （)0,0>>b a 的最大值为12，则ba 32+的最小值为 ▲ ．三、解答题：本大题共5小题，共72分。

闵行区2010学年第一学期高三年级质量调...

闵行区2010学年第一学期高三年级质量调研考试数学文科.doc闵行区2010年第一学期高三年级质量调研考试数学文科-数学-txt预览-第1页学校_______________________ 班级__________ 准考证号_________ 姓名______________ …………………………密○………………………………………封○………………………………………○线…………………………闵行区 2010 学年第一学期高三年级质量调研考试数学试卷（文科）考生注意： 1．答卷前，考生先将自己的姓名、学校填写清楚，并填涂准考证号，请仔细核对．答题时客观题用 2B 铅笔按要求涂写，主观题用黑色水笔填写． 2．本试卷共有 23 道题，共 4 页．满分 150 分，考试时间 120 分钟． 3．考试后只交答题纸，试卷由考生自己保留．一. 填空题（本大题满分56 分）本大题共有 14 题，考生应在答题纸上相应编号的空格内直接填写结果，每个空格填对得 4 分，否则一律得零分．．= i ，其中 i 是虚数单位，则实数 b+ 0 的一个根是 2 = c + bx +2 1．已知关于 x 的实系数方程 x___ .= 3 2 1 y = b2 y + ___, 5．系数矩阵为 a2 x = 3 的解是 x = b1 y + 6 的焦距为． 1 2 的线性方程组 a1 x = 3 y + b 等于． 2 2 4．椭圆2 x - (2,1) ，则 2a =1,2) ， b - (= 3．若向量 a ρρρρ 2 的解集是 x >1 ．2．不等式)({{x0 ，则 f ( x1 ) 与 0 的大小关系 2< x 的零点，且 x1 - ( ) x =． 2 1 9 ．若 x0 是函数 f ( x) = a)9 的展开式中， x 2 的系数是，则实数 a - 3tan 2 x 的图像向右平移 1 个单位，得到的图像对应的函数解析式是． 21 8．在 ( 3 x = 8 7．将函数 y θ的值为． 1 cos θ，则sin 2-= 2 15 θsinlg a6 的值等于．+ 10 ，则 lg a4 =6．已知是． 10．在各项均为正数的等比数列 {a n } 中，若 a511．有甲、乙、丙、丁四人参加广州亚运会某项射击选拔赛的平均成绩依次是8.5、8.8、9.1、 9.1，方差依次是 1.7、2.1、1.7、2.5，则参加亚运会该项目角逐的最佳人选是．a ，若 p 是 q 的充分不必要条件，则 a 的取值范围是．≤ 2 ；条件 q : x ≤ 1 +12．已知条件 p : x= 2 +满足 an }an {13．数列an= 2 ，则 a24 =1 ，若 a1 = 6 ， a2 +an．g ( x2 ) 恒成立；> D ， f ( x1 ) ∈ d ，则对任意 x1、 2 >14．设定义在 D 上的两个函数 f ( x ) 、 g ( x) ，其值域依次是 [ a， ] 和[c， ] ，有下列 4 个命 b d 题：x ①若 ad ；> g ( x2 ) 成立，则必有 a > D ，使 f ( x1 ) ∈x ②若存在 x1、 20 ． [答]（ y 1 x O (D) ） x ） 17．将一颗质地均匀的骰子先后抛）= 1 - 2 y + 0 ．（D） x = 1 - 2 y - 0 ． (B) x = 2 - y + 0 ． (C) 2 x = 1 + 2 y - 0 的法向量垂直的直线方程是[答]（（A） x =2 - 2 y - g ( x) 恒成立．其中正确的命题是（请写出所有正确命题的序号）．二. 选择题（本大题满分 20 分）本大题共有 4 题，每题只有一个正确答案.考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得 5 分，否则一律得零分． 15．过点（1，0）且与直线 x > D ， f ( x) ∈ d ，则对任意 x > d ；④若 a > g ( x) 恒成立，则必有 a > D ， f ( x) ∈③若对任意 x2 的图像是⊕ 1 = b) ，则函数 f ( x) ≤ a ( a = b ⊕x 16．定义运算 ab)>b (a {y 1 O (B)y 1 O (A) xy 1 x O (C)掷 3 次，至少出现一次 6 点向上的概率是[答]（ (A)．闵行区2010年第一学期高三年级质量调研考试数学文科-数学-txt预览-第2页5 216(B)25 ． 216(C)31 ． 216(D)91 ． 216= an +Λ+ a2 +N* ）是等比数列，且 a1 ∈（ n }an {2 2 2 18．设1) ，则 an 的表达式为 3-1 n (41-n1 (A)2 ．-[答]（） n1 ．-2n-(B)2)-(±1 或-2n±(C)．1 ．-2n±(D)ABC 的外接圆的面积．∆ 6 ，求=ABC 的三内角 A、B、C 所对的边分别为a、b、c ，且（1）求角 B 的大小；（2）若 b ∆三. 解答题（本大题满分74 分）本大题共有 5 题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤． 19.（本题满分 12 分）本题共有 2 个小题，每小题满分各6 分．已知b-0． c a =c -b a+a4 y 相交于不同的两点 A、B ，O 为坐标原点．=20.（本题满分 14 分）本题共有 2 个小题，每小题满分各 7 分．若斜率为 2 的动直线 l 与抛物线 x 260 ，求直线 l 在 y 轴上截距的取值范围．≤ OB ⋅（1）求线段 AB 中点 P的轨迹方程；（2）若 OAρρυυυυυυ8) ， A、B 在 MN 上的射影 P、Q 之间距离为 12km ，现计划修普通公路把这两个城镇与高速公路相连接，若普通公路造价为 50 万元/ km ；而每个与高速公路连接的立交出入口修建费用为 200 万元．设计部门提交了以下三种修路方案：方案①：两城镇各修一条普通公路到高速公路，并各修一个立交出入口；方案②：两城镇各修一条普通公路到高速公路上某一点 K ，并在 K 点修一个公共立交出入口；方案③：从 A 修一条普通公路到 B ，再从 B 修一条普通公路到高速公路，也只修一个立交出入口．请你为这两个城镇选择一个省钱的修路方案． A akm P M B 8km N Q>21.（本题满分 14 分）如图，在一条笔直的高速公路 MN 的同旁有两个城镇 A、B ，它们与 MN 的距离分别是akm 与 8km(a⋅log (4 a 2 = R ）为偶函数．（1）求常数 k 的值；（2）当 x 取何值时函数 f ( x ) 的值最小？并求出 f ( x ) 的最小值；（3）设 g (x) ∈ 1) x （ x - (k - 1) + log 4 (4x =22.（本题满分 16 分）本题共有 3 个小题，第(1)小题满分 4 分，第(2)小题满分 5 分，第(3) 小题满分 7 分．已知函数 f ( x)x0） ) 3≠ a （a -4 ，且函数 f ( x ) 与 g ( x) 的图像有且只有一个公共闵行区2010年第一学期高三年级质量调研考试数学文科-数学-txt预览-第3页点，求实数 a 的取值范围．1 1) ， 1) ，- (∈1 ，对任意 x、y -=1，上， f ( ) -23.（本题满分 18 分）本题共有 3 个小题，第 1 小题满分 3 分，第2 小题满分 8 分，第 3小题满分 7 分．已知函数 f ( x ) 定义在区间 (2 f ( ) ； 1) 2 （2）证明数列 { f ( an )} 是等比数列，并求 f (an )的表达式和 lim bn 的值；=1，内求一个实数 t ，使得 f (t ) -． f (a1 )f (a2 ) f (a3 ) f ( an ) 1 （1）在 (=设 bn +Λ+++ xy 1 1 1 1 + an1 +2 2 1 =1 +，an = y 1 ， ) 成立，又数列 {an} 满足 a1 +2an xf (= f ( y ) +恒有 f ( x)∞→n1 2成立？若存在，求出 m 的最 4< N* ，都有 bn ∈ N* ，使得对任意 n ∈8 （3）是否存在 m -m小值；若不存在，请说明理由．闵行区 2010 学年第一学期高三年级质量调研考试数学试卷参考答案与评分标准4 ； 4． 2； 2． (0, ) ； 5．（理）-一. 填空题． 1．1 23． 5；，（文）3=2 yy ++2x x{3 =11==xy {；6．1 ； 42) ； 10．（理）0，（文）2； 13．（理）- 3tan(2 x =7． y-8．1 ； 2；)∞+1, [ 0 ； 12．>9． f ( x1 )11．丙；3 ，（文）3； 14．①④． 7（2 分）= 0 ，又 cos B = ac - b - c +二. 选择题． 15．B； 16．A； 17．D；18．C 2 2 2 三. 解答题．19. 解：（1）由已知得 a2 2 24 时等号成立)（2 分）= c = 16 (当且仅当 a ≤ ac ⇒ 2 ac ≥ c + a = 60 （6 分） 2ac 2ac 2 （2）(理) 由 8 =，（4 分）∴ B ==οb ac 1 -c +a4 时，分）（5= c =ABC 面积的最大值为 4 3 ．即当且仅当 a ∆4 3， 2 2 2 =⨯ 4 ⨯=ο1 1 3 ac sin 60闵行区2010年第一学期高三年级质量调研考试数学文科-数学-txt预览-第4页=ABC ∆∴ S（4 分）（6 分）=（2）(文) 由正弦定理得， 2 R．（6 分）πABC 的外接圆的面积为 12∆，即π 12= 2 3 ，分） sin B 3 ∴ S外接圆=（2 （4 =2 b ，分）∴ R ⋅6b ， l 与 C 的交点坐标分别为 A( x1，y1 )、B( x2，y2 ) ，点 P( x，y ) ，由+ 2 x =20.解：（1）设 l 的方程为 y{b+ 2x = 0 ， y = 4b - 8 x - x 2 ⇒ 4 y =x 2（2 分）60≤ OB ⋅由 OA ρρυυυυυυ b ，（2 分） 16 = 1 2 =4b，y1 y2 -=10 ．（6 （7 分） 2 2 x x 2 （文）（2）由（1）知 x1 x2 ≤ b <4-4 ，∴ -> 10 ，分）注意到 b ≤ b ≤26 - 85 （4 分）解得⨯ 16 ≤ 2b) + (16 + 64 = y2 ) + ( y1 + x2 ) + ( x1 = OB | +| OA = 2 2 2 由 | OQ| ρρ 2 υυυυυυ 2 ρυυυ 2b （2 分）+ 16 = 2b + x2 ) + 2( x1 = y2 +8 ， y1 = x2 + 4) ．（7 分）（2）（理）由（1）知 x1 > 4( y = 2 故所求的轨迹方程为 x ⎩ 4 > 8 + b = b + 1 2 ⨯ 2=y ⎪x + x ⎩⎪⎪4b -=4 2x1 x2 = 1 （4 分）= x ⎨ 8 ，依题意，= x2 + x1 ⎨得⎪ x2 + x ⎪ 0 >4b ⨯ 4 +8)2 - (=∆⎧4 ->b ⎪⎧ 16) 万元；（3 分）方案②：取 B 关于MN 的对称点 B ' ，连 AB ' 与 MN 交于 K ，在 K 修一个出入口，则路程最短，共需资金：+ 50(a = 400 + a) + 50(8 = a)km 普通公路和两个立交出入口，所需资金为 A1 + 10 ．（7 分） 21.解：方案①：共修 (8 ≤ b <4-4 ，∴ -> 10 （6 分）注意到 b ≤ b ≤6 - 60 （4 分）解得≤ b2 +4b-= y1 y2 +得 x1x212] 万元+ 144 + 8) 2 - 50[ (a = 200 + 8] + 122 + 8) 2 - 50[ (a = 4] 万元；方案③：连接 AB 沿 ABQ 修路，在 Q 修一个出入口，共需资金： A3+ 144 + 8) 2 + 50[ (a = 200 + 122 + 8) 2 + 50 (a =A2A3 ，（12 分）故选择方案（3）．（6 分）> A2 > 8 ，比较大小有 A1>由于 a（9 分）（14 分）1) x 对所有- (k - 1) + log 4 (4 x = 1) x - (k + 1) + x -22.解：（1）∵ f ( x ) 为偶函数，故 log 4 (4（2= k ∴ R 都成立，∈ 0 对所有 x = 3) x - R 都成立，分）即 (2k ∈x - 1) + log 4 (4 x =（2）由（1）得 f ( x)3 ．分）（4 2（2 分）log 4 ． 2x 2= 1 x ，即 f ( x) +4x+ log 4 (2 x ⎩ 3 ⎩ 3 ⎩ 3 ⎪⎪② ΛΛΛΛ 0> a - 2 x ⋅a ⎪< 2 > x 4 ， 42 ⎨ x 4 或⎨ 2 ，由②得⎨3 可变形为⎪⎪① ΛΛ a- 2 ⋅ a = x ⎪ 0 <a ⎧0 >a ⎧ 1 4 x + 4x ⎧） 2 3 * a) （- 2 x ⋅ log 4 (a =- 1) + 0 时，分） f ( x ) 的最小值是．分） x 2 2 2 x 4 （3）（理）解法 1 由方程log 4 (4 x =，故当且仅当 x = log 4 2 ≥1 1 1 （3 （5 )⎩⎩ 3 ⎪ 3 ⎪<t < 0> t⎨，或⎨ t ，则= x 4 令 2 ⎪ 4 ⎪ 0 <a ⎧ 0 >a ⎧⎩ 3 ⎩⎩ 3 ⎪ 3 ⎪② ΛΛΛΛ 0> a - 2 x ⋅a ⎪ 4 < 2 > x 4 ， 2 ⎨ x 4 或⎨2 ，由②得⎨3 可变形为⎪⎪① ΛΛ a- 2 ⋅ a = x ⎪ 0 <a ⎧ 0 >a ⎧ 14 x + 4x ⎧） 2 3 * a) （- 2 x ⋅ log 4 (a =- 1) +（-3，1]时，无交点 . （7 分） x 4 （文）由方程 log 4 (4 x ∈ a-)时，一个交点，（∞(1,+⋃{-3}∈， 3）时，两个交点， a ∞-∈ 1 （5 分）综上:a ≤ a < -3 ⇒) 无交点∞(1,+⋃{-3}∈讨论得a ⇒)式只有一个正根* (⇒1 （4 分）一个交点- a ⎩⎪0 >1 -⎪ 1) - 3(a ⎪3 （3 分）-< a ⇒ 0 >⎨⇒)式两相异正根* (⇒ 4a 两个交点⎪⎪ 0 >ς⎪⎧ 0 3 3 = 1 - t ⋅ a - 1)t 2 -(a ⇒ 0 = 1 - 2 x ⋅ a - 1)(2 x )2 - (a ⇒ 4 4 （2 分）⎩ 3 ⎪ 0 > 4 a - 2 x ⋅a ⎪ 2 3 ⎨⇒）* a) （- 2 x ⋅ log 4 (a =- 1) +解法 2： log 4 (4 x ⎪ 3 a x 4 - 2 ⋅ a = 2x ⎪ 1 4 x + 4x ⎧ 1 时，函数 f ( x ) 与 g ( x) 的图像没有公共点．（7 分）≤ a < 0 或 0 < a <3 - 1 时，函数 f ( x ) 与 g ( x) 的图像有且只有一个公共点；当>3 或 a -=3 时，函数f ( x ) 与 g ( x) 的图像有两个不同的公共点；当 a -<）无解．（5 分）综上所述，当 a * 1 时方程（≤ a < 0 ，或 0 < a <3 -）有两解；当当*3 时，方程（-<）有且只有一个解；（4 分） a *3 时方程（-= 34 t 当 a -+3 75 3 t 3t -≤+ 1 = 0 ， a < 34 -+ 3t ≤4 -时，< t <）有且只有一个解；（3 分） 25 75 16 当3 * 1 ，此时方程（> 0 ，3 t t ∴ a > 34 -+ 34 单调递增，∴ 3t -+时， 3t > 34 t 25 75 75 当t -+ 75 3t + 34t - 75 3t + 1= 2 ．（2 分）+ 1= 16t 16 则 a ⎩⎩3 3 ⎪⎪ 2 ⨯ 4 - (2 ) ⨯ 3 <t < 3> x 2 x t⎨，或⎨ t ，则= 3 + 2 x ⨯25 ，令 4 ⎪ 25 ⎪ 3 + 2x ⨯ 0 4 <a ⎧ 0 >a ⎧+ 1 =由①得 a，满足题意，分）（5 4 2=3 ，则 t -=2 ，不合题意，舍去，若 a -=，则 t =3 ， 3 4 3 1 若 a -=或 a = 0 时， a = 1) - 4(a + a) - (=∆ a 不存在， 3 4 2 3 当⇒ 0 > 0 ，∴ h( ) <1 -= 0 时， h(0) < 1 ，（4 分） 3 4 当 a > a ⇒ 0 < 1)h( ) - 0 时， (a > 1 （2 分） 3 3 4 ∴当 a - at - 1)t 2 - (a = 0 ，设 h(t ) = 1 - 2 x ⋅4 4 a1 时，函数 f ( x ) 与 g ( x) 的图像有且只有一个公共点. （7 分）>3 或a -=∴当 a - 1)(2 x ) 2 -由①得 (a闵行区2010年第一学期高三年级质量调研考试数学文科-数学-txt预览-第5页2 2⨯+（3 分） 1 1 2 2 2 5 5 1= f ( ) ，∴ t = f ( 2 2 ) = f ( ) +f ( ) = 2 f ( ) = 1 1 1 4 4 23.解：（1） f (t ) +1 1f (= f ( y ) +1 ，且 f ( x) -= f ( ) = f (a1 ) Θ（2）1 2xy+ y ) 1 +xan f ( an )⋅ an + an 1 +2 2 1 = 2 f (an ) ，即= f (an ) + f (an ) = f( n ) = f ( )=1 ) + f (an ∴1 ) + an f (an +2an a=1 . （4 分）∴ lim bn -2n-=1为首项， 2 为公比的等比数列，∴ f (an ) -∴ { f ( an )} 是以∞→n（2 分）（8 分）2-2 . 1 1-=1 -- N 恒成立，2 ∴ m 的最小正整数值为 12 。

崇文区200-2010学年度高三第一学期期末统一练习(数学文)

AB, PB 的中点．
P
（Ⅰ）求证： OD ∥平面 PAC ；
（Ⅱ）求证：平面 PAB ⊥平面 ABC ；（Ⅲ）求三棱锥 P ABC 的体积．
D
（17）（本小题共 13 分）
A C
O
B
某中学高中学生有 900 名，学校要从中选出 9 名同学作为国庆 60 周年庆祝活动的志愿者.已知高一有
400 名学生，高二有 300 名学生，高三有 200 名学生.为了保证每名同学都有参与的资格，学校采用分层抽
（10）一个几何体的三视图如图所示，其中俯视图为正三角形，则该几何体的表面积为 ___________.
4
2
主（正）视图
侧（左）视图
俯视图
（11）在V ABC 中， AB 3, BC 13, AC 4 ，则 A ___________， SV ABC ___________..w
44
2
（16）（共 14 分）
（Ⅰ）O, D 分别为 AB, PB 的中点，
OD ∥ PA
又 PA 平面 PAC ， OD 平面 PAC OD ∥平面 PAC .
----------5 分
（Ⅱ）连结 OC ， OP
AC CB 2 ， O 为 AB 中点， AB 2 , OC ⊥ AB ， OC 1 .
x2 2 y2 2,
由

y

x
1,
得
3y2 2 y 1 0 ，解得
y1

1,
y2

1 3
．
∴
SPOQ

1 2
OF

y1

y2
1 2

顺义区2010届高三第一次统练数学试卷(文科)

顺义区2010届高三第一次统练数学试卷（文科）本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

考试时间120分钟。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，选出符合题目要求的一项.1. 在复平面内，复数(1)z i i =⋅+对应的点位于 ( ) A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限2.已知向量(1,)a y =r ，(4,)b y =-r，且a r 与b r 垂直，则y 等于（）A.2B.2-.C.2±.D.4 3.命题:p “2,0x R x x ∃∈-<”，那么命题p ⌝为 ( ) A. 2,0x R x x ∃∈-≥ B. 2,0x R x x ∃∈-> C. 2,0x R x x ∀∈-≥ D. 2,0x R x x ∀∈-<4.在等差数列{}n a 中，23a =，47a =，15k a =，则k 等于 ( ) A. 6 B.7 C.8 D.95.“ 12πα=”是“1sin 22α=”的（） A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.对任意非零实数a 、b ，若a b ⊗的运算原理如图所示，则221log 163-⎛⎫⊗ ⎪⎝⎭的值为 ( )A.23 B.1 C.54D.27.已知集合{}*|120,A x x x N =≤≤∈，任取x A ∈，则对数2log x 是一个正整数的概率是 ( ) A.13 B.14 C.15 D. 1108.设x 、y 满足约束条件1048000x y x y x y -+≥⎧⎪--≤⎪⎨≥⎪⎪≥⎩若目标函数z ax by =+ (0,0)a b >>的最大值为12，则34a b+的最小值为（） A. 2 B. 2512C. 4D. 4912第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9.若3sin 5θ=，且θ是第二象限角，则cos θ=_____________. 10.在ABC V 中，a 、b 、c 分别是角A 、B 、C 的对边，已知3b =，c =030A =，则a =_________.11.如果一个几何体的三视图如图所示（长度单位：cm ）,则此几何体的体积是______________3cm .12.直线35150x y -+=经过椭圆22221x y a b+= ()0a b >>的两个顶点，则该椭圆的离心率为______________.13.已知二次函数()y f x =的图象关于直线1x =对称，且在点(0,(0))f 处切线的斜率2k =-，则'(2)f =____________.14.若数列{}n a 满足12,(01)1,(1)n n n n n a a a a a +≤≤⎧=⎨->⎩ 且156a =，则2010a =__________.三．解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤 15．（本小题共13分）已知函数2211()sin 2(cos sin )22f x x x x =--，求：（1）函数()f x 的最小正周期； (2) 函数()f x 的最大值及相应的x 值.16．（本小题共13分）俯视图侧视图正视图2222如图:已知在矩形ABCD 中，5,3AB BC ==,沿对角线BD 把ABD V 折起，使A 移到1A 点,过点1A 作1AO ⊥平面BCD ,垂足O 恰好落在CD 上. （1）求证：1BC A D ⊥ (2)求三棱锥1A BCD -的体积17．（本小题共13分）为了解某高中校开展冬季长跑锻炼的情况，拟采取分层抽样的方法，从高一、高二、高三年级中抽取5个班进行调查.已知该校高一、高二、高三年级分别有5、10、10个班.（1）求从高一、高二、高三年级中应分别抽取班级的个数; （2）若从抽取的5个班中随机抽取2个班，进行调查结果对比,用列举法计算这2个班分别有高二、高三各一个班的概率. 18．（本小题共14分）已知函数321()3f x x x ax a =-+-,()a R ∈在1-=x 时取得极值. （1）求a 的值及()f x 的单调区间;（2）若对任意[]0,4x ∈，()f x λ<恒成立,求实数λ的取值范围. 19．（本小题共14分）已知椭圆:C 12222=+by a x )0(>>b a过点，离心率12e =.（1）求椭圆C 的方程；（2）设Q 是椭圆C 上的一点，过点Q 的直线l 交x 轴于(1,0)F -，交y 轴于点M .若||2||MQ QF =u u u r u u u r，求直线l 的斜率.20．（本小题共13分）在数列{}n a 中，已知10a p =>且21log ()21n n a a n +=+.(1) 若数列{}n a 是等差数列，求的p 值； (2) 求数列{}n a 的前n 项和n S .OA 1DCBA顺义区2009--------2010学年度第一学期期末质量监测9．45-；323；12．45；13．2；14．23；三．解答题（本大题共6小题，共80分） 15. （本小题共13分）解：解：（1）()f x =2211sin 2(cos sin )22x x x =-- 1(sin 2cos 2)2x x =-————3分=)24x π-————6分 ∴T π= ————8分（2）()f x 11分，此时38x k ππ=+，k z ∈———13分. 15．（本小题共13分）（1）证明：Q 1AO ⊥平面BCD BC ⊂平面BCD ∴1AO BC ⊥———2分由已知ABCD 是矩形 ∴BC DC ⊥，1DC AO O =I ∴BC ⊥平面1A DC ————4分 ∴1BC A D ⊥ ————6分（2）由（1）知1BC AC ⊥，5AB =，3BC =∴14AC = 又5DC =，13A D =————8分∴22211DC AC A D =+，∴11A D AC ⊥ ————10分 ∴1125AO =11163A BCD BCD V S A O -==V ————13分 17．（本小题共13分）（1）班级总数25个，样本容量与总体中个体数的比为51255=—2分 ∴从高一、高二、高三年级中分别抽取的班级数为1、2、2. ——5分（2）设1A 为在高一年级中抽得的1个班级，1B 、2B 为在高二年级中抽得的2个班级，1C 、2C 为在高三年级中抽得的2个班级；————7分全部抽取可能结果有11121112(,)(,)(,)(,)A B A B A C A C 12)1112(,(,)(,)B B B C B C 212212(,)(,)(,)B C B C C C共10种结果————9分其中抽取的2个班分别有高二、高三各一个班的共4种可能—11分故所求概率为42105=. ————13分 18．（本小题共14分）解：（1）定义域x R ∈2'()2f x x x a =-+，——2分令'(1)0f -=得3a =- ————4分∴321()333f x x x x =--+，2'()23f x x x =--∴()f x 在(),1-∞-，()3,+∞单调递增，————6分在()1,3-单调递减————8分（2）Q []0,4x ∈≤，()f x 在[]0,3单调递减，在[]3,4单调递增——10分又(0)3f =，11(4)3f =-∴在[]0,4上，max ()3f x =————12分 ∴3λ> ————14分19．（本小题共14分）解：（1）由已知b =12c e a ==∴2a =，1c = ————4分∴椭圆C 的方程为：22143x y +=————6分（2）由已知直线l 的斜率k 存在，设直线l 的方程为：(1)y k x =+————7分则(0,)M k ，设11(,)Q x y ，由于Q 、F 、M 三点共线，且||2||MQ QF =u u u r u u u r ∴2MQ QF =±u u u r u u u r即：1111(,)2(1,)x y k x y -=±+ ————8分解得112x y k =-⎧⎨=-⎩，或11233x ky ⎧=-⎪⎪⎨⎪=⎪⎩∴(2,)Q k --或2(,)33k Q -————10分 Q 点Q 在椭圆上，将点Q 代入椭圆C 的方程解得0k =，————12分或k =±14分 20．（本小题共13分）解：（1）由()21log 21n n a a n +=+∴2112n n n a a ++=————2分Q 10a p =>∴3212a a ⋅=∴322a p =，5322a a =∴523222a p a ==Q {}n a 是等差数列，∴2132a a a =+∴p =5分（2）Q 2112n n n a a ++= ∴1122n n n n a a ++⋅=⋅，∴11122n nn na a ++⋅=. 令2n n n ab =∴11n n b b +=即11n nb b +=，211n n n b b b ++==； ∴13521k b b b b -===⋅⋅⋅==⋅⋅⋅ 2462k b b b b ===⋅⋅⋅==⋅⋅⋅———7分又12p b =，22b p= ∴212k p b -=，22k b p =. 而2n n n a b =，∴2122212122k k k k a b p ----==⋅，22122122k k k k a b p+==()k N +∈ ————9分当2n k =时21232135212462()()n k kk k S S a a a a a a a a a a a a -==+++⋅⋅⋅+=+++⋅⋅⋅+++++⋅⋅⋅+0242235211(2222)(222)k k p p-+=+++⋅⋅⋅++++⋅⋅⋅+ 232221212(12)1212k k p p --=⋅+⋅-- （此时2k n =） 33321122212()333n n n n S p p p p+---=+=+ ————11分同理：当21n k =-时,此时12n k +=132********()3n n n k k k S S S a p p p++--==-=+-()k N +∈.————13分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2010学年第一学期徐汇区高三年级数学学科
学习能力诊断卷（文科试卷）
（考试时间：120分钟，满分150分） 2011.1
一．填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分。

1、函数12
log (1)y x =-的定义域为。

2、抛物线24y x =的准线方程是。

3、方程4220x x +-=的解是。

4、若3sin 5
θ=-
，则行列式
cos sin sin cos θθθ
θ
= 。

5、已知向量(2,3),(4,7)a b ==-
，则向量b 在向量a 的方向上的投影为。

6、若1n
x x ⎛
⎫- ⎪⎝
⎭展开式的第4项含3x ,则n 的值为。

7、已知无穷等比数列{}n a 的各项和为4，则首项1a 的取值范围是。

8、若函数()()(2)f x x a bx a =++（常数,a b R ∈）是偶函数，且它的值域为(,4]-∞，则该函数的解析式()f x = 。

9、一颗骰子投两次, 记第一次得到的数值为a , 第二次得到的数值为b , 将它们作为关于x y 、的二元一次方程组322
ax by x y +=⎧⎨
+=⎩，的系数, 则方程组有唯一解的概率为。

（用数字作答）
10、已知函数()y f x =存在反函数1
()y f
x -=，若函数(1)y f x =+的图象经过点(3,1)，则函数
1
()y f
x -=的图象必经过点。

11、若函数)1l g()(2
--=ax x x f 在区间),1(+∞上是增函数，则a 的取值范围是。

12、在数列{}n a 中，13a =，点*
)(1,)n
n N >∈在直线0x y --=上，则
2
l i m
(1)
n n a n →∞
+= 。

13、已知x 是1，2，3，x ，5，6，7这七个数据的中位数，且1，3，2,x y -这四个数据的平均数为1，则1y x
-
的最小值为。

14、定义平面向量之间的一种运算“*”如下：对任意的(,),(,)a m n b p q == ，令*a b mq np
=-。

给出以下四个命题：（1）若a 与b 共线，则*0a b = ；（2）**a b b a = ；（3）对任意的R λ∈，有()*(*)a b a b λλ=
；
（4）2222
(*)()a b a b a b +⋅=⋅ 。

（注：这里a b ⋅ 指a 与b 的数量积）其中所有真命题的序号是。

二．选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生
应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分。

15、已知a ，b 都是实数，则“b a >”是“22b a >”的（）（A ）充分不必要条件（B ）必要不充分条件
（C ）充分必要条件（D ）既不充分又不必要条件
16、以下向量中，能成为以行列式形式表示的直线方程1
01
2101
1
x
y
=的一个法向量的是（）（A ）()1,2n =-- ；（B ）()2,1n = ；（C ）()1,2n =- ；（D ）()2,1n =-
；
17、在直角坐标平面xOy 中，已知点(3,2)A ，点B 在圆2
2
1x y +=上运动，动点P 满足AP PB =
，
则点P 的轨迹是（）
（A ）圆（B ）椭圆（C ）抛物线（D ）直线 18、函数x
x x x
e e y e e
--+=
-的图像大致为 ( )
B
C
三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤。

19．（本题满分12分）第（1）小题满分4分，第（2）小题满分8分。

已知关于x 的不等式
01
a x x -≥+的解集为P ，不等式11x -<的解集为Q 。

（1）若3a =，求P ；（2）若P Q P ⋃=，求正数a 的取值范围。

20．（本题满分14分）第（1）小题满分6分，第（2）小题满分8分。

在A B C ∆中，角A 、B 、C 的对边分别为a 、b 、c ，且s i n c o s s i n c o s 3s i n c o s C
B B
C A
B
+=。

（1）求cos B 的值；（2）若2BA BC ⋅=
，且22=b ，求a 和c 的值。

21．（本题满分14分）第（1）小题满分6分，第（2）小题满分8分。

设函数[)(),0,1
a f x x x x =+
∈+∞+。

（1）当2a =时，求函数()f x 的最小值；
（2）当01a <<时，试判断函数()f x 的单调性，并证明。

22．（本题满分16分）第（1）小题满分5分，第（2）小题满分5分，第（3）小题满分6分。

各项均为正数的数列{}n a 的前n 项和为n S ，满足2*2(1)()n n n S a a n N +=+∈。

（1）求数列{}n a 的通项公式；（2）若数列{}n b 满足*
112,2()n n
b b b n N +==∈，数列{}n
c 满足
*
,21(),2n n n
a n k c k N
b n k =-⎧=∈⎨=⎩，
数列{}n c 的前n 项和为n T ，当n 为偶数时，求n T ；（3）若数列*
4(21)()3
n n P n N =
⋅-∈，
甲同学利用第（2）问中的n T ，试图确定n n T P -的值是否可以等于20？为此，他设计了一个程序
（如图），但乙同学认为这个程序如果被执行会是一个“死循环”（即程序会永远循环下去，而无法结束），你是否同意乙同学的观点？请说明理由。

23．（本题满分18分）第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分8分。

圆锥曲线上任意两点连成的线段称为弦。

若圆锥曲线上的一条弦垂直于其对称轴，我们将该弦称之为曲线的垂轴弦。

已知椭圆C ：
2
2
14
x
y +=。

（1）过椭圆C 的右焦点作一条垂直于x 轴的垂轴弦M N ，求M N 的长度；
（2）若点P 是椭圆C 上不与顶点重合的任意一点，
M N 是椭圆C 的短轴，直线M P N P 、分别交x 轴于点
(,0)E E x 和点(,0)F F x （如右图），求E F x x ⋅的值；
（3）在（2）的基础上，把上述椭圆C 一般化为
222
2
1(0)x y a b a
b
+=>>，M N 是任意一条垂直于
x 轴的垂轴弦，其它条件不变，试探究E F x x ⋅是否为定值？（不需要证明）；请你给出双曲线
222
2
1(0,0)x y a b a
b
-
=>>中相类似的结论，并证明你的结论。

2010学年第一学期徐汇区高三年级数学学科
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
一、填空题（本大题共14题，每题4分，满分56分）
1. 2. 3.
4. __
5. _
6.
7. __ 8. _ 9.
10. 11. 12.
13. 14.
二、选择题（本大题共4题，每题5分，满分20分）本大题必须使用2B铅笔填涂 15．[ A ] [ B ] [ C ] [ D ] 16．[ A ] [ B ] [ C ] [ D ]
17．[ A ] [ B ] [ C ] [ D ] 18．[ A ] [ B ] [ C ] [ D ]
三、解答题（本大题共5题，满分74分）。