小波实验报告一维Haar小波2次分解
haar小波变换分解和复原

haar小波变换分解和复原
Haar小波变换是一种常用的图像处理方法,它通过使用低通和高通滤波器,将图像信息逐层分解剥离开来。
具体来说,Haar小波变换对图像的分解可以看做如下图所示的滤波过程:
1. 首先进行行滤波,沿着列方向进行。
2. 然后下采样。
3. 对上一步得到的结果进行列滤波,沿着行方向。
4. 最后下采样。
通过以上步骤,可以获得4个不同的频带,一个近似分量、三个细节分量(水平、垂直、对角线),将所有的结果组合为一张图。
若对所得的近似分量继续进行这样的滤波过程,即可得到塔式分解。
在进行Haar小波变换分解和复原时,需要注意处理细节和调整参数,以获得最佳的效果。
如果你需要更详细的信息或代码示例,请提供更多上下文或提供具体要求,我将尽力为你解答。
小波分解与重构原理

“小波工程应用”实验报告一维信号离散小波分解与重构(去噪)的VC实现一、目的在理解了离散小波变换的基本原理和算法的基础上,通过设计VC程序对简单的一维信号在加上了高斯白噪声之后进行Daubechies小波、Morlet小波和Haar小波变换,从而得到小波分解系数;再通过改变分解得到的各层高频系数进行信号的小波重构达到消噪的目的。
在这一程序实现的过程中能直观地理解信号小波分解重构的过程和在信号消噪中的重要作用,以及在对各层高频系数进行权重处理时系数的选取对信号消噪效果的影响。
二、基本原理1、信号的小波分解与重构原理在离散小波变换(DWT)中,我们在空间上表示信号,也就是说对于每一个在上表示的信号能用在上面提到的两个空间中的基函数来表示。
Where and are the coefficients of the scale metric space (j-1) which are obtained after the Decomposing the coefficient of the scale metric space j . Analogously we could reconstruct theby and .我们在尺度度量空间对系数进行分解得到在尺度度量空间的两个系数和。
同样的,我们也能从两个系数和通过重构得到系数。
如上图中的分解与重构我们可以通过一定的滤波器组来实现(也就是小波变换算法)。
当小波和尺度在空间内是正交的,我们就可以用内积公式计算得到系数和:下面是内积计算方法的具体公式:具体的系数计算过程如下:对于上面的小波分解过程,通过分别设计高通滤波器和低通滤波器两组滤波器的系数(数组g[]和h[])即可实现,特别是对于离散小波变换,程序算法相对简单。
而重构也只是分解的逆过程,重构算法和分解的算法是相对应而互逆的。
2、小波去噪原理一般来说,噪声信号多包含在具有较高频率细节中,在对信号进行了小波分解之后,再利用门限阈值等形式对所分解的小波系数进行权重处理,然后对小信号再进行重构即可达到信号去噪的目的。
小波分析实验报告

实验四一、实验目的理解小波阈值去噪法原理。
对所得的去噪效果进行分析。
二、实验要求在载入原始图片后,对图片进行含噪和消噪处理,再对所得的图片效果进行分析。
三、主要内容载入原始图片,对原始图片添加一个随机噪声,得出含噪图片。
用sym6小波对图像进行1层分解,设置一个全局阈值,对图像分解系数,将低频系数进行重构,得出消噪后的图像。
再与原图像,含噪图像一起进行分析比较。
运行代码如下clear all;load woman;subplot(2,2,1);image(X);colormap(map);xlabel('(a)原始图像');axis square;init=2055615866;randn('seed',init);x=X+48*randn(size(X));subplot(2,2,2);image(x);colormap(map);xlabel('(b)含噪图像');axis square;%用sym6小波对图像进行1层分解t1=wpdec2(x,1,'sym6');%设置一个全局阈值thr=10.358;%对图像分解系数t2=wpthcoef(t1,0,'s',thr);%对低频系数进行重构x1=wprcoef(t1,1);subplot(2,2,3);image(x1);运行结果四、思考体会小波去噪的根本任务是在小波域将信号的小波变换与噪声的小波变换有效的分离。
噪声的能量分布于整个小波域内,小波分解后,信号的小波系数幅值要大于噪声的系数幅值,也可以认为,幅值比较大的小波系数一般以信号为主,而比较小的系数在很大程度上是噪声。
于是,采用阈值的方法可把信号系数保留,而把大部分噪声系数减少至零。
将含噪信号在各尺度上进行小波分解,保留大尺度(低分辨率)下的全部系数,对于小尺度(高分辨率)下的小波系数,设定一个阈值,幅值不超过阈值的小波系数设置为零,幅值高于该阈值的小波系数或者完整保留,或者做相应的收缩处理,最后将处理后的小波系数利用逆小波变换进行重构,恢复出有效信号。
Haar小波分析

Haar⼩波分析⼀尺度函数与⼩波函数基本尺度函数定义为:,对其向右平移任意 k 个单位,构成函数族,该函数族在空间中正交,证明如下:1 ;2 当 m 不等于 k 时,函数族构成⼀组正交基,并形成⼦空间。
在⼦空间中,任意函数均可表⽰为的线性组合,。
将函数族构造宽度缩⼩⼀半,则可形成宽度为的⼀组正交基,,同样,该函数族在空间中正交,并形成⼦空间。
在⼦空间中,任意函数均可表⽰为的线性组合,。
通过以上举例可得:设 j 为⾮负整数,j 级函数⼦空间可表⽰为,其对应正交基包括:,观察中可有中线性组合(中任意函数均可⽤中函数线性组合表达),则为得⼦空间。
各个⼦空间之间存在如下关系:。
使⽤不同⼦空间中尺度函数得线性组合,可以阶梯近似任意连续函数。
在噪声滤除应⽤中,需要提取⼀些属于(⾼频信息)但不属于(低频信息)的⽅法,⼩波函数即描述了这部分信息,也即⼩波函数描述相对于的正交补空间。
根据以上描述,⼩波函数应该满⾜⼀些特性:1 ⼩波函数仍然位于空间中,则他应该是空间基函数的线性组合;2 ⼩波函数位于⼦空间中,则它应于正交。
空间的基本⼩波函数表⽰为:,该函数位于空间,且与正交。
同样对⼩波函数向右平移 k 个单位,构成函数族:,该函数族在空间中正交。
空间的基本⼩波函数表⽰为:,该函数族在空间中正交。
使⽤尺度函数与⼩波函数,可以将空间中函数进⾏分解:,其中为空间中的⼩波函数,继续以上分解,可得:⼆ Haar分解1 将函数离散化为,该函数位于空间中;2 由于,可以将空间中该函数分解为(更平滑尺度函数)与(⼩波函数),根据尺度函数与⼩波函数定义,有如下关系:(根据图形可验证结论正确),进⼀步有:;3 观察到分解⽅式不⼀致,需要将原函数改写为:;4 对改写后的分别使⽤更平滑尺度函数与对应⼩波函数再次改写,有:,整理得:;5 令,继续分解直到,可得:,其中,为相应的⼩波分量。
三 Haar重构1 函数被分解为,其中,;2 (根据图形可验证结论正确),进⼀步有:3 重构为;4 重构为;5 ,其中,由组合;6 继续重构与,直到重构。
10.28小波分解总结
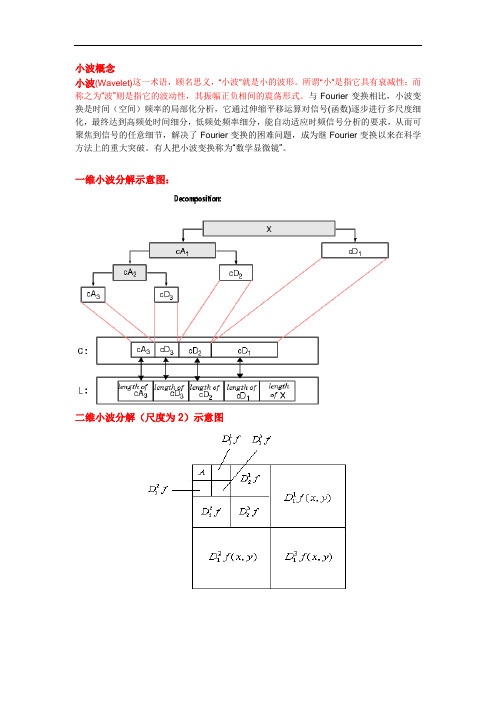
小波概念小波(Wavelet)这一术语,顾名思义,“小波”就是小的波形。
所谓“小”是指它具有衰减性;而称之为“波”则是指它的波动性,其振幅正负相间的震荡形式。
与Fourier变换相比,小波变换是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier变换的困难问题,成为继Fourier变换以来在科学方法上的重大突破。
有人把小波变换称为“数学显微镜”。
一维小波分解示意图:二维小波分解(尺度为2)示意图二维小波分解常用函数:1)[C,S] = WAVEDEC2(X,N,'wname');该函数实现小波的N尺度(层次)分解,得到分解系数C,S为数组,存放各尺度频率的尺寸。
2)A = APPCOEF2(C,S,'wname',N);提取指定尺度N上的低频系数3)D = DETCOEF2(O,C,S,N);提取分解结构[C,S]中指定尺度N上的高频系数,O = 'h' (or 'v' or 'd', respectively), at level N.1 <= N <= size(S,1)-2[H,V,D] = DETCOEF2('all',C,S,N)4)X = WRCOEF2('type',C,S,'wname',N);'type' = 'a',('h','v' or 'd', respectively),单支重构,即重构指定尺度N上的某个频率部分5)X = WAVEREC2(C,S,'wname')多尺度图像分解后重构6)CAT(DIM,A,B) concatenates the arrays A and B along the dimension DIM.沿着行或者列来进行向量的合成,可以用于小波分解后的系数C的重新组合。
两层离散小波分解

两层离散小波分解
两层离散小波分解是一种信号处理技术,用于将原始信号分解成不同频率的小波系数。
这种分解方法常用于处理非平稳信号,能够更好地捕捉信号的时频特性,对于分析和处理信号具有重要意义。
在进行两层离散小波分解时,首先需要选择适当的小波基函数。
小波基函数是一组特定形式的函数,可以用来分解信号并提取其中的特征信息。
常用的小波基函数包括Daubechies小波、Haar小波、Morlet小波等,选择合适的小波基函数对于分解结果的质量至关重要。
接下来,在选择好小波基函数之后,需要对原始信号进行两次离散小波变换。
第一次分解得到的结果包含了信号的低频成分和高频成分,再对低频成分进行第二次分解,得到更细节的频率信息。
通过这样的分层分解过程,可以将原始信号分解成不同尺度和频率的小波系数,从而更好地理解信号的时频特性。
两层离散小波分解在信号处理领域有着广泛的应用。
例如,在医学影像处理中,可以利用两层离散小波分解提取出不同频率的图像特征,对医学图像进行分析和诊断。
在通信领域,可以利用这种分解方法对信号进行压缩和去噪处理,提高通信的可靠性和效率。
此外,在金融数据分析、地震信号处理等领域,两层离散小波分解也都有着重要的应用价值。
总之,两层离散小波分解是一种强大的信号处理工具,能够有效地分析和处理非平稳信号,提取出信号的时频特性。
在各个领域都有着广泛的应用前景,对于进一步深化对信号特性的理解和提高信号处理效率具有重要意义。
haar小波变换分解和复原 -回复

haar小波变换分解和复原-回复正如您所提到的,本文将介绍haar小波变换的分解与复原过程。
首先,我们将解释什么是小波变换,然后详细描述haar小波变换的分解过程,并给出该过程的示例,最后介绍如何通过分解过程实现图像复原。
小波变换是一种数学工具,用于将信号或图像分解成不同频率的子信号或子图像。
它在信号处理中拥有广泛的应用,可以帮助我们提取信号或图像的特征、降噪、压缩等。
haar小波变换是一种离散小波变换的类型,其中使用到了haar小波函数。
haar小波变换是最简单、最容易理解的小波变换之一,因此我们将以haar小波变换为例进行分解和复原。
首先,让我们了解haar小波变换的分解过程。
haar小波变换的分解包括两个步骤:平滑过程和细节过程。
在平滑过程中,我们将信号或图像的奇偶项进行平均,得到一个平滑的低频子信号或子图像。
而在细节过程中,我们将信号或图像的奇偶项进行差分,得到一个细节的高频子信号或子图像。
通过不断重复这两个过程,我们可以将信号或图像逐渐分解成低频和高频子信号或子图像的组合。
接下来,我们将通过一个简单的示例来展示haar小波变换的分解过程。
假设我们有一个8个像素的一维信号[1, 2, 3, 4, 5, 6, 7, 8]。
首先,我们将该信号的奇偶项进行平均,得到第一层的低频子信号[1.5, 3.5, 5.5, 7.5]和高频子信号[-0.5, -0.5, -0.5, -0.5]。
其中,低频子信号表示信号的整体趋势,而高频子信号表示信号的细节或局部变化。
然后,我们继续对低频子信号进行同样的分解过程,得到第二层的低频子信号[2.5, 6.5]和高频子信号[-1, -1]。
最后,在第三层分解中,我们得到最终的低频子信号[4.5]和高频子信号[0]。
现在,让我们来了解如何通过haar小波变换的分解过程实现图像的复原。
首先,我们将使用上述示例中的低频和高频子信号来说明复原的过程。
对于低频子信号,我们可以选择保留其中一部分低频分量,并舍弃其他频率的分量。
【优质】小波实验报告-推荐word版 (7页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==小波实验报告篇一:小波分析实验报告小波分析实验报告姓名班级:学号:成绩: 教师签名篇二:小波课程实验报告小波变换与信号时频分析实验报告院班级:姓名:学号:指导老师:哈尔滨工业大学二维图像信号的小波分解与重构1.1 实验目的结合小波多分辨率分解与重构原理,掌握利用MATLAB实现二维图像信号小波分解与重构的具体实现方法,重点理解二维图像信号分解与重构过程中小波基选择、图像信号边缘延拓方式对于分解和重构质量的影响,进而加深对于小波正交特性、完善重建特性的理解。
1.2 实验内容主要利用MATLAB提供的小波工具箱Wavelet Toolbox实现小波分解与重构,具体包括:(1)小波基的选择(要求三种以上小波基)(2)延拓方式的选择(3)分解过程中的抽样与非抽样(4)重构结果的分析,要求分析不同小波基、不同延拓方式、抽样/非抽样对于小波重构的影响(5)分析小波对于图像信号表示的方向特性1.3 实验步骤1. 小波变换Matlab实现编程实现图片的分解与重构,程序如下:dwtmode('zpd');X=imread('BARB.BMP');X=im2double(X);nbcol = 255;[cA1,cH1,cV1,cD1] = dwt2(X,'haar');cod_X=wcodemat(X,nbcol);cod_cA1=wcodemat(cA1,nbcol);cod_cH1=wcodemat(cH1,nbcol);cod_cV1=wcodemat(cV1,nbcol);cod_cD1=wcodemat(cD1,nbcol);dec2d = [cod_cA1,cod_cH1;cod_cV1,cod_cD1];X1=idwt2(cA1,cH1,cV1,cD1,'haar');cod_X1=wcodemat(X1,nbcol);subplot(221);imshow(X,[],'InitialMagnification','fit');title('orig image');subplot(222);imshow(dec2d,[],'InitialMagnification','fit');title('dec image');subplot(223);imshow(cod_cA1,[],'InitialMagnification','fit');title('appro image');subplot(224);imshow(cod_X1,[],'InitialMagnification','fit');title('syn image');在Zero-padding延拓方式下,分别取Haar、db3、sym小波基得到的图像分解与重构的结果如下:1) Haar小波基orig imagedec imageappro imagesyn image2) Db3小波基orig imagedec imageappro imagesyn image3) Sym3小波基orig imagedec imageappro imagesyn image在采用db4小波实现图像的分析和重构,分别采用四种不同的延拓方式,得到的的结果如下:1) extension mode为Zero-padding模式,分解与重构的结果为orig imagedec imageappro imagesyn image。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、题目:一维Haar 小波2次分解
二、目的:编程实现信号的分解与重构
三、算法及其实现:离散小波变换
离散小波变换是对信号的时-频局部化分析,其定义为:/2200()(,)()(),()()j j Wf j k a f t a t k dt f t L R φ+∞---∞=-∈⎰ 本实验实现对信号的分解与重构:
(1)信号分解:用小波工具箱中的dwt 函数来实现离散小波变换,函数dwt 将信号分解为两部分,分别称为逼近系数和细节系数(也称为低频系数和高频系数),实验中分别记为cA1,cD1,它们的长度均为原始信号的一半,但dwt 只能实现原始信号的单级分解。
在本实验中使用小波函数db1来实现单尺度小波分解,即:
[cA1,cD1]=dwt(s,’db1’),其中s 是原信号;再通过[cA2,cD2]=dwt(cA1,’db1’)进行第二次分解,长度又为cA2的一半。
(2)信号重构:用小波工具箱中的upcoef 来实现,upcoef 是进行一维小波分解系数的直接重构,即:
A1 = upcoef('a',cA1,'db1'); D1 = upcoef('a',cD1,'db1')。
四、实现工具:Matlab
五、程序代码:
%装载leleccum 信号
load leleccum;
s = leleccum(1:3920);
%用小波函数db1对信号进行单尺度小波分解
[cA1,cD1]=dwt(s,'db1');
subplot(3,2,1);
plot(s);
title('leleccum 原始信号');
%单尺度低频系数cA1向上一步的重构信号
A1 = upcoef('a',cA1,'db1');
%单尺度高频系数cD1向上一步的重构信号
D1 = upcoef('a',cD1,'db1');
subplot(3,2,3);
plot(A1);
title('单尺度低频系数cA1向上一步的重构信号');
subplot(3,2,5);
plot(D1);
title('单尺度高频系数cD1向上一步的重构信号');
[cA1,cD1]=dwt(cA1,’db1');
subplot(3,2,2);
plot(s);
title('leleccum 第一次分解后的cA1信号');
%第二次分解单尺度低频系数cA2向上一步的重构信号
A2= upcoef('a',cA2,'db1',2);
%第二次分解单尺度高频系数cD2向上一步的重构信号
D2 = upcoef('a',cD2,'db1',2);
subplot(3,2,4);
plot(A2);
title('第二次分解单尺度低频系数cA2向上一步的重构信号');
subplot(3,2,6);
plot(D2);
title('的二次分解单尺度高频系数cD2向上一步的重构信号');
六、运行结果:
七、结果分析:。
