第八章 习题解答
教材第八章习题解答
第八章氧化还原反应和电化学习题解答1．回答下列问题。
（1）怎样利用电极电势来确定原电池的正负极，并计算原电池的电动势？（2）怎样理解介质的酸性增强，KMnO 4的电极电势代数值增大、氧化性增强？（3）Nernst 方程式中有哪些影响因素？它与氧化态及还原态中的离子浓度、气体分压和介质的关系如何？（4）区别概念：一次电池与二次电池、可逆电池与不可逆电池。
（5）介绍几种不同原电池的性能和使用范围。
（6）什么是电化学腐蚀，它与化学腐蚀有何不同？ （7）防止金属腐蚀的方法主要有哪些？各根据什么原理？ 【解答】（1）电极电势值高的电极做正极，电极电势值低的电极做负极。
原电池的电动势等于正极的电动电势减去负极的电极电势。
（2）根据电极反应：-+-2+42M nO +8H +5e =M n +4H O2442284c(M n)0.0592M nO M nO c ()()lg M nM nc(M nO )5c(H )()cc+--ΘΘ++-ΘΘϕ=ϕ-+⋅由电极电势的能斯特公式可知，介质酸性增强时，H +浓度增大，42M nO ()M n-+ϕ代数值增大，电对中MnO 4-的氧化性增强。
（3）对于电极反应 -a(O x)+ze b(R ed) 电极电势的Nernst 方程为：bR e d aO x (c /c )R T (O x /R e d )(O x /R e d )lnzF(c /c )ΘΘΘϕ=ϕ-影响电极电势大小的因素：a ）浓度对电极电势的影响 电对中氧化态的离子浓度(或气体分压)增大时，电极电势增加；还原态的离子浓度(或气体分压)增大时，电极电势降低。
b ）酸度对电极电势的影响 对于有H +或OH -参加的电极反应，溶液酸度的变化会对电极电势产生影响，对于没有H +或OH -参加的电极反应，溶液酸度的变化对电极电势的影响很小。
（4）一次电池是指电池放电到活性物质耗尽只能废弃而不能再生和重复使用的电池。
物理学第3版习题解答_第8章光的波动性
. B
解： （1） 以 A 为原点
x1
B
. A
x
A
图 8-35 习题 8-5 用图
-1
本题需补充一平面简谐波以速度 u = 20 m ⋅ s 沿直线传播
t x y = A cos[ 2 π( − ) + ϕ ] λ = uT = 10 m ，根据 T λ ， 有
y = A cos[2π(
t x π − )− ] 0.5 10 2
x1 = 0.04 cos(2t + π 6) x 2 = 0.03 cos(2t − π 6)
试写出合振动的表达式。
解 合振动的振幅为
2 A = A12 + A2 + 2 A1 A2 cos(ϕ 2 − ϕ1 )
⎛ π π⎞ = 0.04 2 + 0.03 2 + 2 × 0.03 × 0.04 × cos⎜ − − ⎟ ⎝ 6 6⎠ = 0.06m
第八章习题解答
8-1 一物体沿 x 轴作简谐振动，振幅为 0.12m，周期为 2s。当 t = 0 时，位移为 0.06m，且 向 x 轴正方向运动。求：(1)初相；(2) t = 0.5s 时，物体的位置；(3)在 x = -0.06m 处， 且向 x 轴负向方向运动。物体从这一状态回到平衡位置的最短时间。 解：
−1
8-8 波长为 589.3nm 的钠光照在一双缝上，在距双缝 200cm 的观察屏幕上测量 10 个条纹的 宽度为 2.2cm，试计算双缝之间的距离。
解：根据 ∆x =
D λ 有 d = 0.536 mm d
8-9 在杨氏干涉实验中，若双缝间距为 0.40mm，在距双缝 100cm 的光屏上出现干涉条纹。 现测得相邻两条明纹中心的间距为 1.5mm，求入射光的波长。
理论力学习题解答第八章
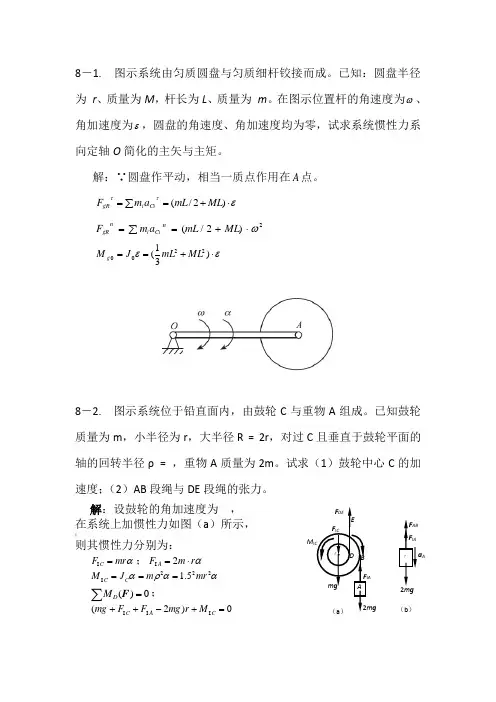
8－1. 图示系统由匀质圆盘与匀质细杆铰接而成。
已知：圆盘半径为 r 、质量为M ，杆长为L 、质量为 m 。
在图示位置杆的角速度为ω、角加速度为ε，圆盘的角速度、角加速度均为零，试求系统惯性力系向定轴O 简化的主矢与主矩。
解：∵圆盘作平动，相当一质点作用在A 点。
εττ⋅+==∑)2/(ML mL a m F Ci i gR 2)2/(ω⋅+==∑ML mL a m F n Ci i ngR εε⋅+==)31(2200ML mL J M g8－2. 图示系统位于铅直面内，由鼓轮C 与重物A 组成。
已知鼓轮质量为m ，小半径为r ，大半径R = 2r ，对过C 且垂直于鼓轮平面的轴的回转半径ρ = ，重物A 质量为2m 。
试求（1）鼓轮中心C 的加速度；（2）AB 段绳与DE 段绳的张力。
解：设鼓轮的角加速度为， 在系统上加惯性力如图（a ）所示， |则其惯性力分别为：αmr F C =I ；αr m F A ⋅=2I ααρα222I 5.1mr m J M C C === ∑=0)(F D M ；0)2(I I I =+-++C A C M r mg F F mg？AM I CF I Cm g F DE （a ）A B 《D E2gF A F I A F AB （b ）g g r a C 2145.132=+==α ∑=0y F ；02I I =--+-mg mg F F F A C DE ；mg mr mg F DE 21593=-=α 取重物A 为研究对象，受力如图（b ）所示，∑=0y F ；02I =-+mg F F A AB ；mg mg mr mg F AB 2134)2141(222=-=-=α：8－3. 11－15重力的大小为100N 的平板置于水平面上，其间的摩擦因数f = ，板上有一重力的大小为300N ，半径为20cm 的均质圆柱。
圆柱与板之间无相对滑动，滚动摩阻可略去不计。
第八章习题解答
第八章 机械波一、选择、填空题：1、若一平面简谐波的波动方程为y=A cos （Bt-Cx ）（SI ），式中A 、B 、C 为正值恒量，则（ ）。
A.波速为C ；B.周期为1/B ；C.波长为2π/C ；D.角频率为B /2π。
答案 C解：)(2cos λ-π=xT t A y 与y =A cos （Bt -Cx ）比较即得答案。
2、一平面谐波，沿X 轴正向传播，波速u =100m ·s -1，t =0时的波形图如图8-1所示。
从波形图可知：（1）波长λ= 振幅A = 频率υ= 周期T =（2）波动方程为 （3）在t=0时，判定下列各质点振动速度的方向：x =0.3m 处。
v方向x =0.4m 处，v方向x =0.5m 处，v方向x =0.6m 处，v方向（4）写出x =0.4m 处的质点振动的方程图8-1解答：（1）λ=0.8m A =0.2mυ=125Hz T =0.008s(2)⎪⎭⎫ ⎝⎛-=8.01252cos 2.0x t y π (3) 0.3m 处，振动沿y 正向。
0.4m 处，0=v0.5m 处，振动沿y 负向。
0.6m 处，振动沿y 负向。
(4) ()ππ-=t y 250cos 2.03、如图8-2所示，有一平面简谐波沿x 轴正向传播，某时刻，P 1点的相位为8π，则P 2点的相位为 ，经时间t=T /4，P 1点的相位为_______ , P 2点相位为 ，由此可见，波的传播是 的传播。
图8-2 解答：P 1点和P 2点的相位差： 221πϕϕϕ=-=∆（1）πϕπϕ57 , 821.== （2）πϕπππϕ8 , 8.52821==+=（3）波的传播是相位的传播。
4、有一平面简谐波沿x 轴正向传播，已知t =1s 时刻的波形图线是I ，t =2s 时刻的波形图线为Ⅱ，如图8-3所示，则此波的波动方程为（ ）。
图8-3A ． m )232(cos 20+-=x t y π.B ．m )4(cos 20xt y -=π.C ．m )214(cos 20+-=x t y π.D ．m )234(cos 20+-=x t y π.答案 D解：由图知：1-s m 4124m,20⋅=-==u A . 1-s 2 , s 2ππω===T T 可得； []ϕπ+-=)4(c o s 20xt y .对于波线I 上的O 点：. 0 , 0 , s 1 , 0<===v y t x其振动的相位为：)10( , 22,=+=+k k ππϕπ)2( , 23ππϕ-=∴5、在弦线上有一简谐波，其表达式是()SI x t y ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=32002.02cos 02.01ππ为了在此弦线上形成驻波，并且在x =0处为一波节，此弦线上还应有一简谐波，其表达式为：（ ）。
运筹学答案第八章
page 24 8 August 2024
School of Management
运筹学教程
第八章习题解答
8.15 如图8-59，发点S1，S2分别可供应10和15个 单边位上，数收为c点ij。t1，t2可以接收10和25个单位，求最大流，
page 25 8 August 2024
School of Management
运筹学教程
第八章习题解答
8.11 求图8-56中v1到各点的最短路。
page 17 8 August 2024
School of Management
运筹学教程
第八章习题解答
page 18 8 August 2024
School of Management
运筹学教程
第八章习题解答
8.12 求图8-57网络中各顶点间的最短路。
page 31 8 August 2024
School of Management
运筹学教程
第八章习题解答
page 32 8 August 2024
School of Management
运筹学教程
第八章习题解答
心B货1B，中18，B心.22B，的02，运B某3B输每种3。能天货A力需物1，由、求A2单分个2的位别仓库运为库存费9At量，如1，分5表At别，28运—为64t送。每，到天各求31仓运个3t库费配，到最货9t配；省中
20 0 36 14 32
D(4)
0
20
18
0
32
12
48
9
0
V1 V2 V3 V4 V5
V1 0 5 16 19 12
V2 20 0 36 14 32
第八章习题解答
习题八答案1． 试比较多谐振荡器、单稳态触发器、施密特触发器的工作特点，并说明每种电路的主要用途。
答：多谐振荡器是一种自激振荡电路，不需要外加输入信号，它没有稳定状态，只有两个暂稳态。
暂稳态间的相互转换完全靠电路本身电容的充电和放电自动完成。
改变外接R 、C 定时元件数值的大小，可调节振荡频率。
施密特触发器具有回差特性，它有两个稳定状态，有两个不同的触发电平。
施密特触发器可将任意波形变换成矩形脉冲，输出脉冲宽度取决于输入信号的波形和回差电压的大小。
单稳态触发器有一个稳定状态和一个暂稳态。
输入信号起到触发电路进入暂稳态的作用，其输出脉冲的宽度取决于电路本身 R 、C 定时元件的数值。
改变 R 、C 定时元件的数值可调节输出脉冲的宽度。
多谐振荡器是常用的矩形脉冲产生电路。
施密特触发器和单稳态触发器是两种常用的整形电路。
施密特触发器可用来进行整形、幅度鉴别、构成多谐振荡器等。
单稳态触发器常用于脉冲的延时、定时和整形等。
２．在图8.2所示５５５集成定时器中，输出电压uo 为高电平ＵＯＨ、低电平ＵＯＬ及保持原来状态不变的输入信号条件各是什么？假定ＵＣＯ端已通过0.01μF 接地，u D 端悬空。
答：当1=R 时， TR U <3V CC ，则C 2输出低电平， 1=Q ，OH o U u =。
当1=R 时， TH U >32V CC ，TR U >3V CC ，则C 1输出低电平、C 2输出高电平，1=Q 、0=Q ，OL o U u =。
当1=R 时， TH U <32V CC，TR U >3V CC ，则C 1C 2输出均为高电平，基本RS 触发器保持原来状态不变，因此o u 保持原来状态不变。
３．在图8.3所示多谐振荡器中，欲降低电路振荡频率，试说明下面列举的各种方法中，哪些是正确的，为什么？1） 加大R 1的阻值； 2） 加大R 2的阻值； 3） 减小C 的容量。
答：根据式（8-2）()ln221121C R R T f +==可知，1）2）两种方法是正确的。
概率论与数理统计习题解答(第8章)
第八章 假 设 检 验三、解答题1. 某种零件的长度服从正态分布，方差σ2 = 1.21，随机抽取6件，记录其长度（毫米）分别为32.46，31.54，30.10，29.76，31.67，31.23在显著性水平α = 0.01下，能否认为这批零件的平均长度为32.50毫米？ 解：这是单个正态总体均值比较的问题，若设该种零件的长度),(~2σμN X ，则需要检验的是：00:μμ=H 01:μμ≠H由于2σ已知，选取nX Z σμ0-=为检验统计量，在显著水平α = 0.01下，0H 的拒绝域为：}|{|}|{|005.02Z z Z z ≥=≥α查表得 2.575829005.0=Z ，现由n =6, 31.1266711∑===ni i x n x ,1.1=σ, 50.320=μ计算得：3.0581561.132.5-31.126670==-=nX z σμ005.0Z z >可知，z 落入拒绝域中，故在0.01的显著水平下应拒绝0H ，不能认为这批零件的平均长度为32.50毫米。
EXCEL 实验结果：2. 正常人的脉搏平均每分钟72次，某医生测得10例“四乙基铅中毒”患者的脉搏数如下：54，67，68，78，70，66，67，65，69，70已知人的脉搏次数服从正态分布，问在显著水平α = 0.05下，“四乙基铅中毒”患者的脉搏和正常人的脉搏有无显著差异？解：这是单个正态总体均值比较的问题，若设“四乙基铅中毒”患者的脉搏数),(~2σμN X ，则需要检验的是：0:μμ=H1:μμ≠H由于方差未知，选取ns X T 0μ-=为检验统计量，在显著水平α = 0.05下，0H 的拒绝域为：)}9(|{|)}1(|{|2/05.02t t n t t ≥=-≥α查表得 2.26215716)9(025.0=t ，现由n =10, 67.411∑===n i i x n x , ()35.155555611122∑==--=n i i x x n s ， 计算得2.45335761035.1555556724.670=-=-=nsX t μ)9(025.0t t >可知，t 落入拒绝域中，故在0.05的显著水平下应拒绝0H ，“四乙基铅中毒”患者的脉搏和正常人的脉搏有显著差异。
高等数学第八章习题解答
习题8.11. 设有一平面薄板（不计其厚度），占有Oxy 平面上的闭区域D ，薄板上分布着面密度为(,)x y μμ=的电荷，且(,)x y μ在D 上连续，试用二重积分表达该板上的全部电荷Q 。
解：据题意，薄板区域D 是Oxy 平面上的有界闭域，(,)x y μ是定义在D 上的面密度函数，那么用任意曲线把D 分成n 个可求面积的小区域12,,n σσσ ，以i σ∆表示小区域的面积，这些小区域构成了D 的一个分割T ，在每个i σ上任取一点(,)i i εη，那么电荷Q 即为D 上的一个积分和1(,)ni i i i Q u εησ==∆∑。
当d 足够小时，1(,)(,)ni i i i DQ u u x y d εησσ==∆=∑⎰⎰2. 下列二重积分表达怎样的空间立体的体积？试画出下列空间立体的图形：（1）()221Dx y d σ++⎰⎰，其中区域D 是圆域221x y +≤；解：（1）在圆域221x y +≤上以抛物面2221z x y =++为顶的曲顶柱体的体积。
（2）Dyd σ⎰⎰，其中区域D 是三角形域0,0,1x y x y ≥≥+≤；解： 在三角形域D 上以平面z y =为顶的柱体的体积。
z 轴x 轴y 轴（1） （2） 3. 设12231()D I x y d σ=+⎰⎰, 其中D 1={(x , y )|-1≤x ≤1, -2≤y ≤2 ;又22232()D I x y d σ=+⎰⎰, 其中D 2={(x , y )|0≤x ≤1, 0≤y ≤2}.试利用二重积分的几何意义说明I 1与I 2的关系.解 I 1表示由曲面z =(x 2+y 2)3与平面x =±1, y =±2以及z =0围成的立体V 的体积.I 2表示由曲面z =(x 2+y 2)3与平面x =0, x =1, y =0, y =2以及z =0围成的立体V 1的体积.显然立体V 关于yOz 面、xOz 面对称, 因此V 1是V 位于第一卦限中的部分, 故 V =4V 1, 即I 1=4I 2. 3. 利用二重积分的定义证明: (1)Dd σσ=⎰⎰ (其中σ为D 的面积;证明 由二重积分的定义可知,1(,)lim (,)ni i i i Df x y d f λσξησ→==∆∑⎰⎰其中∆σi 表示第i 个小闭区域的面积. 此处f (x , y )=1, 因而f (ξ, η)=1, 所以 01lim lim ni i Dd λλσσσσ→→==∆==∑⎰⎰.(2)(,)(,)DDkf x y d k f x y d σσ=⎰⎰⎰⎰ (其中k 为常数);证明 011(,)lim (,)lim (,)n ni i i i i i i i Dkf x y d kf k f λλσξησξησ→→===∆=∆∑∑⎰⎰1lim (,)(,)ni i i i Dk f k f x y d λξησσ→==∆=∑⎰⎰.(3)12(,)(,)(,)DD D f x y d f x y d f x y d σσσ=+⎰⎰⎰⎰⎰⎰,其中D =D 1⋃D 2, D 1、D 2为两个无公共内点的闭区域.证明 将D 1和D 2分别任意分为n 1和n 2个小闭区域1i σ∆和2i σ∆,n 1+n 2=n , 作和1211122212111(,)(,)(,)n n ni i i i i i i i i i i i f f f ξησξησξησ===∆=∆+∆∑∑∑.令各1i σ∆和2i σ∆的直径中最大值分别为λ1和λ2, 又λ=ma x (λ1，λ2), 则有1lim (,)n i i i i f λξησ→=∆∑121112221212011lim (,)lim (,)n n i i i i i i i i f f λλξησξησ→→===∆+∆∑∑,即 12(,)(,)(,)DD D f x y d f x y d f x y d σσσ=+⎰⎰⎰⎰⎰⎰.4. 根据二重积分的性质, 比较下列积分大小:(1)2()Dx y d σ+⎰⎰与, 3()Dx y d σ+⎰⎰ 其中积分区域D 是由x 轴, y 轴与直线x +y =1所围成;解 区域D 为: D ={(x , y )|0≤x , 0≤y , x +y ≤1}, 因此当(x , y )∈D 时, 有(x +y )3≤(x +y )2, 从而3()Dx y d σ+⎰⎰≤2()Dx y d σ+⎰⎰.(2)2()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰其中积分区域D 是由圆周(x -2)2+(y -1)2=2所围成;解 区域D 如图所示, 由于直线x +y =1与圆(x -2)2+(y -1)2=2相切，故D 位于直线x +y =1的上方, 所以当(x , y )∈D 时, x +y ≥1, 从而(x +y )3≥(x +y )2, 因而 23()()DDx y d x y d σσ+≤+⎰⎰⎰⎰.(3)ln()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰其中D 是三角形闭区域, 三角顶点分别为(1,0), (1, 1), (2, 0);解 区域D 如图所示, 显然当(x , y )∈D 时, 1≤x +y ≤2, 从而0≤ln(x +y )≤1, 故有 [ln(x +y )]2≤ ln(x +y ),因而 2[ln()]ln()+≤+⎰⎰⎰⎰DDx y d x y d σσ.(4)ln()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰其中D ={(x , y )|3≤x ≤5. 0≤y ≤1}.解 区域D 如图所示, 显然D 位于直线x +y =e 的上方, 故当(x , y )∈D 时, x +y ≥e , 从而ln(x +y )≥1,因而 [ln(x +y )]2≥ln(x +y ),故 2ln()[ln()]DDx y d x y d σσ+≤+⎰⎰⎰⎰.5. 利用二重积分的性质估计下列积分的值:(1)()DI xy x y d σ=+⎰⎰, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤1};解 因为在区域D 上0≤x ≤1, 0≤y ≤1, 所以 0≤xy ≤1, 0≤x +y ≤2, 进一步可得0≤xy (x +y )≤2,于是 0()2DDDd xy x y d d σσσ≤+≤⎰⎰⎰⎰⎰⎰,即 0()2Dxy x y d σ≤+≤⎰⎰.(2)22sin sin DI x yd σ=⎰⎰, 其中D ={(x , y )| 0≤x ≤π, 0≤y ≤π};解 因为0≤sin 2x ≤1, 0≤sin 2y ≤1, 所以0≤sin 2x sin 2y ≤1. 于是可得 220sin sin 1DDDd x yd d σσσ≤≤⎰⎰⎰⎰⎰⎰,即 2220sin sin Dx yd σπ≤≤⎰⎰.(3)(1)DI x y d σ=++⎰⎰, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤2};解 因为在区域D 上, 0≤x ≤1, 0≤y ≤2, 所以1≤x +y +1≤4, 于是可得 (1)4DDDd x y d d σσσ≤++≤⎰⎰⎰⎰⎰⎰,即 2(1)8Dx y d σ≤++≤⎰⎰.22(49)DI x y d σ=++⎰⎰, 其中D ={(x , y )| x 2+y 2 ≤4}.解 在D 上, 因为0≤x 2+y 2≤4, 所以 9≤x 2+4y 2+9≤4(x 2+y 2)+9≤25.于是 229(49)25DDDd x y d d σσσ≤++≤⎰⎰⎰⎰⎰⎰,222292(49)252Dx y d πσπ≤++≤⋅⋅⎰⎰,即 2236(49)100Dx y d πσπ≤++≤⎰⎰.习题8.21. 化二重积分(,)Df x y dxdy ⎰⎰为二次积分(写出两种积分次序).(1)D ={(x , y )| |x |≤1, |y |≤1}; 解 D 为矩形区域, 所以1111(,)(,)Df x y dxdy dx f x y dy --=⎰⎰⎰⎰,1111(,)(,)Df x y dxdy dy f x y dx --=⎰⎰⎰⎰.(2)D 是由y 轴, y =1及y =x 围成的区域; 解 若将D 表示为0≤x ≤1, x ≤y ≤1, 则 11(,)(,)xDf x y dxdy dx f x y dy =⎰⎰⎰⎰.若将D 表示为0≤y ≤1, 0≤x ≤y , 则 1(,)(,)yDf x y dxdy dy f x y dx =⎰⎰⎰⎰.(3)D 是由x 轴, y =ln x 及x =e 围成的区域; 解 若将D 表示为1≤x ≤e , 0≤y ≤ln x , 则 ln 10(,)(,)ex Df x y dxdy dx f x y dy =⎰⎰⎰⎰.若将D 表示为0≤y ≤1, e y ≤x ≤e , 则 1(,)(,)y eeDf x y dxdy dy f x y dx =⎰⎰⎰⎰.(4)D 是由x 轴, 圆x 2+y 2-2x =0在第一象限的部分及直线x +y =2围成的区域; 解 若将D 表示为0≤x ≤1,0y ≤≤1≤x ≤2, 0≤y ≤2-x , 则12201(,)(,)(,)xDf x y dxdy dx f x y dy dx f x y dy -=+⎰⎰⎰⎰⎰.若将D 表示为0≤y ≤1; 12x y ≤≤-, 则 1201(,)(,)yDf x y dxdy dy f x y dx -=⎰⎰⎰⎰(5)D 是由x 轴与抛物线y =4-x 2在第二象限的部分及圆x 2+y 2-4y =0第一象限部分围成的区域. 解 若将D 表示为-2≤x ≤0, 0≤y ≤4-x 2及0≤x ≤2,22y ≤≤ 则242222(,)(,)(,x Df x y dxdy dx f x y dy dx f x y --=+⎰⎰⎰⎰⎰⎰,若将D 表示为0≤y ≤4, x ≤ 则 40(,)(,)Df x y dxdy dy f x y dx =⎰⎰⎰.2. 交换二次积分的次序:(提示: 交换二次积分的次序, 要先根据原积分写出积分区域不等式, 再根据不等式画出积分区域, 然后根据图形写出另一种形式的积分区域不等式, 最后由不等写出二次积分)(1)228812(,)(,)x xxdx f x y dy dx f x y dy +⎰⎰⎰⎰.解 积分区域为D ={(x , y )|1≤x ≤2, x ≤y ≤x 2}⋃{(x , y )|2≤x ≤8, x ≤y ≤8}. 积分区域还可以表示为D ={(x , y )|1≤y ≤4,x ≤y }⋃{(x , y )|4≤y ≤8, 2≤x ≤y }, 于是 原式=48142(,)(,)y ydy f x y dx dy f x y dx +⎰⎰⎰.(2)12201(,)(,)yydy f x y dx dy f x y dx -+⎰⎰⎰⎰.解 积分区域为D ={(x , y )|0≤y ≤1, 0≤x ≤y }⋃{(x , y )|1≤y ≤2, 0≤x ≤2-y }.积分区域还可以表示为xO y281D ={(x , y )|0≤x ≤1, x ≤y ≤2-x }, 于是 原式=120(,)x xdx f x y dy -⎰⎰. （3） 14(4)(,)y dy f x y dx -⎰⎰；解：积分区域{}2442,20|),(x y x x y x D -≤≤+≤≤=，214(4)040224(,)(,)(,);y x Dx f x y d dy f x y dx dx f x y dy σ---+∴==⎰⎰⎰⎰⎰⎰（4） 11(,)dx f x y dy ⎰；解：积分区域{}{212(,)|01,0(,)|12,0D x y y x y D x y y x =≤≤≤≤⋃=≤≤≤≤21212001(,)(,)(,)(,)y D D f x y d f x y d dy f x y dx dy f x y dxσσ=+=+⎰⎰⎰⎰⎰⎰⎰原式（5）224(,)x x f x y dy -⎰⎰。
第八章刚体的平面运动习题解答
故
向
即
8-21图8-48所示机构中，圆轮A的半径R=0.2m，圆轮B的半径r=0.1m，两轮均在水平轨道上作纯滚动。在图示瞬时，A轮上C点在最高位置，轮心速度vA=2m/s，加速度aA=2m/s2，试求轮B滚动的角速度和角加速度。
图8-48
加速度分析
圆轮A
杆BC
故
向
8-22轮O在水平面上作纯滚动，如图8-49所示。轮缘上固定销钉B，此销钉可在摇杆O1A的槽内滑动，并带动摇杆绕轴O1转动。已知轮心O的速度是一常量，vO=0.2m/s，轮的半径R=0.5m，图示位置时，O1A是轮的切线，摇杆与水平面的夹角为 。试求该瞬时摇杆的角速度和角加速度。
图8-59
以O为动点，杆AB为动系
(1)速度分析
(2)加速度分析
圆轮O
以O为基点，分析C点
向y
8-33图8-60所示机构中，已知曲柄OA以匀角速度 绕定轴O转动，OA=100mm，l=500mm。在图示位置， ，试确定杆BD的角速度和角加速度。
图8-60
以A为动点，杆AB为动系
(1)速度分析
(2)加速度分析
图8-33
瞬心法
基点法
8-7在如图8-34所示的筛动机构中，筛子BC的摆动是由曲柄连杆机构所带动。已知曲柄长OA=0.3m，转速为n=40r/min。当筛子运动到与点O在同一水平线上时， ，试求此时筛子BC的速度。
图8-34
速度投影定理
8-8长为l=1.2m的直杆AB作平面运动，某瞬时其中点C的速度大小为vC=3m/s，方向与AB的夹角为 ，如图8-35所示。试求此时点A可能有的最小速度以及该瞬时杆AB的角速度。
8-20半径为r的圆盘可在半径为R的固定圆柱面上纯滚动，滑块B可在水平滑槽内滑动，如图8-47所示。已知r=125mm，R=375mm；杆AB长l=250mm。图示瞬时，vB=500mm/s，aB=750mm/s2；O、A、O1三点位于同一铅垂线上，试求此时圆盘的角加速度。
第8章习题解答
第8章思考题及习题8参考答案一、填空1. 单片机存储器的主要功能是存储和。
答：程序、数据。
2．假设外部数据存储器2000H单元的内容为80H，执行下列指令后累加器A中的内容为。
MOV P2，#20HMOV R0，#00HMOVX A，@R0答：80H。
3．在存储器扩展中，无论是线选法还是译码法最终都是为扩展芯片的端提供控制信号。
答：片选。
4．起止范围为0000H～3FFFH的数据存储器的容量是 KB。
答：16KB。
5．在AT89S52单片机中，PC和DPTR都用于提供地址，但PC是为访问存储器提供地址，而DPTR是为访问存储器提供地址。
答：程序、数据。
6．11条地址线可选个存储单元，16KB存储单元需要条地址线。
答：2K，14。
7．4KB RAM存储器的首地址若为0000H，则末地址为 H。
答：0FFF。
8．若单片机外扩32KB 数据存储器的首地址若为4000H，则末地址为 H。
答：BFFF9. 设计一个以AT89S52单片机为核心的系统，如果不外扩程序存储器，使其内部8KB闪烁程序存储器有效，则其引脚应该接。
答：EA*，+5V10．74LS138是具有3个输入的译码器芯片，其输出常作片选信号，可选中片芯片中的任一芯片，并且只有1路输出为电平，其它输出均为电平。
答：8，低，高；二、单选1．区分AT89S51单片机片外程序存储器和片外数据存储器的最可靠方法是。
A．看其位于地址范围的低端还是高端B．看其离AT89S51单片机芯片的远近C．看其芯片的型号是ROM还是RAMD．看其是与RD信号连接还是与PSEN信号连接答：D2．访问片外数据存储器的寻址方式是。
A.立即寻址B.寄存器寻址C.寄存器间接寻址D.直接寻址答：C3．若要同时扩展4片2KB的RAM和4片4KB的ROM，则最少需要根地址线。
A、12B、13C、14D、154．当EA=1时，AT89S52单片机可以扩展的外部程序存储器的最大容量为。
A． 64KB B．60KB C．58KB D．56KB答：D5. 若某数据存储器芯片地址线为12根,那么它的存储容量为。
第8章习题解答
第8章习题解答一. 选择题1. 关于类和对象，不正确的说法是（）A. 类是一种数据类型，它封装了数据和函数B. 类是对某一类对象的抽象C. 可以基于类这种数据类型定义类的引用D. 一个类的对象只有一个【答案】D【解析】类是一种数据类型，可以基于“类”这种数据类型定义多个称为“对象”的变量。
2. 类定义的外部，可以被访问的类的成员有（）A. public 的类成员B. public或private的类成员C. private或protected的类成员D. public或private 的类成员【答案】A【解析】类的成员数据或成员函数的访问属性分为三种情况：private、public和protected，即私有访问属性、公有访问属性和保护访问属性，类定义的外部只能访问公有访问属性的成员。
3 关于this 指针，说法错误的是（）A. this指针必须显式说明B. 当创建一个对象后，this 指针就指向该对象C. 成员函数拥有this指针D. 静态成员函数拥有this指针【答案】D【解析】this指针是一种特殊的指针，它指向成员函数当前操作的数据所属的对象。
不同的对象调用相同的成员函数时，this指针将指向不同的对象，也就可以访问不同对象的成员数据。
而静态成员函数是一个类的所有对象共享的成员，而不仅仅是某一对象的成员。
因此，可以在没有任何对象存在的情况下，可以使用静态成员函数，而使用this指针必须有明确的对象所指。
4. 调用形式参数为普通对象的函数时，系统会自动调用相应类的（）A. 名字不同于类名的一般成员函数B. 构造函数C. 析构函数D. 拷贝构造函数【答案】D【解析】若函数的形参为类的对象，调用函数时，实参赋值给形参，系统自动调用拷贝构造函数实现拷贝赋值。
5. 定义某类的对象后，再删除该对象，系统会自动调用（）A. 名字不同于类名的一般成员函数B. 拷贝构造函数C. 构造函数D. 析构函数【答案】D【解析】当对象生存期结束时，需要调用析构函数，释放对象所占的内存空间。
高等数学课后答案第八章习题详细解答
习 题 8-11．设有一个面薄板（不计其厚度），占有xOy 面上的闭区域D ，薄板上分布有面密度为(,)x y μμ=的电荷，且(,)x y μ在D 上连续，试用二重积分表达该板上的全部电荷Q ．解 用一组曲线将D 分成n 个小闭区域i σ∆，其面积也记为(1,2,,)i i n σ∆=.任取一点(,)i i i ξησ∈∆,则i σ∆上分布的电量(,)i i i Q μξησ∆≈∆.通过求和、取极限，便得到该板上的全部电荷为1lim (,)(,)d ,ni i i i DQ x y λμξησμσ→==∆=∑⎰⎰其中1max{i i nλσ≤≤=∆的直径}．2. 设12231()d D I x y σ=+⎰⎰其中1{(,)11,22}D x y x y =-≤≤-≤≤；又22232()d D I x y σ=+⎰⎰其中2{(,)01,02}D x y x y =≤≤≤≤．试利用二重积分的几何意义说明1I 与2I 之间的关系．解 由二重积分的几何意义知，1I 表示底为1D 、顶为曲面223()z x y =+的曲顶柱体1Ω的体积；2I 表示底为2D 、顶为曲面223()z x y =+的曲顶柱体2Ω的体积．由于位于1D 上方的曲面223()z x y =+关于yOz 面和zOx 面均对称，故yOz 面和zOx 面将1Ω分成四个等积的部分，其中位于第一卦限的部分即为2Ω．由此可知124I I =．3. 利用二重积分定义证明： (1) d ()DD σσσ=⎰⎰其中为的面积；(2) (,)d (,)d ()DDkf x y k f x y k σσ=⎰⎰⎰⎰其中为常数；(3)12(,)d (,)d (,)d ,DD D f x y f x y f x y σσσ=+⎰⎰⎰⎰⎰⎰其中12D DD =，1D 、2D 为两个无公共内点的闭区域.证 (1) 由于被积函数(,)1f x y ≡，故由二重积分定义得11d lim (,)lim lim .nniiii i i Df λλλσξησσσσ→→→===∆=∆==∑∑⎰⎰(2) 011(,)d lim (,)lim (,)(,)d .nni i i i i i i i DDkf x y kf k f k f x y λλσξησξησσ→→===∆=∆=∑∑⎰⎰⎰⎰(3) 因为函数(,)f x y 在闭区域D 上可积，故不论把D 怎样分割，积分和的极限总是不变的，因此在分割D 时，可以使1D 和2D 的公共边界永远是一条分割线。
第八章 电解质溶液习题解答
第八章 习题解答1、在300K 和100kPa 压力下，用惰性电极电解水以制备氢气。
设所用直流电的强度为5A ，电流效率为100%。
来电解稀H 2SO 4溶液，如欲获得1m 3氢气，须通电多少时间？如欲获得1m 3氧气，须通电多少时间？已知在该温度下水的饱合蒸气压为3565Pa 。
解 电解时放出气体的压力为 p=(100000-3565)Pa=96435Pa 1m 3气体的物质的量为311(96435)(1)/()38.6637(8.314)(300)Pa m n pV RT mol J K mol K --⨯===⋅⋅⨯ 氢气在阴极放出，电极反应为 2H ++2e －→H 2(g) 根据法拉第定律，It=ξzF=(Δn B /νB )·zF ， t=(Δn B /νB I)·zF 放氢时，12=H ν，z=2，11(38.6637)2(96500)1492418.821(5)mol t C mol s C s --=⨯⨯⋅=⨯⋅。
氧气在阳极放出，电极反应为 2H 2O-4e －→O 2(g)+4H + 放氧时，12=O ν，z=4，11(38.6637)4(96500)2984837.641(5)mol t C mol s C s --=⨯⨯⋅=⨯⋅。
2、用电解NaCl 水溶液的方法制备NaOH ，在通电一段时间后，得到了浓度为1.0mol·dm -3的NaOH 溶液0.6dm 3，在与之串联的铜库仑计中析出了30.4g 的Cu(s)。
试计算该电解池的电流效率。
解 析出Cu(s)的反应为Cu 2++2e －→Cu电解NaCl 水溶液制备NaOH 的反应为 阴极上的反应 2H 2O+2e －→2OH -+H 2(g) 阳极上的反应 2Cl --2e －→Cl 2(g)电解总反应为 2H 2O+2NaCl →Cl 2(g)+H 2(g)+ 2NaOH即铜库仑计中若析出1molCu(s)，则理论上在电解池中可得到2 mol 的NaOH 。
普通化学第八章课后习题解答
第八章氧化还原反应参考答案P 169【综合性思考题】：给定电对体系：Fe 3+/Fe 2+ 和 Ag +/Ag ，已知V FeFe 771.023/=++θϕ，V Ag Ag 799.0/=+θϕ，K θSPFe(OH)3=2.64×10-39，K θSPFe(OH)2=4.87×10-17， K θSPAgI =1.0×10-17，42)(100.136⨯=-θCN fFe K ，35)(100.146⨯=-θCN fFe K ，V I I535.0/2=-θϕ解答下列问题：①在标态下，两电对组成原电池。
写出电池反应，计算εθ ，求电池反应的平衡常数K θ ，写出电池符号。
解：∵V Ag Ag 799.0/=+θϕ>V Fe Fe 771.023/=++θϕ ∴正极：Ag +/Ag ，负极：Fe 3+/Fe 2+εθ=)(028.0771.0799.023//V Fe Fe Ag Ag =-=-+++θθϕϕ根据0592.0lg θθεn K =求K θ473.00592.0028.01lg =⨯=θK解得K θ=2.97电池符号：(-）Pt(s)|Fe 2+(c 1),Fe 3+(c 2)||Ag +(c 3)|Ag(+)②在[Fe 3+]=1.0mol/L ，[Fe 2+]=0.10mol/L ，[Ag +]=1.0mol/L 状态，写出电池反应，计算ε ，求电池反应的平衡常数，写出电池符号。
解：∵]lg[10592.0//++=++Ag AgAg Ag Ag θϕϕ )(799.0]0.1lg[0592.0799.0V =+=][][lg 10592.023//2323+++=++++Fe Fe Fe Fe Fe Feθϕϕ )(8302.0]10.0[]0.1[lg 0592.0771.0V =+=又：∵Ag Ag Fe Fe //23+++>ϕϕ∴正极：Fe 3+/Fe 2+ ，负极：Ag +/Ag 正极(发生还原反应)：Fe 3++e=Fe 2+负极（发生还原反应）：Ag-e=Ag +电池反应：Fe 3++Ag=Fe 2++Ag +Ag Ag Fe Fe//23+++-=-=-+ϕϕϕϕε=0.8302-0.799 =0.0312(V)根据0592.0lg θθεn K =求K θ0592.0(1lg )//23Ag Ag Fe Fe K +++-⨯=θθθϕϕ473.00592.0)799.0771.0(1-=-⨯=解得K θ=0.336电池符号：(-）Ag(s)|Ag +(c 1)||Fe 3+(c 2)，Fe 2+(c 3)|Pt(s)(+)③向电对Fe 3+/Fe 2+体系中加碱调节pH=7.0，计算?23/=++Fe Fe ϕ 解：加入碱，使pH=7.0时，有：pOH=14-pH=7.0，-lg[OH -]=7.0(mol/L) [OH -]=10-7此时发生：Fe 3++3OH -=Fe(OH)3↓ K 1θFe 2++2OH -=Fe(OH)2↓ K 2θ 平衡时：θθ3)(,3311][][1OH Fe SP K OH Fe K =⋅=-+ 1737383)(,3100.4]10[100.4][][3---+⨯=⨯==OH K Fe OH Fe SP θ同理：θθ2)(,2221][][1OH Fe SP K OH Fe K =⋅=-+ 227162)(,2100.8]10[100.8][][2---+⨯=⨯==OH K Fe OH Fe SP θ 根据bad Ox n d Ox d Ox ][Re ][lg0592.0)Re /()Re /(+=θϕϕ ][][lg 0592.023//2323+++=++++Fe Fe Fe Fe Fe Feθϕϕ)(135.0100.8100.4lg 0592.0771.0217V -=⨯⨯⨯+=-- ④向电对Fe 3+/Fe 2+体系中加入足量KCN ，使平衡时L mol CN CN Fe CN Fe /0.1][])([])([4636===---，推断θϕ--4636)(/)(CN Fe CN Fe 、++23/Fe Fe ϕ与θϕ++23/Fe Fe间的大小关系。
第八章 习题答案
第八章 习题解答8-1考虑并回答下面的问题：（a ）在确定非线性元件的描述函数时，要求非线性元件不是时间的函数，并要求有斜对称性，这是为什么？（b ）什么样的非线性元件是无记忆的？什么样的非线性元件是有记忆的？它们的描述函数各有什么特点？（c ）线性元件的传递函数与非线性元件的描述函数，有什么是相同的？有什么是不同的？线性元件可以有描述函数吗？非线性元件可以有传递函数吗？（d ）非线性系统线性部分的频率特性曲线与非线性元件的负倒描述函数曲线相交时，系统一定能产生稳定的自激振荡吗？ 解：（a ）描述函数法只能用来研究非线性定常系统的特性，这要求非线性元件的特性不随时间发生变化。
在用描述函数法研究非线性系统的自振特性时，要求在正弦输入下非线性特性的输出没有直流分量，这要求非线性元件的特性是斜对称的。
（b ）一般情况下用代数方程描述的非线性特性是无记忆的，根据非线性环节当前的输入就可以决定非线性环节的输出。
用微分方程描述的非线性特性是有记忆的，不能简单地根据非线性环节当前的输入决定非线性环节的输出。
无记忆非线性特性的描述函数一般为实数，有记忆非线性特性的描述函数一般为复数。
（c ）线性元件的传递函数与非线性元件的描述函数都是元件的外部描述。
线性元件的传递函数表述的是元件输出拉氏变换与输入拉氏变换之比，而非线性元件的描述函数表示的是元件在正弦输入下输出基波特性。
由传递函数可以得到系统的频率特性，而描述函数一般不是频率的函数，线性元件可以有描述函数，但传递函数只适用于线性系统，非线性系统没有传递函数。
（d ）只有稳定的交点才对应稳定的自激振荡。
8-2设非线性元件的输入、输出特性为35135()()()()y t b x t b x t b x t =++证明该非线性元件的描述函数为2413535()48N A b b A b A =++式中A 为非线性元件输入正弦信号的幅值。
解：由于非线性特性是单值斜对称的，所以10A =，10φ=。
(完整版)大学物理学(课后答案)第8章
第八章课后习题解答一、选择题8-1如图8-1所示，一定量的理想气体，由平衡态A 变到平衡态B ，且它们的压强相等，即=A B p p 。
则在状态A 和状态B 之间，气体无论经过的是什么过程，气体必然[ ](A) 对外作正功 (B) 内能增加 (C) 从外界吸热 (D) 向外界放热分析：由p V -图可知，A A B B p V p V =，即知A B T T <，则对一定量理想气体必有B A E E >，即气体由状态A 变化到状态B ，内能必增加。
而作功、热传递均是过程量，与具体的热力学过程相关，所以（A ）、（C ）、（D ）不是必然结果，只有（B ）正确。
8-2 两个相同的刚性容器，一个盛有氢气，一个盛有氦气（均视为刚性分子理想气体）。
开始时它们的压强和温度都相同。
现将3 J 热量传给氦气，使之升高到一定的温度。
若使氢气也升高同样的温度，则应向氢气传递热量为[ ](A) 6 J (B) 3 J (C) 5 J (D) 10 J分析：由热力学第一定律Q E W =∆+知在等体过程中Q E =∆。
故可知欲使氢气和氦气升高相同的温度，由理想气体的内能公式2m i E R T M '∆=∆，知需传递的热量之比22222:():():5:3HHe H He H He H He H Hem m Q Q i i i i M M ''===。
故正确的是（C ）。
8-3 一定量理想气体分别经过等压、等温和绝热过程从体积1V 膨胀到体积2V ，如图8-3所示，则下述正确的是[ ]习题8-1图(A) A C →吸热最多，内能增加(B) A D →内能增加，作功最少(C) A B →吸热最多，内能不变(D) A C →对外作功，内能不变分析：根据p V -图可知图中A B →为等压过程，A C →为等温过程，A D →为绝热过程。
又由理想气体的物态方程pV vRT =可知，p V -图上的pV 积越大，则该点温度越高，因此图中D A B C T T T T <==，又因对于一定量的气体而言其内能公式2i E vRT =，由此知0AB E ∆>，0AC E ∆=，0AD E ∆<。
第八章-氧化还原滴定法-习题解答
第八章氧化还原滴定法1. 答：标准电极电位E′是指在一定温度条件下（通常为25℃）半反应中各物质都处于标准状态，即离子、分子的浓度（严格讲应该是活度）都是1mol/l（或其比值为1）（如反应中有气体物质，则其分压等于1.013×105Pa，固体物质的活度为1）时相对于标准氢电极的电极电位。
电对的条件电极电位（E0f）是当半反应中氧化型和还原型的浓度都为1或浓度比为，并且溶液中其它组分的浓度都已确知时，该电对相对于标准氢电极电位（且校正了各种外界因素影响后的实际电极电位，它在条件不变时为一常数）。
由上可知，显然条件电位是考虑了外界的各种影响，进行了校正。
而标准电极电位则没有校正外界的各种外界的各种因素。
影响条件电位的外界因素有以下3个方面；（1）配位效应；（2）沉淀效应；（3）酸浓度。
2．答：一般讲，两电对的标准电位大于0.4V（K>106），这样的氧化还原反应，可以用于滴定分析。
实际上，当外界条件（例如介质浓度变化、酸度等）改变时，电对的标准电位是要改变的，因此，只要能创造一个适当的外界条件，使两电对的电极电位超过0.4V ，那么这样的氧化还原反应也能应用于滴定分析。
但是并不是平衡常数大的氧化还原反应都能应用于氧化还原滴定中。
因为有的反应K虽然很大，但反应速度太慢，亦不符合滴定分析的要求。
3. 答：影响氧化还原反应速度的主要因素有以下几个方面：1）反应物的浓度；2）温度；3）催化反应和诱导反应。
4. 答：1）高锰酸钾法．2MnO4+5H2O2+6H+==2Mn2++5O2↑+8H2O.MnO2+H2C2O4+2H+==Mn2++2CO2+2H2O2) 重铬酸甲法. Cr2O72-+14H++Fe2+===2Cr3++Fe3++7H2OCH3OH+Cr2O72-+8H+===CO2↑+2Cr3++6H2O3)碘量法 3I2+6HO-===IO3-+3H2O，2S2O32-+I2===2I-+2H2OCr2O72-+6I-+14H+===3I2+3Cr3++7H2O5. 答：应用于氧化还原滴定法的反应，必须具备以下几个主要条件：（1）反应平衡常数必须大于106，即△E>0.4V。
第8章 气体动理论习题解答
习题8-1 设想太阳是由氢原子组成的理想气体，其密度可当成是均匀的。
若此理想气体的压强为1.35×1014 Pa 。
试估计太阳的温度。
（已知氢原子的质量m = 1.67×10-27 kg ，太阳半径R = 6.96×108 m ，太阳质量M = 1.99×1030 kg ）解：mR MVm M mn 3π)3/4(===ρK 1015.1)3/4(73⨯===Mkm R nk p T π8-2 目前已可获得1.013×10-10 Pa 的高真空，在此压强下温度为27℃的1cm 3体积内有多少个气体分子？解：3462310/cm 1045.2103001038.110013.1⨯=⨯⨯⨯⨯===---V kT p nV N 8-3 容积V ＝1 m 3的容器内混有N 1＝1.0×1023个氢气分子和N 2＝4.0×1023个氧气分子，混合气体的温度为 400 K ，求： （1） 气体分子的平动动能总和；（2）混合气体的压强。
解：（1）J 1014.41054001038.123)(233232321⨯=⨯⨯⨯⨯⨯=+=-∑N N kT tε（2）Pa kT n p i323231076.21054001038.1⨯=⨯⨯⨯⨯==-∑8-4 储有1mol 氧气、容积为1 m 3的容器以v =10 m/s 的速率运动。
设容器突然停止，其中氧气的80%的机械运动动能转化为气体分子热运动动能。
问气体的温度及压强各升高多少？（将氧气分子视为刚性分子）解：1mol 氧气的质量kg 10323-⨯=M ，5=i由题意得T R Mv ∆=⋅ν25%80212K 102.62-⨯=∆⇒TT R V p RT pV ∆=⋅∆⇒=ννpa 52.0102.631.82=⨯⨯=∆=∆∴-VTR p 8-5 一个具有活塞的容器中盛有一定量的氧气，压强为1 atm 。
大学应用物理第八章习题解答
第8章 磁场8-10一均匀密绕直螺线管的半径为 ，单位长度上有 匝线圈，每匝线圈中的电流为 ，用毕奥—萨伐尔定律求此螺线管轴线上的磁场。
分析：由于线圈密绕，因此可以近似地把螺线管看成一系列圆电流的紧密排列，且每一匝圆电流在轴线上任一点的磁场均沿轴向。
解： 取通过螺线管的轴线并与电流形成右旋的方向（即磁场的方向）为x 轴正向，如习题8-10图解（a ）所示。
在螺线管上任取一段微元dx ，则通过它的电流为dI nIdx =，把它看成一个圆线圈，它在轴线上O 点产生的磁感应强度dB 为2022322()R nIdxdB R x μ=+ 由叠加原理可得，整个螺线管在O 点产生的磁感应强度B 的大小为由图可知12122212221212cos os ()()x x R x R x ββ==++ c ，代入上式并整理可得式中12ββ和分别为x 轴正向与从O 点引向螺线管两端的矢径r 之间的夹角。
讨论：（1）若螺线管的长度远远大于其直径，即螺线管可视为无限长时，20β=，1βπ=，则有上式说明，无限长密绕长直螺线管内部轴线上各点磁感应强度为常矢量。
理论和实验均证明：在整个无限长螺线管内部空间里，上述结论也适用。
即无限长螺线管内部空间里的磁场为均匀磁场，其磁感应强度B 的大小为0nI μ，方向与轴线平行；（2）若点O 位于半无限长载流螺线管一端，即12πβ=，20β＝或12πβ=，2βπ＝时，无论哪一种情况均有nI B 021μ=------(8-19) 可见半无限长螺线管端面中心轴线上磁感应强度的大小为管内的一半；综上所述，密绕长直螺线管轴线上各处磁感应强度分布见习题8-10图解（b ）所示，从图中也可看出，长直螺线管内中部的磁场可以看成是均匀的。
习题8-10图解（a ）习题8-10图解（b ）8-11两根长直导线互相平行地放置，导线内电流大小相等，均为I ＝10A ，方向相同，如图8-49题图(左)所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第八章 习题解答
题 8-1 试用相位平衡条件和幅度平衡条件，判断图中各电路是否可能产生正弦波振荡，简述理由。
解：(a)不能振荡，o o
A F 18090~90o ϕϕ==+-因，而，故不能满足相位平衡条件。
(b) 不能振荡，虽然电路能够满足相位平衡条件，但当o F 0ϕ=时，13
F
=&，而电压跟随器的1A
=&，故不能同时满足幅度平衡条件。
(c) 不能振荡，o o o A F F 180RC 0~180180o ϕϕϕ==因，两节电路的，但当接近时，其输
出电压接近于零，故不能同时满足幅度平衡条件。
(d) 不能振荡，放大电路为同相接法，A 0o
ϕ=，选频网络为三节RC 低通电路，
o o F 0~270ϕ=-，但欲达到o F 0ϕ=，只能使频率f=0。
(e)可能振荡，差分放大电路从VT2的集电极输出时A 0o
ϕ=，而选频网络为RC 串并联电路，当f=f0时，o
F 0ϕ=，满足相位平衡条件。
① 判断电路是否满足正弦波振荡的相位平衡条件。
如不满足，修改电路接线使之满足(画在图上)。
② 在图示参数下能否保证起振荡条件？如不能，应调节哪个参数，调到什么值？ ③ 起掁以后，振荡频率f o =?
④ 如果希望提高振荡频率f o ，可以改变哪些参数，增大还是减小？
⑤ 如果要求改善输出波形，减小非线性失真，应调节哪个参数，增大还是减小？
本题意图是掌握文氏电桥RC 振荡电路的工作原理及其振荡频率和起振条件的估算方法。
解：①o o
0A F 0f f 0ϕϕ===因，当时，，故满足相位平衡条件。
②因F e 1F F e 1R 2R ,R R >2R =5.4k <Ω故不能满足起振条件，应调整，使。
③038
11
Hz 5300Hz=5.3kHz 2231010f RC ππ-=
=≈⨯⨯⨯
④可减小R 或C 。
⑤可减小R F 。
题 8-7 试用相位平衡条件判断图P8-7所示电路中，哪些可能产生正弦波振荡？哪些不能？简单说明理由。
解：本题的意图是掌握产生正弦振荡的相位平衡条件，并根据上述条件判断具有LC 选频网络的电路能否产生振荡。
(a) 不能振荡，o o
A F 0180ϕϕ==，，不满足相位平衡条件。
(b) 可能振荡，o o
A F 180180ϕϕ==，，满足相位平衡条件。
(c) 不能振荡，o o
A F 1800ϕϕ==，，不满足相位平衡条件。
(d) 可能振荡，o o
A F 00ϕϕ==，，满足相位平衡条件。
(e) 可能振荡，本电路实际上就是一个电容三点式振荡电路。
(f) 可能振荡，o o
A F 00ϕϕ==，，满足相位平衡条件。
① 将图中左右两部分正确连接起来，使之能够产生正弦波振荡。
②估算振荡频率f o 。
③ 如果电容C 3短路，此时 f o
=?
本题的意图是根据相位平衡条件完成（射同基异）完成电容三点式改进型振荡电路的连线，使之能够振荡；分别估算电容三点式及其改进型振荡电路的振荡频率，并进行比较。
解：①J 接M ，K 接P ，H 接N 。
②60311
311Hz 3.5610Hz 3.56MHz 2220.21010f LC LC π--=
≈==⨯=⨯⨯⨯ππ
③60312
12
12
Hz 0.9210Hz 920kHz 20.210150102f C C L C C ππ--=
=
=⨯=⋅⨯⨯⨯⨯+
题 8-16 在图P8-16所示的矩形波发生电路中，假设集成运放和二极管均为理想的，已知电阻R=10kΩ，R 1＝12kΩ，R 2＝15kΩ，R 3＝2kΩ，电位器R W ＝100kΩ，电容C ＝0.01μF ，稳压管的稳压值U z =±6V 。
如果电位器的滑动端调在中间位置：
① 画出输出电压u o 的电容上电压 u c 的波形。
② 估算输出电压的振荡周期T 。
③ 分别估算输出电压和电容上的峰值U om 和U cm 。
0U +
c t
U -+U Z
u o 0t -U Z
T
T2
T1
本题意图是理解矩形波发生电路的工作原理和输出波形，并估算其输出电压幅值和振荡周期。
解：①输出电压u o 和电容上电压 u c 的波形如图。
②48
1W 22212T 2(0.5R )ln 1261010ln(1)1.15(ms)15
R R C R -⎛⎫⨯=++
=⨯⨯⨯+= ⎪⎝⎭ ③
om Z 1cm T Z 12U U 6V
R 12
U =U =U 6V 2.7V
R +R 1215
===⨯=+
（资料素材和资料部分来自网络，供参考。
可复制、编制，期待你的好评与关注）。