机械原理--速度瞬心习题讲解学习
机械原理课件瞬心例题
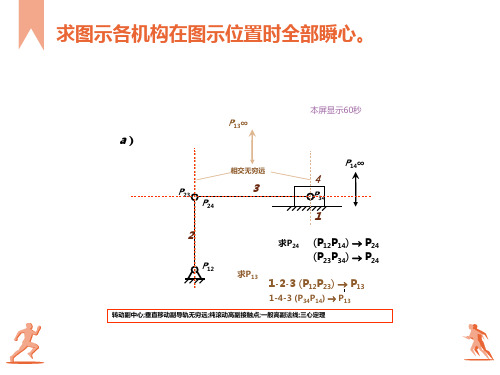
b)
P13
求P24
(P12P14) P24 (P23P34) P24
本屏显示60秒
P34 3
2
4
P12
P14∞
P24
求P13
1
1-2-3 (P12P23) P13
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
水平方向无穷远处有P12，通过P12作竖线连接P14
比1/ 3 。
解： 1. 绘机构运动简图 2.求瞬心P13 3.求1/ 3
1 P36 P13 3 P16 P13
求P13
1-2-3 (P12P23) P13
1-6-3 (P36P16) P13
2
P23
P12 4
P13
P36 5
ห้องสมุดไป่ตู้
3
6
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
求P24
(P12P14) P24
(P23P34) P24
c)
P13
M
P23
2
P12
P14
4
3
P24
求P13 1-2-3 (P12P23) P13
1
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
在图示的齿轮-连杆组合机构中, 试用瞬心法求齿轮1和3的传动
该线与通过P23P34的斜线相交于倾斜方向无穷远点
P12∞
c)
求P24
(P12P14) P24
机械原理中的速度瞬心讲解
机械原理中的速度瞬心讲解速度瞬心是机械原理中的一个重要概念，它在机械传动、运动学和动力学问题的研究中扮演着至关重要的角色。
本文将从定义、原理、应用以及相关公式等多个角度对速度瞬心进行详细讲解。
一、定义和原理速度瞬心是指在机械运动过程中，质点速度矢量的方向和瞬心所在直线方向相重合的点。
简单来说，速度瞬心就是质点瞬时速度的方向与它所在直线方向的交点。
在机械运动过程中，瞬时速度是质点在某一瞬间的瞬时速度，它的大小是瞬时速度的矢量，方向是切线方向。
而速度瞬心则是质点的速度矢量方向与瞬心所在直线方向相重合的点。
速度瞬心的计算方法有很多，其中最常用的方法是使用切线的性质。
在曲线运动中，我们可以通过将切线向后延长，找到两条切线的交点，这个交点就是速度瞬心。
二、速度瞬心的应用速度瞬心在机械工程中有广泛的应用，尤其在运动学和动力学的问题分析中起到了重要作用。
下面以几个具体的例子来说明速度瞬心的应用。
1. 齿轮传动齿轮传动中，速度瞬心常用来确定传动比和齿轮的尺寸。
在两个齿轮相互啮合时，它们的速度瞬心位于齿轮啮合线上，通过计算速度瞬心的位置，可以确定齿轮的啮合情况、传动比和齿轮的尺寸。
2. 曲柄连杆机构曲柄连杆机构中，速度瞬心可用于分析和计算连杆的运动规律。
通过计算连杆各个位置的速度瞬心，可以得到连杆的位移、速度和加速度等参数，从而研究连杆运动的特性和工作原理。
3. 自行车前叉自行车前叉是一种常见的悬挂系统，其原理基于速度瞬心。
在自行车行驶过程中，前叉通过改变前轮的速度瞬心位置来调整悬挂系统的刚度。
通过调整速度瞬心的位置，可以使得前叉对不同路面的冲击吸收能力更好，提高骑行的舒适性和稳定性。
三、速度瞬心的计算方法计算速度瞬心的方法有多种，下面介绍几种常见的计算方法。
1. 直接法直接法是速度瞬心计算的最基本方法，它适用于已知点的速度矢量和所在直线方向的情况。
根据已知点的速度矢量和所在直线的方向，我们可以直接求解速度瞬心。
机械原理及其计算机辅助_ 机构的运动分析_
P34 P24
P13
P12
1
2
ω2
P14
4
P23 3
小结
1. 速度瞬心的概念；
2. 速度瞬心的求解 （1）通过运动副直接相联的两构件的瞬心位置确定
——用定义。 （2）不直接相联两构件的瞬心位置确定
——三心定理。
泰 州 学 院
2-3 用瞬心法作平面机构的速度分析（3）
五、 基于Solidworks的瞬心法平面机构的速度分析
如图中构件1、2的 瞬心用P12表示。
2-3 用速度瞬心作平面机构的速度分析
二、机构中瞬心的数目
由N个构件组成的机构, 其瞬心总数为K N ( N 1) 2
2-3 用速度瞬心作平面机构的速度分析
三、机构中瞬心位置的确定
1. 通过运动副直接相联两构件的瞬心位置确定（用定义）
1.转动副联接两构件的瞬 心在转动副中心。
3.若为纯滚动, 接触点即 为瞬心；
2.移动副联接两构件的瞬心在 垂直于导路方向的无穷远处。
4.若既有滚动又有滑动, 则瞬心 在高副接触点处的公法线上。
2.不直接相联两构件的瞬心位置确定
三心定理: 三个彼此作平面相对运动的构件的 三个瞬心必位于同一直线上。（同学们可课后自己证明）
三、机构中瞬心位置的确定
3. 求构件上某点的速度V或构件的角速度w。
二、优点
1. 本质依然是瞬心法，速度分析概念清楚，求解简单； 2. 可以充分发挥计算机绘图软件的优势，作图快捷，修改方便；且可
以用实际尺寸作图，不需要考虑比例尺的问题； 3. 图纸幅面不受限制，没有瞬心点落在纸面外的困扰； 4. 精度很高，媲美解析法。 5. 当原动件位置变化时，可利用同一个机构运动简图，不需重复作图
机械设计基础第一章 1-3速度瞬心
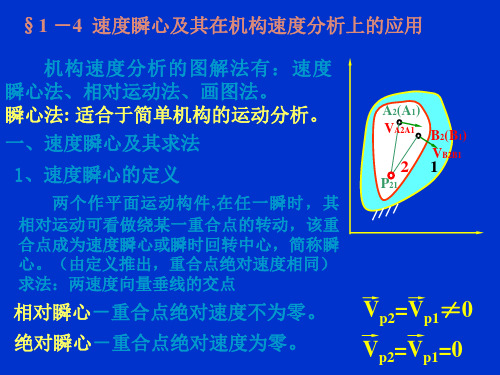
相对瞬心位于两绝对瞬心的同一侧时 两构件转向相同 转向相同。 相对瞬心位于两绝对瞬心的同一侧时，两构件转向相同。 同一侧 相对瞬心位于两绝对瞬心之间时，两构件转向相反。 相对瞬心位于两绝对瞬心之间时 两构件转向相反。 之间 转向相反
2
P12 ω2
1
P233 ω3 P13
4.用瞬心法解题步骤 4.用瞬心法解题步骤 绘制机构运动简图； ①绘制机构运动简图； ②求瞬心的位置； 求瞬心的位置； 求出相对瞬心的速度; ③求出相对瞬心的速度; ④求构件绝对速度V或角速度ω。 求构件绝对速度V或角速度ω 瞬心法的优缺点： 瞬心法的优缺点： 适合于求简单机构的速度， ①适合于求简单机构的速度，机构复杂时因 瞬心数急剧增加而求解过程复杂。 瞬心数急剧增加而求解过程复杂。 ②有时瞬心点落在纸面外。 有时瞬心点落在纸面外。 ③仅适于求速度V,使应用有一定局限性。 仅适于求速度V 使应用有一定局限性。 求速度
∞ 1 6 2 3 P13 4 P14 1 P36 P26 P35 P12 P46 4 P34 P25 2 P45 5 P56 P23 3 ∞ P16 6 P24 P15
5
二、速度瞬心在机构速度分析中的应用 1.凸轮机构直动从动件求线速度 凸轮机构直动从动件求线速度
3 P23 n2 ∞
已知凸轮转速ω 求推杆的速度。 已知凸轮转速ω1，求推杆的速度。 解： 直接观察求瞬心P 、 ①直接观察求瞬心 13、 P23 。 ②根据三心定律和公法线 n－n求瞬心的位置 12 。 求瞬心的位置P － 求瞬心的位置 ③求瞬心P12的速度 。 求瞬心 V2＝V P12＝μl(P13P12)·ω1 ω 长度P 直接从图上量取。 长度 13P12直接从图上量取。 ω1 1
机械原理瞬心法求速度习题
机械原理瞬心法求速度习题引言机械原理是工程力学的一部分，研究物体的运动及力学效应。
在机械原理中，瞬心法是一种常用的分析方法，用于求解物体的速度和加速度。
本文将通过解答一些瞬心法求速度的习题，加深对机械原理的理解。
问题一有一个直径为1m的转盘，上面有一个固定在轴上的活动滑块。
滑块到轴的距离为0.5m。
转盘以5 rad/s的角速度逆时针旋转。
求滑块上某点P的速度。
首先，我们需要确定滑块上的点P的位置。
由于滑块到轴的距离为0.5m，而转盘的直径为1m，因此点P的位置位于滑块上与轴对称的位置，距离轴0.5m。
我们可以使用瞬心法来求解滑块上点P的速度。
瞬心法的基本原理是，在运动过程中，物体的速度等于通过瞬时转动中心与物体上的某一点所作的相对速度。
在本题中，我们可以选择转盘的轴作为瞬时转动中心。
因此，我们需要确定点P相对于转动中心的位置向量和其相对于转动中心的速度向量。
点P相对于转动中心的位置向量为[0.5, 0]，即P的横坐标为0.5m，纵坐标为0，代表距离转动中心0.5m。
点P相对于转动中心的速度向量为[0, R * ω]，其中R 为转盘的半径，即0.5m，ω为转盘的角速度，即5 rad/s。
代入数值计算，得到速度向量为[0, 2.5]，即P点的速度大小为2.5 m/s，方向为垂直于转盘的切线方向。
问题二一个直径为0.8m的小车以2 rad/s的角速度逆时针旋转。
小车上有一根长1.2m的杆，杆上距离小车中心0.6m处有一个质量为1kg的小球。
求小球的速度大小和方向。
我们可以使用瞬心法来求解小球的速度。
同样地，选择小车的中心作为瞬时转动中心。
首先，我们需要确定小球相对于转动中心的位置向量和其相对于转动中心的速度向量。
小球相对于转动中心的位置向量为[0.6, 0]，即小球距离转动中心0.6m。
小球相对于转动中心的速度向量为[0, R * ω]，其中R为小车直径的一半，即0.4m，ω为小车的角速度，即2 rad/s。
速度瞬心法
N＝1/2×4×(4一1)＝6 转动副中心A、B、C、D各为瞬心P12、 P23、P34、P14，由三心定理可知，P13、 P12、P23三个瞬心位于同一直线上；P13、 P14、P34也应位于同一直线上。因此， P12 P23和P14 P34两直线的交点就是瞬心 P13。
同理，直线P14 P12和直线P34 P23的交 点就是瞬心P24。 因为构件1是机架，所以P12、P13、P14是 绝对瞬心,而P23、P34、P24是相对瞬心。
P12 P23
3、机构瞬心位置的确定
（1）直接观察法 （利用定义） 适用于求通过运动副直接相联的两构件瞬心位置。
P12 P12 2 ∞ 1 n 1 2 n
1
2
1
2
P12
t
t
V12
（2）三心定律
定义：三个彼此作平面运动的构件共有三个瞬 心，且它们位于同一条直线上。此法特别适用 于两构件不直接相联的场合。
P13 n
相对瞬心位于两绝对瞬心之间，两构件转向相反。
3.求传动比 定义：两构件角速度之比传动比。 ω 3 /ω 2 ＝ P12P23 / P13P23 P12 ω 2 推广到一般： 1 ω i /ω j ＝P1jPij / P1iPij
2
P233 ω 3 P13
结论:
①两构件的角速度之比等于绝对瞬心至相对 瞬心的距离之反比。 ②角速度的方向为：
3 P23 n2 ∞
已知凸轮转速ω 1，求推杆的速度。
ω 11
P13
V2 P12 n
③求瞬心P12的速度 。 V2＝V P12＝μ l(P13P12)· ω1
长度P13P12直接从图上量取。
2.求角速度 a)铰链机构 已知构件2的转速ω 2，求构件4的角速度ω 4 。 解：①瞬心数为 6个 ②直接观察能求出 4个
机械原理课件瞬心例题
结论和总结
通过学习瞬心的例题和应用，我们对机械原理有了更深入的理解。瞬心是机 械系统中一个重要且复杂的问题，但它也为我们设计和优化机械系统提供了 丰富的信息。
机械Байду номын сангаас理课件瞬心例题
通过这个课件，我们来学习机械原理中的瞬心问题。了解如何计算瞬心，解 决瞬心问题，并探讨瞬心在机械系统中的应用和与平衡的关系。
题目瞬心分析
通过这个例题，我们将深入研究一个机械系统的瞬心问题。通过分析瞬心的 位置和大小，我们可以预测系统的运动和平衡状态。
计算瞬心的方法
了解瞬心的计算方法对于解决机械系统中的问题至关重要。我们将学习如何利用几何和力学原理来计算瞬心的 位置和大小。
解决瞬心问题的策略
当机械系统出现瞬心问题时，我们需要采取一些策略来解决它们。这些策略 可能涉及平衡调整、轴向调整或其他方法。
瞬心在机械系统中的应用
瞬心在机械系统中有许多重要应用。它可以帮助我们设计更稳定和高效的机械系统，提高性能和可靠性。
瞬心与平衡的关系
瞬心与机械系统的平衡有着密切的关系。深入理解瞬心的概念和计算方法可 以帮助我们更好地理解和控制机械系统的平衡状态。
机械原理 瞬心法求速度.
2.确定瞬心的位置
34
P
P24
P 13
A B
P12
C
P 14
P23
3.利用瞬心，由“图”求v3。 因P13是构件1、3的同速重合点，
v3 vP13 1lP
13P 14
VP13 1lP
1P P 13 14 l
P 13 14
3.利用瞬心，由“图”求v3。
得： 从机构位置图中量出图长: P13P14=12.3mm，
(1)两构件组成运动副
根据瞬心的定义，通过观察直接确定两构件的瞬心 位置
两构件组成纯滚动高副
接触点就是其瞬心。 两构件组成滚动兼滑动高副 瞬心在接触点处两高副元素的 公法线n-n上。
1
2
(2)两构件不组成运动副
不直接接触的两构 件，用三心定理确定 其瞬心的位置.
三心定理：
作平面运动的三个构件的三个瞬心位于同一直线上。
v3 vP
注意：
13
1P 13P 14l
m/s
=10×0.0123×2=0.246
图解法的特点体现在直接从“机构位置 图”中量出两点之间的距离。
瞬心法小结
直接利用待求构件和已知构件的相对瞬心，来建立两 者的运动关系。 图解法的特点体现在从“机构位置图”中直接量出两 点之间的距离。 瞬心法适于对构件数较少的机构进行速度分析，不受 机构类型的限制。
下课
1机械原理用速度瞬心法对机构进行速度分析用速度瞬心法对机构进行速度分析瞬心的概念瞬心数目位置例题定义瞬心就是两构件上瞬时绝对速度相同的重合点即等速重合点
机械原理
用速度瞬心法对机构进行速度分析
用速度瞬心法对机构进行速度分析 瞬心 瞬 心 的 概 念
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
机械原理--速度瞬心
习题
习题 > 答案
一.概念
1.当两构件组成转动副时,其相对速度瞬心在转动副的圆心处;组成移动副时,其瞬心在垂直于移动导路的无穷远处;组成滑动兼滚动的高副时,其瞬心在接触点两轮廓线的公法线上.
2.相对瞬心与绝对瞬心相同点是都是两构件上相对速度为零,绝对速度相等的点 ,而不同点是相对瞬心的绝对速度不为零,而绝对瞬心的绝对速度为零 .
3.速度影像的相似原理只能用于同一构件上的两点,而不能用于机构不同构件上的各点.
4.速度瞬心可以定义为互相作平面相对运动的两构件上,相对速度为零,绝对速度相等的点.
5.3个彼此作平面平行运动的构件共有 3 个速度瞬心,这几个瞬心必位于同一条直线上 .含有6个构件的平面机构,其速度瞬心共有 15 个,其中 5 个是绝对瞬心,有 9 个相对瞬心.
二.计算题
1、
2.关键:找到瞬心P36
6 Solution:
The coordinates of joint B are
y B=ABsinφ=0.20sin45°=0.141m
x B=ABsinφ=0.20sin45°=0.141m
The vector diagram of the right Fig is drawn by representing the RTR (BBD) dyad. The vector equation, corresponding to this loop, is written as
r B+ r-r D=0 or r=D-B
r= and r=γ.
Where
When the above vectorial equation is projected on the x and y axes, two scalar equations are obtained:
r*cos(φ3+π)=x D -x B =-0.141m
r*sin(φ3+π)=y D -y B =-0.541m
Angle φ3 is obtained by solving the system of the two previous scalar equations:
tgφ3=141.0541
.0 ⇒φ3=75.36°
The distance r is
r=)cos(3πϕ+-B
D x x =0.56m
The coordinates of joint C are x C =CDcosφ3=0.17m y C =CDsinφ3-AD=0.27m
For the next dyad RRT (CEE), the right Fig, one can write
Cecos(π- φ4)=x E - x C Cesin(π- φ4)= y E - y C
Vector diagram represent the RRT (CEE) dyad.
When the system of equations is solved, the unknowns φ4 and x E are obtained: φ4=165.9° x E =-0.114m
7. Solution: The origin of the system is at A, A≡0; that is,
x A =y A =0.
The coordinates of the R joints at B are x B =l 1cosφ y B = l 1sinφ
For the dyad DBB (RTR), the following equations can be written with respect to the sliding line CD:
mx B - y B +n=0 y D =mx D +n
With x D =d 1, y D =0 from the above system, slope m of link CD and intercept n can be calculated:
m=111cos sin d l l -ϕϕ n=ϕϕ
cos sin 1111l d l d - The coordinates x C and y C of the center of the R joint C result from the system of two equations:
y C =mx C +n=ϕϕϕϕcos sin cos sin 111
1111l d l d x d l l C -+-,
(x C - x D )2+(y C - y D )2=l 2
3
Because of the quadratic equation, two solutions are abstained for x C and y C .For continuous motion of the mechanism, there are constraint relations for the Choice of the correct solution; that is x C < x B < x D and y C >0
For the last dyad CEE (RRT), a position function can be written for joint E:
(x C -x E )2+(y C -h)2=l 2
4
The equation produces values for x 1E and x 2E , and the solution x E >x C is selected for continuous motion of the mechanism.。