速度瞬心例题
工程力学-速度瞬心法
示位置的速度瞬心P 。
得
ω
O
ψ vB
对三角形ABP应用正弦定理得 B
x
又 vA R ，代入上式得
( ) 10
例题
例题2
§2 刚体的平面运动
A
如图所示，半径为R的车
轮，沿直线轨道作纯滚动
D
O vO B （无滑动的滚动），已知轮
心O以匀速vO前进。求轮缘上
C
A，B，C和D各点的速度。
11
例题
例题2
b 2
？
vB
vCA
vCB vC
把
x 上式投影到 x 轴得
所以
方向如图
vC vB vCB 式分别投影到x，y轴上
于是得
22
例题
例题5
§2 刚体的平面运动
图示平面机构中，曲柄OA=100 mm，以角速度ω = 2
rad·s－1转动。连杆AB带动摇杆CD，并拖动轮E 沿水
平面滚动。已知CD = 3CB，图示位置时A，B，E 三点
7
(3)根据已知条件及分析与判断画出速度矢量图。
(4)求解未知速度矢量的大小。
两点速度关系
vB vA vBA
大小 ？
？
方向
速度投影定理 vA AB vB AB
矢量方程
6项中最多 2项未知
标量方程
速度瞬心法 :先通过已知速度量找出刚体该瞬时 速度瞬心位置，再求未知点的速度。
8
例题
例 题 1-续
此时速度瞬心在无穷远处 ----瞬时平动
6
（4）平面图形沿某固定曲面作纯滚动，则任意 瞬时速度瞬心为二者的接触点。
vO
O
P
P
5.求解刚体平面运动问题的基本步骤
机械原理 瞬心法求速度.
2.确定瞬心的位置
34
P
P24
P 13
A B
P12
C
P 14
P23
3.利用瞬心，由“图”求v3。 因P13是构件1、3的同速重合点，
v3 vP13 1lP
13P 14
VP13 1lP
1P P 13 14 l
P 13 14
3.利用瞬心，由“图”求v3。
得： 从机构位置图中量出图长: P13P14=12.3mm，
(1)两构件组成运动副
根据瞬心的定义，通过观察直接确定两构件的瞬心 位置
两构件组成纯滚动高副
接触点就是其瞬心。 两构件组成滚动兼滑动高副 瞬心在接触点处两高副元素的 公法线n-n上。
1
2
(2)两构件不组成运动副
不直接接触的两构 件，用三心定理确定 其瞬心的位置.
三心定理：
作平面运动的三个构件的三个瞬心位于同一直线上。
v3 vP
注意：
13
1P 13P 14l
m/s
=10×0.0123×2=0.246
图解法的特点体现在直接从“机构位置 图”中量出两点之间的距离。
瞬心法小结
直接利用待求构件和已知构件的相对瞬心，来建立两 者的运动关系。 图解法的特点体现在从“机构位置图”中直接量出两 点之间的距离。 瞬心法适于对构件数较少的机构进行速度分析，不受 机构类型的限制。
下课
1机械原理用速度瞬心法对机构进行速度分析用速度瞬心法对机构进行速度分析瞬心的概念瞬心数目位置例题定义瞬心就是两构件上瞬时绝对速度相同的重合点即等速重合点
机械原理
用速度瞬心法对机构进行速度分析
用速度瞬心法对机构进行速度分析 瞬心 瞬 心 的 概 念
速度瞬心例题-all
瞬时平动
工
程
力
AB 0
学
第
vB vA r
9
章
刚 体 的 平 面 运 动
版权所有 钟艳玲 张强
A
vr A
O
OA r
vA r P
vr B B
9
例 曲柄 OA 作定轴转动，通过连杆 AB 带动圆轮 B 沿直线轨
道在作图纯 示滚位动置。时已(1知) 轮：心O速A=度r，ω；vr0B=(2c)on圆st轮.，的圆角轮速半度径为；rB(。3)试连求
例 用速度瞬心法求解 9-2，并求 AB 杆中点 M 之速度。
工 解 (1) 分别做vr A，vr B 垂线交于点 P 即为 AB 速度瞬心
程
(2) 根据速度分布规律有
力
学
vA AP
P B
第 9 章
刚 体 的 平
vA vA AP l sin
vB BP
l cos vA l sin
OA r
B 点为 AB 杆速度瞬心
vA r
工
程 力
vB 0
vr A
学
第 9
AB
vA AB
章
O
AB
A
vr B
B
刚
r 3 转向如图
体
3r 3
的
平
面
运
动
7
版权所有 钟艳玲 张强
工 程 力 学
第 9 章
刚 体 的 平 面 运 动
版权所有 钟艳玲 张强
(b) 60位置如图
P 点为 AB 杆速度瞬心
OA r P
复习专题——瞬心
图2-4（a）两构件以转动副联接
②两构件以移动副联接，构件1各点相对构件 2的移动速度都平行于导路方向，则瞬心 P12位于垂直于移动副导路的无穷远处。
图2-4（b） 两构件以移动副联接
③两构件作纯滚动时，接触点无相对速度， 接触点就是瞬心P12 。
图2-4（c） 两构件作纯滚动
④两构件组成高副时，由于构件间具有两个相对运动自 由度,不能确定构件1上某点对构件2的相对速度的大小, 因而不能确定瞬心P12的确定位置。从两构件必须保持 接触出发，可知构件1上M点的相对速度必定沿着高副 公切线tt的方向，所以瞬心P12虽不能完全确定，但必 位于高副的公法线NN上。
1
1
2 VM1 VM2
A
P13
M（M1，M2）
B
3
2
P23
若将重合点M（M1，M2）选在AB线上
1
1
2 VM1 VM2
A
P13
B
2
P23
M（M1，M2） 3
调整重合点M（M1，M2）在AB线 上的位置可使VM1=VM2
1
1
2
A
P13
VM1
VM2
B
3
2
P23
M（M1，M2）
*三心定理—— 彼此作平面运动的三个构件有三个速度瞬心， 它们位于同一条直线上。 Vp1=AP*1
3
2
1
1
2
3
1
1
2
2
3
2
1
1
2
3
现寻求构件1、2间的瞬心p12。
1
1
2
A
P13
B
3
2
P23
任选两构件的重合点M（M1，M2） 由于VM1 VM2 ，所以M不是1、2的瞬心
机械原理第四章速度瞬心及其应用一类教资
4.4 共轭曲线与共轭曲线机构（自学）
构件1曲线K1和构件2曲线K2 在点Q高副接触。
构件1、2之间的速度瞬心在点P
瞬心线S1是速度瞬心P 相对于构件1的轨迹线。
瞬心线S2是速度瞬心P 相对于构件2的轨迹线。
曲线K2包络了曲线K1的各个位置， 称K2为包络曲线， K1为被包络曲线
（大小、方向相等）
确定瞬心小结
4.2 速度瞬心在机构速度分析中的应用
P23
∞
P13
P12
情形1：求线速度
已知凸轮转速ω1，求推杆的速度。
求解过程： ①直接观察求瞬心P13、 P23 。
③求瞬心P12的速度 。
V2＝V P12＝μl(P13P12)·ω1
长度P13P12直接从图上量取。
ω1
1
2
3
P12
2
3
4
ω2
v2
P14→∞
P34
例题：如图所示的带有一移动副的平面四杆机构中, 已知原动件2以角速度w2等速度转动, 现需确定机构在图示位置时从动件4的速度v4。
求解过程：确定机构瞬心如图所示
P24 在P23、P34 连线和P12、P14 连线上。
P24
P13
ω2
情形2：求角速度
求解过程：①瞬心数为
高副低代的含义: 根据一定条件对平面高副机构的中高副虚拟地用低副来代替的方法。
高副低代的条件： ①代替前后机构的自由度不变； ②代替前后机构的瞬时速度和瞬时加速度不变。
高副低代的方法1
高副两元素均为圆弧
高副元素为非圆曲线
用一个含有两个低副的虚拟构件来代替高副，且两低副位置分别在两高副两元素接触点处的曲率中心。
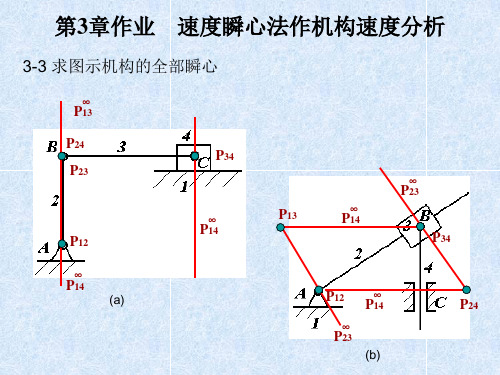
速度瞬心法作机构速度分析.
P12
ω3
P14 P13 B
V /P 23 P 13 VC / P 34 P 13
2）当φ=165°时，构件3的BC线上（或延长线） 速度最小的点E的位置及其速度大小
3 VC / lP
34 P 13
2.65(rad / s)
VE 3 EP 13 L 365.7(mm / s)
ω3=ω2=0
vB 2 vB3 vB 2 B3
大小 方向
VC3=0 p’
⊥AB
0 ？ ⊥BD
？
//CD
aB2 aB 3 a aB 2 B 3 a
n t B3 r
大小 方向 √ B→A 0
k B 2 B3
b2’ (c3’)
b3’
?
⊥ BD
?
∥CD
230 vB2B3
t ' aB p ' b 3 3 3 a 2 lBD l BD
2 aB3 aB1 1 l AB
ω2=ω3=0
aB3 aB 2 aB 2 a
n t
大小 方向 √ B→A
t
r B3 B 2
0
a
k B3 B 2
大小 方向
vC 3 vB3 vC 3B3
？
√
⊥AB 0 ⊥ BC
0
?
⊥ BC
?
20 2 vB3B2
∥BC
大小
' 3 ' 3
(c3’ ) p’
第3章作业 速度瞬心法作机构速度分析
3-3 求图示机构的全部瞬心
P13 P24 P23 P13 P14 P34
∞
∞
P34 P23 P14
5.2、速度瞬心(3-2)
（a） （b）
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
8-7
速度瞬心（3-2） 练习题2
讲述完毕 ！
图示桁架中,假如杆1、杆2、杆3中的某一根杆突然被剪断,那么剪断
后右半部分框架DKEB刚开始运动时的速度瞬心在哪里？
vD
vC
vCD
vB
vBD
↕ ↕↔ ↕
8-8
8-5
速度瞬心（3-2）
3) 平面图形上A、B两点的速度矢都垂直于AB连线时
4) 平面图形上A、B两点的速度矢同向平行,且都不与AB连线垂直时
瞬时平动≠平行移动
aB
aA
aAnB
a
t AB
8-6
大小： ? √
方向：
0√
√√
速度瞬心（3-2）
至此，本次课讲述完毕，现在做两道习题 ！
练习题1
下列平面图形所示速度哪种情况是可能的？
vB
rAB
rAB
B点是平面图形上的任意一点
某时刻平面运动图形上速度为零的点,称为该时刻平面 图形的速度瞬心
定理 5.2-2
平面运动图形上任意一点的速度都等于该点绕平面图形速度瞬心 的定轴转动速度.
8-2
速度瞬心（3-2）
以O为基点 速度瞬心: C点
这与前面第4.1节例题4.1-2的计算分析结果相同吗？
速度瞬心3281定理522abababb点是平面图形上的任意一点某时刻平面运动图形上速度为零的点称为该时刻平面图形的速度瞬心平面运动图形上任意一点的速度都等于该点绕平面图形速度瞬心的定轴转动速度
速度瞬心（3-2）
8-1
速度瞬心（3-2）
vB vA vAB
若 vA 0
机械原理课件瞬心例题
在设计过程中，合理利用瞬心，可以调整机构的动态响应， 降低外部激励对机构的影响，从而减小振动和冲击。
实现机构的轻量化和紧凑化
通过优化瞬心的位置和数量，可以减小机构的整体尺寸， 实现机构的轻量化和紧凑化设计。
瞬心的合理配置有助于减少机构中的运动副数量和传动元 件，从而减小机构的重量和体积，实现轻量化和紧凑化的 目标。
随着计算机技术的发展， 越来越多的机械设计软件 提供了计算机辅助计算瞬 心的功能。
具体步骤
在软件中输入机构的参数 和运动条件，软件会自动 计算出机构的瞬心位置。
应用场景
广泛应用于各种复杂机械 系统的设计和分析中，大 大提高了设计效率。
BIG DATA EMPOWERS TO CREATE A NEW ERA
04
瞬心的计算方法
BIG DATA EMPOWERS TO CREATE A NEW
ERA
平面机构的瞬心计算方法
瞬心定义
应用场景
平面机Байду номын сангаас中，瞬时速度为零的点称为 瞬心。
在平面连杆机构、凸轮机构等中，瞬 心的计算对于确定机构的运动特性十 分重要。
瞬心计算公式
对于两构件，若它们的相对速度为零 ，则它们之间的相对瞬心位置可以通 过求解相对速度的叉乘为零的方程得 到。
详细描述
在球面机构中，如球面齿轮或球面蜗 杆，瞬心通常位于球心。通过分析瞬 心位置，可以确定机构在运动过程中 的位置和运动轨迹，有助于优化机构 的设计和运动性能。
瞬心在万向联轴器中的应用
总结词
万向联轴器中的瞬心点是连接两轴的点 ，对于实现两轴间的等角传递运动至关 重要。
VS
详细描述
在万向联轴器中，瞬心是连接两轴的点， 它确保了两轴间的等角传递运动。通过合 理选择瞬心的位置，可以优化万向联轴器 的运动性能，减小传动误差，提高传动效 率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基本要求了解平面机构运动分析的目的和方法，以及机构位置 图、构件上各点的轨迹和位置的求法。
掌握速度瞬心位置 的确定。
了解用速度瞬心求解速度的方法。
掌握用相对运 动图解法作机构的速度和加速度的分析。
熟练掌握影像法 的应用。
搞清用解析法中的矩阵法作机构的速度和加速度 的分析，最后要达到会编程序上机作习题的程度。
基本概念题与答案1. 什么是速度瞬心，机构瞬心的数目如何计算 答：瞬心：两个构件相对速度等于零的重合点。
2. 速度瞬心的判定方法是什么直观判定有几种 答：判定方法有两种：直观判定和三心定理，直观判定有四种： （1）两构件组成转动副的轴心。
（2）两构件组成移动副，瞬心在无穷远处。
（3）纯滚动副的按触点， （4）高副接融点的公法线上。
3. 速度瞬心的用途是什么 答：用来求解构件的角速度和构件上点的速度，但绝对不能求加速度和角加速度， 在四杆机构中用瞬心法求连杆和从动件上任一点的速度和角速度最方便。
4. 平面机构运动分析的内容、目的和方法是什么 答：内容：构件的位置、角位移、角速度、角加速度、构件上点的轨迹、位移、 速度、加速度。
目的：改造现有机械的性能，设计新机械。
方法：图解法、解析法、实验法。
5. 用相对运动图解法求构件的速度和加速度的基本原理是什么 答：基本原理是理论力学中的刚体平面运动和点的复合运动。
6. 什么是基点法什么样的条件下用基点法动点和基点如何选择 答：基点法：构件上某－点的运动可以认为是随其上任选某一点的移动和绕其点 的转动所合成的方法。
求同一构件上两点间的速度和加速度关系时用基点法，动点和基点选在运动要素己 知多的铰链点。
7 用基点法进行运动分析的步骤是什么 答：（ 1）选长度比例尺画机构运动简图（2）选同一构件上已知运动要素多的铰链点作动点和基点， 已知量的大小和方向。
（3）选速度和加速度比例尺及极点 P 、P '按已知条件画速度和加速度多边形,第四章平面机构的运动分析 K = N (N-1) / 2列矢量方程， 标出求解未知量的大小和方向。
（4）对所求的量进行计算和判定方向。
8 ．什么是运动分析中的影像原理又称什么方法注意什么 答：影像原理：已知同－构件上两点的速度或加速度求另外－点的速度和加速度， 则这三点速度或加速度矢端所围成的三角形与这三点在构件上围成的三角形相似，这就 称作运动分析中的影像法，又称运动分析中的相拟性原理。
注意：三点必须在同一构件上，对应点排列的顺序同为顺时针或逆时针方向。
9．什么是速度和加速度极点答：在速度和加速度多边形中 绝对速度为零或 绝对加速度为零的点，并且是绝对 速度或绝对加速度的出发点。
10. 速度和加速度矢量式中的等号，在速度和加速度多边形中是哪一点 答：箭头对顶的点。
11. 在机构运动分析中应用重合点法的基本原理是什么答：点的复合运动。
12. 重合点法在什么倩况下应用 答：两个活动构件有相对运动时，求重合点的速度和加速度。
13. 应用重合点进行运动分析时，什么情况下有哥氏加速度 答：当牵连角速度和重会点间相对速度不等于零时，有哥氏加速度，若其中之一等 于零，则哥氏加速度等于零。
大小 为： a B1B2 = 2 co 2V B 1B2 方向为：也1B2的矢量按牵连角速度O2方向旋转90 0。
14. 应用重合点法进行运动分析时的步骤是什么 答：（ 1） （2） （3） （4） （5）典型例题例3-1 图（a ）和（b ）分别为移动导杆机构和正切机构的运动简图，其长度比例尺卩L = 2 mm/mm 图中的构件1均为原动件，且已知o i = 10rad /s 。
试分别求出其全部 瞬心点，并用瞬心法分别求出：构件 3的速度V 3、构件2上速度为零的点12和构件2的角速度O 2o解 这两个机构均为含有两个移动副的四杆机构，各有六个瞬心点。
但因导路的形 状不同，故瞬心点的位置不尽相同。
（ 1 ） 移动导杆机构其六个瞬心点的位置如图（a ）所示。
其中：P14在A 点，P12在B 点；P23在导路的曲 率中心C 处（而不是在无穷远处！这点应该注意），Ps 34在与导路垂直的无穷远处；根据三心定理，P13在 P14和Ps 34连线与P12和P23连线的交点处，P24在 P14和P12连线与P23 和Ps 34连线的交点处。
例 3-1 图 L = 2 mm / mm ，卩 v = 0.04 m /s / mm因为构件1的角速度o 1已知，而构件3为平移运动，所以可利用 P 13求出构件3的速度 v 3= V p13 =o 1L AP13=o 1AR 31 L =10X 30X 2=600mrTKs 方向：向右。
选择比例尺画机构运动简图。
选运动要素已知多的铰链点为重合点，列速度，加速度矢量方程。
选速度比例尺和速度极点画速度多边形。
选加速度比例尺和加速度极点画加速度多边形图。
回答所提出的问题。
(a) 构件2上速度为零的点I 2，就是构件2与机架4的瞬心点 在图示位置上，构件2绕P 24（ 12）点作瞬时定轴转动，其角速度 的速度V P12求出，即：v方向：逆时针。
（2 ）正切机构六个瞬心点的位置如图（b ）所示。
请注意利用三心定理求 P 13和P 24的方法。
构件3的平移速度V 3,可利用瞬心点P 13求出V 3 = V P13 = O 1L A p13 =O 1AR 3 y L = 10 X 38X 2 = 760 mm / s 方向：向下。
构件2上速度为零的点|2，即为瞬心P 24。
由于构件2与构件1构成移动副，二者之间没有相对转动，因此O 2 = O 1 = 10 rad / s 逆时针方向例3-2 在图（a ）所示的机构中，已知：L AB = 38mm L CE = 20mm L DE = 50mm X D =150mm y D = 60mm 构件1以逆时针等角速度o 1 = 20 rad / s 转动。
试求出此机构的全部瞬 心点，并用向量多边形法求出构件 3的角速度 O 3和角加速度£ 3,以及点E 的速度V E 和加速度a Eo解（1）求速度瞬心P 14在A 点，P 12在B 点, P 34在D 点，P "23在与导路CE 相垂直的无穷远处，这四个瞬心容易求出，如图（a ）所示。
根据三心定理， P 13既在P 14和P 34的连线上，又在P 12和 P ”23的连线上，因此，过B （ P 12 ）点作导路CE 的垂线，与AD 连线的交点即为P 13点；同理， 过D （ P 34）点作导路CE 的垂线，与AB 连线的延长线的交点即为 P 24点。
（2 ）速度分析 取长度比例尺 卩L = 4 mm/mm,按给定条件作出机构运动简图，如图（ (b)P 24 (V P24= 0) oCO2可通过瞬心点P l2P12= V B =O 1 L AB = o t ABy L = 10 X 22 X 2 = 440 mm / s o 2 = V P12 / L I2B = V P12 / ( I 2BXy L ) = 440 / ( 20 X 2) = 11 radb ）所示。
在PFP HPl4此机构中，构件2为作平面运动的构件，且运动副 点，动系选在构件 3上。
为求得重合点，需将构件 属于构件3的牵连运动点B3。
其中，V B2 取速度比例尺卩Pb 2= V B 2/ v =760/20 = 38mm取速度极点P 作速度多边形Pb 2b 3如图（c ） 贝y 3 3 = V B3 / L BD = Pb 3 V / BD L = 方向：顺时针。
由于滑块2与导杆3之间没有相对转动，因此 3 2 = 3 3 = rad / s至此，在构件3上已经有了 D 和B 两个点的速度已知（注意： D 为固定铰链，V D=0, a D = 0,为运动已知点，这一点易被忽略）， 所以，可以用影像法来求构件 3上E 点B 点的运动已知，因此，应选 B2为动 1向B 点扩大， 得到与B 2点重合的、方向 大小V B2丄ABB3丄BD+ VB2B3// CEAB3 1=L AB 3 1 = 38 V = 20 mm / s / mm X 20 = 760 mm / s 。
贝y V B2 o的代表线段长度为所示。
X 20 / 31 X 4 = rad / 9)23的速度。
为此，在图（c ）中作 △ pb 3e S △ DBE ，得e 点，则 X 20 = 230 mm / s v E = pe 3 v （ 3）加速度分析由于动系（构件 3 ） D 点作定轴转动，所以存在哥氏加速度。
其加速度方程为 a B2 = 方向 B 7A 大小 L 2AB 3 1 其中：n a B2 = L AB 3 a n B3 = L BD 3 B a 2 1 2 3 k B2B37 n B3 + 7D 已知 7 7 7 t t k a B3 + a B2B3 + a B2B3丄 BD // CE 丄 CE 已知2 =38 X 20 = BD3 = 2 3 3v B2B3 = 2 3 3 取加速度比例尺3 量的代表线段。
2 = 15200 mm / s 2 22 L3 23 = 31 X 4X = 2620 mm/s 2 2b 2b 33 v = 2 XXX 20 = 2484 mm/s 22 a = 500 mm/s /mm,选极点p ‘在图（d ）中依次作出上述各已知向 p p k在此基础上作出加速度多边形，如图（ n a B2 / n a B3 / ka B2B3 3= 30.4 mm = 5.24 mm = 4.97 mm d ）所示。
则 3 a / BD 3 L 2 15200 /500 2620 / 500 2484 / 500 £ 3 = a B3 / L BD = n 3 b 3 = 39 X 500 / 31 X 4 = rad/s 2方向：顺时针。
利用影像原理，在图（d ）中，连P P b 3,作 △ P ‘ b 3 ‘ e ‘ sA D BE ,得e ‘点，贝U p 'e 即为 a E 的代表线段，其大小为 22a E = p e 3 a = 16X500 = 8000 mm / s 2 = 8 m / s 2例3 - 3图（a ）所示为一四铰链机构的机构运动简图、速度多边形和加速度多边2 形，作图的比例尺分别为：3 L = 2 mm/mm 3 v = 20 mm/s/mm 、3 a = 200 mm/s /mmo 已知 原动件 1 以匀角速度3 1 = 10 rad / s 顺时针方向转动。
要求： （ 1）根据两个向量多边形分别列出相应的速度和加速度向量方程，井将各个向量标在 向量多边形中相应的代表线段旁边。