速度瞬心例题
理论力学
例4-14 图示机构中，曲柄OO′=l，以匀角速度1绕定轴
O转动，同时带动可绕曲柄一端的轴销O′转动的轮Ⅱ沿
固定轮Ⅰ滚动而不滑动。已知轮Ⅱ的半径为r,求在图示
位置轮缘上A、B两点的加速度aA及aB，A点在OO′的延 长线上，而B点位于通过O′点并与OO′垂直的半径上。
其中 vA OAl 0.2m/s aA O2Al 0.4m/s2 vBA ql 0.05m/s
aBnA q2l 0.025m/s2 aBτ A ql 0.0866m/s2
图中各速度、加 速度的方向都按真实 方向画出。
vA A aA
OA
C aBnA aBA vBA
B
O
O1
把速度与加速度的矢量方程分别投影到x、y轴，得到
杆BE长 2l 。此瞬时OA铅直，且与BE夹角为45°。
求该瞬时杆OA的角速度和角加速度。
A aBE
vB
B
45
aB
a
n BE
O l
D
v
E
A
vr
ar
ve
ae
vB B
aB
aen 45
OA
OA
O l
D
v E
l l
例4-16 AB长为l，滑块A可沿摇杆OC的长槽滑动。摇
杆OC以匀角速度绕O轴转动，滑块B以匀速v=l沿水平
解: (1)明确基点。 (2)用绝对角速度与绝对
B aO’
A aBO’ aO’
O’aAO’
aB
C
aO’ r
vO’
Ⅱ
1
角加速度计算。
O Ⅰ
例 图示机构中，曲柄OA=r，以匀角速度0绕O轴转动。
平面机构运动分析思考题与习题
平面机构运动分析一、基本概念1、速度瞬心和机构中速度瞬心的数目1) 瞬心的定义瞬心：相对作平面运动的两构件上瞬时相对速度为零的点（即等速重合点）称为速度瞬心，简称瞬心。
瞬时等速重合点。
绝对速度瞬心：如果两构件之一是静止的，即绝对速度为零的瞬心称为绝对速度瞬心。
相对速度瞬心：如果两个构件都是运动的，即绝对速度不为零的瞬心称为相对速度瞬心。
2) 瞬心数目因为发生相对运动的任意两构件间都有一个瞬心，如果一个机构由m个构件组成，则瞬心数K为：2. 瞬心位置的确定（1）当两构件直接以运动副链接时，按定义确定:1) 当两构件组成转动副时，转动副的转动中心是它们的瞬心；2) 当两构件组成移动副时，瞬心位于导路垂线无穷远处；3) 当两构件组成纯滚动的高副时，接触点就是其速度瞬心；4) 当两构件组成滑动兼滚动的高副时，瞬心位于接触点的公法线上，具体还需据其它条件确定；（2） 对于不直接接触的构件，其瞬心可用三心定理来确定。
三心定理：作相对运动的三个构件共有三个瞬心，这三个瞬心位于一条直线上。
3、矢量图解法原理：1）用一条“有向线段”对应“一个矢量”2）作图遵循“同侧首末相连，两侧起点相同”的原则4、速度、加速度影响定理1）使用场合：统一构件，知2求3。
2）ΔBCD(机构位置图)∽Δbcd（速度多边形）∽Δb’c’d’（加速度多边形）。
3）字母排列顺序一致。
二、思考题1、机构运动分析的目的和任务是什么？图解法和解析法各有何优缺点？2、什么是速度瞬心？绝对瞬心和相对瞬心有何异同点？3．什么是“三心定理”？在确定不直接相联的两构件瞬心位置时，可能会出现什么情况（指不便于作图的情况）？三、练习题1、在图1示曲柄滑块机构中，原动件曲柄以等角速度ω1=5rad/s 逆时针转动。
已知机构尺寸：a=0.30m,b=0.6m。
1）试用瞬心法确定机构在ϕ1=60º位置时滑块3的速度2）用矢量图解法求滑块3的速度，构件2的角速度ω23）求BC上中点D的速度图1 图22、图2所示正弦机构中，已知：曲柄AB以等角速度转动，ω1=5rad/s，l AB=0.1m。
机械原理课件瞬心例题
结论和总结
通过学习瞬心的例题和应用，我们对机械原理有了更深入的理解。瞬心是机 械系统中一个重要且复杂的问题，但它也为我们设计和优化机械系统提供了 丰富的信息。
机械Байду номын сангаас理课件瞬心例题
通过这个课件，我们来学习机械原理中的瞬心问题。了解如何计算瞬心，解 决瞬心问题，并探讨瞬心在机械系统中的应用和与平衡的关系。
题目瞬心分析
通过这个例题，我们将深入研究一个机械系统的瞬心问题。通过分析瞬心的 位置和大小，我们可以预测系统的运动和平衡状态。
计算瞬心的方法
了解瞬心的计算方法对于解决机械系统中的问题至关重要。我们将学习如何利用几何和力学原理来计算瞬心的 位置和大小。
解决瞬心问题的策略
当机械系统出现瞬心问题时，我们需要采取一些策略来解决它们。这些策略 可能涉及平衡调整、轴向调整或其他方法。
瞬心在机械系统中的应用
瞬心在机械系统中有许多重要应用。它可以帮助我们设计更稳定和高效的机械系统，提高性能和可靠性。
瞬心与平衡的关系
瞬心与机械系统的平衡有着密切的关系。深入理解瞬心的概念和计算方法可 以帮助我们更好地理解和控制机械系统的平衡状态。
理论力学(刘又文 彭献)答案第4章
§4.2 思考解析
思考 4-1 已知平面图形 S 的运动方程，试写出 S 上给定点 M 的运动方程， 以及该点的速度和加速度解析表达式。 答：设已知 x A = f1 (t ),
y A = f 2 (t ), ϕ = f3 (t ) 。则 M 点运动方程为
xM = x A + AM cos ϕ = f1 (t ) + AM cos f3 (t ) yM = y A + AM sin ϕ = f 2 (t ) + AM sin f3 (t ) M 点速度和加速度分量分别为
n τ aCv = aO + aC + aC vO vO n τ 其中， aC = Rω 2 , aC = Rα = a0 ，方向与 a0 相反。 vO vO
110
故
n aCv = aC ， aCv = Rω 2 = vO
2 v0 R
以 Cv 为基点，M 点的加速度如图 b 所示。 故
n 2 2 aM = (aMC − aCv ) + (aτ ( Rω 2 ) 2 + (2 Rα ) 2 = 2 a0 + MCv ) = v 4 v0 4R2
所以
xM = r cos ω t + AM cos ϕ ， yM = r sin ω t − AM sin ϕ
对时间 t 求一阶和二阶导数便得 M 点的速度和加速度坐标分量。
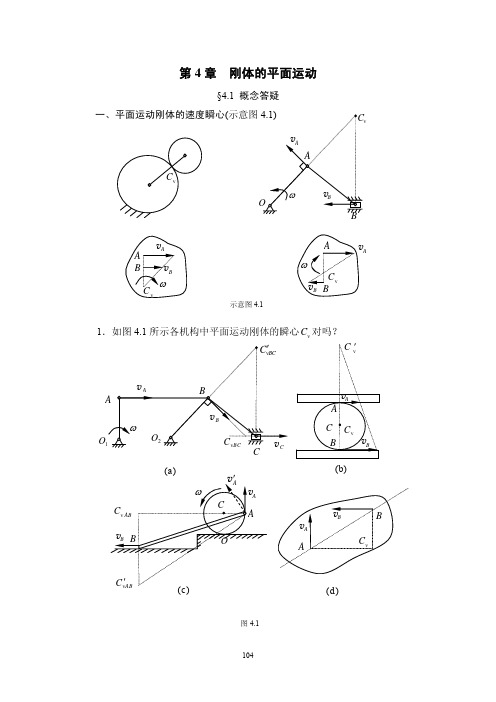
思考 4-4
试求图 a、b、c 中各平面运动刚体的速度瞬心 Cv 。
ω
B
A B
C v
A
ω
(b) (c)
(a)
ω
C
A B
B
A
ω
Cv
vC vB
瞬心法求速度
OA r v A r
P
AB
vA vA AP 3 3 OA
AB
r 转向如图 3r 3 vA v B AB BP
A
2 3 OA 3
2 3 r 3
O
vA
60
vB v BA
(c) 90 位置如图 瞬时平动
v DC
M
A
vBC
平面图形内任意点的速度等于该点随图 形绕速度瞬心转动的速度。
速度的分布情况
vM
C
vM vMC MC
M
平面图形内各点速度的大小与该点到速度 瞬心的距离成正比；速度的方向垂直于该点到 速度瞬心的连线，指向图形转动的一方。
三、速度瞬心的确定方法示例
⑴ 平面图形沿一固定表面只滚不滑 速度瞬心：图形与固定面的接触点C
D B O2
A
O1
3、从已知求未知
例8-6 椭圆规尺的A端以速度 v A沿x 轴的负向运动，如图所示，
AB=l。求B端的速度以及尺AB的角速度。
解：⑴ 分析各物体的运动
尺AB作平面运动
滑块A、B作平移
y vB
B
⑵利用瞬心法求解 找出速度瞬心的位置:C
C
vA vA AB AC l sin
解 (1) O1O2 做定轴转动
vO2 O1O2 H ( r1 r2 ) H
vA A
II
vB
v O2
B
(2) 轮 II 在轮 I 上做纯滚动，其接 触点 P 为其速度瞬心 H O1 I
O2
P
vC
vO2 r2 2
2
东南大学机械设计考试瞬心法
瞬 心 法一、单项选择题（每小题1分）在下列每小题的四个备选答案中选出一个正确的答案，并将其字母标号填入题干的括号内。
1、在两构件的相对速度瞬心处，瞬时重合点间的速度应为（ A ）。
A. 两点间相对速度为零，但两点的绝对速度不等于零B. 两点间相对速度不等于零，但其中一点的绝对速度等于零C. 两点间相对速度不等于零，且两点的绝对速度也不等于零D. 两点间的相对速度和绝对速度都等于零2、两构件作相对运动时，其瞬心是指（ C ）的重合点。
A. 绝对速度等于零B. 绝对速度和相对速度都等于零C. 绝对速度不一定等于零，但绝对速度相等或相对速度等于零D. 相对速度不等于零3、速度瞬心是指两构件上（ B ）为零的重合点。
A. 绝对速度B. 相对速度C. 绝对速度不D. 相对速度不二、填空题（每空1分）1、当两构件组成转动副时，其瞬心就是 转动中心位置 。
2、当求机构中不直接组成运动副两构件间的瞬心位置时，可应用 三心定理 来求。
三、分析题（每小题6分）1、对于下列机构的图示位置：①试确定机构的所有速度瞬心位置；②若已知原动件1的角速度ω1，试列出求从动件3运动速度ω3的表达式。
——4分113133ωωDP AP =——2分2、对于下列机构的图示位置：①试确定机构的所有速度瞬心位置；②若已知原动件1的角速度ω1，P 12P 24∞——4分0113133==ωωDP AP ——2分 3、对于下列机构的图示位置：①试确定机构的所有速度瞬心位置；②若已知原动件1的角速度ω1，试列出求从动件3运动速度v 3的表达式。
——4分1133ωAP v =——2分4、对于下列机构的图示位置：①试确定机构的所有速度瞬心位置；②若已知原动件1的角速度ω1，试列出求从动件3运动速度v 3的表达式。
——4分01133==ωAP v ——2分5、对于下列机构的图示位置：①试确定机构的所有速度瞬心位置；②若已知原动件1的角速度ω1，试列出求从动件3运动速度ω3的表达式。
理论力学-高教出版-刘又文、彭献著-第4章
ϕ
x
思考 4-1 图
My = f 2′′(t ) − AM [sin f 3 (t ) ⋅ f 3′2 (t ) − cos f 3 (t ) ⋅ f 3′′(t ) ] 。 aMy = v
思考 4-2 问题 4-4 图中，若 vC 不为常数时， aC 有何变化？
v
课
后 答
Mx = f1′′ aMx = v (t ) + AM [ cos f3 (t ) ⋅ f3′2 (t ) + sin f3 (t ) ⋅ f3′′(t )] ；
2r
C
aw .
B
r/2
ω0
O
Ι
vA
后 答
vC = 2rω 2 (轮Ⅱ上 C 点速度的大小)
课
而 故
ω2 =
vC = 6rω 0 (亦为轮Ⅲ上 C 点速度的大小)
轮Ⅲ上 B 点速度 v B ，亦为杆 OB 上 B 点的速度，其大小为
案
再求轮Ⅲ的瞬心。因为
v A 3rω 0 = = 3ω 0 r r
所以轮Ⅲ的瞬心为 v B 、 v C 两矢量端连线与 CB 连线延长线的交点 Cv3 。 由几何关系有
所以 又
vB = v Ae = Rω 0 vC cos 60 D = vB cos 30 D
109
b
vC cos 60 = v A cos 30
D
案
D
网
于是由
ω0
O
v Ae
m
所以
aC = (aCx ) 2 + (aCy ) 2 =
v4 v4 A + B l12 l22
所以 故
vC = 3Rω 0
ω BC =
机械设计基础第一章-1-3速度瞬心
绝对瞬心－重合点绝对速度为零。
A2(A1) VA2A1
2
P21
B2(B1)
VB2B1
1
Vp2=Vp1≠0 Vp2=Vp1=0
由定义推出的特点：
①该点涉及两个构件。
②绝对速度相同，相对速度为零。（重合点）
③相对回转中心。 2、瞬心数目 若机构中有n个构件，则
P13
1 23
P13 P34
③求瞬心P24的速度 。 VP24＝μl(P24P12)·ω2
VP24
P23 3
2 ω2
1
（令构件2绕绝对瞬心P12旋转，得VP24 ） P24 P12
4
ω4
P14
VP24＝μl(P24P14)·ω4（绕绝对瞬心P14旋转）
ω4 ＝ω2·(P24P12)/ P24P14 方向: 与ω2相同。
P36 2
3 P13
P26
P35
P25
2
P12
P46 5
P14 1
P15
∞ P16
6 P56
二、速度瞬心在机构速度分析中的应用
1.凸轮机构直动从动件求线速度 3 P23 ∞
已知凸轮转速ω1，求推杆的速度。
解： ①直接观察求瞬心P13、 P23 。
②根据三心定律和公法线
n2
ω1 1 V2
三心定理的证明：
（用反证法证明）
如右图所示的三个构件组 成的一个机构，设构件1为固定 件。若P23不与P12、P13共线 （同一直线），而在任意一点 C，则C点在构件2和构件3上的 绝对速度的方向不可能一致， 即绝对速度不相等。而只有C 点在P12、P13连成的直线上， 重合点速度方向才可能一致。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章平面机构的运动分析基本要求了解平面机构运动分析的目的和方法，以及机构位置图、构件上各点的轨迹和位置的求法。
掌握速度瞬心位置的确定。
了解用速度瞬心求解速度的方法。
掌握用相对运动图解法作机构的速度和加速度的分析。
熟练掌握影像法的应用。
搞清用解析法中的矩阵法作机构的速度和加速度的分析，最后要达到会编程序上机作习题的程度。
基本概念题与答案1.什么是速度瞬心，机构瞬心的数目如何计算答：瞬心：两个构件相对速度等于零的重合点。
K = N (N-1) / 22.速度瞬心的判定方法是什么直观判定有几种答：判定方法有两种：直观判定和三心定理，直观判定有四种：（1）两构件组成转动副的轴心。
（2）两构件组成移动副，瞬心在无穷远处。
（3）纯滚动副的按触点，（4）高副接融点的公法线上。
3.速度瞬心的用途是什么答：用来求解构件的角速度和构件上点的速度，但绝对不能求加速度和角加速度，在四杆机构中用瞬心法求连杆和从动件上任一点的速度和角速度最方便。
4.平面机构运动分析的内容、目的和方法是什么答：内容：构件的位置、角位移、角速度、角加速度、构件上点的轨迹、位移、速度、加速度。
目的：改造现有机械的性能，设计新机械。
方法：图解法、解析法、实验法。
5.用相对运动图解法求构件的速度和加速度的基本原理是什么答：基本原理是理论力学中的刚体平面运动和点的复合运动。
6.什么是基点法什么样的条件下用基点法动点和基点如何选择答：基点法：构件上某－点的运动可以认为是随其上任选某一点的移动和绕其点的转动所合成的方法。
求同一构件上两点间的速度和加速度关系时用基点法，动点和基点选在运动要素己知多的铰链点。
7 用基点法进行运动分析的步骤是什么答：（1）选长度比例尺画机构运动简图（2）选同一构件上已知运动要素多的铰链点作动点和基点，列矢量方程，标出已知量的大小和方向。
（3）选速度和加速度比例尺及极点P、P′按已知条件画速度和加速度多边形，求解未知量的大小和方向。
（4）对所求的量进行计算和判定方向。
8 ．什么是运动分析中的影像原理又称什么方法注意什么答：影像原理：已知同－构件上两点的速度或加速度求另外－点的速度和加速度，则这三点速度或加速度矢端所围成的三角形与这三点在构件上围成的三角形相似，这就称作运动分析中的影像法，又称运动分析中的相拟性原理。
注意：三点必须在同一构件上，对应点排列的顺序同为顺时针或逆时针方向。
9．什么是速度和加速度极点答：在速度和加速度多边形中绝对速度为零或绝对加速度为零的点，并且是绝对速度或绝对加速度的出发点。
10.速度和加速度矢量式中的等号，在速度和加速度多边形中是哪一点答：箭头对顶的点。
11.在机构运动分析中应用重合点法的基本原理是什么答：点的复合运动。
12.重合点法在什么倩况下应用答：两个活动构件有相对运动时，求重合点的速度和加速度。
13.应用重合点进行运动分析时，什么情况下有哥氏加速度答：当牵连角速度和重会点间相对速度不等于零时，有哥氏加速度，若其中之一等于零，则哥氏加速度等于零。
大小为： a k B1B2= 2ω2V B1B2方向为：V B1B2的矢量按牵连角速度ω2方向旋转 900。
14.应用重合点法进行运动分析时的步骤是什么答：（1）选择比例尺画机构运动简图。
（2）选运动要素已知多的铰链点为重合点，列速度，加速度矢量方程。
（3）选速度比例尺和速度极点画速度多边形。
（4）选加速度比例尺和加速度极点画加速度多边形图。
（5）回答所提出的问题。
典型例题例3-1 图（a）和（b）分别为移动导杆机构和正切机构的运动简图，其长度比例尺μL＝2 mm/mm。
图中的构件1均为原动件，且已知ω1＝10rad／s 。
试分别求出其全部瞬心点，并用瞬心法分别求出：构件3的速度V3、构件2上速度为零的点I2和构件2的角速度ω2。
解这两个机构均为含有两个移动副的四杆机构，各有六个瞬心点。
但因导路的形状不同，故瞬心点的位置不尽相同。
（1）移动导杆机构其六个瞬心点的位置如图（a）所示。
其中：P14在A点，P12在B点；P23在导路的曲率中心O处（而不是在无穷远处！这点应该注意），P∞34在与导路垂直的无穷远处；根据三心定理，P13在P14和P∞34连线与P12和P23连线的交点处，P24在P14和P12连线与P23和P∞34连线的交点处。
例 3-1 图μL＝2 mm / mm，μv＝0.04 m /s / mm因为构件1的角速度ω1已知，而构件3为平移运动，所以可利用P13求出构件3的速度 v3＝v p13＝ω1L AP13＝ω1AP13μL=10×30×2=600mm／s 方向：向右。
（a）（b）构件2上速度为零的点I2，就是构件 2 与机架 4 的瞬心点 P24（v P24＝0）。
在图示位置上，构件2绕P24（I2）点作瞬时定轴转动，其角速度ω2可通过瞬心点P12的速度v P12求出，即：v P12＝ v B＝ω1L AB＝ω1ABμL＝ 10×22×2 ＝ 440 mm / s ∴ω2＝ v P12 / L I2B＝ v P12 / （ I2B×μL）＝ 440 /（ 20×2） = 11 rad ／s方向：逆时针。
（2）正切机构六个瞬心点的位置如图（b）所示。
请注意利用三心定理求P13和P24 的方法。
构件3的平移速度 v3，可利用瞬心点P13求出v3＝ v P13＝ω1L Ap13＝ω1AP13μL＝ 10×38×2 ＝ 760 mm / s方向：向下。
构件 2上速度为零的点I2，即为瞬心 P24。
由于构件 2与构件 1构成移动副，二者之间没有相对转动，因此ω2＝ω1＝ 10 rad / s 逆时针方向例3-2 在图（a）所示的机构中，已知：L AB＝38mm，L CE＝20mm，L DE = 50mm，x D =150 mm，y D＝60mm；构件1以逆时针等角速度ω1＝20 rad / s转动。
试求出此机构的全部瞬心点，并用向量多边形法求出构件 3 的角速度ω3和角加速度ε3，以及点 E 的速度v E和加速度 a E。
解（1）求速度瞬心P14在A点，P12在B点，P34在 D点，P∞23在与导路 CE 相垂直的无穷远处，这四个瞬心容易求出，如图（a）所示。
根据三心定理，P13既在P14和P34的连线上，又在P12和P ∞23的连线上，因此，过B（P12）点作导路CE的垂线，与AD连线的交点即为P13点；同理，过 D（P34）点作导路 CE 的垂线，与 AB 连线的延长线的交点即为 P24点。
（2）速度分析取长度比例尺μL = 4 mm/mm，按给定条件作出机构运动简图，如图（b）所示。
在此机构中，构件 2 为作平面运动的构件，且运动副 B 点的运动已知，因此，应选B2为动点，动系选在构件 3上。
为求得重合点，需将构件 3 向 B 点扩大，得到与 B2点重合的、属于构件3的牵连运动点B3。
按“重合点法”列出的速度方程式为：→→→v B2 = v B3 + v B2B3方向⊥AB ⊥BD ∥CE大小 L ABω1其中，v B2＝ L ABω1＝ 38×20 ＝ 760 mm / s。
取速度比例尺μv＝ 20 mm / s / mm。
则 v B2的代表线段长度为pb2＝v B2/μv＝760/20＝38mm取速度极点 P 作速度多边形 pb2b3如图（c）所示。
则ω3＝ v B3 / L BD＝ pb3μv/ BDμL＝×20 / 31×4 ＝ rad / s方向：顺时针。
由于滑块2与导杆3之间没有相对转动，因此ω2＝ω3＝ rad / s至此，在构件 3 上已经有了 D 和 B 两个点的速度已知（注意：D为固定铰链，v D ＝0，a D＝0，为运动已知点，这一点易被忽略），所以，可以用影像法来求构件 3上 E 点的速度。
为此，在图（c）中作△pb3e ∽△DBE ，得 e 点，则v E＝ pe μv＝×20 ＝ 230 mm / s（3）加速度分析由于动系（构件 3）绕 D点作定轴转动，所以存在哥氏加速度。
其加速度方程为→→→→→a n B2 = a n B3 + a t B3 + a t B2B3 + a k B2B3方向 B→A B→D ⊥BD ∥CE ⊥CE大小 L ABω21已知已知其中：a n B2＝ L ABω21＝ 38×202＝ 15200 mm / s2a n B3＝ L BDω23＝BDμLω23＝ 31×4×＝ 2620 mm/s 2a k B2B3 ＝ 2ω3v B2B3 ＝ 2ω3b2b3μv＝ 2×××20 ＝ 2484 mm/s2取加速度比例尺μa＝500 mm/s2/mm，选极点p′在图（d）中依次作出上述各已知向量的代表线段。
p′b2′＝ a n B2/ μa＝ 15200 / 500 ＝ 30.4 mmp′n3′＝ a n B3/ μa＝ 2620 / 500 ＝ 5.24 mmk′b2′＝ a k B2B3 3/μa＝ 2484 / 500 ＝ 4.97 mm在此基础上作出加速度多边形，如图（d）所示。
则ε3＝ a t B3 / L BD＝ n3′b3′μa/ BDμL＝ 39×500 / 31×4 ＝ rad/s2 方向：顺时针。
利用影像原理，在图（d）中，连p′b3，作△p′b3′e′∽△DBE ，得 e′点，则 p′e′即为 a E的代表线段，其大小为a E＝ p′e′μa＝ 16×500 ＝ 8000 mm / s2＝ 8 m / s2例 3－3 图（a）所示为一四铰链机构的机构运动简图、速度多边形和加速度多边形，作图的比例尺分别为：μL＝2 mm/mm、μv＝20 mm/s/mm、μa＝200 mm/s2/mm。
已知原动件 1 以匀角速度ω1 = 10 rad / s 顺时针方向转动。
要求：（1）根据两个向量多边形分别列出相应的速度和加速度向量方程，井将各个向量标在向量多边形中相应的代表线段旁边。
（2）求出构件 2 和 3 的角速度ω2 、ω3和角加速度ε2、ε3。
（3）在构件 1、2 和 3 上分别求出速度为 v x＝ 300 mm / s（方向为 p→x ）的点 x1、x2和 x3 。
（4）求出构件 2 上速度为零的点 I2和加速度为零的点 Q2 。
（5）求出 I2点的加速度 a I 2和 Q2 点的速度 v Q2 。
解（ 1）速度和加速度向量方程分别为→→→v c＝ v B＋ v CB→→→→→a n c十 a t c＝ a n B十 a n cB十 a t cB多边形中各线段所代表的向量如图（b）所示。