高三数学复习基础训练题
高三数学基础训练题测试试卷
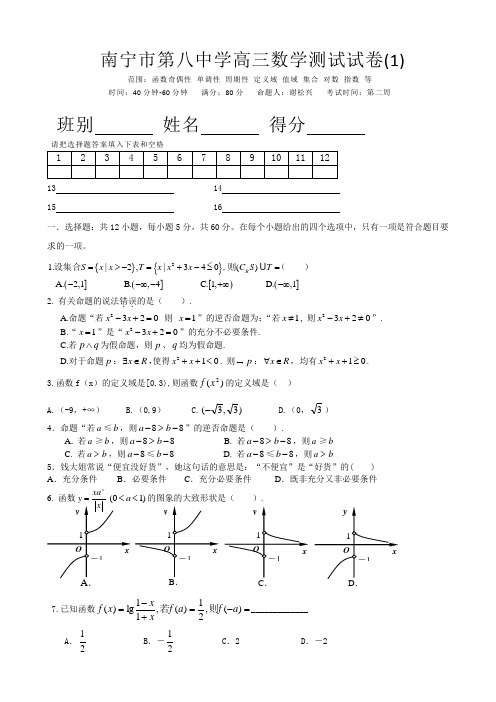
南宁市第八中学高三数学测试试卷(1)范围:函数奇偶性 单调性 周期性 定义域 值域 集合 对数 指数 等 时间:40分钟-60分钟 满分:80分 命题人:谢松兴 考试时间:第二周班别 姓名 得分请把选择题答案填入下表和空格13 14 15 16一.选择题:共12小题,每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
{}{}(](][)(]21.|2,|340() A.2,1 B.,4 C.1, D.,1R S x x T x x x C S T =>-=+-≤=--∞-+∞-∞设集合,则( )2. 有关命题的说法错误..的是( ). A.命题“若2320x x -+= 则 1x =”的逆否命题为:“若1x ≠, 则2320x x -+≠”.B.“1x =”是“2320x x -+=”的充分不必要条件.C.若p q ∧为假命题,则p 、q 均为假命题.D.对于命题p :x R ∃∈,使得210x x ++<. 则⌝p :x R ∀∈, 均有210x x ++≥. 3.函数f (x )的定义域是[0,3),则函数)(2x f 的定义域是( ) A.(-9,+∞) B.(0,9) C.)3,3(- D.(0,3)4.命题“若a ≤b ,则8a ->8b -”的逆否命题是( ).A. 若a ≥b ,则8a ->8b -B. 若8a ->8b -,则a ≥bC. 若a >b ,则8a -≤8b -D. 若8a -≤8b -,则a >b5.钱大姐常说“便宜没好货”,她这句话的意思是:“不便宜”是“好货”的( ) A .充分条件B .必要条件C .充分必要条件D .既非充分又非必要条件x1)<的图象的大致形状是().7.已知函数=-=+-=)(,21)(,11lg )(a f a f x x x f 则若_____________A .21B .-21 C .2 D .-28.函数221()1x f x x -=+, 则(2)1()2f f =__________A .1B .-1C .35D .35-9. 已知函数2(4),()(1)(4)x x f x f x x ⎧<=⎨-≥⎩,那么(5)f 的值为( ).A. 32B. 16C. 8D. 6410.已知定义在R 上的函数()f x ,对任意,x y R ∈满足()()()f x f y f x y +=+,则( ).A .()f x 为奇函数B .()f x 为偶函数C .()f x 既为奇函数又为偶函数D .()f x 既非奇函数又非为偶函数3( )1A.()B.()C. ()D.()sin f x x f x x x f x x f x xx ∞=-==+=11.下列函数中,既是奇函数又在(0,+)内单调递增的函数是12. 现有四个函数①x x y sin ⋅= ②x x y cos ⋅= ③|cos |x x y ⋅= ④xx y 2⋅=的部分图象如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是A .①④②③B . ①④③②C . ④①②③D . ③④②① 二.填空题: 本大题共4小题, 每小题20分, 共20分. 13.f(x)为奇函数且周期T =2,若f( -0.5)=9则f(8.5)=_______ 14.若函数))(12()(a x x xx f -+=为奇函数,则a=15.已知偶函数f (x )在[0,+∞)单调递减,f (2)=0,若f (x ﹣1)>0,则x 的取值范围是 _________()()()()()()()()()()()()()16.R 6,31230343f x f x f x y f x f x f x f x f x x +=-=--=-已知定义在上的函数满足:且是奇函数,给出以下四个命题:是周期函数,关于点,对称,是偶函数,关于直线对称.其中一定是真命题是南宁市第八中学高三数学测试试卷(2)范围:函数图像 对数 指数 等时间:40分钟-60分钟 满分:80分 命题人:许正敏谢松兴 考试时间:第三周班别 姓名 得分请把选择题答案填入下表13 14 15 16一.选择题:共12小题,每小题5分,共60分。
高三数学基础训练题2

高三数学基础训练题(2) 2013/8/16一:选择题(5分一题,每题只有一个正确选项)1.已知集合A ={x |x =a +16,a ∈Z },B ={x |x =b 2-13,b ∈Z },C ={x |x =c 2+16,c ∈Z },则A 、B 、C 之间的关系是________.A .AB =C B .B A C C .B =C AD .B C A2.定义A ⊗B ={z |z =xy +xy,x ∈A ,y ∈B }.设集合A ={0,2},B ={1,2},C ={1},则集合(A ⊗B )⊗C的所有元素之和为________A .6B .8C .10D .183.设函数y =f (x )满足f (x +1)=f (x )+1,则函数y =f (x )与y =x 图象交点的个数可能是________个.A .0B .2C .无数D .0或无数4.已知f (x )=log 3x +2,x ∈[1,9],则函数y =[f (x )]2+f (x 2)的最大值是________.A .3B .8C .13D .185. 已知f (x )=|x |+|x -1|,若g (x )=f (x )-a 的零点个数不为0,则a 的最小值为________.A .1B .2C .3D .-16.已知函数图象C ′与C :y (x +a +1)=ax +a 2+1关于直线y =x 对称,且图象C ′关于 点(2,-3)对称,则a 的值为__________.A .1B .2C .3D .-1 二.填空题(5分一题)7.已知定义在R 上的函数f (x )满足f (x )=-f (x +32),且f (-2)=f (-1)=-1,f (0)=2,f (1)+f (2)+…+f (2009)+f (2010)=________.8.已知函数f (x )是R 上的偶函数,且在(0,+∞)上有f ′(x )>0,若f (-1)=0,那么关于x 的不等式xf (x )<0的解集是________. 三.解答题(每题12分)9.已知:f (x )=log 3x 2+ax +bx ,x ∈(0,+∞),是否存在实数a ,b ,使f (x )同时满足下列三个条件:(1)在(0,1]上是减函数,(2)在[1,+∞)上是增函数,(3)f (x )的最小值是1.若存在,求出a 、b ;若不存在,说明理由.10.已知函数y=f(x)是定义在R上的周期函数,周期T=5,函数y=f(x)(-1≤x≤1)是奇函数,又知y=f(x)在[0,1]上是一次函数,在[1,4]上是二次函数,且在x=2时函数取得最小值-5.(1)证明:f(1)+f(4)=0;(2)求y=f(x),x∈[1,4]的解析式;(3)求y=f(x)在[4,9]上的解析式.11.已知函数f(x)满足f(log a x)=aa2-1(x-x-1),其中a>0且a≠1.(1)对于函数f(x),当x∈(-1,1)时,f(1-m)+f(1-m2)<0,求实数m的集合;(2)x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.12.设函数f (x )=ax 2+bx +c ,且f (1)=-a 2,3a >2c >2b ,求证:(1)a >0且-3<b a <-34;(2)函数f (x )在区间(0,2)内至少有一个零点;(3)设x 1、x 2是函数f (x )的两个零点,则2≤|x 1-x 2|<574.高三数学基础训练题(2)答案解析 2013/8/16一:选择题(5分一题,每题只有一个正确选项)1.已知集合A ={x |x =a +16,a ∈Z },B ={x |x =b 2-13,b ∈Z },C ={x |x =c 2+16,c ∈Z },则A 、B 、C 之间的关系是________.解析:用列举法寻找规律.答案:A B =C2.定义A ⊗B ={z |z =xy +xy,x ∈A ,y ∈B }.设集合A ={0,2},B ={1,2},C ={1},则集合(A ⊗B )⊗C的所有元素之和为________.解析:由题意可求(A ⊗B )中所含的元素有0,4,5,则(A ⊗B )⊗C 中所含的元素有0,8,10,故所有元素之和为18.答案:18由等式x 3+a 1x 2+a 2x +a 3=(x +1)3+b 1(x +1)2+b 2(x +1)+b 3定义一个映射f (a 1,a 2,a 3)=(b 1,b 2,b 3),则f (2,1,-1)=________.解析:由题意知x 3+2x 2+x -1=(x +1)3+b 1(x +1)2+b 2(x +1)+b 3, 令x =-1得:-1=b 3;再令x =0与x =1得⎩⎪⎨⎪⎧-1=1+b 1+b 2+b 33=8+4b 1+2b 2+b 3,解得b 1=-1,b 2=0.答案:(-1,0,-1)3.设函数y =f (x )满足f (x +1)=f (x )+1,则函数y =f (x )与y =x 图象交点的个数可能是________个. 解析:由f (x +1)=f (x )+1可得f (1)=f (0)+1,f (2)=f (0)+2,f (3)=f (0)+3,…本题中如果f (0)=0,那么y =f (x )和y =x 有无数个交点;若f (0)≠0,则y =f (x )和y =x 有零个交点.答案:0或无数 4.已知f (x )=log 3x +2,x ∈[1,9],则函数y =[f (x )]2+f (x 2)的最大值是________.解析:∵函数y =[f (x )]2+f (x 2)的定义域为⎩⎪⎨⎪⎧1≤x ≤9,1≤x 2≤9,∴x ∈[1,3],令log 3x =t ,t ∈[0,1], ∴y =(t +2)2+2t +2=(t +3)2-3,∴当t =1时,y max =13.答案:135. 已知f (x )=|x |+|x -1|,若g (x )=f (x )-a 的零点个数不为0,则a 的最小值为________.解析:作f (x )的图象,如图,g (x )=f (x )-a =0,即f (x )=a ,当a =1时,g (x )有无数个零点;当a >1时,g (x )有2个零点;∴a 的最小值为1.答案:16. (2010年安徽合肥模拟)已知函数图象C ′与C :y (x +a +1)=ax +a 2+1关于直线y =x 对称,且图象C ′关于点(2,-3)对称,则a 的值为__________.解析:∵C ′与C :y (x +a +1)=ax +a 2+1关于直线y =x 对称,∴C ′为x (y +a +1)=ay +a 2+1.整理得,y +1+a =1-ax -a.∵C ′关于点(2,-3)对称,∴a =2.答案:2 二.填空题(5分一题)7.已知定义在R 上的函数f (x )满足f (x )=-f (x +32),且f (-2)=f (-1)=-1,f (0)=2,f (1)+f (2)+…+f (2009)+f (2010)=________.解析:f (x )=-f (x +32)⇒f (x +3)=f (x ),即周期为3,由f (-2)=f (-1)=-1,f (0)=2,所以f (1)=-1,f (2)=-1,f (3)=2,所以f (1)+f (2)+…+f (2009)+f (2010)=f (2008)+f (2009)+f (2010)=f (1)+f (2)+f (3)=0.答案:08.已知函数f (x )是R 上的偶函数,且在(0,+∞)上有f ′(x )>0,若f (-1)=0,那么关于x 的不等式xf (x )<0的解集是________.解析:在(0,+∞)上有f ′(x )>0,则在(0,+∞)上f (x )是增函数,在(-∞,0)上是减函数,又f (x )在R 上是偶函数,且f (-1)=0,∴f (1)=0.从而可知x ∈(-∞,-1)时,f (x )>0;x ∈(-1,0)时,f (x )<0;x ∈(0,1)时,f (x )<0;x ∈(1,+∞)时,f (x )>0.∴不等式的解集为(-∞,-1)∪(0,1)答案:(-∞,-1)∪(0,1).三.解答题(每题12分)9.已知:f (x )=log 3x 2+ax +bx ,x ∈(0,+∞),是否存在实数a ,b ,使f (x )同时满足下列三个条件:(1)在(0,1]上是减函数,(2)在[1,+∞)上是增函数,(3)f (x )的最小值是1.若存在,求出a 、b ;若不存在,说明理由.解:∵f (x )在(0,1]上是减函数,[1,+∞)上是增函数,∴x =1时,f (x )最小,log 31+a +b1=1.即a +b =2.设0<x 1<x 2≤1,则f (x 1)>f (x 2).即x 12+ax 1+b x 1>x 22+ax 2+bx 2恒成立.由此得(x 1-x 2)(x 1x 2-b )x 1x 2>0恒成立.又∵x 1-x 2<0,x 1x 2>0,∴x 1x 2-b <0恒成立,∴b ≥1.设1≤x 3<x 4,则f (x 3)<f (x 4)恒成立.∴(x 3-x 4)(x 3x 4-b )x 3x 4<0恒成立.∵x 3-x 4<0,x 3x 4>0,∴x 3x 4>b 恒成立.∴b ≤1.由b ≥1且b ≤1可知b =1,∴a =1.∴存在a 、b ,使f (x )同时满足三个条件.10.已知函数y =f (x )是定义在R 上的周期函数,周期T =5,函数y =f (x )(-1≤x ≤1)是奇函数,又知y =f (x )在[0,1]上是一次函数,在[1,4]上是二次函数,且在x =2时函数取得最小值-5.(1)证明:f (1)+f (4)=0;(2)求y =f (x ),x ∈[1,4]的解析式;(3)求y =f (x )在[4,9]上的解析式.解:(1)证明:∵f (x )是以5为周期的周期函数,∴f (4)=f (4-5)=f (-1), 又∵y =f (x )(-1≤x ≤1)是奇函数,∴f (1)=-f (-1)=-f (4),∴f (1)+f (4)=0.(2)当x ∈[1,4]时,由题意可设f (x )=a (x -2)2-5(a >0),由f (1)+f (4)=0,得a (1-2)2-5+a (4-2)2-5=0,∴a =2,∴f (x )=2(x -2)2-5(1≤x ≤4).(3)∵y =f (x )(-1≤x ≤1)是奇函数,∴f (0)=0,又知y =f (x )在[0,1]上是一次函数,∴可设f (x )=kx (0≤x ≤1),而f (1)=2(1-2)2-5=-3,∴k =-3,∴当0≤x ≤1时,f (x )=-3x ,从而当-1≤x <0时,f (x )=-f (-x )=-3x ,故-1≤x ≤1时,f (x )=-3x .∴当4≤x ≤6时,有-1≤x -5≤1,∴f (x )=f (x -5)=-3(x -5)=-3x +15.当6<x ≤9时,1<x -5≤4,∴f (x )=f (x -5)=2[(x -5)-2]2-5=2(x -7)2-5.∴f (x )=⎩⎪⎨⎪⎧-3x +15, 4≤x ≤62(x -7)2-5, 6<x ≤9.11.已知函数f (x )满足f (log a x )=a a 2-1(x -x -1),其中a >0且a ≠1.(1)对于函数f (x ),当x ∈(-1,1)时,f (1-m )+f (1-m 2)<0,求实数m 的集合; (2)x ∈(-∞,2)时,f (x )-4的值恒为负数,求a 的取值范围.解:令log a x =t (t ∈R ),则x =a t ,∴f (t )=a a 2-1(a t -a -t ),∴f (x )=a a 2-1(a x -a -x ).∵f (-x )=a a 2-1(a -x -a x )=-f (x ),∴f (x )是R 上的奇函数.当a >1时,a a 2-1>0,a x 是增函数,-a -x 是增函数,∴f (x )是R 上的增函数;当0<a <1,a a 2-1<0,a x 是减函数,-a -x 是减函数,∴f (x )是R 上的增函数.综上所述,a >0且a ≠1时,f (x )是R 上的增函数.(1)由f (1-m )+f (1-m 2)<0有f (1-m )<-f (1-m 2)=f (m 2-1),∴⎩⎪⎨⎪⎧1-m <m 2-1,-1<1-m <1,-1<m 2-1<1.解得m ∈(1,2).(2)∵f (x )是R 上的增函数,∴f (x )-4也是R 上的增函数,由x <2,得f (x )<f (2), ∴f (x )-4<f (2)-4,要使f (x )-4的值恒为负数,只需f (2)-4≤0,即a a 2-1(a 2-a -2)-4≤0,解得2-3≤a ≤2+3, ∴a 的取值范围是2-3≤a ≤2+3且a ≠1.12.设函数f (x )=ax 2+bx +c ,且f (1)=-a 2,3a >2c >2b ,求证:(1)a >0且-3<b a <-34;(2)函数f (x )在区间(0,2)内至少有一个零点;(3)设x 1、x 2是函数f (x )的两个零点,则2≤|x 1-x 2|<574.证明:(1)∵f (1)=a +b +c =-a2,∴3a +2b +2c =0.又3a >2c >2b ,∴3a >0,2b <0,∴a >0,b <0.又2c =-3a -2b ,由3a >2c >2b ,∴3a >-3a -2b >2b .∵a >0,∴-3<b a <-34.(2)∵f (0)=c ,f (2)=4a +2b +c =a -c ,①当c >0时,∵a >0,∴f (0)=c >0且f (1)=-a2<0,∴函数f (x )在区间(0,1)内至少有一个零点.②当c ≤0时,∵a >0,∴f (1)=-a2<0且f (2)=a -c >0,∴函数f (x )在区间(1,2)内至少有一个零点.综合①②得f (x )在(0,2)内至少有一个零点.(3)∵x 1、x 2是函数f (x )的两个零点,则x 1、x 2是方程ax 2+bx +c =0的两个根,∴x 1+x 2=-ba,x 1x 2=c a =-32-b a ,∴|x 1-x 2|=(x 1+x 2)2-4x 1x 2= (-b a )2-4(-32-b a )= (b a +2)2+2.∵-3<b a <-34,∴2≤|x 1-x 2|<574.。
高三数学复习练习题

高三数学复习练习题一、选择题1. 若函数 f(x) = 2x + 5,则 f(3) 的值为:A) 6B) 9C) 11D) 132. 已知函数 f(x) = ax^2 + bx + c 的图像经过点(1, 3),(-2, 2),(0, 1),则 a, b, c 的值分别为:A) a = 2, b = -3, c = 2B) a = 2, b = -2, c = 3C) a = -2, b = 3, c = -2D) a = -2, b = 2, c = -33. 设直线 L1 的方程为 y = 2x + 1,直线 L2 过点(2, 3)且与直线L1 垂直,则直线 L2 的方程为:A) y = -2x - 1B) y = -2x + 7C) y = 1/2x + 4D) y = 1/2x - 14. 已知等差数列 {an} 的公差为 3,若 a1 = 2,an = 20,则该等差数列的项数是:A) 5B) 6C) 7D) 85. 设函数 f(x) = x^2 + bx + c 与 x 轴有两个交点,则 f(x) = 0 的根是:A) 无解B) 一个解C) 两个相等的解D) 两个不等的解二、填空题6. 若 f(x) = x^3 + 2x^2 - 3x + k 与 y 轴交于点(0, 4),则 k 的值为______。
7. 已知等差数列 {an} 的通项公式为 an = 2n - 5,则 a5 = ______。
8. 在平面直角坐标系中,点 A(4,2)和点 B(k,-2)关于 y 轴对称,求 k 的值为______。
9. 若 log2(x^2 - 1) = 3,则 x 的值为______。
10. 函数 f(x) = ax^2 + bx + c 在点(1, 3)处的导数为 2,求 c 的值为______。
11. 已知函数 f(x) = log(2x + a),当 x = 3 时,f(x) = 2,则 a 的值为______。
高三数学复习习题集

高三数学复习习题集一、代数1. 已知函数 f(x) = 2x + 5,求 f(3) 的值。
2. 解方程:2x - 5 = 3x + 4。
3. 化简以下代数式:(a + b)² - (a - b)²。
4. 已知函数 f(x) = 3x² + 2x + 1,求 f(-2) 的值。
5. 解方程组:2x + y = 7x - y = -1二、几何1. 在直角三角形 ABC 中,∠C = 90°,AC = 5 cm,BC = 12 cm,求 AB 的长度。
2. 已知正方形 ABCD 的边长为 6 cm,求对角线 AC 的长度。
3. 在四边形 ABCD 中,已知 AB = 5 cm,BC = 3 cm,CD = 7 cm,求 AD 的长度。
4. 在菱形 ABCD 中,已知 BD = 8 cm,AC = 6 cm,求对角线 AC 的长度。
5. 在等腰梯形 ABCD 中,AB ∥ CD,AB = 8 cm,BC = 6 cm,CD = 14 cm,求AD的长度。
三、概率与统计1. 一副扑克牌中,从中随机取出一张牌,求取到黑牌的概率。
2. 有一袋中装有5个红球,3个蓝球,从中不放回地取2个球,求取到一红一蓝的概率。
3. 一班学生参加考试,成绩的平均值为80分,方差为20。
已知有一位同学得了90分,求该同学的成绩对整体平均值的偏离程度。
4. 一张筛选题调查问卷中,有5个选项供选择,共有100份问卷,每份问卷选择答案时等概率出现在5个选项上,并且相互独立。
求选项A被选择的平均次数。
5. 一组数据为:2,4,6,8,10。
求该组数据的中位数和众数。
四、三角函数1. 已知sinθ = 3/5,求cosθ 的值。
2. 已知 tanA = 3/4,求 sinA 的值。
3. 已知 cosB = 4/5,求 sinB 的值。
4. 已知tanθ = √3,求cotθ 的值。
5. 已知 sinA = 1/2,cosB = 3/5,求 tan(A + B) 的值。
高三一轮数学复习备考试卷归纳

高三一轮数学复习备考试卷归纳高三年级数学复习试题一、选择题:本大题共8小题,每小题5分,共40分..1.若复数的实部与虚部相等,则实数()A(A)(B)(C)(D)2.已知,猜想的表达式为().A.B.C.D.3.等比数列中,,则“”是“”的B(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件4.从甲、乙等名志愿者中选出名,分别从事,,,四项不同的工作,每人承担一项.若甲、乙二人均不能从事工作,则不同的工作分配方案共有B(A)种(B)种(C)种(D)种5.已知定义在上的函数的对称轴为,且当时,.若函数在区间()上有零点,则的值为A(A)或(B)或(C)或(D)或6.已知函数,其中.若对于任意的,都有,则的取值范围是D(A)(B)(C)(D)7.已知函数有且仅有两个不同的零点,,则BA.当时,,B.当时,,C.当时,,D.当时,,8.如图,正方体中,为底面上的动点,于,且,则点的轨迹是A(A)线段(B)圆弧(C)椭圆的一部分(D)抛物线的一部分第Ⅱ卷(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.设等差数列的公差不为,其前项和是.若,,则______.510.的展开式中的系数是.16011.设.若曲线与直线所围成封闭图形的面积为,则______.12.在直角坐标系中,点与点关于原点对称.点在抛物线上,且直线与的斜率之积等于,则______.13.数列的通项公式,前项和为,则___________。
301814.记实数中的_大数为,_小数为.设△的三边边长分别为,且,定义△的倾斜度为(ⅰ)若△为等腰三角形,则______;1(ⅱ)设,则的取值范围是______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题共14分)已知函数.(Ⅰ)当时,求曲线在点处的切线方程;(Ⅱ)讨论的单调性;(III)若存在_大值,且,求的取值范围.(18)(共14分)解:(Ⅰ)当时,..所以.又,所以曲线在点处的切线方程是,即.(Ⅱ)函数的定义域为,.当时,由知恒成立,此时在区间上单调递减.当时,由知恒成立,此时在区间上单调递增.当时,由,得,由,得,此时在区间内单调递增,在区间内单调递减. (III)由(Ⅱ)知函数的定义域为,当或时,在区间上单调,此时函数无_大值.当时,在区间内单调递增,在区间内单调递减,所以当时函数有_大值._大值.因为,所以有,解之得.所以的取值范围是.16.(本小题满分13分)已知函数的一个零点是.(Ⅰ)求实数的值;(Ⅱ)设,求的单调递增区间.(Ⅰ)解:依题意,得,………………1分即,………………3分解得.………………5分(Ⅱ)解:由(Ⅰ)得.………………6分………………7分………………8分………………9分.………………10分由,得,.………………12分所以的单调递增区间为,.………………13分117.(本小题满分13分)已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.(1)求数列{bn}的通项公式bn;(2)设数列{an}的通项an=loga(1+)(其中a0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与logabn+1的大小,并证明你的结论.(1)解:设数列{bn}的公差为d,由题意得,∴bn=3n-2(2)证明:由bn=3n-2知Sn=loga(1+1)+loga(1+)+…+loga(1+)=loga[(1+1)(1+)…(1+)]而logabn+1=loga,于是,比较Sn与logabn+1的大小比较(1+1)(1+)…(1+)与的大小.取n=1,有(1+1)=取n=2,有(1+1)(1+推测:(1+1)(1+)…(1+)(_)①当n=1时,已验证(_)式成立.②假设n=k(k≥1)时(_)式成立,即(1+1)(1+)…(1+)则当n=k+1时,,即当n=k+1时,(_)式成立由①②知,(_)式对任意正整数n都成立.于是,当a1时,Snlogabn+1,当0a1时,snlogabn+1 p=18.(本小题满分13分)已知函数,,其中.(Ⅰ)求的极值;(Ⅱ)若存在区间,使和在区间上具有相同的单调性,求的取值范围.18.(本小题满分13分)(Ⅰ)解:的定义域为,………………1分且.………………2分①当时,,故在上单调递减.从而没有极大值,也没有极小值.………………3分②当时,令,得.和的情况如下:↘↗故的单调减区间为;单调增区间为.从而的极小值为;没有极大值.………………5分(Ⅱ)解:的定义域为,且.………………6分③当时,显然,从而在上单调递增.由(Ⅰ)得,此时在上单调递增,符合题意.………………8分④当时,在上单调递增,在上单调递减,不合题意.……9分⑤当时,令,得.和的情况如下表:↘↗当时,,此时在上单调递增,由于在上单调递减,不合题意.………………11分当时,,此时在上单调递减,由于在上单调递减,符合题意.综上,的取值范围是.………………13分19.(本小题满分14分)如图,椭圆的左焦点为,过点的直线交椭圆于,两点.当直线经过椭圆的一个顶点时,其倾斜角恰为.(Ⅰ)求该椭圆的离心率;(Ⅱ)设线段的中点为,的中垂线与轴和轴分别交于两点.记△的面积为,△(为原点)的面积为,求的取值范围.19.(本小题满分14分)(Ⅰ)解:依题意,当直线经过椭圆的顶点时,其倾斜角为.………………1分设,则.………………2分将代入,解得.………………3分所以椭圆的离心率为.………………4分(Ⅱ)解:由(Ⅰ),椭圆的方程可设为.………………5分设,.依题意,直线不能与轴垂直,故设直线的方程为,将其代入,整理得.………………7分则,,.………………8分因为,所以,.………………9分因为△∽△,所以………………11分.………………13分所以的取值范围是.………………14分(20)(本小题共13分)设是由个有序实数构成的一个数组,记作:.其中称为数组的“元”,称为的下标.如果数组中的每个“元”都是来自数组中不同下标的“元”,则称为的子数组.定义两个数组,的关系数为.(Ⅰ)若,,设是的含有两个“元”的子数组,求的_大值;(Ⅱ)若,,且,为的含有三个“元”的子数组,求的_大值.(20)(共13分)解:(Ⅰ)依据题意,当时,取得_大值为2.(Ⅱ)①当是中的“元”时,由于的三个“元”都相等,及中三个“元”的对称性,可以只计算的_大值,其中.由,得.当且仅当,且时,达到_大值,于是.②当不是中的“元”时,计算的_大值,由于,所以.,当且仅当时,等号成立.即当时,取得_大值,此时.综上所述,的_大值为1.高三数学复习试题整理一、选择题。
人教版新高三数学起始考复习练习题含答案

新高三数学起始考复习练习题1学校:___________姓名:___________班级:___________考号:___________新高三数学起始考复习练习题1学校:___________姓名:___________班级:___________考号:___________一、解答题1.在等差数列{}n a 中,38a =,724a a a =+. (1)求数列{}n a 的通项公式; (2)设1n nb na =,求数列{}n b 的前n 项和n S .2.记n S 为等差数列{}n a 的前n 项和,已知36a =-,728S =-. (1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.3.等差数列{}n a 中,1239a a a ++=,12n n a a +-=. (1)求{}n a 的通项公式; (2)求{}2nn a +的前n 项和nS.4.如图,在四棱锥P ABCD -中,PD ⊥底面ABCD ,底面ABCD 为矩形,E 为PC 的中点,且3PD =,2AD =,4AB =. (1)求证:PA 平面BDE ;(2)若点F 为线段PC 上一点,且AF BD ⊥,求四棱锥F ABCD -的体积.5.如图,已知PA ⊥平面ABCD ,ABCD 为矩形,M N 、分别为AB PC 、的中点,,2,PA AD AB AD ===.(1)求证:MN ∥平面PAD ; (2)求证:面MPC ⊥平面PCD ; (3)求点B 到平面MNC 的距离.6.如图所示,在四棱锥P ABCD -中,四边形ABCD 为矩形,PAD ∆为等腰三角形,APD 90︒∠=,平面PAD ⊥平面ABCD ,且1,2,,AB AD E F ==分别为,PC BD的中点.(1)证明://EF 平面PAD ; (2)证明:平面PDC ⊥平面PAD ; (3)求三棱锥E ABD -的体积.7.已知函数2()cos 2cos f x x x x =+. (I )求()f x 最小正周期; (Ⅱ)求()f x 在闭区间,63ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.8.已知函数())cos()f x x x ωϕωϕ=+++,0,02πωϕ⎛⎫><< ⎪⎝⎭的图像经过点3π⎛⎝且相邻两条对称轴间的距离为π. (1)求函数()f x 的解析式和单调减区间; (2)若将()f x 的图像上所有点的横坐标变为原来的13,纵坐标不变,得到函数()h x 的图像,求函数()h x 在区间,63ππ⎛⎫⎪⎝⎭上的值域.9.在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b 2+c 2-a 2=bc . (1)求角A 的大小;(2)设函数2()sin cos 222x x xf x =,当f (B )取最大值时,判断△ABC 的形状.10.在ABC ∆中,已知角,,A B C 的对边分别为,,a b c ,且cos cos a B b A b c -=+. (1)求角A 的大小;(2)若4a =,b c +=ABC ∆的面积.11.在ABC ∆中,已知()cos cos 2sin cos 0B A A C +-=. (1)求角C 的余弦值;(2)若BC =,AB 边上的中线CD =,求ABC ∆的面积.12.已知函数()222cos 1f x x x =--,x ∈R(1)求函数()f x 的最小正周期;(2)设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且c =()0f C =,()sin sin 2sin 2C B A A +-=,求ABC ∆的面积.13.已知椭圆C :()222210x y a b a b+=>>的右焦点为()1,0F ,点()2,0A 在椭圆C 上,过F 点的直线l 与椭圆C 交于不同两点M 、N . (1)求椭圆C 的方程;(2)设直线l 斜率为1,求线段MN 的长;(3)设线段MN 的垂直平分线交y 轴于点()00,p y ,求0y 的取值范围.14.已知椭圆C 的焦点为1F (-和2F ,长轴长为6,设直线y=x+2交椭圆C 于A 、B 两点.求:(1)椭圆C 的标准方程; (2)弦AB 的中点坐标及弦长.15.已知椭圆22221(0)x y E a b a b =+=>>CH 在椭圆上.(1)求椭圆E 的方程;(2)①直线:(0)l y kx m k =+≠与椭圆E 交于两点,A B .求AB 的弦长;②若直线l 与椭圆E 交于两点,A B .且线段AB 的垂直平分线经过点10,2⎛⎫⎪⎝⎭,求AOB∆的面积的最大值.(O 为原点)16.已知椭圆C :22221(0)x y a b a b+=>>的短轴长为12,直线l :()1y k x =-与椭圆C 交于不同的两点M ,N ,A 为椭圆C 的左顶点.(1)求椭圆C 的标准方程;(2)当AMN ∆的面积为7时,求l 的方程.一、解答题1.在等差数列{}n a 中,38a =,724a a a =+. (1)求数列{}n a 的通项公式; (2)设1n nb na =,求数列{}n b 的前n 项和n S .【答案】(1)22n a n =+(2)22nn +【解析】 【分析】(1)利用等差数列的性质可求出1,a d ,进而可求出{}n a 的通项公式;(2)()1121n n b na n n ==+11121n n ⎛⎫=- ⎪+⎝⎭,由裂项相消求和法可求出n S . 【详解】解:(1)设等差数列{}n a 的公差为d ,则()11n a a n d +-=.因为37248,a a a a =⎧⎨=+⎩所以11112863a d a d a d a d +=⎧⎨+=+++⎩,解得14a =,2d =,所以数列{}n a 的通项公式为22n a n =+. (2)由题意知()1121n n b na n n ==+11121n n ⎛⎫=- ⎪+⎝⎭, 所以111111122231n S n n ⎛⎫=-+-++-= ⎪+⎝⎭1112122n n n ⎛⎫-= ⎪++⎝⎭. 【点睛】本题考查了等差数列的通项公式的求法,考查了利用裂项相消求数列的前n 项和,属于基础题.2.记n S 为等差数列{}n a 的前n 项和,已知36a =-,728S =-. (1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.【答案】(1)212n a n =-;(2)2212111( 5.5)4n S n n n =-=--,30-. 【解析】 【分析】(1)先求出公差d 和首项1a ,可得通项公式;(2)由(1)可得前n 项和n S ,由二次函数性质可得最小值(只要注意n 取正整数). 【详解】(1)设{}n a 的公差为d ,由题意得126a d +=-,17(3)28a d +=-, 解得110a =-,2d =.所以{}n a 的通项公式为212n a n =-. (2)由(1)得22(10212)12111( 5.5)24n n n S n n n -+-==-=--因为*n N ∈所以当5n =或6n =时,n S 取得最小值,最小值为-30. 【点睛】本题考查等差数列的通项公式和前n 项和公式,方法叫基本量法. 3.等差数列{}n a 中,1239a a a ++=,12n n a a +-=. (1)求{}n a 的通项公式; (2)求{}2nn a +的前n 项和nS.【答案】(1)21n a n =-;(2)2122n n S n +=+-.【解析】 【分析】(1)由12n n a a +-=得出等差数列{}n a 的公差为2,再利用1239a a a ++=,得出1a 的值,再利用等差数列的通项公式求出数列{}n a 的通项公式; (2)求出数列{}2nn a +的通项公式,再利用分组求和法求出nS.s【详解】(1)12n n a a +-=Q ,∴等差数列{}n a 的公差为2,()()1231111222369a a a a a a a ∴++=++++⨯=+=,解得11a =,因此,()12121n a n n =+-=-; (2)()2212nnn a n ∴+=-+,()()()()123123252212nn S n ⎡⎤∴=+++++++-+⎣⎦L()()123135212222nn =++++-+++++⎡⎤⎣⎦L L()()2121212122212nn n n n+-+-=+=+--,因此,2122n n S n +=+-.【点睛】本题考查等差数列的通项与分组求和法,对于等差数列通项,一般利用首项和公差建立方程组求解,对于等差与等比相加所构成的新数列,一般利用分组求和法进行求和,考查计算能力,属于基础题。
高三数学复习练习题及答案x

停课辅导期间数学专用材料一、集合与简易逻辑1.已知集合A={x| -2≤x ≤7 }, B={x|m+1<x <2m -1},若A ∪B=A ,B≠∅,则函数m 的取值范围是____ A .-3≤m ≤4 B .-3<m <4 C .2<m <4 D . m ≤42.已知集合A={x x 2+(p+2)x+1=0, p ∈R },若A ∩R +=φ。
则实数P 的取值范围为 。
3.命题“若△ABC 有一内角为3π,则△ABC 的三内角成等差数列”的逆命题是( )A .与原命题真值相异B .与原命题的否命题真值相异C .与原命题的逆否命题的真值不同D .与原命题真值相同【参考答案】1. P ∈(-4,+∞) 2. D 3. D二、函数: 研究函数的问题一定要注意定义域优先的原则。
4.判断函数f(x)=(x -1)x x-+11的奇偶性为_______________5.函数y=3472+++kx kx kx 的定义域是一切实数,则实数k 的取值范围是_________6.设函数f(x)=132-+x x ,函数y=g(x)的图象与函数y=f -1(x+1)的图象关于直线y=x 对称,则g (3)=_____________7. 方程log 2(9x -1-5)-log 2(3 x -1-2)-2=0的解集为______________【参考答案】4. k ⎪⎭⎫⎢⎣⎡∈43,0 5. 非奇非偶 6. g ( 3 ) = 27 7. {x x = 2}三、数列8.x=ab 是a 、x 、b 成等比数列的( ) A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件 9.已知数列{a n }的前n 项和S n =a n -1(a 0,≠∈a R ),则数列{a n}___________ A.一定是A ²P B.一定是G ²PC.或者是A ²P 或者是G ²PD.既非等差数列又非等比数列10.A ²P {a n }中, a 1=25, S 17=S 9,则该数列的前____项之和最大,其最大值为_____。
高三数学复习基础题试卷

一、选择题(每题5分,共50分)1. 若函数$f(x) = x^3 - 3x^2 + 4$的图像关于点$(1,1)$对称,则$f(0)$的值为:A. 0B. 1C. 2D. 32. 已知等差数列$\{a_n\}$的前$n$项和为$S_n$,若$S_3 = 12$,$S_5 = 30$,则$a_1$的值为:A. 2B. 3C. 4D. 53. 下列函数中,在区间$(0, +\infty)$上单调递减的是:A. $y = 2^x$B. $y = \log_2 x$C. $y = x^2$D. $y = \sqrt{x}$4. 在平面直角坐标系中,点$A(2,3)$关于直线$x+y=1$的对称点为$B$,则$|AB|$的值为:A. $\sqrt{10}$B. $2\sqrt{10}$C. $\sqrt{5}$D. $2\sqrt{5}$5. 若$\sin A = \frac{1}{2}$,$\cos B = \frac{\sqrt{3}}{2}$,则$\sin(A+B)$的值为:A. $\frac{1}{2}$B. $\frac{\sqrt{3}}{2}$C.$\frac{1}{2}\sqrt{3}$ D. $\frac{\sqrt{3}}{2}\sqrt{3}$6. 若等比数列$\{a_n\}$的公比为$q$,且$a_1 + a_2 + a_3 = 9$,$a_4 + a_5 + a_6 = 27$,则$q$的值为:A. 1B. 3C. 2D. $\frac{1}{3}$7. 在$\triangle ABC$中,$a=3$,$b=4$,$c=5$,则$\cos A$的值为:A. $\frac{1}{2}$B. $\frac{1}{3}$C. $\frac{2}{3}$D.$\frac{3}{4}$8. 下列不等式中,正确的是:A. $x^2 + 1 > 0$B. $\sqrt{x} > x$C. $\log_2 x > x$D.$\frac{1}{x} > x$9. 已知函数$f(x) = x^3 - 3x^2 + 4$,则$f'(x)$的值为:A. $3x^2 - 6x$B. $3x^2 - 6$C. $3x^2 + 6x$D. $3x^2 + 6$10. 在$\triangle ABC$中,若$A:B:C=2:3:4$,则$\cos A$的值为:A. $\frac{1}{2}$B. $\frac{\sqrt{3}}{2}$C. $\frac{1}{3}$D. $\frac{2}{3}$二、填空题(每题5分,共50分)1. 函数$f(x) = ax^2 + bx + c$的图像开口向上,且顶点坐标为$(1,2)$,则$a$、$b$、$c$的值分别为______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年高三数学基础训练题(1)1.设集合}4|||{<=x x A ,}034|{2>+-=x x x B ,则集合{A x x ∈|且B A x I ∉}= 。
2.下列说法中:(1)若22y x =,则y x =;(2)等比数列是递增数列的一个必要条件是公比大于1;(3)2≥a 的否定是;(4)若3>+b a ,则1>a 或2>b 。
其中不正确的有 。
3.设集合}2|||{<-=a x x A ,}1212|{<+-=x x x B ,且B A ⊆,则实数a 的取值范围是 。
4.已知二次函数)0(3)(2≠-+=a bx ax x f 满足)4()2(f f =,则)6(f = 。
5.计算:3121log 24lg539--⎛⎫- ⎪⎝⎭= 。
6.已知函数1)(2++=x bax x f 的值域是[-1,4 ],则b a 2的值是 。
7.若函数3)2(2+++=x a x y ,][b a x ,∈的图象关于直线1=x 对称,则=b 。
8.函数)(x f y =的图象与x x g )41()(=的图象关于直线y=x 对称,那么)2(2x x f -的单调减区间是 。
9.函数1)(---=a x x a x f 的反函数)(1x f -的图象的对称中心是(-1,3),则实数a = 。
10.)(x f y =是R 上的减函数,且)(x f y =的图象经过点A (0,1)和B (3,-1),则不等式1|)1(|<+x f 的解集为 。
11.已知函数⎩⎨⎧>≤+=0,log 0,1)(2x x x x x f ,若1))((0-=x f f ,则0x 的取值范围是 .12.已知函数),1,1(,5sin )(-∈+=x x x x f 如果,0)1()1(2<-+-a f a f 则a 的取值范围是____。
13.关于x 的方程aa x -+=535有负根,则a 的取值范围是 。
14.已知函数)(x f 满足:对任意实数21,x x ,当21x x <时,有)()(21x f x f <,且)()()(2121x f x f x x f ⋅=+写出满足上述条件的一个函数: 。
15.定义在区间)1,1(-内的函数)(x f 满足)1lg ()()(2+=--x x f x f ,则)(x f = 。
16.已知函数x x f 2log )(=,2)(y x y x F +=,,则)1),41((f F 等于 。
17.对任意]1,1[-∈a ,函数a x a x x f 24)4()(2-+-+=的值恒大于零,那么x 的取值范围是 。
18.若函数⎭⎬⎫⎩⎨⎧+=x x x f 241log ,log 3min )(,其中{}q p ,min 表示q p ,两者中的较小者,则2)(<x f 的解为 。
19.已知函数f (x )=l og 2(x +1),若-1<a <b <c ,且abc ≠0,则a a f )(、bb f )(、c c f )(的大小关系是 。
20.若方程042)4(4=+⋅++x x a 有解,则实数a 的取值范围是 . 21.等差数列{}n a 前n 项之和为n S ,若31710a a -=,则19S 的值为 。
22.已知数列{}n a 中,3,6011+=-=+n n a a a ,那么||||||3021a a a +++Λ的值为 。
23.已知等差数列{}n a 前n 项的和n s ,若22,m n s m s n =则65a a 的值是 。
24.已知一个等差数列前五项的和是120,后五项的和是180,又各项之和是360,则此数列共有项。
25.设等比数列{}n a 中,每项均是正数,且8165=a a ,则 =+++1032313log log log a a a Λ 。
26.一个项数为偶数的等比数列,首项是1,且所有奇数项之和是85,所有偶数项之和是170,则此数列共有 项。
27.设331)(+=xx f ,利用课本中推导等差数列前n 项和的公式的方法,可求得: )13()12()11()0()10()11()12(f f f f f f f ++++++-+-+-ΛΛ的值为28.已知数列{}n a 的通项12)12(-⋅+=n n n a ,前n 项和为n S ,则n S = 。
29.数列Λ,841,631,421,2112222++++前n 项的和等于 。
30.数列{}n a 中,)2(112,1,21121≥+===-+n a a a a a n n n ,则其通项公式为=n a 。
2007年高三数学基础训练题(2)31.函数x y 2sin =的图象按向量平移后,所得函数的解析式是12cos +=x y ,则=(只需写出满足条件的一个向量) 32.函数)632cos(32sin)(π-+=x x x f 的图象相邻的两条对称轴间的距离是 。
33.函数)42sin(π+-=x y 的单调增区间是 。
34.已知41)4tan(,52)tan(=-=+πββα,则=+)4tan(πα 。
35.οοοο42tan 18tan 342tan 18tan ++=_______________。
36.函数)10cos(5)20sin(300-++=x x y 的最大值是 。
37.已知,54cos ),0,2(=-∈x x π则=x 2tan 。
38.已知tan 2,α=则=+ααα2sin cos sin __ __。
39.如果4π≤x ,那么函数x x x f sin cos )(2+=的最小值是 。
40.函数2cos sin +=x xy 的最大值为 。
41.已知1||||||=+==,则||-= 。
42.若非零向量,满足||||-=+,则α与β所成角的大小为 。
43.与向量(12,5)a =r平行的单位向量是_____________。
44.在直角坐标平面上,向量)1,4(=OA ,向量)3,2(-=OB ,两向量在直线l 上的正射影长度相等,则直线l 的斜率为45.设平面向量=(-2,1),=(1,λ),若a 与b 的夹角为钝角,则λ的取值范围是 。
46.已知向量)sin 2,cos 2(),2,2(),0,2(αα===,则向量,的夹角范围是 。
47.将函数x y 2=的图象按向量 →a 平移后得到62+=x y 的图象,给出以下四个命题:①→a 的坐标可以是)0,3(-; ②→a 的坐标可以是)0,3(-和)6,0(; ③→a 的坐标可以是)6,0(; ④→a 的坐标可以有无数种情况。
上述说法正确的是 。
48.某人在静水中游泳的速度为4千米/时,水的流向是由西向东,水流速度为22千米/时,则此人必须朝与水流方向成__*___度角时,才能沿正北方向前进 。
49.在△ABC 中,BC =1,∠B =3π,当△ABC 的面积为3时,=∠C tan 。
50.若△ABC 三边长AB =5,BC =7,AC =8,则BC AB ⋅等于 。
51.函数)1(122)(2->+++=x x x x x f 的图象的最低点的坐标是 。
52.已知正实数y x ,满足121=+yx ,则y x 2+的最小值为_________________。
53.设实数y x b a ,,,满足3,12222=+=+y x b a , 则by ax +的取值范围为____________。
54.04<<-k 是函数12--=kx kx y 恒为负值的___________条件。
55.不等式)(062R x x x ∈<--的解集是 。
56. 若不等式20x mx nx a++≥+的解集为{|31,2}x x x -≤<-≥或,则n m a ++=57.关于x 的不等式|log ||log |2121x x x x +<-的解集为 。
58.若1>a ,10<<b ,且1)12(log >-x b a,则实数x 的范围是 .59.若不等式na n n1)1(2)1(+-+<-对于任意正整数n 恒成立,则实数a 的取值范围是60.实系数一元二次方程022=+-b ax x 的两根分别在区间()1,0和()2,1上,则b a 32+的取值范围是2007年高三数学基础训练题(3)61.从1,3,5,7中任取2个数字,从0,2,4,6,8中任取2个数字,组成没有重复数字的四位数,其中能被5整除的四位数共有 个。
(用数字作答)62.某小组有4个男同学和3个女同学,从这小组中选取4人去完成三项不同的工作,其中女同学至少二人,每项工作至少一人,则不同选派方法的种数为 。
63.现有8名青年,其中有5名青年能胜任英语翻译工作,4名青年能胜任电脑软件设计工作,(其中有一人两项工作都能胜任),现要从中选派5名青年承担一项任务,其中3人从事英语翻译工作,2人从事软件设计工作,则不同的选法种数为 。
64.6人站成一排照相,其中甲,乙,丙三人要站在一起,并且乙,丙要站在甲的两边,则不同的排法种数共有种。
65. 现有6个参加兴趣小组的名额,分给4个班级,每班至少一个,则不同的分配方案共有_____种。
66.把6本书平均分给甲、乙、丙3个人,每人2本,有 种分法,若平均分成3份,每份2本,有 种分法。
67.从集合}20,,3,2,1{Λ中选3个不同的数,使这3个数成递增的等差数列,则这样的数列共有_______组。
68.从6双不同的手套中任取4只,其中恰有一双配对的取法有_______种。
69.从6个正方形拼成的右图的12个顶点中任取3个顶点作为一组,其中可以构成三角形的组数为 。
70、某幢楼从二楼到三楼的楼梯共10级,上楼可以一步上一级,也可以一步上两级,若规定从二楼到三楼用8步走完,则上楼梯的方法有 。
71. 46)1()1(x x -+ 展开式中,3x 的系数是 。
72.设函数6)52()(+=x x f ,则导函数)(/x f 中的3x 的系数是73.42)2(-+x x 展开式中2x 项的系数是 。
74.55443322105)12(x a x a x a x a x a a x +++++=-,则||||||||||54321a a a a a ++++= 。
75.若1001002210100)1()1()1()12(-++-+-+=+x a x a x a a x Λ,则99531a a a a ++++Λ= 。
76.坛中有红球6个,白球4个,今从中任取3个,至少取到一个白球的概率为______.77.从1,2,…..,9这九个数中,随机取2个不同的数,则这两个数的和为偶数的概率是 。
