电磁场作业答案
作业06_第四章时变电磁场

作业06_第四章时变电磁场-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第四章 时变电磁场1. 在无源的自由空间中,已知磁场强度597.210cos(31010)A/m y H t z e -=⨯⨯-,求位移电流密度。
2. 在电导率310S/m γ=、介电常数06εε=的导电媒质中,已知电场强度58210sin(10)x E t e -=⨯π,计算在92.510s t -=⨯时刻,媒质中的传导电流密度c J 和位移电流密度d J 。
3. 在无源区域,已知电磁场的电场强度90.1cos(6.281020.9)V/m x E t z e =⨯-,求空间任一点的磁场强度H 和磁感应强度B 。
4. 一个同轴圆柱型电容器,其内、外半径分别为11cm r =、24cm r =,长度0.5m l =,极板间介质介电常数为04ε,极板间接交流电源,电压为V u t =π。
求极板间任意点的位移电流密度。
5.一个球形电容器的内、外半径分别为a 和b ,内、外导体间材料的介电常数为ε,电导率为γ,在内、外导体间加低频电压sin m u U t ω=。
求内、外导体间的全电流。
6. 已知自由空间中电磁波的两个场量表达式为 20002)V/m x E =t z e ωβ-, 5.32sin()A/m y H =t z e ωβ-式中,20MHz f =,0.42rad/m β==。
求(1)瞬时坡印亭矢量;(2)平均坡印亭矢量;(3)流入图示的平行六面体(长为2m ,横截面积为0.5m 2)中的净瞬时功率。
7. 一个平行板电容器的极板为圆形,极板面积为S ,极板间距离为d ,介质的介电常数和电导率分别为ε,γ,试问:(1). 当极板间电压为直流电压U 时,求电容器内任一点的坡印亭矢量;(2). 如果电容器极板间的电压为工频交流电压cos314u t =,求电容器内任一点的坡印亭矢量及电容器的有功功率和无功功率。
电磁场与电磁波:第三章作业答案
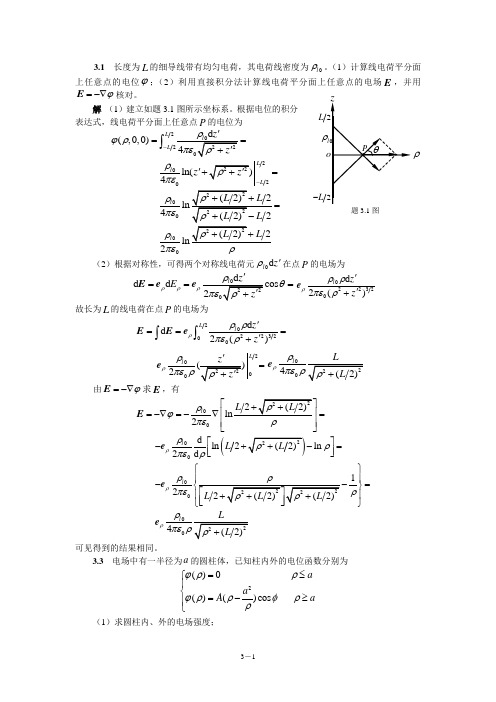
3.1 长度为L 的细导线带有均匀电荷,其电荷线密度为0l ρ。
(1)计算线电荷平分面上任意点的电位ϕ;(2)利用直接积分法计算线电荷平分面上任意点的电场E ,并用ϕ=-∇E 核对。
解 (1)建立如题3.1图所示坐标系。
根据电位的积分表达式,线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε (2)根据对称性,可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ,有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。
3.3 电场中有一半径为a 的圆柱体,已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩(1)求圆柱内、外的电场强度;L L -ρρ题3.1图(2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。
解 (1)由ϕ=-∇E ,可得到a ρ<时, 0ϕ=-∇=Ea ρ>时, ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e(2)该圆柱体为等位体,所以是由导体制成的,其表面有电荷分布,电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷,下列几个函数中哪些是可能的电位的解? (1)cosh y e x -; (2)x e y cos -;(3)cos sin e x x (4)z y x sin sin sin 。
工程电磁场课后答案1(完整)

0.29K
7401
VOH 74LS00
2.9.1 驱动: 负载: 拉电流: 灌电流: 扇出:
2.9.2 VOH > VIH VOL < VIL IOH > IIH IOL > IIL
第三章 组合逻辑电路分析与设计
3.1.2证明(C)A ABC ACD C D E
A ACD (C D )E
(b) _______ ________ _______ ________
A B C D C D A D
( A B)(C D) (C D)( A D)
(C D)( A B D)
AC AD BC BD CD D
AC BC D
3.2.1展开最小项(a) L A(B C) A BC A(B B)(C C) ( A A)BC
mi
3.2.2 (a)
______________________
___________________
AC ABC BC ABC AC BC BC ABC
灌电流多余: (8-4.8)/0.4=8
N=min(8,17)=8
2.4.5
__________________ ____ ____
L AB BC D E
AB BC D E
2.4.6 RP计算 (1)拉电流时
VCC R IP IH 74LS 00 VOH 7401
D=0 选中低位片1;D=1 选中高位片2
01234
56789
1
0
1
A B C D
0
2
0
4.2.9 7位数字译码显示电路
高等电磁场理论习题解答(作业)

⾼等电磁场理论习题解答(作业)第⼀章基本电磁理论1-1 利⽤Fourier 变换, 由时域形式的Maxwell ⽅程导出其频域形式。
(作1-2—1-3)解:付⽒变换和付⽒逆变换分别为:dt e t f F t j ?∞∞-=ωω)()(ωωπωd e F t f tj ?∞∞--=)(21)( 麦⽒⽅程:t D J H ??+=??ρρρtB E ??-=??ρρ0=??B ρρ=??D ρ对第⼀个⽅程进⾏付⽒变换:),(),(),ωωωr H dt e t r H dt e t r H t j tj ρρρρρρ??=??=??=∞∞-∞∞-(左端),(),(),(),(]),(),[ωωωωωωωr D j r J dte t r D j r J dt e t t r D t r J t j tj ρρρρρρρρρρρρ+=+=??+=??∞∞-∞∞-(右端(时谐电磁场) =??∴),(ωr H ρρ),(),(ωωωr D j r J ρρρρ+同理可得:()()ωωω,,r B j r H ??ρρ-=??()0,=??ωr B ρ()()ωρω,,r r D ?ρ?=??上⾯四式即为麦式⽅程的频域形式。
1-2 设各向异性介质的介电常数为=300420270εε当外加电场强度为 (1) 01E x e E =;(2)02E y e E =;(3) 03E z e E =;(4) )2(04y x E e e E +=;(5))2(05y x E e e E +=求出产⽣的电通密度。
(作1-6)解:()),(,t r E t r D ?Θ?=ε=333231232221131211εεεεεεεεεz y x D D D 即z y x E E E 将E 分别代⼊,得:=??=??????????027003000420270000111E E D D D z y x εε )?2?7(001y x E D +=ε?=??=??????????042003000420270000322E E D D D z y x εε )?4?2(002y x E D +=ε? ????=??=??????????300003000420270000333E E D D D z y x εε z E D ?3003ε=? ??==010110230004202700000444E E E D D D z y x εε )?10?11(004y x E D +=ε? ==08160230004202700000555E E E D D D z y x εε )?8?16(005y x E D +=ε? 1-3 设各向异性介质的介电常数为=4222422240εε试求:(1) 当外加电场强度)(0z y x E e e e E ++=时,产⽣的电通密度D ;(2) 若要求产⽣的电通密度004E x εe D =,需要的外加电场强度E 。
2020年西南大学作业答案[1081]电磁场与电磁波
![2020年西南大学作业答案[1081]电磁场与电磁波](https://img.taocdn.com/s3/m/8fbe720671fe910ef02df85e.png)
.
能速与相速相等
.
能速高于相速
.
不定
.
能速低于相速
判断题
21、在导电媒质中,电流从一个电极流向另一个电极,我们把两个电极之间导电媒质中的电流与两极间的电压的比值称
为导电媒质的电阻。( )
.
A.√
.
B.×
22、麦克斯韦对电磁场理论重大贡献的核心是位移电流的假说。( )
.
A.√
.
B.×
23、电位参考点的选取,当电荷分布在无限区域内时,通常选择无穷远点为参考点。( )
.
A.√
.
B.×
41、把场点与源点之间的距离远小于波长λ的区域称为远区。( )
.
A.√
.
B.×
42、孤立导体的电容可认为是把双导体系中一个导体移至无限远处,以无限远处为参考点,则两导体间的电位差就是另
一导体的电位。( )
.
A.√
.
B.×
43、当频率趋近于 TE10 模的截止频率时,因λ/(2a)≈1 传输功率将趋于零。( )
.
A.√
.
B.×
47、有关垂直极化和平行极化的公式有许多重要应用,并且如果把介电常数换成复介电常数,这些公式也可以推广到有耗
媒质。( )
.
A.√
.
B.×
48、在等相位面上电场和磁场均等幅,且任一时刻、任一处能量密度相等。( )
.
A.√
.
B.×
49、驻波可以传输能量。( )
.
A.√
.
B.×
50、在两种媒质分界面上 E 的切向分量总是不连续的。( )
.
A.√
.
B.×
37、静电场是非保守场。( )
工程电磁场作业合辑

d2
2、2
y
图2-29 具有两层介质的平行板电容器
答案:
T2-22 答:欧姆定律 : J E ,其物理意义是电流密度和电场强度成正比,说明电场 是推动大量电荷定向运动从而形成电流的原因,是导电媒质的基本构成关系。
T2-27 答:电流连续性方程由电荷守恒定律推导而来。
积分形式:
J
T2-27 电流连续性方程的特点是什么?
E2-29 一个有两层介质 1 、 2 的平行板电容器,两层介质都具有电导率,分别 为1 和 2 ,参见图 2.29。当外加电压为0 时,求通过电容器的电流和两层介质 分界面上的自由电荷面密度。
x
d1
1、1
E dl 0 :静电场沿任何一个封闭路径的标量线积分为 0。 l
第二讲 作业
E2-5 一个球形电荷分布 f 0 1 r2 b2 存在于区域 0 r b
中,这一电荷分布被一内半径为 ri b ,外半径为 r0 的导体球壳所包 围。计算各处的 E 。
E2-14
已知在园柱形区域( 0
a
)内的电场强度 E
E4-15. 均匀分布面电荷 s 的球,半径为 a ,以角速度 绕其一直径旋转,求磁 矩。
E4-17. 半径为 a 的磁介质球,具有磁化强度为:M ez (Az2 B) ,求磁化电流和 磁荷。
答案
T4-16. 标量磁位m , H m 只有在没有传导电流的区域中成立。用m 来表 征磁场的性质和分布,简化了静磁场的分析和计算,最终可化为求解满足一定边 界条件的拉普拉斯方程,计算方法和求解静电场的方法保持了一致性。其缺点在 于求解的局限性仅限于传导电流为零的区域。
槽绝缘的盖板。槽的电压为 0 ,而盖板的电压为0 ,求槽内的电位函数。
第十二章 电磁感应电磁场(二)作业答案

一. 选择题[ A ] 1 (基础训练4)、两根很长的平行直导线,其间距离为a ,与电源组成闭合回路,如图12-18.已知导线上的电流为I ,在保持I 不变的情况下,若将导线间的距离增大,则空间的(A) 总磁能将增大. (B) 总磁能将减少.(C) 总磁能将保持不变.(D) 总磁能的变化不能确定【解答】212m W L I =,距离增大,φ增大,L 增大, I 不变,m W 增大。
[ D ]2(基础训练7)、如图12-21所示.一电荷为q 的点电荷,以匀角速度作圆周运动,圆周的半径为R .设t = 0 时q 所在点的坐标为x 0 = R ,y 0 = 0 ,以i 、j分别表示x 轴和y 轴上的单位矢量,则圆心处O 点的位移电流密度为: (A)i t R q ωωsin 42π (B) j t Rq ωωcos 42π (C) k R q 24πω (D) )cos (sin 42j t i t Rq ωωω-π 图 12-21 【解答】设在0—t 的时间内,点电荷转过的角度为ωt ,此时,点电荷在O 点产生的电位移矢量为0D E ε=, ()222000cos sin ,444rqR q q E e ti tj R R R R ωωπεπεπε=-=-=-+ 式中的r e 表示从O 点指向点电荷q 的单位矢量。
()2sin cos 4d dD q J ti tj dt R ωωωπ∴==-。
[ C ] 3 (基础训练8)、 如图12-22,平板电容器(忽略边缘效应)充电时,沿环路L 1的磁场强度H 的环流与沿环路L 2的磁场强度H 的环流两者,必有: (A) >'⎰⋅1d L l H ⎰⋅'2d L l H . (B) ='⎰⋅1d L l H ⎰⋅'2d L l H .(C) <'⎰⋅1d L l H ⎰⋅'2d L l H. (D) 0d 1='⎰⋅L l H .【解答】全电流是连续的,即位移电流和传导电流大小相等、方向相同。
电磁感应与电磁场作业纸答案

第10章 电磁感应与电磁场一、选择题1、一导体圆线圈在均匀磁场中运动,在下列情况下,会产生感应电流的是( D )A .线圈沿磁场方向平移B .线圈以自身直径为轴转动,轴与磁场方向平行C .线圈沿垂直于磁场方向平移D .线圈以自身直径为轴转动,轴与磁场方向垂直 2、将磁铁从迅速插入和缓慢插入金属环,若两种情况下磁铁的起始位置和终了位置均相同,则关于两种情况环中的感应电动势和感生电量的说法正确的是( C )A .感应电动势不同;感生电量也不同B .感应电动势相同,感生电量也相同;C .感应电动势不同,感生电量相同;D .感应电动势相同,感生电量不同. 3、如图所示,A 为闭合的导体环,B 为有间隙的导体环,则当磁铁分别移近A 和B 时,关于A 和B 的运动描述正确的是( A )A .A 环被排斥,B 环不动 B .A 环被吸引,B 环不动C .A 环被吸引,B 环被吸引D .A 环被排斥,B 环被排斥4、在感应电场中电磁感应定律可写成⎰-=•L K dtdl d E φ ,式中K E 为感应电场的电场强度。
此式表明( D )A. 闭合曲线L 上K E处处相等 B. 感应电场是保守力场。
C .感应电场的电力线不是闭合曲线D .在感应电场中不能像对静电场那样引入电势的概念 5、关于长直螺线管线圈的自感,以下说法正确的是( D ) A 、螺线管中通有的电流越大,自感也越大; B 、螺线管横截面通过的磁通量越大,自感也越大C 、在单位长度匝数不变的情况下,真空中螺线管长度越长,自感就越大;D 、在单位长度匝数不变的情况下,真空中螺线管体积越大,自感就越大6、如图,矩形区域为均匀稳恒磁场,半圆形闭合导线回路在纸面内绕轴O 作逆时钟方向匀角速度转动,O 点是圆心且恰好落在磁场的边缘上,半圆形闭合导线完全在磁场外时开始计时。
图(A)--(D)的t -ε函数图像中哪一条属于半圆形导线回路中产生的感应电动势(A )7、如图所示的闭合线圈abcda 均位于匀强磁场中,当磁场不断减小时,回路中不产生感应电流的是( B )8、如图所示,两个圆环形导体a 、b 互相垂直地放置,且圆心重合,当它们的电流I 1、和I 2同时发生变化时,则( D )(A) a 导体产生自感电流,b 导体产生互感电流(B) 两导体同时产生自感电流和互感电流(C) b 导体产生自感电流,a 导体产生互感电流;(D)两导体只产生自感电流,不产生互感电流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.6在圆柱坐标系中电荷分布为ρ={①r/a,r≤a ②0,r>a ,r为场点到z轴的距离,a为常数。
求电场强度。
解:电场强度只有沿r方向分量,选取长度为l的圆柱
(1)时
代入(1)得:
时
代入(1)得:
2.7在直角坐标系中电荷分布为ρ(x,y,z)={①ρ0 ∣x∣≤a②0 ∣x∣>a求电场强度。
解:电场与,均无关,电场强度只有沿方向分量,
(1)时
代入(1)得:
时为有限值所以
时
代入(1)得:
在处连续,所以
2.16已知电场强度为E=3x+4y-5z,试求点(0,0,0)与点(1,2,1)之间的电压解:
2.26两同心导体球壳半径分别为a、b,两导体之间有两层介质,介电常数分别为ε1、ε2,介质界面半径为c,内外导体球壳电位分别为V和0,求两导体球壳之间的电场和球壳上的电荷面密度,以及介质分界面上的束缚电荷面密
度。
解:两球壳之间电介质不带电电位分布满足拉普拉斯方程
选取球坐标则有:
代入边界条件
由上式可得:
在介质与导体分界面上的电荷密度
介质分界面上没有自由电荷感应电荷面密度为:
2.32同轴圆柱形电容器内、外半径分别为a、b,导体之间一半填充介电常数为ε1的介质,另一半填充介电常数为ε2的介质,如图所示,当电压为V时,求电容器中的电场和电荷分布。
解:电介质不带电电位分布满足拉普拉斯方程
电场强度只有沿r方向分量,选取圆柱坐标则有:
又,则
又因为两极板之间的电压是V
在介质与导体分界面上的电荷密度
在侧
在侧
2.43内外半径分别为a、b的导电球壳内距球心为d(d<a)处有一点电荷q,当(1)导电球壳电位为0;(2)导电球壳电位为v;(3)导电球壳上的总电量为Q;分别求导电球壳内外的电位分布。
解:(1)导体球壳电位为0,点电荷在球壳内所以球壳外电位均为零
在导体球外距离球心O为f
的镜像位置B处放置一镜像
电荷q’要保持导体球壳C处
电位为零则有
则
,
导体球内距离球心r处的电位为:
其中
(2)因为球壳是一等位体,球壳内的电位分布应在第一步计算基础上加上球壳电位V。
球壳内的电位分布为:
球壳外的电位分布为球心一镜像电荷产
生的电位,并且在求外壳产生的电位为
V ,则有:
球壳外电位分布为:
(3)当导体球壳上总电量为Q时,导体球壳的电位为:
球壳内的电位分布为:
球壳外电位分布为:
3.7同轴电缆内导体半径为10cm,外导体半径为40cm,内外导体之间有两层煤质。
内层从10cm到20cm,煤质的参数为σ1=50μS/m,εrl=2;外层从20cm 到40cm,煤质的参数为σ2=100μS/m,εr2=
4.求⑴每区域单位长度的电容;⑵每区域单位长度的电导;⑶单位长度的总电容;⑷单位长度的总电导。
(1)每个区域单位长度的电容:
(2)应用静电比拟可得
每个区域单位长度的电导:
(3)两电容是串联,单位长度总电容为:
(4)利用静电比拟,单位长度总电导为:
3-13 圆球形电容器内导体半径为a,外导体内半径为c,内外导体之间填充两层介电常数分别为,电导分别为的非理想介质,两层非理想介质分界面半径为b,如果内外
导体间电压为V,求电容器中的电场及界面上的电荷密度。
解:由于圆球形电容器内填充两层非理想介质,有电流流过,设电流为I。
在圆球形电容器内取一半径为的球面,流过此球面的电流密度为,则由得
或
电场强度为
电压为
由此求出电流与电压的关系后,电场为
内导体表面的电荷密度为
外导体内表面的电荷密度为
媒质分界面的(驻立)电荷密度为
4-4、真空中导线绕成的回路形状如图所示,电流为I。
求半圆中心处的磁场。
(c)
题4-4 图
解:设垂直于纸面向内的方向为z方向。
由例4-2知,半径为a的半圆中心处的磁场为
(1)因为在载流长直导线的延长线上磁场为零,因此
(2)由例4-1知,本题半无限长的载流长直导线在距离为a处的磁场为
因此本题磁场为半圆环的磁场与两半无限长的直导线的磁场之和
(3)本题磁场为电流方向相反的两不同半径的半圆环的磁场之和,即
4-18、已知真空中位于xoy平面的表面电流为,求磁感应强度。
解:由于在无限大的平面上有均匀电流,因此产生匀强磁场。
磁场方向在y方向,跨电流面取一长为L的矩形回路,利用安培环路定律得
因此
写成矢量形式为
4-20、壁很薄的、半径为的导体圆筒导体圆筒上的电流面密度上的电流在圆筒外产生
的磁场为,求导体圆筒上的电流面密度。
解:当导体圆筒上的电流面密度为,由安培环路定律
当为以导体圆筒上的电流面密度的轴线为中心,半径为的圆时
因此
5.10已知在空气中
在圆球坐标系中,求。
解:
由
5.11已知在空气中
在圆球坐标系中,求。
解:在圆球坐标系中
利用关系式得
上式代入得
6-4.均匀平面电磁波在真空中沿=1/(+)方向传播, =10,求,(y,z,t),,(y,z,t),
解:则k=2π,
==10
=1/Z*
=/24π(-)
(y,z,t)= 10cos(2πc/λt-(π)(y+z))
(y,z,t)= 1/12π(-)cos(2πc/λt-(π)(y+z))
==(5/6π)(+)
6-8、求=100kHz,1MHz,100MHz,10GHz时电磁波在铝(σ=3.6*10/欧米, ε=1, μ
=1)中的集肤深度.
解:δ=1/=
=100kHz,δ=2.6526*10 m
=1MHz, δ= 8.3882*10m
=100MHz, δ= 8.3882*10m
=10GHz, δ= 8.3882*10m
6-13、设,其中σ=0.5*10(1/欧米),求在的群速和相速。
解:。
