合肥工业大学计算方法复化梯形公式实验
复化梯形公式和复化Simson公式

数值计算方法上机题目3一、计算定积分的近似值:要求:(1)若用复化梯形公式和复化Simpson 公式计算,要求误差限71021-⨯=ε,分别利用他们的余项估计对每种算法做出步长的事前估计; (2)分别利用复化梯形公式和复化Simpson 公式计算定积分;(3)将计算结果与精确解比较,并比较两种算法的计算量。
1.复化梯形公式程序:程序1(求f (x )的n 阶导数:syms xf=x*exp(x) %定义函数f (x )n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2:clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x),换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))'%因fminbnd()函数求的是表达式的最小值,且要求表达式带引号,故取负号,以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点,也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0 for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示:用复化梯形算法计算的结果 Tn= 7.3891等分数 n=7019已知值与计算值的误差 R= 2.8300e-0082. Simpson公式程序:程序1:(求f(x)的n阶导数):syms xf=x*exp(x) %定义函数f(x)n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2:clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x),换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数,输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd()函数求的是表达式的最小值,且要求表达式带引号,故取负号,一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点,也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值,故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示:用Simpson公式计算的结果 Sn= 7.3891等分数 n=24已知值与计算值的误差 R= 2.7284e-008用复化梯形公式计算的结果为:7.3891,与精确解的误差为:2.8300e-008。
复化梯形公式求积分

武汉工程大学计算机科学与工程学院计算方法》实验报告日期:年月日实验内容设计分析复化数值积分:将区间[a,b]n 等分,取等距节点x i a ih,iba0,1,2,..., n, hn 由定积分的区间可加性,有nf x dxxix i 1f x dx在每个小区间上利用梯形积分公式有x ii f x dx x i 1 h f x i 1 f x i 2i 1 ih n1T n f a f b 2 f x i一般记 2 i1 称做n+1 点复化梯形积分公式。
数学公式:b h n1f xdx f a f b 2 f x ia 2 i1算法描述:i1Step1:输入a,b 和正整数n;Step2:置h=(b-a)/n;Step3:F=f(a)+f(b);l=0;Step4:对j=1,2,⋯,n 循环执行5;Step5:置x=a+jh; l+=f(x);Step6:置T=h(F+2l)/2 Step7:输出T;程序源代码:#include<iostream>#include<math.h>using namespacestd;<<endl; cout<<" 请输入把 0 到 1 的范围几等分?int m1; cin>>m1;EchelonIntegral(m1); cout<<endl; char answer1;cout<<" 是否要继续求该算法? (y/n)"<<"\t"; cin>>answer1;while(answer1=='y'){cout<<"请输入把 0到 1的范围几等分? "<<"\t"; cin>>m1;EchelonIntegral(m1); //3. 直线求积分; cout<<endl;cout<<" 是否要继续求该算法? (y/n)"<<"\t"; cin>>answer1; }cout<<endl;}cout<<"用梯形积分公式求积分1/(1+pow(sin(x),2))的值测试用例实验总结复化数值积分就是为了减少数值积分的误差,可以把积分区间分成若干小区间,在每个小区间上采取低阶数值积分公式,然后把这些小区间上的数值积分结果加起来作为函数在整个区间上的近似,类似于分段差值。
复化梯形公式求积分-推荐下载
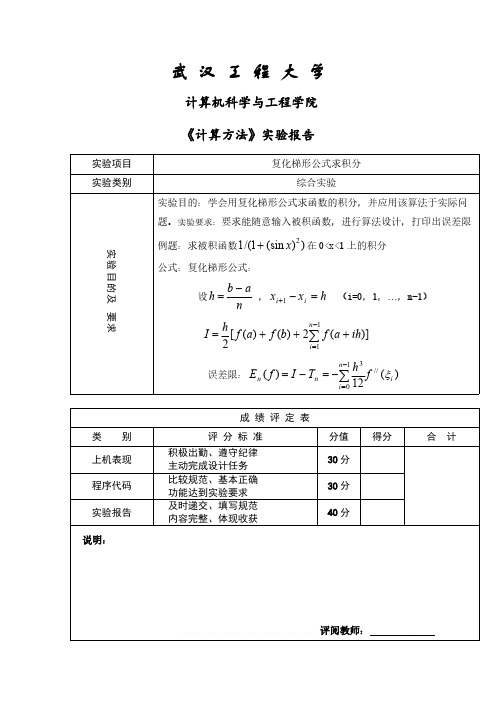
武汉工程大学计算机科学与工程学院《计算方法》实验报告实验项目复化梯形公式求积分实验类别综合实验实验目的及要求实验目的:学会用复化梯形公式求函数的积分,并应用该算法于实际问题。
实验要求:要求能随意输入被积函数,进行算法设计,打印出误差限例题:求被积函数在0<x<1上的积分))(sin1/(12x+公式:复化梯形公式:设,(i=0,1,…,n-1)nabh-=hxx ii=-+1])(2)()([211∑-=+++=niihafbfafhI误差限:)(12)(//13ininnfhTIfEξ∑-=-=-=成绩评定表类别评分标准分值得分合计上机表现积极出勤、遵守纪律主动完成设计任务30分程序代码比较规范、基本正确功能达到实验要求30分实验报告及时递交、填写规范内容完整、体现收获40分说明:评阅教师:日 期: 年 月 日实 验 内 容设计分析复化数值积分:将区间[a,b]n 等分,取等距节点n ab h n i ih a x i -==+=,,...,2,1,0,由定积分的区间可加性,有()()dxx f dx x f bani x x ii ⎰∑⎰=-=11在每一个小区间上利用梯形积分公式有()()()[]i i x x x f x f hdx x f ii +≈-⎰-112一般记()()()⎥⎦⎤⎢⎣⎡++=∑-=1122n i i n x f b f a f h T 称做n+1点复化梯形积分公式。
数学公式:()()()()⎥⎦⎤⎢⎣⎡++≈∑⎰-=1122n i i bax f b f a f h dx x f 算法描述:Step1:输入a,b 和正整数n ;Step2:置h=(b-a)/n;Step3:F=f(a)+f(b);l=0;Step4:对j=1,2,…,n 循环执行5;Step5:置x=a+jh; l+=f(x);Step6:置T=h(F+2l)/2Step7:输出T;程序源代码:#include<iostream>#include<math.h>using namespace std;double f(double x)//求函数的值;{return1/(1+pow(sin(x),2.0));}void EchelonIntegral(int n)//梯形积分{double y=0;double h=(1.0-0.0)/n;for(int i=0;i<=n;i++){double a=0.0+i*h,b=0.0+(i+1)*h;y=y+h*(f(a)+f(b))/2.0;}cout<<"对应所求的梯形求积分为"<<y<<endl;double En=0.0;double mid=(0.0+1.0)/2.0;double x=mid,p=2*sin(2*x)*sin(2*x)*(1+sin(x)*sin(x))-2*cos(2*x)*pow(1+sin(x)*sin(x),2);double f2d=p/pow(1+sin(x)*sin(x),2);for(i=0;i<n;i++){En=En+pow(h,3)/12.0*f2d;}cout<<"误差为"<<En<<endl;}/*void ParabolicIntegral(int n)//抛物线积分{double y=0;double t=(1.0-0.0)/n;for(int i=0;i<n;i++){double a=0.0+i*t,b=0.0+(i+1)*t;y=y+t*(f(a)+f(b)+4*f((a+b)/2.0))/6.0;}cout<<"对应所求的抛物线求积分为"<<y<<endl;}*/void main(){cout<<"*********************用梯形积分公式求积分1/(1+pow(sin(x),2))的值****************"<<endl;cout<<"请输入把0到1的范围几等分?"<<"\t";int m1;cin>>m1;EchelonIntegral(m1);cout<<endl;char answer1;cout<<"是否要继续求该算法?(y/n)"<<"\t";cin>>answer1;while(answer1=='y'){cout<<"请输入把0到1的范围几等分?"<<"\t";cin>>m1;EchelonIntegral(m1);//3.直线求积分;cout<<endl;cout<<"是否要继续求该算法?(y/n)"<<"\t";cin>>answer1;}cout<<endl;}计算机科学与工程学院测试用例计算机科学与工程学院实验总结复化数值积分就是为了减少数值积分的误差,可以把积分区间分成若干小区间,在每个小区间上采取低阶数值积分公式,然后把这些小区间上的数值积分结果加起来作为函数在整个区间上的近似,类似于分段差值。
合肥工业大学计算方法复化梯形公式实验

《计算方法》实验报告学号 姓名 班级 实验项目名称 ■、实验名称 实验二数值积分 实验二 数值积分二、实验目的: (1) (2) (3) (4) 熟悉复化梯形方法、复化 Simpson 方法、梯形递推算法、龙贝格算法; 能编程实现复化梯形方法、复化 Simpson 方法、梯形递推算法、龙贝格算法; 理解并掌握自适应算法和收敛加速算法的基本思想;分析实验结果体会各种方法的精确度,建立计算机求解定积分问题的感性认识 三、实验内容及要求 (1) 设计复化梯形公式求积算法,编制并调试相应的函数子程序 (2) 设计复化辛浦生求积算法,编制并调试相应的函数子程序 1 sin x (3)用龙贝格算法计算 曲d x 0x 输入:积分区间,误差限 输出:序列Tn ,Sn ,Cn,Rn 及积分结果(参考书本 P81的表2-5) 取 n=2, 4, 8, 16,精确解为 0.9460831 四、实验原理及算法描述 在许多实际问题中,常常需要计算定积分 b f (x)dx 的值。
根据微积分学基本定理,若被积函 a 数f(x)在区间[a,b ]上连续,只要能找到 f(x)的一个原函数 F(x),便可利用牛顿 -莱布尼兹公式 b f (x) F(b) F(a)求得积分值。
a 但是在实际使用中,往往遇到如下困难,而不能使用牛顿 -莱布尼兹公式。
找不到用初等函数表示的原函数 虽然找到了原函数,但因表达式过于复杂而不便计算 f(x)是由测量或计算得到的表格函数由于以上种种困难,有必要研究积分的数值计算问题。
bb 利用插值多项式P n (x)f (x)则积分 f (x)dx 转化为P n (x)dx ,显然易算。
a a插值型求积公式。
最简单的插值型求积公式是梯形公式和 Simpson 公式,。
当求积结点提供较多,可以分段使用少结点的梯形公式和Simpson 公式,并称为复化梯形公式、复化 Simpson 公式。
如步长未知,可以通过误差限的控制用区间逐次分半的策略自动选取步长的方法称自适应算法。
用复合梯形求积公式求积实验报告

用复合梯形求积公式求积实验报告学院:计算机学院班级:信计0902班姓名:***学号:**********1、实验目的1)观察复化梯形公式和复化辛普森公式随区间数n 增加各自误差的减少规律;研究广义积分的数值计算如何将其转化为普通积分,再由已有数值积分方法进行计算;2)利用复化梯形公式和复化辛普森公式计算定积分,编程实现。
2、实验内容分别用复化梯形公式和复化辛普森公式计算定积分,研究随着n 增加各自误差的减少规律dx e I x ⎰+=201,取n=2,4,8,16,精确值为I=4.006994。
3、实验原理原理:将区间[a,b]等分成N 个子区间[x(k),x(k+1)](k=0,1,…..,N -1),h=(b-a )/N ,在每个子区间[x(k),x(k+1)]上使用体形公式,可求得结果。
4、设计思想用上述的的公式来计算dx x x I ⎰=10ln ,然后再将积分区间[0,1]进行n 等分,得到n 个小区间[x i ,x i+1](i=0,1,2,…,n-1),每个小区间的长度为h=(b-a)/n,其中x i =a+i*h 。
按∑⎰-=++==101)]()([2)(n i i i ba x f x f h dx x f T ∑-=++=10)()]()([2n i i x f h b f a f h 进行计算。
5、程序框图6、对应程序#include<iostream.h>#include<math.h>double fun1(double a,double h,int n){int i;double sum=0,m;for(i=1;i<=n-1;i++){m=a+i*h;if(m==0)continue;sum=sum+sqrt(m)*log(m);}return sum;}double get(double a){if(a==0)a=0.00001;return sqrt(a)*log(a);}void main(){double a=0,b=1;int n;while(1){cout<<"请输入要等分的子区间个数(n>0):";cin>>n;double h;double T,f0,f1,f2;h=(b-a)/n;f0=get(a);f1=fun1(a,h,n);f2=get(b);T=h/2*(f0+2*f1+f2);cout<<"步长h为:"<<h<<endl;cout<<"复化梯形公式计算结果T="<<T<<endl;}}7、实验结果8、实验体会通过本次实验我熟悉了用复化梯形公式求数值积分的全过程,并更加熟悉的掌握了复化梯形公式原理。
合工大计算方法实验报告

《计算方法》试验报告班级:学号:姓名:实验一、牛顿下山法1 实验目的(1)熟悉非线性方程求根简单迭代法,牛顿迭代及牛顿下山法 (2)能编程实现简单迭代法,牛顿迭代及牛顿下山法 (3)认识选择迭代格式的重要性 (4) 对迭代速度建立感性的认识;分析实验结果体会初值对迭代的影响2 实验内容(1)用牛顿下山法解方程013=--x x (初值为0.6)输入:初值,误差限,迭代最大次数,下山最大次数输出:近似根各步下山因子(2)设方程f(x)=x 3- 3x –1=0 有三个实根 x *1=1.8793 , x *2=-0.34727 ,x *3=-1.53209现采用下面六种不同计算格式,求 f(x)=0的根 x *1 或x *2 x = 213xx +; x = 313-x ;x = 313+x ; x = 312-x ;x = x13+;x = x - ()1133123---x x x输入:初值,误差限,迭代最大次数输出:近似根、实际迭代次数 3 算法基本原理求非线性方程组的解是科学计算常遇到的问题,有很多实际背景.各种算法层出不穷,其中迭代是主流算法。
只有建立有效的迭代格式,迭代数列才可以收敛于所求的根。
因此设计算法之前,对于一般迭代进行收敛性的判断是至关重要的。
牛顿法也叫切线法,是迭代算法中典型方法,只要初值选取适当,在单根附近,牛顿法收敛速度很快,初值对于牛顿迭代 至关重要。
当初值选取不当可以采用牛顿下山算法进行纠正。
一般迭代:)(1k k x x φ=+ 0)()(=⇔=x f x x φ 牛顿公式:)()(1k k k k x f x f x x '-=+ 牛顿下山公式:)()(1k k k k x f x f x x '-=+λ图3.1一般迭代算法流程图 下山因子 ,,,,322121211=λ 下山条件|)(||)(|1k k x f x f <+4 算法描述一般迭代算法见流程图牛顿下山算法见流程图:5、代码:#include <iostream>#include <fstream>#include <cmath>using namespace std;class srrt{private:int n;double *a, *xr, *xi;图3.2牛顿下山算法流程图⇐⇐⇐⇐srrt (int nn){n = nn;a = new double[n+1]; //动态分配内存xr = new double[n];xi = new double[n];}void input (); //由文件读入代数方程系数void srrt_root (); //执行牛顿下山法void output (); //输出根到文件并显示~srrt (){ delete [] a, xr, xi; }};void srrt::input () //由文件读入代数方程系数{int i;char str1[20];cout <<"\n输入文件名: ";cin >>str1;ifstream fin (str1);if (!fin){ cout <<"\n不能打开这个文件" <<str1 <<endl; exit(1); } for (i=n; i>=0; i--) fin >>a[i]; //读入代数方程系数fin.close ();}void srrt::srrt_root () //执行牛顿下山法{int m,i,jt,k,is,it;double t,x,y,x1,y1,dx,dy,p,q,w,dd,dc,c;double g,u,v,pq,g1,u1,v1;m=n;while ((m>0)&&(fabs(a[m])+1.0==1.0)) m=m-1;if (m<=0){cout <<"\n程序工作失败!" <<endl;return;}for (i=0; i<=m; i++) a[i]=a[i]/a[m];for (i=0; i<=m/2; i++){w=a[i]; a[i]=a[m-i]; a[m-i]=w;k=m; is=0; w=1.0;jt=1;while (jt==1){pq=fabs(a[k]);while (pq<1.0e-12){xr[k-1]=0.0; xi[k-1]=0.0; k=k-1;if (k==1){xr[0]=-a[1]*w/a[0]; xi[0]=0.0;return;}pq=fabs(a[k]);}q=log(pq); q=q/(1.0*k); q=exp(q);p=q; w=w*p;for (i=1; i<=k; i++){ a[i]=a[i]/q; q=q*p; }x=0.0001; x1=x; y=0.2; y1=y; dx=1.0;g=1.0e+37;l40:u=a[0]; v=0.0;for (i=1; i<=k; i++){p=u*x1; q=v*y1;pq=(u+v)*(x1+y1);u=p-q+a[i]; v=pq-p-q;}g1=u*u+v*v;if (g1>=g){if (is!=0){it=1;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}else{it=1;while (it==1){t=t/1.67; it=0;x1=x-t*dx;y1=y-t*dy;if (k>=50){p=sqrt(x1*x1+y1*y1);q=exp(85.0/k);if (p>=q) it=1;}}if (t>=1.0e-03) goto l40;if (g>1.0e-18){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}}if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{g=g1; x=x1; y=y1; is=0;if (g<=1.0e-22){if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{u1=k*a[0]; v1=0.0;for (i=2; i<=k; i++){p=u1*x; q=v1*y; pq=(u1+v1)*(x+y);u1=p-q+(k-i+1)*a[i-1];v1=pq-p-q;}p=u1*u1+v1*v1;if (p<=1.0e-20){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{dx=(u*u1+v*v1)/p;dy=(u1*v-v1*u)/p;t=1.0+4.0/k;it=1;while (it==1){t=t/1.67; it=0;x1=x-t*dx;y1=y-t*dy;if (k>=50){p=sqrt(x1*x1+y1*y1);q=exp(85.0/k);if (p>=q) it=1;}}if (t>=1.0e-03) goto l40;if (g>1.0e-18){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}}}if (k==1) jt=0;else jt=1;}}void srrt::output () //输出根到文件并显示{int k;char str2[20];cout <<"\n输出文件名: ";cin >>str2;ofstream fout (str2);if (!fout){ cout <<"\n不能打开这个文件" <<str2 <<endl; exit(1); } for (k=0; k<n; k++){fout <<xr[k] <<" " <<xi[k] <<endl;cout <<xr[k] <<" +j " <<xi[k] <<endl;}fout.close ();}void main () //主函数{srrt root(6);root.input (); //由文件读入代数方程系数root.srrt_root (); //执行牛顿下山法root.output (); //输出根到文件并显示}6、输入输出输出结果如下:7、分析体会牛顿下山法作为计算方法课程中重要的知识点,在看书学习时较易大致理解其思路,但上级编写代码时却是有难度的。
利用复化梯形公式、复化simpson 公式计算积分

1、运用复化梯形公式、复化simpson公式计算积分
2、比较计算误差与实际误差
实验原理(算法流程图或者含注释旳源代码)
取n=2,3,…,10分别运用复化梯形公式、复化simpson公式计算积分 ,并与真值进行比较,并画出计算误差与实际误差之间旳曲线。
运用复化梯形公式旳程序代码如下:
function f=fx(x)
functionf=fx1(x)
f=x.^4;
a=0;%积分下线
b=1;%积分上线
T=[];%用来装不同n值所计算出旳成果
forn=2:10
h=(b-a)/(2*n);%步长
x=zeros(1,2*n+1);%给节点定初值
for i=1:2*n+1
x(i)=a+(i-1)*h;%给节点赋值
end
y=x.^4;%给相应节点处旳函数值赋值
实
验
结
果
分
析
及
心
得
体
会
上图是运用复化梯形公式所画出旳误差。其中:红线是计算误差,‘*’号是实际误差。-0.0017是计算误差。0.0417、0.0185、0.0104、0.00670.0046、0.0034、0.0026、0.0021、0.0017是n值分别为2到10旳实际误差。
上图是运用复化simpson公式所画出旳误差。其中:红线是计算误差,‘*’号是实际误差。
t=0;
for i=1:n
t=t+h/3*(y(2*i-1)+4*y(2*i)+y(2*i+1));%运用复化simpson公式求值
end
T=[T,t];%把不同n值所计算出旳成果装入T中
end
选用复合梯形公式-复合Simpson公式-计算

数值分析实验 三班级:10信计2班 学号:59 姓名:王志桃 分数一·问题提出:选用复合梯形公式,复合Simpson 公式,计算(1) I =dx x ⎰-4102sin 4 ()5343916.1≈I(2) I = dx x x⎰1sin ()9460831.0,1)0(≈=I f(3) I = dx xe x⎰+1024(4) I = ()dx x x ⎰++10211ln二·实验要求:1.编制数值积分算法的程序2.分别用两种算法计算同一个积分,并比较计算结果3.分别取不同步长()/ a b h -=n ,试比较计算结果(如n = 10, 20等)4.给定精度要求ε,试用变步长算法,确定最佳步长三·实验流程图:复化梯形公式:输入 端点 a , b 正整数 n直接计算TN=h/2*[f(a)+2∑f(x k )+f(b)] k=1,2…,n-1输出 定积分近似值TN复化Simpson 公式输入 端点 a , b 正整数 n输出 定积分近似值SN(1) 置h=(b-a)/(2n)(2) F0=f(a)+f(b) , F1=0 , F2=0(3) 对j=1,2,…,2n-1循环执行步4到步5(4) 置x=a+jh(5) 如果j 是偶数,则F2=F2+f(x),否则F1=F1+f(x)(6) 置SN=h(F0+4F1+2F2)/3(7) 输出SN,停机四·源程序:#include<iostream>#include<math.h>using namespace std;#define n 20//此为步长double f1(double x){double y;y=sqrt(4-sin(x)*sin(x));return y;}double f2(double x){if(x==0)return 1;double y;y=sin(x)/x;return y;}double f3(double x){double y;y=exp(x)/(4+x*x);return y;}double f4(double x){double y;y=log(1+x)/(1+x*x);return y;}int main(){int j;double e=0.000001,h,F0,F1,F2,a,b,x,S;cout<<"利用复化Simpson公式求积分"<<endl;//1a=0;b=0.25*3.141592;h=(b-a)/(2*n);F0=f1(a)+f1(b);F1=F2=0;for(j=1;j<2*n;j++){x=a+j*h;if(j%2==0)F2=F2+f1(x);elseF1=F1+f1(x);}S=((F0+F1*4+F2*2)*h)/3;cout<<"第一个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//2a=0;b=1;h=(b-a)/(2*n);F0=f2(a)+f2(b);F1=F2=0;for(j=1;j<2*n;j++){x=a+j*h;if(j%2==0)F2=F2+f2(x);elseF1=F1+f2(x);}S=(F0+F1*4+F2*2)*h/3;cout<<"第二个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//3a=0;b=1;h=(b-a)/(2*n);F0=f3(a)+f3(b);F1=F2=0;for(j=1;j<2*n;j++){x=a+j*h;if(j%2==0)F2=F2+f3(x);elseF1=F1+f3(x);}S=(F0+F1*4+F2*2)*h/3;cout<<"第三个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//4a=0;b=1;h=(b-a)/(2*n);F0=f4(a)+f4(b);F1=F2=0;for(j=1;j<2*n;j++){x=a+j*h;if(j%2==0)F2=F2+f4(x);elseF1=F1+f4(x);}S=(F0+F1*4+F2*2)*h/3;cout<<"第四个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl<<endl;cout<<"利用复化梯形公式求积分"<<endl;//1a=0;b=0.25*3.141592;h=(b-a)/n;F0=f1(a)+f1(b);F1=0;for(j=1;j<n;j++){x=a+j*h;F1=F1+f1(x);}S=((F0+F1*2)*h)/2;cout<<"第一个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//2a=0;b=1;h=(b-a)/n;F0=f2(a)+f2(b);F1=0;for(j=1;j<n;j++){x=a+j*h;F1=F1+f2(x);}S=((F0+F1*2)*h)/2;cout<<"第二个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//3a=0;b=1;h=(b-a)/n;F0=f3(a)+f3(b);F1=0;for(j=1;j<n;j++){x=a+j*h;F1=F1+f3(x);}S=((F0+F1*2)*h)/2;cout<<"第三个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//4a=0;b=1;h=(b-a)/n;F0=f4(a)+f4(b);F1=0;for(j=1;j<n;j++){x=a+j*h;F1=F1+f4(x);}S=((F0+F1*2)*h)/2;cout<<"第四个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;return 0;}五.实验结果六.实验心得:通过本次实验,我掌握了求数值积分的各种方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cin>>x>>y>>z;
cout<<"根据龙贝格算法求出的精确值为:"<<longbeige(x, y, z)<<endl;
cout<<"K"<<" "<<"T"<<" "<<"S"<<" "<<"C"<<" "<<"R"<<endl;
cout<<"0"<<" "<<tixing(0, 1, 1)<<endl;
复化梯形公式
复化Simpson公式
梯形递推公式
加权平均公式:
龙贝格算法大大加快了误差收敛的速度,由梯形序列O(h2)提高到龙贝格序列的O(h8)
五、程序代码及实验结果
1.主程序
intmain()
{
//cout << longbeige(0, 1, 0.0000001);
cout<<"请输入你的区间和误差限度:"<<endl;
(1)找不到用初等函数表示的原函数
(2)虽然找到了原函数,但因表达式过于复杂而不便计算
(3)f(x)是由测量或计算得到的表格函数
由于以上种种困难,有必要研究积分的数值计算问题。
利用插值多项式 则积分 转化为 ,显然易算。 称为插值型求积公式。最简单的插值型求积公式是梯形公式和Simpson公式,。当求积结点提供较多,可以分段使用少结点的梯形公式和Simpson公式,并称为复化梯形公式、复化Simpson公式。如步长未知,可以通过误差限的控制用区间逐次分半的策略自动选取步长的方法称自适应算法。梯形递推公式给出了区间分半前后的递推关系。由梯形递推公式求得梯形序列,相邻序列值作线性组合得Simpson序列, Simpson序列作线性组合得柯特斯序列, 柯特斯序列作线性组合的龙贝格序列。若|R2-R1|<,则输出R2;否则…依此类推。如此加工数据的过程叫龙贝格算法,如下图所示:
(4)分析实验结果体会各种方法的精确度,建立计算机求解定积分问题的感性认识
三、实验内容及要求
(1)设计复化梯形公式求积算法,编制并调试相应的函数子程序
(2)设计复化辛浦生求积算法,编制并调试相应的函数子程序
(3)用龙贝格算法计算
输入:积分区间,误差限
输出:序列Tn,Sn,Cn,Rn及积分结果(参考书本P81的表2-5)
取n=2,4,8,16,精确解为0.9460831
四、实验原理及算法描述
在许多实际问题中,常常需要计算定积分 的值。根据微积分学基本定理,若被积函数f(x)在区间[a,b]上连续,只要能找到f(x)的一个原函数F(x),便可利用牛顿-莱布尼兹公式 求得积分值。
但是在实际使用中,往往遇到如下困难,而不能使用牛顿-莱布尼兹公式。
cout<<"4"<<" "<<tixing(0, 1, 16)<<" "<<xingbusheng(0, 1, 8)<<" "<<((double(16 / 15))* xingbusheng(0, 1, 4)) - (double(1 / 15))*xingbusheng(0, 1, 2)<<" "<<longbeige(0, 1,0.00000001)<<endl;;
cout<<"the result "<<4<<" is "<<longbeige(0, 1, 0.00000001);
return0;
}
2.复化梯形公式子程序:
doubletixing(doublea,doubleb,intn)
{
doublefa = f(a);
doublefb = f(b);
doubleh = (b-a) /n;
cout<<"1"<<" "<<tixing(0, 1, 2)<<" "<<xingbusheng(0, 1, 1)<<endl;
cout<<"2"<<" "<<tixing(0, 1, 4)<<" "<<xingbusheng(0, 1, 2)<<" "<<((double(16/15))* xingbusheng(0, 1, 2)) -(double(1/15))*xingbusheng(0, 1, 1)<<endl;
{
doubleh = (b-a) /n;
doublefa = f(a);
doublefb = f(b);
//double s = fb - fa;
doublex =a;
doublefxk12 = 0.0;
doublefxk = 0.0;
/*for (int k = 1; k <=n; k++)
{
x = x + h / (2.0);
doublefxk = 0.0;
for(intk = 1; k <=n- 1; k++)
{
doublexk =a+ k*h;
fxk = f(xk) + 2.0)*(fa + 2.0*fxk + fb);
returnres;
}
3.复化辛浦生公式子程序:
doublexingbusheng(doublea,doubleb,intn)
《计算方法》实验报告
学号
姓名
班级
实验项目名称
实验二 数值积分
一、实验名称
实验二数值积分
二、实验目的:
(1)熟悉复化梯形方法、复化Simpson方法、梯形递推算法、龙贝格算法;
(2)能编程实现复化梯形方法、复化Simpson方法、梯形递推算法、龙贝格算法;
(3)理解并掌握自适应算法和收敛加速算法的基本思想;
fxk12 = fxk12 + f(x);
}
for(intk = 1; k <=n- 1; k++)
cout<<"3"<<" "<<tixing(0,1,8)<<" "<<xingbusheng(0,1,4)<<" "<<((double(16 / 15))* xingbusheng(0, 1, 4)) - (double(1 / 15))*xingbusheng(0, 1, 2)<<" "<<longbeige(0, 1, 0.000000001)<<endl;
double fx = f(x);
s = s + 4.0*f(x);
x = x + h / (2.0);
s = s + 2.0*f(x);
}
s = (h / 6.0)*s;
return s;*/
for(intk = 0; k <=n- 1; k++)
{
doublexk1 =a+ k*h;
x = xk1 + h / 2.0;
