ch3 双变量线性回归模型(数学)-1
第二章:双变量线性回归分析
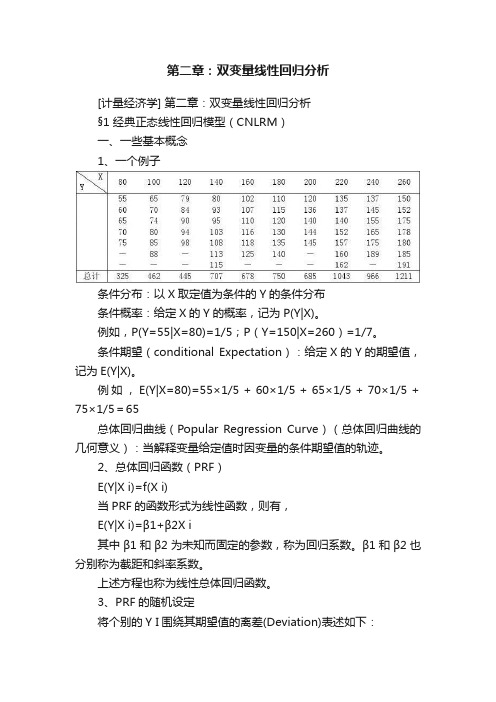
第二章:双变量线性回归分析[计量经济学] 第二章:双变量线性回归分析§1 经典正态线性回归模型(CNLRM)一、一些基本概念1、一个例子条件分布:以X取定值为条件的Y的条件分布条件概率:给定X的Y的概率,记为P(Y|X)。
例如,P(Y=55|X=80)=1/5;P(Y=150|X=260)=1/7。
条件期望(conditional Expectation):给定X的Y的期望值,记为E(Y|X)。
例如,E(Y|X=80)=55×1/5+60×1/5+65×1/5+70×1/5+75×1/5=65总体回归曲线(Popular Regression Curve)(总体回归曲线的几何意义):当解释变量给定值时因变量的条件期望值的轨迹。
2、总体回归函数(PRF)E(Y|X i)=f(X i)当PRF的函数形式为线性函数,则有,E(Y|X i)=β1+β2X i其中β1和β2为未知而固定的参数,称为回归系数。
β1和β2也分别称为截距和斜率系数。
上述方程也称为线性总体回归函数。
3、PRF的随机设定将个别的Y I围绕其期望值的离差(Deviation)表述如下:u i=Y i-E(Y|X i)或Y i=E(Y|X i)+u i其中u i是一个不可观测的可正可负的随机变量,称为随机扰动项或随机误差项。
4、“线性”的含义“线性”可作两种解释:对变量为线性,对参数为线性。
本课“线性”回归一词总是指对参数β为线性的一种回归(即参数只以它的1次方出现)。
模型对参数为线性?模型对变量为线性?是不是是LRM LRM不是NLRM NLRM注:LRM=线性回归模型;NLRM=非线性回归模型。
5、随机干扰项的意义随机扰动项是从模型中省略下来的而又集体地影响着Y 的全部变量的替代物。
显然的问题是:为什么不把这些变量明显地引进到模型中来?换句话说,为什么不构造一个含有尽可能多个变量的复回归模型呢?理由是多方面的:(1)理论的含糊性(2)数据的欠缺(3)核心变量与周边变量(4)内在随机性(5)替代变量(6)省略原则(7)错误的函数形式6、样本回归函数(SRF )(1)样本回归函数iY ?=1?β+2?βi X 其中Y ?=E(Y|X i )的估计量;1?β=1β的估计量;2β=2β的估计量。
线性回归模型双变量线性回归模型

3.相关程度的度量—相关系数
总体线性相关系数:
Cov( X ,Y )
Var( X )Var(Y )
其中:Var(X ) ——X 的方差;Var(Y ) ——Y的方差
Cov( X ,Y ) ——X和Y的协方差
样本线性相关系数:
XY
__
__
( Xi X )(Yi Y )
__
__
( Xi X )2 (Yi Y )2
回归的现代意义: 一个应变量对若干解释变量 依存关系 的研究
回归的目的(实质): 由固定的解释变量去 估计应变量的平均值
注意几个概念
● Y 的条件分布
当解释变量 X 取某固定值时(条件),Y 的值不 确定,Y 的不同取值形成一定的分布,即Y 的条
件分布。
Y
● Y 的条件期望
对于 X的每一个取值, 对 Y 所形成的分布确
2110 2225 2319 2321 2365 2398 2487 2513 2538 2567 2610 2710
2388 2426 2488 2587 2650 2789 2853 2934 3110
1650 1900 2150 2400 2650
5000 2464 2589 2790 2856 2900 3021 3064 3142 3274
均值 E(Y的X偏i )差为 , 显u然i 是随机变u i量,则有
ui Yi E(Yi Xi ) Yi 1 2 Xi
或 Yi 1 2 Xi ui
•
ui
•
Xi X
3.如何理解总体回归函数
●实际的经济研究中总体回归函数通常是未知的, 只能根据经济理论和实践经验去设定。“计量” 的目的就是寻求PRF。
计量经济学ch3 双变量回归的估计

∑ sd (βˆ2 ) = var(βˆ2 ) = σ / xi2
同理,有
(3.12)
∑ ∑ var(βˆ1) = n
X
2 i
xi2
σ
2
⇒
sd (βˆ1 )
=σ
X
2 i
,
n xi2
(3.13)
总体方差σ 2 和标准差σ 是未知的,故需要用样本予以估计:
uˆi = yi − βˆ2 xi = β2 xi + (ui − u ) − βˆ2 xi = (β2 − βˆ2 )xi + (ui − u )
uˆ
2 i
)
/
∂βˆ
2
=
∂(
(Yi − βˆ1 − βˆ2 X i )2 ) / ∂βˆ2 = −2
(Yi − βˆ1 − βˆ2 X i )X i = −2
uˆi X i = 0
由此得到
∑ ∑ (Yi − βˆ1 − βˆ2 Xi ) = uˆi = 0 ∑ ∑ (Yi − βˆ1 − βˆ2 Xi )Xi = uˆi Xi = 0
6
为什么如此要求?
8.X 值要有变异性,即对于一个给定的样本,X 的值不能全部相同, 也就是说,X 的方差必须是一个有限的正数。
为什么如此要求?
9.正确设定了模型,或者说,所用的模型不存在设定误差。 所谓设定问题,在本书中包括: (1)模型应包括哪些变量, (2)模型的函数形式(如线性还是非线性), (3)对模型的变量和扰动应有哪些假定等。
E(kiui ) = 0)
3. βˆi (i = 1,2) 在所有线性无偏估计量中具有最小方差 (具有最小方差
的估计量称为有效估计量)。
第三章 双变量回归模型-估计问题

RSS) 则表示残差平方和(residual sum of squares, 则表示残差平方和
• n-2 是被称为自由度 是被称为自由度(degrees of freedom, df)的个数 的个数 •
1-21
的性质: 第四节 OLS的性质:高斯 马尔科夫定理 的性质 高斯-马尔科夫定理
(
)
(
)
(1)
(
)
(
)
(2)
1-8
正规方程(normal equations)及其解 正规方程 及其解
ˆ ˆ ∑ Yi = n β 1 + β 2 ∑ X i ˆ ˆ Y i X i = β 1 ∑ X i + β 2 ∑ X i2 ∑
ˆ = n ∑ X iYi − ∑ X i ∑ Yi = β2 n ∑ X i2 − ( ∑ X i ) 2 ˆ ˆ β1 = Y − β 2 X
ˆ var( β 2 ) = ˆ se ( β 2 ) =
∑
σ
x i2 x i2
σ
2 i 2 i
∑ ˆ )= ∑ X σ var( β n∑ x ˆ )=σ ∑ X se ( β n∑ x
1 1
2
2 i 2 i
1-20
第三节 OLS 估计的精度
σ
•
2
的估计
ˆ σ2 =
ui的 σ 2的OLS估计量
ˆ ˆ E β1 = β1 , E β 2 = β 2
量中具有最小方差
1-22
拟合优度的度量: 第五节 拟合优度的度量:判定系数 r2
拟合优度( 拟合优度(goodness of fit)是指样本回归线与样本 ) 观测值之间的拟合程度。 观测值之间的拟合程度。 判定系数r 判定系数 2 (Coefficient of determination)或R2 就 或 是衡量样本回归线对数据拟合程度的总度量。 是衡量样本回归线对数据拟合程度的总度量。 如何计算呢? 如何计算呢?
第二章 线性回归的思想:双变量回归模型

二、总体回归函数
从图2.2我们可以看出,条件均值E (Y/Xi)是Xi 的函数,即:
E(Y/Xi)= f (Xi)
(2.1)
其中,f (Xi)表示解释变量Xi 的某个函数 。在我们的引例中,E(Y/Xi)是Xi 的一个线 性函数。
式(2.1)就是总体回归函数,简称 总体回归。它表明在给定Xi 下Y 的分布 的总体均值与Xi有函数关系,就是说它 给出了Y 的均值是怎样随X 值的变化而 变化的。
2.在经济学中,经济学家要研究个人
消费支出与个人可支配收入的依赖关系。
这种分析有助于估计边际消费倾向,就是
可支配收入每增加一元引起消费支出的平
均变化。
3.在企业中,我们很想知道人们对企
业产品的需求与广告费开支的关系。这种
研究有助于估计出相对于广告费支出的需
求弹性,即广告费支出每变化百分之一的
需求变化百分比,这有助于制定最优广告
函数f (Xi)采取什么函数形式,是一个
需要解决的重要问题。在实际经济系统
中,我们不会得到总体的全部数据,因
而就无法据已知数据确定总体回归函数 的函数形式。同时,对总体回归函数的 形式只能据经济理论与经验去推断。
例如,我们可以假定消费支出与收入有 线性关系。则总体回归函数为
E(Y / X i ) 1 2 X i
有异,但图2.2清楚地表明随着收入的增
加,消费支出平均地说也在增加。就是
说,散点图启示我们,Y 的条件均值随X
的增加而增加。
如果我们观察图2.2中那些代表Y 的
各个条件均值的粗圆点,则表明这些条
件平均值落在一根有正斜率的直线上。
我们称这根直线叫做总体回归线,它是
Y 对X 的回归。
计量经济学之双变量线性回归模型.

8
例:一个假想的社区有100户家庭组成,要研 究该社区每月家庭消费支出Y 与每月家庭可支 配收入X 的关系。 即如果知道了家庭的月收入, 能否预测该社区家庭的平均月消费支出水平。 为达到此目的,将该100户家庭划分为组内收 入差不多的10组,以分析每一收入组的家庭消 费支出。
变量间的关系包括: 确定性关系或函数关系:研究的是确定 现象非随机变量间的关系。
圆面积 f , 半径 半径2
统计依赖或相关关系:研究的 阳光, 施肥量
4
对变量间统计依赖关系的考察主要是通过相关 分析(correlation analysis)或回归分析 (regression analysis)来完成的。
15
“线性”一词的含义:
1、模型就变量而言是线性的
例如: E (Y X i ) 0 1 X i 2、模型就参数而言是线性的 例如: E (Y X i ) 0 1 X
2 i
E (Y X i ) 0 1 X i
1 E (Y X i ) 0 1 X
注:在计量经济学中,从回归理论的发展、 参数的估计方法来说,主要考虑的是模型就 参数而言是线性的情形。
估计
Yi E(Y | X i ) ui 0 1 X i ui
这就要求我们必须找到合适的方法使得SRF ˆ (i 0,1)尽可能接 尽可能地接近PRF,或者说使
i
近i (i 0,1)。
24
2.2 模型的基本假设
一、 对变量和模型的假定
1)重复抽样中,解释变量 X i 是一组固定的值或
样本残差或剩余项(residual), ˆi。 也可看成是ui的估计量u
双变量回归模型估计问题课件
在应用双变量回归模型进行预测之前,需要对模型进行假设检验,以确保模型的有效性和可靠性。
03
CHAPTER
双变量回归模型大样本可以提供更稳定和准确的估计。
异常值可能对估计稳定性产生负面影响。在回归分析中,需要谨慎处理异常值,以避免对估计稳定性的不良影响。
总结词
在气候变化对农业产量影响的案例中,可以选择一些与农业产量密切相关的气候因素作为自变量,如温度、降雨量、光照等。通过双变量回归模型,可以建立这些气候因素与农业产量之间的线性关系,并利用历史数据来估计模型的参数。通过预测未来气候因素的变动,可以进一步预测未来农业产量的变化趋势,为农业生产和资源管理提供决策依据。
详细描述
06
CHAPTER
结论与展望
01
总结了双变量回归模型估计问题的基本概念、方法和应用场景。
02
分析了双变量回归模型估计问题中存在的挑战和问题,如多重共线性、异方差性等。
03
介绍了解决这些问题的常用方法和技巧,如主成分分析、岭回归等。
04
强调了双变量回归模型估计问题在实践中的重要性和应用价值。
最小二乘法具有很多优点,例如它对数据的要求较低、计算相对简单等,因此在回归分析中得到了广泛应用。
模型的假设主要包括线性假设、误差项独立同分布假设、误差项无偏性假设等。
对假设的检验可以通过一些统计方法进行,例如残差分析、Jarque-Bera检验等。如果模型的假设不满足,则需要对模型进行调整或重新设定。
双变量回归模型估计问题课件
目录
引言双变量回归模型基础双变量回归模型的估计问题解决双变量回归模型估计问题的方法实际案例分析结论与展望
01
CHAPTER
引言
03
估计问题是指在使用回归模型时,如何准确地估计未知的参数值。
3.1双变量线性回归分析的基本概念
随机误差项的意义(引入原因) (1)理论的含糊性; (2)数据的欠缺; (3)众多细小因素对因变量的综合影响; (4)变量的观测误差的影响; (5)模型设定误差的影响; (6)变量内在随机性的影响; (7) 省略原则。
回归模型存在两个特点:
建立在某些假定条件不变前提下抽象出来 的回归函数不能百分之百地再现所研究的 经济过程。 也正是由于这些假定与抽象,才使我们能 够透过复杂的经济现象,深刻认识到该经 济过程的本质。
由上图发现:随着收入的增加,消费支出Y“平 均地说”也在增加,且Y的条件均值均落在一根 正斜率的直线上。这条直线称为总体回归直线。
概念(二)
当解释变量Xi取给定值时因变量Yi的条件期望 值或条件均值的轨迹称为总体回归曲线 (population regression curve)。 总体回归直线(Population regression line, PRL )
二、线性的含义
线性回归模型有两种解释: (1)对变量为线性 (2)对参数为线性
三、 PRF的随机设定以及随机误差项的性质 和意义
PRF说明了在给定的收入水平下,该社区家庭的 平均消费支出随收入变化的规律。 但对某一个别的家庭,其消费支出可能与该平均 水平有偏差。 ui Yi E(Y | X i )
总体回归函数PRF的随机设定形式 含义:它表明因变量除了受解释变量的系统 性影响外,还受其他因素的随机性影响。 由于函数中引入了随机项,成为计量经济学 模型,因此也称为总体回归模型。
随机误差项的性质
随机误差项是所有可能影响因变量,但又 未能包括到回归模型中来的被忽略变量的 替代(surrogate)或代理(proxy)变量。 E(ui| Xi)=0
经济计量学第二讲 双变量回归模型及其估计问题
东北财经大学数量经济系
第四节 两个说明性例子
第四节 两个说明性例子
例一:1970-1980年间美国的咖啡消费 例二:利用1980-1991年数据建立的美国
凯恩斯消费函数
东北财经大学数量经济系
东北财经大学数量经济系
第三节
双变量回归模型的估计问题(2)
2 ˆ 2 ˆ (Y Y ) u
2 ˆ ˆ (Y b 1 b 2 X )
min
ˆ2 u ˆ b 1 ˆ2 u ˆ b 2
ˆ ˆ 2 (Y b 1 b 2 X ) 0
ˆ ˆ 2 ( Y b 1 b 2 X )( X ) 0
密 度 true
ˆ b2 d
东北财经大学数量经济系
b2
ˆ b2 + d
ˆ b2
第三节
双变量回归模型的估计问题(11)
五、判定系数r2:“拟合优度”的度量
(一)判定系数的意义 1.判定系数R2的含义 2.文图或巴伦坦图
东北财经大学数量经济系
第三节
双变量回归模型的估计问题(12)
(二)判定系数R2的计算 1.总平方和(TSS)的计算及分解 2.判定系数R2的计算公式 3.判定系数R2与相关系数的关系 4.相关系数r 的性质
ˆ ˆ b1 Y b 2 X
东北财经大学数量经济系
第三节
数值性质
双变量回归模型的估计问题(5)
是指由于运用最小二乘法而得以成立的那 些性质而不管数据是如何产生的。
统计性质
是指仅在数据产生的方式满足一定的假设 下才得以成立的那些性质。
数 值 性 质
1.OLS估计量是纯粹由可观测的量表达式,是容易计算的; 2.OLS估计量是点估计量; 3.一旦从样本数据得到OLS估计值,便可画出样本回归线。
计量经济学 两变量线性回归
消费性支出 y 585 576
1983
1984
686
834 1075 1293 1437
615
726 992 1170 1282
例3-1 上海市人均居民收 入和人均消费支出数据 (1981-2002)
1985 1986 1987
1988
1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002
i i i
最小。
23
1.最小二乘估计(OLS)(续)
核心:残差平方和 ei 2 最小。
min V ei Yi (a bX i )
2 i i
i
2
一阶条件为: V 0 a V 0 b
24
1.最小二乘估计(OLS)(续)
V 2 (Yi a bX i ) 0 a V 2 (Yi a bX i ) X i 0 b
(Y a bX ) 0
i i
(Yi a bX i ) X i 0
正规方程组
ei 0 利用残差记号ei可以 i 把正规方程组写为: e X 0 i i i
25
参数α和β的最小二乘估计量a和b
由正规方程 组得到:
Yi na b X i X iYi a X i b X i 2
3
1.模型建立
建立两变量线性回归模型必须有理论和现实 根据 一个例子: 凯恩斯绝对收入假设消费理论:消费(Y) 是由收入(X )唯一决定的,是收入的线性 函数: Y=+X 要利用经验和数据分布情况来判断变量 间的关系是否是线性关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在满足基本假设条件下,对一元线性回归模型: Yi 0 1 X i ui
随机抽取n组样本观测值(Xi, Yi)(i=1,2,…n)。
假如模型的参数估计量已经求得,为 那么Yi服从如下的正态分布:
3、总体回归函数(PRF) 回归分析关心的是根据解释变量的已知或给
定值,考察被解释变量的总体均值,即当解 释变量取某个确定值时,与之统计相关的被 解释变量所有可能出现的对应值的平均值。
E (Y | X i ) f ( X i )
例1 一个假想的社区有100户家庭组成,要研究 该社区每月家庭消费支出Y与每月家庭可支配收 入X的关系。 即如果知道了家庭的月收入,能否 预测该社区家庭的平均月消费支出水平。 为达到此目的,将该100户家庭划分为组内 收入差不多的10组,以分析每一收入组的家庭消 费支出。
注意 ①不线性相关并不意味着不相关。 ②有相关关系并不意味着一定有因果关系。 ③相关分析对称地对待任何(两个)变量,两 个变量都被看作是随机的。回归分析对变量 的处理方法存在不对称性,即区分应变量 (被解释变量)和自变量(解释变量):前 者是随机变量,后者不是。
回归分析构成计量经济学的方法论基础,其主要内 容包括: (1)根据样本观察值对经济计量模型参数进行估 计,求得回归方程; (2)对回归方程、参数估计值进行显著性检验; (3)利用回归方程进行分析、评价及预测。
第三章 经典单方程计量经济学模型: 双变量线性回归模型
一、回归分析概述 二、双变量线性回归模型的参数估计 三、最小二乘估计量的性质 四、拟合优度的测度 五、双变量回归中的区间估计和假设检验 六、双变量线性回归模型的应用——预测 小结:本章知识结构图
一、回归分析概述
1、变量间的关系 2、相关分析与回归分析
(3)代表众多影响不重要因;
(6)变量的内在随机性。
5、样本回归函数(SRF)
问题:能从一次抽样中获得总体的近似的信息 吗?如果可以,如何从抽样中获得总体的近似 信息? 例2 在例1的总体中有如下一个样本,能否从 该样本估计总体回归函数PRF?
顺便指出 ,记 则有
ˆ ˆ yi Yi Y
ˆ ˆ ˆ ˆ ˆ yi ( 0 1 X i ) ( 0 1 X e ) ˆ (X X ) 1 e
1 i n
i
可得
ˆ ˆ yi 1 xi
(**)
(**)式也称为样本回归函数的离差形式。 注意:
ˆ ˆ ˆ Q (Yi Yi ) (Yi ( 0 1 X i )) 2
2 1 1 n n
最小。
最小二乘法的基本原理:用使估计的剩余平方和最小的原 则确定样本回归函数。
方程组(*)称为正规方程组(normal equations)。
记
1 2 x (X i X ) X n X i 1 xi yi ( X i X )(Yi Y ) X iYi n X i Yi
表 3.1.3 家庭消费支出与可支配收入的一个随机样本 Y X 800 1100 1400 594 638 1122 1700 2000 2300 1155 1408 1595 2600 1969 2900 2078 3200 2585 3500 2530
回答:能
• 该样本的散点图(scatter diagram):
表1
某社区家庭每月收入与消费支出统计表 1400 869 913 924 979 1012 1045 1078 1122 1155 1188 1210 每月家庭可支配收入 X(元) 1700 2000 2300 2600 1023 1100 1144 1155 1210 1243 1254 1298 1331 1364 1408 1430 1485 1254 1309 1364 1397 1408 1474 1496 1496 1562 1573 1606 1650 1716 2900 1969 1991 2046 2068 2101 2189 2233 2244 2299 2310 3200 2090 2134 2178 2266 2354 2486 2552 2585 2640 3500 2299 2321 2530 2629 2860 2871
含义:总体回归函数(PRF)说明被解释变量 Y的平均状态(总体条件期望)随解释变量X变 化的规律。
• 函数形式:可以是线性或非线性的。
• 例1中,可将居民消费支出看成是其可支配收入 的线性函数,即:
E (Y | X i ) 0 1 X i
为一线性函数。其中,0,1是未知参数,称为 回归系数(regression coefficients)。
满足假设1-4的线 性回归模型称为古 典(或经典)线性 回归模型
2、参数的普通最小二乘估计(OLS)
给定一组样本观测值(Xi, Yi)(i=1,2,…n)要求样本 回归函数尽可能好地拟合这组值.
普通最小二乘法(Ordinary least squares, OLS)给出 的判断标准是:二者之差的平方和
Yi E (Y | X i ) ui 0 1 X i ui
二、双变量线性回归模型的参 数估计 1、双变量线性回归模型的基本假设
2、参数的普通最小二乘估计(OLS) 3、参数估计的极大似然法(ML)
双变量线性回归模型只有一个解释变量,其一般形 式为:
Y 0 1 X u
在计量经济学中,往往以小写字母表示对均 值的离差。
例3 在上述家庭可支配收入-消费支出例中,对于所 抽出的一组样本,求参数的估计值。
表3 Y X 800 1100 1400 594 638 1122 家庭消费支出与可支配收入的一个随机样本 1700 2000 2300 1155 1408 1595 2600 1969 2900 2078 3200 2585 3500 2530
显然,此形式是总体回归函数的随机设定形式,称 其为总体回归模型,由于随机扰动项的引入,使其 成为了计量经济模型。
由模型
Yi E (Y | X i ) ui 0 1 X i ui
可看出:给定收入水平Xi ,个别家庭的支出Yi除了受X的系统 性或确定性影响外,还受其它随机性或非确定性影响,ui即 为这些影响因素的综合代表。 在总体回归函数中引入随机扰动项,主要有下面几个方 面的原因: (1)代表未知的影响因素; (2)代表残缺数据;
2,800 2,400
2,000
1,600
Y
1,200
800
400 0 1,000 2,000 X 3,000 4,000
画一条直线尽可能地拟合该散点图,由于样本取 自总体,可以用该直线近似地代表总体回归线。该 直线称为样本回归线。 ˆ ˆ ˆ 记样本回归线的函数形式为: Yi f ( X i ) 0 1 X i 称为样本回归函数(sample regression function,SRF)
2 i 2 2 i
ˆ xi y i 1 x i2 上述参数估计量可以写成: Y X ˆ ˆ 1 0 称为OLS估计量的离差形式(deviation form)。
由于参数的估计结果是通过最小二乘法得到 的,故称为普通最小二乘估计量(ordinary least squares estimators)。
• 注意:这里将样本回归线看成总体回归线的近似 替代
则
ˆ Yi 为E (Y | X i )的估计量; ˆ 为 的估计量 i 0,1). (
i i
• 样本回归函数的随机形式/样本回归模型: 同样地,样本回归函数也有如下的随机形式:
ˆ ˆ ˆ ˆ Yi Yi ui 0 1 X i ei
4、随机扰动项
总体回归函数说明在给定的收入水平Xi下,该 社区家庭平均的消费支出水平。 但对某一个别的家庭,其消费支出可能与该平 均水平有偏差。
记ui=Yi-E(Y|Xi),称为Yi围绕它的期望值E(Y|Xi ) 的离差,它是一个不可观测的随机变量,称其 为随机扰动项或随机误差项。
Y 由此可得例1的如下结果: i 0 1 X i ui
2. 相关分析与回归分析
对变量间统计依赖关系的考察主要是通过相关 分析或回归分析来完成的.
正相关 线性关系不相关 相关系数: 1 XY 1 负相关 有因果关系 回归分析 统计依赖关系 正相关 无因果关系 相关分析 非线性关系不相关 负相关
21450 21285 2145 2635
15510 2585
在给定解释变量Xi条件下被解释变量Y 的期望轨迹称为总体回归线,或更一般 地称为总体回归曲线。
• 相应的函数:
E (Y | X i ) f ( X i )
称为(双变量)总体回归函数(population regression function, PRF)。
由EViews软件计算得下面结果:
因此,由该样本估计的回归方程为:
ˆ Yi 103 .1717 0.777010 X i
3、参数估计的极大似然法(ML)
极大似然法(Maximum Likelihood,简称ML), 也称最大似然法,是不同于最小二乘法的另一种 参数估计方法,是从最大似然原理出发发展起来 的其他估计方法的基础。 基本原理: 对于极大似然法,当从模型总体随机抽取n组 样本观测值后,最合理的参数估计量应该使得从 模型中抽取该n组样本观测值的概率最大。即
3、总体回归函数(PRF)
4、随机扰动项 5、样本回归函数(SRF)
1. 变量间的关系
(1)确定性关系或函数关系:研究的是确定现
象非随机变量间的关系。
