黑龙江省哈尔滨市第六中学2016届高三地理上学期10月月考试题(含答案)
黑龙江省哈尔滨市第六中学高二地理10月月考试题

哈尔滨市第六中学2020届10月阶段性总结高二地理试题一.选择题(1~20题,每题1分,21~40题每题2分,共计60分)读我国西北某地区新垦区位置图,回答1~2题。
1.该流域新垦区A.区域的界线与行政边界一致B.区域内部农业生产无相似性C.区域发展的决定性因素是水源D.与非农垦区相互独立2.图中行政中心与新垦区的区域空间结构分别表现为A.面状与点状B.线状与岛状C.点状与岛状 D.点状与面状德国慕尼黑大学的一位教授是这样看待中国的:他首先把中国分成东部与西部,再分别分成南北两部分,形成如图中所示①②③④四块区域,并把四块区域命名为“黄色中国”、“绿色中国”、“银色中国”和“金色中国”。
读图,完成3~4题。
3.关于图中各区域说法正确的是A.决定各区域差异的基本因素是气候和地貌 B.各区域间具有明确的界限C.各区域内部没有明显的分异 D.各区域间不存在广泛的联系4.各色分区组合正确的是A.④—“金色中国” B.①—“银色中国”C.③—“绿色中国” D.②—“黄色中国”夜晚,我漫步在银行、公司、商店、事务所密集的街头。
高楼耸立夜空,像陡峻的山峰,墙壁是透明的玻璃,好像水晶宫。
五颜六色的街灯闪闪烁烁,远远近近,高高低低,时隐时现,走在路上,就像浮游在布满繁星的天空。
汽车如风如龙,飞驰而过,车上的尾灯,似无数条红色丝带不断地向远方延伸。
结合所学知识,回答5~7题。
5.上述材料所描述的区域处于区域发展的阶段A. 传统农业为主体B. 工业化C. 高效益的综合发展D. 高水平的开发6.该区域A. 对外开放程度较低B. 经济以“自给自足”为主C. 劳动力由农业向制造业大规模转移D. 加工制造业向资金密集型和技术密集型全面升级7.推动该区域经济增长的主要部门有( )①科技、教育②金融、贸易③信息、旅游④钢铁、普通服装A. ②③④B. ①③④C. ①②④D. ①②③下图为某城区发展变化示意图。
读图完成8~9题。
8.该城区由Ⅰ到Ⅱ的发展过程中( )①交通运输方式增多②经济发展水平提升③区域开放程度提高④区域环境质量改善A.①② B.②③ C.③④ D.②④9.该城区工业( )①产品联系紧密②技术协作密切③规模效应增强④企业竞争激烈A.①② B.②③ C.③④ D.①③苏州市自1987年形成“二三一”产业主导格局之后,经过近30年的发展,逐渐形成了“三二一”格局,产业结构实现历史性跨越。
2016届黑龙江省哈尔滨市第六中学高三上学期期中考试试题地理卷解析

【试卷综析】本试卷是高三年级期中考试试卷,其中1—40题选择题,41、42、43题为综合题。
考查了高中地理的全部内容。
以基础知识和基本技能为载体,以能力测试为主导,在注重考查学科核心知识的同时,突出考查考纲要求的基本能力,重视学生科学素养的考查。
本试题重点考查点为地球运动相关知识点、太阳直射点的移动、城市化、世界地理、土地的利用类型、水土保持、等高线地形图、自然景观、我国雨带推移规律、洋流、地图基本知识、晨昏线变化分析、地球的宇宙环境、水利工程建设对河流的影响、板块边界类型等,考查知识点侧重自然地理方面,图文资料丰富,设问较好,题量和难度适中,是一套不错的考试题。
哈尔滨市第六中学2015-2016学年度上学期期中考试高三地理试题选择题(共40小题,1—20每小题1分,21—40每小题2分,共60分。
在每题给出的四个选项中,只有一项是最符合题目要求的。
))【题文】 C4 J1读“某地区农业经济发展生产布局模式图”,分析回答1~3题。
1、该地区的气候类型是A、地中海气候B、亚热带季风气候C、温带季风气候D、山地气候2、该模式改造的主要农业区位因素是A.热量条件 B.地形条件 C.生态条件 D.水源条件3、该地区冬半年的多发的自然灾害是A.暴雨、洪涝 B.火山、地震 C.冻雨、雪灾 D.滑坡、泥石流【答案】【知识点】本题考查区域自然环境和利用改造。
【答案解析】1.B 2.D 3.C解析:第1题,根据图中信息可知,该地以水田为主,且有较多水利设施,因此应当是亚热带季风气候。
第2题,通过图中的集水雨柜、蓄水池、管渠引水等信息可以看出改造的主要是水源条件。
第3题,该地冬季易受到来自北方的冷空气带来冻雨、雪灾。
【思路点拨】本题要认真分析图表信息,难度较小。
【题文】 E2 D2下图为某季节北印度洋局部海域示意图,据此完成4~5题。
4.图中①虚线代表的地理事物可能是A .深海沟B .1月0℃等温线C .板块生长边界D .岛弧链5.判断右图代表的季节及图中洋流的流向A .夏季 向东北流B .夏季 向西南流C .冬季 向东北流D .冬季 向西南流【答案】【知识点】本题考查板块构造和北印度洋季风洋流。
黑龙江省哈尔滨市第六中学2018-2019学年高二地理上学期期末考试试题(含解析)

一、选择题。
(每小题1.5分,共40道选择题60分)读北半球经纬线俯视图,完成下列各题。
1. 如果一架飞机从A地飞往B地,最近的飞行的方向是()A. 一直向东B. 一直向西C. 一直向东南D. 先向西北,再向西南2. 如果AB所在的纬度为60度,则纬线段AB的长度为()A. 10000kmB. 5000kmC. 2500kmD. 3000km【答案】1. D 2. B【解析】试题分析:【1题详解】球面上最近距离的走向,是大圆的劣弧。
所以方向是先向西北,再向西南。
选择C项。
【2题详解】把地球看成正球体所有纬线线都算大圆,赤道是一个最大的大圆,长度为4万千米,经度60°是赤道圈的长度的一半2万千米,AB占纬线的四分之一,即5 000 km.【考点定位】经线和纬线【名师点睛】利用经纬网定“最短航线”地球上两点间最短航线为球面最短距离,即经过两点的大圆劣弧长度。
(注:所谓大圆指过地心的平面与球面的交线)(1)同一经线上的两点,其最短距离的劣弧线就在经线上(如图中弧AB)。
(2)同一纬线上的两点,其最短距离的劣弧线向较高纬度凸起(如图中同一条纬线上MK之间的最短航线是弧MPK,而不是弧MQK,赤道上除外)。
(3)晨昏线上的两点,由于晨昏线本身就是一个大圆,故两点最短线就是两点之间的较短晨昏线(即劣弧线)。
2018年6月21日,国务院关于同意设立“中国农民丰收节”的批复发布,同意自2018年起,将每年农历秋分节气那一天设立为“中国农民丰收节”。
将极大调动起亿万农民的积极性、主动性、创造性,提升亿万农民的荣誉感、幸福感、获得感。
回答下列各题。
3. 国务院批复发布农民丰收节的当天,太阳直射点接近下图中的哪个位置()A. ①B. ②C. ③D. ④4. 全国农民在庆祝首届丰收节时,我国昼夜情况接近哪幅图()A. B.C. D.5. 我国华北地区的一句农谚所言:“白露早,寒露迟,秋分种麦正当时”,种麦时,地球位于公转轨道中的哪个位置()A. AB. BC. CD. D【答案】3. B 4. B 5. B【解析】【3题详解】国务院批复发布农民丰收节的当天为6月21日,6月22日前后太阳直射北回归线,故B正确。
黑龙江省哈尔滨市高三上学期地理10月月考试卷
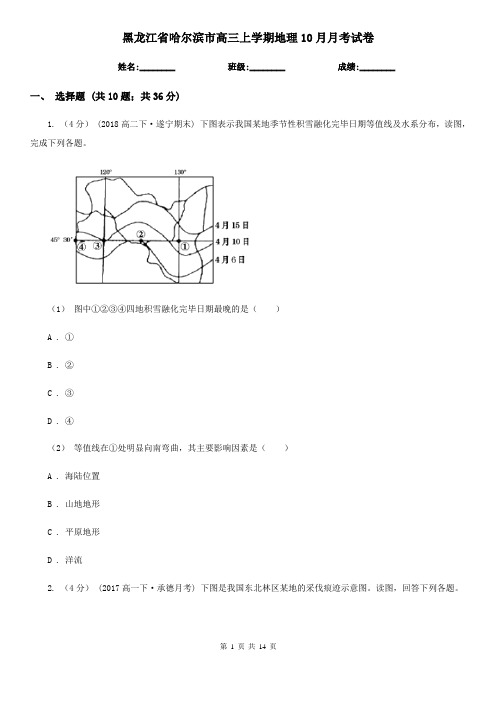
黑龙江省哈尔滨市高三上学期地理10月月考试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共36分)1. (4分) (2018高二下·遂宁期末) 下图表示我国某地季节性积雪融化完毕日期等值线及水系分布,读图,完成下列各题。
(1)图中①②③④四地积雪融化完毕日期最晚的是()A . ①B . ②C . ③D . ④(2)等值线在①处明显向南弯曲,其主要影响因素是()A . 海陆位置B . 山地地形C . 平原地形D . 洋流2. (4分) (2017高一下·承德月考) 下图是我国东北林区某地的采伐痕迹示意图。
读图,回答下列各题。
(1)图中甲、乙、丙、丁所代表的方位及判断依据组合正确的是()A . 北、南、西、东——热量、光照B . 东、西、南、北——地形、水源C . 南、北、东、西——土壤、水源D . 西、东、南、北——地形、光照(2)这种采伐方式带来的后果,不可能是()A . 水旱灾害频繁B . 沙尘天气加重C . 物种减少D . 地震灾害3. (4分)(2020·祁阳模拟) 兴凯湖是中俄边界上的湖泊,由大小两湖组成,仅涨水时相通。
两湖之间有宽约1千米的天然沙坝(沙坝上生长着茂密的森林),在特定时间,该区域常见“大湖波浪滔天,小湖温柔恬静”的奇特现象。
结合图文信息,完成下面小题。
(1)该区域出现“大湖波浪滔天,小湖温柔恬静”奇特现象的时间最有可能是()A . 夏季B . 秋季C . 春季D . 冬季(2)关于图中沙坝相关特征描述正确的是:()①沙坝出露的面积夏季大于冬季②沙坝夏季的增长速度大于冬季③沙坝可净化水质,改良土壤④沙坝北侧植被比南侧长势更好A . ①②B . ②④C . ②③D . ①④4. (2分) (2016高二下·宁夏期中) 读我国某地区气温、降水量和蒸发量年内分布示意图,该地区位于我国的()A . 华北地区B . 华南地区C . 青藏地区D . 西南地区5. (2分)某地正午时,北京时间为12点16分,则该地经度为:A . 116°EB . 124°EC . 104°ED . 136°E6. (4分) (2017高二下·成都月考) 下图为乌鲁木齐和昌吉市≥10 ℃的年积温变化图(单位:℃/年)。
黑龙江省哈尔滨市第六中学校2022-2023学年高三上学期10月月考数学试题

黑龙江省哈尔滨市第六中学校2022-2023学年高三上学期10月月考数学试题一、单选题1.已知集合(){}2=log 1<0A x x -,4=0+1x B xx -≥⎧⎫⎨⎬⎩⎭,则()A B ⋂=R ð( ) A .()1,1-B .()2,4C .(][]1,12,4-⋃D .[][]1,12,4-⋃ 2.在等比数列{}n a 中,1a ,13a 是方程213160x x -+=的两根,则2127a a a 的值为( ) AB.C .4D .4±3.某学习小组的学习实践活动是测量图示塔AB 的高度.他们选取与塔底在同一水平面内的两个测量基点C ,D ,测得3BCD π∠=,4BDC π∠=,且基点C ,D间的距离为(30m CD =+,同时在点C 处测得塔顶A 的仰角为6π,则塔高AB 为( )A .20mB.C .40mD.4.下列说法正确的是( )A .命题“2x ∀>,ln 1x x ≤-”的否定是“02x ∃≤,00ln 1x x >-”B .命题p :0x ∃∈R ,02010ax ax ++≤,若命题p 是假命题,则04a <<C .“0a b ⋅<”是“a ,b 的夹角为钝角”的充分不必要条件D .ABC 中,A B >是sin sin A B >的充要条件5.向量OA ,OB 满足0OA OB ⋅=,点C 在以点O 为圆心的劣弧AB 上,OC xOA yOB =+uu u r uu r uu u r,则2x y +的最大值为( )6.已知函数()f x 定义域为R ,()1f x -为奇函数,()1f x +为偶函数,当[]1,3x ∈时,()f x kx m =+,若()()031f f -=-,则()2022f =( )A .1-B .1C .2-D .27.已知函数()()π=sin 2+>0,0<<2f x x ωϕωϕ⎛⎫ ⎪⎝⎭的部分图象如图所示,则下列结论正确的是( )A .()f x 的图象关于点,03π⎛⎫- ⎪⎝⎭对称B .()f x 在区间π0,2⎡⎤⎢⎥⎣⎦的最小值为C .()f x 在[]0,π上的单调递增区间为π0,6⎡⎤⎢⎥⎣⎦D .将()f x 图象的横坐标变为原来的()1>0t t 倍,纵坐标不变得到函数()g x ,若()12g x =在[]0,π上有且只有三个不等实根,则41<3t ≤8.若关于x 的不等式ln x a e x a -≥+对一切正实数x 恒成立,则实数a 的取值范围是( )A .1,e ⎛⎫-∞ ⎪⎝⎭B .(],e -∞C .(],1-∞D .(],2∞-二、多选题9.下列关于复数的四个命题正确的是( ) A .若2z =,则4z z ⋅= B .若()72i3i z +=+,则z 的共轭复数的虚部为1C .若1i 1z +-=,则1i z --的最大值为3D .若复数1z ,2z 满足12z =,22z =,121z z +=,则12z z -=10.已知等差数列{}n a 的前n 项和为n S ,若23a =,77S =,则( ) A .5n a n =- B .若210m n a a a a +=+,则116m n+的最小值为2512C .n S 取到最大值时,5n =D .设2nn n a b =,则数列{}n b 的最小项为164- 11.设锐角三角形ABC 的对边分别为a ,b ,c ,若cos cos a a B b A +=,则( ) A .22b a ac -= B .2B A = C .04A π<<D.)2b ca+∈12.平面向量a ,b ,c ,满足1a =,2b =且()a ab ⊥-,2,30c a c b <-->=︒r r r r,则下列说法正确的是( )A.2a b +=r r B .a 在b 方向上的投影向量为12bC .c的最大值是2 D .若向量m 满足2m a ⋅=u r r,则()m m b⋅-u r u r r 的最小值为54三、填空题13.记n S 为等差数列{}n a 的前n 项和.若32236S S =+,则公差d =_______.14.通过研究正五边形和正十边形的作图,古希腊数学家毕达哥拉斯发现了黄金分割率,黄金分割率的值也可以用2sin18︒2sin18=︒.记2sin18m =︒,则=______.15.已知O 是ABC 的外心,若22AC AB AB AO AC AO mAO AB AC⋅+⋅=uuu r uu u r uu u r uuu r uuu r uuu r uuu r uu u r uuu r,且sin sin B C +=m 的最大值为______.16.已知函数()()()222e 1e x x f x a a x x =+-++有三个不同的零点1x ,2x ,3x ,且123x x x <<,则3122312111e e e x x x x x x ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为______.四、解答题17.已知函数()2sin cos 3f x x x π⎛⎫=- ⎪⎝⎭.(1)求函数()f x 的最小正周期及单调递增区间; (2)在锐角ABC 中,若()f AACBC =ABC 的面积. 18.设n S 是正项等比数列{}n a 的前n 项和,且26S =,430S =. (1)求数列{}n a 的通项公式; (2)设()121n n n b n n a ++=+,求数列{}n b 的前n 项和n T .19.在ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,ABC 的面积214S a =. (1)cos B b =-,求sin sin CB的值; (2)求c bb c+的最大值.20.已知等差数列{}n b 满足32b =,251681b b b b =++,数列{}n a 的前n 项和2124n n S b +=⋅-,*n ∈N(1)求数列{}n a ,{}n b 的通项公式;(2)记数列{}n n a b 的前n 项和为n T ,若226825n n kT n a n n >-+对一切*n ∈N 恒成立,求正整数k 的最小值.21.已知函数()2x x f x e ae -=+-,()2g x x =(1)讨论()f x 的单调性;(2)设()()()h x f x g x =-.若函数()h x 有相同零点和极值点0x ,求()h x 的最小值.22.已知函数()21e xf x x =+-.(1)求曲线()=y f x 在点()()0,0P f 处的切线方程;(2)设函数()()()ln 1g x f x a x =-+有三个零点,求实数a 的取值范围.参考答案:1.C【分析】根据对数函数的单调性化简集合A ,根据分式不等式的解法化简集合B ,结合集合的补集和交集的定义进行求解即可.【详解】不等式()2log 1<0x -可化为()22log 1<log 1x -,所以011x <-<, 所以12x <<,所以()1,2A =, 不等式40+1xx -≥可化为()()4+10x x ->或=4x ,所以14x -<?,所以(]=1,4B -,所以(][)R 12A ,,=-∞+∞ð,所以()A B ⋂=R ð(][]1,12,4-⋃, 故选:C. 2.C【分析】由已知条件结合一元二次方程根与系数的关系,利用等比数列的性质求解. 【详解】113,a a 是方程213160x x -+=的两根,11311313,16a a a a ∴+=⋅=,21131132127>0,>0,===16a a a a a a a ∴⋅⋅,又等比数列{}n a 中奇数项符号相同,可得74a =21271644a a a ⋅∴==. 故选:C . 3.A【分析】设,AB x =则BC =,利用正弦定理即得解. 【详解】解:设,AB x =则BC . 由题得53412CBD ππππ∠=--=. 51sinsin()12642πππ=+==在△BCD20x ∴=. 所以塔高20m. 故选:A4.D【分析】对于A ,利用含量词的命题的否定即可判断;对于B ,由p 是假命题可得p ⌝:x ∀∈R ,210ax ax ++>为真命题,分=0a 和0a ≠进行讨论即可;对于C ,利用“,a b 的夹角为钝角”的充要条件即可判断;对于D ,利用正弦定理和三角形性质即可求解.【详解】对于A ,由含量词的命题的否定知,命题“2x ∀>,ln 1x x ≤-”的否定是“02x ∃>,00ln 1x x >-”,故不正确;对于B ,因为命题p 是假命题,所以p ⌝:x ∀∈R ,210ax ax ++>为真命题, 当=0a 时,不等式为10>恒成立;当0a ≠时,需满足2>0Δ=4<0a a a -⎧⎨⎩,解得04a <<, 综上所述,a 的取值范围为{}0<4a a ≤,故不正确;对于C ,“,a b 的夹角为钝角”的充要条件是“0a b ⋅<且a 不平行于b ”,所以“0a b ⋅<”是“a ,b 的夹角为钝角”的必要不充分条件,故不正确;对于D ,若A B >,由三角形中“大边对大角”可知,a b >,由正弦定理可知,sin sin A B >; 若sin sin A B >,由正弦定理可知,a b >,从而A B >, 故“A B >”是“sin sin A B >”的充要条件,故正确, 故选:D 5.D【分析】由OC xOA yOB =+uu u r uu r uu u r两边平方可得,x y 的关系,设(),m x y =,()2,1n =由数量积的性质求2x y +的最大值.【详解】因为OC xOA yOB =+uu u r uu r uu u r,两边平方可得()()()222222OC x OA xyOA OB y OB =+⋅+uuu r uu r uu r uu u r uu u r ,因为0OA OB ⋅=,所以()()()22222OC x OA y OB =+uu u r uu r uu u r ,因为点C 在以点O 为圆心的劣弧AB 上,所以OC OA OB ==uuu r uu r uu u r,且0x ≥,0y ≥,所以221x y +=, 设(),m x y =,()2,1n =,则2m n x y ?+,又=cos ,m n m n m n m n ⋅⋅⋅≤⋅,当且仅当m ,n 同向时等号成立,所以2x y +?x y ==故选:D. 6.B【分析】由题意表示出()1(1)--=--f x f x 与()1(1)f x f x -+=+,令=1x ,=0x ,=2x ,结合题目所给条件列式求解,k m ,再由两式化简可推导出()f x 的周期为8T =,从而代入计算. 【详解】因为()1f x -为奇函数,所以()1(1)--=--f x f x ①; 又()1f x +为偶函数,所以()1(1)f x f x -+=+②; 令=1x ,由②得:()(2)20==+f f k m ,又()33=+f k m , 所以()()032(3)1f f k m k m k -=+-+=-=-,得=1k , 令=0x ,由①得:()()1(1)10-=--⇒-=f f f ; 令=2x ,由②得:()1(3)0-==f f , 所以()3330f k m m =+=⇒=-. 得[]1,3x ∈时,()3f x x =-,结合①②得,()2()(2)(4)()(8)(4)()f x f x f x f x f x f x f x f x +=-=--⇒+=-⇒+=-+=, 所以函数()f x 的周期为8T =,所以()()()()()20222528662231f f f f =⨯+==-=--=. 故选:B 7.D【分析】由图象求出()f x 的解析式,再结合三角函数的性质与图像逐项分析即得. 【详解】由图可知,1(0)sin 2f ϕ==, 又π02ϕ<<,所以π6ϕ=, 所以由五点作图法可知4ππ3π362ω⋅+=,得1ω=,所以()πsin 26f x x ⎛⎫=+ ⎪⎝⎭,对于A ,由π2ππ133sin 6f ⎛⎫-⎛⎫+ ⎪⎝⎭=-=- ⎪⎝⎭,所以A 错误;对于B ,当π0,2x ⎡⎤∈⎢⎥⎣⎦时,ππ7π2,666x ⎡⎤+∈⎢⎥⎣⎦,所以1πsin 2126x ⎛⎫-≤+≤ ⎪⎝⎭,所以()f x 在区间π0,2⎡⎤⎢⎥⎣⎦的最小值为12-,所以B 错误;对于C ,当[]0,πx ∈,则ππ13π2,666x ⎡⎤⎢⎥⎣∈⎦+, 由πππ2,662x ⎡+∈⎤⎢⎥⎣⎦,可得π0,6x ⎡⎤∈⎢⎥⎣⎦,由π13π22π,66x +∈⎡⎤⎢⎥⎣⎦,可得11π,π12x ⎡⎤∈⎢⎥⎣⎦, 所以()f x 在[]0,π上的单调递增区间为π0,6⎡⎤⎢⎥⎣⎦,11π,π12⎡⎤⎢⎥⎣⎦,故C 错误; 对于D ,由题可得()πsin 26g x tx ⎛⎫+ ⎝=⎪⎭,因为()12g x =在[]0,π上有且只有三个不等实根,所以π1sin 262tx ⎛⎫+= ⎪⎝⎭在[]0,π上有且只有三个不等实根,由[]0,πx ∈,可得πππ2,2π666tx t ⎡⎤+∈+⎢⎥⎣⎦,作出正弦函数的图象,由图象可知ππ5π2π2π2π666t +≤+<+,即413t ≤<,故D 正确. 故选:D. 8.C【分析】构造函数()(0)x a f x e lnx a x -=-->,将原不等式转化为求解函数()f x 的最小值,通过导数判断函数的单调性研究函数的最值,得到000x a e lnx a ---…,再利用基本不等式进行求解即可.【详解】解:设()(0)x a f x e lnx a x -=-->,则()0f x …对一切正实数x 恒成立,即()0min f x …, 由1()x a f x e x -'=-,令1()x a h x e x -=-,则21()0x ah x e x -'=+>恒成立,所以()h x 在(0,)+∞上为增函数,当0x →时,()h x →-∞,当x →+∞时,()h x →+∞, 则在(0,)+∞上,存在0x 使得0()0h x =,当00x x <<时,()0h x <,当0x x >时,()0h x >,故函数()f x 在0(0,)x 上单调递减,在0(x ,)∞+上单调递增,所以函数()f x 在0x x =处取得最小值为000()0x a f x e lnx a -=--…, 因为001x aex -=,即00x a lnx -=-, 所以0010x a a x +--…恒成立,即0012a x x+…,又0012x x +=…,当且仅当001x x =,即01x =时取等号,故22a …,所以1a …. 故选:C .【点睛】方法点睛:不等式恒成立问题常见方法:① 分离参数()a f x ≤恒成立(min ()a f x ≤即可)或()a f x ≥恒成立(max ()a f x ≥即可);② 数形结合(()y f x = 图象在()y g x = 上方即可);③ 讨论最值min ()0f x ≥或max ()0f x ≤恒成立;④ 讨论参数. 9.ACD【分析】根据复数模、共轭复数的积运算即可判断A ,由复数除法的运算及共轭复数、虚部的概念判断B ,根据复数模的几何意义及圆的性质判断C ,利用复数的加减运算、模的运算求解可判断D.【详解】设i,(,R)z a b a b =+∈,对A ,2224z a b =⇒+=,22i)(i (4)z a b a b a z b +-=+⋅==,故正确;对B ,()72i3i z(2i)3i z +=+⇒-=+,所以3i (3i)(2i)55iz 1i 2i (2i)(2i)5++++====+--+, z 1i =-,其虚部为1-,故错误;对C ,由1i 1z +-=的几何意义,知复数z 对应的动点Z 到定点(1,1)-的距离为1, 即动点Z 的轨迹为以(1,1)-为圆心,1为半径的圆,1i z --表示动点Z 到定点(1,1)的距离,由圆的性质知,max 1i 13z --==,故正确; 对D ,设12=+i,=+i,(,,,R)z m n z c d m n c d ∈,因为12z =,22z =, 所以22224+=4m n c d +=,,又121z z +=,所以+=1,+m c n d 所以+=2mc nd -,所以12=|()+(z z m c n d ---.故选:ACD 10.AD【分析】求得等差数列{}n a 的通项公式判断选项A ;求得116m n+的最小值判断选项B ;求得n S 取到最大值时n 的值判断选项C ;求得数列{}n b 的最小项判断选项D.【详解】由11+=37?67+=72a d a d ⎧⎪⎨⎪⎩,可得1=4=1a d -⎧⎨⎩, 则等差数列{}n a 的通项公式为5n a n =-,则选项A 判断正确; 若210m n a a a a +=+,则21012m n +=+= 则116116116125(17)(178)12121212m n n m m n m n m n +⎛⎫+=+⨯=++≥+= ⎪⎝⎭ (当且仅当1248,55m n ==时等号成立) 又,m n ∈Z ,则116m n +的最小值为不为2512.则选项B 判断错误; 等差数列{}n a 中,123456432101a a a a a a =>=>=>=>=>=->则等差数列{}n a 的前n 项和n S 取到最大值时,=4n 或5n =.则选项C 判断错误; 设2n n n a b =,则52n n n b -=,则111546222n n n n n n n n b b +++----=-= 则12345678b b b b b b b b >>>>>=<<则数列{}n b 的最小项为766561264b b -===-.则选项D 判断正确 故选:AD 11.ABD【分析】利用余弦定理可判断A ,利用正弦定理结合三角恒等变换可判断B ,结合条件可得角A 的范围可判断C ,利用正弦定理及三角函数的性质可判断D. 【详解】因为cos cos a a B b A +=,所以22222222a c b b c a a a b ac bc +-+-+⋅=⋅, 整理可得22=b a ac -,故A 正确;由cos cos a a B b A +=,可得sin sin cos sin cos A A B B A +=, 所以()sin sin cos sin cos sin A B A A B B A =-=-,所以A B A =-或πA B A +-=(舍去),即2B A =,故B 正确;因为ABC △为锐角三角形,所以π0<<2π0<=2<2π0<=π3<2A B A C A -⎧⎪⎪⎪⎨⎪⎪⎪⎩,解得ππ<<64A ,故C 错误;由题可得()sin 2sin 3sin sin sin sin A A b c B C a A Aπ+-++==, sin 2sin 2cos cos 2sin sin A A A A A A++=22cos 2cos cos2A A A =++ 24cos 2cos 1A A =+-,又ππ<<64AA所以)+b ca∈,故D 正确. 故选:ABD 12.ACD【分析】利用向量的数量积运算律和模的运算求解2a b +r r,根据投影向量定义求解a 在b 方向上的投影向量,构造如图所示的几何图形集合几何意义求c 的最小值,作出满足题意的几何图形求解()m m b ⋅-的最小值.【详解】因为1a =,2b =且()a ab ⊥-,所以()20a a b a a b ⋅-=-⋅=,所以1a b ⋅=,1cos ,2a b a ba b⋅=,所以a ,b 的夹角为60,因为()222224423a b a ba b a b +=+=++⋅=,所以A 正确;a 在b 方向上的投影向量为1cos ,4ba ab b b ⋅=,所以B 错误;如图,作半径都等于2且公共弦长等于2的两个圆中, 2,,,OA a OB b OC c ===则2,AC c a BC c b =-=-,因为30ACB ∠=,所以2,30c a c b --=︒,符合题意, 由图可知,当OC 同过两圆的圆心时c 最大,此时c 的最大值等于圆心距加半径为2, 所以C 正确;作,,OA a OB b ==如图,222222()23AB b a b a b a OB OA =-=+-⋅==-, 所以90OAB ∠=,令OM m =,由2m a ⋅=得cos 2OM AOM ∠=, 在射线OA 上取点E ,使得2OE =,过E 作直线l OA ⊥,则有点M 在直线l 上,取OB 中点C ,过C 作CD l ⊥,垂足为D , 连接,,BM CM OM ,()()()()()m m b OM BM OC CM BC CM OC CM OC CM ⋅-=⋅=+⋅+=+⋅-+2222151124CM OC CD OA AE ⎛⎫=-≥-=+-= ⎪⎝⎭, 当且仅当,M D 重合时取得等号,所以()m m b ⋅-的最小值为54. 所以D 正确. 故选:ACD.【点睛】结合向量间的关系作出满足题意的几何图形,利用几何意义求解相关最值问题是向量最值问题有效的手段. 13.2【分析】转化条件为()112+226a d a d =++,即可得解.【详解】由32236S S =+可得()()123122+36a a a a a +=++,化简得31226a a a =++, 即()112+226a d a d =++,解得2d =. 故答案为:2.14.【分析】将2sin18m =︒代入,根据恒等变换公式化简,即可求得结果 【详解】2sin18m =︒Q ,2sin144m -⋅︒4sin 182sin 36︒-︒===故答案为:15.32##1.5【分析】设三角形ABC 的外接圆的半径为r ,根据向量数量积的几何定义可得22211222b c c b mr c b ⋅+⋅=,从而可得22bc mr =,从而可得222m b br r =⋅,又sin sin B C +=正弦定理可得sin 2b B r =,sin 2cC r =,从而可得22b c r r+ 【详解】设三角形ABC 的外接圆的半径为r ,2||||2()||||AC AB AB AO AC AO m AO AB AC ⋅+⋅=, ∴根据向量数量积的几何定义可得:22211222b c c b mr c b ⋅+⋅=,即22bc mr =,∴=222m b c r r⋅,又sin sin B C +=sin 2b B r =,sin 2cC r =,∴22b c r r+ ∴2322()22224b cm b b r r r r +=⋅≤=,当且仅当22b c r r =时,即ABC △为等边三角形时取等号,∴324m ≤,32m ∴≤,∴实数m 的最大值为32. 故答案为:3216.4【分析】先将题给条件转化为()()2+1++2=0e e x x x x a a -⎛⎫⎪⎝⎭有三个不同的零点1x ,2x ,3x ,且123<<x x x ,再转化为()()2+1++2=0t a t a -有二根12,t t ,且121<0,0<<et t ,进而利用根与系数关系求得3122312111e e e x x x x x x ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值 【详解】()()()()()22222e 1e =e 12e e xxxx x x xf x a a x x a a ⎡⎤⎛⎫=+-++-+++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,又2e >0x ,则()()2+1++2=0e e x x x x a a -⎛⎫⎪⎝⎭有三个不同的零点1x ,2x ,3x ,且123<<x x x ,令()e xx g x =,则1()e x x g x -'=, 当>1x 时()<0g x ',()g x 单调递减;当<1x 时()>0g x ',()g x 单调递增 则()g x 在=1x 时取得最大值1(1)=eg ,>0x 时()>0g x ,令e xx t =,则1e t ≤ 则()()2+1++2=0t a t a -必有二根12,t t ,且121<0,0<<et t则12121,2t t a t t a +=+=+ 则1e x x t =有一解1<0x ,2ex xt =有二解23,x x 且230<<1<x x 故()()3122223121211111e e ex x x x x x t t ⎛⎫⎛⎫⎛⎫---=-- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭[][]221212=1(+)+=1(+1)++2=4t t t t a a --故答案为:417.(1)函数()f x 的最小正周期为π,单调递增区间为5,,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦【分析】(1)由三角恒等变换化简解析式,求出周期,再由正弦函数的单调性求解即可;(2)由()f A sin 23A π⎛⎫=-= ⎪⎝⎭A ,利用余弦定理可求得AB 边的长,再利用三角形的面积公式可求得结果. (1)()22sin cos cos sin sin sin cos 33f x x x x x x x ππ⎛⎫=+= ⎪⎝⎭)1cos211sin2sin2sin 22223x x x x x π-⎛⎫=+==- ⎪⎝⎭ 所以函数()f x 的最小正周期为22T ππ== 由222,232k x k k Z πππππ-+≤-≤+∈得出5,1212k x k k Z ππππ-+≤≤+∈ 故函数()f x 的单调递增区间为5,,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦(2)()f A sin 23A π⎛⎫=-=⎪⎝⎭因为02A π<<,则22333A πππ-<-<,所以233A ππ-=,可得3A π=,由余弦定理可得222232cos23BC AB AC AB AC AB π==+-⋅=+,即210AB -=,因为0AB >,解得AB = 此时,AB 为最长边,角C 为最大角,此时222cos 02AC BC AB C AC BC+-=>⋅,则角C 为锐角,所以,11sin 22ABCSAB AC A =⋅=18.(1)2n n a =;(2)1112(1)2n n T n +=-+⋅.【分析】(1)由等比数列前n 项和公式列方程组求得1,a q ,得通项公式; (2)用裂项相消法求和. (1)设{}n a 的公比为q ,显然1q ≠,0q >,由题意1141+=6(1)=301a a q a q q--⎧⎪⎨⎪⎩,解得1=2=2a q ⎧⎨⎩(负数舍去).所以1222n nn a -=⨯=;(2) 由(1)11211(1)22(1)2n n n n n b n n n n +++==-+⋅⋅+⋅,所以2231111111()()[]122222322(1)2n n n T n n+=-+-++-⋅⋅⋅⋅⋅+⋅1112(1)2n n +=-+⋅.19.1; (2)【分析】(1)已知214S a =,由面积公式和余弦定理得π)4c b A b c +=+,由已知及正弦定理和三角恒等变换得π4A =,则有c b b c+=. (2)由π)4c b A b c +=+,结合正弦函数性质求最值..(1)ABC 的面积211sin 42S a bc A ==,有22sin a bc A =,由余弦定理,2222sin 2cos a bc A b c bc A ==+-,得2sin 2cos c bA A bc=+-,即π2sin +2cos)4c bA A A b c +==+, cosB b -cos sin A B CB =-,由[]sin sin()sin()sin coscos sin C A B A B A B A B =π-+=+=+, i n c n n cos sin sin os si A A B C B B A B B =--=sin sin 0A B B -=,ABC 中sin 0B ≠,∴cos A =(0,π)A ∈,则π4A =,∴π)4c b A b c +=+=c t b =,则有1t t+=1t ,由正弦定理,sin 1sin C cB b==. (2)由(1)有:π)4c b A b c +=+,A 为ABC 的内角,当π4A =时,c bb c +有最大值20.(1)12n n a +=,12n n b +=; (2)3【分析】(1)由等差数列的基本量法求得n b ,由1(2)n n n a S S n -=-≥求得n a ; (2)用错位相减法求得和n T ,代入不等式化简后转化为用基本不等式求函数的最值. (1)设数列{}n b 的公差为d ,则225168(22)1222325b d b b b d d d +==++-++++,12d =, 所以112(3)22n n b n +=+-⨯=, 1=1b ,224n n S +=-,311244a S ==-=,2n ≥时,211124(24)2n n n n n n a S S +++-=-=---=,1=4a 也适用,所以12n n a +=;(2)由(1)(1)2nn n a b n =+⋅,22232(1)2n n T n =⨯+⨯+++⋅,231222322(1)2n n n T n n +=⨯+⨯++⋅++⋅,两式相减得2314222(1)2n n n T n +-=++++-+⋅1114(12)4(1)2212n n n n n -++-=+-+⋅=-⋅-,所以12n n T n +=⋅.所以不等式226>8+25n n kT n a n n -即为26>8+25nk n n -, 又266258258n n n n n =-++-,2510n n +≥=,当且仅当5n =时等号成立, 所以26825n n n -+的最大值是63108=-,故3k ≥, 所以k 的最小值是3.21.(1)当0a ≤ 时,()f x 在R 上单调递增;当>0a 时,()f x在)∞上单调递增,在(-∞上单调递减. (2)()h x 的最小值为0.【分析】(1)先函数求导,对参数进行分类讨论得出结论(2)构造函数对函数求导,利用已知条件求出参数,分析问题,将参数的值代入表达式中求出函数的最小值. (1)由()e e 2x xf x a -=+-,所以()e e x x f x a -'=-,当0a ≤ 时,()0f x '≥,此时()f x 在R 上单调递增, 当0a > 时,由()0f x '>,有x >()f x在)+∞上单调递增, 由()0f x '<,有x <()f x在(-∞上单调递减, 综上所述:当0a ≤ 时,()f x 在R 上单调递增;当0a > 时,()f x在)+∞上单调递增,在(-∞上单调递减. (2)由()()()2e 2x x e a h x g x xf x ---==+-所以()e e 2x xa x x h --'=-,又函数()h x 有相同零点和极值点0x ,所以有0000200e +e 2=0e e 2=0x x x x a x a x --⎧--⎪⎨--⎪⎩,两式相加得:02002e 22x x x =++, 令()22e 22x p x x x =---,则()2e 22xp x x '=--,设()2e 22x s x x =--,则()2e 2xs x '=-,所以()s x 在(),0-∞上单调递减,在()0,+∞上单调递增,所以()()00s x s ≥=, 所以()p x 单调递增,由()00p =可得00x =,=1a ,所以()22x x e x e x h -+--=,所以()2x x e x h x e ---'=,设()2x xe e x t x --=-所以()120xxx e t e '+-≥=,当且仅当=0x 时取等号. 所以()h x '在R 单调递增,又()00h '=所以当0x >时,()0'>h x ,所以()h x '在(0,)+∞上单调递增, 当0x <时,()0'<h x ,所以()h x '在(,0)-∞上单调递减 所以()min 0)0(h x h == 故()h x 的最小值为0. 22.(1)=y x (2)(0,1)【分析】(1)求得(0),(0)f f ',利用导数的几何意义得出切线的方程;(2)求出()g x 的导数,通过分类讨论a 的范围,求出函数的单调区间,结合函数的零点个数确定a 的范围即可. (1)()21e x f x x =+-,()2e x f x '=-∴,则(0)0,(0)1f f '==,因此,曲线()y f x =在点()()0,0P f 处的切线方程为y x =.(2)()21e ln(1),(1)x g x x a x x =+--+>-,则()(1)e 2()2e 11x xa x a g x x x ⎡⎤-++-⎣⎦'=---=++, 设h ()()(1)e 2xx a x =++-,则()(2)e 2x h x x '=+-,显然()h x '在(1,)-+∞内递增且(0)0h '=, 所以,在(1,0)x ∈-时,()0,()h x h x <'单调递减, 在(0,)x ∈+∞时,()0,()h x h x >'单调递增, 所以()h x 有极小值(0)1h a =-,又(1)h a -=,①当1a ≥时,()0h x ≥在(1,)x ∈-+∞恒成立,即()0g x '≤,所以()g x 在区间(1,)-+∞内单调递减,最多一个零点,不符合题意; ②当01a <<时,(1)0,(0)0,(2)0h h h -><>, 所以存在12(1,0),(0,2)x x ∈-∈使得()()120h x h x ==, 则在()11,x -内,()0h x >,()0,()g x g x <'单调递减, 在()12,x x 内,()0h x <,()0,()g x g x >'单调递增, 在()2,x +∞内,()0h x >,()0,()g x g x <'单调递减,又()()12(0)0g x g g x <=<,则()g x 在()12,x x 上有且只有一个零点0, 又2(2)5e ln30g a =--<,则()g x 在()2,x +∞上有且只有一个零点,又4411544442e e e e 12e 11eln e 2e e 2e e 130a a a a a a ag a ----------⎛⎫⎛⎫-=-+-+--=->> ⎪⎝⎝⎭+⎪ ⎭,则()g x 在()11,x -上有且只有一个零点,所以函数()g x 恰有三个零点;③当0a ≤时,在(1,0]-内()(0)0h x h <<,又()2(2)(3)e (3)02ah a a a a a --=+->+->-,结合()h x 的单调性可知,存在0(0,)x ∈+∞,使得()00h x =,在()01,x -内,()0h x <,()0g x '>,()g x 单调递增, 在()0,x +∞内,()0h x >,()0g x '<,()g x 单调递减, 函数()g x 最多两个零点,不合题意. 综上所述,实数a 的取值范围是(0,1).。
地理丨黑龙江省哈尔滨市第三中学2025届高三10月月考地理试卷及答案

哈三中2024-2025学年度上学高三十月月考地理试卷第Ⅰ卷选择题一、选择题:本题共30小题,每小题1.5分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
湖南省湘阴县樟树镇处于南洞庭湖平原与峨形山脉交接的丘岗山地,三面环水,年均气温为17.1℃。
国家地理标志产品“樟树港辣椒”是当地农民经过200多年栽培选育而成的具有明显地方特色的农产品,始终沿用传统的露地轮作栽培方法,以施用农家有机肥或商品有机肥为主,一般于“五一节”前开始上市,常年栽培面积徘徊在267公顷左右,大户栽培面积也只有0.2~0.4公顷。
据此完成1~2题。
1.樟树港辣椒风味独特主要得益于A.种植历史悠久B.栽培方式传统C.地理环境独特D.地势起伏和缓2.樟树港辣椒产业化发展的主要限制性因素是A.种植方式B.种植规模C.品牌效应D.市场规模第七次全国人口普查数据显示,某省2020年人口总数为7461万人。
据学者判断,该省人口规模已达到峰值,到2030年将降至7437万人。
图1示意该省2020年和2030年的人口金字塔。
据此完成3~4题。
图13.与2020年相比,2030年该省人口结构呈现出A.少儿人口占比增加B.劳动力人口结构年轻化C.老年人口中的女性占比减少D.高龄人口在老年人口中占比增加4.面对该省未来人口结构问题,建议采取的积极应对措施包括①渐进式延迟退休年龄②完善社会养老保障体系③全面鼓励生育政策④加快工业化和城市化进程A.①②B.①③C.②④D.③④区域性人口回流是指流动人口由跨省流动转为省内流动,亦或由省内跨市流动转为市内跨县流动的返迁流动行为。
图2示意近年我国区域性回流人口在不同行政等级城镇的分布。
据此完成5~7题。
图25.关于图2的叙述,说法正确的是A.全国省会城市和直辖市接受的区域性回流人口最多B.东部地区的省会城市是区域性人口回流主要目的地C.西部地区的县级城市对区域性回流人口吸引力最强D.中部地区普通地级城市的区域性人口回流占比最高6.与县级城市相比,普通地级城市区域性人口回流占比高的主要原因是①二、三产业发展水平更高②占地面积更广大③工资水平和生活成本更高④公共服务更完善A.①②B.②③C.①④D.②④7.针对我国人口区域性回流现象,下列应对措施合理的是A.提高直辖市能源工业、重化工业比重B.扶持技能型劳动力丰富的普通地级城市发展C.调整直辖市产业结构,扩大就业空间D.全面落实城市落户、住房、医疗、教育等平等化苏格兰高地的天空岛,也叫斯凯岛,是英国的世外桃源,岛上几乎没有天然树木,图3为该岛地理位置、当地局部地貌景观和传统民居景观。
2023届高三10月月考政治试卷带参考答案和解析(黑龙江省哈尔滨市第六中学)

选择题随着智能手机的功能越来越强大,MP3(音乐播放器)、电子词典、掌上游戏机等电子产品正慢慢淡出人们的视野。
这说明()①市场竞争导致商品优胜劣汰②商品使用价值会影响人的消费选择③功能不同的商品会相互替代④商品使用价值因替代品出现而减小A. ①②B. ①③C. ②④D. ③④【答案】A【解析】本题考查商品的基本属性和互为替代品的知识。
MP3(音乐播放器)、电子词典、掌上游戏机等电子产品正慢慢淡出人们的视野,是市场竞争的结果,①符合题意。
智能手机的功能越来越强大,能够满足人们越来越多的需要,促使更多的人选择购买智能手机,②符合题意。
使用价值是商品的自然属性,不同商品的使用价值在质上是不同的,不能进行量的比较,④说法错误。
两种商品的功能相同或相近,可以满足人们的同一需要,这两种商品才能相互替代,③表述错误。
故选A。
选择题汽车行业属于资本密集型行业,行业的劳动生产率较高。
当前,家用轿车价格普遍较低,我国已经进入了汽车社会。
从根本上说,汽车变得相对便宜的原因是A. 汽车质量下降B. 社会需求量大C. 汽车行业社会必要劳动时间缩短D. 汽车供给量大【答案】C【解析】题干中要求选的是汽车变得相对便宜的根本原因是什么,这应该从商品的价值量上找,商品的价值量由生产该商品的社会必要劳动时间决定的,汽车行业的劳动生产率提高,从而缩短了生产汽车的社会必要劳动时间,使得汽车的价值量下降,也就是价格降低,使汽车进入寻常百姓家,我国进入汽车社会。
C项符合题意;汽车质量下降与当前实际不符合,A项观点错误;供求影响价格,若社会需求量大,会导致汽车价格上升,而不是下降,B项不合题意;D项不是根本原因,D项不合题意。
答案选C。
选择题最低工资制度旨在保护低收入劳动者的合法权益,因此最低工资应高于劳动力市场供需平衡时的工资水平。
2017年,我国有22个地区提高了最低工资标准。
在其他条件不变的情况下,如图中(P代表劳动力价格,Q代表劳动力数量,D、S分别代表需求曲线和供给曲线,P1、P2分别表示变化前后的劳动力价格)能正确反映这一变化的是A.B.C.D.【答案】A【解析】本题考查实现收入分配的公平。
黑龙江省哈尔滨市第六中学2016届高三上学期12月月考地理试卷Word版含答案

2014届哈六中高二地理考试一.选择题(1-20题每题1分,21—40题每题2分,共计60分)2013年7月30日,我国西北某地出现强沙尘暴。
图1示意该地当日14时~24时气温、气压随时间的变化。
据此完成1~2题。
1. 强沙尘暴经过该地的时间段是A .16时~17时B .17时~18时C .18时~19时D .19时~20时 2.与正常情况相比,强沙尘暴经过时,该地A .气温水平差异减小B .水平气压梯度增大C .地面吸收太阳辐射增多D .大气逆辐射减弱圣劳伦斯河(图3a )是一条著名的“冰冻之河”。
图3b 示意蒙特利尔年内各月气温和降水量。
据此完成3~5题。
3.蒙特利尔附近河段结冰期大致为A .2个月B .3个月C . 4个月D .5个月 4.据图示信息推测,冬季可能不结冰的河段位于A .安大略湖至普雷斯科特河段B .普雷斯科特至康沃尔河段C .蒙特利尔至魁北克河段D .魁北克以下河口段 5.减少该河凌汛危害的可行措施是①加深河道 ②绿化河堤 ③分段拦冰 ④拓宽河道 A .①② B.②③ C.③④ D.①④受强冷空气影响,预计2015年3月10日8时,南疆盆地、西北地区东部、华北、东北地区南部、黄淮、江淮、江汉、江南北部等地气温下降6~10℃。
读亚洲局部区域此时海平面等压线分布图(图3)(单位:hPa ),回答6-8题。
6.下列关于乌兰巴托、北京、郑州、合肥、东京五地的叙述,正确的是 A.乌拉巴托上升气流较强 B.东京、北京处于阴雨天气C.东京和合肥的气压差低于15百帕D.合肥的风速大于北京处7.由图可知,N 地与乌兰巴托气压的最大差是A.16帕B.18帕C.24帕D.21帕 8.由此可知以下说法错误的是气压/hp b气温气压图1气温/℃A.受冷空气影响,京津冀等地的霾可能会逐渐减弱消散B.西北地区的大气能见度会降低C.黑龙江、吉林等地出行时需关注封路信息D.影响我国中东部地区的天气系统为锋面气旋图4为部分经纬线图,30°N纬线与120°E经线相交于①地,①、②、③、④地位于同一经线圈上,且①与②、②与③之间纬度差均为15°,N为北极点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈尔滨市第六中学2016届十月月考地理试题一.选择题(1-20题每题1分,21—40题每题2分,共计60分)1. 亚洲贝加尔湖和北美五大湖的形成原因分别是:①地壳陷落②熔岩阻塞③冰川侵蚀④海底抬升⑤河床阻塞A.①和②B.③和⑤C.①和③D.②和④下图中甲、乙、丙、丁表示四条著名山脉。
读图回答2~3题。
2.下列关于甲、乙、丙、丁四山脉位置的说法,正确的是A.甲位于国界线上B.乙位于大洲分界线上C.丙位于俄罗斯地形分界线上D.丁位于我国地势阶梯分界线上3.四幅图中A.a、b两地相距约2 200千米 B.d地位于c地的东北方向C.e地和f地分属不同的国家 D.g地和h地内力作用强烈读世界四区域简图(阴影部分表示陆地),完成4~6题:4.甲、乙、丙、丁所示区域中,气候类型相同的是A.甲和乙B.乙和丙C.乙和丁D.甲和丙5.图中A、B两地的主导产业相似,都是A.电子工业B.钢铁工业C.麻纺织工业D.石油化工6.下面关于甲、乙、丙、丁四个区域的叙述,不正确的是A.图中四个城市A、B、C、D都不是所在国的首都B.目前B地跨国公司在D地所在国建立了许多分公司C.四区域河流的补给类型都以雨水补给为主,所以汛期都出现在夏季D.丁区域有世界著名的金融中心右图为世界某地区图。
读图回答7~8题。
7.下列关于该地区地理事物的叙述,正确的是A.该地区位于西半球和北半球B.该地区山势雄伟,景色优美C.该地区终年温和多雨D.该地区植被为荒漠8.当自西向东通过图中海峡的轮船顺风顺水时,下列说法正确的是A.南极正处于科学考察的有利时期B.开普敦正值多雨季节C.北京受亚洲低压影响 D.伦敦正午太阳高度达一年中最大值马达加斯加地广人稀,水稻种植有着得天独厚的优越性,全国各地都有栽培,但仍不能完全自给。
2008年9月25日上午11:30(北京时间),马达加斯加政府选派的10名农业专家抵湘(中国湖南),正式向杂交水稻之父袁隆平拜师学艺。
读图回答9~11题。
9.①地稻米产区与湖南省稻米产区相似的区位条件是A.灌溉水源丰富,机械化程度高B.气候类型相同,土壤肥沃C.地势平坦,高温期与多雨期一致D.精耕细作,技术条件优越10.马达加斯加稻米不能自给的原因是A.粮食需求量增长过快B.农业技术落后,产量低C.岛国,种植面积有限D.国际市场稻米价格低廉11.下列地理事物(或现象)的成因与图中②地自然带成因最接近的是A.撒哈拉沙漠直逼非洲西海岸 B.东非高原出现热带草原带C.南半球亚寒带针叶林带缺失 D.澳大利亚东北部的热带雨林带读“某地区地形剖面图”,完成12~13题。
12、图中高地可能是A、巴塔哥尼亚高原B、大分水岭C、安第斯山D、巴西高原13、图中地形剖面最低处,可能位于A、巨大的裂谷带上B、太平洋板块和美洲板块张裂处C、深海盆中部D、南极洲板块和美洲板块俯冲带上读30°N附近四个地区简图,回答14~15题。
14.①、②、③、④四城市气候特征相似的是A.①和② B.②和③ C.③和④ D.①和④15.关于图中四城市的叙述正确的是A.①为该国最大的城市和港口B.②附近海域有著名渔场C.③为该国重要的金融中心 D.④所在地区有飓风灾害右图世界某区域图,回答16~17题。
16.下列四图中,正确表示A处气候资料的是17.关于图中B处农业地域类型的叙述,正确的是A.混合农业,专业化程度高B.大牧场放牧业,对国际市场依赖性大C.商品谷物农业,经营规模大D.季风水田农业,水利工程量大读右下图,回答18~19题。
18.图中四国为了保证本国能源长期稳定供应,可采取的应对措施是A.甲国利用其丰富的天然气资源替代石油B.乙国从其东面邻国大量进口石油C.丙国大量动用石油战略储备D.丁国利用甘蔗等作物生产生物能源19.有关图中四国应对粮食安全问题的叙述,正确的是A.甲国保护耕地,提高单位面积粮食产量B.乙国加大开垦力度,扩大耕地面积C.丙国大量进口小麦,提高粮食安全储量D.丁国利用生物转化能源,减少粮食出口下图为“世界某区域海洋与陆地自然带分布图”。
读图,完成20~22题。
20.图中洋流的名称是A.加那利寒流B.西澳大利亚寒流C.本格拉寒流D.秘鲁寒流21.X地降水主要集中在A.12月至次年2月B.3~5月C.6~8月D.9~11月22.沿X——Y——Z自然景观的变化是A.阔叶林——森林草原——荒漠B.硬叶林——草原——荒漠C.落叶林——草原——荒漠D.雨林——稀树草原——荒漠读印度及周边国家轮廓图,据此回答23~24题。
23.有关印度地理特征的叙述,正确的是A.绝大部分领土在热带B.是亚洲耕地面积最大、产粮最多的国家C.印度河是印度最主要的河流D.恒河三角洲是印度重要的产棉区24.关于该区域自然环境的叙述,正确的是A.地形以山地为主B.自西向东降水量逐渐减少C.河流水量大、水位季节变化小D.蕴藏有丰富的煤、铁、锰等矿产资源读右图,世界某区域图,完成25~26题。
25.与图中沙漠形成主导原因相同的地区是①阿拉伯半岛的沙漠②安第斯山南段东侧的沙漠③澳大利亚中西部的沙漠④塔里木盆地的沙漠A.①③ B.①②C.②④ D.③④26.图示季节,沿河流各段及周边区域地理现象的描述不正确的是A.①→②河段正值丰水期B.②→③河段水量减少C.③→④河段沿岸草木枯黄D.④→⑤河段森林茂密下图为亚洲某国年降水量分布图。
读图回答27~29题。
山峰城市河流国界年等降水量线(mm )湖泊3905100100200100图 2200甲丁乙丙116°116°100°52°52°44°44°27. 据图示信息推断,甲、乙、丙、丁四城市中,人口数量最多的应是A. 甲城市B. 乙城市C. 丙城市D. 丁城市28. 针对该国面临的突出生态环境问题,应采取的主要防治措施是A. 调整农作物熟制B. 大面积营造水土保持林C. 广泛建设人工水域D. 实施林草结合的防风固沙工程 29. 下列结论的依据,所用图示信息正确的是 A. 河流稀少,有内流河,所以该国为内陆国B. 中、东部城市分布较多,故该国中、东部为平原C. 位于温带地区,导致该国1月平均气温在0℃以下D. 降水稀少且呈带状分布,使该国植被景观东西延伸、南北更替欧洲鳗孵化于马尾藻海,幼体随着洋流到达欧洲西部沿海,然后进入河流生活,成年后回到马尾藻海,产卵后死亡。
读下图,完成30-31题。
30.欧洲鳗从马尾藻海西南部迁往欧洲,首先借助的洋流属于①以副热带为中心的大洋环流 ②以副极地为中心的大洋环流 ③暖流④寒流 A .①③B .①④C .②③D .②④31.甲地自然环境深受海洋影响,在河流水文特征方面表现为A .流量稳定、水量丰富B .含沙量小、冰期短C .水量丰富、落差小D .流速缓慢、流量稳定 读下图为中国科考队南极考察示意图,完成32--33题。
32.由长城站往东,依次经过的大洋是A.太平洋、印度洋、大西洋B.大西洋、太平洋、印度洋C.大西洋、印度洋、太平洋D.太平洋、大西洋、印度洋33.12月18日,考察队到达距南极中山站12海里外的陆缘冰区,经过仔细研究,决定放弃原先的冰上运货计划,改用直升飞机往中山站调运物资。
其原因可能是A.空运速度快,运输方便B.气温偏高,陆缘冰出现了松软和开裂C.冰上行走不便D.气温偏低,不宜长时间野外活动某探险协会组织“火山主题探险旅游”,目的地分别为下图中甲、乙、丙、丁四个半岛或岛屿上的火山。
完成34~35 题。
34.图中某一地火山附近的板块边界类型与其它三地不同,它是A.甲 B.乙 C.丙 D.丁35.在甲、乙、丙、丁四地附近还可以欣赏到的特色景观依次是A.肥美草原牧场、高峻海岸山脉、旖旎峡湾风光、填海造陆工程B.高峻海岸山脉、填海造陆工程、肥美草原牧场、旖旎峡湾风光C.高峻海岸山脉、旖旎峡湾风光、肥美草原牧场、填海造陆工程D.填海造陆工程、旖旎峡湾风光、高峻海岸山脉、肥美草原牧场下图甲、乙分别为某区域城市和乡村两种不同景观,景观与当地某种资源短缺有关。
完成36—37题。
甲乙36.图示两景观共同反映了某区域的环境特征,则该区域最可能位于A .拉美B .西亚C .西欧D .东亚 37.关于该区域叙述正确的是A .图甲景观与石油开采相关B .图甲景观主要用于收集太阳能C .图乙景观中心区为井D .图乙景观种植的农作物为水稻下图为45ºN 附近某区域的遥感影像,其中深色部分为植被覆盖区,浅色部分为高原荒漠区;终年冰雪覆盖的山峰海拔3424米,距海约180千米.读图2,完成38~40题。
38. 导致图示区域内降水差异的主导因素是A. 大气环流B. 地形C. 纬度位置D. 洋流 39. 该区域位于A. 亚欧大陆太平洋沿岸地区B. 亚欧大陆大西洋沿岸地区C. 北美洲大西洋沿岸地区D. 北美洲太平洋沿岸地区 40. 该区域中山脉西坡山麓的自然植被属于A. 常绿阔叶林B. 常绿硬叶林C. 针阔叶混交林D. 草原二.综合题41.读“欧洲部分区域图”,分析回答有关问题。
(20分) (1)图中字母表示的地理事物名称分别是(4分)A________(海域),B________(海域), C________(河流),D____________(山脉)。
(2)简述①国地形、地势的主要特点。
(3分)高原荒漠区植被覆盖区山峰山脉 0 12N(3)分析图示地区1月份等温线分布的特点,并分析其原因。
(4分)(4)说出图示区域国家的主要气候类型、特点及形成原因。
(6分)(5)②国阴影区域种植的主要农作物是________,与本国西部地区相比,该区域发展种植业有什么优越的气候条件?(3分)42.阅读资料,完成下列问题。
(20分)材料一:下图为亚洲某国示意图材料二:该国盛产番红花,番红花喜冷凉湿润。
(1)分析图中卡维尔盐沼含盐较高的原因。
(6分)(2)根据材料,判断ABC三地中哪一个最适合大面积种植番红花,并说明理由。
(8分)(3)你认为图示国家是否应该大力发展炼油工业,并说明理由。
(6分)河阿尔卑斯山(4分) (2)东南部以高原和山地为主,西北部以平原为主;东南较高,西北较低(或地势由东南向西北倾斜)。
(3分)(3)特点:等温线走向大致与海岸线平行,温度值由沿海向内陆逐渐降低。
原因:该区域位于欧洲西部,气候深受北大西洋暖流影响;离海洋越远,大陆性越强,冬季气温越低。
(4分)(4)温带海洋性气候冬季温和夏季凉爽,气温日较差和年较差小,降水较多且季节分配较均匀常年受西风影响,沿岸有北大西洋暖流经过,增温增湿。
(5)小麦与西部地区相比,该区域地处西风带的背风地带,晴天较多(降水较少),光热资源较为丰富,有利于发展种植业。
