六年级数学创新思维训练一

合集下载

六年级趣味数学思维训练题50道及答案

六年级趣味数学思维训练题50道及答案(1) 【图形分割】如图，要求把正方形分成四块，两个正方形共分为八块，使每块的大小和形状都相同，而且都带一个○．(2) 【图形面积】如图所示，在正方形ABCD 中，红色，绿色正方形的面积分别是52和13，且红，绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点，另一个顶点位于绿色正方形两条对角线的交点，求黄色正方形面积.(3) 【行程问题】龟兔进行10000米跑步比赛。

兔每分钟跑400米，龟每分钟跑80米，兔每跑5分钟歇25分钟，谁先到达终点？(4) 【统筹规划】有1993名少先队员分散在一条公路上值勤宣传交通法规，问完成任务后应该在公路的什么地点集合，可以使他们从各自的宣传岗位沿公路走到集合地点的路程总和最小.(5) 【行程问题】已知猫跑5步的路程与狗跑3步的路程相同；猫跑7步的路程绿黄红D C B A与兔跑5步的路程相同．而猫跑3步的时间与狗跑5步的时间相同；猫跑5步的时间与兔跑7步的时间相同，猫，狗，兔沿着周长为300米的圆形跑道，同时同向同地出发．问当它们出发后第一次相遇时各跑了多少路程？(6)【逻辑推理】在S岛上居住着100个人，其中一些人总是说假话，其余人则永远说真话，岛上的每一位居民崇拜三个神之一：太阳神，月亮神和地球神．向岛上的每一位居民提三个问题：⑴您崇拜太阳神吗？⑴您崇拜月亮神吗？⑴您崇拜地球神吗？对第一个问题有60人回答：“是”；对第二个问题有40人回答：“是”；对第三个问题有30人回答：“是”．他们中有多少人说的是假话？(7)【统筹规划】小明骑在牛背上赶牛过河．共有甲，乙，丙，丁4头牛．甲牛过河需要1分钟，乙牛过河需要2分钟，丙牛过河需要5分钟，丁牛过河需要6分钟．每次只能赶两头牛过河，那么小明要把这4头牛都赶到对岸，最小要用__________分钟.(8)【不定方程】庙里有若干个大和尚和若干个小和尚，已知7个大和尚每天共吃41个馒头，29个小和尚每天共吃11个馒头，平均每个和尚每天恰好吃一个馒头．问：庙里至少有多少个和尚？(9)【行程问题】有两支香，第一支长34厘米；第二支长18厘米，同时点燃后，都是平均每分钟燃掉2厘米，多少分钟后第一支香的长度是第二支香的长度的3倍(10)【年龄问题】同学们可能知道，歌星，影星一般都不愿意公开自己的年龄。

六年级数学思维操(数学水平提升题)

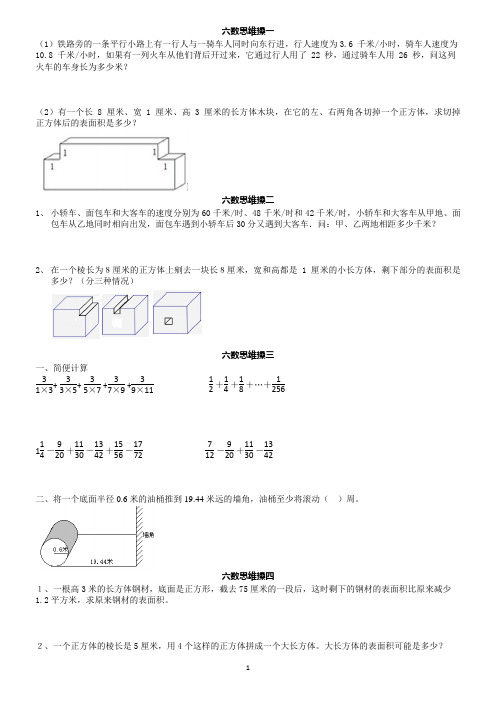
六数思维操一（1）铁路旁的一条平行小路上有一行人与一骑车人同时向东行进，行人速度为3.6 千米/小时，骑车人速度为 10.8 千米/小时，如果有一列火车从他们背后开过来，它通过行人用了 22 秒，通过骑车人用 26 秒，问这列火车的车身长为多少米？（2）有一个长 8 厘米、宽 1 厘米、高 3 厘米的长方体木块，在它的左、右两角各切掉一个正方体，求切掉正方体后的表面积是多少？六数思维操二 1、小轿车、面包车和大客车的速度分别为60千米/时、48千米/时和42千米/时，小轿车和大客车从甲地、面包车从乙地同时相向出发，面包车遇到小轿车后30分又遇到大客车．问：甲、乙两地相距多少千米？2、在一个棱长为８厘米的正方体上剜去一块长８厘米，宽和高都是1厘米的小长方体，剩下部分的表面积是多少？（分三种情况）六数思维操三一、简便计算31×3+ 33×5+ 35×7 +37×9 +39×1112 ＋14 ＋18 ＋…＋1256114 －920 ＋1130 －1342 ＋1556 －1772 712 －920 ＋1130 －1342二、将一个底面半径 0.6 米的油桶推到 19.44 米远的墙角，油桶至少将滚动（）周。

六数思维操四１、一根高3米的长方体钢材，底面是正方形，截去75厘米的一段后，这时剩下的钢材的表面积比原来减少1.2平方米，求原来钢材的表面积。

２、一个正方体的棱长是5厘米，用4个这样的正方体拼成一个大长方体。

大长方体的表面积可能是多少？六数思维操五（来源：小学生数学报）１、一个长方体，前面与上面的面积和是 209 平方厘米，这个长方体的长、宽、高都是以厘米为单位的质数。

这个长方体的表面积是多少？２、如图，从一个棱长为 5 厘米的正方体木料上，剜去一个长是 5 厘米、宽和高都是 1 厘米的小长方体木块有三种方法，剩余部分的表面积分别是多少？３、如图，有一个正方体被切成 24 个小长方体，这些长方体的表面积之和为 162 平方厘米，那么原正方体的表面积是多少平方厘米？六数思维操六1、一个水果盒长２０厘米，宽１５厘米，高３０厘米，现在要在它的四周贴商标纸，如果商标纸的接头处为３厘米，这张商标纸的面积至少是多少平方分米？2、有一队伍以 1.4 米／秒的速度行军，末尾有一通讯员因有事要通知排头，以 2.6 米／秒的速度从末尾赶到排头并立即返回队尾，共用了 10 分 50 秒。

六年级数学思维题

六年级数学思维题
以下是一些适合六年级学生的数学思维题：
1. 填数字游戏：在一个3x3的方格中，填写数字1~9，使得每行、每列和每个小方格内的数字都不重复。

2. 图形拼图：给出不同形状的几何图形，要求将它们拼接成一个完整的图形。

可以通过切分和旋转进行拼接。

3. 数字游戏：给出一组数字，要求通过加、减、乘、除等运算，得到指定的目标数字。

可以使用括号调整运算的优先级。

4. 数学解谜：给出一些数学问题或条件，要求通过逻辑推理和分析，找到正确的答案或结论。

例如：有5个小球，其中1个比其他的重一些，通过天平称量最少需要几次？
5. 立体图形识别：给出一些立体图形的正视图、俯视图或侧视图，要求识别出对应的立体图形，并计算其体积或表面积。

这些数学思维题可以培养学生的逻辑思考能力、计算能力和空间想象能力，同时也可以激发学生的学习兴趣和创造力。

1/ 1。

六年级思维训练001-答案

01.从六个数字1，2，3，4，5，6中任意选取两个组成两位数，如果其中的6也可以换成9使用，一共可以组成（40）个不同的两位数。

解：组成两位数的情况=普通情况+6作9的情况普通情况：6×5=30;6作9的情况:有一位必选9，剩下的排数位2×5=10;30+10=40(个）02.两个自然数a和b,它们的最大公因数是14，最小公倍数是280，那么它们的和a+b是（294）或（136）。

解：方法：短除模型14xy=280,xy=20;x,y=1;只有两组可能解：൝x=1y=20，ቊx=4y=5；则൝a=14b=280，ቊa=56b=70；则a+b=294或136.03.从7开始，把7的倍数一直写下去，一直到994，成为一个很大的数：71421……987994.这个数是（411）位数。

解：994是7的142倍；7是7的1倍，也是唯一的个位数7的倍数；从7的2倍14一直到7的14倍98，一共有13个是两位数的7的倍数；从7的15倍105一直到7的142倍994，一共有128个是三位数的7的倍数；1×1+2×13+3×128=411(位）。

04.有一泓泉水，泉水不断从泉底涌出，并且每分钟涌出的泉水一样多。

如果用8台抽水机10小时可以把全部的水抽干；如果用12台抽水机6小时可以把全部的水抽干.那么如果用14台抽水机（5）小时可以把全部的水抽干。

解：设一台抽水机一小时抽一份水；则10小时抽了8×10=80份水；6小时抽了12×6=72份水；水速：80−72÷10−6=2份每小时；原来水量：80−10×2=60份水；设14台抽水机x小时抽完所有水14x=60+2xx=505.六（1）班和六（2）班的人数之和在100人左右。

如果排成3列不多不少；如果排成5列少2人；如果排成7列少4人。

这两个班一共有（102）人。

解：将条件用同余式表示：a≡0mod3,a≡2mod5,a≡4mod7;即a最小是3,5,7−3=10206.在▲ABC中，E是AC的中点，且BD=2DC，AD和BE交于F,则▲BDF的面积:四边形DCEF的面积=（8:7）。

寒假用：六年级数学思维训练专题一至专题十电子教材

这就是逻辑推理问题。

例1:甲、乙、丙、丁4位同学中有一位同学假日去敬老院做了好事，老师了解情况，4人分别回答如下：甲说：“不是我做的。

”乙说：“是甲做的。

”丙说：“不是我做的。

”丁说：“是乙做的。

”他们4人中只有一人说的是真话，你知道是谁做的好事吗？【跟进练习】A、B、C、D、E、F六位同学参加了学校组织的“一站到底”的角逐，对于谁是冠军，甲、乙、丙、丁四人有以下猜测。

甲说：冠军不是A就是B；乙说：冠军不是C；丙说：D、E、F都不可能是冠军；丁说：冠军是D、E、F中的一个人。

比赛结果，这四人中只有一人猜测是正确的，请判断谁是冠军？例2:一次学校举行田径运动会，A、B、C、D、E五个班取得了团体前五名，发奖后有人问他们的名次，回答是：A班代表说：“B是第三名，C是第五名。

”B班代表说：“D是第二名，E是第四名。

”C班代表说：“A是第一名，E是第四名。

”D班代表说：“C是第一名，B是第二名。

”E班代表说：“D是第二名，A是第三名。

”最后，他们都补充说：“我们的话是半真半假的。

”请你判断一下，他们各个班的名次。

【跟进练习】甲、乙、丙、丁四位同学的运动衫上印有不同的号码。

赵说：“甲是2号，乙是3号.”钱说：“丙是4号，乙是2号.”孙说：“丁是2号，丙是3号.”李说：“丁是4号，甲是1号.”又知道赵、钱、孙、李每人都只说对了一半，那么丙的号码是几？例3:赵、钱、孙、李四位老师进行乒乓球比赛，并决出了一、二、三、四名，已知：（1）赵老师的名次比钱老师的名次靠前；（2）孙老师和李老师喜欢一起下象棋；（3）第一名和第三名在这次比赛中才认识的；（4）第二名不会开电动车，也不会下象棋；（5）钱老师和李老师每天都是开电动车一起上班。

六年级上册拓展思维练习题

六年级上册拓展思维练习题一、数学拓展思维题1. 整数思维拓展题在数轴上标出-3、-2、0、1、4五个数，然后画出两个点A和B，使得点A的坐标为-2，点B的坐标为1。

连接点A和B，并延长线段AB与数轴的交点为C，请问C点的坐标是多少？2. 几何思维拓展题给定一个正方形ABCD，其中AB的边长为5cm。

在BC边上取一点E，使得AE与AD垂直且AE的长度为3cm。

连接BE，并延长线段BE与AD的交点为F。

请问AF的长度是多少？3. 逻辑思维拓展题班级里有30个学生，其中一半是男生，一半是女生。

若男生穿白色衣服的有3人，女生穿白色衣服的有7人，且男生和女生都只会穿白色和蓝色两种颜色的衣服。

问男生和女生一共有多少人穿蓝色衣服？4. 应用思维拓展题一包红豆种子可以种植20棵豆苗。

现在小明接收到5包红豆种子，他想用这些种子种植尽可能多的豆苗。

请问小明最多可以种植多少棵豆苗？如果有剩余的种子，剩余多少颗？二、语文拓展思维题请阅读以下短文，并回答问题：小明有一文具盒，里面有许多铅笔、钢笔和橡皮擦。

小明想要将这些文具按照以下条件进行排序：1. 铅笔的数量比钢笔的数量多5支；2. 钢笔的数量比橡皮擦的数量多3支；3. 铅笔、钢笔和橡皮擦的总数量是18支。

请问小明的文具盒里分别有多少支铅笔、钢笔和橡皮擦？2. 写作拓展题描述一下你参观博物馆的经历。

你可以写下你参观的博物馆是什么，展览中有哪些内容，你对其中的哪些展品感兴趣等等。

注意：请在文章中划分合适的段落，并使用恰当的过渡词。

三、英语拓展思维题1. 词汇拓展题请用英语写一段短文，该段落包括以下8个单词，每个单词只能用一次，可以使用其不同形式：apple, watch, car, school, run, big, happy, rain。

提示：你可以写一段关于一个孩子在下雨天快乐地跑回学校的故事。

请阅读以下短文，并回答问题：Tom is a 10-year-old boy. He loves playing basketball and he is very good at it. Every day after school, he goes to the basketball court near his house to practice. One day, when he was practicing, it started to rain. But Tom didn't want to stop playing, so he kept playing basketball in the rain. His mom saw him and called him back, worried that he would catch a cold. Tom smiled and said, "Mom, playing basketball in the rain makes me feel so alive!"1. What does Tom love to do?2. What did he do when it started to rain?3. How did his mom feel about him playing in the rain?4. How did Tom feel about playing basketball in the rain?以上是六年级上册拓展思维练习题，包括数学、语文和英语三个科目的思维拓展题。

小学数学六年级思维训练练习题及答案

小学数学六年级思维训练练习题及答案题目一：计算题（共20分）1. 58 + 97 = _____2. 135 - 82 = _____3. 5 * 7 = _____4. 49 ÷ 7 = _____5. 爸爸买了25颗苹果，妈妈买了30颗苹果，一共有多少颗苹果？答：_____题目二：填空题（共15分）1. 将200打九折后的价格是_____元。

2. 8 × 9 = _____。

3. 13 × 7 = _____。

4. 450 ÷ 9 = _____。

5. 圆的周长公式是____。

题目三：选择题（共15分）1. 一个正方形的周长是20米，边长是 _____ 米。

（A）4 （B）5 （C）102. 一个矩形的长是12厘米，宽是6厘米，则矩形的周长是 _____ 厘米。

（A）12 （B）18（C）363. 12 ÷ 3 = _____。

（A）3 （B）4 （C）54. 52 + 29 = _____。

（A）81 （B）82 （C）925. 如果一块长方体的长是5米，宽是3米，高是2米，它的体积是_____ 立方米。

（A）10 （B）15 （C）30题目四：应用题（共20分）小明在一个陶瓷艺术品展览会上看到了一块瓷砖，它的形状是一个边长为12厘米的正方形，格子之间有一层花纹线。

若每个格子的边长是1厘米，请计算出这块瓷砖上有多少个格子？答：_____题目五：解答题（共30分）1. 把32厘米长的一根铁丝剪成两段，一段比另一段长16厘米，这两段各是多长？答：_____2. 一个长方形的长和宽的比是3:2，它的周长是30厘米，这个长方形的长和宽各是多少厘米？答：_____3. 5个小朋友准备把50元钱按比例分成3份和2份，按这个比例每份应该分多少钱？答：_____4. 如果一辆汽车每小时行驶100公里的速度行驶8小时，那么它开了多远？答：_____5. 一辆电车每小时行驶40公里，一辆汽车每小时行驶60公里。

六年级数学思维训练题(有答案及解析)

一、兴趣篇1．甲、乙两队进行象棋对抗赛，甲队的三人是张、王、李，乙队的三人是赵、钱、孙，按照以往的比赛成绩看，张能胜钱，钱能胜李，李能胜孙，但是第一轮的三场比赛他们都没有成为对手．请问：第一轮比赛的分别是谁对谁？2．甲、乙、丙、丁与小强五位同学一起比赛象棋，每两人都要比赛一盘．到现在为止，甲已经赛了4盘，乙赛了3盘，丙赛了2盘，丁赛了1 盘．问：小强已经赛了几盘？分别与谁赛过？3．甲、乙、丙三名选手参加马拉松比赛，起跑后甲处在第一的位置，在整个比赛过程中，甲的位置共发生了7次变化．比赛结束时甲是第几名？（注：整个比赛过程中没有出现三人跑在同一位置的情形．）4．有10名选手参加乒乓球单打比赛，每名选手都要和其它选手各赛一场，而且每场比赛都分出胜负，请问：（1）总共有多少场比赛？（2）这10名选手胜的场数能否全都相同？（3）这10名选手胜的场数能否两两不同？5．6支足球队进行单循环比赛，即每两队之间都比赛一场．每场比赛胜者得3分，负者得0分，平局各得1分，请问：（1）各队总分之和最多是多少分？最少是多少分？（2）如果在比赛中出现了6场平局，那么各队总分之和是多少？6．红、黄、蓝三支乒乓球队进行比赛，每队派出3名队员参赛．比赛规则如下：参赛的9名队员进行单循环赛决出名次，按照获胜场数进行排名，并按照排名获得一定的分数，第一名得9分，第二名得8分，…，第九名得1分；除产生个人名次外，每个队伍还会计算各自队员的得分总和，按团体总分的高低评出团体名次．最后，比赛结果没有并列名次．其中个人评比的情况是：第一名是一位黄队队员，第二名是一位蓝队队员，相邻的名次的队员都不在同一个队．团体评比的情况是：团体第一的是黄队，总分16分；第二名是红队，第三名是蓝队．请问：红队队员分别得了多少分？7．5支球队进行单循环赛，每两队之间比赛一场，每场比赛胜者得3分，负者得0分，打平则双方各得1分，最后5支球队的积分各不相同，第三名得了7分，并且和第一名打平．请问：这5支球队的得分，从高到低依次是多少？8．有A、B、C三支足球队，每两队比赛一场，比赛结果为：A：两胜，共失2球；B：进4球，失5球；C：有一场踢平，进2球，失8球．则A与B两队间的比分是多少？9．一次考试共有10道判断题，正确的画“√”，错误的画“×”，每道题10分，满分为100分．甲、乙、丙、丁4名同学的解答及甲、乙、丙3名同学得分如下表所示．丁应得分．题号学生1 2 3 4 5 6 7 8 9 1得分甲××√√××√×√√70 乙×√×√√××√√×70 丙√×××√√√×××60 丁×√×√√×√×√×10．赵、钱、孙、李、周5户人家，每户至少订了A、B、C、D、E这5种报纸中的一种．已知赵、钱、孙、李分别订了其中的2、2、4、3种报纸，而A、B、C、D这4种报纸在这5户人家中分别有1、2、2、2家订户．周姓订户订有这5种报纸中的几种？报纸E在这5户人家中有几家订户？二、拓展篇11．编号为1、2、3、4、5、6的同学进行围棋比赛，每2个人都要赛1盘．现在编号为1、2、3、4、5的同学已经赛过的盘数和他们的编号数相等．请问：编号为6的同学赛了几盘？12．五行（火水木金土）相生相克，其中每一个元素都生一个，克一个，被一个生和被一个克，水克火是我们熟悉的，有一个俗语叫做“兵来将挡，水来土掩”，是说土能克水．另外，水能生木，火能生土．请把五行的相生相克关系画出来．13．A、B、C、D、E、F六个国家的足球队进行单循环比赛（即每队都与其他队赛一场），每天同时在3个场地各进行一场比赛，已知第一天B对D，第二天C对E，第三天D对F，第四天B对C请问：第五天与A队比赛的是哪支队伍？14．A、B、C三个篮球队进行比赛，规定每天比赛一场，每场比赛结束后，第二天由胜队与另一队进行比赛，败队则休息一天，如此继续下去，最后结果是A队胜10场，B队胜12场，C队胜14场，则A队共打了几场比赛？15．甲、乙、丙、丁四名同学进行象棋比赛，每两人都比赛一场，规定胜者得2分，平局各得1分，输者得0分，请问：（1）一共有多少场比赛？（2）四个人最后得分的总和是多少？（3）如果最后结果甲得第一，乙、丙并列第二，丁是最后一名，那么乙得了多少分？16．五支足球队进行循环赛，即每两个队之间都要赛一场，每场比赛胜者得2分，输者得0分，平局两队各得1分．比赛结果各队得分互不相同．已知：①第一名的队没有平过；②第二名的队没有输过；③第四名的队没有胜过，问：第一名至第五名各得多少分？全部比赛共打平过几场？17．4支足球队进行单循环比赛，即每两队之间都比赛一场．每场比赛胜者得3分，负者得0 分，平局各得1分．比赛结果，各队的总得分恰好是4个连续的自然数．问：输给第一名的队的总分是多少？18．甲、乙、丙、丁、戊五个同学的各科考试成绩如表，已知：①每门功课五个人的分数恰巧分别为l、2、3、4、5；②五个人的总分互不相同，且从高到低的顺序排列是：甲、乙、丙、丁、戊；③丙有四门功课的分数相同．请你把表格补充完整．语文数学英语音乐美术总分田24乙丙丁 4戊 3 519．一次足球赛，有A、B、C、D四个队参加，每两队都赛一场，按规则，胜一场得2分，平一场得1分，负一场得0分．比赛结束后，B队得5分，A队得1分．所有场次共进了9个球，B队进球最多，共进了4个球，C队共失了3个球，D队1个球也未进，A队与C队的比赛比分是2：3．问：A队与B队的比赛比分是多少？20．A、B、C、D四个足球队进行循环比赛．赛了若干场后，A、B、C三队的比赛情况如表：问：D赛了几场？D赛的几场的比分各是多少？场数胜平负进球失球A 3 2 1 0 2 0B 2 1 1 0 4 3C 2 0 0 2 3 6D21．九个外表完全相同的小球，重量分别是1，2，…，9．为了加以区分，它们都被贴上了数字标签，可是有一天，不知被哪个调皮鬼重新乱贴了一通．我们用天平做了两次称量，得到如下结果：（1）①②＞③④⑤⑥⑦；（2）③⑧=⑦，请问：⑨号小球的重量是多少？22．A、B、C、D、E五位同学分别从不同的途径打听到五年级数学竞赛获得第一名的那位同学的情况：A打听到的：姓李，是女同学，13岁，东城区；B打听到的：姓张，是男同学，11岁，海淀区；C打听到的：姓陈，是女同学，13岁，东城区；D打听到的：姓黄，是男同学，11岁，西城区；E打听到的：姓张，是男同学，12岁，东城区．’实际上第一名同学的情况在上面都出现过，而且这五位同学的消息都仅有一项正确，那么第一名的同学应该是哪个区的，今年多少岁呢？三、超越篇23．在一次射击练习中，甲、乙、丙三位战士打了四发子弹，全部中靶，其中命中情况如下：（1）每人四发子弹命中的环数各不相同；（2）每人四发子弹命中的总环数均为17环；（3）乙有两发命中的环数分别与甲其中两发一样，乙另外两发命中的环数与丙其中两发一样；（4）甲与丙只有一发环数相同；（5）每人每发子弹的最好成绩不超过7环．问：甲与丙命中的相同环数是几？24．一次象棋比赛共有10位选手参加，他们分别来自甲、乙、丙3个队．每人都与其余9人比赛一盘，每盘胜者得1分，负者得0分，平局各得0.5分．结果乙队平均得分为3.6分，丙队平均得分为9分，那么甲队平均得多少分？25．A、B、C、D、E这5支足球队进行循环赛，每两队之间比赛一场．每场比赛胜者得3分，负者得0分，打平则双方各得1分，最后5支球队的积分各不相同，从高到低依次为D、A、E、B、C又已知5支球队当中只有A没输过，只有C没赢过，而且B战胜了E．请问：战胜过C的球队有哪些？26．10名选手参加象棋比赛，每两名选手间都要比赛一次，已知胜一场得2分，平一场得1分，负一场不得分．比赛结果：选手们所得分数各不相同，前两名选手都没输过，前两名的总分比第三名多20分，第四名得分与后四名所得总分相等，问：前六名的分数各为多少？27．现有A、B、C共3支足球队举行单循环比赛，即每两队之间都要比赛一场．比赛积分的规定是胜一场积2分，平一场积1分，负一场积0分，表1是一张记有比赛详细情况表格，但是，经过核对，发现表中恰好有4个数字是错误的，请你把正确的结果填入表2中．表1场数胜负平进球失球积分A 22 0 1 0 2 3B 21 1 0 3 6 2C 12 1 2 0 1 1 表2场数胜负平进球失球积分ABC28．9个小朋友从前到后站成一列．现在将红黄蓝三种颜色的帽子各三顶分别戴在这些小朋友的头上．每个小朋友都只能看到站在他前面的小朋友帽子的颜色．后来统计了一下，发现他们看到的红颜色帽子的总次数等于他们看到的黄颜色帽子的总次数，也等于他们看到的蓝颜色帽子的总次数．已知从前往后数第三个小朋友戴着红帽子，第六个小朋友戴着黄帽子，请问：最后一个小朋友戴着什么颜色的帽子？29．有A、B、C三支球队进行比赛，每一轮比赛三个队之间各赛一场．每队胜一场得2分，平一场得1分，负一场不得分．如果三支球队共比赛了7轮，最后A胜的场数最多，B输的场数最少，C的得分最高＜这些都没有并列）．请问：A得了多少分？30．阿奇和8个好朋友去李老师家玩，李老师给每人发了一顶帽子，并在每个人的帽子上写了一个两位数，这9个两位数互不相同，且每个小朋友只能看见别人帽子上的数．李老师在纸上写了一个自然数A，问这9位同学：“你们知道自己帽子上的数能否被A整除吗？知道的请举手，”结果有4人举手．李老师又问：“现在你们知道自己帽子上的数能否被24整除吗？知道的请举手．”结果有6人举手．已知阿奇两次都举手了，并且这9位同学都足够聪明且从不说谎．请问：除了阿奇之外的人帽子上8个两位数的总和是多少？参考答案与试题解析一、兴趣篇1．甲、乙两队进行象棋对抗赛，甲队的三人是张、王、李，乙队的三人是赵、钱、孙，按照以往的比赛成绩看，张能胜钱，钱能胜李，李能胜孙，但是第一轮的三场比赛他们都没有成为对手．请问：第一轮比赛的分别是谁对谁？【分析】张能胜钱，说明第一轮只会碰赵或者孙；钱能胜李，说明第一轮只会碰赵或者孙；钱能胜李，说明第一轮只会碰张，或者是王；而李能胜孙，说明第一轮只会碰赵或者钱；由于都没有碰到对手，说明钱只能对上王，遇张不行，故王与钱；而李由于只能碰赵或者钱，在钱有对手的情况下只能选赵，故李与赵，最后得出张与孙．【解答】解：根据上述分析可知：张能胜钱，说明第一轮只会碰赵或者孙；钱能胜李，说明第一轮只会碰张，或者是王；李能胜孙，说明第一轮只会碰赵或者钱综上所述：第一轮比赛是张与孙，王与钱，李与赵答：第一轮比赛是张与孙，王与钱，李与赵．2．甲、乙、丙、丁与小强五位同学一起比赛象棋，每两人都要比赛一盘．到现在为止，甲已经赛了4盘，乙赛了3盘，丙赛了2盘，丁赛了1 盘．问：小强已经赛了几盘？分别与谁赛过？【分析】这道题按照常规思路似乎不太好解决，我们画个图试试，用五个点分别表示参加比赛的五个人，如果某两人已经赛过，就用线段把代表这两个人的点连接起来，因为甲已经赛了4盘，除了甲以外还有4个点，所以甲与其他4个点都有线段相连（见下图），根据图即可做出解答．【解答】解：用五个点分别表示参加比赛的五个人，如果某两人已经赛过，就用线段把代表这两个人的点连接起来，因为甲已经赛了4盘，除了甲以外还有4个点，所以甲与其他4个点都有线段相连（见左下图），因为丁只赛了1盘，所以丁只与甲有线段相连，因为乙赛了3盘，除了丁以外，乙与其他三个点都有线段相连（见右上图），因为丙赛了2盘，右上图中丙已有两条线段相连，所以丙只与甲、乙赛过，由上页右图清楚地看出，小强赛过2盘，分别与甲、乙比赛，答：小强赛过2盘，分别与甲、乙比赛．3．甲、乙、丙三名选手参加马拉松比赛，起跑后甲处在第一的位置，在整个比赛过程中，甲的位置共发生了7次变化．比赛结束时甲是第几名？（注：整个比赛过程中没有出现三人跑在同一位置的情形．）【分析】据题意可知，甲原为第一名（奇数），第一次位置交换后，甲成了第二名（偶数）；第二次位置交换后，甲不是第二名，成了第一名或第三名（奇数）；第三次位置变化后，不管之前甲处于第一名还是第三名，这次甲肯定又成了第二名（偶数），…；所以可以知道，当甲交换了奇数次位置时，甲一定是第二名；偶数次时，甲一定不在第二名．【解答】解：据题意可知，当甲与共交换了奇数次位置时，甲一定是第二名；偶数次时，甲一定不在第二名．所以甲共交换了7次位置时，7是奇数，则甲一定是在第二名．答：比赛的结果甲是第二名．4．有10名选手参加乒乓球单打比赛，每名选手都要和其它选手各赛一场，而且每场比赛都分出胜负，请问：（1）总共有多少场比赛？（2）这10名选手胜的场数能否全都相同？（3）这10名选手胜的场数能否两两不同？【分析】（1）因为每一个选手都和其他选手进行一场比赛，属于单循环赛制中，参赛人数与比赛场数的关系为：比赛场数=×参赛人数×（人数﹣1），由此代入求得问题；【解答】解：（1）×10×（10﹣1）=45（场），答：一共要进行45场比赛．（2）45÷10=4（个）…5（场）（不相同，有余数．）答：这10名选手胜的场数不相同．（3）45可以分成1，2，3，4，5，6，7，8，9，0的数列（有五列，是整数，可以）答：这10名选手胜的场数可以两两不同．5．6支足球队进行单循环比赛，即每两队之间都比赛一场．每场比赛胜者得3分，负者得0分，平局各得1分，请问：（1）各队总分之和最多是多少分？最少是多少分？（2）如果在比赛中出现了6场平局，那么各队总分之和是多少？【分析】（1）6支足球队进行单循环比赛，即每两队之间都比赛一场，所以一个球队赛5场，加入五场全胜，则得分最多是：3×5=15分；有一个球队5场全负，得分最少是0分．（2）出现了6场平局，得12分，一共1赛15场，剩下9场就是输或者赢了，9×3=27分，那么总分就是：12+27=39分．【解答】解：（1）每支球队赛5场，全胜得分最多：5×3=15（分）最少得分就是全输得0分：答：各队总分之和最多是15分，最少是0分．（2）6×5÷2=15（场）6×2+（15﹣6）×3=12+27=39（分）答：那么各队总分之和是39分．6．红、黄、蓝三支乒乓球队进行比赛，每队派出3名队员参赛．比赛规则如下：参赛的9名队员进行单循环赛决出名次，按照获胜场数进行排名，并按照排名获得一定的分数，第一名得9分，第二名得8分，…，第九名得1分；除产生个人名次外，每个队伍还会计算各自队员的得分总和，按团体总分的高低评出团体名次．最后，比赛结果没有并列名次．其中个人评比的情况是：第一名是一位黄队队员，第二名是一位蓝队队员，相邻的名次的队员都不在同一个队．团体评比的情况是：团体第一的是黄队，总分16分；第二名是红队，第三名是蓝队．请问：红队队员分别得了多少分？【分析】首先总分是45分，黄队16分，红蓝共29分，又团队第一的是黄队且比赛结果没有并列名次，故只能是红队15分，蓝队14分．第一名是一位黄队队员有9分，第二名是一位蓝队队员有8分，即黄队另两名队员共有7分，蓝队另两名队员共有6分，又每名队员至少1分故第三名是一位红队队员有7分，即红队另两名队员共有8分．．又相邻的名次的队员都不在同一个队故第四名的得6分的队员是黄队，此时黄队最后一名队员1分．故得5分的不是蓝队队员，不然蓝队又有一名队员1分矛盾．故得5分为红队队员，此时红队有一名是3分．故剩下的蓝队为4分和2分，刚好共6分．故得分情况如下：黄：9、6、1 蓝：8、4、2 红：7、5、3，据此解答即可．【解答】解：1．由于1到9名分数分别是9到1分，那么总共9人总分就是45分2．由于团队第一名16分，第二名只能是小于等于15，第三名小于等于14．而总分是45．所以第二，第三只能分别是15分，14分．（因为16+15+14=45，没有其他组合等于45分）因此第二名红对共得15分．3．由于单打前两名分别由黄队和蓝队的队员获得．因此红对个人得分最多的一个小于等于7分．又因为相邻名次没有同队的人员，所以红对的三人得分可能是7，5，3或者7，4，2等几种（没有列全）．但是红队总分能达到15分的组合只有7+5+3=15．所以红对队员分别得了7，5，3分．答：红队队员分别得了7，5，3分．7．5支球队进行单循环赛，每两队之间比赛一场，每场比赛胜者得3分，负者得0分，打平则双方各得1分，最后5支球队的积分各不相同，第三名得了7分，并且和第一名打平．请问：这5支球队的得分，从高到低依次是多少？【分析】由于5支足球队进行单循环赛，每两队之间进行一场比赛，则每一队都要和其它四队赛一场，即每支球队进行了4场比赛，全胜得12分，第三名得了7分，并且和第一名打平得一分，那么另三场只能是两胜一负，因各队得分都不相同，第一名平一场，如平再负一场就和第三名得分一样，如果再平一场就得8分，这都不符合题意，所以剩下三场只能胜，积3×3+1=10分，也就是胜2、4、5名，第二名只能是三胜一负，积3×3+0=9分．也就是胜3、4、5名；第三名胜4、5，负2，平1；第四名为负1、2、3，第五名也负1、2、3又因各队比分不同则4胜5积3分，第五名全负，积0分．【解答】解：由题意可知，每支球队进行了4场比赛，第三名得了7分，并且和第一名打平，那么另三场只能是两胜一负；因各队得分都不相同，第一名平一场，另三场只能胜，积3×3+1=10分，也就是胜2、4、5名；第二名只能是三胜一负，积3×3+0=9分．也就是胜3、4、5；第三名胜4、5，负2，平1；第四名为负1、2、3，第五名也负1、2、3名；又因各队比分不同则4胜5积3分，则第五名全负，积0分；即：第一名：10分，第二名：9分，第三名：7分，第四名：3分，第五名：0分．答：第一名：10分，第二名：9分，第三名：7分，第四名：3分，第五名：0分．8．有A、B、C三支足球队，每两队比赛一场，比赛结果为：A：两胜，共失2球；B：进4球，失5球；C：有一场踢平，进2球，失8球．则A与B两队间的比分是多少？【分析】A两战两胜，C有一场平说明比赛胜负情况如下：A胜B A胜C B平C；而B C 的比分：0：0 这种情况不存在因为A共失球两个而B C共进球6个1：1 同上2：2 适合条件B另外两个球攻入A的球门3：3 不存在C共进球两个所以得出B：C 为2：2则C另外6个失球失给A，B剩下两个进球，3个失球是跟A比赛的时候故可得出结论：A胜B 3比2A胜C 6比0B平C 2比2【解答】解：总进球=总失球A进球+4+2=2+5+8A进球=9A全胜那么B与C打平又因为B比C多进2球那么B对A进的球比C对A进的球多2个又因为A只失2球那么B对A进2球C对A进0球那么B：C=2：2那么A：B=3；2答：A与B两队间的比分是3：2．9．一次考试共有10道判断题，正确的画“√”，错误的画“×”，每道题10分，满分为100分．甲、乙、丙、丁4名同学的解答及甲、乙、丙3名同学得分如下表所示．丁应得90分．题号学生1 2 3 4 5 6 7 8 9 1得分甲××√√××√×√√70 乙×√×√√××√√×70 丙√×××√√√×××60 丁×√×√√×√×√×【分析】观察甲与乙的答案可知，A、B有1、4、6、9这四道题答案相同，6道题答案不同．因为每人都是70分，所以4道答案相同的题都答对了，6道答案不同的题各对了3道；由此可知第1、4、6、9题的答案分别是×、√、×、√；又丙的1、4、6、9题的答案分别是√、×、√、×；所以丙的这四道题答错，又丙得60分，所以丙的其他题目全部答对，即2，3，5，7，8，10的答案分别是×，×、√、√、×、×．由此可知，这10道题的答案分别是：据此即能得出丁得多少分．【解答】解：由于A、B有1、4、6、9这四道题答案相同，6道题答案不同．且每人都是70分，所以4道答案相同的题都答对了，6道答案不同的题各对了3道；由此可知第1、4、6、9题的答案分别是×、√、×、√；由于丙的1、4、6、9题的答案分别是√、×、√、×；所以丙的这四道题答错，又丙得60分，所以丙的其他题目全部答对，即2，3，5，7，8，10的答案分别是×，×、√、√、×、×．这10道题的答案分别是：所以丁的只的2题，扣10分，得90分．故答案为：90．10．赵、钱、孙、李、周5户人家，每户至少订了A、B、C、D、E这5种报纸中的一种．已知赵、钱、孙、李分别订了其中的2、2、4、3种报纸，而A、B、C、D这4种报纸在这5户人家中分别有1、2、2、2家订户．周姓订户订有这5种报纸中的几种？报纸E在这5户人家中有几家订户？【分析】通过分析可知：赵钱孙李一共订了：2+2+4+3=11份A，B，C，D一共订了：1+2+2+2=7份根据题意，周至少订了1份5人一共最少订了11+1=12份那么订E的就有12﹣7=5户如果周订的不止1份，假设周至少订了2份那么5人订报总数至少为11+2=13份那么订E的至少有：13﹣7=6户，这与一共有5户矛盾所以周只能订1种，订E的有5户【解答】解：赵钱孙李订的份数：2+2+4+3=11份A，B，C，D订的份数：1+2+2+2=7份根据题意可知周至少订了1份所以5人一共最少订了11+1=12份那么订E的就有12﹣7=5户如果周订的不止1份，假设周至少订了2份那么5人订报总数至少为11+2=13份那么订E的至少有：13﹣7=6户，这与一共有5户矛盾所以周只能订1种，订E的有5户答：周姓订户订有这5种报纸中的1种，报纸E在这5户人家中有5家订户．二、拓展篇11．编号为1、2、3、4、5、6的同学进行围棋比赛，每2个人都要赛1盘．现在编号为1、2、3、4、5的同学已经赛过的盘数和他们的编号数相等．请问：编号为6的同学赛了几盘？【分析】从5号队员开始讨论，他和另外5个队员各赛了1场，由此得出1号只跟5号赛了1场，由此类推即可得出结果．【解答】解：因为是每2个人都要赛1盘，所以可以这样推理：①5号赛了5场，说明他与1，2，3，4，6，各赛了1场；②1号赛1场，那么1号只跟5号赛了1场；③4号赛了4场，除了跟5号赛1场，另外3场是跟2，3，6号；④那么2号此时分别和5号、4号已赛了2场；④3号赛了3场，除了和4号，5号之外，又和6号赛了1场．将上述推理过程用图表示为：答：此时6号已经赛了3场．12．五行（火水木金土）相生相克，其中每一个元素都生一个，克一个，被一个生和被一个克，水克火是我们熟悉的，有一个俗语叫做“兵来将挡，水来土掩”，是说土能克水．另外，水能生木，火能生土．请把五行的相生相克关系画出来．【分析】五行有‘五行相生’和‘五行相克’，‘五行相生’是互相生旺的意思，表示生成化育，‘五行相克’就是互相反驳、互相战斗、制衡．五行相生：水生木→木生火→火生土→土生金→金生水五行相克：木克土→土克水→水克火→火克金→金克木据此解答即可．【解答】解：根据五行相生：水生木→木生火→火生土→土生金→金生水五行相克：木克土→土克水→水克火→火克金→金克木得出图为：13．A、B、C、D、E、F六个国家的足球队进行单循环比赛（即每队都与其他队赛一场），每天同时在3个场地各进行一场比赛，已知第一天B对D，第二天C对E，第三天D对F，第四天B对C请问：第五天与A队比赛的是哪支队伍？【分析】因“A、B、C、D、E、F六个国家的足球队单循环比赛（即每队都与其他队赛一场），每天同时在3个场地各进行一场比赛”，根据已经进行的比赛场次进行推理，据此解答即可．【解答】解：第二天A不能对B，否则A对B、D对F与第三天D对F矛盾，所以应当B 对F、A对D．第三天A也不能对B，否则C对E与第二天C对E矛盾，应当B对E（不能B对C，与第四天矛盾），A对C．第四天B对C，D对E，A对F，所以第五天A对B．答：第五天与A队比赛的是B支队伍．14．A、B、C三个篮球队进行比赛，规定每天比赛一场，每场比赛结束后，第二天由胜队与另一队进行比赛，败队则休息一天，如此继续下去，最后结果是A队胜10场，B队胜12场，C队胜14场，则A队共打了几场比赛？【分析】根据题意，扣除A、B、C分别赢的场次，得出A、B、C各打了几场，即可得出A 总共打了几场．【解答】解：由A队先取得10连胜，这样BC队就各输5场再由B队取得12连胜，这样AC队就各输6场最后C队取得14连胜，这样AB队就各输7场从A来看，每负一场就休息了一场，总共有10+12+14=36场比赛，A胜了10场，剩下26场是负和休息，那么A负了13场，休息了13场，赛了10+13=23场．同理，B胜了12场，剩下24场是负和休息，那么B负了12场，休息了12场，赛了12+12=24场．C胜了14场，剩下22场是负和休息，那么C负了11场，休息了11场，赛了14+11=25场．答：则A队共打了23场比赛．15．甲、乙、丙、丁四名同学进行象棋比赛，每两人都比赛一场，规定胜者得2分，平局各得1分，输者得0分，请问：（1）一共有多少场比赛？（2）四个人最后得分的总和是多少？。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

六年级数学创新思维训练一
A卷
1.（1）计算下列各题，你能发现从1起求若干奇数和的规律吗？
1＋3=
1＋3＋5=
1＋3＋5＋7=
1＋3＋5＋7＋9=
（2）求1＋3+5+ (99)
（3）想一想，怎样计算下列各数的和。

101，103，105， (199)
2.用花、白两种正方形的瓷砖拼成大的正方形图形，要求中间用白瓷砖，四周一圈用花瓷砖（如下图所示）。

（1）填写下列表格。

想一想，这些数量之间有什么关系？
（2）如果所拼的图形中，用了100块白瓷砖，那么，花瓷砖用了多少块？（3）如果所拼的图形中用了100块花瓷砖，那么白瓷砖用了多少块？
3.用若干相同的小等边三角形，可以拼成大的等边三角形。

（如下图所示）
（1）填写下面表格，想一想，小三角形的个数与大三角形的层数有什么关系？
（2）如果拼成的大三角形有 30层.那么共用了多少个小三角形？
4.把一张长方形纸对折再对折，然后在折叠着的角上剪一刀，纸的中间就剪出了一个洞（如下图所示）。

（1）填写下面表格。

想一想，对折的次数与剪出洞的个数有什么关系？
（2）如果对折了10次后，再在折叠着的角上剪一刀，那么这张纸上共剪出了多少个洞？
5.用火柴棒搭成两排大小相等的正方形（如下图所示）。

（1）填写下面表格，想一想，小正方形的个数与所用火柴棒的根数有什么关系？
（2）如果搭12个这样的正方形，那么需要多少根火柴？
（3）用157根火柴可以搭成这样的正方形多少个？
6.第一次把一根一米长的木棒锯成相等的两段，第二次再把锯成的两段各锯成相等的两段。

至少经过几次这样的操作后，每段木棒的长度小于1厘米？
7.如果在下面45个空格内分别填上这空格所在行和所在列的两个数的和。

问这45个数的总和是多少？
8.已知1995年元旦是星期日，2000年的元旦是星期几？
9.从长方形左下方的顶点发出一道光束，光线按45°角前进，碰到正方形的边即呈45。

角折射，最后从长方形顶点射出（如下图）。

这样，光线从发出点到终点共通过6个小方格。

（1）调查光线通过的小正方形个数与长边、宽边上小正方形个数的关系。

光线通过的正方形个数与长边、宽边上的正方形个数有什么关系？
（2）用你发现的规律计算下面各题。