2013高考数学(理科)小题限时训练7
2013届高考理科数学复习演练套题(含答案)
2013届高考理科数学复习演练套题(含答案)(时间：40分钟满分：60分)一、填空题(每小题5分，共40分)1．不等式|2x－1|＜3的解集为________．解析①当2x－1≥0，即x≥12时，不等式变为2x－1＜3，得x＜2，∴12≤x ＜2.②当2x－1＜0即x＜12时，不等式变为－(2x－1)＜3即x＞－1，∴－1＜x＜12，综上不等式解集为{x|－1＜x＜2}．答案(－1,2)2．已知x＞0，则函数y＝x(1－x2)的最大值为________．解析∵y＝x(1－x2)，∴y2＝x2(1－x2)2＝2x2(1－x2)(1－x2)•12.∵2x2＋(1－x2)＋(1－x2)＝2，∴y2≤122x2＋1－x2＋1－x233＝427.当且仅当2x2＝1－x2，即x＝33时取等号．∴y≤239.∴y的最大值为239.答案2393．(2011•江西卷)对于x∈R，不等式|x＋10|－|x－2|≥8的解集为________．解析法一(零点分段法)由题意可知，x≤－10，－x－10＋x－2≥8或－10＜x＜2，x＋10＋x－2≥8或x≥2，x＋10－x＋2≥8，解得x≥0，故原不等式的解集为{x|x≥0}．法二(几何意义法)如图，在数轴上令点A、B的坐标分别为－10，2，在x轴上任取一点P，其坐标设为x，则|PA|＝|x＋10|，|PB|＝|x－2|，观察数轴可知，要使|PA|－|PB|≥8，则只需x≥0.故原不等式的解集为{x|x≥0}．答案{x|x≥0}4．(2011•陕西)若不等式|x＋1|＋|x－2|≥a对任意x∈R恒成立，则a 的取值范围是________．解析由于|x＋1|＋|x－2|≥|(x＋1)－(x－2)|＝3.所以只需a≤3即可．答案(－∞，3]5．若不等式|x＋1|＋|x－3|≥a＋4a对任意的实数x恒成立，则实数a 的取值范围是________．解析当a＜0时，显然成立；当a＞0时，∵|x＋1|＋|x－3|的最小值为4，∴a＋4a≤4.∴a＝2..综上可知a的取值范围是(－∞，0)∪{2}．答案(－∞，0)∪{2}6．设x，y，z∈R，若x2＋y2＋z2＝4，则x－2y＋2z的最小值为________时，(x，y，z)＝________.解析∵(x－2y＋2z)2≤(x2＋y2＋z2)12＋(－2)2＋22]＝4×9＝36，∴x－2y ＋2z最小值为－6，此时x1＝y－2＝z2.又∵x2＋y2＋z2＝4，∴x＝－23，y＝43，z＝－43.答案－6－23，43，－437．若对任意x＞0，xx2＋3x＋1≤a恒成立，则a的取值范围是________．解析∵a≥xx2＋3x＋1＝1x＋1x＋3对任意x＞0恒成立，设u＝x＋1x＋3，∴只需a≥1u恒成立即可．∵x＞0，∴u≥5(当且仅当x＝1时取等号)．由u≥5，知0＜1u≤15，∴a≥15.答案15，＋∞8．已知h＞0，a，b∈R，命题甲：|a－b|＜2h：命题乙：|a－1|＜h 且|b－1|＜h，则甲是乙的________条件．解析|a－b|＝|a－1＋1－b|≤|a－1|＋|b－1|＜2h，故由乙能推出甲成立，但甲成立不能推出乙成立，所以甲是乙的必要不充分条件．答案必要不充分二、解答题(共20分)9．(10分)已知关于x的不等式|ax－2|＋|ax－a|≥2(a＞0)．(1)当a＝1时，求此不等式的解集；(2)若此不等式的解集为R，求实数a的取值范围．解(1)当a＝1时，不等式为|x－2|＋|x－1|≥2.由绝对值的几何意义知，不等式的意义可解释为数轴上的点x到1、2的距离之和大于等于2.∴x≥52或x≤12.∴不等式的解集为xx≤12或x≥52.注也可用零点分段法求解．(2)∵|ax－2|＋|ax－a|≥|a－2|，∴原不等式的解集为R等价于|a－2|≥2，∴a≥4或a≤0，又a＞0，∴a≥4.10．(10分)对于任意实数a(a≠0)和b，不等式|a＋b|＋|a－2b|≥|a|(|x －1|＋|x－2|)恒成立，试求实数x的取值范围．解原不等式等价于|a＋b|＋|a－2b||a|≥|x－1|＋|x－2|，设ba＝t，则原不等式变为|t＋1|＋|2t－1|≥|x－1|＋|x－2|对任意t恒成立．因为|t＋1|＋|2t－1|＝3t，t≥12，－t＋2，－1＜t＜12，－3t，t≤－1，在t＝12时取到最小值为32.所以有32≥|x－1|＋|x－2|＝2x－3，x≥2，1，1＜x＜2，3－2x，x≤1，解得x∈34，94.。
2013年高考数学(全国卷)理科及答案
2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(理科)注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号标黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。
4. 考试结束，将试题卷和答题卡一并交回。
第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题。
每小题5分，共50分。
在每个小题给出的四个选项中，只有一项是符合题目要求的。
（1）已知集合M=｛x|(x+1)2 < 4,x∈R｝，N=｛-1，0，1，2，3｝，则M∩N=（）（A）｛0，1，2｝（B）｛-1，0，1，2｝（C）{-1，0，2，3} （D）{0，1，2，3}（2）设复数z满足（1-i）z=2 i，则z= （）（A）-1+i （B）-1-i （C）1+i （D）1-i（3）等比数列｛a n｝的前n项和为S n，已知S3 = a2 +10a1 ，a5 = 9，则a1= （）（A）（B）-（C）（D）-（4）已知m，n为异面直线，m⊥平面α，n⊥平面β。
直线l满足l ⊥m，l ⊥n，l β，则（）（A）α∥β且l ∥α（B）α⊥β且l⊥β（C）α与β相交，且交线垂直于l （D）α与β相交，且交线平行于l（5）已知（1+ɑx）(1+x)5的展开式中x2的系数为5，则ɑ=（A）-4 （B）-3 （C）-2 （D）-1（6）执行右面的程序框图，如果输入的N=10，那么输出的s=（A）1+ + +…+（B ）1++ +…+（C ）1+ + +…+（D ）1++ +…+（7）一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是（1，0，1），（1，1，0），（1，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx 平面为搞影面，则得到正视图可以为(A) (B) (C) (D)（8）设ɑ=log 36,b=log 510,c=log 714,则（A ）c ＞b ＞a （B ）b ＞c ＞a（C ）a ＞c ＞b (D)a ＞b ＞c（9）已知a ＞0，x ，y 满足约束条件 ,若z=2x+y 的最小值为1，则a=(A)(B) (C)1 (D)2（10）已知函数f(x)=x2+αx2+bx+，下列结论中错误的是（A ）∑x α∈R f(x α)=0（B ）函数y=f(x)的图像是中心对称图形（C ）若x α是f(x)的极小值点，则f(x)在区间（-∞,x α）单调递减（D ）若xn 是f （x ）的极值点，则f 1(x α)=0（11）设抛物线y2=3px(p ≥0)的焦点为F ，点M 在C 上，|MF|=5若以MF 为直径的园过点（0，3），则C 的方程为（A ）y2=4x 或y2=8x （B ）y2=2x 或y2=8x（C ）y2=4x 或y2=16x （D ）y2=2x 或y2=16x（12）已知点A （-1，0）；B （1，0）；C （0，1），直线y=ax+b(a>0)将△ABC 分割为面积相等的两部分，则b 的取值范围是x ≥1, x+y ≤3, y ≥a(x-3). {（A）（0，1）(B)（1-，1/2）( C)（1-，1/3）(D)[ 1/3, 1/2）第Ⅱ卷本卷包括必考题和选考题，每个试题考生都必修作答。
2013年高考数学理知识与能力测试题
OF
即有
DF
EF
，又根据相交弦定理 DF· EF＝ BF· AF
PF
可推出 BF OB 2 ，从而 PF PB 1
PF AP 6
PF
3
∴ PF＝ 3
ab
ab
（ 2） ∵ PF QF，
∴c a2
c
1 ∴ a b,e 2
a2
cc
c
c
(3) 略。
三、 15．解： (1) 依题知，
得 f (x) m? n
3 sin x cos x cos2 x
2 )
3
当t
13 ln 时， 0
et
2 ， P2 P1 0 ， P2
P1 ；
2
3
当 t 1 ln 3 时， e t 2 ， P2 P1 0 ， P2 P1 ；
2
3
当t
13 ln 时， e
t
2 ， P2 P1 0 ， P2
P1 ；
2
3
13
故当 t
ln 时，飞机 A 安全；
2
当t
13 ln 时，飞机 A 与飞机 B 一样安全；
2
2
设 m (x1, y1 , z1 ) 是平面 C ' EF 的一个法向量，则
2
A． 1
B． 1
3
3
C．
1
1
D．
2
6
2
6
11
-2
2
4
6
8
10
12
O 2 -1
x
3 -2
3
-3
-4
6．某工厂生产产品， 用传送带将产品放入下一工序， 质检人员每隔 t 分钟在传进带上某一固定位置取一件检验， 这种抽样方法是
2013高考数学(理科)小题限时训练2
2013高考数学（理科）小题限时训练二15小题共75分，时量：45分钟，考试时间：2012年8月23日第6节 姓名一、选择题：本大题共8小题，每小题5分，共40分． 1、设集合{1,2}A =,则满足{1,2,3}A B ⋃=的集合B 的个数是（ ）A ． 1B ．3C ．4D ．8 2、下列函数中，在其定义域内既是奇函数又是减函数的是 （ ） A ．R x x y ∈-=,3 B ．R x x y ∈=,sinC ．R x x y ∈=,D ．R x x y ∈=,)21(3、函数)13lg(13)(2++-=x xx x f 的定义域是 （ ）A ．),31(+∞-B ．)31,(--∞C ．)31,31(-D ．)1,31(-4、已知函数⎩⎨⎧>≤=+.0,log ,0,3)(21x x x x f x 若()30>x f ，则0x 的取值范围是 （ ）A ．80>xB ．00<x 或80>x ．C ．800<<x ．D ．00<x 或800<<x ．5、,1xy x =-已知函数则下列四个命题中错误的是 （ ） A ．该函数图象关于点（1，1）对称； B ．该函数的图象关于直线2y x =-对称； C ．该函数在定义域内单调递减；D ．将该函数图象向左平移一个单位，再向下平移一个单位后与函数xy 1=的图象重合 6、函数(1)||xxa y a x =>的图像大致形状是 （ ）7、若方程m m x x 无实数解，则实数+=-21的取值范围是 （ ）AB CD[](1)1(1)))A B C D -∞---∞-+∞+∞ 、，、、，8、函数)6(log )(ax x f a -=在]2,0[上为减函数，则a 的取值范围是（ ） （A ）)1,0(（B ）)3,1(（C ）)3,0(（D ）),3[+∞二、填空题：本大题共7小题，每小题5分，共35分．9、若方程0422=+-mx x 的两根满足一根大于2，一根小于1，则m 的取值范围是10、设,0.(),0.x e x g x lnx x ⎧≤=⎨>⎩则1(())2g g =__________．11、函数()lg 3f x x x =+-的零点的个数是____________． 12、设定义在R 上的函数)(x f 同时满足以下条件：①0)()(=-+x f x f ；②)2()(+=x f x f ；③当10<≤x 时，12)(-=x x f 。
2013年高考数学(理科)模拟卷
2017学年第一学期浙江“七彩阳光”联盟期中联考高三年级数学学科 参考答案一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.答案B 。
解：1a bi i +=-+Q ， 21a b ∴+=。
3.答案A 。
解析：若222log loglog ()a b a b +≥+，则ab a b ≥+。
又0,0a b >>， 则有ab a b ≥+≥4ab ≥，故充分性成立；若4,1a b ==，满足4ab ≥，但22log log 2a b +=，22log ()log 52a b +=>， 即222log log log ()a b a b +≥+不成立，故必要性不成立，故选A.4.答案D.解：所取3个球中没有红球的概率是34137435C p C ==，所取3个球中恰有1个红球的概率是12342371835C C p C ==，则所取3个球中至多有1个红球的概率是122235p p p =+=。
5.答案C ．解8511820,0a a a a =+>∴>Q ，则115158151502a a S a +=⨯=>。
又7869780,0a a a a a a +=+<∴<-<，则113137131302a a S a +=⨯=<。
而1141469147()02a a S a a +=⨯=+<，则满足0n S <的正整数n 的最大值是14。
6答案A. 解析：222()2a b a b a b a b a ba b ++-=+++-+-r r r r r r r r r r r r Q g222222a a b b a a b b =+++-+r r r r r r r r g g444sin()αβ=+=+-。
02παβ<-<Q ，24()8a b a b ∴<++-<r r r r，2a b a b ∴<++-<r r r r7.答案C.解法1：设点A 在第一象限，由222b y x a x y c ⎧=⎪⎨⎪+=⎩和0x >，得x a y b =⎧⎨=⎩，即得(,)A a b 。
2013年全国高考理科数学试题(带答案)：三角函数
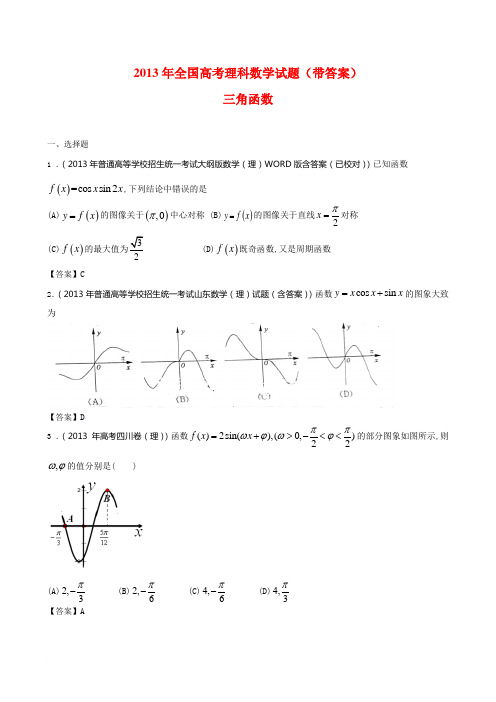
2013年全国高考理科数学试题（带答案）三角函数一、选择题1 ．（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知函数()=cos sin 2f x x x ,下列结论中错误的是(A)()y f x =的图像关于(),0π中心对称 (B)()y f x =的图像关于直线2x π=对称(C)()f x 的最大值为2(D)()f x 既奇函数,又是周期函数 【答案】C2．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））函数cos sin y x x x =+的图象大致为【答案】D3 ．（2013年高考四川卷（理））函数()2sin(),(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( )(A)2,3π-(B)2,6π-(C)4,6π-(D)4,3π【答案】A4．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））已知210cos 2sin ,=+∈αααR ,则=α2tan A.34 B. 43C.43-D.34-【答案】C5 ．（2013年高考陕西卷（理））设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=,则△ABC 的形状为(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定 【答案】B6．（2013年普通高等学校招生统一考试天津数学（理）试题（含答案））在△ABC 中, ,3,4AB BC ABC π∠===则sin BAC ∠ =【答案】C7 ．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））将函数sin(2)y x ϕ=+的图象沿x轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为 (A) 34π (B) 4π (C)0 (D) 4π-【答案】B8 ．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=且a b >,则B ∠= A.6π B.3π C.23π D.56π【答案】A9 ．（2013年上海市春季高考数学试卷(含答案)）既是偶函数又在区间(0 )π，上单调递减的函数是( ) (A)sin y x = (B)cos y x = (C)sin 2y x = (D)cos 2y x =【答案】B10．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））04cos50tan 40-= ( )21 【答案】C11．（2013年高考湖南卷（理））在锐角中ABC ∆,角,A B 所对的边长分别为,a b .若2sin ,a B A =则角等于A.12π B.6π C.4π D.3π 【答案】D12．（2013年高考湖北卷（理））将函数()sin y x x x R =+∈的图像向左平移()0m m >个长度单位后,所得到的图像关于y 轴对称,则m 的最小值是( ) A.12πB.6π C.3π D.56π【答案】B 二、填空题13．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））ABC ∆中,090=∠C ,M 是BC的中点,若31sin =∠BAM ,则=∠BAC sin ________.【答案】314．（2013年高考新课标1（理））设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______【答案】. 15．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））如图ABC ∆中,已知点D 在BC 边上,AD ⊥AC,sin 3BAC AB AD ∠===则BD 的长为_______________16．（2013年上海市春季高考数学试卷(含答案)）函数2sin y x =的最小正周期是_____________【答案】2π17．（2013年高考四川卷（理））设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是_________.【答案】18．（2013年高考上海卷（理））若12cos cos sin sin ,sin 2sin 223x y x y x y +=+=,则sin()________x y +=【答案】2sin()3x y +=. 19．（2013年高考上海卷（理））已知△ABC 的内角A 、B 、C 所对应边分别为a 、b 、c,若22232330a ab b c ++-=,则角C 的大小是_______________(结果用反三角函数值表示)【答案】1arccos3C π=- 20．（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知α是第三象限角,1sin 3a =-,则cot a =____________.【答案】21．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））函数)42sin(3π+=x y 的最小正周期为___________.【答案】π22．（2013年上海市春季高考数学试卷(含答案)）在ABC ∆中,角 A B C 、、所对边长分别为 a b c 、、,若5 8 60a b B ===，，,则b=_______【答案】723．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））设ABC ∆的内角,,A B C 所对边的长分别为,,a b c .若2b c a +=,则3sin 5sin ,A B =则角C =_____.【答案】π3224．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））设θ为第二象限角,若1tan()42πθ+=,则sin cos θθ+=________.【答案】25．（2013年高考江西卷（理））函数2sin 2y x x =+的最小正周期为T 为_________.【答案】π26．（2013年上海市春季高考数学试卷(含答案)）函数4sin 3cos y x x =+的最大值是_______________【答案】5 三、解答题27．（2013年高考北京卷（理））在△ABC 中,a =3,b B =2∠A .(I)求cos A 的值; (II)求c 的值.【答案】解:(I)因为a =3,b =2,∠B =2∠A . 所以在△AB C 中,由正弦定理得3sin sin 2A A=.所以2sin cos sin 3A A A =.故cos 3A =.(II)由(I)知cos A =,所以s i n A ==.又因为∠B=2∠A,所以21c o s 2c o s 13B A =-=.所以sin B ==.在△ABC 中,sin sin()sin cos cos sin C A B A B A B =+=+=. 所以sin 5sin a Cc A==.28．（2013年高考陕西卷（理））已知向量1(cos ,),,cos2),2x x x x =-=∈a b R , 设函数()·f x =a b . (Ⅰ) 求f (x)的最小正周期.(Ⅱ) 求f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】解:(Ⅰ) ()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x .最小正周期ππ==22T . 所以),62sin()(π-=x x f 最小正周期为π.(Ⅱ) 上的图像知，在，由标准函数时，当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈.]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f . 所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为21,1-.29．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））在ABC 中,内角,,A B C 的对边分别是,,a b c ,且222a b c +=.(1)求C ; (2)设()()2cos cos cos cos cos A B A B ααα++==求tan α的值. 【答案】由题意得30．（2013年普通高等学校招生统一考试天津数学（理）试题（含答案））已知函数2()26sin cos 2cos 41,f x x x x x x π⎛⎫=++- ⎪+⎝⎭∈R .(Ⅰ) 求f (x )的最小正周期;(Ⅱ) 求f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】31．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））设向量)(),sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I)若.a b x =求的值； (II)设函数()(),.f x a b f x =求的最大值【答案】32．（2013年高考上海卷（理））(6分+8分)已知函数()2sin()f x x ω=,其中常数0ω>;(1)若()y f x =在2[,]43ππ-上单调递增,求ω的取值范围;(2)令2ω=,将函数()y f x =的图像向左平移6π个单位,再向上平移1个单位,得到函数()y g x =的图像,区间[,]a b (,a b R ∈且a b <)满足:()y g x =在[,]a b 上至少含有30个零点,在所有满足上述条件的[,]a b 中,求b a -的最小值.【答案】(1)因为0ω>,根据题意有34202432ππωωππω⎧-≥-⎪⎪⇒<≤⎨⎪≤⎪⎩ (2) ()2sin(2)f x x =,()2sin(2())12sin(2)163g x x x ππ=++=++1()0sin(2)323g x x x k πππ=⇒+=-⇒=-或7,12x k k Z ππ=-∈,即()g x 的零点相离间隔依次为3π和23π,故若()y g x =在[,]a b 上至少含有30个零点,则b a -的最小值为2431415333πππ⨯+⨯=. 33．（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=. (I)求B(II)若sin sin A C =,求C . 【答案】34．（2013年高考四川卷（理））在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且232cos cos sin()sin cos()25A B B A B B A C ---++=-. (Ⅰ)求cos A 的值;(Ⅱ)若a =5b =,求向量BA 在BC 方向上的投影.【答案】解:()I 由()()232cos cos sin sin cos 25A B B A B B A C ---++=-,得 ()()3cos 1cos sin sin cos 5A B B A B B B -+---=-⎡⎤⎣⎦, 即()()3cos cos sin sin 5A B B A B B ---=-,则()3cos 5A B B -+=-,即3cos 5A =-()II 由3cos ,05A A π=-<<,得4sin 5A =,由正弦定理,有sin sin a b A B =,所以,sin sin b A B a ==. 由题知a b >,则A B >,故4B π=.根据余弦定理,有(22235255c c ⎛⎫=+-⨯⨯- ⎪⎝⎭,解得1c =或7c =-(舍去).故向量BA 在BC方向上的投影为cos 2BA B =35．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））设△ABC 的内角,,A B C 所对的边分别为,,a b c ,且6a c +=,2b =,7cos 9B =. (Ⅰ)求,a c 的值; (Ⅱ)求sin()A B -的值.【答案】解:(Ⅰ)由余弦定理2222cos b a c ac B =+-,得()222(1cos )b ac ac B =+-+,又6a c +=,2b =,7cos 9B =,所以9ac =,解得3a =,3c =.(Ⅱ)在△ABC中,sin B ==,由正弦定理得sin sin a B A b ==,因为a c =,所以A 为锐角,所以1cos 3A ==因此sin()sin cos cos sin 27A B A B A B -=-=.36．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））已知函数()4cos sin (0)4f x x x πϖϖϖ⎛⎫=⋅+> ⎪⎝⎭的最小正周期为π.(Ⅰ)求ϖ的值; (Ⅱ)讨论()f x 在区间[]0,2上的单调性.【答案】解: (Ⅰ)2)42sin(2)12cos 2(sin 2)cos (sin cos 22++=++=+⇒πωωωωωωx x x x x x122=⇒=⇒ωπωπ.所以1,2)42sin(2)(=++=ωπx x f (Ⅱ) ；解得，令时，当8242]4,4[)42(]2,0[ππππππππ==++∈+∈x x x x 所以.]28[]8,0[)(上单调递减，上单调递增；在在πππx f y =37．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））已知函数()sin()(0,0)f x x ωϕωϕπ=+><<的周期为π,图像的一个对称中心为(,0)4π,将函数()f x 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移2π个单位长度后得到函数()g x 的图像.(1)求函数()f x 与()g x 的解析式; (2)是否存在0(,)64x ππ∈,使得0000(),(),()()f x g x f x g x 按照某种顺序成等差数列?若存在,请确定0x 的个数;若不存在,说明理由(3)求实数a 与正整数n ,使得()()()F x f x ag x =+在(0,)n π内恰有2013个零点.【答案】解:(Ⅰ)由函数()sin()f x x ωϕ=+的周期为π,0ω>,得2ω=又曲线()y f x =的一个对称中心为(,0)4π,(0,)ϕπ∈故()sin(2)044f ππϕ=⨯+=,得2πϕ=,所以()cos 2f x x =将函数()f x 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得cos y x =的图象,再将cos y x =的图象向右平移2π个单位长度后得到函数()sin g x x =(Ⅱ)当(,)64x ππ∈时,1sin 2x <<10cos 22x << 所以sin cos 2sin cos 2x x x x >>问题转化为方程2cos 2sin sin cos 2x x x x =+在(,)64ππ内是否有解设()sin sin cos 22cos 2G x x x x x =+-,(,)64x ππ∈ 则()cos cos cos 22sin 2(2sin )G x x x x x x '=++- 因为(,)64x ππ∈,所以()0G x '>,()G x 在(,)64ππ内单调递增又1()064G π=-<,()04G π=> 且函数()G x 的图象连续不断,故可知函数()G x 在(,)64ππ内存在唯一零点0x ,即存在唯一的0(,)64x ππ∈满足题意 (Ⅲ)依题意,()sin cos 2F x a x x =+,令()sin cos 20F x a x x =+=当sin 0x =,即()x k k Z π=∈时,cos 21x =,从而()x k k Z π=∈不是方程()0F x =的解,所以方程()0F x =等价于关于x 的方程cos 2sin xa x=-,()x k k Z π≠∈ 现研究(0,)(,2)x πππ∈U 时方程解的情况 令cos 2()sin xh x x=-,(0,)(,2)x πππ∈U 则问题转化为研究直线y a =与曲线()y h x =在(0,)(,2)x πππ∈U 的交点情况22cos (2sin 1)()sin x x h x x +'=,令()0h x '=,得2x π=或32x π= 当x 变化时,()h x 和()h x '变化情况如下表当0x >且x 趋近于0时,()h x 趋向于-∞ 当x π<且x 趋近于π时,()h x 趋向于-∞ 当x π>且x 趋近于π时,()h x 趋向于+∞ 当2x π<且x 趋近于2π时,()h x 趋向于+∞故当1a >时,直线y a =与曲线()y h x =在(0,)π内有无交点,在(,2)ππ内有2个交点; 当1a <-时,直线y a =与曲线()y h x =在(0,)π内有2个交点,在(,2)ππ内无交点; 当11a -<<时,直线y a =与曲线()y h x =在(0,)π内有2个交点,在(,2)ππ内有2个交点由函数()h x 的周期性,可知当1a ≠±时,直线y a =与曲线()y h x =在(0,)n π内总有偶数个交点,从而不存在正整数n ,使得直线y a =与曲线()y h x =在(0,)n π内恰有2013个交点;当1a =±时,直线y a =与曲线()y h x =在(0,)(,2)πππU 内有3个交点,由周期性,20133671=⨯,所以67121342n =⨯= 综上,当1a =±,1342n =时,函数()()()F x f x ag x =+在(0,)n π内恰有2013个零点38．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分14分.已知(cos ,sin )(cos ,sin )a b ααββ=＝，,παβ<<<0. (1)若||2a b -=,求证:a b ⊥;(2)设(0,1)c =,若a b c +=,求βα,的值.【答案】解:(1)∵2||=- ∴2||2=- 即()22222=+-=-,又∵1sin cos ||2222=+==αα,1sin cos ||2222=+==ββ∴222=-∴0=∴⊥(2)∵)1,0()sin sin ,cos (cos =++=+βαβα ∴⎩⎨⎧=+=+1sin sin 0cos cos βαβα即⎩⎨⎧-=-=βαβαsin 1sin cos cos两边分别平方再相加得:βsin 221-= ∴21sin =β ∴21sin =α ∵παβ<<<0 ∴πβπα61,65==39．（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））已知函数()12f x x π⎛⎫=- ⎪⎝⎭,x ∈R .(Ⅰ) 求6f π⎛⎫- ⎪⎝⎭的值; (Ⅱ) 若3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,求23f πθ⎛⎫+ ⎪⎝⎭.【答案】(Ⅰ)1661244f πππππ⎛⎫⎛⎫⎛⎫-=--=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;(Ⅱ) 222cos 2sin 233124f ππππθθθθθ⎛⎫⎛⎫⎛⎫+=+-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,所以4sin 5θ=-, 所以24sin 22sin cos 25θθθ==-,227cos 2cos sin 25θθθ=-=- 所以23f πθ⎛⎫+⎪⎝⎭cos 2sin 2θθ=-72417252525⎛⎫=---= ⎪⎝⎭. 40．（2013年高考湖南卷（理））已知函数2()sin()cos().()2sin 632xf x x xg x ππ=-+-=.(I)若α是第一象限角,且()5f α=求()g α的值; (II)求使()()f x g x ≥成立的x 的取值集合.【答案】解: (I)533sin 3)(sin 3sin 23cos 21cos 21sin 23)(==⇒=++-=ααf x x x x x x f . 51cos 12sin 2)(,54cos )2,0(,53sin 2=-===⇒∈=⇒ααααπααg 且(II)21)6sin(cos 21sin 23cos 1sin 3)()(≥+=+⇒-≥⇒≥πx x x x x x g x f Z k k k x k k x ∈+∈⇒++∈+⇒],322,2[]652,62[6ππππππππ41．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分16分.如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲.乙两位游客从A 处下山,甲沿AC 匀速步行,速度为min /50m .在甲出发min 2后,乙从A 乘缆车到B ,在B 处停留min 1后,再从匀速步行到C .假设缆车匀速直线运动的速度为min /130m ,山路AC 长为m 1260,经测量,1312cos =A ,53cos =C . (1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?【答案】解:(1)∵1312cos =A ,53cos =C ∴），（、20π∈C A ∴135sin =A ,54sin =C∴[]6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B ）（）（π 根据sinB sinC AC AB =得m C ACAB 1040sin sinB== (2)设乙出发t 分钟后,甲.乙距离为d,则1312)50100(1302)50100()130(222⨯+⨯⨯-++=t t t t d ∴)507037(20022+-=t t d∵13010400≤≤t 即80≤≤t ∴3735=t 时,即乙出发3735分钟后,乙在缆车上与甲的距离最短.(3)由正弦定理sinBsinA ACBC =得50013565631260sin sinB ===A AC BC (m) 乙从B 出发时,甲已经走了50(2+8+1)=550(m),还需走710 m 才能到达C 设乙的步行速度为V min /m ,则350710500≤-v ∴3507105003≤-≤-v ∴14625431250≤≤v ∴为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在⎥⎦⎤⎢⎣⎡14625,431250范围内 法二:解:(1)如图作BD ⊥CA 于点D ,设BD =20k ,则DC =25k ,AD =48k , AB =52k ,由AC =63k =1260m, 知:AB =52k =1040m.(2)设乙出发x 分钟后到达点M , 此时甲到达N 点,如图所示. 则:AM =130x ,AN =50(x +2),CBA由余弦定理得:MN 2=AM 2+AN 2-2 AM ·AN cos A =7400 x 2-14000 x +10000, 其中0≤x ≤8,当x =3537 (min)时,MN 最小,此时乙在缆车上与甲的距离最短.(3)由(1)知:BC =500m,甲到C 用时:126050 =1265(min).若甲等乙3分钟,则乙到C 用时:1265 +3=1415 (min),在BC 上用时:865 (min) .此时乙的速度最小,且为:500÷865 =125043m/min.若乙等甲3分钟,则乙到C 用时:1265 -3=1115 (min),在BC 上用时:565 (min) .此时乙的速度最大,且为:500÷565 =62514 m/min.故乙步行的速度应控制在[125043 ,62514]范围内.42．（2013年高考湖北卷（理））在ABC ∆中,角A ,B ,C 对应的边分别是a ,b ,c .已知()cos 23cos 1A B C -+=.(I)求角A 的大小;(II)若ABC ∆的面积S =,5b =,求sin sin B C 的值.【答案】解:(I)由已知条件得:cos23cos 1A A +=22cos 3cos 20A A ∴+-=,解得1cos 2A =,角60A =︒(II)1sin 2S bc A ==4c ⇒=,由余弦定理得:221a =,()222228sin a R A == 25sin sin 47bc B C R ∴==43．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））△ABC 在内角,,A B C的对边分别为,,a b c ,已知cos sin a b C c B =+. (Ⅰ)求B ;(Ⅱ)若2b =,求△ABC 面积的最大值.CBADMN【答案】44．（2013年高考新课标1（理））如图,在△ABC中,∠ABC=90°,AB= 3 ,BC=1,P 为△ABC内一点,∠BPC=90°(1)若PB=12,求PA;(2)若∠APB=150°,求tan∠PBA[【答案】(Ⅰ)由已知得,∠PBC=o 60,∴∠PBA=30o ,在△PBA 中,由余弦定理得2PA =o 1132cos3042+-=74;(Ⅱ)设∠PBA=α,由已知得,PB=sin α,在△PBA 中,由正弦定理得,o sin sin(30)αα=-,化简得4sin αα=, ∴tan αtan PBA ∠. 45．（2013年上海市春季高考数学试卷(含答案)）本题共有2个小题,第一小题满分4分,第二小题满分9分.在平面直角坐标系xOy 中,点A 在y 轴正半轴上,点n P 在x 轴上,其横坐标为n x ,且{}n x 是首项为1、公比为2的等比数列,记1n n n P AP θ+∠=,n N *∈. (1)若31arctan3θ=,求点A 的坐标; (2)若点A的坐标为(0,求n θ的最大值及相应n 的值.[解](1) (2)【答案】[解](1)设(0 )A t ，,根据题意,12n n x -=.由31arctan 3θ=,知31tan 3θ=,而3443343223443()4tan tan()321x x t x x t t t OAP OAP x x t x x t t tθ--=∠-∠===+⋅++⋅, 所以241323t t =+,解得4t =或8t =. 故点A 的坐标为(0 4)，或(0 8)，. (2)由题意,点n P 的坐标为1(20)n -，,1tan n n OAP -∠=. 111212tan tan()1n n n n n n n OAP OAP θ--+-=∠-∠===.n+≥,所以tan nθ≤=当且仅当2nn=,即4n =时等号成立. 易知0 tan 2n y x πθ<<=，在(0 )2π，上为增函数,因此,当4n =时,n θ最大,其最大值为arctan4. 46．（2013年高考江西卷（理））在△ABC 中,角A,B,C 所对的边分别为a,b,c,已知cosC+(conA-sinA)cosB=0.(1) 求角B 的大小;若a+c=1,求b 的取值范围【答案】解:(1)由已知得cos()cos cos cos 0A B A B A B -++=即有sin sin cos 0A B A B =因为sin 0A ≠,所以sin 0B B =,又cos 0B ≠,所以tan B =又0B π<<,所以3B π=.(2)由余弦定理,有2222cos b a c ac B =+-.因为11,cos 2a c B +==,有22113()24b a =-+. 又01a <<,于是有2114b ≤<,即有112b ≤<.。
2013年全国高考理科数学试题分类汇编7：立体几何Word版含答案
2013年全国高考理科数学试题分类汇编7：立体几何一、选择题1 ．（2013 年高考新课标1（理））如图, 有一个水平放置的透明无盖的正方体容器, 容器高8cm,将一个球放在容器口, 再向容器内注水, 当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度, 则球的体积为（）A．50033cm B．86633cm C．137233cm D．204833cm【答案】 A2 ．（2013 年普通高等学校招生统一考试广东省数学（理）卷（纯WORD版））设m,n 是两条不同的直线, , 是两个不同的平面, 下列命题中正确的是（）A．若, m , n , 则m n B．若// , m , n , 则m // nC．若m n , m , n , 则D．若m , m // n, n // , 则【答案】 D3 ．（2013 年上海市春季高考数学试卷( 含答案) ）若两个球的表面积之比为1: 4, 则这两个球的体积之比为（）A．1: 2 B．1: 4 C．1: 8 D．1:16【答案】 C4 ．（2013 年普通高等学校招生统一考试大纲版数学（理）WORD版含答案（已校对））已知正四棱柱A BCD ABC D 中AA1 2AB , 则CD 与平面BDC1 所成角的正弦值等于（）1 1 1 1A．23B．33C．23D．13【答案】 A5 ．（2013 年高考新课标1（理））某几何体的三视图如图所示, 则该几何体的体积为（）A．16 8 B．8 8 C．16 16 D．8 16【答案】 A6 ．（2013 年高考湖北卷（理））一个几何体的三视图如图所示, 该几何体从上到下由四个简单几何体组成, 其体积分别记为V1 , V2 , V3 , V4 , 上面两个简单几何体均为旋转体, 下面两个简单几何体均为多面体, 则有（）A．V1 V2 V4 V3 B．V1 V3 V2 V4 C．V2 V1 V3【答案】 C7 ．（2013 年高考湖南卷（理））已知棱长为 1 的正方体的俯视图是一个面积为 1 的正方形,则该正方体的正视图的面积不可．能．．等于（）A．1 B． 2 C．2-12D．2+12【答案】 C8 ．（2013 年普通高等学校招生统一考试广东省数学（理）卷（纯WORD版））某四棱台的三视图如图所示, 则该四棱台的体积是122正视图侧视图11第5 题图俯视图（）14 16A．4 B．3 C．3 D．6【答案】 B9 ．（2013 年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD版含答案））已知m,n为异面直线, m 平面, n 平面. 直线l 满足l m,l n,l ,l , 则（）A．// , 且l // B．, 且lC．与相交, 且交线垂直于l D．与相交, 且交线平行于l【答案】 D10．（2013 年普通高等学校招生统一考试山东数学（理）试题（含答案））已知三棱柱9ABC A B C1 1 1的侧棱与底面垂直, 体积为4, 底面是边长为 3 的正三角形. 若P 为底面A1B1C1的中心, 则PA 与平面ABC 所成角的大小为（）5A．12 B．3 C．4 D．6【答案】 B11．（2013 年普通高等学校招生统一考试重庆数学（理）试题（含答案））某几何体的三视图如题5 图所示,则该几何体的体积为（）A．5603B．5803C．200 D．240【答案】 C12．（2013 年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））已知三棱柱ABC A B C的 6 个顶点都在球O 的球面上, 若1 1 1AB 3，AC 4 , AB AC , AA1 12, 则球O 的半径为（）A．3172B．210 C．132D．310【答案】 C13．（2013 年高考江西卷（理））如图, 正方体的底面与正四面体的底面在同一平面上, 且AB CD , 正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为m,n , 那么m n（）A．8 B．9 C．10 D．11【答案】 A14．（2013 年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD版含答案））一个四面体的顶点在空间直角坐标系O xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),,(画0,该0,四0)面体三视图中的正视图时, 以zOx平面为投影面, 则得到正视图可以为（）A．B．C．D．【答案】 A15．（2013 年普通高等学校招生统一考试安徽数学（理）试题（纯WORD版））在下列命题中, 不是公．理．的是（）A．平行于同一个平面的两个平面相互平行B．过不在同一条直线上的三点, 有且只有一个平面C．如果一条直线上的两点在一个平面内, 那么这条直线上所有的点都在此平面内D．如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线【答案】 A16．（2013 年普通高等学校招生统一考试浙江数学（理）试题（纯WORD版））在空间中, 过点A 作平面的垂线, 垂足为B , 记B f ( A). 设, 是两个不同的平面, 对空间任意一点P , Q1 f [ f ( P)], Q2 f [ f ( P)] , 恒有PQ1 PQ2 , 则（）A．平面与平面垂直B．平面与平面所成的( 锐) 二面角为045C．平面与平面平行D．平面与平面所成的( 锐) 二面角为060【答案】 A17．（2013 年高考四川卷（理））一个几何体的三视图如图所示, 则该几何体的直观图可以是【答案】 D二、填空题18．（2013 年高考上海卷（理））在xOy 平面上, 将两个半圆弧 2 2( x 1) y 1(x 1) 和2 2(x 3) y 1(x 3)、两条直线y 1 和y 1围成的封闭图形记为D,如图中阴影部分. 记 D 绕y 轴旋转一周而成的几何体为, 过(0, y )(| y | 1) 作的水平截面, 所得截面面积为 24 1 y 8 , 试利用祖暅原理、一个平放的圆柱和一个长方体, 得出的体积值为__________【答案】 22 16 .19．（2013 年高考陕西卷（理））某几何体的三视图如图所示, 则其体积为___ _____.3 2111【答案】320．（2013 年普通高等学校招生统一考试大纲版数学（理）WORD版含答案（已校对））已知圆O和圆K 是球O 的大圆和小圆, 其公共弦长等于球O 的半径,3OK , 且圆O与圆K 所2在的平面所成的一个二面角为60 , 则球O的表面积等于______.【答案】1621．（2013 年高考北京卷（理））如图, 在棱长为 2 的正方体ABCD- A1B1C1D1 中, E为BC的中点, 点P在线段D1E上, 点P到直线CC1 的距离的最小值为__________.D 1 C 1A1D PB1CEAB2 5 【答案】522．（2013 年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD版含附加题））如图, 在三棱柱 A B C ABC1 中, D，E，F 分别是AB，AC，AA1 的中点, 设三棱1 1锥 F ADE 的体积为V , 三棱柱A1B1C1 ABC 的体积为V2 , 则1V1 :V____________.2CBAFCEA D【答案】1: 24B23．（2013 年普通高等学校招生统一考试浙江数学（理）试题（纯WORD版））若某几何体的三视图( 单位:cm) 如图所示, 则此几何体的体积等于________ 2cm .4332正视图侧视图3俯视图（第12 题图）【答案】2424．（2013 年普通高等学校招生统一考试安徽数学（理）试题（纯WORD版））如图, 正方体ABCD ABC D 的棱长为1,P 为BC的中点,Q 为线段CC1 上的动点, 过点A,P,Q 的平1 1 1 1面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号).①当01 1 3CQ 时,S 为四边形; ②当CQ 时,S 为等腰梯形; ③当CQ 时,S 与2 2 41C D 的交点R满足 1 1C R ; ④当1 13 34CQ 1时,S 为六边形; ⑤当CQ 1时,S 的面积6为. 2【答案】①②③⑤25．（2013 年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））某几何体的三视图如图所示, 则该几何体的体积是____________.【答案】16 1626．（2013 年普通高等学校招生统一考试福建数学（理）试题（纯WORD版））已知某一多面体内接于一个简单组合体, 如果该组合体的正视图. 测试图. 俯视图均如图所示, 且图中的四边形是边长为 2 的正方形, 则该球的表面积是_______________【答案】1227．（2013 年上海市春季高考数学试卷( 含答案) ）在如图所示的正方体A BCD ABC D 中,1 1 1 1异面直线A1B 与B1C 所成角的大小为_______D1 C1A1B1D CA B【答案】3WORD文档三、解答题28．（2013 年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(I) 求证: 平面PAC 平面PBC；(II) 若AB 2，AC 1，PA 1，求证：二面角 C PB A的余弦值.【答案】WORD文档29．（2013 年普通高等学校招生统一考试重庆数学（理）试题（含答案））如图, 四棱锥P ABCD 中, PA 底面ABCD , BC CD 2, AC 4, ACB ACD , F 为PC 的中3 点, AF PB .(1) 求PA 的长; (2) 求二面角 B AF D 的正弦值.【答案】1．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD版））如图,圆锥顶点为p.底面圆心为o, 其母线与底面所成的角为22.5 °. AB 和CD 是底面圆O 上的两条平行的弦, 轴OP 与平面PCD 所成的角为60°.( Ⅰ) 证明: 平面PAB 与平面PCD 的交线平行于底面; ( Ⅱ) 求cos COD .【答案】解: ( Ⅰ) 设面面直线且面面PAB PCD m, AB/ /CD CD PCD AB/ / PCDAB / /直线m AB 面ABCD 直线m // 面ABCD .所以, 面PAB与面PCD的公共交线平行底面ABCD .( Ⅱ)PO设底面半径为.r,线段CD的中点为F，则OPF 60 .由题知tan 22.5r, tan 60 OFPOtan 60 tan 22.5OFrcosCOD2, tan 4512 t antan22 .5222.5.cos COD 2 2 COD cos CODcos 1 tan 22.5 2 -1,2 2 1[ 3( 2 - 1,)] 2 3(3 2 2 )cos COD 17- 12 2.所以cos COD 17 -12 2 . 法二:1．（2013 年普通高等学校招生统一考试浙江数学（理）试题（纯WORD版））如图, 在四面体A BCD 中, AD 平面BCD , BC CD, AD 2, BD 2 2 . M 是AD 的中点, P是BM 的中点, 点Q 在线段AC 上, 且AQ 3QC .(1) 证明: PQ // 平面BCD ;(2) 若二面角 C BM D 的大小为060 , 求BDC 的大小.AMPQDBC（第20 题图）【答案】解: 证明( Ⅰ) 方法一: 如图6, 取MD 的中点 F , 且M 是AD 中点, 所以AF 3 FD . 因为P 是BM 中点, 所以PF / /BD ; 又因为( Ⅰ)AQ 3QC 且AF 3FD , 所以QF / / BD , 所以面PQF / / 面BDC , 且PQ 面BDC , 所以PQ / / 面BDC ;方法二: 如图7 所示, 取BD 中点O , 且P 是BM 中点, 所以1PO/ / MD ; 取CD 的三等2分点H , 使DH 3CH , 且AQ 3QC , 所以/ / 1 / / 1QH AD MD , 所以4 2P O// Q H P /Q/ ,O且H OH BCD , 所以PQ / / 面BDC ;( Ⅱ) 如图8 所示, 由已知得到面ADB 面BDC , 过C 作CG BD 于G , 所以CG BMD , 过G 作GH BM 于H , 连接CH , 所以CHG 就是C BM D 的二面角; 由已知得到BM 8 1 3, 设BDC , 所以CD CG CBcos ,sin CD 2 2 cos ,CG 2 2 cos sin , BC 2 2 sin , BD CD BD,在RT BCG 中, BCG sin BG BG 2 2 sin2BC, 所以在RT BHG中,HG22 2 sin21 2 2 sinHG , 所以在RT CHG 中3 3tan CHG tan60 3 CGHG2 2 cos sin22 2 sin3tan 3 (0,90 ) 60 BDC 60 ;2．（2013 年上海市春季高考数学试卷( 含答案) ）如图, 在正三棱锥ABC A1B1C1 中, AA1 6 ,异面直线B C 与1 AA 所成角的大小为1 6, 求该三棱柱的体积.A1 C1B1A CB【答案】[ 解] 因为C C1 AA1 .所以B CC 为异面直线BC1 与AA1 . 所成的角, 即BC1C =1 6 .在Rt BC C 中,13BC CC tan BC C 6 2 3 ,1 13从而32S BC 3 3 , ABC4因此该三棱柱的体积为V S ABC AA1 3 3 6 18 3 .3．（2013 年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD版含附加题））本小题满分14 分.如图, 在三棱锥S ABC 中, 平面SAB 平面SBC , AB BC , AS AB , 过A 作AF SB , 垂足为 F , 点E，G 分别是棱SA，SC 的中点.求证:(1) 平面EFG // 平面ABC ; (2) BC SA.SE GFCAB【答案】证明:(1) ∵AS AB , AF SB∴F分别是SB的中点∵E.F 分别是SA.SB的中点∴EF∥AB又∵EF 平面ABC, AB 平面ABC∴EF∥平面ABC同理:FG∥平面ABC又∵EF FG=F, EF.FG 平面ABC∴平面EFG // 平面ABC(2) ∵平面SAB 平面SBC平面SAB 平面SBC =BCAF 平面SABAF⊥SB∴AF⊥平面SBC 又∵BC 平面SBC∴AF⊥BC又∵AB BC , AB AF=A, AB.AF 平面SAB ∴BC⊥平面SAB 又∵SA 平面SAB∴BC⊥SA4．（2013 年高考上海卷（理））如图, 在长方体ABCD-A1B1C1D1 中,AB=2,AD=1,A 1A=1, 证明直线BC1 平行于平面DA1C,并求直线BC1 到平面D1AC的距离.D CABA1D1B1C1【答案】因为ABCD-A1B1C1D1 为长方体, 故AB// C1D1, AB C1D1 ,故ABC1D1 为平行四边形, 故B C1 // AD1, 显然 B 不在平面 D1AC上, 于是直线BC1 平行于平面DA1C;直线BC1 到平面D1AC的距离即为点 B 到平面D1AC的距离设为h考虑三棱锥ABCD1 的体积, 以ABC为底面, 可得V1 1 1( 1 2) 13 2 3而ADC 中, AC D1C5, AD1 2 , 故1 SAD C1321 3 12 2所以, V h h , 即直线BC .1 到平面D1AC的距离为3 2 3 3 35．（2013 年高考湖北卷（理））如图, AB 是圆O 的直径, 点C 是圆O 上异于A,B 的点, 直线PC 平面ABC , E , F 分别是PA, PC 的中点.(I) 记平面BEF 与平面ABC 的交线为l , 试判断直线l 与平面PAC 的位置关系, 并加以证明;(II) 设(I) 中的直线l 与圆O 的另一个交点为 D , 且点Q 满足 1DQ CP . 记直线PQ2 与平面ABC 所成的角为, 异面直线PQ 与EF 所成的角为, 二面角 E l C 的大小为, 求证: sin sin sin .第19 题图【答案】解:(I) EF AC , AC 平面ABC , EF 平面ABC EF 平面ABC又EF 平面BEFEF ll 平面PAC(II) 连接DF,用几何方法很快就可以得到求证.( 这一题用几何方法较快, 向量的方法很麻烦, 特别是用向量不能方便的表示角的正弦. 个人认为此题与新课程中对立体几何的处理方向有很大的偏差.)WORD文档6．（2013 年普通高等学校招生统一考试广东省数学（理）卷（纯WORD版））如图1, 在等腰直角三角形ABC 中, A 90 , BC 6, D,E分别是AC, AB 上的点, CD BE 2, O 为BC 的中点. 将ADE 沿DE 折起, 得到如图 2 所示的四棱锥 A BCDE , 其中A O 3 .( Ⅰ) 证明: A O 平面BCDE ; ( Ⅱ) 求二面角 A CD B 的平面角的余弦值.CO.BAD ECO BA DE 图1 图2【答案】( Ⅰ) 在图 1 中, 易得O C 3, AC 3 2, AD 2 2ACO BDEH连结OD ,OE , 在OCD 中, 由余弦定理可得2 2 2 cos45 5 ODOC CD OC CD由翻折不变性可知 A D 2 2 ,所以 2 2 2A O OD A D , 所以A O OD ,理可证 A O OE , 又OD OE O , 所以 A O 平面BCDE . ( Ⅱ) 传统法: 过O作OH CD 交CD 的延长线于H , 连结A H , 因为A O 平面BCDE , 所以 A H CD ,所以 A HO 为二面角 A CD B 的平面角.结合图 1 可知, H 为AC 中点, 故3 2OH , 从而22 2 30A H OH OA2cos A HO 所以O HA H155, 所以二面角 A CD B 的平面角的余弦值为15z5A.向量法: 以O 点为原点, 建立空间直角坐标系O xyz如图所示,则A 0,0, 3 , C 0, 3,0 , D 1, 2,0 所以CA 0,3, 3 , DA 1,2, 3 CDxO向量法图EBy设n x, y,z 为平面A CD 的法向量, 则n CA n DA 0, 即3y 3z 0x 2y3z 0, 解得y xz 3x, 令x 1, 得n 1, 1, 3由( Ⅰ) 知, OA 0,0, 3 为平面CDB 的一个法向量,所以cos n, O An OAn OA3 1553 5, 即二面角 A CD B 的平面角的余弦15 值为. 57．（2013 年普通高等学校招生统一考试天津数学（理）试题（含答案））如图, 四棱柱ABCD- A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB// DC, AB⊥AD, AD= CD= 1, AA1 = AB= 2, E 为棱AA1 的中点.( Ⅰ) 证明B1C1⊥CE;( Ⅱ) 求二面角B1- CE- C1 的正弦值.( Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1 所成角的正弦值为的长.26, 求线段AM【答案】8．（2013 年高考新课标1（理））如图, 三棱柱ABC-A1B1C1 中,CA=CB,AB=A A1, ∠BA A1=60° .( Ⅰ) 证明AB⊥A1C;( Ⅱ) 若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.【答案】 ( Ⅰ) 取 AB 中点 E,连结 CE, A B , 1A E ,1∵AB=AA 1 , BAA 1 =60 , ∴ BAA 1是正三角形 , ∴ A E ⊥AB, ∵CA=CB,∴CE ⊥AB,∵C EA 1E =E, ∴AB ⊥面CEA 1 ,1∴AB ⊥ A C ;1( Ⅱ) 由( Ⅰ) 知 EC ⊥AB, EA 1 ⊥AB,又∵面 ABC ⊥面 A BB A , 面 ABC ∩面 ABB 1A 1 =AB, ∴EC ⊥面ABB 1 A 1 ,∴EC ⊥EA 1,1 1∴EA,EC, E A 两两相互垂直 , 以 E 为坐标原点 , EA 的方向为 x 轴正方向 ,| EA | 为单位1长度, 建立如图所示空间直角坐标系 O xyz ,有 题 设 知A(1,0,0),A (0,3 ,0),C(0,0, 3 ),B(-1,0,0),则1BC =(1,0, 3 ), BB 1 = AA 1 =(-1,0, 3 ), A 1C =(0,- 3 , 3 ),设 n =(x, y, z) 是平面 CBB C 的法向量 , 1 1则nn B C BB 10 0, 即 x 3z 0 x 3y 0, 可取 n =(3,1,-1),∴cos n , A C =1n | n ||A C 1 A 1C |10 5,∴直线A1C 与平面BB1C1C所成角的正弦值为1059．（2013 年高考陕西卷（理））如图, 四棱柱ABCD- A1B1C1D1 的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,AB AA1 2 .( Ⅰ) 证明: A1C⊥平面BB1D1D;( Ⅱ) 求平面OCB1 与平面BB1 D1D的夹角的大小.D1C1A1B1DCOAB【答案】解:( Ⅰ) A1O 面ABCD,且BD 面ABCD, A O BD ; 又因为, 在正1方形AB CD 中, AC BD；且A1O AC A,所以BD 面A1 AC且A1C 面A1AC，故A1C BD .在正方形AB CD中,AO = 1 . RT A1OA中，A O 1.在1设.B1D1的中点为E1，则四边形A1OCE1为正方形，所以A1C E1O又BD BB1 D1D,E1O BB1 D1D . BD E1O O面面，且，所以由以上三点得A1C 面BB1 D1D .( 证毕)( Ⅱ) 建立直角坐标系统, 使用向量解题.以O为原点, 以OC为X 轴正方向, 以OB为Y轴正方向. 则B（0,1, 0）,C (1，0，0), A1(0，0，1), B1(1,1,1) A1C (1, 0, 1) .由( Ⅰ) 知, 平面BB 1 A C OB OC （）1D1D的一个法向量n (1,0, 1), (1,1,1) ,1,0, 0 .1 1设平面OCB1 的法向量为D1C1 ,则0, 0，n2 n OB n OC2 1 2A1B1解得其中一个法向量为n2 ( 0,1, -1).DCOcos | cos| n n | 1 11 2n ,n| .1 12| n | | n | 2 21 2A B所以, 平面OCB1 与平面BB1D1D的夹角为310 ．（2013 年高考江西卷（理））如图, 四棱锥P A B C中, PA 平面ABCD, E为BD的中点, G为PD的中点，3DAB DCB ,EA EB AB 1，PA , 连接CE 并延长交AD 于F .2(1) 求证: AD 平面CFG ;(2) 求平面BCP 与平面DCP 的夹角的余弦值.【答案】解:(1) 在ABD 中, 因为E 是BD 的中点, 所以EA EB ED AB 1,故,BAD ABE AEB ,2 3因为DAB DCB , 所以EAB ECB ,从而有FED FEA ,故E F AD, AF FD , 又因为PG GD,所以FG ∥PA .又PA 平面ABCD ,所以GF AD,故AD 平面CFG .(3) 以点 A 为坐标原点建立如图所示的坐标系, 则3 3A(0,0,0), B(1,0,0), C( , ,0), D (0, 3,0) ,2 2(4)3P (0,0, ) , 故21 3 3 3 3 3 3 BC ( ，，0), CP ( ，, ), C D ( , ,0)2 2 2 2 2 2 21 3y12 2设平面BCP 的法向量n (1, y , z ),则1 1 1,3 3 3y z1 12 2 2解得y1z12333 , 即 3 2n (1, , ).13 3设平面DCP 的法向量n2 (1, y2 ,z2 ) , 则3 3y22 23 3 3y z2 22 2 2y, 解得 2z223,即n2 (1, 3,2) . 从而平面 B C P与平面 D C P的夹角的余弦值为cos n n1 2n n1 243169824.11 ．（2013 年高考四川卷（理））如图, 在三棱柱A BC A B C中, 侧棱1 1 AA 底面1ABC , A B AC 2AA , BAC 120 , D,D1分别是线段BC, B1C1 的中点, P 是线1段AD 的中点.( Ⅰ) 在平面ABC 内, 试作出过点P 与平面A BC 平行的直线l , 说明理由, 并证明直线1l 平面ADD1A1;( Ⅱ) 设( Ⅰ) 中的直线l 交AB 于点M , 交AC 于点N , 求二面角 A A M N 的余弦1值.CDA PBC1D1A1B1【答案】解: 如图, 在平面ABC 内, 过点P 做直线l // BC , 因为l 在平面ABC 外,1BC 在平面A BC 内, 由直线与平面平行的判定定理可知, l // 平面A1BC .1由已知, AB AC , D 是BC 的中点, 所以, BC AD , 则直线l AD .因为AA1 平面ABC , 所以AA1 直线l . 又因为AD, AA1 在平面ADD1A1 内, 且AD与A A 相交, 所以直线平面ADD1A11解法一:连接A1P , 过A 作AE A1P于E , 过E 作EF A1M 于F , 连接AF .由知, MN 平面AEA, 所以平面AEA1 平面A1MN .1所以AE 平面AMN , 则A1M AE.1所以A M平面AEF , 则A1M AF .1故AFE 为二面角 A AM N 的平面角( 设为).1设A A1 1 , 则由 A B 2A 1 C , A BAC A 120 , 有BAD 60 , AB 2, AD 1 .又P 为AD 的中点, 所以M 为AB 的中点, 且1AP , AM 1 ,2在5Rt AAP 中, A1P ; 在Rt A1AM 中,12A1M 2 .AA AP从而,1AEA P11 5,AFAA AM 1A M11 2, 所以 sinAE AF 2 5. 所以222 15 cos 1 sin155.故二面角 AA 1M N 的余弦值为155解法二 :设A A 1 1. 如图 , 过 A 1 作 A 1E 平行于B 1C 1 , 以 A 1 为坐标原点 , 分别以 A 1E,A 1D 1 , AA 1 的 方向为 x 轴, y 轴, z轴的正方向 , 建立空间直角坐标系Oxyz ( 点O 与点A 重合).1则 A 1 0,0,0 , A 0,0,1 .因为 P 为 AD 的中点 , 所以 M , N 分别为 AB, AC 的中点 , 故3 13 1 M, ,1 ,N , ,1 , 2 22 2所以3 1A M, A 1A0,0,1 , NM 3,0,0 ., ,112 2设平面 A AM 的一个法向量为n 1 x 1,y 1,z 1 , 则1nA M 11n A A,11,n A M0,11即故有n A A0,113 1x , y,z, ,1 0,1 1 12 2x , y,z0,0,1 0,1 1 13 1x y z从而 1 1 12 20,z122.6取x1 1, 则y1 3 , 所以n1 1, 3,0 .设平面A MN 的一个法向量为n2 x2 , y2,z2 , 则1n A M 2 1n NM2 ,,即n A M2 1n NM20,0,故有3 1x , y , z , ,1 0,2 2 22 2x , y ,z3,0,0 0,2 2 2从而3 1x y z2 2 22 20,3x 0.2取y2 2, 则z2 1, 所以n2 0,2, 1 . 设二面角A A1M N 的平面角为, 又为锐角,则cos n n1 2n n1 21, 3,0 0,2, 1 152 5 5.故二面角A A1M N 的余弦值为15 512．（2013 年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD版含附加题））本小题满分10 分.如图, 在直三棱柱A B C ABC中, AB AC , AB AC 2 , AA1 4 , 点D 是1 1 1BC 的中点(1) 求异面直线A1B 与C1D 所成角的余弦值(2) 求平面A DC 与ABA1 所成二面角的正弦值.1【答案】 本题主要考察异面直线 . 二面角 . 空间向量等基础知识以及基本运算 , 考察运用空间向量解决问题的能力 .解:(1) 以 A B, AC, AA 为为单位正交基底建立空间直角坐标系A xyz ,1则 A(0,0,0) B (2,0,0) , C ( 0,2,0) ,A (0,0,4) , D (1,1,0) , C 1 (0,2,4)1∴ A 1B (2,0, 4) , A 1 B (1, 1, 4) ∴cos A B, 1C D1A B 1A 1BCD1C D118 20 183 10 10∴异面直线 A 1 B 与C 1D 所成角的余弦值为3 10 10(2)AC (0,2,0)是平面ABA 的的一个法向量1设平面 ADC 1 的法向量为m (x, y, z) , ∵ AD (1,1,0), AC 1(0,2,4)由 mAD, m AC1∴x2y y 4z 0 0取 z 1, 得 y2, x 2 , ∴平面ADC 的法向量为 m (2, 2 ,1)1设平面 ADC 1 与A BA 1 所成二面角为∴cos cosAC m 4 2AC, m , 得2 3 3AC msin53∴平面ADC 与ABA1 所成二面角的正弦值为15 313．（2013 年普通高等学校招生统一考试大纲版数学（理）WORD版含答案（已校对））如图, 四棱锥P ABCD 中, ABC BAD 90 ，BC 2 AD, PAB与PAD 都是等边三角形.(I) 证明: PB CD ; (II) 求二面角 A PD C 的大小.【答案】14．（2013 年普通高等学校招生统一考试山东数学（理）试题（含答案））如图所示, 在三棱锥P ABQ 中, PB 平面ABQ , BA BP BQ , D,C, E, F 分别是A Q,B ,Q A,P的中B点P, AQ 2BD , PD 与EQ 交于点G , PC 与FQ 交于点H ,连接GH .( Ⅰ) 求证: AB GH ; ( Ⅱ) 求二面角 D GH E 的余弦值.【答案】解:( Ⅰ) 证明: 因为D,C,E, F分别是AQ, BQ, AP, BP 的中点,所以EF ∥AB , DC ∥AB , 所以EF ∥DC ,又EF 平面PCD , DC 平面PCD ,所以EF ∥平面PCD ,又EF 平面EFQ , 平面EFQ 平面PCD GH ,所以EF ∥GH ,又EF ∥AB ,所以AB ∥GH .( Ⅱ) 解法一: 在△ABQ 中, AQ 2BD , AD DQ ,所以ABQ=90 , 即A B BQ , 因为PB 平面ABQ , 所以AB PB ,又BP BQ B, 所以AB 平面PBQ , 由( Ⅰ) 知AB ∥GH ,所以GH 平面PBQ , 又FH 平面PBQ , 所以GH FH , 同理可得GH HC , 所以FHC 为二面角 D GH E 的平面角, 设BA BQ BP 2 , 连接PC ,在Rt △FBC 中, 由勾股定理得, FC 2 ,在Rt △PBC 中, 由勾股定理得, PC 5 ,又H 为△PBQ 的重心, 所以1 5 HC PC3 3FH5 3同理,在△FHC 中, 由余弦定理得cos FHC5 5249 95 529,4即二面角 D GH E 的余弦值为5.解法二: 在△ABQ 中, AQ 2BD , AD DQ ,所以ABQ 90 , 又PB 平面ABQ , 所以BA, BQ, BP 两两垂直,以B 为坐标原点, 分别以BA, BQ, BP 所在直线为x 轴, y 轴, z轴, 建立如图所示的空间直角坐标系, 设BA BQ BP 2 , 则E (1,0,1) , F (0,0,1) , Q (0,2,0) , D (1,1,0) , C (0,1,0) P (0,0, 2) ,, 所以EQ ( 1 , 2 ,, FQ (0,2, 1) , DP ( 1,1,2) , CP (0, 1,2) ,设平面EFQ 的一个法向量为m(x , y ,z)1 1 1,由m EQ 0, m FQ 0 ,x 2y z 01 1 1得2y z 01 1取y1 1, 得m (0,1,2) .设平面PDC 的一个法向量为n (x2 , y2 ,z2) 由n DP 0, n CP 0 ,x y 2z 02 2 2得y2z 0 2 2取z2 1, 得n (0,2,1). 所以cos m, nm nm n454因为二面角 D GH E 为钝角, 所以二面角 D GH E 的余弦值为5. 15．（2013 年高考湖南卷（理））如图5, 在直棱柱ABCD A1B1C1D 中，AD / /BC , BAD 90 ,AC BD, BC 1, AD AA1 3.1(I) 证明: A C B D ; (II) 求直线1 B C与平面ACD 所成角的正弦值.1 1 1【答案】解: ( Ⅰ) ABCD A1B1C1D1是直棱柱BB1 面ABCD,且BD 面ABCD BB1 AC又.AC BD,且BD BB1 B, AC 面BDB1。
2013年全国统一高考真题数学试卷(理科)(新课标ⅰ)(含答案及解析)
2013年全国统一高考数学试卷（理科）（新课标Ⅰ）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的.1．（5分）已知集合A={x|x2﹣2x＞0}，B={x|﹣＜x＜}，则（）A．A∩B=∅B．A∪B=R C．B⊆A D．A⊆B2．（5分）若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（）A．﹣4B．C．4D．3．（5分）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是（）A．简单的随机抽样B．按性别分层抽样C．按学段分层抽样D．系统抽样4．（5分）已知双曲线C：（a＞0，b＞0）的离心率为，则C的渐近线方程为（）A．y=B．y=C．y=±x D．y=5．（5分）执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（）A．[﹣3，4]B．[﹣5，2]C．[﹣4，3]D．[﹣2，5] 6．（5分）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（）A．B．C．D．7．（5分）设等差数列{a n}的前n项和为S n，若S m﹣1=﹣2，S m=0，S m+1=3，则m=（）A．3B．4C．5D．68．（5分）某几何体的三视图如图所示，则该几何体的体积为（）A．16+8πB．8+8πC．16+16πD．8+16π9．（5分）设m为正整数，（x+y）2m展开式的二项式系数的最大值为a，（x+y）2m+1展开式的二项式系数的最大值为b，若13a=7b，则m=（）A．5B．6C．7D．810．（5分）已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）A．B．C．D．11．（5分）已知函数f（x）=，若|f（x）|≥ax，则a的取值范围是（）A．（﹣∞，0]B．（﹣∞，1]C．[﹣2，1]D．[﹣2，0] 12．（5分）设△A n B n C n的三边长分别为a n，b n，c n，△A n B n C n的面积为S n，n=1，2，3…若b1＞c1，b1+c1=2a1，a n+1=a n，，，则（）A．{S n}为递减数列B．{S n}为递增数列C．{S2n﹣1}为递增数列，{S2n}为递减数列D．{S2n﹣1}为递减数列，{S2n}为递增数列二.填空题：本大题共4小题，每小题5分.13．（5分）已知两个单位向量，的夹角为60°，=t+（1﹣t）．若•=0，则t=．14．（5分）若数列{a n}的前n项和为S n=a n+，则数列{a n}的通项公式是a n=．15．（5分）设当x=θ时，函数f（x）=sinx﹣2cosx取得最大值，则cosθ=．16．（5分）若函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，则f（x）的最大值为．三、解答题：解答应写出文字说明，证明过程或演算步骤.17．（12分）如图，在△ABC中，∠ABC=90°，AB=，BC=1，P为△ABC内一点，∠BPC=90°．（1）若PB=，求PA；（2）若∠APB=150°，求tan∠PBA．18．（12分）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．（Ⅰ）证明AB⊥A1C；（Ⅱ）若平面ABC⊥平面AA1B1B，AB=CB=2，求直线A1C与平面BB1C1C所成角的正弦值．19．（12分）一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n．如果n=3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n=4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为，且各件产品是否为优质品相互独立．（Ⅰ）求这批产品通过检验的概率；（Ⅱ）已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X（单位：元），求X的分布列及数学期望．20．（12分）已知圆M：（x+1）2+y2=1，圆N：（x﹣1）2+y2=9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．（Ⅰ）求C的方程；（Ⅱ）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P 的半径最长时，求|AB|．21．（12分）已知函数f（x）=x2+ax+b，g（x）=e x（cx+d），若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2．（Ⅰ）求a，b，c，d的值；（Ⅱ）若x≥﹣2时，f（x）≤kg（x），求k的取值范围．四、请考生在第22、23、24题中任选一道作答，并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分，不涂，按本选考题的首题进行评分.22．（10分）（选修4﹣1：几何证明选讲）如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．（Ⅰ）证明：DB=DC；（Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径．23．已知曲线C1的参数方程为（t为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ．（1）把C1的参数方程化为极坐标方程；（2）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．24．已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．（Ⅰ）当a=﹣2时，求不等式f（x）＜g（x）的解集；（Ⅱ）设a＞﹣1，且当x∈[﹣，]时，f（x）≤g（x），求a的取值范围．2013年全国统一高考数学试卷（理科）（新课标Ⅰ）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的.1．（5分）已知集合A={x|x2﹣2x＞0}，B={x|﹣＜x＜}，则（）A．A∩B=∅B．A∪B=R C．B⊆A D．A⊆B【考点】1D：并集及其运算；73：一元二次不等式及其应用．【专题】59：不等式的解法及应用；5J：集合．【分析】根据一元二次不等式的解法，求出集合A，再根据的定义求出A∩B和A∪B．【解答】解：∵集合A={x|x2﹣2x＞0}={x|x＞2或x＜0}，∴A∩B={x|2＜x＜或﹣＜x＜0}，A∪B=R，故选：B．【点评】本题考查一元二次不等式的解法，以及并集的定义，属于基础题．2．（5分）若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（）A．﹣4B．C．4D．【考点】A5：复数的运算．【专题】5N：数系的扩充和复数．【分析】由题意可得z==，再利用两个复数代数形式的乘除法法则化简为+i，由此可得z的虚部．【解答】解：∵复数z满足（3﹣4i）z=|4+3i|，∴z====+i，故z的虚部等于，故选：D．【点评】本题主要考查复数的基本概念，两个复数代数形式的乘除法法则的应用，属于基础题．3．（5分）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是（）A．简单的随机抽样B．按性别分层抽样C．按学段分层抽样D．系统抽样【考点】B3：分层抽样方法．【专题】21：阅读型．【分析】若总体由差异明显的几部分组成时，经常采用分层抽样的方法进行抽样．【解答】解：我们常用的抽样方法有：简单随机抽样、分层抽样和系统抽样，而事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．了解某地区中小学生的视力情况，按学段分层抽样，这种方式具有代表性，比较合理．故选：C．【点评】本小题考查抽样方法，主要考查抽样方法，属基本题．4．（5分）已知双曲线C：（a＞0，b＞0）的离心率为，则C的渐近线方程为（）A．y=B．y=C．y=±x D．y=【考点】KC：双曲线的性质．【专题】5D：圆锥曲线的定义、性质与方程．【分析】由离心率和abc的关系可得b2=4a2，而渐近线方程为y=±x，代入可得答案．【解答】解：由双曲线C：（a＞0，b＞0），则离心率e===，即4b2=a2，故渐近线方程为y=±x=x，故选：D．【点评】本题考查双曲线的简单性质，涉及的渐近线方程，属基础题．5．（5分）执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（）A．[﹣3，4]B．[﹣5，2]C．[﹣4，3]D．[﹣2，5]【考点】3B：分段函数的解析式求法及其图象的作法；EF：程序框图．【专题】27：图表型；5K：算法和程序框图．【分析】本题考查的知识点是程序框图，分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算一个分段函数的函数值，由条件为t＜1我们可得，分段函数的分类标准，由分支结构中是否两条分支上对应的语句行，我们易得函数的解析式．【解答】解：由判断框中的条件为t＜1，可得：函数分为两段，即t＜1与t≥1，又由满足条件时函数的解析式为：s=3t；不满足条件时，即t≥1时，函数的解析式为：s=4t﹣t2故分段函数的解析式为：s=，如果输入的t∈[﹣1，3]，画出此分段函数在t∈[﹣1，3]时的图象，则输出的s属于[﹣3，4]．故选：A．【点评】要求条件结构对应的函数解析式，要分如下几个步骤：①分析流程图的结构，分析条件结构是如何嵌套的，以确定函数所分的段数；②根据判断框中的条件，设置分类标准；③根据判断框的“是”与“否”分支对应的操作，分析函数各段的解析式；④对前面的分类进行总结，写出分段函数的解析式．6．（5分）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（）A．B．C．D．【考点】LG：球的体积和表面积．【专题】11：计算题；5F：空间位置关系与距离．【分析】设正方体上底面所在平面截球得小圆M，可得圆心M为正方体上底面正方形的中心．设球的半径为R，根据题意得球心到上底面的距离等于（R﹣2）cm，而圆M的半径为4，由球的截面圆性质建立关于R的方程并解出R=5，用球的体积公式即可算出该球的体积．【解答】解：设正方体上底面所在平面截球得小圆M，则圆心M为正方体上底面正方形的中心．如图．设球的半径为R，根据题意得球心到上底面的距离等于（R﹣2）cm，而圆M的半径为4，由球的截面圆性质，得R2=（R﹣2）2+42，解出R=5，∴根据球的体积公式，该球的体积V===．故选：A．【点评】本题给出球与正方体相切的问题，求球的体积，着重考查了正方体的性质、球的截面圆性质和球的体积公式等知识，属于中档题．7．（5分）设等差数列{a n}的前n项和为S n，若S m﹣1=﹣2，S m=0，S m+1=3，则m=（）A．3B．4C．5D．6【考点】83：等差数列的性质；85：等差数列的前n项和．【专题】11：计算题；54：等差数列与等比数列．【分析】由a n与S n的关系可求得a m+1与a m，进而得到公差d，由前n项和公式及S m=0可求得a1，再由通项公式及a m=2可得m值．【解答】解：a m=S m﹣S m﹣1=2，a m+1=S m+1﹣S m=3，所以公差d=a m﹣a m=1，+1S m==0，m﹣1＞0，m＞1，因此m不能为0，得a1=﹣2，所以a m=﹣2+（m﹣1）•1=2，解得m=5，另解：等差数列{a n}的前n项和为S n，即有数列{}成等差数列，则，，成等差数列，可得2•=+，即有0=+，解得m=5．又一解：由等差数列的求和公式可得（m﹣1）（a1+a m﹣1）=﹣2，m（a1+a m）=0，（m+1）（a1+a m+1）=3，可得a1=﹣a m，﹣2a m+a m+1+a m+1=+=0，解得m=5．故选：C．【点评】本题考查等差数列的通项公式、前n项和公式及通项a n与S n的关系，考查学生的计算能力．8．（5分）某几何体的三视图如图所示，则该几何体的体积为（）A．16+8πB．8+8πC．16+16πD．8+16π【考点】L!：由三视图求面积、体积．【专题】16：压轴题；27：图表型．【分析】三视图复原的几何体是一个长方体与半个圆柱的组合体，依据三视图的数据，得出组合体长、宽、高，即可求出几何体的体积．【解答】解：三视图复原的几何体是一个长方体与半个圆柱的组合体，如图，其中长方体长、宽、高分别是：4，2，2，半个圆柱的底面半径为2，母线长为4．∴长方体的体积=4×2×2=16，半个圆柱的体积=×22×π×4=8π所以这个几何体的体积是16+8π；故选：A．【点评】本题考查了几何体的三视图及直观图的画法，三视图与直观图的关系，柱体体积计算公式，空间想象能力9．（5分）设m为正整数，（x+y）2m展开式的二项式系数的最大值为a，（x+y）2m+1展开式的二项式系数的最大值为b，若13a=7b，则m=（）A．5B．6C．7D．8【考点】DA：二项式定理．【专题】5P：二项式定理．【分析】根据二项式系数的性质求得a和b，再利用组合数的计算公式，解方程13a=7b求得m的值．【解答】解：∵m为正整数，由（x+y）2m展开式的二项式系数的最大值为a，以及二项式系数的性质可得a=，同理，由（x+y）2m+1展开式的二项式系数的最大值为b，可得b==．再由13a=7b，可得13=7，即13×=7×，即13=7×，即13（m+1）=7（2m+1），解得m=6，故选：B．【点评】本题主要考查二项式系数的性质的应用，组合数的计算公式，属于中档题．10．（5分）已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）A．B．C．D．【考点】K3：椭圆的标准方程．【专题】5D：圆锥曲线的定义、性质与方程．【分析】设A（x1，y1），B（x2，y2），代入椭圆方程得，利用“点差法”可得．利用中点坐标公式可得x1+x2=2，y1+y2=﹣2，利用斜率计算公式可得==．于是得到，化为a2=2b2，再利用c=3=，即可解得a2，b2．进而得到椭圆的方程．【解答】解：设A（x1，y1），B（x2，y2），代入椭圆方程得，相减得，∴．∵x1+x2=2，y1+y2=﹣2，==．∴，化为a2=2b2，又c=3=，解得a2=18，b2=9．∴椭圆E的方程为．故选：D．【点评】熟练掌握“点差法”和中点坐标公式、斜率的计算公式是解题的关键．11．（5分）已知函数f（x）=，若|f（x）|≥ax，则a的取值范围是（）A．（﹣∞，0]B．（﹣∞，1]C．[﹣2，1]D．[﹣2，0]【考点】7E：其他不等式的解法．【专题】16：压轴题；59：不等式的解法及应用．【分析】由函数图象的变换，结合基本初等函数的图象可作出函数y=|f（x）|的图象，和函数y=ax的图象，由导数求切线斜率可得l的斜率，进而数形结合可得a的范围．【解答】解：由题意可作出函数y=|f（x）|的图象，和函数y=ax的图象，由图象可知：函数y=ax的图象为过原点的直线，当直线介于l和x轴之间符合题意，直线l为曲线的切线，且此时函数y=|f（x）|在第二象限的部分解析式为y=x2﹣2x，求其导数可得y′=2x﹣2，因为x≤0，故y′≤﹣2，故直线l的斜率为﹣2，故只需直线y=ax的斜率a介于﹣2与0之间即可，即a∈[﹣2，0]故选：D．【点评】本题考查其它不等式的解法，数形结合是解决问题的关键，属中档题．12．（5分）设△A n B n C n的三边长分别为a n，b n，c n，△A n B n C n的面积为S n，n=1，2，3…若b1＞c1，b1+c1=2a1，a n+1=a n，，，则（）A．{S n}为递减数列B．{S n}为递增数列C．{S2n﹣1}为递增数列，{S2n}为递减数列D．{S2n﹣1}为递减数列，{S2n}为递增数列【考点】82：数列的函数特性；8H：数列递推式．【专题】16：压轴题；54：等差数列与等比数列；55：点列、递归数列与数学归纳法．=a n可知△A n B n C n的边B n C n为定值a1，由b n+1+c n+1﹣【分析】由a n+12a1=及b1+c1=2a1得b n+c n=2a1，则在△A n B n C n中边长B n C n=a1为定值，另两边A n C n、A n B n的长度之和b n+c n=2a1为定值，由此可知顶点A n在以B n、C n为焦点的椭圆上，根据b n+1﹣c n+1=，得b n﹣c n=，可知n→+∞时b n→c n，据此可判断△A n B n C n的边B nC n的高h n随着n的增大而增大，再由三角形面积公式可得到答案．【解答】解：b1=2a1﹣c1且b1＞c1，∴2a1﹣c1＞c1，∴a1＞c1，∴b1﹣a1=2a1﹣c1﹣a1=a1﹣c1＞0，∴b1＞a1＞c1，又b1﹣c1＜a1，∴2a1﹣c1﹣c1＜a1，∴2c1＞a1，∴，由题意，+a n，∴b n+1+c n+1﹣2a n=（b n+c n﹣2a n），∴b n+c n﹣2a n=0，∴b n+c n=2a n=2a1，∴b n+c n=2a1，由此可知顶点A n在以B n、C n为焦点的椭圆上，﹣c n+1=，∴=a1﹣b n，又由题意，b n+1﹣a1=，∴b n﹣a1=，∴b n+1∴，c n=2a1﹣b n=，∴[][]=[﹣]单调递增（可证当n=1时＞0）故选：B．【点评】本题主要考查由数列递推式求数列通项、三角形面积海伦公式，综合考查学生分析解决问题的能力，有较高的思维抽象度，是本年度全国高考试题中的“亮点”之一．二.填空题：本大题共4小题，每小题5分.13．（5分）已知两个单位向量，的夹角为60°，=t+（1﹣t）．若•=0，则t=2．【考点】9H：平面向量的基本定理；9O：平面向量数量积的性质及其运算．【专题】5A：平面向量及应用．【分析】由于•=0，对式子=t+（1﹣t）两边与作数量积可得=0，经过化简即可得出．【解答】解：∵，，∴=0，∴tcos60°+1﹣t=0，∴1=0，解得t=2．故答案为2．【点评】熟练掌握向量的数量积运算是解题的关键．14．（5分）若数列{a n}的前n项和为S n=a n+，则数列{a n}的通项公式是a n=（﹣2）n﹣1．【考点】88：等比数列的通项公式．【专题】54：等差数列与等比数列．【分析】把n=1代入已知式子可得数列的首项，由n≥2时，a n=S n﹣S n﹣1，可得数列为等比数列，且公比为﹣2，代入等比数列的通项公式分段可得答案．【解答】解：当n=1时，a1=S1=，解得a1=1当n≥2时，a n=S n﹣S n﹣1=（）﹣（）=，整理可得，即=﹣2，故数列{a n}从第二项开始是以﹣2为首项，﹣2为公比的等比数列，故当n≥2时，a n=（﹣2）n﹣1，经验证当n=1时，上式也适合，故答案为：（﹣2）n﹣1【点评】本题考查等比数列的通项公式，涉及等比数列的判定，属基础题．15．（5分）设当x=θ时，函数f（x）=sinx﹣2cosx取得最大值，则cosθ=﹣．【考点】GP：两角和与差的三角函数；H4：正弦函数的定义域和值域．【专题】16：压轴题；56：三角函数的求值．【分析】f（x）解析式提取，利用两角和与差的正弦函数公式化为一个角的正弦函数，由x=θ时，函数f（x）取得最大值，得到sinθ﹣2cosθ=，与sin2θ+cos2θ=1联立即可求出cosθ的值．【解答】解：f（x）=sinx﹣2cosx=（sinx﹣cosx）=sin（x﹣α）（其中cosα=，sinα=），∵x=θ时，函数f（x）取得最大值，∴sin（θ﹣α）=1，即sinθ﹣2cosθ=，又sin2θ+cos2θ=1，联立得（2cosθ+）2+cos2θ=1，解得cosθ=﹣．故答案为：﹣【点评】此题考查了两角和与差的正弦函数公式，同角三角函数间的基本关系，以及正弦函数的定义域与值域，熟练掌握公式是解本题的关键．16．（5分）若函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，则f（x）的最大值为16．【考点】57：函数与方程的综合运用；6E：利用导数研究函数的最值．【专题】11：计算题；16：压轴题；51：函数的性质及应用；53：导数的综合应用．【分析】由题意得f（﹣1）=f（﹣3）=0且f（1）=f（﹣5）=0，由此求出a=8且b=15，由此可得f（x）=﹣x4﹣8x3﹣14x2+8x+15．利用导数研究f（x）的单调性，可得f（x）在区间（﹣∞，﹣2﹣）、（﹣2，﹣2+）上是增函数，在区间（﹣2﹣，﹣2）、（﹣2+，+∞）上是减函数，结合f（﹣2﹣）=f（﹣2+）=16，即可得到f（x）的最大值．【解答】解：∵函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，∴f（﹣1）=f（﹣3）=0且f（1）=f（﹣5）=0，即[1﹣（﹣3）2][（﹣3）2+a•（﹣3）+b]=0且[1﹣（﹣5）2][（﹣5）2+a•（﹣5）+b]=0，解之得，因此，f（x）=（1﹣x2）（x2+8x+15）=﹣x4﹣8x3﹣14x2+8x+15，求导数，得f′（x）=﹣4x3﹣24x2﹣28x+8，令f′（x）=0，得x1=﹣2﹣，x2=﹣2，x3=﹣2+，当x∈（﹣∞，﹣2﹣）时，f′（x）＞0；当x∈（﹣2﹣，﹣2）时，f′（x）＜0；当x∈（﹣2，﹣2+）时，f′（x）＞0；当x∈（﹣2+，+∞）时，f′（x）＜0∴f（x）在区间（﹣∞，﹣2﹣）、（﹣2，﹣2+）上是增函数，在区间（﹣2﹣，﹣2）、（﹣2+，+∞）上是减函数．又∵f（﹣2﹣）=f（﹣2+）=16，∴f（x）的最大值为16．故答案为：16．【点评】本题给出多项式函数的图象关于x=﹣2对称，求函数的最大值．着重考查了函数的奇偶性、利用导数研究函数的单调性和函数的最值求法等知识，属于中档题．三、解答题：解答应写出文字说明，证明过程或演算步骤.17．（12分）如图，在△ABC中，∠ABC=90°，AB=，BC=1，P为△ABC内一点，∠BPC=90°．（1）若PB=，求PA；（2）若∠APB=150°，求tan∠PBA．【考点】HP：正弦定理；HR：余弦定理．【专题】58：解三角形．【分析】（I）在Rt△PBC，利用边角关系即可得到∠PBC=60°，得到∠PBA=30°．在△PBA中，利用余弦定理即可求得PA．（II）设∠PBA=α，在Rt△PBC中，可得PB=sinα．在△PBA中，由正弦定理得，即，化简即可求出．【解答】解：（I）在Rt△PBC中，=，∴∠PBC=60°，∴∠PBA=30°．在△PBA中，由余弦定理得PA2=PB2+AB2﹣2PB•ABcos30°==．∴PA=．（II）设∠PBA=α，在Rt△PBC中，PB=BCcos（90°﹣α）=sinα．在△PBA中，由正弦定理得，即，化为．∴．【点评】熟练掌握直角三角形的边角关系、正弦定理和余弦定理是解题的关键．18．（12分）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．（Ⅰ）证明AB⊥A1C；（Ⅱ）若平面ABC⊥平面AA1B1B，AB=CB=2，求直线A1C与平面BB1C1C所成角的正弦值．【考点】LW：直线与平面垂直；LY：平面与平面垂直；MI：直线与平面所成的角．【专题】5F：空间位置关系与距离；5G：空间角．【分析】（Ⅰ）取AB的中点O，连接OC，OA1，A1B，由已知可证OA1⊥AB，AB ⊥平面OA1C，进而可得AB⊥A1C；（Ⅱ）易证OA，OA1，OC两两垂直．以O为坐标原点，的方向为x轴的正向，||为单位长，建立坐标系，可得，，的坐标，设=（x，y，z）为平面BB1C1C的法向量，则，可解得=（，1，﹣1），可求|cos ＜，＞|，即为所求正弦值．【解答】解：（Ⅰ）取AB的中点O，连接OC，OA1，A1B，因为CA=CB，所以OC⊥AB，由于AB=AA1，∠BAA1=60°，所以△AA1B为等边三角形，所以OA1⊥AB，又因为OC∩OA1=O，所以AB⊥平面OA1C，又A1C⊂平面OA1C，故AB⊥A1C；（Ⅱ）由（Ⅰ）知OC⊥AB，OA1⊥AB，又平面ABC⊥平面AA1B1B，交线为AB，所以OC⊥平面AA1B1B，故OA，OA1，OC两两垂直．以O为坐标原点，的方向为x轴的正向，||为单位长，建立如图所示的坐标系，可得A（1，0，0），A1（0，，0），C（0，0，），B（﹣1，0，0），则=（1，0，），=（﹣1，，0），=（0，﹣，），设=（x，y，z）为平面BB1C1C的法向量，则，即，可取y=1，可得=（，1，﹣1），故cos＜，＞==，又因为直线与法向量的余弦值的绝对值等于直线与平面的正弦值，故直线A1C与平面BB1C1C所成角的正弦值为：．【点评】本题考查直线与平面所成的角，涉及直线与平面垂直的性质和平面与平面垂直的判定，属难题．19．（12分）一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n．如果n=3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n=4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为，且各件产品是否为优质品相互独立．（Ⅰ）求这批产品通过检验的概率；（Ⅱ）已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X（单位：元），求X的分布列及数学期望．【考点】CG：离散型随机变量及其分布列；CH：离散型随机变量的期望与方差．【专题】5I：概率与统计．【分析】（Ⅰ）设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，第二次取出的4件产品全是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，这批产品通过检验为事件A，依题意有A=（A1B1）∪（A2B2），且A1B1与A2B2互斥，由概率得加法公式和条件概率，代入数据计算可得；（Ⅱ）X可能的取值为400，500，800，分别求其概率，可得分布列，进而可得期望值．【解答】解：（Ⅰ）设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，第二次取出的4件产品全是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，这批产品通过检验为事件A，依题意有A=（A1B1）∪（A2B2），且A1B1与A2B2互斥，所以P（A）=P（A1B1）+P（A2B2）=P（A1）P（B1|A1）+P（A2）P（B2|A2）==（Ⅱ）X可能的取值为400，500，800，并且P（X=800）=，P（X=500）=，P（X=400）=1﹣﹣=，故X的分布列如下：X 400 500 800P故EX=400×+500×+800×=506.25【点评】本题考查离散型随机变量及其分布列涉及数学期望的求解，属中档题．20．（12分）已知圆M：（x+1）2+y2=1，圆N：（x﹣1）2+y2=9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．（Ⅰ）求C的方程；（Ⅱ）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P 的半径最长时，求|AB|．【考点】J3：轨迹方程；J9：直线与圆的位置关系．【专题】5B：直线与圆．【分析】（I）设动圆的半径为R，由已知动圆P与圆M外切并与圆N内切，可得|PM|+|PN|=R+1+（3﹣R）=4，而|NM|=2，由椭圆的定义可知：动点P的轨迹是以M，N为焦点，4为长轴长的椭圆，求出即可；（II）设曲线C上任意一点P（x，y），由于|PM|﹣|PN|=2R﹣2≤4﹣2=2，所以R ≤2，当且仅当⊙P的圆心为（2，0）R=2时，其半径最大，其方程为（x﹣2）2+y2=4．分①l的倾斜角为90°，此时l与y轴重合，可得|AB|．②若l的倾斜角不为90°，由于⊙M的半径1≠R，可知l与x轴不平行，设l与x轴的交点为Q，根据，可得Q（﹣4，0），所以可设l：y=k（x+4），与椭圆的方程联立，得到根与系数的关系利用弦长公式即可得出．【解答】解：（I）由圆M：（x+1）2+y2=1，可知圆心M（﹣1，0）；圆N：（x﹣1）2+y2=9，圆心N（1，0），半径3．设动圆的半径为R，∵动圆P与圆M外切并与圆N内切，∴|PM|+|PN|=R+1+（3﹣R）=4，而|NM|=2，由椭圆的定义可知：动点P的轨迹是以M，N为焦点，4为长轴长的椭圆，∴a=2，c=1，b2=a2﹣c2=3．∴曲线C的方程为（x≠﹣2）．（II）设曲线C上任意一点P（x，y），由于|PM|﹣|PN|=2R﹣2≤3﹣1=2，所以R≤2，当且仅当⊙P的圆心为（2，0）R=2时，其半径最大，其方程为（x﹣2）2+y2=4．①l的倾斜角为90°，则l与y轴重合，可得|AB|=．②若l的倾斜角不为90°，由于⊙M的半径1≠R，可知l与x轴不平行，设l与x轴的交点为Q，则，可得Q（﹣4，0），所以可设l：y=k（x+4），由l于M相切可得：，解得．当时，联立，得到7x2+8x﹣8=0．∴，．∴|AB|===由于对称性可知：当时，也有|AB|=．综上可知：|AB|=或．【点评】本题综合考查了两圆的相切关系、直线与圆相切问题、椭圆的定义及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式等基础知识，需要较强的推理能力和计算能力及其分类讨论的思想方法．21．（12分）已知函数f（x）=x2+ax+b，g（x）=e x（cx+d），若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2．（Ⅰ）求a，b，c，d的值；（Ⅱ）若x≥﹣2时，f（x）≤kg（x），求k的取值范围．【考点】3R：函数恒成立问题；6H：利用导数研究曲线上某点切线方程．【专题】16：压轴题；53：导数的综合应用．【分析】（Ⅰ）对f（x），g（x）进行求导，已知在交点处有相同的切线及曲线y=f （x）和曲线y=g（x）都过点P（0，2），从而解出a，b，c，d的值；（Ⅱ）由（I）得出f（x），g（x）的解析式，再求出F（x）及它的导函数，通过对k的讨论，判断出F（x）的最值，从而判断出f（x）≤kg（x）恒成立，从而求出k的范围．【解答】解：（Ⅰ）由题意知f（0）=2，g（0）=2，f′（0）=4，g′（0）=4，而f′（x）=2x+a，g′（x）=e x（cx+d+c），故b=2，d=2，a=4，d+c=4，从而a=4，b=2，c=2，d=2；（Ⅱ）由（I）知，f（x）=x2+4x+2，g（x）=2e x（x+1）设F（x）=kg（x）﹣f（x）=2ke x（x+1）﹣x2﹣4x﹣2，则F′（x）=2ke x（x+2）﹣2x﹣4=2（x+2）（ke x﹣1），由题设得F（0）≥0，即k≥1，令F′（x）=0，得x1=﹣lnk，x2=﹣2，①若1≤k＜e2，则﹣2＜x1≤0，从而当x∈（﹣2，x1）时，F′（x）＜0，当x∈（x1，+∞）时，F′（x）＞0，即F（x）在（﹣2，x1）上减，在（x1，+∞）上是增，故F（x）在[﹣2，+∞）上的最小值为F（x1），而F（x1）=﹣x1（x1+2）≥0，x≥﹣2时F（x）≥0，即f（x）≤kg（x）恒成立．②若k=e2，则F′（x）=2e2（x+2）（e x﹣e﹣2），从而当x∈（﹣2，+∞）时，F′（x）＞0，即F（x）在（﹣2，+∞）上是增，而F（﹣2）=0，故当x≥﹣2时，F（x）≥0，即f（x）≤kg（x）恒成立．③若k＞e2时，F′（x）＞2e2（x+2）（e x﹣e﹣2），而F（﹣2）=﹣2ke﹣2+2＜0，所以当x＞﹣2时，f（x）≤kg（x）不恒成立，综上，k的取值范围是[1，e2]．【点评】此题主要考查利用导数研究曲线上某点切线方程，函数恒成立问题，考查分类讨论思想，解题的关键是能够利用导数工具研究函数的性质，此题是一道中档题．四、请考生在第22、23、24题中任选一道作答，并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分，不涂，按本选考题的首题进行评分.22．（10分）（选修4﹣1：几何证明选讲）如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．（Ⅰ）证明：DB=DC；（Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径．【考点】NC：与圆有关的比例线段．【专题】5B：直线与圆．【分析】（I）连接DE交BC于点G，由弦切角定理可得∠ABE=∠BCE，由已知角平分线可得∠ABE=∠CBE，于是得到∠CBE=∠BCE，BE=CE．由已知DB⊥BE，可知DE为⊙O的直径，Rt△DBE≌Rt△DCE，利用三角形全等的性质即可得到DC=DB．（II）由（I）可知：DG是BC的垂直平分线，即可得到BG=．设DE的中点为O，连接BO，可得∠BOG=60°．从而∠ABE=∠BCE=∠CBE=30°．得到CF⊥BF．进而得到Rt△BCF的外接圆的半径=．【解答】（I）证明：连接DE交BC于点G．由弦切角定理可得∠ABE=∠BCE，而∠ABE=∠CBE，∴∠CBE=∠BCE，BE=CE．又∵DB⊥BE，∴DE为⊙O的直径，∠DCE=90°．∴△DBE≌△DCE，∴DC=DB．（II）由（I）可知：∠CDE=∠BDE，DB=DC．故DG是BC的垂直平分线，∴BG=．设DE的中点为O，连接BO，则∠BOG=60°．从而∠ABE=∠BCE=∠CBE=30°．∴CF⊥BF．∴Rt△BCF的外接圆的半径=．【点评】本题综合考查了圆的性质、弦切角定理、等边三角形的性质、三角形全等、三角形的外接圆的半径等知识，需要较强的推理能力、分析问题和解决问题的能力．23．已知曲线C1的参数方程为（t为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ．（1）把C1的参数方程化为极坐标方程；（2）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．【考点】Q4：简单曲线的极坐标方程；QH：参数方程化成普通方程．【专题】11：计算题；35：转化思想；4R：转化法；5S：坐标系和参数方程．【分析】（1）曲线C1的参数方程消去参数t，得到普通方程，再由，能求出C1的极坐标方程．（2）曲线C2的极坐标方程化为直角坐标方程，与C1的普通方程联立，求出C1与C2交点的直角坐标，由此能求出C1与C2交点的极坐标．【解答】解：（1）将，消去参数t，化为普通方程（x﹣4）2+（y﹣5）2=25，即C1：x2+y2﹣8x﹣10y+16=0，将代入x2+y2﹣8x﹣10y+16=0，得ρ2﹣8ρcosθ﹣10ρsinθ+16=0．∴C1的极坐标方程为ρ2﹣8ρcosθ﹣10ρsinθ+16=0．（2）∵曲线C2的极坐标方程为ρ=2sinθ．∴曲线C2的直角坐标方程为x2+y2﹣2y=0，。
2013高考数学押题卷：高三理科数学高考押题卷（带答案）
2013年⾼考数学(理)押题精粹（课标版）（30道选择题+20道⾮选择题）⼀．选择题（30道）1.设集合，，若，则的值为（）A．0 B．1 C． D．2. 已知是实数集，集合，，则 ( )A. B.C. D.3.已知i为虚数单位，则复数等于（）A．-1-i B．-1+i C．1+i D．1—i4.复数在复平⾯上对应的点不可能位于A．第⼀象限 B．第⼆象限 C．第三象限 D．第四象限5. “ ”是“⽅程表⽰焦点在y轴上的椭圆”的（）A．充分⽽不必要条件 B．必要⽽不充分条件C．充要条件 D．既不充分也不必要条件6.若命题“ R，使得 ”为假命题，则实数m的取值范围是（）（A）（B）（C）（D）7.⼀个算法的程序框图如右，则其输出结果是（）A.0B.C. D.8.下⾯的程序框图中，若输出的值为，则图中应填上的条件为（）A． B． C． D．9.右图是函数在区间上的图象．为了得到这个函数的图象，只需将的图象上所有的点（）A．向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变B．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变C．向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变D．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变10.已知则的值（ ）A．随着k的增⼤⽽增⼤B．有时随着k的增⼤⽽增⼤,有时随着k的增⼤⽽减⼩C．随着k的增⼤⽽减⼩D．是⼀个与k⽆关的常数11.关于函数的四个结论:P1:值为 ;P2:最⼩正周期为 ;P3:单调递增区间为 Z;P4:图象的对称中⼼为 Z.其中正确的有（ ）A．1 个 B．2个 C．3个 D．4个12. 是两个向量，，，且，则与的夹⾓为（）（A）（B）（C）（D）13.已知a,b是两个互相垂直的单位向量,且c•a=c•b=1,,则对任意正实数t, 的最⼩值是（ ）A． B． C． D．14.⼀个⼏何体的三视图如右图所⽰，则它的体积为（）A． B．15．正⽅形的边长为 ,中⼼为 ,球与正⽅形所在平⾯相切于点,过点的球的直径的另⼀端点为 ,线段与球的球⾯的交点为 ,且恰为线段的中点,则球的体积为（ ）A． B． C． D．16.不等式组表⽰⾯积为1的直⾓三⾓形区域，则的值为（）Ａ. B. C. D.17.设函数， . 若当时，不等式恒成⽴，则实数的取值范围是（）.A. B. C. D.18、⼀个盒⼦⾥有3个分别标有号码为1，2，3的⼩球，每次取出⼀个，记下它的标号后再放回盒⼦中，共取3次，则取得⼩球标号值是3的取法有（）A.12种B. 15种C. 17种D.19种19、⼆项式的展开式中常数项是（）A．28 B．-7 C．7 D．-2820、⾼三毕业时，甲，⼄，丙等五位同学站成⼀排合影留念，已知甲，⼄相邻，则甲丙相邻的概率为（） A. B. C. D.⼀、某苗圃基地为了解基地内甲、⼄两块地种植的同⼀种树苗的长势情况，从两块地各随机抽取了10株树苗测量它们的⾼度，⽤茎叶图表⽰上述两组数据，对两块地抽取树苗的⾼度的平均数和中位数进⾏⽐较，下⾯结论正确的是（）A． B．C． D．22、公差不为0的等差数列{ }的前21项的和等于前8项的和．若，则k＝（）A．20 B．21 C．22 D．2323、已知数列为等⽐数列，，，则的值为（）A． B． C． D．24. 已知分别是双曲线的左、右焦点,过且垂直于轴的直线与双曲线交于两点,若是锐⾓三⾓形,则该双曲线离⼼率的取值范围是（ ）A． B． C． D．25．圆－2x＋my－2＝0关于抛物线＝4y的准线对称，则m的值为（）A.1B. 2C. 3D. 426．已知抛物线的焦点到准线的距离为 , 且上的两点关于直线对称, 并且 , 那么 =（ ）A． B． C．2 D．327．如果函数图像上任意⼀点的坐标都满⾜⽅程，那么正确的选项是（）(A) 是区间（0，）上的减函数，且(B) 是区间（1，）上的增函数，且(C) 是区间（1，）上的减函数，且(D) 是区间（1，）上的减函数，且28．定义在R上的奇函数，当 ≥0时，则关于的函数（0＜＜1）的所有零点之和为（）（A）1- （B）（C）（D）29．的展开式中, 的系数等于40,则等于（ ）A． B． C．1 D．30．已知函数 ,,设函数，且函数的零点均在区间内，则的最⼩值为（）A． B． C． D．⼆．填空题（8道）31.已知A ,B(0,1)),坐标原点O在直线AB上的射影为点C,则 = .32.在的展开式中，含项的系数是________.（⽤数字作答）33.若实数、满⾜，且的最⼩值为，则实数的值为__34.已知四⾯体的外接球的球⼼在上,且平⾯ , , 若四⾯体的体积为 ,则该球的体积为_____________35.已知是曲线与围成的区域，若向区域上随机投⼀点，则点落⼊区域的概率为．36.公⽐为4的等⽐数列中,若是数列的前项积,则有也成等⽐数列,且公⽐为；类⽐上述结论，相应的在公差为3的等差数列中，若是的前项和，则有⼀相应的等差数列，该等差数列的公差为_____________.37.在中,⾓所对的边分别为 ,且 ,当取值时,⾓的值为_______________38.已知抛物线的准线为 ,过点且斜率为的直线与相交于点 ,与的⼀个交点为 ,若 ,则等于____________三．解答题（12道）39、中，，，分别是⾓的对边，向量， , ．（1）求⾓的⼤⼩；（2）若，，求的值．40、已知等差数列的⾸项，公差．且分别是等⽐数列的．（Ⅰ）求数列与的通项公式；（Ⅱ）设数列对任意⾃然数均有 … 成⽴，求 … 的值.41、⼀次考试中，五名同学的数学、物理成绩如下表所⽰：学⽣（1）请在直⾓坐标系中作出这些数据的散点图，并求出这些数据的回归⽅程；（2）要从名数学成绩在分以上的同学中选⼈参加⼀项活动，以表⽰选中的同学的物理成绩⾼于分的⼈数，求随机变量的分布列及数学期望的值．42、⼗⼀黄⾦周，记者通过随机询问某景区110名游客对景区的服务是否满意，得到如下的列联表：性别与对景区的服务是否满意 单位：名男⼥总计满意 50 30 80不满意 10 20 30总计 60 50 110(1)从这50名⼥游客中按对景区的服务是否满意采取分层抽样，抽取⼀个容量为5的样本，问样本中满意与不满意的⼥游客各有多少名？(2)从(1)中的5名⼥游客样本中随机选取两名作深度访谈，求选到满意与不满意的⼥游客各⼀名的概率；(3)根据以上列联表，问有多⼤把握认为“游客性别与对景区的服务满意”有关附：P( )0.050 0.025 0.010 0.0053.841 5.024 6.635 7.87943、如图在四棱锥中,底⾯是边长为的正⽅形,侧⾯底⾯，且 ,设、分别为、的中点．(Ⅰ) 求证： //平⾯；(Ⅱ) 求证：⾯平⾯；(Ⅲ) 求⼆⾯⾓的正切值．44、已知椭圆 : 的焦距为 ,离⼼率为 ,其右焦点为 ,过点作直线交椭圆于另⼀点 .(Ⅰ)若 ,求外接圆的⽅程;(Ⅱ)若过点的直线与椭圆相交于两点、，设为上⼀点，且满⾜（为坐标原点），当时，求实数的取值范围.45. 已知定点A(1，0), B为x轴负半轴上的动点，以AB为边作菱形ABCD,使其两对⾓线的交点恰好落在y轴上.(1) 求动点D的轨迹五的⽅程.(2) 若四边形MPNQ的四个顶点都在曲线E上，M，N关于x轴对称，曲线E在M点处的切线为l，且PQ//l①证明直线PN与QN的斜率之和为定值；②当M的横坐标为，纵坐标⼤于O, =60°时，求四边形MPNQ的⾯积46. 对于函数f（x）（x∈D），若x∈D时，恒有＞成⽴，则称函数是D上的J函数．（Ⅰ）当函数f（x）＝m lnx是J函数时，求m的取值范围；（Ⅱ）若函数g（x）为（0，＋∞）上的J函数，①试⽐较g（a）与 g（1）的⼤⼩；②求证：对于任意⼤于1的实数x1，x2，x3，…，xn，均有g（ln（x1＋x2＋…＋xn））＞g（lnx1）＋g（lnx2）＋…＋g（lnxn）．47. 设函数，．(Ⅰ)讨论函数的单调性；(Ⅱ）如果存在，使得成⽴，求满⾜上述条件的整数；（Ⅲ）如果对任意的，都有成⽴，求实数的取值范围．48.选修4-1:⼏何证明选讲.如图，过圆E外⼀点A作⼀条直线与圆E交B,C两点，且AB= AC,作直线AF与圆E相切于点F，连接EF交BC于点D,⼰知圆E的半径为2， =30.(1)求AF的长.(2)求证：AD=3ED.49. 在直⾓坐标系中,以原点为极点, 轴的正半轴为极轴建坐标系.已知曲线 ,已知过点的直线的参数⽅程为：，直线与曲线分别交于两点.（1）写出曲线和直线的普通⽅程；（2）若成等⽐数列,求的值．50. 选修4-5：不等式选讲设（1）当，求的取值范围；（2）若对任意x∈R，恒成⽴，求实数的最⼩值．2013年⾼考数学(理)押题精粹（课标版）【参考答案与解析】⼆．选择题（30道）1.【答案】A2.【答案】D【点评】:集合问题是⾼考必考内容之⼀，题⽬相对简单.集合的表⽰法有列举法、描述法、图⽰法三种，⾼考中与集合的运算相结合，不外乎上述⼏种题型。
【免费下载】13年高考真题理科数学7立体几何
2013高考真题分类汇编：立体几何1．【2013新课标】如图，有一个水平放置的透明无盖的正方体容器,容器高8，将一个球放在容器口，再向容器内注水，当球cm 面恰好接触水面时测得水深为6，如果不计容器的厚度，则球的cm 体积为( )（A ）（B ） （C ） （D ）35003cm π38663cm π313723cm π320483cm π2．【2013广东】设是两条不同的直线，是两个不同的,m n ,αβ平面，下列命题中正确的是( )（A ）若，，，则αβ⊥m α⊂n β⊂m n⊥（B ）若，，，则//αβm α⊂n β⊂//m n（C ）若，，，则m n ⊥m α⊂n β⊂αβ⊥（D ）若，，，则m α⊥//m n //n βαβ⊥3．【2013湖北8】一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为，，，，上面两个简单几何体均为1V 2V 3V 4V 旋转体，下面两个简单几何体均为多面体，则有( )（A ） （B ）1243V V V V <<<1324V V V V <<<（C ） （D ）2134V V V V <<<2314V V V V <<<4．【2013大纲版】已知正四棱柱中1111ABCD A B C D -，则与平面所成角的正弦值等于( )12AA AB =CD 1BDC（A ） （B （C （D ）2315．【2013新课标】某几何体的三视图如图所示，则该几何体的体积为( ) （A ） （B ） （C ） （D ）168π+88π+1616π+816π+6．【2013湖南】已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能等于() （A ）1（B（C ）（D ）)12)12+7．【2013新课标】已知n m ,为异面直线，⊥m 平面α，⊥n 平面β。
2013届高考数学理科模拟卷
天利图书2013年普通高等学校招生全国统一考试数学（理科）注意事项:1．答题前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2．每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。
不能答在试题卷上。
一、选择题：本大题共10小题，每小题5分，共50分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知集合}023|{2>-+=x x x M ，}1|{≥=x x N ，则=⋂N MA ．),1(∞+-B ．)3,1[C ．)3,1(D ．),3(∞+ 2．若复数i z +=1(i 是虚数单位)，则A ．01222=--z z B ．01222=+-z z C ．0222=--z z D ．0222=+-z z 3．已知0>a 且1≠a ，则0log >b a 是0)1)(1(>--b a 的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件4．某程序框图如图所示，该程序运行后输出的k 的值是 A ．12 B ．13 C ．14 D ．155．不等式组⎪⎩⎪⎨⎧≥≤--≥+-x a y y x y x 013032表示一个锐角三角形所围成的平面区域，则实数a 的取值范围是A ．)3,(--∞B ．),21(∞+-C ．)21,3(-- D ．)2,31(6．设8822108)(x a x a x a a a x +⋯+++=-，若685-=+a a ， 则实数a 的值为A ．12B ．13C ． 2D ．37．如图，正方体D C B A ABCD ''''-中，M 为BC 边 的中点，点P 在底面D C B A ''''和侧面C D CD ''上 运动并且使C PA C MA '∠='∠，那么点P 的轨迹是 A ．两段圆弧 B ．两段椭圆弧 C ．两段双曲线弧 D ．两段抛物线弧8．如图，在扇形OAB 中，︒=∠60AOB ，C 为弧AB 上与B A ,不重合．．．的一个动点，y x +=，若)0(,>+=λλy x u 存在最大值，则λ的取值范围为A ．)1,21(B ．)2,21(C ．)3,31( D ．)3,1(9．设椭圆)0(12222>>=+b a b ya x 的上顶点为A ，点C B , 在椭圆上，且左、右焦点21,F F 分别在等腰三角形ABC 两腰AB 和AC 上. 若椭圆的离心率33=e ,则原点O 是ABC ∆的 A ．内心 B ．外心 C ．重心 D ．垂心 10．设函数)10)(10)(10()(322212c x x c x x c x x x f +-+-+-=)10(42c x x +-B'D (第4题))10(52c x x +-，设集合*921},,,{}0)(|{N x x x x f x M ⊆⋯===，设 54321c c c c c ≥≥≥≥，则=-51c cA ．14B ．16C ．18D ． 20非选择题部分 (共100分)二、填空题：本大题共7小题，每小题4分，共28分。
2013山东省高考数学(理科)模拟题及答案_7
2013山东省高考数学（理科）模拟题7本试卷分第I 卷和第II 卷两部分，共4页。
满分150分。
考试用时120分钟。
考试结束后，将本试卷和答题卡一并交回。
注意事项：1．答卷前，考生务必用0.5毫米黑色墨水签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上。
2．第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。
3．第II 卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4．填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。
第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合{|03},{|2,1}xA x xB y y x =≤≤==>，则A ∩B 为A ．[0，3]B ．(2,3]C ．[3,)+∞D ．[1，3]2．若复数（a +i ）2在复平面内对应的点在y 轴负半轴上，则实数a 的值是A ．－lB ．1C D3．在等差数列{n a }中，811162a a =+，则数列{n a }前9项的和S 9等于A ．24B ．48C ．72D ．1084．下图给出的是计算1001...81614121+++++的一个程序框图，其中判断框内应填入的条件是A ．50<iB ．50>iC ．25<iD ．25>i5．某小区有排成一排的7个车位，现有3辆不同型号的车需要停放，如果要求剩余的4个车位连在一起， 那么不同的停放方法的种数为A ．16B ．18C ．24D ．326．若2log 3a =，3log 2b =，4log 6c =,则下列结论正确的是A ．b a c <<B ．a b c <<C ．c b a <<D ．b c a <<7．已知半径为5的球O 被互相垂直的两个平面所截，得到的两个圆的公共弦为4，若其中的一圆的半径为4，则另一圆的半径为ABC ．D8．一个几何体的三视图如图所示（单位长度：cm ），俯视图中圆与四边形相切，且该几何体的体积为33cm ，则该几何体的高h 为A ．cm πB ．(cm π+C ．(cm π+D ．(3cm π+9．由曲线21y x =-、直线x=0、x=2和x 轴围成的封闭图形的面积可表示为A ．22(1)x dx -⎰B ．22|1|x dx -⎰C ．22|(1)|x dx -⎰D ．22221(1)(1)x dx x dx -+-⎰⎰10．设函数()2sin +4f x x πωω=（）(>0)与函数()cos(2)(||)2g x x πφφ=+≤的对称轴完全相同，则φ的值为A ．4πB ．4π-C ．2πD ．2π-11．设1e 、2e 为焦点在x 轴且具有公共焦点1F 、2F 的标准椭圆和标准双曲线的离心率，O 为坐标原点，P 是两曲线的一个公共点，且满足的值为A ．2 BCD ．112．已知函数31,0()3,0x x f x xx x ⎧+>⎪=⎨⎪+≤⎩，则函数a x x f y -+=)2(2（2a >）的零点个数不可能为A ．3B ．4C ．5D ．6第Ⅱ卷本卷包括必考题和选考题两部分，第13题至第21题为必考题，第22题至第24题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题4分，共16分，13．若4234512345(1)x m x a x a x a x a x a x -=++++，其中62-=a ，则54321a a a a a ++++的值为 ．14．已知z=2x +y ，x ，y 满足,2,,y x x y x a ≥⎧⎪+≤⎨⎪≥⎩且z 的最大值是最小值的4倍，则a 的值是 。
2013高考数学(理科)小题限时训练12
2013高考数学（理科）小题限时训练十二15小题共75分，时量：45分钟，考试时间：2012年9月27日第6节 姓名一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若M ＝{x ||x －1|<2}，N ＝{x |x (x －3)<0}，则M ∩N ＝ A.{x |0<x <3} B.{x |－1<x <2} C.{x |－1<x <3} D.{x |－1<x <0}2.已知函数f (x )＝sin(2x －π4)，若存在α∈(0，π)，使得f (x ＋α)＝f (x ＋3α)恒成立，则α的值是A.π6B.π3C.π4D.π23.已知α，β是两个不同的平面，m ，n 是两条不同的直线，又知α∩β＝m ，且n ⊄α，n ⊄β，则“n ∥m ”是“n ∥α且n ∥β”的A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件4.6名同学安排到3个宿舍，每个宿舍两人，其中甲必须在一号宿舍，乙和丙均不能到三号宿舍，则不同的安排方法种数为A.6B.9C.12D.185.若f (x )＝f 1(x )＝x 1＋x ，f n (x )＝f n －1[f (x )](n ≥2，n ∈N *)，则f (1)＋f (2)＋…＋f (n )＋f 1(1)＋f 2(1)＋…＋f n (1)＝A.nB.9n ＋1C.nn ＋1D.16.已知m 是一个给定的正整数，如果两个整数a ，b 被m 除得的余数相同，则称a 与b 对模m 同余，记作a ≡b (mod m )，例如：5≡13(mod4).若22010≡r (mod7)，则r 可以为A.2008B.2009C.2010D.20117.在△ABC 所在的平面内有一点P ，满足P A ＋PB ＋PC ＝AB ，则△PBC 与△ABC 的面积之比是A.13B.12C.23D.348.若函数y ＝f (x )(x ∈R )满足f (x ＋2)＝f (x )，且x ∈(－1,1]时，f (x )＝1－x 2， 函数g (x )＝l g ︱x ︱，则函数h (x )＝f (x )－g (x )在区间[－5,10]内零点的个数为A.12B.14C.13D.8二、填空题：本大题共7小题，每小题5分，共35分，把答案填在答题卡中对应题号后的横线上.9.已知a 是实数，(a －i)(1－i)i是纯虚数，则a 的值是 .10.若x 1，x 2，x 3，…，x 2009，x 2010的方差是2，则3(x 1－1),3(x 2－1)，…，3(x 2009－1),3(x 2010－1)的方差是 .11.已知某一几何体的正视图与侧视图如图所示，则在下列图形中，可以是该几何体的俯视图的图形为 (填你认为正确的图序号)12.已知函数f (x )＝－x 2＋ax －2b .若a ，b 都是区间[0,4]内的数，则使f (1)>0成立的概率是 .13.某机构对小学生作业负担的情况进行调查，设每个学生平均每天作业的时间为x (单位：分钟)，且x ～N (60,100)，已知P (x ≤50)＝0.159.现有1000名小学生接受了此项调查，下图是此次调查中某一项的流程图，则输出的结果大约是 .14.已知关于x 的方程9x－(4＋a )·3x＋4＝0有两个实数解x 1，x 2，则x 21＋x 22x 1x 2的最小值是 .15.对有10个元素的总体{1,2,3，…，10}进行抽样，先将总体分成两个子总体A ＝{1,2,3,4}和B ＝{5,6,7,8,9,10}，再从A 和B 中分别随机抽取2个元素和3个元素组成样本，用P ij 表示元素i 和j 同时出现在样本中的概率，则P 15＝ ，所有P ij (1≤i <j ≤10)的和等于 .参考答案一、选择题1.A2.D3.C4.B5.A6.C7.C 解：由P A ＋PB ＋PC ＝AB 得P A ＋PB ＋BA ＋PC ＝0，即PC ＝2AP ，所以点P 是CA 边上的三等分点，故S △PBC ∶S △ABC ＝2∶3.8.B 解：如图，当x ∈[0,5]时，结合图象知f (x )与g (x )共有5个交点，故在区间[－5,0]上共有5个交点；当x ∈(0,10]时，结合图象知共有9个交点，故函数h (x )＝f (x )－g (x )在区间[－5,10]上共有14个零点.二、填空题9.－1 10.18 11.①② 12.96413.15914.2 解：原方程可化为(3x )2－(4＋a )·3x ＋4＝0，∴3x 1·3x 2＝4，∴x 1＋x 2＝2log 32，∴x 1x 2≤(log 32)2.∴x 21＋x 22x 1x 2＝(x 1＋x 2)2－2x 1x 2x 1x 2＝4(log 32)2x 1x 2－2≥2. 15.1410 解：(1)由题意有：P 15＝C 13·C 25C 24·C 36＝14.(2)当1≤i <j ≤4时，P ij ＝1C 24＝16，这样的P ij 共有C 24个，故所有P ij (1≤i <j ≤4)的和为16·6＝1；当5≤i <j ≤10时，P ij ＝C 14·C 22C 36＝15.这样的P ij 共有C 26＝15个，故所有P ij (5≤i <j ≤10)的和为15·15＝3； 当1≤i ≤4,5≤j ≤10时，P ij ＝14，这样的P ij 共有4·6＝24，所有P ij (1≤i ≤4,5≤j ≤10)的和为24·14＝6，综上所述，所有P ij (1≤i <j ≤10)的和等于1＋3＋6＝10.。
2013年全国统一高考数学试卷(理科)(大纲版)(含解析版)
2013年全国统一高考数学试卷（理科）（大纲版）一、选择题：本大题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设集合A={1，2，3}，B={4，5}，M={x|x=a+b，a∈A，b∈B}，则M中元素的个数为（）A．3B．4C．5D．62．（5分）=（）A．﹣8B．8C．﹣8i D．8i3．（5分）已知向量=（λ+1，1），=（λ+2，2），若（+）⊥（﹣），则λ=（）A．﹣4B．﹣3C．﹣2D．﹣14．（5分）已知函数f（x）的定义域为（﹣1，0），则函数f（2x+1）的定义域为（）A．（﹣1，1）B ．C．（﹣1，0）D ．5．（5分）函数f（x）=log2（1+）（x＞0）的反函数f﹣1（x）=（）A ．B ．C．2x﹣1（x∈R）D．2x﹣1（x＞0）6．（5分）已知数列{a n}满足3a n+1+a n=0，a2=﹣，则{a n}的前10项和等于（）A．﹣6（1﹣3﹣10）B ．C．3（1﹣3﹣10）D．3（1+3﹣10）7．（5分）（1+x）3（1+y）4的展开式中x2y2的系数是（）A．5B．8C．12D．188．（5分）椭圆C ：的左、右顶点分别为A1、A2，点P在C上且直线PA2斜率的取值范围是[﹣2，﹣1]，那么直线PA1斜率的取值范围是（）A ．B ．C ．D ．9．（5分）若函数f（x）=x2+ax +是增函数，则a的取值范围是（）A．[﹣1，0]B．[﹣1，+∞）C．[0，3]D．[3，+∞）10．（5分）已知正四棱柱ABCD﹣A1B1C1D1中，AA1=2AB，则CD与平面BDC1所成角的正弦值等于（）A ．B ．C ．D ．11．（5分）已知抛物线C：y2=8x的焦点为F，点M（﹣2，2），过点F且斜率为k的直线与C交于A，B 两点，若，则k=（）A ．B ．C ．D．212．（5分）已知函数f（x）=cosxsin2x，下列结论中不正确的是（）A．y=f（x）的图象关于（π，0）中心对称B ．C ．D．f（x）既是奇函数，又是周期函数二、填空题：本大题共4小题，每小题5分.13．（5分）已知α是第三象限角，sinα=﹣，则co tα=．14．（5分）6个人排成一行，其中甲、乙两人不相邻的不同排法共有种．（用数字作答）15．（5分）记不等式组所表示的平面区域为D．若直线y=a（x+1）与D有公共点，则a 的取值范围是．16．（5分）已知圆O和圆K是球O的大圆和小圆，其公共弦长等于球O的半径，，则球O的表面积等于．三、解答题：解答应写出文字说明、证明过程或演算步骤.17．（10分）等差数列{a n}的前n项和为S n．已知S3=a22，且S1，S2，S4成等比数列，求{a n}的通项式．18．（12分）设△ABC的内角A，B，C的内角对边分别为a，b，c，满足（a+b+c）（a﹣b+c）=ac．（Ⅰ）求B．（Ⅱ）若sinAsinC=，求C．19．（12分）如图，四棱锥P﹣ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是等边三角形．（Ⅰ）证明：PB⊥CD；（Ⅱ）求二面角A﹣PD﹣C的大小．20．（12分）甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判，设各局中双方获胜的概率均为，各局比赛的结果都相互独立，第1局甲当裁判．（Ⅰ）求第4局甲当裁判的概率；（Ⅱ）X表示前4局中乙当裁判的次数，求X的数学期望．21．（12分）已知双曲线C ：=1（a＞0，b＞0）的左、右焦点分别为F1，F2，离心率为3，直线y=2与C 的两个交点间的距离为．（I）求a，b；（II）设过F2的直线l与C的左、右两支分别相交于A、B两点，且|AF1|=|BF1|，证明：|AF2|、|AB|、|BF2|成等比数列．22．（12分）已知函数．（I）若x≥0时，f（x）≤0，求λ的最小值；（II）设数列{a n}的通项a n=1+．2013年全国统一高考数学试卷（理科）（大纲版）参考答案与试题解析一、选择题：本大题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设集合A={1，2，3}，B={4，5}，M={x|x=a+b，a∈A，b∈B}，则M中元素的个数为（）A．3B．4C．5D．6【考点】13：集合的确定性、互异性、无序性；1A：集合中元素个数的最值．【专题】11：计算题．【分析】利用已知条件，直接求出a+b，利用集合元素互异求出M中元素的个数即可．【解答】解：因为集合A={1，2，3}，B={4，5}，M={x|x=a+b，a∈A，b∈B}，所以a+b的值可能为：1+4=5、1+5=6、2+4=6、2+5=7、3+4=7、3+5=8，所以M中元素只有：5，6，7，8．共4个．故选：B．【点评】本题考查集合中元素个数的最值，集合中元素的互异性的应用，考查计算能力．2．（5分）=（）A．﹣8B．8C．﹣8i D．8i【考点】A5：复数的运算．【分析】复数分子、分母同乘﹣8，利用1的立方虚根的性质（），化简即可．【解答】解：故选：A．【点评】复数代数形式的运算，是基础题．3．（5分）已知向量=（λ+1，1），=（λ+2，2），若（+）⊥（﹣），则λ=（）A．﹣4B．﹣3C．﹣2D．﹣1【考点】9T：数量积判断两个平面向量的垂直关系．【专题】5A：平面向量及应用．【分析】利用向量的运算法则、向量垂直与数量积的关系即可得出．【解答】解：∵，．∴=（2λ+3，3），．∵，∴=0，∴﹣（2λ+3）﹣3=0，解得λ=﹣3．故选：B．【点评】熟练掌握向量的运算法则、向量垂直与数量积的关系是解题的关键．4．（5分）已知函数f（x）的定义域为（﹣1，0），则函数f（2x+1）的定义域为（）A．（﹣1，1）B ．C．（﹣1，0）D ．【考点】33：函数的定义域及其求法．【专题】51：函数的性质及应用．【分析】原函数的定义域，即为2x+1的范围，解不等式组即可得解．【解答】解：∵原函数的定义域为（﹣1，0），∴﹣1＜2x+1＜0，解得﹣1＜x ＜﹣．∴则函数f（2x+1）的定义域为．故选：B．【点评】考查复合函数的定义域的求法，注意变量范围的转化，属简单题．5．（5分）函数f（x）=log2（1+）（x＞0）的反函数f﹣1（x）=（）A ．B ．C．2x﹣1（x∈R）D．2x﹣1（x＞0）【考点】4R：反函数．【专题】51：函数的性质及应用．【分析】把y看作常数，求出x：x=，x，y互换，得到y=log2（1+）的反函数．注意反函数的定义域．【解答】解：设y=log2（1+），把y看作常数，求出x：1+=2y，x=，其中y＞0，x，y互换，得到y=log2（1+）的反函数：y=，故选：A．【点评】本题考查对数函数的反函数的求法，解题时要认真审题，注意对数式和指数式的相互转化．6．（5分）已知数列{a n}满足3a n+1+a n=0，a2=﹣，则{a n}的前10项和等于（）A．﹣6（1﹣3﹣10）B ．C．3（1﹣3﹣10）D．3（1+3﹣10）【考点】89：等比数列的前n项和．【专题】11：计算题；54：等差数列与等比数列．【分析】由已知可知，数列{a n}是以﹣为公比的等比数列，结合已知可求a1，然后代入等比数列的求和公式可求【解答】解：∵3a n+1+a n=0∴∴数列{a n}是以﹣为公比的等比数列∵∴a1=4由等比数列的求和公式可得，S10==3（1﹣3﹣10）故选：C．【点评】本题主要考查了等比数列的通项公式及求和公式的简单应用，属于基础试题7．（5分）（1+x）3（1+y）4的展开式中x2y2的系数是（）A．5B．8C．12D．18【考点】DA：二项式定理．【专题】11：计算题．【分析】由题意知利用二项展开式的通项公式写出展开式的通项，令x的指数为2，写出出展开式中x2的系数，第二个因式y2的系数，即可得到结果．【解答】解：（x+1）3的展开式的通项为T r+1=C3r x r令r=2得到展开式中x2的系数是C32=3，（1+y）4的展开式的通项为T r+1=C4r y r令r=2得到展开式中y2的系数是C42=6，（1+x）3（1+y）4的展开式中x2y2的系数是：3×6=18，故选：D．【点评】本题考查利用二项展开式的通项公式解决二项展开式的特定项问题，本题解题的关键是写出二项式的展开式，所有的这类问题都是利用通项来解决的．8．（5分）椭圆C ：的左、右顶点分别为A1、A2，点P在C上且直线PA2斜率的取值范围是[﹣2，﹣1]，那么直线PA1斜率的取值范围是（）A ．B ．C ．D ．【考点】I3：直线的斜率；KH：直线与圆锥曲线的综合．【专题】5D：圆锥曲线的定义、性质与方程．【分析】由椭圆C ：可知其左顶点A1（﹣2，0），右顶点A2（2，0）．设P（x0，y0）（x0≠±2），代入椭圆方程可得．利用斜率计算公式可得，再利用已知给出的的范围即可解出．【解答】解：由椭圆C ：可知其左顶点A1（﹣2，0），右顶点A2（2，0）．设P（x0，y0）（x0≠±2），则，得．∵=，=，∴==，∵，∴，解得．故选：B．【点评】熟练掌握椭圆的标准方程及其性质、斜率的计算公式、不等式的性质等是解题的关键．9．（5分）若函数f（x）=x2+ax +是增函数，则a的取值范围是（）A．[﹣1，0]B．[﹣1，+∞）C．[0，3]D．[3，+∞）【考点】6B：利用导数研究函数的单调性．【专题】53：导数的综合应用．【分析】由函数在（，+∞）上是增函数，可得≥0在（，+∞）上恒成立，进而可转化为a ≥﹣2x 在（，+∞）上恒成立，构造函数求出﹣2x 在（，+∞）上的最值，可得a的取值范围．【解答】解：∵在（，+∞）上是增函数，故≥0在（，+∞）上恒成立，即a ≥﹣2x 在（，+∞）上恒成立，令h（x）=﹣2x，则h′（x）=﹣﹣2，当x ∈（，+∞）时，h′（x）＜0，则h（x）为减函数．∴h（x）＜h （）=3∴a≥3．故选：D．【点评】本题考查的知识点是利用导数研究函数的单调性，恒成立问题，是导数的综合应用，难度中档．10．（5分）已知正四棱柱ABCD﹣A1B1C1D1中，AA1=2AB，则CD与平面BDC1所成角的正弦值等于（）A ．B ．C ．D ．【考点】MI：直线与平面所成的角．【专题】15：综合题；16：压轴题；5G：空间角；5H：空间向量及应用．【分析】设AB=1，则AA1=2，分别以的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，设=（x，y，z）为平面BDC1的一个法向量，CD与平面BDC1所成角为θ，则sinθ=||，在空间坐标系下求出向量坐标，代入计算即可．【解答】解：设AB=1，则AA1=2，分别以的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，如下图所示：则D（0，0，2），C1（1，0，0），B（1，1，2），C（1，0，2），=（1，1，0），=（1，0，﹣2），=（1，0，0），设=（x，y，z）为平面BDC1的一个法向量，则，即，取=（2，﹣2，1），设CD与平面BDC1所成角为θ，则sinθ=||=，故选：A．【点评】本题考查直线与平面所成的角，考查空间向量的运算及应用，准确理解线面角与直线方向向量、平面法向量夹角关系是解决问题的关键．11．（5分）已知抛物线C：y2=8x的焦点为F，点M（﹣2，2），过点F且斜率为k的直线与C交于A，B 两点，若，则k=（）A ．B ．C ．D．2【考点】9O：平面向量数量积的性质及其运算；K8：抛物线的性质．【专题】11：计算题；5D：圆锥曲线的定义、性质与方程．【分析】斜率k存在，设直线AB为y=k（x﹣2），代入抛物线方程，利用=（x1+2，y1﹣2）•（x2+2，y2﹣2）=0，即可求出k的值．【解答】解：由抛物线C：y2=8x得焦点（2，0），由题意可知：斜率k存在，设直线AB为y=k（x﹣2），代入抛物线方程，得到k2x2﹣（4k2+8）x+4k2=0，△＞0，设A（x1，y1），B（x2，y2）．∴x1+x2=4+，x1x2=4．∴y1+y2=，y1y2=﹣16，又=0，∴=（x1+2，y1﹣2）•（x2+2，y2﹣2）==0∴k=2．故选：D．【点评】本题考查直线与抛物线的位置关系，考查向量的数量积公式，考查学生的计算能力，属于中档题．12．（5分）已知函数f（x）=cosxsin2x，下列结论中不正确的是（）A．y=f（x）的图象关于（π，0）中心对称B ．C ．D．f（x）既是奇函数，又是周期函数【考点】H1：三角函数的周期性；HW：三角函数的最值．【专题】11：计算题；57：三角函数的图像与性质．【分析】根据函数图象关于某点中心对称或关于某条直线对称的公式，对A、B两项加以验证，可得它们都正确．根据二倍角的正弦公式和同角三角函数的关系化简，得f（x）=2sinx（1﹣sin2x），再换元：令t=sinx，得到关于t的三次函数，利用导数研究此函数的单调性可得f（x）的最大值为，故C不正确；根据函数周期性和奇偶性的定义加以验证，可得D项正确．由此可得本题的答案．【解答】解：对于A，因为f（π+x）=cos（π+x）sin（2π+2x）=﹣cosxsin2x，f（π﹣x）=cos（π﹣x）sin（2π﹣2x）=cosxsin2x，所以f（π+x）+f（π﹣x）=0，可得y=f（x）的图象关于（π，0）中心对称，故A正确；对于B，因为f （+x）=cos （+x）sin（π+2x）=﹣sinx（﹣sin2x）=sinxsin2x，f （﹣x）=cos （﹣x）sin（π﹣2x）=sinxsin2x，所以f （+x）=f （﹣x），可得y=f（x）的图象关于直线x=对称，故B正确；对于C，化简得f（x）=cosxsin2x=2cos2xsinx=2sinx（1﹣sin2x），令t=sinx，f（x）=g（t）=2t（1﹣t2），﹣1≤t≤1，∵g（t）=2t（1﹣t2）的导数g'（t）=2﹣6t2=2（1+t）（1﹣t）∴当t∈（﹣1，﹣）时或t ∈（，1）时g'（t）＜0，函数g（t）为减函数；当t ∈（﹣，）时g'（t）＞0，函数g（t）为增函数．因此函数g（t）的最大值为t=﹣1时或t=时的函数值，结合g（﹣1）=0＜g （）=，可得g（t ）的最大值为．由此可得f（x ）的最大值为而不是，故C不正确；对于D，因为f（﹣x）=cos（﹣x）sin（﹣2x）=﹣cosxsin2x=﹣f（x），所以f（x）是奇函数．因为f（2π+x）=cos（2π+x）sin（4π+2x）=cosxsin2x=f（x），所以2π为函数的一个周期，得f（x）为周期函数．可得f（x）既是奇函数，又是周期函数，得D 正确．综上所述，只有C项不正确．故选：C．【点评】本题给出三角函数式，研究函数的奇偶性、单调性和周期性．着重考查了三角恒等变换公式、利用导数研究函数的单调性和函数图象的对称性等知识，属于中档题．二、填空题：本大题共4小题，每小题5分.13．（5分）已知α是第三象限角，sinα=﹣，则cotα=2．【考点】GG：同角三角函数间的基本关系．【专题】56：三角函数的求值．【分析】根据α是第三象限的角，得到cosα小于0，然后由sinα的值，利用同角三角函数间的基本关系求出cosα的值，进而求出cotα的值．【解答】解：由α是第三象限的角，得到cosα＜0，又sinα=﹣，所以cosα=﹣=﹣则cotα==2故答案为：2【点评】此题考查学生灵活运用同角三角函数间的基本关系化简求值，是一道基础题．学生做题时注意α的范围．14．（5分）6个人排成一行，其中甲、乙两人不相邻的不同排法共有480种．（用数字作答）【考点】D9：排列、组合及简单计数问题．【专题】11：计算题．【分析】排列好甲、乙两人外的4人，然后把甲、乙两人插入4个人的5个空位中即可．【解答】解：6个人排成一行，其中甲、乙两人不相邻的不同排法：排列好甲、乙两人外的4人，有中方法，然后把甲、乙两人插入4个人的5个空位，有种方法，所以共有：=480．故答案为：480．【点评】本题考查了乘法原理，以及排列的简单应用，插空法解答不相邻问题．15．（5分）记不等式组所表示的平面区域为D．若直线y=a（x+1）与D有公共点，则a 的取值范围是[，4] ．【考点】7C：简单线性规划．【专题】16：压轴题；59：不等式的解法及应用．【分析】本题考查的知识点是简单线性规划的应用，我们要先画出满足约束条件的平面区域，然后分析平面区域里各个角点，然后将其代入y=a（x+1）中，求出y=a（x+1）对应的a的端点值即可．【解答】解：满足约束条件的平面区域如图示：因为y=a（x+1）过定点（﹣1，0）．所以当y=a（x+1）过点B（0，4）时，得到a=4，当y=a（x+1）过点A（1，1）时，对应a=．又因为直线y=a（x+1）与平面区域D有公共点．所以≤a≤4．故答案为：[，4]【点评】在解决线性规划的小题时，我们常用“角点法”，其步骤为：①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证，求出最优解．16．（5分）已知圆O和圆K是球O的大圆和小圆，其公共弦长等于球O的半径，，则球O的表面积等于16π．【考点】LG：球的体积和表面积．【专题】16：压轴题；5F：空间位置关系与距离．【分析】正确作出图形，利用勾股定理，建立方程，即可求得结论．【解答】解：如图所示，设球O的半径为r，AB是公共弦，∠OCK是面面角根据题意得OC=，CK=在△OCK中，OC2=OK2+CK2，即∴r2=4∴球O的表面积等于4πr2=16π故答案为16π【点评】本题考查球的表面积，考查学生分析解决问题的能力，属于中档题．三、解答题：解答应写出文字说明、证明过程或演算步骤.17．（10分）等差数列{a n}的前n项和为S n．已知S3=a22，且S1，S2，S4成等比数列，求{a n}的通项式．【考点】85：等差数列的前n项和；88：等比数列的通项公式．【专题】11：计算题；54：等差数列与等比数列．【分析】由，结合等差数列的求和公式可求a2，然后由，结合等差数列的求和公式进而可求公差d，即可求解通项公式【解答】解：设数列的公差为d由得，3∴a2=0或a2=3由题意可得，∴若a2=0，则可得d2=﹣2d2即d=0不符合题意若a2=3，则可得（6﹣d）2=（3﹣d）（12+2d）解可得d=0或d=2∴a n=3或a n=2n﹣1【点评】本题主要考查了等差数列的通项公式及求和公式的应用，等比数列的性质的简单应用，属于基础试题18．（12分）设△ABC的内角A，B，C的内角对边分别为a，b，c，满足（a+b+c）（a﹣b+c）=ac．（Ⅰ）求B．（Ⅱ）若sinAsinC=，求C．【考点】GP：两角和与差的三角函数；HR：余弦定理．【专题】58：解三角形．【分析】（I）已知等式左边利用多项式乘多项式法则计算，整理后得到关系式，利用余弦定理表示出cosB，将关系式代入求出cosB的值，由B为三角形的内角，利用特殊角的三角函数值即可求出B的度数；（II）由（I）得到A+C的度数，利用两角和与差的余弦函数公式化简cos（A﹣C），变形后将cos（A+C）及2sinAsinC的值代入求出cos（A﹣C）的值，利用特殊角的三角函数值求出A﹣C的值，与A+C 的值联立即可求出C的度数．【解答】解：（I）∵（a+b+c）（a﹣b+c）=（a+c）2﹣b2=ac，∴a2+c2﹣b2=﹣ac，∴cosB==﹣，又B为三角形的内角，则B=120°；（II）由（I）得：A+C=60°，∵sinAsinC=，cos（A+C）=，∴cos（A﹣C）=cosAcosC+sinAsinC=cosAcosC﹣sinAsinC+2sinAsinC=cos（A+C）+2sinAsinC=+2×=，∴A﹣C=30°或A﹣C=﹣30°，则C=15°或C=45°．【点评】此题考查了余弦定理，两角和与差的余弦函数公式，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．19．（12分）如图，四棱锥P﹣ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是等边三角形．（Ⅰ）证明：PB⊥CD；（Ⅱ）求二面角A﹣PD﹣C的大小．【考点】LW：直线与平面垂直；M5：共线向量与共面向量．【专题】11：计算题；5G：空间角．【分析】（I）取BC的中点E，连接DE，过点P作PO⊥平面ABCD于O，连接OA、OB、OD、OE．可证出四边形ABED是正方形，且O为正方形ABED的中心．因此OE⊥OB，结合三垂线定理，证出OE⊥PB，而OE是△BCD的中位线，可得OE∥CD，因此PB⊥CD；（II）由（I）的结论，证出CD⊥平面PBD，从而得到CD⊥PD．取PD的中点F，PC的中点G，连接FG，可得FG∥CD，所以FG⊥PD．连接AF，可得AF⊥PD，因此∠AFG为二面角A﹣PD﹣C的平面角，连接AG、EG，则EG∥PB，可得EG⊥OE．设AB=2，可求出AE、EG、AG、AF和FG的长，最后在△AFG中利用余弦定理，算出∠AFG=π﹣arccos，即得二面角A﹣PD﹣C的平面角大小．【解答】解：（I）取BC的中点E，连接DE，可得四边形ABED是正方形过点P作PO⊥平面ABCD，垂足为O，连接OA、OB、OD、OE∵△PAB与△PAD都是等边三角形，∴PA=PB=PD，可得OA=OB=OD因此，O是正方形ABED的对角线的交点，可得OE⊥OB∵PO⊥平面ABCD，得直线OB是直线PB在内的射影，∴OE⊥PB∵△BCD中，E、O分别为BC、BD的中点，∴OE∥CD，可得PB⊥CD；（II）由（I）知CD⊥PO，CD⊥PB ∵PO、PB是平面PBD内的相交直线，∴CD⊥平面PBD∵PD⊂平面PBD，∴CD⊥PD取PD的中点F，PC的中点G，连接FG，则FG为△PCD有中位线，∴FG∥CD，可得FG⊥PD连接AF，由△PAD是等边三角形可得AF⊥PD，∴∠AFG为二面角A﹣PD﹣C的平面角连接AG、EG，则EG∥PB∵PB⊥OE，∴EG⊥OE，设AB=2，则AE=2，EG=PB=1，故AG==3在△AFG中，FG=CD=，AF=，AG=3∴cos∠AFG==﹣，得∠AFG=π﹣arccos，即二面角A﹣PD﹣C的平面角大小是π﹣arccos．【点评】本题给出特殊的四棱锥，求证直线与直线垂直并求二面角平面角的大小，着重考查了线面垂直的判定与性质、三垂线定理和运用余弦定理求二面的大小等知识，属于中档题．20．（12分）甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判，设各局中双方获胜的概率均为，各局比赛的结果都相互独立，第1局甲当裁判．（Ⅰ）求第4局甲当裁判的概率；（Ⅱ）X表示前4局中乙当裁判的次数，求X的数学期望．【考点】CB：古典概型及其概率计算公式；CH：离散型随机变量的期望与方差．【专题】5I：概率与统计．【分析】（I）令A1表示第2局结果为甲获胜，A2表示第3局甲参加比赛时，结果为甲负，A表示第4局甲当裁判，分析其可能情况，每局比赛的结果相互独立且互斥，利用独立事件、互斥事件的概率求解即可．（II）X的所有可能值为0，1，2．分别求出X取每一个值的概率，列出分布列后求出期望值即可．【解答】解：（I）令A1表示第2局结果为甲获胜．A2表示第3局甲参加比赛时，结果为甲负．A表示第4局甲当裁判．则A=A1•A2，P（A）=P（A1•A2）=P（A1）P（A2）=；（Ⅱ）X的所有可能值为0，1，2．令A3表示第3局乙和丙比赛时，结果为乙胜．B1表示第1局结果为乙获胜，B2表示第2局乙和甲比赛时，结果为乙胜，B3表示第3局乙参加比赛时，结果为乙负，则P（X=0）=P（B1B 2）=P（B1）P（B2）P （）=．P（X=2）=P （B3）=P （）P（B3）=．P（X=1）=1﹣P（X=0）﹣P（X=2）=．从而EX=0×+1×+2×=．【点评】本题考查互斥、独立事件的概率，离散型随机变量的分布列和期望等知识，同时考查利用概率知识解决问题的能力．21．（12分）已知双曲线C ：=1（a＞0，b＞0）的左、右焦点分别为F1，F2，离心率为3，直线y=2与C 的两个交点间的距离为．（I）求a，b；（II）设过F2的直线l与C的左、右两支分别相交于A、B两点，且|AF1|=|BF1|，证明：|AF2|、|AB|、|BF2|成等比数列．【考点】K4：椭圆的性质；KH：直线与圆锥曲线的综合．【专题】14：证明题；15：综合题；16：压轴题；35：转化思想；5D：圆锥曲线的定义、性质与方程．【分析】（I）由题设，可由离心率为3得到参数a，b的关系，将双曲线的方程用参数a表示出来，再由直线建立方程求出参数a即可得到双曲线的方程；（II）由（I）的方程求出两焦点坐标，设出直线l的方程设A（x1，y1），B（x2，y2），将其与双曲线C的方程联立，得出x1+x2=，，再利用|AF1|=|BF1|建立关于A，B坐标的方程，得出两点横坐标的关系，由此方程求出k的值，得出直线的方程，从而可求得：|AF2|、|AB|、|BF2|，再利用等比数列的性质进行判断即可证明出结论．【解答】解：（I ）由题设知=3，即=9，故b2=8a2所以C的方程为8x2﹣y2=8a2将y=2代入上式，并求得x=±，由题设知，2=，解得a2=1所以a=1，b=2（II）由（I）知，F1（﹣3，0），F2（3，0），C的方程为8x2﹣y2=8 ①由题意，可设l的方程为y=k（x﹣3），|k|＜2代入①并化简得（k2﹣8）x2﹣6k2x+9k2+8=0设A（x1，y1），B（x2，y2），则x1≤﹣1，x2≥1，x1+x2=，，于是|AF1|==﹣（3x1+1），|BF1|==3x2+1，|AF1|=|BF1|得﹣（3x1+1）=3x2+1，即故=，解得，从而=﹣由于|AF2|==1﹣3x1，|BF2|==3x2﹣1，故|AB|=|AF2|﹣|BF2|=2﹣3（x1+x2）=4，|AF2||BF2|=3（x1+x2）﹣9x1x2﹣1=16因而|AF2||BF2|=|AB|2，所以|AF2|、|AB|、|BF2|成等比数列【点评】本题考查直线与圆锥曲线的综合关系，考查了运算能力，题设条件的转化能力，方程的思想运用，此类题综合性强，但解答过程有其固有规律，一般需要把直线与曲线联立利用根系关系，解答中要注意提炼此类题解答过程中的共性，给以后解答此类题提供借鉴．22．（12分）已知函数．（I）若x≥0时，f（x）≤0，求λ的最小值；（II）设数列{a n}的通项a n=1+．【考点】6E：利用导数研究函数的最值；8E：数列的求和；8K：数列与不等式的综合．【专题】16：压轴题；35：转化思想；53：导数的综合应用；54：等差数列与等比数列．【分析】（I）由于已知函数的最大值是0，故可先求出函数的导数，研究其单调性，确定出函数的最大值，利用最大值小于等于0求出参数λ的取值范围，即可求得其最小值；（II）根据（I）的证明，可取λ=，由于x＞0时，f（x）＜0得出，考察发现，若取x=，则可得出，以此为依据，利用放缩法，即可得到结论【解答】解：（I）由已知，f（0）=0，f′（x）==，∴f′（0）=0欲使x≥0时，f（x）≤0恒成立，则f（x）在（0，+∞）上必为减函数，即在（0，+∞）上f′（x）＜0恒成立，当λ≤0时，f′（x）＞0在（0，+∞）上恒成立，为增函数，故不合题意，若0＜λ＜时，由f′（x）＞0解得x ＜，则当0＜x ＜，f′（x）＞0，所以当0＜x ＜时，f（x）＞0，此时不合题意，若λ≥，则当x＞0时，f′（x）＜0恒成立，此时f（x）在（0，+∞）上必为减函数，所以当x＞0时，f（x）＜0恒成立，综上，符合题意的λ的取值范围是λ≥，即λ的最小值为（II）令λ=，由（I）知，当x＞0时，f（x）＜0，即取x=，则于是a2n﹣a n +=++…++====＞=ln2n﹣lnn=ln2所以【点评】本题考查了数列中证明不等式的方法及导数求最值的普通方法，解题的关键是充分利用已有的结论再结合放缩法，本题考查了推理判断的能力及转化化归的思想，有一定的难度。
2013年全国高考理科数学试题分类汇编三角函数
2013年全国高考理科数学试题分类汇编三角函数一、选择题1 ．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））已知210cos 2sin ,=+∈αααR ,则=α2tan A.34 B. 43C.43-D.34-【答案】C2 ．（2013年高考陕西卷（理））设△ABC的内角A , B , C 所对的边分别为a , b ,c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定【答案】B3 ．（2013年普通高等学校招生统一考试天津数学（理）试题（含答案））在△ABC中,,3,4AB BC ABC π∠==则sin BAC ∠ =【答案】C4 ．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））将函数sin(2)y x ϕ=+的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为(A) 34π (B) 4π(C)0 (D) 4π-【答案】B5 ．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=且a b >,则B ∠=A.6πB.3πC.23πD.56π【答案】A6 ．（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知函数()=cos sin 2f x x x ,下列结论中错误的是(A)()y f x =的图像关于(),0π中心对称 (B)()y f x =的图像关于直线2x π=对称(C)()f x 的最大值为2(D)()f x 既奇函数,又是周期函数【答案】C7 ．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））函数cos sin y x x x=+的图象大致为【答案】D8 ．（2013年高考四川卷（理））函数()2sin(),(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( )(A)2,3π- (B)2,6π- (C)4,6π- (D)4,3π【答案】A9 ．（2013年上海市春季高考数学试卷(含答案)）既是偶函数又在区间(0 )π，上单调递减的函数是( )(A)sin y x = (B)cos y x = (C)sin 2y x = (D)cos 2y x =【答案】B10．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））004cos50tan 40-=( )2D.1 【答案】C11．（2013年高考湖南卷（理））在锐角中ABC ∆,角,A B 所对的边长分别为,a b .若2sin ,a B A =则角等于 A.12π B.6π C.4π D.3π 【答案】D12．（2013年高考湖北卷（理））将函数()sin y x x x R =+∈的图像向左平移()0m m >个长度单位后,所得到的图像关于y 轴对称,则m 的最小值是( ) A.12π B. 6π C. 3πD.56π【答案】B 二、填空题13．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））ABC∆中,090=∠C ,M 是BC 的中点,若31sin =∠BAM ,则=∠BAC sin ________.14．（2013年高考新课标1（理））设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______【答案】. 15．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））如图ABC ∆中,已知点D 在BC 边上,AD ⊥AC,sin 3BAC AB AD ∠===则BD 的长为_______________16．（2013年上海市春季高考数学试卷(含答案)）函数2sin y x =的最小正周期是_____________【答案】2π17．（2013年高考四川卷（理））设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是_________.18．（2013年高考上海卷（理））若12cos cos sin sin,sin 2sin 223x y x y x y +=+=,则sin()________x y +=【答案】2sin()3x y +=. 19．（2013年高考上海卷（理））已知△ABC 的内角A 、B 、C 所对应边分别为a 、b 、c,若22232330a ab bc ++-=,则角C 的大小是_______________(结果用反三角函数值表示)【答案】1arccos 3Cπ=-20．（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知α是第三象限角,1sin 3a =-,则cot a =____________.【答案】21．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））函数)42sin(3π+=x y 的最小正周期为___________.【答案】π22．（2013年上海市春季高考数学试卷(含答案)）在ABC ∆中,角 A B C 、、所对边长分别为 a b c 、、,若5 8 60a b B ===，，,则b=_______ 【答案】723．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））设ABC ∆的内角,,A B C 所对边的长分别为,,a b c .若2b c a +=,则3sin 5sin ,A B =则角C =_____.【答案】π3224．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））设θ为第二象限角,若1tan()42πθ+=,则sin cos θθ+=________.【答案】5-25．（2013年高考江西卷（理））函数2sin 2sin y x x =+的最小正周期为T 为_________.【答案】π26．（2013年上海市春季高考数学试卷(含答案)）函数4sin 3cos y x x =+的最大值是_______________【答案】5 三、解答题27．（2013年高考北京卷（理））在△ABC中,a =3,b ,∠B =2∠A .(I)求cos A 的值; (II)求c 的值.【答案】解:(I)因为a =3,b ,∠B =2∠A . 所以在△ABC 中,由正弦定理得3sin sin 2A A =.所以2sin cos sin 3A A A =.故cos 3A =.(II)由(I)知cos A =,所以sin A ==.又因为∠B=2∠A,所以21cos 2cos 13B A =-=.所以sin B ==.在△ABC 中,sin sin()sin cos cos sin C A B A B A B =+=+=. 所以sin 5sin a Cc A==.28．（2013年高考陕西卷（理））已知向量1(cos ,),,cos2),2x x x x =-=∈a b R , 设函数()·f x =a b .(Ⅰ) 求f (x)的最小正周期.(Ⅱ) 求f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】解:(Ⅰ)()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x . 最小正周期ππ==22T . 所以),62sin()(π-=x x f 最小正周期为π.(Ⅱ)上的图像知，在，由标准函数时，当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈.]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f .所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为21,1-.29．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））在ABC 中,内角,,A B C 的对边分别是,,a b c ,且222a b c +=.(1)求C ; (2)设()()2cos cos cos cos cos A B A B ααα++==,求tan α的值.【答案】由题意得30．（2013年普通高等学校招生统一考试天津数学（理）试题（含答案））已知函数2()26sin cos 2cos 41,f x x x x x x π⎛⎫=++- ⎪+⎝⎭∈R .(Ⅰ) 求f (x )的最小正周期;(Ⅱ) 求f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】31．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））设向量)(),sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I)若.a b x =求的值； (II)设函数()(),.f x a b f x =求的最大值【答案】32．（2013年高考上海卷（理））(6分+8分)已知函数()2sin()f x x ω=,其中常数0ω>;(1)若()y f x =在2[,]43ππ-上单调递增,求ω的取值范围;(2)令2ω=,将函数()y f x =的图像向左平移6π个单位,再向上平移1个单位,得到函数()y g x =的图像,区间[,]a b (,a b R ∈且a b <)满足:()y g x =在[,]a b 上至少含有30个零点,在所有满足上述条件的[,]a b 中,求b a -的最小值.【答案】(1)因为0ω>,根据题意有34202432ππωωππω⎧-≥-⎪⎪⇒<≤⎨⎪≤⎪⎩ (2) ()2sin(2)f x x =,()2sin(2())12sin(2)163g x x x ππ=++=++1()0sin(2)323g x x x k πππ=⇒+=-⇒=-或7,12x k k Z ππ=-∈,即()g x 的零点相离间隔依次为3π和23π,故若()y g x =在[,]a b 上至少含有30个零点,则b a -的最小值为2431415333πππ⨯+⨯=. 33．（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=. (I)求B (II)若1sin sin 4A C =,求C . 【答案】34．（2013年高考四川卷（理））在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且232cos cos sin()sin cos()25A B B A B B A C ---++=-. (Ⅰ)求cos A 的值;(Ⅱ)若a =5b =,求向量BA 在BC 方向上的投影.【答案】解:()I 由()()232cos cos sin sin cos 25A B B A B B A C ---++=-,得 ()()3cos 1cos sin sin cos 5A B B A B B B -+---=-⎡⎤⎣⎦, 即()()3cos cos sin sin 5A B B A B B ---=-,则()3cos 5A B B -+=-,即3cos 5A =-()II 由3cos ,05A A π=-<<,得4sin 5A =,由正弦定理,有sin sin a bA B=,所以,sin sin 2b A B a ==. 由题知a b >,则A B >,故4B π=.根据余弦定理,有(22235255c c ⎛⎫=+-⨯⨯- ⎪⎝⎭,解得1c =或7c =-(舍去).故向量BA 在BC 方向上的投影为cos BA B =35．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））设△ABC 的内角,,A B C 所对的边分别为,,a b c ,且6a c +=,2b =,7cos 9B =. (Ⅰ)求,a c 的值; (Ⅱ)求sin()A B -的值.【答案】解:(Ⅰ)由余弦定理2222cos b a c ac B =+-,得()222(1cos )b ac ac B =+-+,又6a c +=,2b =,7cos 9B =,所以9ac =,解得3a =,3c =.(Ⅱ)在△ABC 中,sin 9B ==,由正弦定理得sin sin 3a B A b ==,因为a c =,所以A 为锐角,所以1cos 3A ==因此sin()sin cos cos sin A B A B A B -=-=.36．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））已知函数()4cos sin (0)4f x x x πϖϖϖ⎛⎫=⋅+> ⎪⎝⎭的最小正周期为π.(Ⅰ)求ϖ的值; (Ⅱ)讨论()f x 在区间[]0,2上的单调性.【答案】解:(Ⅰ)2)42sin(2)12cos 2(sin 2)cos (sin cos 22++=++=+⇒πωωωωωωx x x x x x122=⇒=⇒ωπωπ.所以1,2)42sin(2)(=++=ωπx x f(Ⅱ) ；解得，令时，当8242]4,4[)42(]2,0[ππππππππ==++∈+∈x x x x 所以.]28[]8,0[)(上单调递减，上单调递增；在在πππx f y =37．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））已知函数()sin()(0,0)f x x ωϕωϕπ=+><<的周期为π,图像的一个对称中心为(,0)4π,将函数()f x 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移2π个单位长度后得到函数()g x 的图像.(1)求函数()f x 与()g x 的解析式;(2)是否存在0(,)64x ππ∈,使得0000(),(),()()f x g x f x g x 按照某种顺序成等差数列?若存在,请确定0x 的个数;若不存在,说明理由.(3)求实数a 与正整数n ,使得()()()F x f x ag x =+在(0,)n π内恰有2013个零点.【答案】解:(Ⅰ)由函数()sin()f x x ωϕ=+的周期为π,0ω>,得2ω=又曲线()y f x =的一个对称中心为(,0)4π,(0,)ϕπ∈故()sin(2)044f ππϕ=⨯+=,得2πϕ=,所以()cos 2f x x =将函数()f x 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得cos y x =的图象,再将cos y x =的图象向右平移2π个单位长度后得到函数()sin g x x =(Ⅱ)当(,)64x ππ∈时,1sin 2x <<,10cos 22x << 所以sin cos 2sin cos 2x x x x >>问题转化为方程2cos 2sin sin cos 2x x x x =+在(,)64ππ内是否有解设()sin sin cos 22cos 2G x x x x x =+-,(,)64x ππ∈则()cos cos cos 22sin 2(2sin )G x x x x x x '=++-因为(,)64x ππ∈,所以()0G x '>,()G x 在(,)64ππ内单调递增又1()064G π=-<,()04G π=> 且函数()G x 的图象连续不断,故可知函数()G x 在(,)64ππ内存在唯一零点0x ,即存在唯一的0(,)64x ππ∈满足题意(Ⅲ)依题意,()sin cos 2F x a x x =+,令()sin cos 20F x a x x =+=当sin 0x =,即()x k k Z π=∈时,cos 21x =,从而()x k k Z π=∈不是方程()0F x =的解,所以方程()0F x =等价于关于x 的方程cos 2sin xa x=-,()x k k Z π≠∈ 现研究(0,)(,2)x πππ∈U 时方程解的情况 令cos 2()sin xh x x=-,(0,)(,2)x πππ∈U 则问题转化为研究直线y a =与曲线()y h x =在(0,)(,2)x πππ∈U 的交点情况22cos (2sin 1)()sin x x h x x +'=,令()0h x '=,得2x π=或32x π= 当x 变化时,()h x 和()h x '变化情况如下表当0x >且x 趋近于0时,()h x 趋向于-∞当x π<且x 趋近于π时,()h x 趋向于-∞ 当x π>且x 趋近于π时,()h x 趋向于+∞ 当2x π<且x 趋近于2π时,()h x 趋向于+∞故当1a >时,直线y a =与曲线()y h x =在(0,)π内有无交点,在(,2)ππ内有2个交点;当1a <-时,直线y a =与曲线()y h x =在(0,)π内有2个交点,在(,2)ππ内无交点;当11a -<<时,直线y a =与曲线()y h x =在(0,)π内有2个交点,在(,2)ππ内有2个交点由函数()h x 的周期性,可知当1a ≠±时,直线y a =与曲线()y h x =在(0,)n π内总有偶数个交点,从而不存在正整数n ,使得直线y a =与曲线()y h x =在(0,)n π内恰有2013个交点;当1a =±时,直线y a =与曲线()y h x =在(0,)(,2)πππU 内有3个交点,由周期性,20133671=⨯,所以67121342n =⨯=综上,当1a =±,1342n =时,函数()()()F x f x ag x =+在(0,)n π内恰有2013个零点38．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分14分.已知(cos ,sin )(cos ,sin )a b ααββ=＝，,παβ<<<0. (1)若||2a b -=,求证:a b ⊥;(2)设(0,1)c =,若a b c +=,求βα,的值.【答案】解:(1)∵2||=- ∴2||2=- 即()22222=+-=-,又∵1sin cos ||2222=+==ααa a ,1sin cos ||2222=+==ββb b ∴222=-∴0=b a ∴b ⊥a(2)∵)1,0()sin sin ,cos (cos b a =++=+βαβα ∴⎩⎨⎧=+=+1sin sin 0cos cos βαβα即⎩⎨⎧-=-=βαβαsin 1sin cos cos 两边分别平方再相加得:βsin 221-= ∴21sin =β ∴21sin =α ∵παβ<<<0 ∴πβπα61,65==39．（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））已知函数()12f x x π⎛⎫=- ⎪⎝⎭,x ∈R .(Ⅰ) 求6f π⎛⎫- ⎪⎝⎭的值; (Ⅱ) 若3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,求23f πθ⎛⎫+ ⎪⎝⎭.【答案】(Ⅰ)1661244f πππππ⎛⎫⎛⎫⎛⎫-=--=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;(Ⅱ) 222cos 2sin 233124f ππππθθθθθ⎛⎫⎛⎫⎛⎫+=+-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为3cos 5θ=,3,22πθπ⎛⎫∈⎪⎝⎭,所以4sin 5θ=-,所以24sin 22sin cos 25θθθ==-,227cos 2cos sin 25θθθ=-=- 所以23f πθ⎛⎫+ ⎪⎝⎭cos2sin 2θθ=-72417252525⎛⎫=---= ⎪⎝⎭. 40．（2013年高考湖南卷（理））已知函数2()sin()cos().()2sin 632x f x x x g x ππ=-+-=.(I)若α是第一象限角,且()f α=求()g α的值; (II)求使()()f x g x ≥成立的x 的取值集合.【答案】解:(I)533sin 3)(sin 3sin 23cos 21cos 21sin 23)(==⇒=++-=ααf x x x x x x f .51cos 12sin 2)(,54cos )2,0(,53sin 2=-===⇒∈=⇒ααααπααg 且(II)21)6sin(cos 21sin 23cos 1sin 3)()(≥+=+⇒-≥⇒≥πx x x x x x g x f Z k k k x k k x ∈+∈⇒++∈+⇒],322,2[]652,62[6ππππππππ 41．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分16分.如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲.乙两位游客从A 处下山,甲沿AC匀速步行,速度为min /50m .在甲出发min 2后,乙从A 乘缆车到B ,在B 处停留min 1后,再从匀速步行到C .假设缆车匀速直线运动的速度为min /130m ,山路AC 长为m 1260,经测量,1312cos =A ,53cos =C . (1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?【答案】解:(1)∵1312cos =A ,53cos =C ∴），（、20π∈C A ∴135sin =A ,54sin =C∴[]6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B ）（）（π CB A根据sinB sinC AC AB =得m C ACAB 1040sin sinB==(2)设乙出发t 分钟后,甲.乙距离为d,则1312)50100(1302)50100()130(222⨯+⨯⨯-++=t t t t d ∴)507037(20022+-=t t d∵13010400≤≤t 即80≤≤t ∴3735=t 时,即乙出发3735分钟后,乙在缆车上与甲的距离最短.(3)由正弦定理sinBsinA ACBC =得50013565631260sin sinB ===A AC BC (m) 乙从B 出发时,甲已经走了50(2+8+1)=550(m),还需走710 m 才能到达C设乙的步行速度为V min /m ,则350710500≤-v ∴3507105003≤-≤-v ∴14625431250≤≤v ∴为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在⎥⎦⎤⎢⎣⎡14625,431250范围内 法二:解:(1)如图作BD ⊥CA 于点D , 设BD =20k ,则DC =25k ,AD =48k ,AB =52k ,由AC =63k =1260m,知:AB =52k =1040m.(2)设乙出发x 分钟后到达点M , 此时甲到达N 点,如图所示. 则:AM =130x ,AN =50(x +2),由余弦定理得:MN 2=AM 2+AN 2-2 AM ·AN cos A =7400 x 2-14000 x +10000, 其中0≤x ≤8,当x =3537 (min)时,MN 最小,此时乙在缆车上与甲的距离最短.(3)由(1)知:BC =500m,甲到C 用时:126050 =1265(min).若甲等乙3分钟,则乙到C 用时:1265 +3=1415 (min),在BC 上用时:865(min) .此时乙的速度最小,且为:500÷865 =125043m/min.若乙等甲3分钟,则乙到C 用时:1265 -3=1115 (min),在BC 上用时:565(min) .此时乙的速度最大,且为:500÷565 =62514 m/min.故乙步行的速度应控制在[125043 ,62514]范围内.42．（2013年高考湖北卷（理））在ABC∆中,角A ,B ,C 对应的边分别是a ,b ,c .已知()cos23cos 1A B C -+=. (I)求角A 的大小;(II)若ABC ∆的面积S =,5b =,求sin sin B C 的值.【答案】解:(I)由已知条件得:cos23cos 1A A +=CB AD MN22cos 3cos 20A A ∴+-=,解得1cos 2A =,角60A =︒ (II)1sin 2S bc A ==4c ⇒=,由余弦定理得:221a =,()222228sin a R A ==25sin sin 47bc B C R ∴==43．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））△ABC在内角,,A B C 的对边分别为,,a b c ,已知cos sin a b C c B =+. (Ⅰ)求B ;(Ⅱ)若2b =,求△ABC 面积的最大值.【答案】44．（2013年高考新课标1（理））如图,在△ABC中,∠ABC=90°,AB=3 ,BC=1,P为△ABC内一点,∠BPC=90°(1)若PB=12,求PA;(2)若∠APB=150°,求t an∠PBA【答案】(Ⅰ)由已知得,∠PBC=o 60,∴∠PBA=30o ,在△PBA 中,由余弦定理得2PA=o 1132cos3042+-=74; (Ⅱ)设∠PBA=α,由已知得,PB=sin α,在△PBA 中,由正弦定理得o sin sin(30)αα=-,化简得4sin αα=, ∴tan α,∴tan PBA ∠. 45．（2013年上海市春季高考数学试卷(含答案)）本题共有2个小题,第一小题满分4分,第二小题满分9分.在平面直角坐标系xOy 中,点A 在y 轴正半轴上,点n P 在x 轴上,其横坐标为n x ,且{}n x 是首项为1、公比为2的等比数列,记1n n n P AP θ+∠=,n N *∈.(1)若31arctan 3θ=,求点A 的坐标;(2)若点A的坐标为(0,求n θ的最大值及相应n 的值.[解](1)(2)【答案】[解](1)设(0 )A t ，,根据题意,12n n x -=.由31arctan 3θ=,知31tan 3θ=, 而3443343223443()4tan tan()321x x t x x t t t OAP OAP x x t x x t t tθ--=∠-∠===+⋅++⋅, 所以241323t t =+,解得4t =或8t =. 故点A 的坐标为(0 4)，或(0 8)，.(2)由题意,点n P 的坐标为1(2 0)n -，,1tan n n OAP -∠=111212tan tan()12n n n n n n n n OAP OAP θ--+-=∠-∠===+.因为2n n ≥所以tan 4n θ≤=,当且仅当2n n =即4n =时等号成立. 易知0 tan 2n y x πθ<<=，在(0 )2π，上为增函数, 因此,当4n =时,n θ最大,其最大值为arctan4. 46．（2013年高考江西卷（理））在△ABC 中,角A,B,C 所对的边分别为a,b,c,已知cosC+(conA-sinA)cosB=0.(1) 求角B 的大小;若a+c=1,求b 的取值范围【答案】解:(1)由已知得cos()cos cos cos 0A B A B A B -++=即有sin sin cos 0A B A B = 因为sin 0A ≠,所以sin 0B B =,又cos 0B ≠,所以tan B =又0B π<<,所以3B π=. (2)由余弦定理,有2222cos b a c ac B =+-. 因为11,cos 2a c B +==,有22113()24b a =-+.又01a <<,于是有2114b ≤<,即有112b ≤<.。
2013高考数学(理科)小题限时训练4
2013高考数学（理科）小题限时训练四15小题共75分，时量：45分钟，考试时间：2012年8月30日第6节 姓名一、选择题：本大题共8小题，每小题5分，共40分．1．命题：00R,21x x ∃∈≥的否定是A ．00R,21x x ∃∈<B ．00R,21x x ∃∉≥C ．R,21x x ∀∈≥D ．R,21x x ∀∈<2．下列函数中，在区间(0，2)上为增函数的是A ．y ＝－x ＋1B ．12y x = C ．y ＝x 2－4x ＋5 D ．1y x=3．设全集U ＝R ，集合A ＝{x | x(x ＋3)＜0}，B ＝{x | x ＜－1}，则右图中阴影部分表示的集合为A ．{x |－3＜x ＜－1}B ．{x |－1≤x ＜0}C ．{x |－3＜x ＜0}D ．{x |－1＜x ＜0}4．方程log 3x ＋x －3＝0的实数解所在的区间是A ．(0，1)B ．A ．(1，2)C ．(2，3)D ．(3，4)5．设函数f(x)是定义在R 上的以3为周期的奇函数，若f(1)＞1且23(2)1a f a -=+，则 A ．23a < B ．213a a <≠-且 C ．213a a ><-或 D ．213a -<< 6．在一次数学实验中，运用计算器采集到如下一组数据：则y 关于x 的函数关系与下列最接近的函数(其中a 、b 、c 为待定系数)是A ．y ＝a ＋bxB ．y ＝a ＋b xC ．y ＝ax 2＋bD ．b y a x=+ 7．已知函数f(x)＝(x －a)(x －b)(其中a ＞b)，若f(x)的图象如右图所示，则函数g(x)＝a x ＋b 的图象大致为A B C D8．已知函数13()ln 144f x x x x=-+-，g(x)＝x 2－2bx ＋4，若对任意x 1∈(0，2)，存在x 2∈[1，2]，使f(x 1)≥g(x 2)，则实数b 的取值范围是A ．17(2,]8B ．[1，＋∞]C ．17[,)8+∞ D ．[2，＋∞] 二、填空题：本大题共7小题，每小题5分，共35分． 9．幂函数f(x)＝x α(α为常数)的图象经过，则f(x)的解析式是 ．10．已知f(x)是偶函数，它在[0，＋∞)上是 增函数，若f(lgx)＜f(1)，则x 的取值范围是 ．11．如图所示的程序框图运行后，输出的S 的值是 ．12．若函数()(4)2(1)2xa f x a x x ⎧⎪=⎨-+≤⎪⎩是R 上的单调递增函数，则实数a 的取值范围是 ．13．先作与函数1ln 3y x=-的图象关于原点对称的图象，再将所得图象向右平移3个单位得到图象C 1．又y ＝f(x)的图象C 2与C 1关于y ＝x 对称，则y ＝f(x)的解析式是 ．14．已知函数f(x)的定义域为[－1，5]，部分对应值如下表：f(x)的导函数y ＝f ′(x)的图象如图所示：则f(x)的单调递增区间是 ；f(x)的最大值是 ．15．定义min{p ，q}表示p 、q 中的较小者，若函数214()min{log ,3log }f x x x =+，则满足f(x)＜2的x 的取值范围是 ．参考答案DBBC DBAC9．12()f x x10．1(,10)1011． 31 12． [4，8)13． y＝e x 14． [－1，0]和[2，4] 2 15． (0，4)∪(4，＋∞)。
三年高考2013_2015高考数学试题分项版专题07不等式理(含解析)
第七章 不等式一、选择题1. 【2013高考北京理第8题】设关于x ，y 的不等式组210,0,0x y x m y m -+>⎧⎪+<⎨⎪->⎩表示的平面区域内存在点P (x 0，y 0)，满足x 0－2y 0＝2，求得m 的取值范围是( )． A ．4,3⎛⎫-∞ ⎪⎝⎭ B ．1,3⎛⎫-∞ ⎪⎝⎭ C ．2,3⎛⎫-∞-⎪⎝⎭ D ．5,3⎛⎫-∞- ⎪⎝⎭ 【答案】C【名师点睛】本题考查线性规划有关知识,本题属于基础题，近几年高考线性规划为必考基础题，线性规划考试题型有两种，一种是求目标函数的最值或范围，但目标函数变化多样，有截距型、距离型、斜率型等；另一种是线性规划逆向思维型，提供目标函数的最值，反求参数的范围，本题属于第二类，对可行域提出相应的要求，求参数m 的取值范围.2. 【2014高考北京理第6题】若x 、y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩，且z y x =-的最小值为4-，则k 的值为（ ）A ．2B ．2-C ．12 D ．12-【名师点睛】本题考查线性规划有关知识,本题属于基础题，近几年高考线性规划为必考基础题，线性规划考试题型有两种，一种是类似本题求目标函数的最值或范围，但目标函数变化多样，有截距型、距离型、斜率型等；另一种是线性规划逆向思维型，提供目标函数的最值，反求参数.3. 【2015高考北京，理2】若x ，y 满足010x y x y x -⎧⎪+⎨⎪⎩≤，≤，≥，则2z x y =+的最大值为（ ）A ．0B ．1C ．32D ．2【答案】D【解析】如图，先画出可行域，由于2z x y =+，则1122y x z =-+，令0Z =，作直线12y x =-，在可行域中作平行线，得最优解(0,1)，此时直线的截距最大，Z 取考点定位：本题考点为线性规划的基本方法【名师点睛】本题考查线性规划解题的基本方法，本题属于基础题,要求依据二元一次不等式组准确画出可行域，利用线性目标函数中直线的纵截距的几何意义，令0z =，画出直线12y x =-，在可行域内平移该直线，确定何时z 取得最大值，找出此时相应的最优解，依据线性目标函数求出最值，这是最基础的线性规划问题.4.【2015高考广东，理6】若变量x ，y 满足约束条件⎪⎩⎪⎨⎧≤≤≤≤≥+2031854y x y x 则y x z 23+=的最小值为（ ） A ．531 B. 6 C. 523 D. 4 【答案】C ．【名师点睛】本题主要考查学生利用二元一次不等式组所表示的平面区域解决线性规划的应用，数形结合思想的应用和运算求解能力，本题关键在于正确作出二元一次不等式组所表示的可行域和准确判断目标函数直线出取得最小值的可行解，属于容易题．5. 【2014高考广东卷.理.3】若变量x .y 满足约束条件11y xx y y ≤⎧⎪+≤⎨⎪≤-⎩，且2z x y =+的最大值和最小值分别为M 和m ，则M m -=( )A .8B .7C .6D .5【答案】C【考点定位】本题考查线性规划中线性目标函数的最值，属于中等题.【名师点晴】本题主要考查的是线性规划，属于中等题．线性规划类问题的解题关键是先正确画出不等式组所表示的平面区域，然后确定目标函数的几何意义，通过数形结合确定目标函数何时取得最值．解题时要看清楚是求“最大值”还是求“最小值”，否则很容易出现错误；画不等式组所表示的平面区域时要通过特殊点验证，防止出现错误．6. 【 2013湖南4】若变量,x y 满足约束条件211y xx y y ≤⎧⎪+≤⎨⎪≥-⎩，2x y +则的最大值是A ．5-2B ．0C ．53D ．52【答案】 C【解析】 区域为三角形，直线u = x + 2y 经过三角形顶点最大时，35)32,31(=u 选C【考点定位】线性规划【名师点睛】本题给出二元一次不等式组，求目标函数z 的最大值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题，解决问题的关键是正确做出可行域，根据目标觳觫性质进行分析计算即可.7.【2015高考山东，理5】不等式152x x ---<的解集是（ ）（A ）（-，4） （B ）（-，1） （C ）（1，4） （D ）（1，5） 【答案】A【名师点睛】本题考查了含绝对值的不等式的解法，重点考查学生利用绝对值的意义将含绝对值的不等式转化为不含绝对值的不等式（组）从而求解的能力，本题属中档题.8. 【2015高考山东，理6】已知,x y 满足约束条件020x y x y y -≥⎧⎪+≤⎨⎪≥⎩，若z ax y =+的最大值为4，则a = （ ）（A ）3 （B ）2 （C ）-2 （D ）-3 【答案】B【解析】不等式组020x y x y y -≥⎧⎪+≤⎨⎪≥⎩在直角坐标系中所表示的平面区域如下图中的阴影部分所示，若z ax y =+的最大值为4，则最优解可能为1,1x y == 或2,0x y == ，经检验，2,0x y ==是最优解，此时2a = ；1,1x y ==不是最优解.故选B.【考点定位】简单的线性规划问题.【名师点睛】本题考查了简单的线性规划问题，通过确定参数a 的值，考查学生对线性规划的方法理解的深度以及应用的灵活性，意在考查学生利用线性规划的知识分析解决问题的能力.9. 【2014山东.理9】 已知,x y 满足约束条件10230x y x y --≤⎧⎨--≥⎩，当目标函数(0,0)z ax by a b =+>>在该约束条件下取到最小值22a b +的最小值为（ ）【答案】B【名师点睛】本题考查简单线性规划、二次函数的图象和性质.此类问题的基本解法是“图表法”，即通过画可行域及直线ax ＋by =0，平移直线ax ＋by =0，观察其在y 轴的纵截距变化情况，得出最优解.要注意y 的系数正负不同时，结论恰好相反.本题属于小综合题，由以往单纯考查线性规划问题，转变成此类题，增大了解题的难度，也给人耳目一新的感觉.10. 【2013山东，理12】设正实数x ，y ，z 满足x 2－3xy ＋4y 2－z ＝0，则当xyz取得最大值时，212x y z+-的最大值为( )． A ．0 B ．1 C ．94D ．3【答案】：B【解析】：由x 2－3xy ＋4y 2－z ＝0得2234x xy y z -+，即xy z≤1，当且仅当x 2＝4y 2时成立，又x ，y 为正实数，故x ＝2y .此时将x ＝2y 代入x 2－3xy ＋4y 2－z ＝0得z ＝2y 2，所以222121211+1x y z y y y ⎛⎫+-=-+=-- ⎪⎝⎭，当1=1y ，即y ＝1时，212x y z+-取得最大值为1，故选B. 【名师点睛】本题考查基本不等式、二次函数性质等.解答本题的关键，是利用转化与化归思想，利用分组结合法，创造应用基本不等式的条件，通过适当的代换，逐步转化成可用二次函数的图象和性质等有关结论解答的情形.本题属于能力题，是一道难题.在考查基本不等式、二次函数性质等基础知识的同时，考查了考生的逻辑推理能力、运算能力、转化与化归思想.11.【2015高考陕西，理9】设()ln ,0f x x a b =<<，若p f =，()2a bq f +=，1(()())2r f a f b =+，则下列关系式中正确的是（ ） A ．q r p =< B ．q r p => C ．p r q =<D ．p r q => 【答案】C【名师点晴】本题主要考查的是基本不等式和基本初等函数的单调性，属于容易题．解题时一定要注意检验在使用基本不等式求最值中是否能够取得等号，否则很容易出现错误．本题先判断2a b+ 12. 【2015高考陕西，理10】某企业生产甲、乙两种产品均需用A ，B 两种原料．已知生产1吨每种产品需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为（ ）A ．12万元B ．16万元C ．17万元D ．18万元【答案】D【名师点晴】本题主要考查的是线性规划，属于容易题．线性规划类问题的解题关键是先正确画出不等式组所表示的平面区域，然后确定目标函数的几何意义，通过数形结合确定目标函数何时取得最值．解题时要看清楚是求“最大值”还是求“最小值”，否则很容易出现错误；画不等式组所表示的平面区域时要通过特殊点验证，防止出现错误．13. 【2014新课标，理9】设x,y满足约束条件70310350x yx yx y+-⎧⎪-+⎨⎪--⎩≤≤≥，则2z x y=-的最大值为（）A. 10B. 8C. 3D. 2【答案】B【名师点睛】本题考查了线性规划问题的解法，本题属于基础题，要求学生根据所给二元一次不等式组画所表示平面区域，然后根据目标函数的几何意义，由图形直观地观察得到目标函数的最优解，从而求出目标函数的最大值，本题有两个关键点：一是平面区域必须作正确，且要有一定的精度；二是目标函数的几何意义必须理解正确才能正确作出答案.14. 【2013课标全国Ⅱ，理9】已知a ＞0，x ，y 满足约束条件1,3,3.x x y y a x ≥⎧⎪+≤⎨⎪≥(-)⎩若z ＝2x ＋y的最小值为1，则a ＝( )．A ．14 B ．12C ．1D ．2 【答案】：B【名师点睛】本题考查线性规划问题的解法，本题属于基础题，要求学生根据所给二元一次不等式组画所表示平面区域，然后根据目标函数的几何意义，由图形直观地观察得到目标函数的最优解，从而用参数a 表示出目标函数的最小值，本题有两个关键点：一是平面区域必须作正确，且要有一定的精度；二是目标函数的几何意义必须理解正确才能正确作出答案. 15. 【2014四川，理4】若0a b >>，0c d <<，则一定有（ ） A ．a b c d > B ．a b c d < C ．a b d c > D ．a b d c< 【答案】D 【解析】试题分析：110,0,0c d c d d c<<∴->->->-> ，又0,0,a b a ba b d c d c>>∴->->∴<.选D 【考点定位】不等式的基本性质.【名师点睛】不等式的基本性质:同向同正可乘性0a b ac bd c d >>⎧⇒>⎨>>⎩,可推：00a b a bc d d c>>⎧⇒>⎨>>⎩. 16.【2015高考四川，理9】如果函数()()()()21281002f x m x n x m n =-+-+≥≥，在区间122⎡⎤⎢⎥⎣⎦，上单调递减，则mn 的最大值为（ ）（A ）16 （B ）18 （C ）25 （D ）812【答案】B【考点定位】函数与不等式的综合应用.【名师点睛】首先弄清抛物线的开口方向和对称轴，结合所给单调区间找到m 、n 满足的条件，然后利用基本不等式求解.本题将函数的单调性与基本不等式结合考查，检测了学生综合运用知识解题的能力.在知识的交汇点命题，这是高考的一个方向，这类题往往以中高档题的形式出现.17. 【2014课标Ⅰ，理9】不等式组1,24,x y x y +≥⎧⎨-≤⎩的解集为D,有下面四个命题：1:(x,y)D,x 2y 2p ∀∈+≥-， 2:(x,y)D,x 2y 2p ∃∈+≥， 3:(x,y)D,x 2y 3p ∀∈+≤ 4:(x,y)D,x 2y 1p ∃∈+≤-，其中的真命题是（ ）A ．23,p pB ．12,p pC ．13,p pD ．14,p p 【答案】B【解析】画出可行域，如图所示，设2x y z +=，则1y x 22z=-+，当直线l 过点(2,1)A -时，z 取到最小值，min 22(1)0z =+⨯-=，故2x y +的取值范围为20x y +≥，所以正确的命题是12,p p ，选B ．【考点定位】1、线性规划；2、存在量词和全称量词．【名师点睛】本题考查命题的真假判断与应用，线性规划和存在量词和全称量词，着重考查考生的数形结合能力，熟练作图和正确分析是解决本题的关键，本题的综合性很强. 18.【2013高考重庆理第3－6≤a ≤3)的最大值为( )． A ．9 B ．92 C ．3 D ．2【答案】B【考点定位】基本不等式或配方法求最值.【名师点睛】本题考查了用基本不等式或配方法求最值，本题属于基础题，注意自变量的取值范围，在用基本不等式求最值时注意一正、二定、三相等缺一不可.19. 【2014，安徽理5】y x ,满足约束条件⎪⎩⎪⎨⎧≥+-≤--≤-+02202202y x y x y x ，若ax y z -=取得最大值的最优解不唯一．．．，则实数a 的值为 （ ） A ，121-或 B ．212或 C ．2或1 D ．12-或 【答案】D ．考点：1．线性规划求参数的值．【名师点睛】线性规划问题中的目标函数一般都有明显的几何意思，如直线在y 轴上的截距、斜率、距离等，要根据目标函数的几何意义灵活应用.对于含参数的目标函数，如z ax by =+型，可变形为斜截式，进而考查y 轴上截距的取值范围.20. 【2013，安徽理6】已知一元二次不等式()<0f x 的解集为{}1|<-1>2x x x 或，则(10)>0x f 的解集为（ ）A ．{}|<-1>lg2x x x 或B ．{}|-1<<lg2x xC ．{}|>-lg2x xD ．{}|<-lg2x x【答案】D ．【命题立意】考查不等式的解法．【名师点睛】对于一元二次不等式求解的问题，首先要考虑到二次项前面系数的正负，通俗的解法是将二次项前系数变为正数，然后来进行求解.另外，要熟悉指数运算和对数运算性质，如0112,22,1log ,0log 1a a a ====.21. 【2013，安徽理9】在平面直角坐标系中，o 是坐标原点，两定点,A B 满足2,OA OB OA OB === 则点集,1,,|P OP OA OB R λμλμλμ==++≤∈ 所表示的区域的面积是 （ ）A．．．．【答案】D ． 【解析】方法一：由2,OA OB OA OB === 得1cos ,2OA OB OA OB OA OB ⋅==，所以,OA OB 的夹角是60°．设(),P x y ，A （2，0），则(B ，所以由OP OA OB λμ=+得2x y λμ=+⎧⎪⎨=⎪⎩，解得12x λμ⎧=-⎪⎪⎨⎪=⎪⎩代入1λμ+≤得112x ≤．等价于0112y x ⎧≤≤⎪⎨+≤⎪⎩或0112y y x ⎧⎪≤⎪⎪≤⎨⎪⎪≤⎪⎩或0112y y x ⎧⎪≥⎪⎪≥⎨⎪⎪-≤⎪⎩或0112y x ⎧≥≥⎪⎨-+≤⎪⎩，对应的平面区域是一个以(((),(2,0),1,,2,0--为顶点的矩形，边长分别是2和，所以面积为D ． 方法二：考察三点共线向量知识:1,,,,=++=μλμλ其中是线外一点则三点共线若PC PB PA P C B A ．32cos 4cos ||||πθθθ=⇒==⋅⋅=⋅．建立直角坐标系，设A(2，0)，).(10,0).31(含边界内在三角形时，，则当OAB P B ≤+≥≥μλμλ344=⨯=的面积三角形的面积根据对称性，所求区域OAB S ，所以选D ．【命题立意】考查向量的运算以及不等式组对应的平面区域．【名师点睛】要解决好本题，需要熟知平面向量中的一个结论.,A B 两点确定一条直线AB ，P 是线外一点，若PC PA PB λμ=+且1λμ+=，则C 点在直线AB 上；若PC PA PB λμ=+且1λμ+<，则C 点在直线AB 与P 点构成的区域内；若PC PA PB λμ=+且1λμ+>，则C 点在直线AB 与P 点构成的区域外，并与P 点分别在直线AB 两侧.22. 【2013天津，理2】设变量x ，y 满足约束条件360,20,30,x y x y y +-≥⎧⎪--≤⎨⎪-≤⎩则目标函数z ＝y －2x的最小值为( )．A ．－7B ．－4C ．1D ．2 【答案】A考点定位：本题考点为利用线性规划的基本方法，求目标函数的最值.【名师点睛】本题考查线性规划解题的基本方法，本题属于基础题,要求依据二元一次不等式组准确画出可行域，利用线性目标函数中直线的纵截距的几何意义，令0z =，画出直线=2y x，在可行域内平移该直线，确定何时z 取得最大值，找出此时相应的最优解，依据线性目标函数求出最值，这是最基础的线性规划问题. 线性规划考试题型有两种，一种是求目标函数的最值或范围，但目标函数变化多样，有截距型、距离型、斜率型等；另一种是线性规划逆向思维型，提供目标函数的最值，反求参数的范围，本题属于第二类，对可行域提出相应的要求，求参数的取值范围.23. 【2014天津，理2】设变量x ，y 满足约束条件0,20,12,y x y y x +-⎧≥--≤≥⎪⎨⎪⎩则目标函数2z x y=+的最小值为 （ ）（A ）2 （B ）3 （C ）4 （D ）5 【答案】B ．【名师点睛】本题考查线性规划解题的基本方法，本题属于基础题,要求依据二元一次不等式组准确画出可行域，利用线性目标函数中直线的纵截距的几何意义，令0z =，画出直线=2y x，在可行域内平移该直线，确定何时z 取得最大值，找出此时相应的最优解，依据线性目标函数求出最值，这是最基础的线性规划问题. 线性规划考试题型有两种，一种是求目标函数的最值或范围，但目标函数变化多样，有截距型、距离型、斜率型等；另一种是线性规划逆向思维型，提供目标函数的最值，反求参数的范围，本题属于第二类，对可行域提出相应的要求，求参数的取值范围.24. 【2015高考天津，理2】设变量,x y 满足约束条件2030230x x y x y +≥⎧⎪-+≥⎨⎪+-≤⎩ ，则目标函数6z x y =+的最大值为( )（A ）3 （B ）4 （C ）18 （D ）40 【答案】C【解析】不等式2030230x x y x y +≥⎧⎪-+≥⎨⎪+-≤⎩所表示的平面区域如下图所示，当6z x y =+所表示直线经过点(0,3)B 时，z 有最大值18.【考点定位】线性规划.【名师点睛】本题主要考查线性规划与二元一次不等式的几何意义，将二元一次不等式（组）的几何意义与求线性目标函数的最值问题结合在一起，考查线性相关问题和数形结合的数学思想，同时考查学生的作图能力与运算能力.本题中不等式所表示的平面区域为不封闭区域，与平时教学中的练习题有出入，是易错问题.25.【2014湖北卷7】由不等式组⎪⎩⎪⎨⎧≤--≥≤0200x y y x 确定的平面区域记为1Ω，不等式组⎩⎨⎧-≥+≤+21y x y x ，确定的平面区域记为2Ω，在1Ω中随机取一点，则该点恰好在2Ω内的概率为（ ） A.81 B.41 C. 43 D.87 【答案】D考点：不等式组表示的平面区域，面积型的几何概型，中等题.【名师点睛】将一元二次不等式组所表示的平面区域和几何概型联系在一起，重点考查几何概型，其解题的关键是正确地画出一元二次不等式组所表示的平面区域.能较好的考查学生准确作图能力和灵活运用基础知识解决实际问题的能力.26. 【2015高考湖北，理10】设x ∈R ，[]x 表示不超过x 的最大整数. 若存在实数t ，使得[]1t =，2[]2t =，…，[]n t n = 同时成立．．．．，则正整数n 的最大值是（ ） A ．3 B ．4 C ．5 D ．6 【答案】B【名师点睛】这类问题一般有两种：[]x 表示不超过x 的最大整数；{}x 表示不小于x 的最大整数. 应注意区别.27.【2015高考福建，理5】若变量,x y满足约束条件20,0,220,x yx yx y+≥⎧⎪-≤⎨⎪-+≥⎩则2z x y=-的最小值等于 ( )A．52- B．2- C．32- D．2【答案】A【名师点睛】本题考查线性规划，要正确作图，首先要对目标函数进行分析，什么时候目标函数取到最大值，解该类题目时候，往往还要将目标直线的斜率和可行域边界的斜率比较，否则很容易出错，属于基础题．28. 【2013山东，理6】在平面直角坐标系xOy中，M为不等式组220,210,380x yx yx y--≥⎧⎪+-≥⎨⎪+-≤⎩所表示的区域上一动点，则直线OM斜率的最小值为( )．A．2 B．1 C．13- D．12-【答案】：C【解析】：不等式组表示的区域如图阴影部分所示，结合斜率变化规律，当M位于C点时OM斜率最小，且为13-，故选C.【名师点睛】本题考查简单线性规划、直线的斜率公式.此类问题的基本解法是“图表法”，即通过画可行域，观察OM 斜率变化情况，经简单计算，做出结论. 本题属于小综合题，也是常见题目，故考生易于正确解答.29. .【2014辽宁理11】当[2,1]x ∈-时，不等式32430ax x x -++≥恒成立，则实数a 的取值范围是（ ）A ．[5,3]--B ．9[6,]8-- C ．[6,2]-- D ．[4,3]--【答案】C 【解析】试题分析：当x =0时，原式恒成立； 当(0,1]x ∈时，原式等价于2max 343()x x a x--≥恒成立； 当[2,0)x ∈-时，原式等价于2min 343()x x a x--≤恒成立；令2343(),[2,0)(0,1]x x f x x x--=∈- ，232343143()x x f x x xx x--==-- ，令1t x =，即3234y t t t =--+，2'981y t t ∴=--+，可知1(1,)9-为y 的增区间，1(,1),(,)9-∞-+∞为y 的减区间，所以当(0,1]x ∈时，即[1,)t ∈+∞时，t =1时max 6y =-，即max ()66f x a =-∴≥-；当[2,0)x ∈-时，即1(,)2t ∈-∞-时，y 在(,1)-∞-上递减，在1(1,]2--上递增，所以t =-1时min 2y =-，即min ()22f x a =-∴≤-；综上，可知a 的取值范围是[6,2]--，故选C .考点：不等式恒成立问题.【名师点睛】本题考查应用导数研究函数的单调性、极值，不等式恒成立问题.解答本题的关键，是利用分类讨论思想、转化与化归思想，通过构造函数研究其单调性、最值，得出结论.本题属于能力题，中等难度.在考查应用导数研究函数的单调性、极值、不等式恒成立问题等基本方法的同时，考查了考生的逻辑推理能力、运算能力、分类讨论思想及转化与化归思想.30. 【2015湖南理2】若变量x ，y 满足约束条件1211x y x y y +≥-⎧⎪-≤⎨⎪≤⎩，则3z x y =-的最小值为（ ）A.-7B.-1C.1D.2 【答案】A.【考点定位】线性规划.【名师点睛】本题主要考查了利用线性规划求线性目标函数的最值，属于容易题，在画可行域时，首先必须找准可行域的范围，其次要注意目标函数对应的直线斜率的大小，从而确定目标函数取到最优解时所经过的点，切忌随手一画导致错解. 二、填空题1.【2013高考广东卷.理.9】不等式x 2＋x －2＜0的解集为__________. 【答案】{x |－2＜x ＜1}【名师点晴】本题主要考查的是一元二次不等式，属于容易题．解题时要注意2x 的系数是否为正数，如果2x 的系数是负数，一定要化为正数，否则很容易出现错误． 2. 【2014高考广东卷.理.9】不等式521≥++-x x 的解集为 . 【答案】(][),32,-∞-+∞.【名师点晴】本题主要考查的是绝对值不等式，属于容易题．解题时一定要注意解与解集的区别，否则很容易出现错误．零点分段法解绝对值不等式的步骤：①求零点；②划区间，去绝对值号；③分别解去掉绝对值的不等式；④取每段结果的并集，注意在分段时不要遗漏区间的端点值．3. 【2014湖南14】若变量y x ,满足约束条件⎪⎩⎪⎨⎧≥≤+≤k y y x x y 4，且y x z +=2的最小值为6-，则____=k . 【答案】2-【解析】求出约束条件中三条直线的交点为()(),,4,k k k k -(),2,2,且不等式组,4y x x y ≤+≤限制的区域如图,所以2k ≤,则当(),k k 为最优解时,362k k =-⇒=-,当()4,k k -为最优解时,()24614k k k -+=-⇒=, 因为2k ≤,所以2k =-,故填2-.【考点定位】线性规划【名师点睛】有关线性规划的题目主要是根据所给不等式组得到对应的可行域，然后根据目标函数满足的条件结合其对应的几何意义进行发现计算即可. 常见的目标函数有： (1)截距型：形如z ax by =+，求这类目标函数的最值常将函数z ax by =+转化为直线的斜截式：1,(0)a y x z b b b =-+≠，通过求直线的截距zb的最值间接求出z 的最值． (2)距离型：形如22()()z x a y b =-+-. (3)斜率型：形如y bz x a-=-.注意：转化的等价性及几何意义． 4. 【2013高考陕西版理第13题】若点(x ，y )位于曲线y ＝|x －1|与y ＝2所围成的封闭区域，则2x －y 的最小值为__________． 【答案】-4【名师点晴】本题主要考查的是线性规划，属于容易题．线性规划类问题的解题关键是先正确画出不等式组所表示的平面区域，然后确定目标函数的几何意义，通过数形结合确定目标函数何时取得最值．解题时要看清楚是求“最大值”还是求“最小值”，否则很容易出现错误；画不等式组所表示的平面区域时要通过特殊点验证，防止出现错误．5. 【2015高考新课标2，理14】若x ，y 满足约束条件1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩，，则z x y =+的最大值为____________．【答案】32【解析】画出可行域，如图所示，将目标函数变形为y x z =-+，当z 取到最大时，直线y x z =-+的纵截距最大，故将直线尽可能地向上平移到1(1,)2D ，则z x y =+的最大值为32．【考点定位】线性规划．【名师点睛】本题考查线性规划，要正确作图，首先要对目标函数进行分析，什么时候目标函数取到最大值，解该类题目时候，往往还要将目标直线的斜率和可行域边界的斜率比较，否则很容易出错，属于基础题．6.【2015高考新课标1，理15】若,x y 满足约束条件10040x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩，则y x 的最大值为 . 【答案】3【解析】作出可行域如图中阴影部分所示，由斜率的意义知，yx是可行域内一点与原点连线的斜率，由图可知，点A （1,3）与原点连线的斜率最大，故yx的最大值为3.【考点定位】线性规划解法【名师点睛】对线性规划问题，先作出可行域，在作出目标函数，利用z 的几何意义，结合可行域即可找出取最值的点，通过解方程组即可求出做最优解，代入目标函数，求出最值，要熟悉相关公式，确定目标函数的意义是解决最优化问题的关键，目标函数常有距离型、直线型和斜率型.7. 【2014年.浙江卷.理13】当实数x，y满足240,10,1,x yx yx+-≤⎧⎪--≤⎨⎪≥⎩时，14ax y≤+≤恒成立，则实数a的取值范围是________.答案：3 1,2⎡⎤⎢⎥⎣⎦【名师点睛】本题主要考查简单线性规划．解决此类问题的关键是正确画出不等式组表示的可行域，将目标函数赋予几何意义；求目标函数的最值的一般步骤为：一画二移三求．其关键是准确作出可行域，理解目标函数的意义．常见的目标函数有：(1)截距型：形如z＝ax＋by.求这类目标函数的最值常将函数z＝ax＋by转化为直线的斜截式：y＝－abx＋zb，通过求直线的截距zb的最值间接求出z的最值．(2)距离型：形如z＝(x－a)2＋(y－b)2.(3)斜率型：形如z＝y bx a --.8. 【2013年.浙江卷.理13】设z＝kx＋y，其中实数x，y满足20,240,240.x yx yx y+-≥⎧⎪-+≥⎨⎪--≤⎩若z的最大值为12，则实数k＝__________. 【答案】：2【解析】：画出可行域如图所示．由可行域知，最优解可能在A (0,2)或C (4,4)处取得． 若在A (0,2)处取得不符合题意；若在C (4,4)处取得，则4k ＋4＝12，解得k ＝2，此时符合题意． 【考点定位】简单的线性规划 【名师点睛】本题主要考查简单线性规划．解决此类问题的关键是正确画出不等式组表示的可行域，将目标函数赋予几何意义；求目标函数的最值的一般步骤为：一画二移三求．其关键是准确作出可行域，理解目标函数的意义．常见的目标函数有：(1)截距型：形如z ＝ax ＋by .求这类目标函数的最值常将函数z ＝ax ＋by 转化为直线的斜截式：y ＝－a b x ＋zb，通过求直线的截距z b的最值间接求出z 的最值．(2)距离型：形如z ＝(x －a )2＋(y －b )2.(3)斜率型：形如z ＝y bx a--.9. 【2015高考浙江，理14】若实数,x y 满足221x y +≤，则2263x y x y +-+--的最小值是 ． 【答案】3.【考点定位】1.线性规划的运用；2.分类讨论的数学思想；3.直线与圆的位置关系【名师点睛】本题主要考查了以线性规划为背景的运用，属于中档题根据可行域是圆及其内部的特点，结合直线与圆的位置关系的判定，首先可以将目标函数的两个绝对值号中去掉一个，再利用分类讨论的数学思想去掉其中一个绝对值号，利用线性规划知识求解，理科试卷的线性规划问题基本考查含参的线性规划问题或者是利用线性规划的知识解决一些非线性的目标函数或可行域的问题，常需考查目标函数或可行域的几何意义求解，在复习时应予以关注.10. 【2013江苏，理9】抛物线y＝x2在x＝1处的切线与两坐标轴围成三角形区域为D(包含三角形内部和边界)．若点P(x，y)是区域D内的任意一点，则x＋2y的取值范围是__________．【答案】1 2,2⎡⎤-⎢⎥⎣⎦．【名师点晴】对于线性目标函数，必须明确线性目标函数的最值一般在可行域的顶点或边界取得，运用数形结合的思想方法求解.同时注意边界直线斜率与目标函数斜率的关系；对于非线性目标函数，应考虑其具有的几何意义，依平面几何知识解答；对于交汇问题应转化为目标函数最值问题处理.11. 【2013江苏，理11】已知f (x )是定义在R 上的奇函数，当x ＞0时，f (x )＝x 2－4x ，则不等式f (x )＞x 的解集用区间表示为__________． 【答案】(－5,0)∪(5，＋∞)．【解析】∵函数f(x)为奇函数，且x ＞0时，f (x )＝x 2－4x ，则f (x )＝224,0,0,0,4,0,x x x x x x x ⎧->⎪=⎨⎪--<⎩∴原不等式等价于20,4,x x x x >⎧⎨->⎩或20,4,x x x x <⎧⎨-->⎩由此可解得x ＞5或－5＜x ＜0. 故应填(－5,0)∪(5，＋∞)．【考点定位】分段函数，函数的奇偶性，一元二次不等式的解法.【名师点晴】利用函数的奇偶性把研究整个函数具有的性质问题转化到只研究部分(一半)区间上的问题，是简化问题的一种途径．若函数f(x)为偶函数，则函数在y 轴两侧单调性相反；若函数f(x)为奇函数，则函数在原点两侧的单调性相同． 12. 【2015高考江苏，7】不等式224x x-<的解集为________.【答案】(1,2).-13.【2013天津，理14】设a ＋b ＝2，b ＞0，则当a ＝__________时，1||2||a a b+取得最小值． 【答案】－2考点定位：本题考点为利用基本不等式求最值问题.【名师点睛】本题考查利用基本不等式求最值，利用基本不等式求最值问题就是灵活应用下列两个重要不等式22,,2;,,a b R a b ab a b R a b +∈+≥∈+≥（当且仅当a=b 时取等号），注意不等式的使用条件，特别是等号取得的条件，第二个更要注意“一正，二定，三相等”，利用基本不等式求最值常用方法有三种，（1）做乘法，（2）1的妙用，（3）等转不等.14. 【2014湖北卷14】设()x f 是定义在()+∞,0上的函数，且()0>x f ，对任意0,0>>b a ，若经过点))(,(a f a ，))(,(b f b -的直线与x 轴的交点为()0,c ，则称c 为b a ,关于函数()x f 的平均数，记为),(b a M f ，例如，当())0(1>=x x f 时，可得2),(ba cb a M f +==，即),(b a M f 为b a ,的算术平均数.（1）当())0_____(>=x x f 时，),(b a M f 为ba ,的几何平均数；（2）当())0_____(>=x x f 时，),(b a M f 为ba ,的调和平均数ba ab+2；。
2013年湖南高考理科数学卷及答案
绝密★启用前2014年普通高等学校招生全国统一考试（湖南卷）数学（理工农医类）本试题卷包括选择题、填空题和解答题三部分,共6页.时量120分钟.满分150分. 一、选择题：本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数i (1i)z =+(i 为虚数单位)在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.某学校有男、女学生各500名.为了解男、女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是 ( ) A .抽签法B .随机数法C .系统抽样法D .分层抽样法3.在锐角中ABC △,角A ,B 所对的边长分别为a ,b .若2sin a B =,则角A 等于( )A .π12B .π6C .π4D .π34.若变量x ,y 满足约束条件2,1,1,y x x y y ⎧⎪+⎨⎪-⎩≤≤≥,则2x y +的最大值是( )A .52-B .0C .53D .525.函数()2ln f x x =的图象与函数2()45g x x x =-+的图象的交点个数为( )A .3B .2C .1D .06.已知a ,b 是单位向量,0=a b .若向量c 满足||1--=c a b ,则||c 的取值范围是( ) A.1] B.2] C.1]D.2]+7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不．可能．．等于( )A .1BCD8.在等腰直角三角形ABC 中,=4AB AC =,点P 是边AB 上异于A ,B 的一点,光线从点P 出发,经BC ,CA 发射后又回到原点P （如图）.若光线QR 经过ABC △的中心,则AP 等于( ) A .2 B .1 C .83D .43二、填空题：本大题共8小题,考生作答7小题,每小题5分,共35分.（一）选做题（请考生在第9,10,11三题中任选两题作答,如果全做,则按前两题记分）9.在平面直角坐标系xOy 中,若l ：,x t y t a =⎧⎨=-⎩（t 为参数）过椭圆C ：3cos ,2sin x y ϕϕ=⎧⎨=⎩（ϕ为参数）的右顶点,则常数a 的值为 . 10.已知,,a b c ∈R ,236a b c ++=,则22249a b c ++的最小值为 .11.如图,的O 中,弦AB ,CD 相交于点P ,2PA PB ==,1PD =,则圆心O 到弦CD 的距离为 .（二）必做题（12～16题）12.若20d 9Tx x =⎰,则常数T 的值为 .13.执行如图所示的程序框图,如果输入1a =,2b =,则输出的a 的值为 .14.设1F ,2F 是双曲线C ：22221(0,0)x y a b a b-=>>的两个焦点,P 是C 上一点.若126PF PF a +=,且12PF F △的最小内角为30,则C 的离心率为 . 15.设n S 为数列{}n a 的前n 项和,1(1)2n n n n S a =--,*n ∈N ,则 （1）3a = . （2）12100S S S +++= .16.设函数()xxxf x a b c =+-,其中0c a >>,0c b >>.（1）记集合{(,,),,}M a b c a b c a b =不能构成一个三角形的三条边长,且=,则(,,)a b c M ∈所对应的()f x 的零点的取值集合为 .（2）若a ,b ,c 是ABC △的三条边长,则下列结论正确的是 .(写出所有正确结论的序号)①(,1)x ∀∈-∞,()0f x >；②x ∃∈R ,使x a ,x b ,x c 不能构成一个三角形的三条边长； ③若ABC △为钝角三角形,则(1,2)x ∃∈,使()0f x =.三、解答题：本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 17.（本小题满分12分）已知函数ππ()sin()cos()6f x x x =-+-,2()2sin 2xg x =.（Ⅰ）若α是第一象限角,且()f α,求()g α的值；（Ⅱ）求使()()f x g x ≥成立的x 的取值集合.18.（本小题满分12分）某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形的顶点）处都种了一株相同品种的作物.根据历年的种植经验,一株该种作这里,两株作物“相近”是指它们之间的直线距离不超过1米.（Ⅰ）从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率； （Ⅱ）从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.19.（本小题满分12分）--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无------------------------------------姓名________________ 准考证号_____________如图,在直棱柱1111ABCD A B C D -中,AD BC ∥,90BAD ∠=,AC BD ⊥,1BC =,13AD AA ==.（Ⅰ）证明：1AC B D ⊥；（Ⅱ）求直线11B C 与平面1ACD 所成角的正弦值.20.（本小题满分13分）在平面直角坐标系xOy 中,将从点M 出发沿纵、横方向到达点N 的任一路径称为M 到N 的一条“L 路径”.如图所示的路径123MM M M N 与路径1MN N 都是M 到N 的“L 路径”.某地有三个新建的居民区,分别位于平面xOy 内三点(3,20)A ,(10,0)B -,(14,0)C 处.现计划在x 轴上方区域（包含x 轴）内的某一点P 处修建一个文化中心.（Ⅰ）写出点P 到居民区A 的“L 路径”长度最小值的表达式（不要求证明）； （Ⅱ）若以原点O 为圆心,半径为1的圆的内部是保护区,“L 路径”不能进入保护区.请确定点P 的位置,使其到三个居民区的“L 路径”长度之和最小.21.（本小题满分13分） 过抛物线E :22(0)x py p =>的焦点F 作斜率分别为1k ,2k 的两条不同的直线1l ,2l ,且122k k +=.1l 与E 相交于点A ,B ,2l 与E 相交于点C ,D .以AB ,CD 为直径的圆M ,圆N （M ,N 为圆心）的公共弦所在直线记为l .（Ⅰ）若10k >,20k >,证明：22FM FN P <；（Ⅱ）若点M 到直线l,求抛物线E 的方程.21.（本小题满分13分）已知0a >,函数()||2x af x x a-=+. （Ⅰ）记()f x 在区间[0,4]上的最大值为()g a ,求()g a 的表达式；（Ⅱ）是否存在a ,使函数()y f x =在区间(0,4)内的图象上存在两点,在该两点处的切线互相垂直？若存在,求a 的取值范围；若不存在,请说明理由.2013年普通高等学校招生全国统一考试（湖南卷）数学（理工农医类）答案解析【解析】i(1i)1z=+=-【提示】利用复数乘法的运算法则及复数的几何意义求解【考点】复数乘法的运算法则，复数集与复平面上的点对应关系2sina B【提示】给出三角形中的边角关系，运用正弦定理求解未知角【考点】正弦定理33⎝⎭333【解析】2()g x x=一直角坐标系内画出函数()f x与()g x有2个不同的交点在位置P'时最远，而21PO=-，21P O'=+，故选A．【提示】令OA a=，OB b=，OD a b=+，OC c=，作出图象，根据图象可求出||c的最2)2(11213)2(121212)(24292)3(a b c a b c a =⨯+⨯+⨯≤++++=，化简得212c ≥，由此可得当且仅当2a =，1b =，2c =时，224a b +PD PC PA PB =，22⎝⎭a22a c <，【解析】n n a S =-n 为偶数时11210021431009923100()()()2222S S S a a a a a a ⎛⎫∴+++=-+-++--++++ ⎪⎝⎭399210010011111111122222232⎛⎫⎛⎫⎛⎫=+++-+++=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭【提示】（1）把给出的数列递推式先分1n =和2n ≥讨论，由此求出首项和2n ≥时的关系式11(1)(1)2n n n n n n a a a -=-+--．对此关系式再分n 为偶数和奇数分别得到当n 为偶数和a 【解析】0c a >>①a ，b ，c ，0c a >>0ac∴<<,1)-∞110x ab c c +->∞则a ，b ，c ③c a >，c上存在零点，故③正确【提示】（1）由集合M 中的元素满足的条件，得到2c a b a ≥+=，求得a的范围，解出函数的零点，利用()xxxf x a b c +-=不等式可得零点x 的取值集合；（2）对于①，把函数式()xxxf x a b c +-=变形为()1xxx x x xa b f x a b c c c c ⎡⎤⎛⎫⎛⎫=+-=+-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦，利用指数函数的单调性即可证得结论成立；解出3sin 5α=，利用同角三角函数的基本关系算出4cos 5α=．由二倍角的余弦公式进行降次，可得()1cos g x x =-，即可算出1()1cos g αα=-=； 【提示】（Ⅰ）确定三角形地块的内部和边界上的作物株数，分别求出基本事件的个数，)ABCD -ABCD ，且面又AC BD ⊥，且1BD BB B =，AC ⊥面BDB ，1B D ⊂面BDB 1AC B D ⊥（Ⅱ）11B C BC AD ∥∥∴直线．建立直角坐标系，用向量解题．设原点在正半轴，AA 设(0,0,0)A ，(3,0,0)，D ，(0,,0)B y ，(1C 则(1,,0)AC y =，(3,BD =-，AC BD ⊥00AC BD y =⇒-+=0y >⇒=，(1,AC ∴=，(3,0,3)AD =设平面A C D ,,)x y z ，则100n A Cn A D ⎧=⎪⇒⎨=⎪⎩平1C D 的一，(1,0,0)B C =1法向3(1,0,0)sin |cos ,|B C n B C θ=⇒=<>==71BD B=，AD与平面【考点】绝对值函数最值（Ⅰ）22FM FN p<已知抛物线的焦点为212(x x p FM k p=-⇒⇒=同理23422x k p⇒==，(FN k p⇒=121)FM FN k k⇒=1k>，2k2122k k k+>⇒21FM FN p k∴=所以，22FM FN p<（Ⅱ）径分1⎡⎛222)0+=211214455k kp p⎪ ⎪++⎝⎭⎝⎭≥抛物线的方程为216x y=求出向量FM和FN2)()f x'=-232)3axx aa+-，2223(2)ax a -+12)4x x a ++【提示】（Ⅰ）利用绝对值的几何意义，分类讨论，结合导数确定函数的单调性，从而可得()g a 的表达式；（Ⅱ）利用曲线()y f x =在两点处的切线互相垂直，建立方程，从而可转化为集合的运算，即可求得结论【考点】导数求分段函数的最值，导数的几何意义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
:()(0,1)x q f x a a a =>≠2012高考数学（理科）小题限时训练七
15小题共75分，时量：45分钟，考试时间：2012年9月12日第6节 姓名 一、选择题（每题5分共40分）
1．集合A={－1，0，1}，B={A x x y y ∈=,cos }，则A B=（ ） A. {0}
B ． {1}
C ．{0，1}
D ．{－1，0，1}
2．已知:p 不等式2
1x a +≤的解集为φ，是减函数，则p 是
q 的（ ）
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要
3．直线
4022
2=+=++y x y x 截圆所得劣弧所对圆心角为 （ ）
A ．6π
B ．3π
C ．2π
D ．32π
4．已知角a 的余弦线是单位长度的有向线段，那么角a 的终边在
（ ）
A ．x 轴上
B ．y 轴上
C ．直线y=x 上
D ．直线y=-x 上
5．若实数,x y 满足
2222111,2x y x y
+=+则有 （ ）
A
．最大值3+B
．最小值3+
C ．最大值6
D ．最小值6
6．复数i
i
+1在复平面中所对应的点到原点的距离为 ( ) A ．
2
1
B ．1
C ．22
D ．2
7． 设非常值函数() ()f x x R ∈是一个偶函数，它的函数图像()y f x =
关于直线2
x =对称，则该函数是 （ ）
A. 非周期函数
B.
周期为
2
的周期函数 C.
D. 周期为2的周期函数 8．对任意正整数n ，定义n 的双阶乘!!n 如下： 当n 为偶数时，!!(2)(4)642n n n n =--∙∙
（4）
（3）（2）
（1
）
当n 为奇数时，
!!(2)(4)531n n n n =--∙∙
现有四个命题：①(2011!!)(2010!!)2011!=， ②2010!!21005!=∙， ③2010!!个位数为0， ④2011!!个位数为5 其中正确的个数为( )
A.1
B.2
C.3
D.4
二、填空题（每题5分共35分）
9．若将右面的展开图恢复成正方体，则ABC ∠的度数为
10．若()(12)(13)(,,1,1)m
n
f x x x m n N m n +=+++∈>>的展开 式中x 的系数为13，则展开式中2
x 的系数是 。
11．在区间[]π,0上随机取一个数x ，x sin 的值介于0到2
1
之间的概率为
12．设圆1O 与圆2O 的半径分别为3和2，124O O =，,A B 为两圆的交点，试求两圆的公共弦AB 的长度是________．
13．在R 上定义运算(1)x y x y ⊗=-,若不等式()()1x a x a -⊗+<对任意实数x 均成立,则a 的
取值范围是__________
14．对于平面上的点集Ω，如果连接Ω中任意两点的线段必定包含于Ω，则称Ω为平面上的凸集，给出平面上4个点集的图形如右（阴影区域及其边界）：其中为凸集的是 （写出所有凸集相应图形的序号）。
15．下表给出一个“直角三角形数阵”：满足每一列成等差数列，从第三行起，每一行的数成等比数列，且每一行的公比相等，记第i 行第j 列的数 为()
*,,ij a i j i j N ≥∈，则ij a =
一、选择题
BBDA BCCC
二、填空题
9．60° 10． 31 11．
3
1
12．4153 13． 23
21<<-a
14． （2）（3） 15． 2
1
+j i。