[高三数学]高考数学压轴题训练题含答案
高考数学高考数学压轴题立体几何多选题分类精编及答案
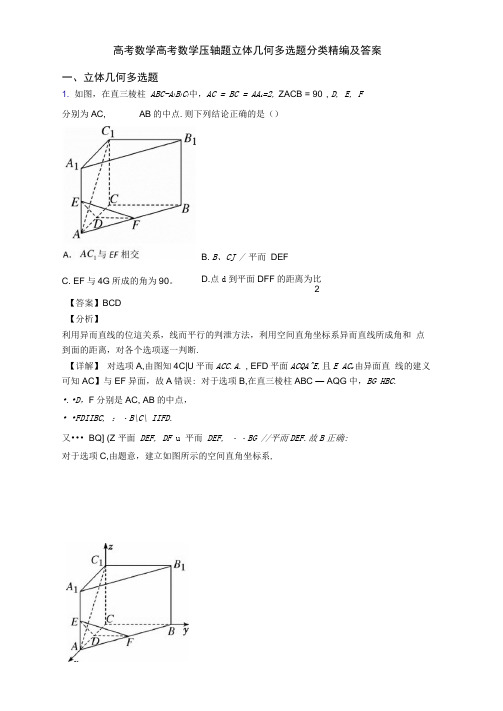
高考数学高考数学压轴题立体几何多选题分类精编及答案一、立体几何多选题1. 如图，在直三棱柱ABC-A}B}C}中，AC = BC = AA i=2, ZACB = 90°, D, E, F分别为AC, AB的中点.则下列结论正确的是（）B. B、CJ /平而DEFD.点d到平面DFF的距离为比C. EF与4G所成的角为90。
2【答案】BCD【分析】利用异而直线的位這关系，线而平行的判泄方法，利用空间直角坐标系异而直线所成角和点到面的距离，对各个选项逐一判断.【详解】对选项A,由图知4C|U平而ACC.A. , EFD平面ACQA^E,且E AC r由异面直线的建义可知AC】与EF异面，故A错误: 对于选项B,在直三棱柱ABC — AQG中，BG HBC.•.•D，F分别是AC, AB的中点，• •FDIIBC, ：・B\C\ IIFD.又••• BQ] (Z 平面DEF, DF u 平而DEF, ・・BG //平而DEF.故B正确:对于选项C,由题意，建立如图所示的空间直角坐标系,则C(0,0, 0), A(2,0t 0), 5(0,2, 0),人(2,0, 2),坊(0,2, 2), C 】(0,0, 2),D(l,o, 0), E(2,0, 1), F(1,1, 0)..\EF = (-1,1, T), AC ；=(—2,0, 2).•.•EFAC ； = 2+0—2 = 0, :.EF 丄 AC ；, 丄 A©.•.•EF 与AC ；所成的角为90。
，故c 正确：对于选项D,设向量匝= (x,y, Z)是平而DEF 的一个法向疑.・••万E = (ho ・ 1) , DF = (0,l, 0),取 X = 1 ♦则 z=—1 ‘ ・••帀=(h 0, —1),设点耳到平而DEF 的距离为d ・二点d 到平而DEF 的距离为空，故D 正确.2故选：BCD【点睛】本题主要考查异而直线的位置关系，线而平行的判定，异而直线所成角以及点到而的距 离，还考查思维能力及综合分析能力，属难题.2. 已知球O 为正方体ABCD-AgD 、的内切球，平而A {C }B 截球O 的而积为24兀, 下列命题中正确的有（）A. 异而直线AC 与所成的角为60。
2024年高考数学(新高考压轴卷)(全解全析)
2024年高考压轴卷【新高考卷】数学·全解全析一、单选题1．已知集合105x A x x ⎧⎫+=≥⎨⎬-⎩⎭，(){}22log 16B x y x ==-，则()R A B ⋂=ð（）A ．()1,4-B ．[]1,4-C ．(]1,5-D ．()4,52．宋代是中国瓷器的黄金时代，涌现出了五大名窑：汝窑、官窑、哥窑、钧窑、定窑．其中汝窑被认为是五大名窑之首．如图1，这是汝窑双耳罐，该汝窑双耳罐可近似看成由两个圆台拼接而成，其直观图如图2所示．已知该汝窑双耳罐下底面圆的直径是12厘米，中间圆的直径是20厘米，上底面圆的直径是8厘米，高是14厘米，且上、下两圆台的高之比是3:4，则该汝窑双耳罐的体积是（）A ．1784π3B ．1884π3C ．2304π3D ．2504π33．如图，左车道有2辆汽车，右车道有3辆汽车等待合流，则合流结束时汽车通过顺序共有（）种.A ．10B ．20C ．60D ．120【答案】A【分析】合流结束时5辆车需要5个位置，第一步从5个位置选2个位置安排左边的2辆汽车，第二步剩下3个位置安排右边的3辆汽车，从而由分步乘法计数原理可得结果.【详解】设左车辆汽车依次为12,A A ，右车辆汽车依次为123,,B B B ，则通过顺序的种数等价于将12,A A 安排在5个顺序中的某两个位置（保持12,A A 前后顺序不变），123,,B B B 安排在其余3个位置（保持123,,B B B 前后顺序不变），123,,B B B ，所以，合流结束时汽车通过顺序共有2353C C 10=.故选：A.4．已知等比数列{}n a 的各项均为负数，记其前n 项和为n S ，若6467813,8S S a a a -=-=-，则2a =（）A ．－8B ．－16C ．－32D ．－485．已知圆C ：22()1x y m +-=，直线l ：()1210m x y m ++++=，则直线l 与圆C 有公共点的必要不充分条件是（）A ．11m -≤≤B ．112m -≤≤C ．10m -≤≤D ．102m ≤≤6．已知函数2()log f x x =，则对任意实数,a b ，“0a b +≤”是“()()0f a f b +≤”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件故选：C.7．已知0.50.2a =，cos2b =，lg15c =，则（）A ．a b c <<B ．c a b <<C ．b c a <<D ．b a c<<8．从椭圆22:1(0)x y C a b a b+=>>外一点()00,P x y 向椭圆引两条切线，切点分别为,A B ，则直线AB 称作点P关于椭圆C 的极线，其方程为00221x x y ya b+=.现有如图所示的两个椭圆12,C C ，离心率分别为12,e e ，2C 内含于1C ，椭圆1C 上的任意一点M 关于2C 的极线为l ，若原点O 到直线l 的距离为1，则2212e e -的最大值为（）A ．12B ．13C ．15D ．14二、多选题9．已知非零复数1z ，2z 在复平面内对应的点分别为1Z ，2Z ，O 为坐标原点，则下列说法正确的是（）A ．若1211z z -=-，则12=z z B ．若1212z z z z +=-，则120OZ OZ ⋅=C ．若1212z z z z +=-，则120z z ⋅=D ．若1212z z z z +=+，则存在实数t ，使得21z tz =10．已知四面体ABCD的一个平面展开图如图所示，其中四边形AEFD是边长为B，C分别为AE，FD的中点，BD=）⊥A．BE CDB．BE与平面DCE所成角的余弦值为15C．四面体ABCD的内切球半径为30D．四面体ABCD的外接球表面积为8π【点睛】11．对于数列{}n a （N n a +∈），定义k b 为1a ，2a ，…，k a 中最大值（1,2,,k n =⋅⋅⋅）（N n +∈），把数列{}n b 称为数列{}n a 的“M 值数列”.如数列2，2，3，7，6的“M 值数列”为2，2，3，7，7，则（）A ．若数列{}n a 是递减数列，则{}n b 为常数列B ．若数列{}n a 是递增数列，则有n na b =C ．满足{}n b 为2，3，3，5，5的所有数列{}n a 的个数为8D ．若()1()2N n n a n -+=-∈，记n S 为{}n b 的前n 项和，则1001002(21)3S =-三、填空题12．已知向量()1,1,4a b == ，且b 在a 上的投影向量的坐标为()2,2--，则a 与b的夹角为.13．已知公比q 大于1的等比数列{}n a 满足135a a +=，22a =.设22log 7n n b a =-，则当5n ≥时，数列{}n b 的前n 项和n S =.14．已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ，过点2F 且斜率为34-的直线与C 交于,A B两点．若112AF F F ⊥，则C 的离心率为；线段AB 的垂直平分线与x 轴交于点D ，则22BF DF =．5.【点睛】方法点睛：椭圆求离心率或者范围关键是找到关于,a c 的齐次式求得.四、解答题15．如图，在平面四边形ABCD ，已知1BC =，3cos 5BCD ∠=-.（1）若AC 平分BCD ∠，且2AB =，求AC 的长；（2）若45CBD ∠=︒，求CD 的长.16．如图，在三棱柱111ABC A B C -中，ABC △是边长为2的正三角形，侧面11BB C C 是矩形，11AA A B =．(1)求证：三棱锥1A ABC -是正三棱锥；(2)若三棱柱111ABC A B C -的体积为221AC 与平面11AA B B 所成角的正弦值．【答案】(1)证明见解析(2)23【分析】（1）根据线面垂直的判定定理及性质定理，证明1A O ⊥平面ABC 即可；（2）建立空间直角坐标系，利用向量法求线面角正弦即可.【详解】（1）分别取AB ，BC 中点D ，E ，连接CD ，AE 交于点O ，则点O 为正三角形ABC 的中心．因为11AA A B CA CB ==，得1CD AB AD AB ⊥⊥，，又11,,A D CD D A D CD =⊂ 平面1A CD ，所以AB ⊥平面1A CD ，又1A O ⊂平面1A CD ，则1AB A O ⊥；取11B C 中点1E ，连接111A E E E ，，则四边形11AA E E 是平行四边形，因为侧面11BB C C 是矩形，所以1BC EE ⊥，又BC AE ⊥，又11,,EE AE E EE AE =⊂ 平面11AA E E ，所以BC ⊥平面11AA E E ，又1A O ⊂平面11AA E E ，则1BC A O ⊥；又AB BC B ⋂=，,AB BC ⊂平面ABC ，所以1A O ⊥平面ABC ，所以三棱锥1A ABC -是正三棱锥．17．某学校为了解本学期学生参加公益劳动的情况，从学校内随机抽取了500名高中学生进行在线调查，收集了他们参加公益劳动时间（单位:小时）分配情况等数据，并将样本数据分成[0,2],(2,4]，(4,6],(6,8],(8,10],(10,12],(12,14],(14,16]，(16,18]九组，绘制成如图所示的频率分布直方图.(1)为进一步了解这500名学生参加公益劳动时间的分配情况，从参加公益劳动时间在(12,14],(14,16],(16,18]三组内的学生中，采用分层抽样的方法抽取了10人，现从这10人中随机抽取3人.记参加公益劳动时间在(14,16]内的学生人数为X ，求X 的分布列和期望；(2)以调查结果的频率估计概率，从该学校所有高中学生中随机抽取20名学生，用“20()P k ”表示这20名学生中恰有k 名学生参加公益劳动时间在(10,12]（单位:小时）内的概率，其中0,1,2,,20k = .当20()P k 最大时，写出k 的值.18．已知双曲线(22:10,0x y C a b a b-=>>）的左右焦点分别为12,F F ，C 的右顶点到直线2:a l x c =的距离为1，双曲线右支上的点到1F 的最短距离为3(1)求双曲线C 的方程；(2)过2F 的直线与C 交于M 、N 两点，连接1MF 交l 于点Q ，证明：直线QN 过x 轴上一定点.【点睛】方法点睛：求解直线过定点问题常用方法如下：（1）“特殊探路，一般证明（2）“一般推理，特殊求解”：即设出定点坐标，根据题设条件选择参数，建立一个直线系或曲线的方程，再根据参数的任意性得到一个关于定点坐标的方程组，以这个方程组的解为坐标的点即为所求点；（3）求证直线过定点()00,x y ，常利用直线的点斜式方程()00y y k x x -=-或截距式y kx b =+来证明.19．函数()e xf x a x=-图像与x 轴的两交点为()()()1221,0,0A x B x x x >，(1)令()()ln h x f x x x =-+，若()h x 有两个零点，求实数a 的取值范围；(2)证明：121x x <；(3)证明：当5a ≥时，以AB 为直径的圆与直线)1y x =+恒有公共点．（参考数据：0.25 2.5e 1.3e 12.2≈≈，）。
高考数学选择填空压轴题45道(附答案)
,
D．
1,
27 e4
21．已知方程
e x 1
x
e2 x1 x aex1
有三个不同的根，则实数
a
的
取值范围为（ ）
A． 1,e
B．
e,
1 2
C． 1,1
D．
1,
1 2
22．函数 f (x) ex1 ex1 a sin （x x R ，e 是自然对数的底数，
a 0 ）存在唯一的零点，则实数 a 的取值范围为( )
38．若不等式 x e2x a x ln x 1恒成立，则实数 a 的取值范
围是__________.
39．已知函数 f x ln x e a x b ，其中 e 为自然对数的底
数.若不等式
f
x
0
恒成立，则
b a
的最小值为_______.
40．已知函数
f
(x)
x
2 cos
x
，在区间上
0,
4
A．
0,
2
B．
0,
2
C． (0,2]
D． (0,2)
23．已知 a 0 ，b R ，且 ex a(x 1) b 对 x R 恒成立，则 a2b 的 最大值为（ ）
A． 1 e5
2
B． 1 e5
3
C． 1 e3
2
D． 1 e3
3
k
24．若关于
x
的不等式
1 x
x
1 27
有正整数解，则实数
16 12
7
4
x
x
3y 6 y
的最小值为________.
8
参考答案，仅供参考
高考数学专题《函数的奇偶性、对称性、周期性》填选压轴题及答案
6．(多选题)函数f(x)的定义域为R，且f(x＋1)与f(x＋2)都为奇函数，则()
A.f(x)为奇函数B.f(x)为周期函数
C.f(x＋3)为奇函数D.f(x＋4)为偶函数
专题03函数的奇偶性、对称性、周期性
【方法点拨】
1.常见的与周期函数有关的结论如下：
(1)如果f(x＋a)＝－f(x)(a≠0)，那么f(x)是周期函数，其中的一个周期T＝2a.
(2)如果f(x＋a)＝ (a≠0)，那么f(x)是周期函数，其中的一个周期T＝2a.
(3)如果f(x＋a)＋f(x)＝c(a≠0)，那么f(x)是周期函数，其中的一个周期T＝2a.
对于 ， 是函数 的一条对称轴，且函数 是周期为4的周期函数，则 是函数 的一条对称轴，
又由函数为奇函数，则直线 是函数 图象的一条对称轴， 正确；
对于 ，函数 在 ， 上有7个零点：分别为 ， ， ，0，2，4，6； 错误；
对于 ， 在区间 ， 上为增函数且其周期为4，函数 在 ， 上为增函数，
又由 为函数 图象的一条对称轴，则函数 在 ， 上为减函数， 正确；
2.函数奇偶性、对称性间关系：
(1)若函数y＝f(x＋a)是偶函数，即f(a＋x)＝f(a－x)恒成立，则y＝f(x)的图象关于直线x＝a对称；一般的，若f(a＋x)＝f(b－x)恒成立，则y＝f(x)的图象关于直线x＝ 对称．
(2)若函数y＝f(x＋a)是奇函数，即f(－x＋a)＋f(x＋a)＝0恒成立，则函数y＝f(x)关于点(a，0)中心对称；一般的，若对于R上的任意x都有f(a＋x)＋f(a－x)＝2b恒成立，则y＝f(x)的图象关于点(a，b)对称.
新高考数学高考数学压轴题多选题专项训练分类精编含解析(2)
一、数列多选题1．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一列数：1，1，2，3，5，…，其中从第三项起，每个数等于它前面两个数的和，后来人们把这样的一列数组成的数列{a n }称为“斐波那契数列”，记S n 为数列{a n }的前n 项和，则下列结论正确的是（ ） A ．a 8＝34 B ．S 8＝54C ．S 2020＝a 2022－1D ．a 1＋a 3＋a 5＋…＋a 2021＝a 2022答案：BCD 【分析】由题意可得数列满足递推关系，依次判断四个选项，即可得正确答案. 【详解】对于A ，可知数列的前8项为1，1，2，3，5，8，13，21，故A 错误； 对于B ，，故B 正确； 对于C ，可解析：BCD 【分析】由题意可得数列{}na 满足递推关系()12211,1,+3nn n aa a aan --===≥，依次判断四个选项，即可得正确答案.【详解】对于A ，可知数列的前8项为1，1，2，3，5，8，13，21，故A 错误； 对于B ，81+1+2+3+5+8+13+2154S ==，故B 正确；对于C ，可得()112nn n a aan +-=-≥，则()()()()1234131425311++++++++++nn n a a a a aa a a aa a a aa+-=----即212++1nnn n S a a aa++=-=-，∴202020221Sa=-，故C 正确；对于D ，由()112n n n a aan +-=-≥可得，()()()135202124264202220202022++++++++a a a a a a a a a aaa=---=，故D 正确.故选：BCD. 【点睛】本题以“斐波那契数列”为背景，考查数列的递推关系及性质，解题的关键是得出数列的递推关系，()12211,1,+3nn n a a a aan --===≥，能根据数列性质利用累加法求解.2．已知数列{}na 中，11a =，1111n na a n n +⎛⎫-=+ ⎪⎝⎭，*n N ∈.若对于任意的[]1,2t ∈，不等式()22212n at a t a a n<--++-+恒成立，则实数a 可能为（ ）A ．－4B ．－2C ．0D ．2答案：AB 【分析】由题意可得，利用裂项相相消法求和求出，只需对于任意的恒成立，转化为对于任意的恒成立，然后将选项逐一验证即可求解. 【详解】 ，， 则，，，，上述式子累加可得：，， 对于任意的恒成立解析：AB 【分析】由题意可得11111n n a a n n n n +-=-++，利用裂项相相消法求和求出122n a n n =-<，只需()222122t a t a a --++-+≥对于任意的[]1,2t ∈恒成立，转化为()()210t a t a --+≤⎡⎤⎣⎦对于任意的[]1,2t ∈恒成立，然后将选项逐一验证即可求解. 【详解】111n n n a a n n++-=，11111(1)1n n a a n n n n n n +∴-==-+++， 则11111n n a a n n n n --=---，12111221n n a a n n n n ---=-----，，2111122a a -=-， 上述式子累加可得：111n a a n n -=-，122n a n n∴=-<， ()222122t a t a a ∴--++-+≥对于任意的[]1,2t ∈恒成立，整理得()()210t a t a --+≤⎡⎤⎣⎦对于任意的[]1,2t ∈恒成立， 对A ，当4a =-时，不等式()()2540t t +-≤，解集5,42⎡⎤-⎢⎥⎣⎦，包含[]1,2，故A 正确；对B ，当2a =-时，不等式()()2320t t +-≤，解集3,22⎡⎤-⎢⎥⎣⎦，包含[]1,2，故B 正确；对C ，当0a =时，不等式()210t t +≤，解集1,02⎡⎤-⎢⎥⎣⎦，不包含[]1,2，故C 错误；对D ，当2a =时，不等式()()2120t t -+≤，解集12,2⎡⎤-⎢⎥⎣⎦，不包含[]1,2，故D 错误，故选：AB. 【点睛】本题考查了裂项相消法、由递推关系式求通项公式、一元二次不等式在某区间上恒成立，考查了转化与划归的思想，属于中档题.3．著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一列数：1，1，2，3，5，…，其中从第三项起，每个数等于它前面两个数的和，后来人们把这样的一列数组成的数列{}na 称为“斐波那契数列”，记Sn为数列{}na 的前n 项和，则下列结论正确的是（ ） A ．68a =B ．733S =C ．13520192022a a a aa++++=D ．22212201920202019a a a aa+++=答案：ABD 【分析】根据，，，计算可知正确；根据，，，，，，累加可知不正确；根据，，，，，，累加可知正确. 【详解】依题意可知，，，， ，，，，故正确； ，所以，故正确； 由，，，，，， 可得，故不解析：ABD 【分析】根据11a =，21a =，21n n n aaa ++=+，计算可知,A B 正确；根据12a a =，342a a a =-，564a a a =-，786a a a =-，，201920202018aaa=-，累加可知C 不正确；根据2121a a a =，222312312()a a a a a a a a =-=-，233423423()a a a a a a a a =-=-，244534534()a a a a a a a a =-=-，，220192019202020182019202020182019()a aaaaaaa=-=-，累加可知D 正确. 【详解】依题意可知，11a =，21a =，21n n naaa ++=+，312112a a a =+=+=，423123a a a =+=+=，534235a a a =+=+=，645358a a a =+=+=，故A 正确；7565813a a a =+=+=，所以712345671123581333S a a a a a a a =++++++=++++++=，故B 正确；由12a a =，342a a a =-，564a a a =-，786a a a =-，，201920202018aaa=-，可得13572019a a a a a+++++=242648620202018a a a a a a a aa+-+-+-++-2020a=，故C 不正确；2121a a a =，222312312()a a a a a a a a =-=-，233423423()a a a a a a a a =-=-，244534534()a a a a a a a a =-=-，，220192019202020182019202020182019()a aaaaaaa=-=-，所以2222212342019a a a a a +++++122312342345342019202020182019a a a a a a a a a a a a a a aaaa=+-+-+-+-20192020aa=，所以22212201920202019a a a aa+++=，故D 正确.故选：ABD. 【点睛】本题考查了数列的递推公式，考查了累加法，属于中档题.4．已知数列{}na 满足112a =-，111n na a +=-，则下列各数是{}n a 的项的有（ ） A ．2-B ．23C ．32D ．3答案：BD 【分析】根据递推关系式找出规律，可得数列是周期为3的周期数列，从而可求解结论． 【详解】 因为数列满足，， ； ； ；数列是周期为3的数列，且前3项为，，3； 故选：． 【点睛】 本题主要解析：BD 【分析】根据递推关系式找出规律，可得数列是周期为3的周期数列，从而可求解结论． 【详解】因为数列{}n a 满足112a =-，111n na a +=-，212131()2a ∴==--； 32131a a==-； 4131112a a a ==-=-； ∴数列{}n a 是周期为3的数列，且前3项为12-，23，3；故选：BD ． 【点睛】本题主要考查数列递推关系式的应用，考查数列的周期性，解题的关键在于求出数列的规律，属于基础题．5．设数列{}na 的前n 项和为*()nS n N ∈，关于数列{}na ，下列四个命题中正确的是（ ） A ．若1*()n naa n N +∈=，则{}na 既是等差数列又是等比数列B ．若2nS An Bn =+(A ，B 为常数，*n N ∈)，则{}na 是等差数列C ．若()11n nS =--，则{}na 是等比数列D ．若{}na 是等差数列，则nS ，2n n SS -，*32()n nS S n N -∈也成等差数列答案：BCD 【分析】利用等差等比数列的定义及性质对选项判断得解. 【详解】选项A: ,得是等差数列，当时不是等比数列，故错; 选项B: ,,得是等差数列，故对; 选项C: ,,当时也成立，是等比数列解析：BCD 【分析】利用等差等比数列的定义及性质对选项判断得解. 【详解】 选项A: 1*()n n a a n N +∈=,10n n aa +∴-=得{}na 是等差数列，当0n a =时不是等比数列，故错; 选项B:2nS An Bn =+,12nn a aA -∴-=,得{}na 是等差数列，故对;选项C: ()11n nS =--,112(1)(2)n nn nS Sa n --∴-==⨯-≥,当1n =时也成立，12(1)n na -∴=⨯-是等比数列，故对;选项D: {}na 是等差数列，由等差数列性质得nS ，2n n SS -，*32()n nS S n N -∈是等差数列，故对; 故选：BCD 【点睛】熟练运用等差数列的定义、性质、前n 项和公式是解题关键.6．朱世杰是元代著名数学家，他所著的《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中涉及一些“堆垛”问题，主要利用“堆垛”研究数列以及数列的求和问题.现有100根相同的圆形铅笔，小明模仿“堆垛”问题，将它们全部堆放成纵断面为等腰梯形的“垛”，要求层数不小于2，且从最下面一层开始，每一层比上一层多1根，则该“等腰梯形垛”应堆放的层数可以是（ ） A ．4B ．5C ．7D ．8答案：BD 【分析】依据题意，根数从上至下构成等差数列，设首项即第一层的根数为，公差即每一层比上一层多的根数为，设一共放层，利用等差数列求和公式，分析即可得解. 【详解】依据题意，根数从上至下构成等差解析：BD 【分析】依据题意，根数从上至下构成等差数列，设首项即第一层的根数为1a ，公差即每一层比上一层多的根数为1d =，设一共放()2n n ≥层，利用等差数列求和公式，分析即可得解. 【详解】依据题意，根数从上至下构成等差数列，设首项即第一层的根数为1a ，公差为1d =，设一共放()2n n ≥层，则总得根数为：()()111110022n n n d n n S na na --=+=+= 整理得120021a n n=+-， 因为1a *∈N，所以n 为200的因数，()20012n n+-≥且为偶数，验证可知5,8n =满足题意. 故选：BD. 【点睛】关键点睛：本题考查等差数列的求和公式，解题的关键是分析题意，把题目信息转化为等差数列，考查学生的逻辑推理能力与运算求解能力，属于基础题.7．公差不为零的等差数列{}na 满足38aa =，n S 为{}n a 前n 项和，则下列结论正确的A ．110S =B ．10nnS S-=（110n ≤≤）C ．当110S >时，5nS S ≥D ．当110S <时，5nS S ≥答案：BC 【分析】设公差d 不为零,由，解得，然后逐项判断. 【详解】 设公差d 不为零, 因为， 所以， 即， 解得， ，故A 错误； ，故B 正确；若，解得，，故C 正确；D 错误； 故选：BC解析：BC 【分析】设公差d 不为零,由38a a =，解得192a d =-，然后逐项判断. 【详解】设公差d 不为零, 因为38a a =， 所以1127a d a d +=+， 即1127a d a d +=--，解得192a d =-， 11191111551155022S a d d d d ⎛⎫=+=⨯-+=≠ ⎪⎝⎭，故A 错误； ()()()()()()221101110910,10102222n n n n n n d d na d n n n a n n S S d ----=+=-=-+=-，故B 正确；若11191111551155022S a d d d d ⎛⎫=+=⨯-+=> ⎪⎝⎭，解得0d >，()()22510525222n d d d n n S n S =-=--≥，故C 正确；D 错误；8．设{}na 是等差数列，nS是其前n 项的和，且56S S <，678S S S =>，则下列结论正确的是（ ） A ．0d > B ．70a =C ．95S S >D ．6S 与7S 均为nS 的最大值答案：BD 【分析】设等差数列的公差为，依次分析选项即可求解. 【详解】根据题意，设等差数列的公差为，依次分析选项： 是等差数列，若，则，故B 正确； 又由得，则有，故A 错误； 而C 选项，，即，可得，解析：BD 【分析】设等差数列{}na 的公差为d ，依次分析选项即可求解.【详解】根据题意，设等差数列{}na 的公差为d ，依次分析选项：{}na 是等差数列，若67SS =，则7670S S a -==，故B 正确；又由56S S <得6560S S a -=>，则有760d a a =-<，故A 错误； 而C 选项，95S S >，即67890a a a a +++>，可得()7820a a+>，又由70a =且0d <，则80a <，必有780a a +<，显然C 选项是错误的.∵56S S <，678S S S =>，∴6S 与7S 均为nS 的最大值，故D 正确；故选：BD. 【点睛】本题考查了等差数列以及前n 项和的性质，需熟记公式，属于基础题.9．已知等差数列{}na 的前n 项和为nS ()*n N ∈，公差0d ≠，690S=，7a 是3a 与9a 的等比中项，则下列选项正确的是（ ） A ．2d =-B ．120a=-C ．当且仅当10n =时，nS 取最大值D ．当0nS <时，n 的最小值为22答案：AD 【分析】运用等差数列的通项公式和求和公式，解方程可得首项和公差，可判断A ，B ；由二次函数的配方法，结合n 为正整数，可判断C ；由解不等式可判断D ． 【详解】等差数列的前n 项和为，公差，由，可解析：AD 【分析】运用等差数列的通项公式和求和公式，解方程可得首项和公差，可判断A ，B ；由二次函数的配方法，结合n 为正整数，可判断C ；由0nS <解不等式可判断D ．【详解】等差数列{}na 的前n 项和为nS，公差0d ≠，由690S =，可得161590a d +=，即12530a d +=，①由7a 是3a 与9a 的等比中项，得2739a a a =，即()()()2111628a d a d a d +=++，化为1100a d +=，②由①②解得120a =，2d =-，则202(1)222na n n =--=-，21(20222)212n S n n n n =+-=-， 由22144124n S n ⎛⎫=--+ ⎪⎝⎭，可得10n =或11时，n S 取得最大值110； 由2102nS n n -<=，解得21n >，则n 的最小值为22.故选：AD 【点睛】本题考查等差数列的通项公式和求和公式，以及等比中项的性质，二次函数的最值求法，考查方程思想和运算能力，属于中档题. 10．下列命题正确的是（ ）A ．给出数列的有限项就可以唯一确定这个数列的通项公式B ．若等差数列{}na的公差0d >，则{}na 是递增数列C ．若a ，b ，c 成等差数列，则111,,a b c可能成等差数列D ．若数列{}na是等差数列，则数列{}12++nn aa也是等差数列答案：BCD 【分析】根据等差数列的性质即可判断选项的正误. 【详解】A 选项：给出数列的有限项不一定可以确定通项公式；B 选项：由等差数列性质知，必是递增数列；C 选项：时，是等差数列，而a = 1，解析：BCD 【分析】根据等差数列的性质即可判断选项的正误. 【详解】A 选项：给出数列的有限项不一定可以确定通项公式；B 选项：由等差数列性质知0d >，{}na必是递增数列；C 选项：1a b c ===时，1111a b c===是等差数列，而a = 1，b = 2，c = 3时不成立；D 选项：数列{}na是等差数列公差为d ，所以11112(1)223(31)nn a aa n d a nd a n d ++=+-++=+-也是等差数列；故选：BCD 【点睛】本题考查了等差数列，利用等差数列的性质判断选项的正误，属于基础题.11．在下列四个式子确定数列{}na 是等差数列的条件是（ ）A ．na knb =+（k ，b 为常数，*n N ∈）； B ．2n naa d +-=（d 为常数，*n N ∈）；C ．()*2120n n n a a a n ++-+=∈N ； D ．{}na 的前n 项和21nSn n =++（*n N ∈）.答案：AC 【分析】直接利用等差数列的定义性质判断数列是否为等差数列． 【详解】A 选项中（，为常数，），数列的关系式符合一次函数的形式，所以是等差数列，故正确，B 选项中（为常数，），不符合从第二项起解析：AC 【分析】直接利用等差数列的定义性质判断数列是否为等差数列． 【详解】A 选项中na knb =+（k ，b 为常数，*n N ∈），数列{}na 的关系式符合一次函数的形式，所以是等差数列，故正确， B 选项中2n naa d +-=（d 为常数，*n N ∈），不符合从第二项起，相邻项的差为同一个常数，故错误； C 选项中()*2120n n n aaa n ++-+=∈N ，对于数列{}na 符合等差中项的形式，所以是等差数列，故正确；D 选项{}na 的前n 项和21nSn n =++（*n N ∈），不符合2nS An Bn =+，所以{}na 不为等差数列．故错误． 故选：AC 【点睛】本题主要考查了等差数列的定义的应用，如何去判断数列为等差数列，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．12．无穷数列{}na 的前n 项和2nSan bn c =++，其中a ，b ，c 为实数，则（ ）A ．{}na 可能为等差数列B ．{}na 可能为等比数列 C ．{}na 中一定存在连续三项构成等差数列 D ．{}na 中一定存在连续三项构成等比数列 答案：ABC 【分析】由可求得的表达式，利用定义判定得出答案． 【详解】 当时，． 当时，． 当时，上式＝． 所以若是等差数列，则所以当时，是等差数列， 时是等比数列；当时，从第二项开始是等差数列．解析：ABC 【分析】由2nS an bn c =++可求得na 的表达式，利用定义判定得出答案．【详解】当1n =时，11a S abc ==++．当2n ≥时，()()221112nnn a S San bn c a n b n c an a b -=-=++-----=-+．当1n =时，上式＝+a b ．所以若{}na 是等差数列，则0.ab a bc c +=++∴=所以当0c时，{}n a 是等差数列， 00a cb ==⎧⎨≠⎩时是等比数列；当0c ≠时，{}na 从第二项开始是等差数列． 故选：A B C 【点睛】本题只要考查等差数列前n 项和nS 与通项公式na 的关系，利用nS 求通项公式，属于基础题．二、等差数列多选题13．在等差数列{}na 中，公差0d ≠，前n 项和为nS，则（ ）A ．4619a a a a >B ．130S >，140S <，则78a a >C ．若915S S =，则n S 中的最大值是12SD ．若2nS n n a =-+，则0a =解析：AD 【分析】对于A ，作差后利用等差数列的通项公式运算可得答案；对于B ，根据等差数列的前n 项和公式得到70a >和780a a +<， 进而可得80a <，由此可知78||||a a <，故B 不正确；对于C ，由915S S =得到，12130a a +=，然后分类讨论d 的符号可得答案；对于D ，由nS 求出na 及1a ，根据数列{}na 为等差数列可求得0a =.【详解】对于A ，因为46191111(3)(5)(8)a a a a a d a d a a d -=++-+215d =，且0d ≠，所以24619150a a a a d -=>，所以4619a a a a >，故A 正确；对于B ，因为130S >，140S <，所以77713()1302a a a +=>，即70a >，787814()7()02a a a a +=+<，即780a a +<，因为70a >，所以80a <，所以7878||||0a a a a -=+<，即78||||a a <，故B 不正确；对于C ，因为915S S =，所以101114150a a a a ++++=，所以12133()0a a +=，即12130a a +=，当0d >时，等差数列{}na 递增，则12130,0a a <>，所以n S 中的最小值是12S ，无最大值；当0d <时，等差数列{}na 递减，则12130,0aa ><，所以n S 中的最大值是12S ，无最小值，故C 不正确；对于D ，若2nS n n a =-+，则11a S a ==，2n ≥时，221(1)(1)nnn a S Sn n a n n a -=-=-+--+--22n =-，因为数列{}n a 为等差数列，所以12120a a =⨯-==，故D 正确.故选：AD 【点睛】关键点点睛：熟练掌握等差数列的通项公式、前n 项和公式是解题关键.14．题目文件丢失！15．已知数列{}na 的前4项为2，0，2，0，则该数列的通项公式可能为（ ）A ．0,2,nn a n ⎧=⎨⎩为奇数为偶数B ．1(1)1n na -=-+C ．2sin 2n n a π=D ．cos(1)1na n π=-+解析：BD 【分析】根据选项求出数列的前4项，逐一判断即可. 【详解】解：因为数列{}na 的前4项为2，0，2，0，选项A ：不符合题设；选项B ：01(1)12,a =-+=12(1)10,a =-+=23(1)12,a =-+=34(1)10a =-+=，符合题设；选项C ：，12sin2,2a π==22sin 0,a π==332sin 22a π==-不符合题设； 选项D ：1cos012,a =+=2cos 10,a π=+=3cos212,a π=+=4cos310a π=+=，符合题设.故选：BD. 【点睛】本题考查数列的通项公式的问题，考查了基本运算求解能力，属于基础题.16．朱世杰是元代著名数学家，他所著的《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中涉及一些“堆垛”问题，主要利用“堆垛”研究数列以及数列的求和问题.现有100根相同的圆形铅笔，小明模仿“堆垛”问题，将它们全部堆放成纵断面为等腰梯形的“垛”，要求层数不小于2，且从最下面一层开始，每一层比上一层多1根，则该“等腰梯形垛”应堆放的层数可以是（ ） A ．4 B ．5 C ．7D ．8解析：BD 【分析】依据题意，根数从上至下构成等差数列，设首项即第一层的根数为1a ，公差即每一层比上一层多的根数为1d =，设一共放()2n n ≥层，利用等差数列求和公式，分析即可得解. 【详解】依据题意，根数从上至下构成等差数列，设首项即第一层的根数为1a ，公差为1d =，设一共放()2n n ≥层，则总得根数为：()()111110022n n n d n n S na na --=+=+=整理得120021a n n=+-， 因为1a *∈N ，所以n 为200的因数，()20012n n+-≥且为偶数， 验证可知5,8n =满足题意. 故选：BD. 【点睛】关键点睛：本题考查等差数列的求和公式，解题的关键是分析题意，把题目信息转化为等差数列，考查学生的逻辑推理能力与运算求解能力，属于基础题. 17．已知数列{}na ：1，1，2，3，5，…其中从第三项起，每个数等于它前面两个数的和，记nS为数列{}na 的前n 项和，则下列结论正确的是（ ）A ．68S a = B ．733S =C ．13520212022a a a aa++++=D ．2222123202020202021a a a a aa++++=解析：BCD 【分析】根据题意写出8a ，6S ，7S ，从而判断A ，B 的正误；写出递推关系，对递推关系进行适当的变形，利用累加法即可判断C ，D 的正误． 【详解】对A ，821a =，620S =，故A 不正确；对B ，761333S S =+=，故B 正确；对C ，由12a a =，342a a a =-，564a a a =-，…，202120222020aaa=-，可得13520212022a a a aa +++⋅⋅⋅+=，故C 正确；对D ，该数列总有21n n n aaa ++=+，2121a a a =，则()222312321a a a a a a a a =-=-，()233423423a a a a a a a a =-=-，…，()220182018201920172018201920172018a a a a a a a a =-=-， 22019a =2019202020192018aaaa-，220202020202120202019a aaaa=-，故2222123202020202021a a a a a a+++⋅⋅⋅+=，故D 正确．故选：BCD 【点睛】关键点睛：解答本题的关键是对CD 的判断，即要善于利用21n n na aa ++=+对所给式子进行变形.18．已知等差数列{}na 的公差不为0，其前n 项和为nS，且12a 、8S 、9S 成等差数列，则下列四个选项中正确的有（ ）A ．59823a a S +=B ．27S S =C ．5S 最小D ．50a =解析：BD【分析】设等差数列{}na 的公差为d ，根据条件12a 、8S、9S 成等差数列可求得1a 与d 的等量关系，可得出na 、nS 的表达式，进而可判断各选项的正误.【详解】设等差数列{}na 的公差为d ，则8118788282S a d a d ⨯=+=+，9119899362S a d a d ⨯=+=+， 因为12a 、8S 、9S 成等差数列，则81922S a S =+，即11116562936a d a a d +=++，解得14a d =-，()()115n a a n d n d ∴=+-=-，()()219122nnn d n n dS na --=+=.对于A 选项，59233412a a d d +=⨯=，()2888942d S d -⨯==-，A 选项错误； 对于B 选项，()2229272d S d -⨯==-，()2779772d S d -⨯==-，B 选项正确；对于C 选项，()2298192224n d d S n n n ⎡⎤⎛⎫=-=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦. 若0d >，则4S 或5S 最小；若0d <，则4S 或5S 最大.C 选项错误；对于D 选项，50a =，D 选项正确.故选：BD. 【点睛】在解有关等差数列的问题时可以考虑化归为a 1和d 等基本量，通过建立方程（组）获得解，另外在求解等差数列前n 项和nS 的最值时，一般利用二次函数的基本性质或者数列的单调性来求解. 19．定义11222n nna a a H n-+++=为数列{}na 的“优值”.已知某数列{}na 的“优值”2n nH =，前n 项和为nS ，则（ ）A ．数列{}na 为等差数列 B ．数列{}na 为等比数列C ．2020202320202S =D ．2S ，4S ，6S 成等差数列解析：AC 【分析】由题意可知112222n n nna a a H n-+++==，即112222n n na a a n -+++=⋅，则2n ≥时，()()111221212n n n n na n n n ---=⋅--⋅=+⋅，可求解出1na n =+，易知{}na 是等差数列，则A 正确，然后利用等差数列的前n 项和公式求出nS ，判断C ，D 的正误.【详解】 解：由112222n n nna a a H n-+++==，得112222n n na a a n -+++=⋅，①所以2n ≥时，()211212212n n n a a an ---+++=-⋅，②得2n ≥时，()()111221212n n n n na n n n ---=⋅--⋅=+⋅， 即2n ≥时，1na n =+，当1n =时，由①知12a =，满足1na n =+．所以数列{}na 是首项为2，公差为1的等差数列，故A 正确，B 错，所以()32n n n S +=，所以2020202320202S =，故C 正确．25S =，414S =，627S =，故D 错， 故选：AC ． 【点睛】本题考查数列的新定义问题，考查数列通项公式的求解及前n 项和的求解，难度一般.20．数列{}n a 满足11,121n n naa a a +==+，则下列说法正确的是（ ） A ．数列1n a ⎧⎫⎨⎬⎩⎭是等差数列B ．数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和2nS n =C ．数列{}na 的通项公式为21nan =-D ．数列{}na 为递减数列解析：ABD【分析】首项根据11,121n n n a a a a +==+得到1112n n a a +-=，从而得到1na ⎧⎫⎨⎬⎩⎭是以首项为1，公差为2的等差数列，再依次判断选项即可.【详解】对选项A ，因为121n n naa a +=+，11a =， 所以121112n n nna a a a ++==+，即1112n na a+-= 所以1n a ⎧⎫⎨⎬⎩⎭是以首项为1，公差为2的等差数列，故A 正确.对选项B ，由A 知：112121nn n a数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和()21212n n n S n +-==，故B 正确. 对选项C ，因为121nn a =-，所以121n a n =-，故C 错误. 对选项D ，因为121n a n =-，所以数列{}n a 为递减数列，故D 正确. 故选：ABD 【点睛】本题主要考查等差数列的通项公式和前n 项和前n 项和，同时考查了递推公式，属于中档题.21．设等差数列{}na 的前n 项和为nS，若39S =，47a =，则（ ）A ．2nS n =B ．223nS n n =-C ．21na n =-D ．35na n =-解析：AC 【分析】利用等差数列{}na 的前n 项和公式、通项公式列出方程组，求出11a =，2d =，由此能求出na 与nS ．【详解】等差数列{}na 的前n 项和为n S ．39S =，47a =，∴31413239237S a d a a d ⨯⎧=+=⎪⎨⎪=+=⎩， 解得11a =，2d =，1(1)221na n n ∴+-⨯=-=．()21212nn nS n +-==故选：AC ． 【点睛】本题考查等差数列的通项公式求和公式的应用，考查等差数列的性质等基础知识，考查运算求解能力，是基础题．22．已知数列{}na 满足：13a =，当2n ≥时，()21111nn a a-=++-，则关于数列{}na 说法正确的是（ ）A ．28a =B ．数列{}na 为递增数列C ．数列{}na 为周期数列D ．22na n n =+解析：ABD【分析】由已知递推式可得数列{}1na +是首项为112a +=，公差为1的等差数列，结合选项可得结果. 【详解】()21111nn a a-=++-得()21111nn a a-+=++，∴1111nn a a-+=++，即数列{}1na +是首项为112a +=，公差为1的等差数列，∴12(1)11na n n +=+-⨯=+，∴22na n n =+，得28a =，由二次函数的性质得数列{}na 为递增数列，所以易知ABD 正确， 故选：ABD. 【点睛】本题主要考查了通过递推式得出数列的通项公式，通过通项公式研究数列的函数性质，属于中档题.23．无穷数列{}na 的前n 项和2nSan bn c =++，其中a ，b ，c 为实数，则（ ）A ．{}na 可能为等差数列 B ．{}na 可能为等比数列 C ．{}na 中一定存在连续三项构成等差数列 D ．{}na 中一定存在连续三项构成等比数列 解析：ABC 【分析】由2nS an bn c =++可求得na 的表达式，利用定义判定得出答案．【详解】当1n =时，11a S abc ==++．当2n ≥时，()()221112nnn a S San bn c a n b n c an a b -=-=++-----=-+．当1n =时，上式＝+a b ．所以若{}na 是等差数列，则0.ab a bc c +=++∴=所以当0c时，{}na 是等差数列， 00a cb ==⎧⎨≠⎩时是等比数列；当0c ≠时，{}na 从第二项开始是等差数列．故选：A B C 【点睛】本题只要考查等差数列前n 项和nS 与通项公式na 的关系，利用nS 求通项公式，属于基础题．24．等差数列{}na 的前n 项和为n S ，若90a <，100a >，则下列结论正确的是（ ）A ．109S S >B ．170S <C ．1819S S >D ．190S>解析：ABD 【分析】先根据题意可知前9项的和最小，判断出A 正确；根据题意可知数列为递减数列，则190a >，又181919S S a =-，进而可知1516S S >，判断出C 不正确；利用等差中项的性质和求和公式可知()01179179172171722aaa Sa <+⨯⨯===，()1191019101921919022aaa S a +⨯⨯===>，故BD 正确.【详解】根据题意可知数列为递增数列，90a <，100a >，∴前9项的和最小，故A 正确； ()11791791721717022a a a S a +⨯⨯===<，故B 正确；()1191019101921919022aaa S a +⨯⨯===>，故D 正确；190a >，181919S S a ∴=-， 1819S S ∴<，故C 不正确. 故选：ABD . 【点睛】本题考查等差数列的综合应用，考查逻辑思维能力和运算能力，属于常考题.三、等比数列多选题25．题目文件丢失！ 26．题目文件丢失！27．在数列{}na 中，如果对任意*n N ∈都有211n n n na a k aa+++-=-（k 为常数），则称{}na 为等差比数列，k 称为公差比.下列说法正确的是（ ） A ．等差数列一定是等差比数列 B ．等差比数列的公差比一定不为0 C ．若32n na =-+，则数列{}na是等差比数列D ．若等比数列是等差比数列，则其公比等于公差比 解析：BCD 【分析】考虑常数列可以判定A 错误，利用反证法判定B 正确，代入等差比数列公式判定CD 正确. 【详解】对于数列{}na ，考虑121,1,1nn n aaa++===，211n n n na aa a+++--无意义，所以A 选项错误；若等差比数列的公差比为0，212110,0n n n n n na aa a a a+++++---==，则1n n a a +-与题目矛盾，所以B 选项说法正确；若32n n a =-+，2113n n n na aa a+++-=-，数列{}n a 是等差比数列，所以C 选项正确； 若等比数列是等差比数列，则11,1n n q a a q -=≠，()()11211111111111n n nn n n n n n na q q a a a q a q q a a a q a q a q q +++--+---===---，所以D 选项正确. 故选：BCD 【点睛】易错点睛：此题考查等差数列和等比数列相关的新定义问题.解决此类问题应该注意： （1）常数列作为特殊的等差数列公差为0； （2）非零常数列作为特殊等比数列公比为1.28．已知数列{}na 的前n 项和为n S 且满足11130(2),3n n n a S S n a -+=≥=，下列命题中正确的是（ ）A ．1n S ⎧⎫⎨⎬⎩⎭是等差数列B ．13n S n= C ．13(1)n a n n =--D ．{}3nS 是等比数列解析：ABD 【分析】由1(2)n n n a S S n -=-≥代入已知式，可得{}n S 的递推式，变形后可证1n S ⎧⎫⎨⎬⎩⎭是等差数列，从而可求得nS ，利用nS 求出na ，并确定3n S 的表达式，判断D．【详解】因为1(2)n n n a S S n -=-≥，1130n n n n S S S S ---+=，所以1113nn S S--=，所以1n S ⎧⎫⎨⎬⎩⎭是等差数列，A 正确；公差为3，又11113S a ==，所以133(1)3nn n S =+-=，13n S n =．B 正确； 2n ≥时，由1n n n a S S -=-求得13(1)n a n n =-，但13a =不适合此表达式，因此C 错； 由13n S n =得1311333n n n S +==⨯，∴{}3n S 是等比数列，D 正确． 故选：ABD． 【点睛】本题考查等差数列的证明与通项公式，考查等比数列的判断，解题关键由1(2)n n n a S S n -=-≥，化已知等式为{}n S 的递推关系，变形后根据定义证明等差数列．29．已知数列{}na 前n 项和为nS.且1a p =，122(2)nn S Sp n --=≥（p 为非零常数）测下列结论中正确的是（ ）A ．数列{}na 为等比数列 B ．1p =时，41516S = C ．当12p =时，()*,m n m n a a a m n N +⋅=∈ D ．3856a a a a +=+解析：AC 【分析】 由122(2)nn S Sp n --=≥和等比数列的定义，判断出A 正确；利用等比数列的求和公式判断B 错误；利用等比数列的通项公式计算得出C 正确，D 不正确． 【详解】由122(2)n n S S p n --=≥，得22p a =. 3n ≥时，1222n n SSp ---=，相减可得120nn a a--=，又2112a a =，数列{}n a 为首项为p ，公比为12的等比数列，故A 正确； 由A 可得1p =时，44111521812S -==-，故B 错误； 由A 可得mnm na a a+⋅=等价为2121122m n m n p p ++⋅=⋅，可得12p =，故C 正确；38271133||||22128a a p p ⎛⎫+=+=⋅ ⎪⎝⎭，56451112||||22128a a p p ⎛⎫+=+=⋅ ⎪⎝⎭， 则3856a a a a +>+，即D 不正确；故选：AC. 【点睛】本题考查等比数列的通项公式和求和公式，考查数列的递推关系式，考查学生的计算能力，属于中档题．30．设等比数列{}na 的公比为q ，其前n 项和为nS，前n 项积为nT ，并且满足条件11a >，671a a >，67101a a -<-，则下列结论正确的是（ ） A ．01q << B ．8601a a <<C ．nS 的最大值为7SD ．nT 的最大值为6T解析：ABD 【分析】先分析公比取值范围，即可判断A，再根据等比数列性质判断B,最后根据项的性质判断C,D. 【详解】若0q <，则67670,00a a a a <>∴<与671a a >矛盾；若1q ≥，则11a >∴671,1a a >>∴67101a a ->-与67101a a -<-矛盾； 因此01q <<，所以A 正确；667710101a a a a -<∴>>>-，因此2768(,1)0a a a =∈，即B 正确；因为0na >，所以n S 单调递增，即n S 的最大值不为7S ，C 错误；因为当7n ≥时，(0,1)na ∈，当16n ≤≤时，(1,)na ∈+∞，所以nT 的最大值为6T ，即D正确； 故选：ABD 【点睛】本题考查等比数列相关性质，考查综合分析判断能力，属中档题.31．记单调递增的等比数列{}na 的前n 项和为nS，若2410a a +=，23464a a a =，则（ ） A ．112n n nSS ++-=B ．12n naC ．21n nS =-D ．121n nS -=-解析：BC 【分析】先求得3a ，然后求得q ，进而求得1a ，由此求得1,,nnn na S SS +-，进而判断出正确选项.【详解】由23464a a a =得3334a =，则34a =．设等比数列{}na 的公比为()0q q ≠，由2410a a +=，得4410q q+=，即22520q q -+=，解得2q 或12q =．又因为数列{}na 单调递增，所以2q，所以112810a a +=，解得11a =．所以12n na，()1122112n nnS ⨯-==--，所以()1121212n n n n n S S ++-=---=.故选：BC 【点睛】本题考查等比数列的通项公式、等比数列的性质及前n 项和，属于中档题.32．已知数列{a n }，{b n }均为递增数列，{a n }的前n 项和为S n ，{b n }的前n 项和为T n ．且满足a n +a n +1＝2n ，b n •b n +1＝2n （n ∈N *），则下列说法正确的有（ ） A ．0＜a 1＜1 B ．1＜b 12＜ C ．S 2n ＜T 2nD ．S 2n ≥T 2n解析：ABC 【分析】利用代入法求出前几项的关系即可判断出a 1，b 1的取值范围，分组法求出其前2n 项和的表达式，分析，即可得解.【详解】∵数列{a n }为递增数列；∴a 1＜a 2＜a 3；∵a n+a n +1＝2n ，∴122324a a a a +=⎧⎨+=⎩； ∴12123212244a a aa a a a +⎧⎨+=-⎩＞＞ ∴0＜a 1＜1；故A 正确．∴S 2n ＝（a 1+a 2）+（a 3+a 4）+…+（a 2n ﹣1+a 2n ）＝2+6+10+…+2（2n ﹣1）＝2n 2； ∵数列{b n}为递增数列；∴b 1＜b 2＜b 3； ∵b n•b n +1＝2n∴122324b b b b =⎧⎨=⎩； ∴2132b b b b⎧⎨⎩＞＞； ∴1＜b 12＜，故B 正确．∵T 2n ＝b 1+b 2+…+b 2n＝（b 1+b 3+b 5+…+b 2n ﹣1）+（b 2+b 4+…+b 2n ）()()()()121212122122nnn b b b b⋅--=+=+-()()122212221n n b b ≥-=-； ∴对于任意的n ∈N*，S 2n ＜T 2n；故C 正确，D 错误．故选：ABC 【点睛】本题考查了分组法求前n 项和及性质探究，考查了学生综合分析，转化划归，数学运算的能力，属于较难题.33．定义在()(),00,-∞⋃+∞上的函数()f x ，如果对于任意给定的等比数列{}na ，数列(){}nf a 仍是等比数列，则称()f x 为“保等比数列函数”.现有定义在()(),00,-∞⋃+∞上的四个函数中，是“保等比数列函数”的为（ ）A ．()2f x x =B ．()2x f x =C ．()f x x =D ．()ln f x x =解析：AC 【分析】直接利用题目中“保等比数列函数”的性质，代入四个选项一一验证即可. 【详解】设等比数列{}na 的公比为q .对于A ，则2221112()()n n n n n nf a a a q f a a a +++⎛⎫=== ⎪⎝⎭ ，故A 是“保等比数列函数”； 对于B ，则111()22()2n n n na a a n a nf a f a ++-+==≠ 常数，故B 不是“保等比数列函数”； 对于C ，则111()()n n n nnnaf a aq f a aa+++=== ，故C 是“保等比数列函数”；对于D ，则11ln ln ln ln ln ()1()ln ln ln ln n n n n nnnnna a q a q q f a f a a a a a++⋅+====+≠ 常数，故D 不是“保等比数列函数”. 故选：AC. 【点睛】本题考查等比数列的定义，考查推理能力，属于基础题.34．已知等比数列{a n }的公比23q =-，等差数列{b n }的首项b 1＝12，若a 9＞b 9且a 10＞b 10，则以下结论正确的有（ ） A ．a 9•a 10＜0 B ．a 9＞a 10C ．b 10＞0D ．b 9＞b 10解析：AD 【分析】设等差数列的公差为d ，运用等差数列和等比数列的通项公式分析A 正确，B 与C 不正确，结合条件判断等差数列为递减数列，即可得到D 正确． 【详解】数列{a n }是公比q 为23-的等比数列，{b n }是首项为12，公差设为d 的等差数列，则8912()3a a =-，91012()3a a =-， ∴a 9•a 1021712()3a =-＜0，故A 正确； ∵a 1正负不确定，故B 错误； ∵a 10正负不确定，∴由a 10＞b 10，不能求得b 10的符号，故C 错误； 由a 9＞b 9且a 10＞b 10，则a 1（23-）8＞12+8d ，a 1（23-）9＞12+9d ，由于910,a a 异号，因此90a <或100a<故 90b <或100b <，且b 1＝12可得等差数列{b n }一定是递减数列，即d ＜0， 即有a 9＞b 9＞b 10，故D 正确． 故选：AD 【点睛】本题考查了等差等比数列的综合应用，考查了等比数列的通项公式、求和公式和等差数列的单调性，考查了学生综合分析，转化划归，数学运算的能力，属于中档题.35．等差数列{}na 的公差为d ，前n 项和为nS，当首项1a 和d 变化时，3813++a a a 是一个定值，则下列各数也为定值的有( )A ．7aB ．8aC ．15SD ．16S解析：BC 【分析】根据等差中项的性质和等差数列的求和公式可得出结果. 【详解】由等差中项的性质可得381383a a a a ++=为定值，则8a 为定值，()11515815152a aS a +==为定值，但()()11616891682a aS a a +==+不是定值.故选：BC. 【点睛】本题考查等差中项的基本性质和等差数列求和公式的应用，考查计算能力，属于基础题.36．对于数列{}na ，若存在正整数()2k k ≥，使得1kk aa-<，1kk a a+<，则称ka 是数列{}na 的“谷值”，k 是数列{}na 的“谷值点”，在数列{}na 中，若98nan n=+-，下面哪些数不能作为数列{}na 的“谷值点”？（ ）A ．3B ．2C ．7D ．5解析：AD。
2023-2024学年高考数学专项复习——压轴题(附答案)
决胜3．已知函数，曲线在处的切线方程为.()2e xf x ax =-()y f x =()()1,1f 1y bx =+(1)求的值：,a b (2)求在上的最值；()f x []0,1(3)证明：当时，.0x >()e 1e ln 0x x x x +--≥4．已知函数，.()()ln 1f x x x a x =-++R a ∈(1)若，求函数的单调区间；1a =()f x (2)若关于的不等式在上恒成立，求的取值范围；x ()2f x a≤[)2,+∞a (3)若实数满足且，证明.b 21a b <-+1b >()212ln f x b <-5．椭圆的离心率是，点是椭圆上一点，过点2222:1(0)x y E a b a b +=>>22()2,1M E 的动直线与椭圆相交于两点.()0,1P l ,A B (1)求椭圆的方程；E (2)求面积的最大值；AOB (3)在平面直角坐标系中，是否存在与点不同的定点，使恒成立？存在，xOy P Q QA PAQB PB=求出点的坐标；若不存在，请说明理由.Q 6．已知函数，.()21ln 2f x a x x⎛⎫=-+ ⎪⎝⎭()()()2R g x f x ax a =-∈(1)当时，0a =（i ）求曲线在点处的切线方程；()y f x =()()22f ,（ii ）求的单调区间及在区间上的最值；()f x 1,e e ⎡⎤⎢⎥⎣⎦(2)若对，恒成立，求a 的取值范围.()1,x ∀∈+∞()0g x <(1)求抛物线的表达式和的值；,t k (2)如图1，连接AC ，AP ，PC ，若△APC 是以(3)如图2，若点P 在直线BC 上方的抛物线上，过点的最大值．12CQ PQ +(1)【基础训练】请分别直接写出抛物线的焦点坐标和准线l 的方程；22y x =(2)【技能训练】如图2所示，已知抛物线上一点P 到准线l 的距离为6，求点P 的坐218y x =标；(3)【能力提升】如图3所示，已知过抛物线的焦点F 的直线依次交抛物线及准()20y ax a =>线l 于点，若求a 的值；、、A B C 24BC BF AF ==，(4)【拓展升华】古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点C 将一条线段分为两段和，使得其中较长一段是全线段与另一AB AC CB AC AB 段的比例中项，即满足：，后人把这个数称为“黄金分割”，把CB 512AC BC AB AC -==512-点C 称为线段的黄金分割点.如图4所示，抛物线的焦点，准线l 与y 轴AB 214y x=(0,1)F 交于点，E 为线段的黄金分割点，点M 为y 轴左侧的抛物线上一点.当(0,1)H -HF 时，求出的面积值.2MH MF=HME 10．已知双曲线的一条渐近线方程的倾斜角为，焦距为4．2222:1(0,0)x y C a b a b -=>>60︒(1)求双曲线的标准方程；C (2)A 为双曲线的右顶点，为双曲线上异于点A 的两点，且．C ,M N C AM AN ⊥①证明：直线过定点；MN ②若在双曲线的同一支上，求的面积的最小值．,M N AMN(1)试用解析几何的方法证明：(2)如果将圆分别变为椭圆、双曲线或抛物线，你能得到类似的结论吗？13．对于数集（为给定的正整数），其中，如果{}121,,,,n X x x x =-2n ≥120n x x x <<<< 对任意，都存在，使得，则称X 具有性质P ．,a b X ∈,c d X ∈0ac bd +=(1)若，且集合具有性质P ，求x 的值；102x <<11,,,12x ⎧⎫-⎨⎬⎩⎭(2)若X 具有性质P ，求证：；且若成立，则；1X ∈1n x >11x =(3)若X 具有性质P ，且，求数列的通项公式．2023n x =12,,,n x x x 14．已知，是的导函数，其中．()2e xf x ax =-()f x '()f x R a ∈(1)讨论函数的单调性；()f x '(2)设，与x 轴负半轴的交点为点P ，在点P()()()2e 11x g x f x x ax =+-+-()y g x =()y g x =处的切线方程为．()y h x =①求证：对于任意的实数x ，都有；()()g x h x ≥②若关于x 的方程有两个实数根，且，证明：()()0g x t t =>12,x x 12x x <．()2112e 11e t x x --≤+-15．在平面直角坐标系中，一动圆经过点且与直线相切，设该动圆圆心xOy 1,02A ⎛⎫ ⎪⎝⎭12x =-的轨迹为曲线K ，P 是曲线K 上一点．(1)求曲线K 的方程；(2)过点A 且斜率为k 的直线l 与曲线K 交于B 、C 两点，若且直线OP 与直线交//l OP 1x =于Q 点．求的值；||||AB ACOP OQ ⋅⋅(3)若点D 、E 在y 轴上，的内切圆的方程为，求面积的最小值．PDE △()2211x y -+=PDE △16．已知椭圆C ：，四点中恰有三()222210x y a b a b +=>>()()1234331,1,0,1,1,,1,22P P P P ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭点在椭圆C 上．(1)求椭圆C 的方程；(2)设直线l 不经过P 2点且与C 相交于A ，B 两点，若直线与直线的斜率的和为，2P A 2P B 1-证明：l 过定点．18．给定正整数k ，m ，其中，如果有限数列同时满足下列两个条件．则称2m k ≤≤{}n a 为数列．记数列的项数的最小值为．{}n a (,)k m -(,)k m -(,)G k m 条件①：的每一项都属于集合；{}n a {}1,2,,k 条件②：从集合中任取m 个不同的数排成一列，得到的数列都是的子列．{}1,2,,k {}n a 注：从中选取第项、第项、…、第项（）形成的新数列{}n a 1i 2i 5i 125i i i <<<…称为的一个子列．325,,,i i i a a a ⋯{}n a (1)分别判断下面两个数列，是否为数列．并说明理由！(33)-，数列；1:1,2,3,1,2,3,1,2,3A 数列．2:1,2,3,2,1,3,1A (2)求的值；(),2G k (3)求证．234(,)2k k G k k +-≥答案：1．(1)极大值为，无极小值2e (2)证明见解析【分析】（1）求导，根据导函数的符号结合极值的定义即可得解；（2）构造函数，利用导数求出函数的最小值，再()21()()()2ln 12F x f x g x x x x x x =+=+->证明即可或者转换不等式为，通过构造函数可得证.()min0F x >()112ln 012x x x +->>【详解】（1）的定义域为，，()f x (0,)+∞()2(1ln )f x x '=-+当时，，当时，，10e x <<()0f x '>1e x >()0f x '<所以函数在上单调递增，在上单调递减，()f x 10,e ⎛⎫ ⎪⎝⎭1,e ⎛⎫+∞ ⎪⎝⎭故在处取得极大值，()f x 1e x =12e e f ⎛⎫= ⎪⎝⎭所以的极大值为，无极小值；()f x 2e （2）设，()21()()()2ln 12F x f x g x x x x x x =+=+->解法一：则，()2ln 1F x x x '=--令，，()()2ln 11h x x x x =-->22()1x h x x x -'=-=当时，，单调递减，当时，，单调递增，12x <<()0h x '<()h x 2x >()0h x '>()h x 又，，，(2)1ln 40h =-<(1)0h =(4)32ln 40h =->所以存在，使得，即．0(2,4)x ∈0()0h x =002ln 10x x --=当时，，即，单调递减，01x x <<()0h x <()0F x '<()F x 当时，，即，单调递增，0x x >()0h x >()0F x '>()F x 所以当时，在处取得极小值，即为最小值，1x >()F x 0x x =故，22000000(11()()12ln )222F x F x x x x x x ≥=+-=-+设，因为，2000122()p x x x =-+0(2,4)x ∈由二次函数的性质得函数在上单调递减，2000122()p x x x =-+(2,4)故，0()(4)0p x p >=所以当时，，即．1x >()0F x >()()0f x g x +>解法二：要证，即证，()0F x >()1()12ln 012p x x x x =+->>因为，所以当时，，单调递减，()124()122x p x x x x -'=-=>()1,4x ∈()0p x '<()p x 当时，，单调递增，()4,x ∞∈+()0p x '>()p x 所以，所以，即.()()4212ln 434ln 20p x p ≥=+-=->()0F x >()()0f x g x +>方法点睛：利用导数证明不等式问题，方法如下：（1）直接构造函数法：证明不等式（或）转化为证明()()f xg x >()()f xg x <（或），进而构造辅助函数；()()0f xg x ->()()0f xg x -<()()()h x f x g x =-（2）适当放缩构造法：一是根据已知条件适当放缩；二是利用常见放缩结论；（3）构造“形似”函数，稍作变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.2．(1)0(2)证明详见解析(3)2a ≤【分析】（1）利用导数求得的最小值.()g x （2）根据（1）的结论得到，利用放缩法以及裂项求和法证得不等式成立.2211ln 1n n ⎛⎫+≤ ⎪⎝⎭（3）由不等式分离参数，利用构造函数法，结合导数求得的取ln (2)10xx x x a x -+--≥a a 值范围.【详解】（1）依题意，，()21ln (,0)2f x x x x t t x =-+∈>R 所以，()()()()ln 1ln 10g x f x x x x x x '==-+=-->，所以在区间上单调递减；()111x g x x x -'=-=()g x ()0,1()()0,g x g x '<在区间上单调递增，()1,+∞()()0,g x g x '>所以当时取得最小值为.1x =()g x ()11ln110g =--=（2）要证明：对任意正整数，都有，(2)n n ≥222211111111e 234n ⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅++< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 即证明，22221111ln 1111ln e234n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅++< ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 即证明，222111ln 1ln 1ln 1123n ⎛⎫⎛⎫⎛⎫++++++< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 由（1）得，即()()()10f xg x g '=≥=ln 10,ln 1x x x x --≥≤-令，所以， *211,2,N x n n n =+≥∈222111ln 111n n n ⎛⎫+≤+-= ⎪⎝⎭所以222222111111ln 1ln 1ln 12323n n ⎛⎫⎛⎫⎛⎫++++++≤+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ，()111111111122312231n n n n <+++=-+-++-⨯⨯-- 111n=-<所以对任意正整数，都有.(2)n n ≥222211111111e 234n ⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅++< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ （3）若不等式恒成立，此时，ln (2)10xx x x a x -+--≥0x >则恒成立，ln 21x x x x x a x -+-≤令，()ln 21xx x x x h x x -+-=令，()()()e 10,e 10x x u x x x u x '=--≥=-≥所以在区间上单调递增，()u x[)0,∞+所以，当时等号成立，()0e 010,e 10,e 1x x u x x x ≥--=--≥≥+0x =所以，()ln e ln 21ln 1ln 212x x x x x x x x x x h x x x -+-+-+-=≥=当时等号成立，所以.ln 0,1x x x ==2a ≤利用导数求函数的最值的步骤：求导：对函数进行求导，得到它的导函数.导函数()f x ()f x '表示了原函数在不同点处的斜率或变化率.找出导数为零的点：解方程，找到使得导()0f x '=数为零的点,这些点被称为临界点，可能是函数的极值点（包括最大值和最小值），检查每个临界点以及区间的端点，并确认它们是否对应于函数的最值.3．(1)，1a =e 2b =-(2)；()max e 1f x =-()min 1f x =(3)证明见解析【分析】（1）利用切点和斜率列方程组，由此求得.,a b （2）利用多次求导的方法求得在区间上的单调性，由此求得在上的最值.()f x []0,1()f x []0,1（3）先证明时，，再结合（2）转化为，从0x >()()e 21f x x ≥-+()21e ln e x x x x x+--≥+而证得不等式成立.【详解】（1），()e 2x f x ax'=-∴，解得：，；()()1e 21e 1f a b f a b ⎧=-=⎪⎨=-=+'⎪⎩1a =e 2b =-（2）由（1）得：，()2e xf x x =-，令，则，()e 2x f x x '=-()e 2x h x x=-()e 2x h x '=-是增函数，令解得.()h x ()0h x '=ln 2x =∴，也即在上单调递减，()h x ()f x '()0,ln2()()0,h x h x '<在上单调递增，()ln2,+∞()()0,h x h x '>∴，∴在递增，()()ln 2ln222ln20h f ==->'()f x []0,1∴；；()()max 1e 1f x f ==-()()min 01f x f ==（3）∵，由（2）得过，()01f =()f x ()1,e 1-且在处的切线方程是，()y f x =1x =()e 21y x =-+故可猜测且时，的图象恒在切线的上方，0x >1x ≠()f x ()e 21y x =-+下面证明时，，设，，0x >()()e 21f x x ≥-+()()()e 21g x f x x =---()0x >∴，∴令，()()e 2e 2x g x x =---'()()()e 2e 2x x x g m x '--==-，()e 2x m x '=-由（2）得：在递减，在递增，()g x '()0,ln2()ln2,+∞∵，，，∴，()03e 0g '=->()10g '=0ln21<<()ln20g '<∴存在，使得，()00,1x ∈()0g x '=∴时，，时，，()()00,1,x x ∈⋃+∞()0g x '>()0,l x x ∈()0g x '<故在递增，在递减，在递增.()g x ()00,x ()0,1x ()1,+∞又，∴当且仅当时取“”，()()010g g ==()0g x ≥1x ==()()2e e 210x g x x x =----≥故，，由（2）得：，故，()e e 21x x xx+--≥0x >e 1x x ≥+()ln 1x x ≥+∴，当且仅当时取“=”，∴，1ln x x -≥1x =()e e 21ln 1x x x x x+--≥≥+即，∴，()21ln 1e e x x x x+--≥+()21e ln e x x x x x+--≥+即成立，当且仅当时“=”成立.()1ln 10e e x x x x +---≥1x =求解切线的有关的问题，关键点就是把握住切点和斜率.利用导数研究函数的单调性，如果一次求导无法求得函数的单调性时，可以考虑利用多次求导来进行求解.利用导数证明不等式恒成立，如果无法一步到位的证明，可以先证明一个中间不等式，然后再证得原不等式成立.4．(1)单调增区间为，单调减区间为；()0,1()1,+∞(2)(],2ln 2-∞(3)证明见解析【分析】（1）求导，再根据导函数的符号即可得解；（2）分离参数可得，构造函数，利用导数求出函数的最小ln 1x x a x ≤-ln (),21x xg x x x =≥-()g x 值即可得解；（3）由，得，则，要证21a b <-+21a b -<-2112()(e )e e 1a a b f x f a b ---≤=+<-+，即证，即证，构造函数()212ln f x b<-222e112ln bb b --+<-22212ln 0eb b b +-<，证明即可.()()()12ln e x h x x x x =>-()1h x <-【详解】（1）当时，，1a =()ln 1,0f x x x x x =-++>，由，得，由，得，()ln f x x '=-()0f x '>01x <<()0f x '<1x >故的单调增区间为，单调减区间为；()f x ()0,1()1,+∞（2），()ln 2,1x xf x a a x ≤∴≤- 令，ln (),21x x g x x x =≥-则，21ln ()(1)x xg x x --'=-令，则，()ln 1t x x x =-+11()1xt x x x -'=-=由，得，由，得，()0t x '>01x <<()0t x '<1x >故在递增，在递减，，()t x ()0,1()1,+∞max ()(1)0t x t ==，所以，()0t x ∴≤ln 1≤-x x 在上单调递增，，()0,()g x g x '≥∴[)2,+∞()min ()2g x g ∴=，(2)2ln 2a g ∴≤=的取值范围；a ∴(],2ln 2-∞（3），221,1b a b a <-+∴-<- 又，在上递增，11()(e )e a a f x f a --≤=+1e a y a -=+ R a ∈所以，2112()(e )e e 1a a b f x f a b ---≤=+<-+下面证明：，222e 112ln b b b --+<-即证，22212ln 0ebb b +-<令，则，21x b =>12ln 0e x x x +-<即，(2ln )e 1xx x -⋅<-令，则，()()()12ln e xh x x x x =>-()22ln 1e xh x x x x '⎛⎫=-+-⋅ ⎪⎝⎭令，则，()2()2ln 11x x x x x ϕ=-+->()()2221122()101x x x x x x ϕ---=--=<>∴函数在上单调递减，()x ϕ()1,+∞，()(1)0x ϕϕ∴<=在递减，()()0,h x h x '∴<(1,)+∞，()()1e 1h x h ∴<=-<-所以.()212ln f x b <-方法点睛：利用导数证明不等式问题，方法如下：（1）直接构造函数法：证明不等式（或）转化为证明()()f xg x >()()f xg x <（或），进而构造辅助函数；()()0f xg x ->()()0f xg x -<()()()h x f x g x =-（2）适当放缩构造法：一是根据已知条件适当放缩；二是利用常见放缩结论；（3）构造“形似”函数，稍作变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.5．(1)22142x y +=(2)2(3)存在，.()0,2Q 【分析】（1）由离心率及过点列方程组求解.()2,1M,a b （2）设直线为与椭圆方程联立，将表达为的函数，由基本不l 1y kx =+1212AOB S x x =⋅- k 等式求最大值即可.（3）先讨论直线水平与竖直情况，求出，设点关于轴的对称点，证得()0,2Q B y B '三点共线得到成立.,,Q A B 'QA PAQB PB=【详解】（1）根据题意，得，解得，椭圆C 的方程为.2222222211c a a b c a b ⎧=⎪⎪⎪=+⎨⎪⎪+=⎪⎩222422a b c ⎧=⎪=⎨⎪=⎩22142x y +=（2）依题意，设，直线的斜率显然存在，()()1122,,,A x y B x y l 故设直线为，联立，消去，得，l 1y kx =+221142y kx x y =+⎧⎪⎨+=⎪⎩y ()2212420k x kx ++-=因为直线恒过椭圆内定点，故恒成立，，l ()0,1P 0∆>12122242,1212k x x x x k k +=-=-++故，()2221212221224212111214414222122AOBk S x x x x x x k k k k ⋅+⎛⎫⎛⎫=⋅=⨯-=⨯-⨯= ⎪ ⎪+⎝-+-⎝++⎭⎭- 令，所以，当且仅当，即时取得214,1t k t =+≥22222211AOB t S t t t=×=×£++1t =0k =等号，综上可知：面积的最大值为.AOB 2（3）当平行于轴时，设直线与椭圆相交于两点，如果存在点满足条件，l x ,C D Q 则有，即，所以点在轴上，可设的坐标为；||||1||||QC PC QD PD ==QC QD =Q y Q ()00,y 当垂直于轴时，设直线与椭圆相交于两点，如果存在点满足条件，l x ,M N Q 则有，即，解得或，||||||||QM PM QN PN =00221212y y --=++01y =02y =所以若存在不同于点的定点满足条件，则点的坐标为；P Q Q ()0,2当不平行于轴且不垂直于轴时，设直线方程为，l x x l 1y kx =+由（2）知，12122242,1212k x x x x k k --+==++又因为点关于轴的对称点的坐标为，B y B '()22,x y -又，，11111211QA y kx k k x x x --===-22222211QB y kx k k x x x '--===-+--.方法点睛：直线与椭圆0Ax By C ++=时，取得最大值2222220a A b B C +-=MON S 6．(1)（i ）；（322ln 220x y +--=(2)11,22⎡⎤-⎢⎥⎣⎦故曲线在点处的切线方程为，()y f x =()()22f ,()()32ln 222y x --+=--即；322ln 220x y +--=（ii ），，()21ln 2f x x x =-+()0,x ∈+∞，()211x f x x x x -'=-+=令，解得，令，解得，()0f x ¢>()0,1x ∈()0f x '<()1,x ∈+∞当时，，1,e e x ⎡⎤∈⎢⎥⎣⎦()()max 112f x f ==-又，，221111ln 1e 2e e 2e f ⎛⎫=-+=-- ⎪⎝⎭()2211e e ln e e 122f =-+=-+其中，()222211111e 1e 1e 20e 2e 222ef f ⎛⎫⎛⎫-=----+=--> ⎪ ⎪⎝⎭⎝⎭故，()()2min 1e e 12f x f ==-+故的单调递增区间为，单调递减区间为；()f x ()0,1()1,+∞在区间上的最大值为，最小值为；()f x 1,e e ⎡⎤⎢⎥⎣⎦12-21e 12-+（2），()21ln 22xg x a x x a ⎭-+⎛=⎪-⎫ ⎝对，恒成立，()1,x ∀∈+∞21ln 202a x x ax ⎛⎫-+-< ⎪⎝⎭变形为对恒成立，ln 122x a xa x<--⎛⎫ ⎪⎝⎭()1,x ∀∈+∞令，则，()(),1,ln x h x x x ∈=+∞()21ln xh x x -'=当时，，单调递增，()1,e x ∈()0h x '>()ln xh x x =当时，，单调递减，()e,+x ∈∞()0h x '<()ln xh x x =其中，，当时，恒成立，()10h =()ln e 1e e e h ==1x >()ln 0x h x x =>故画出的图象如下：()ln x h x x =其中恒过点122y xa a ⎛⎫ ⎪⎝=⎭--(2,1A 又，故在()210111h -'==()ln x h x x =又在上，()2,1A 1y x =-()对于2111644y x x =-+-∴点，即()0,6C -6OC =∵2114,14P m m m ⎛-+- ⎝∴点，3,64N m m ⎛⎫- ⎪⎝⎭∴，22111316624444PN m m m m m⎛⎫=-+---=-+ ⎪⎝⎭∵轴，PN x ⊥∴，//PN OC ∴，PNQ OCB ∠=∠∴，Rt Rt PQN BOC ∴，PN NQ PQ BC OC OB ==∵，8,6,10OB OC BC ===∴，34,55QN PN PQ PN==∵轴，NE y ⊥∴轴，//NE x ∴，CNE CBO ∴，5544CN EN m ==∴，2215111316922444216CQ PQ m m m m ⎛⎫+=-+=--+⎪⎝⎭当时，取得最大值.132m =12CQ PQ+16916关键点点睛：熟练的掌握三角形相似的判断及性质是解决本题的关键.8．(1)详见解析；(2)①具有性质；理由见解析；②P 1346【分析】（1）当时，先求得集合，由题中所给新定义直接判断即可；10n =A （2）当时，先求得集合， 1010n =A ①根据，任取，其中，可得，{}2021|T x x S =-∈02021t x T =-∈0x S ∈0120212020x ≤-≤利用性质的定义加以验证，即可说明集合具有性质；P T P ②设集合有个元素，由（1）可知，任给，，则与中必有个S k x S ∈12020x ≤≤x 2021x -1不超过，从而得到集合与中必有一个集合中至少存在一半元素不超过，然后利1010S T 1010用性质的定义列不等式，由此求得的最大值．P k【详解】（1）当时，，10n ={}1,2,,19,20A = 不具有性质，{}{}|910,11,12,,19,20B x A x =∈>= P 因为对任意不大于的正整数，10m 都可以找到该集合中的两个元素与，使得成立，110b ＝210b m =+12||b b m -=集合具有性质，{}*|31,N C x A x k k =∈=-∈P 因为可取，对于该集合中任一元素，110m =<，（），都有.112231,31c k c k =-=-*12,N k k ∈121231c c k k -=-≠（2）当时，集合，1010n ={}()*1,2,3,,2019,2020,1010N A m m =≤∈ ①若集合具有性质，那么集合一定具有性质．S P {}2021|T x x S =-∈P 首先因为，任取，其中．{}2021|T x x S =-∈02021t x T =-∈0x S ∈因为，所以．S A ⊆{}01,2,3,,2020x ∈ 从而，即，所以．0120212020x ≤-≤t A ∈T A ⊆由具有性质，可知存在不大于的正整数，S P 1010m 使得对中的任意一对元素，都有．s 12,s s 12s s m -≠对于上述正整数，从集合中任取一对元素，m {}2021|T x x S =-∈112021t x -＝，其中，则有．222021t x =-12,x x S ∈1212t t s s m --≠＝所以，集合具有性质P ；{}2021|T x x S =-∈②设集合有个元素，由（1）可知，若集合具有性质，S k S P 那么集合一定具有性质．{}2021|T x x S =-∈P 任给，，则与中必有一个不超过．x S ∈12020x ≤≤x 2021x -1010所以集合与中必有一个集合中至少存在一半元素不超过．S T 1010不妨设中有个元素不超过．S 2k t t ⎛⎫≥ ⎪⎝⎭12,,,t b b b 1010由集合具有性质，可知存在正整数．S P 1010m ≤使得对中任意两个元素，都有．S 12,s s 12s s m -≠所以一定有．12,,,t b m b m b m S +++∉ 又，故．100010002000i b m +≤+=121,,,b m b m b m A +++∈ 即集合中至少有个元素不在子集中，A t S 因此，所以，得．20202k k k t +≤+≤20202k k +≤1346k ≤当时，取，{}1,2,,672,673,,1347,,2019,2020S = 673m =则易知对集合中的任意两个元素，都有，即集合具有性质．S 12,y y 12673y y -≠S P 而此时集合S 中有个元素，因此，集合元素个数的最大值为．1346S 1346解新定义题型的步骤：(1)理解“新定义”——明确“新定义”的条件、原理、方法、步骤和结论.(2)重视“举例”,利用“举例”检验是否理解和正确运用“新定义”;归纳“举例”提供的解题方法.归纳“举例”提供的分类情况.(3)类比新定义中的概念、原理、方法，解决题中需要解决的问题.9．(1)，10,8⎛⎫ ⎪⎝⎭18y =-(2)或()42,4()42,4-(3)14a =(4)或51-35-【分析】（1）根据焦点和准线方程的定义求解即可；（2）先求出点P 的纵坐标为4，然后代入到抛物线解析式中求解即可；（3）如图所示，过点B 作轴于D ，过点A 作轴于E ，证明，推BD y ⊥AE y ⊥FDB FHC ∽出，则，点B 的纵坐标为，从而求出，证明16FD a =112OD OF DF a =-=112a 36BD a =，即可求出点A 的坐标为，再把点A 的坐标代入抛物线解析式AEF BDF ∽123,24a ⎛⎫ ⎪⎝+⎭-中求解即可；（4）如图，当E 为靠近点F 的黄金分割点的时候，过点M 作于N ，则，MN l ⊥MN MF=先证明是等腰直角三角形，得到，设点M 的坐标为，则MNH △NH MN=21,4m m ⎛⎫⎪⎝⎭过点B 作轴于D ，过点BD y ⊥由题意得点F 的坐标为F ⎛ ⎝1FH =当E 为靠近点F 的黄金分割点的时候，过点∵在中，Rt MNH △sin MHN ∠∴，∴是等腰直角三角形，45MHN ︒=MNH △双曲线方程联立，利用韦达定理及题目条件可得，后由题意可得AM AN ⋅= ()()222131t t m -+=-所过定点坐标；②结合①及图形可得都在左支上，则可得，后由图象可得,M N 213m <，后通过令，结合单调性229113m S m +=-223113m λλ⎛⎫+=≤< ⎪⎝⎭()423313f x x x x ⎛⎫=-≤< ⎪⎝⎭可得答案.【详解】（1）设双曲线的焦距为，C 2c 由题意有解得．2223,24,,ba c c ab ⎧=⎪⎪=⎨⎪=+⎪⎩1,3,2a b c ===故双曲线的标准方程为；C 2213y x -=（2）①证明：设直线的方程为，点的坐标分别为，MN my x t =+,M N ()()1122,,,x y x y 由（1）可知点A 的坐标为，()1,0联立方程消去后整理为，2213y x my x t ⎧-=⎪⎨⎪=+⎩x ()222316330m y mty t --+-=可得，2121222633,3131mt t y y y y m m -+==--，()212122262223131m t tx x m y y t t m m +=+-=-=--，()()()()222222222121212122223363313131m t m t m t x x my t my t m y y mt y y t t m m m -+=--=-++=-+=----由，()()11111,,1,AM x y AN x y =-=-有()()()1212121212111AM AN x x y y x x x x y y ⋅=--+=-+++，()()()()22222222222222222132331313131313131t t t t t t m t t t m m m m m m -----++-=--++===------由，可得，有或，AM AN ⊥0AM AN ⋅=1t =-2t =当时，直线的方程为，过点，不合题意，舍去；1t =-MN 1my x =-()1,0当时，直线的方程为，过点，符合题意，2t =MN 2my x =+()2,0-②由①，设所过定点为121224,31x x x x m +==-若在双曲线的同一支上，可知,M N 有12240,31x x x m +=<-关键点睛：求直线所过定点常采取先猜后证或类似于本题处理方式，设出直线方程，通过题一方面：由以上分析可知，设椭圆方程为一方面：同理设双曲线方程为()22221y m x a b +-=，()2222221b x a k x m a b -+=化简并整理得()(2222222112ba k x a mk x a m ---+一方面：同理设抛物线方程为(22x p y =，()212x p k x n =+化简并整理得，由韦达定理可得12220pk x x pn --=2,2x x pk x x pn +=⋅=-（2）构造，故转化为等价于“对任()()()()()13131931x x xx f x k k g x f x +--==+++()()()123g x g x g x +>意，，恒成立”，换元后得到（），分，和1x 2x 3R x ∈()()11k g x q t t -==+3t ≥1k >1k =三种情况，求出实数k 的取值范围.1k <【详解】（1）由条件①知，当时，有，即在R 上单调递增．12x x <()()12f x f x <()f x 再结合条件②，可知存在唯一的，使得，从而有．0R x ∈()013f x =()093x x f x x --=又上式对成立，所以，R x ∀∈()00093x x f x x --=所以，即．0001393x x x --=0009313x x x ++=设，因为，所以单调递增．()93x x x xϕ=++()9ln 93ln 310x x x ϕ'=++>()x ϕ又，所以．()113ϕ=01x =所以；()931x x f x =++（2）构造函数，()()()()()13131931x x xx f x k k g x f x +--==+++由题意“对任意的，，，1x 2x 3R x ∈均存在以，，为三边长的三角形”()()()11113x f x k f x +-()()()22213x f x k f x +-()()()33313x f x k f x +-等价于“对任意，，恒成立”．()()()123g x g x g x +>1x 2x 3R x ∈又，令，()111313x x k g x -=+++1131231333x x x x t ⋅=++≥+=当且仅当时，即时取等号，91x=0x =则（），()()11k g x q t t -==+3t ≥当时，，因为且，1k >()21,3k g x +⎛⎤∈ ⎥⎝⎦()()122423k g x g x +<+≤()3213k g x +<≤所以，解得，223k +≤4k ≤即；14k <≤当时，，满足条件；1k =()()()1231g x g x g x ===当时，，因为且，1k <()2,13k g x +⎡⎫∈⎪⎢⎣⎭()()122423k g x g x ++<≤()3213k g x +<≤所以，即．2413k +≤112k -≤<综上，实数k 的取值范围是．1,42⎡⎤-⎢⎥⎣⎦复合函数零点个数问题处理思路：①利用换元思想，设出内层函数；②分别作出内层函数与外层函数的图象，分别探讨内外函数的零点个数或范围；③内外层函数相结合确定函数交点个数，即可得到复合函数在不同范围下的零点个数.13．(1)14x =(2)证明过程见解析(3)，()112023k n k x --=1k n≤≤【分析】（1）由题意转化为对于，都存在，使得，其中(),m a b =(),n c d =0m n ⋅= ，选取，，通过分析求出；,,,a b c d X ∈()1,,2m a b x ⎛⎫== ⎪⎝⎭ ()(),1,n c d d ==- 14x =（2）取，，推理出中有1个为，则另一个为1，即，()()11,,m a b x x == (),n c d =,c d 1-1X ∈再假设，其中，则，推导出矛盾，得到；1k x =1k n <<101n x x <<<11x =（3）由（2）可得，设，，则有，记11x =()11,m s t =()22,n s t =1212s t t s =-，问题转化为X 具有性质P ，当且仅当集合关于原点对称，得到,,s B s X t X s t t ⎧⎫=∈∈>⎨⎬⎩⎭B ，共个数，由对称性可知也有个数，(){}234,0,,,,n B x x x x -∞=---- ()1n -()0,B +∞ ()1n -结合三角形数阵得到，得到数列为首项为1的等比123212321n n n n n n x x x x x x x x x x -----===== 12,,,n x x x 数列，设出公比为，结合求出公比，求出通项公式.q 2023n x =【详解】（1）对任意，都存在，使得，,a b X ∈,c d X ∈0ac bd +=即对于，都存在，使得，其中，(),m a b =(),n c d =0m n ⋅= ,,,a b c d X ∈因为集合具有性质P ，11,,,12x ⎧⎫-⎨⎬⎩⎭选取，，()1,,2m a b x ⎛⎫== ⎪⎝⎭ ()(),1,n c d d ==-则有，12x d -+=假设，则有，解得，这与矛盾，d x =102x x -+=0x =102x <<假设，则有，解得，这与矛盾，1d =-12x --=12x =-102x <<假设，则有，解得，这与矛盾，1d =12x -+=12x =102x <<假设，则有，解得，满足，12d =14x -+=14x =102x <<故；14x =（2）取，，()()11,,m a b x x == (),n c d =则，()10c d x +=因为，所以，即异号，120n x x x <<<< 0c d +=,c d 显然中有1个为，则另一个为1，即，,c d 1-1X ∈假设，其中，则，1k x =1k n <<101n x x <<<选取，，则有，()()1,,n m a b x x ==(),n s t =10n sx tx +=则异号，从而之中恰有一个为，,s t ,s t 1-若，则，矛盾，1s =-11n x tx t x =>≥若，则，矛盾，1t =-1n n x sx s x =<≤故假设不成立，所以；11x =（3）若X 具有性质P ，且，20231n x =>由（2）可得，11x =设，，则有，()11,m s t =()22,n s t =1212s t t s =-记，则X 具有性质P ，当且仅当集合关于原点对称，,,s B s X t X s t t ⎧⎫=∈∈>⎨⎬⎩⎭B 注意到是集合中唯一的负数，1-X 故，共个数，(){}234,0,,,,n B x x x x -∞=---- ()1n -由对称性可知也有个数，()0,B +∞ ()1n -由于，已经有个数，123421n n n n n nn n n n x x x x x x x x x x x x ----<<<<<< ()1n -对于以下三角形数阵：123421n n n n n n n n n n x x x x x xx x x x x x ----<<<<<< 1111123421n n n n n n n n x x x x xx x x x x --------<<<<< ……3321x x x x <21x x 注意到，123211111n n n x x x x x x x x x x -->>>>> 所以有，123212321n n n n n n x x x x x x x x x x -----===== 从而数列为首项为1的等比数列，设公比为，12,,,n x x x q 由于，故，解得，2023n x =112023n nx q x -==()112023n q -=故数列的通项公式为，.12,,,n x x x ()112023k n k x --=1k n ≤≤集合新定义问题，命题新颖，且存在知识点交叉，常常会和函数或数列相结合，很好的考虑了知识迁移，综合运用能力，对于此类问题，一定要解读出题干中的信息，正确理解问题的本质，转化为熟悉的问题来进行解决，要将“新”性质有机地应用到“旧”性质上，创造性的解决问题.14．(1)答案见解析(2)①证明见解析；②证明见解析【分析】（1）求出的导数，结合解不等式可得答案；()e 2x f x ax'=-（2）①，利用导数的几何意义求得的表达式，由此构造函数，()y h x =()()()F x g x h x =-利用导数判断其单调性，求其最小值即可证明结论；②设的根为，求得其表达式，()h x t=1x '并利用函数单调性推出，设曲线在点处的切线方程为，设11x x '≤()y g x =()0,0()y t x =的根为，推出，从而，即可证明结论.()t x t=2x '22x x '≥2121x x x x ''-≤-【详解】（1）由题意得，令，则，()e 2x f x ax'=-()e 2x g x ax=-()e 2x g x a'=-当时，，函数在上单调递增；0a ≤()0g x '>()f x 'R 当时，，得，，得，0a >()0g x '>ln 2x a >()0g x '<ln 2x a <所以函数在上单调递减，在上单调递增．()f x '(),ln 2a -∞()ln 2,a +∞（2）①证明：由（1）可知，令，有或，()()()1e 1x g x x =+-()0g x ==1x -0x =故曲线与x 轴负半轴的唯一交点P 为．()y g x =()1,0-曲线在点处的切线方程为，()1,0P -()y h x =则，令，则，()()()11h x g x '=-+()()()F x g x h x =-()()()()11F x g x g x '=--+所以，．()()()()11e 2e x F x g x g x '''=-=+-()10F '-=当时，若，，1x <-(],2x ∈-∞-()0F x '<若，令，则，()2,1x --()1()e 2e x m x x =+-()()e 30xm x x '=+>故在时单调递增，．()F x '()2,1x ∈--()()10F x F ''<-=故，在上单调递减，()0F x '<()F x (),1-∞-当时，由知在时单调递增，1x >-()()e 30x m x x '=+>()F x '()1,x ∈-+∞，在上单调递增，()()10F x F ''>-=()F x ()1,-+∞设曲线在点处的切线方程为()y g x =()0,0令()()()()(1e x T x g x t x x =-=+当时，2x ≤-()()2e x T x x =+-'()()2e xn x x =+-设，∴()()1122,,,B x y C x y 1x 又1211,22AB x AC x =+=+依题意，即，则，0bc <02x >()()220220004482x y c x x b =+---因为，所以，2002y x =0022x b c x -=-所以，()()00000242248122424S b c x x x x x -⋅=-++≥-⋅+=-=-当且仅当，即时上式取等号，00422x x -=-04x =所以面积的最小值为8．PDE △方法点睛：圆锥曲线中最值或范围问题的常见解法：（1）几何法，若题目的条件和结论能明显体现几何特征和意义，则考虑利用几何法来解决；（2）代数法，若题目的条件和结论能体现某种明确的函数关系，则可首先建立目标函数，再求这个函数的最值或范围．16．(1)2214x y +=(2)证明见解析(3)存在，7,,777⎛⎫⎛⎫-∞- ⎪ ⎪ ⎪ ⎪⎝+∞⎝⎭⎭ 【分析】（1）根据椭圆的对称性，得到三点在椭圆C 上．把的坐标代入椭圆234,,P P P 23,P P C ，求出，即可求出椭圆C 的方程；22,a b （2）当斜率不存在时，不满足；当斜率存在时，设，与椭圆方程联立，利():1l y kx t t =+≠用判别式、根与系数的关系，结合已知条件得到，能证明直线l 过定点；21t k =--()2,1-（3）利用点差法求出直线PQ 的斜率，从而可得直线PQ 的方程，与抛物线方程联14PQ k t =立，由，及点G 在椭圆内部，可求得的取值范围，设直线TD 的方程为，0∆>2t 1x my =+与抛物线方程联立，由根与系数的关系及，可求得m 的取值范围，进而可求得直线11DA TB k k =的斜率k 的取值范围．2l【详解】（1）根据椭圆的对称性，两点必在椭圆C 上，34331,,1,22P P ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭又的横坐标为1，4P ∴椭圆必不过，()11,1P ∴三点在椭圆C 上．()234330,1,1,,1,22P P P ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭把代入椭圆C ，()3231,20,1,P P ⎛⎫- ⎪ ⎪⎝⎭得，解得，222111314b a b ⎧=⎪⎪⎨⎪+=⎪⎩2241a b ⎧=⎨=⎩∴椭圆C 的方程为．2214x y +=（2）证明：①当斜率不存在时，设,，:l x m =()(),,,A A A m y B m y -∵直线与直线的斜率的和为，2P A 2P B 1-∴，221121A A P A P B y y k k m m m ----+=+==-解得m ＝2，此时l 过椭圆右顶点，不存在两个交点，故不满足．②当斜率存在时，设,，，:l y kx t =+1t ≠()()1122,,,A x y B x y 联立，消去y 整理得，22440y kx tx y =+⎧⎨+-=⎩()222148440k x ktx t +++-=则，，122814kt x x k -+=+21224414t x x k -=+则()()()()222112************111111P A P B x y x y x kx t x kx t y y k k x x x x x x -+-+-++---+=+==,()()()()()()12121222222448218114141144411142t k k kx x t tk t k t k k t t x t x x x +-+=--⋅+-⋅-++===--+-+又，∴，此时，1t ≠21t k =--()()222222644144464161664k t k t k t k ∆=-+-=-+=-故存在k ，使得成立，0∆>∴直线l 的方程为，即21y kx k =--()12y k x +=-∴l 过定点．()2,1-（3）∵点P ，Q 在椭圆上，所以，，2214P P x y +=2214Q Q x y +=两式相减可得，()()()()04PQ P Q P Q P Q y xy x x x y y +-++-=又是线段PQ 的中点，()1,G t -∴，2,2P Q P Q x x x x t+=-=∴直线PQ 的斜率，()144P Q P QP Q P QPQ x x k ty y x y y x +==-=--+∴直线PQ 的方程为，与抛物线方程联立消去x 可得，()114y x t t =++()22164410y ty t -++=由题可知，∴，()2161210t ∆=->2112t >又G 在椭圆内部，可知，∴，故，2114t +<234t <213124t <<设，，由图可知，，221212,,,44y y A y B y ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭223434,,,44y y T y D y ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭2134,y y y y >>∴，()2121216,441y y t y y t +==+当直线TD 的斜率为0时，此时直线TD 与抛物线只有1个交点，不合要求，舍去，设直线TD 的方程为，与抛物线方程联立，消去x 可得，()10x my m =+≠2440y my --=∴，34344,4y y m y y +==-由，可知，即，11//ATB D 11DA TB k k =3142222234214444y y y y y y y y --=--∴，即，1342y y y y +=+1243y y y y -=-∴，()()221212343444y y y y y y y y +-=+-∵，()()()()()222212124161641161210,128y y y y t t t +-=-+=-∈∴，解得，即，()()223434416160,128y y y y m +-=+∈27m <()7,7m ∈-∴直线TD 即的斜率．2l 771,77,k m ⎛⎫⎛⎫=∈-∞- ⎪ ⎪ ⎪ ⎪⎝+∞⎝⎭⎭ 思路点睛：处理定点问题的思路：（1）确定题目中的核心变量（此处设为），k （2）利用条件找到与过定点的曲线的联系，得到有关与的等式，k (),0F x y =k ,x y （3）所谓定点，是指存在一个特殊的点，使得无论的值如何变化，等式恒成立，()00,x y k 此时要将关于与的等式进行变形，直至找到，k ,x y ()00,x y ①若等式的形式为整式，则考虑将含的式子归为一组，变形为“”的形式，让括号中式k ()k ⋅子等于0，求出定点；②若等式的形式是分式，一方面可考虑让分子等于0，一方面考虑分子和分母为倍数关系，可消去变为常数.k 17．(1)1y =-(2)2ln23-+【分析】（1）由题意，将代入函数的解析式中，对函数进行求导，得到1m =()f x ()f x 和，代入切线方程中即可求解；()1f '()1f （2）得到函数的解析式，对进行求导，利用根的判别式以及韦达定理对()g x ()g x 进行化简，利用换元法，令，，可得，12122()()y x x b x x =--+12x t x =01t <<2(1)ln 1t y t t -=-+根据，求出的范围，构造函数，对进行求导，利用导数得到322m ≥t 2(1)()ln 1t h t tt -=-+()h t 的单调性和最值，进而即可求解．()h t 【详解】（1）已知(为常数），函数定义域为，()ln f x x mx =-m (0,)+∞当时，函数，1m =()ln f x x x =-可得，此时，又，11()1x f x x x -'=-=()=01f '()11=f -所以曲线在点处的切线方程为，即.()y f x =()()1,1f (1)0(1)y x --=⨯-1y =-（2）因为，函数定义域为，22()2()2ln 2g x f x x x mx x =+=-+(0,)+∞可得，222(1)()22x mx g x m x x x -+=-+='此时的两根，即为方程的两根，()0g x '=1x 2x 210x mx -+=因为，所以，由韦达定理得，，322m ≥240m ∆=->12x x m +=121=x x 又，所以1212lnx x b x x =-121212121212ln 22()()()()xx y x x b x x x x x x x x =--=--++-，11211211222212()ln 2ln 1x x x x x x x x x x x x --=-=⨯-++令，，所以，12x t x =01t <<2(1)ln 1t y t t -=-+因为，整理得，2212()x x m +=22212122x x x x m ++=因为，则，121=x x 2221212122x x x x m x x ++=等式两边同时除以，得，12x x 212212=x x m x x ++可得，因为，212t m t ++=322m ≥所以，，152t t +≥()()2252=2210t t x x -+--≥解得 或，则，12t ≤2t ≥102t <≤不妨设，函数定义域为，2(1)()ln 1t h t t t -=-+10,2⎛⎤⎥⎝⎦可得，22(1)()0(1)t h t t t -'=-<+所以函数在定义域上单调递减，()h t 此时，min 12()()ln223h t h ==-+故的最小值为．12122()()y x x b x x =--+2ln23-+利用导数求解在曲线上某点处的切线方程，关键点有两点，第一是切线的斜率，第二是切点。
高考数学选填压轴题练习与答案
高考数学选填压轴题练习与答案一．选择题（共25小题）1．数列{a n}满足a1＝1，na n+1＝（n+1）a n+n（n+1），若b n=a n cos2nπ3，且数列{b n}的前n项和为S n，则S11＝（）A．64B．80C．﹣64D．﹣80【解答】解：数列{a n}满足a1＝1，na n+1＝（n+1）a n+n（n+1），则a n+1n+1=a nn+1，可得数列{a nn}是首项为1、公差为1的等差数列，即有a nn=n，即为a n＝n2，则b n=a n cos2nπ3=n2cos2nπ3，则S11=−12（12+22+42+52+72+82+102+112）+（32+62+92）=−12（12+22﹣32﹣32+42+52﹣62﹣62﹣72+82﹣92﹣92+102+112）=−12×（5+23+41+59）＝﹣64．故选：C．2．已知函数f（x）＝sin（ωx+φ）（ω＞0，0＜φ＜π2），f（π6+x）＝﹣f（π6−x），f（π2+x）＝f（π2−x），下列四个结论：①φ=π4；②ω=92+3k（k∈N）；③f（−π2）＝0；④直线x=−π3是f（x）图象的一条对称轴．其中所有正确结论的编号是（）A．①②B．①③C．②④D．③④【解答】解：函数f（x）＝sin（ωx+φ）（ω＞0，0＜φ＜π2），f（x）图象的一条对称轴是直线x=π2，所以f（π2+x）＝f（π2−x），由f （x ）的一个零点为π6， 所以f （π6+x ）＝﹣f （π6−x ），整理得T 4+k ⋅T 2=π2−π6=π3， 所以T =4π3(1+2k)， 故ω=2πT=32+3k （k ∈Z ），故②错误；当k ＝1时，f （x ）＝sin （92x +φ）， 把（π6，0）代入关系式，得到sin （3π4+φ）＝0，由于0＜φ＜π2，所以φ=π4，故①正确；对于f （−π3）＝sin （92⋅π3+π4）≠±1，故④错误； f （−π2）＝sin[92⋅(−π2)+π4]＝sin （﹣2π）＝0，故③正确． 故选：B ．3．已知四面体ABCD 的四个顶点都在以AB 为直径的球R 面上，且BC ＝CD ＝DB ＝2，若四面体ABCD 的体积是4√23，则这个球面的面积是（ ）A ．16πB ．323πC ．4πD ．763π【解答】解：由题意，几何体的直观图如图， 四面体ABCD 的体积是4√23，可得O 到平面BCD 的距离为h ，13×√34×22×2ℎ=4√23，解得h =2√63， 所以外接球的半径为R ＝OB ＝OD ＝OC ＝OA =(2√63)(23√32=2，所以外接球的表面积为：4π×22＝16π． 故选：A ．4．已知函数f （x ）={log 2x ，x ＞114x +1，x ≤1，g （x ）＝f （x ）﹣kx ，若函数g （x ）有两个零点，则k 的取值范围是（ ） A ．（0，14]B ．（0，1eln2） C ．[0，1e）D ．[14，1eln2）【解答】解：函数f （x ）={log 2x ，x ＞114x +1，x ≤1，作出f （x ）的图象与y ＝kx 图象有两个交点，（如图）设y ＝kx 与y ＝log 2x 的切点为（x 0，y 0）， 可得{y 0=kx 0y 0=log 2x 01k =x 0ln2，解得x 0＝e ，∴相切时的斜率k =1eln2．故得f （x ）的图象与y ＝kx 图象有两个交点时，14≤k ＜1eln2． 故选：D ．5．已知F 是椭圆E ：x 2a 2+y 2b 2=1(a ＞b ＞0)的左焦点，椭圆E 上一点P （2，1）关于原点的对称点为Q ，若△PQF 的周长为4√2+2√5．则离心率e ＝（ ）A．√32B．√22C．√33D．√23【解答】解：∵P与Q关于原点对称，则Q（﹣2，﹣1），∴|PQ|＝2√12+22=2√5，又三角形PQF的周长为|QP|+|PF|+|QF|＝4√2+2√5，∴|PF|+|QF|＝4√2，设椭圆的右焦点为M，则由椭圆的性质可得|PF|＝|QM|，∴|QM|+|QF|＝2a＝4√2，得a＝2√2，将点P代入椭圆方程可得：48+1b2=1，解得b=√2，∴c=√a2−b2=√6．则离心率e=ca =√62√2=√32．故选：A．6．对于函数y＝f（x）与y＝g（x），若存在x0，使f（x0）＝g（﹣x0），则称M（x0，f（x0）），N（﹣x0，g（﹣x0））是函数f（x）与g（x）图象的一对“隐对称点”．已知函数f（x）＝m（x+1），g(x)=lnxx，函数f（x）与g（x）的图象恰好存在两对“隐对称点”，则实数m的取值范围为（）A．（﹣1，0）B．（﹣∞，﹣1）C．（0，1）∪（1，+∞）D．（﹣∞，﹣1）∪（﹣1，0）【解答】解：∵f（x）＝m（x+1）恒过定点（﹣1，0），f（x）关于y轴对称的图象的函数解析式为y＝﹣m（x﹣1）依题意可得，y＝﹣m（x﹣1）与g（x）=lnxx有2个交点，由g(x)=lnxx ，得g′（x）=1−lnxx2，当0＜x＜e时，h′（x）＞0，函数g（x）单调递增，当x＞e时，g′（x）＜0，函数g（x）单调递减，而y＝﹣m（x﹣1）恒过定点（1，0），作出函数g（x）=lnxx的图象如图，当直线y＝﹣m（x﹣1）与g(x)=lnxx切于（1，0）时，由导数的几何意义可得，﹣m=1−ln112=1，则要使y ＝﹣m （x ﹣1）与g （x ）=lnx x有2个交点，则﹣m ＞0且﹣m ≠1，∴实数m 的取值范围为（﹣∞，﹣1）∪（﹣1，0）． 故选：D ．7．已知函数f （x ）={|xlnx|，x ＞0|x(x +1)|，x ⩽0，关于x 的方程f 2（x ）+tf （x ）+1＝0（t ∈R ）有8个不同的实数根，则t 的取值范围是（ ） A ．（−1e −e ，+∞） B ．（−2e ，−12）∪（﹣∞，−1e −e ）C ．（﹣∞，−174）D ．（2，+∞）∪（﹣∞，−174）【解答】解：当x ＞0时，f （x ）＝|xlnx |，令F （x ）＝xlnx ，F ′（x ）＝lnx +1， 令F ′（x ）＝lnx +1＝0，解得x =1e，F （1e）=−1e，f （1e）=1e，故当x ＞0时，函数f （x ）在（0，1e ）上单调递增，在（1e ，1）上单调递减，在（1，+∞）上单调递增； 当x ＜0时，可得函数f （x ）在（﹣∞，﹣1）上单调递减，在（﹣1，−12）上单调递增，在（−12，0）上单调递减．又f （−12）=14，f （1e ）=1e ，故刻画出函数f （x ）的大致图象如图：令m ＝f （x ），则已知方程可化为m 2+tm +1＝0．观察图象可知，当m ＞1e 时，只有2个交点；当m =1e 时，有3个交点；当14＜m ＜1e 时，有4个交点； 当0＜m ＜14时，有6个交点．要想满足题意，则只需使得方程m 2+tm +1＝0在（14，1e ）上存在两个不同实数根，或在（1e ，+∞）和（0，14）上各有1个根，方程m 2+tm +1＝0的两根之积为1， 令g （m ）＝m 2+tm +1，由题意，{g(14)＜0g(4)＜0，解得t ＜−174，即t 的取值范围是（﹣∞，−174）．故选：C ．8．在棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中，点P 是正方体棱上一点，若满足|PB |+|PC 1|＝d 的点P 的个数为4．则d 的取值范围为（ ） A ．（√2，2）B ．（√2，2√2）C ．[2，1+√3）D ．（1+√3，2√2）【解答】解：点P 分别在BB 1，BC ，CC 1，B 1C 1上运动时，m 的取值范围是[√2，2]， 当点P 分别在C 1D 1，AB 上运动时，m 的取值范围是[√2，1+√3]， 当点P 分别在棱A 1B 1，CD 上运动时，m 的取值范围是[2，2√2]，当P 分别在棱A 1D 1，DD 1，AD ，AA 1上运动时，m 的取值范围是[√4+2√2，2√2]， 由结合图形可知，点P 在正方体的每一条棱上运动时， 它所在的位置与m 的值是一一对应的， 当|PB |+|PC 1|＝d 的点P 的个数为4， 则d 的取值范围为[2，1+√3）， 故选：C ．9．已知不相等的两个正实数x ，y 满足x 2﹣y ＝4（log 2y ﹣log 4x ），则下列不等式中不可能成立的是（ ）A．x＜y＜1B．y＜x＜1C．1＜x＜y D．1＜y＜x【解答】解：由已知x2﹣y＝4（log2y﹣log4x），因为2log4x＝log2x，所以原式可变形为x2+2log2x＝y+4log2y，令f（x）＝x2+2log2x，g（x）＝x+4log2x，函数f（x）与g（x）均为（0，+∞）上的增函数，且f（x）＝g（y），且f（1）＝g（1），当x＞1时，f（x）＞1，g（y）＞1，y＞1，当x＜1时，f（x）＜1，g（y）＜1，y＜1，要比较x与y的大小，只需比较g（x）与g（y）的大小，g（x）﹣g（y）＝g（x）﹣f（x）＝x+4log2x﹣x2﹣2log2x＝x﹣x2+2log2x，设h（x）＝x﹣x2+2log2x（x＞0），则h'（x）=1−2x+2xln2，故h'（x）在（0，+∞）上单调递减，又h'（1）=−1+2ln2＞0，h'（2）=−3+1ln2＜0，则存在x0∈（1，2）使得h'（x）＝0，所以当x∈（0，x0）时，h'（x）＞0，当x∈（x0，+∞）时，h'（x）＜0，又因为h（1）＝0，h（x0）＞h（1）＝0，h（4）＝﹣12+4＝﹣8＜0，所以当x＜1时，h（x）＜0，当x＞1时，h（x）正负不确定，故当x＜1，y＜1时，h（x）＜0，所以g（x）＜g（y）＜g（1），故x＜y＜1，当x＞1，y＞1时，h（x）正负不定，所以g（x）与g（y）的正负不定，所以x＞y＞1，x＝y＞1，y＞x＞1均有可能，即选项A，C，D均有可能，选项B不可能．故选：B．10．正实数a，b，c满足a+2﹣a＝2，b+3b＝3，c+log4c＝4，则实数a，b，c之间的大小关系为（）A．b＜a＜c B．a＜b＜c C．a＜c＜b D．b＜c＜a【解答】解：c+log4c＝4⇒log4c＝4﹣c，即c 为函数y ＝log 4x 与y ＝4﹣x 的图象交点的横坐标； b +3b ＝3⇒1+3b ＝4﹣b ，即b 为函数y ＝1+3x 与y ＝4﹣x 的图象交点的横坐标； a +2﹣a ＝2⇒2+12a =4−a ，即a 为函数y =2+12x 与y ＝4﹣x 的图象交点的横坐标； 在同一坐标系中画出图象，可得b ＜a ＜c ． 故选：A ．11．《九章算术》是我国古代数学经典名著，堪与欧几里得《几何原本》相媲美的数学名著，在《九章算术》中，将四个面都是直角三角形的四面体称为“鳖臑”．已知某鳖臑A ﹣BCD 的外接球半径为1，则该鳖臑A ﹣BCD 的体积最大值为（ ） A ．49√3B ．427√3C ．94√3D ．316√3【解答】解：四个面都是直角三角形的四面体称为“鳖臑”．如图：某鳖臑A ﹣BCD 的外接球半径为1，可知CD ＝2，设AB ＝a ，BC ＝b ，AD ＝c ， 所以a 2+b 2+c 2＝4，可得4＝a 2+b 2+c 2≥3√(abc)23，所以abc ≤√4333=8√39．当且仅当a ＝b ＝c =2√33时，取等号．该鳖臑A ﹣BCD 的体积：13×12abc ≤16×8√39=4√327． 故选：B ．12．已知抛物线y＝x2+mx﹣2与x轴交于A，B两点，点C的坐标为（3，1），圆Q过A，B，C三点，当实数m变化时，存在一条定直线l被圆Q截得的弦长为定值，则此定直线l方程为（）A．x﹣3y＝0B．3x﹣y+1＝0C．√3x﹣y﹣1＝0D．x−√3y＝0【解答】解：y＝x2+mx﹣2与x轴交于A，B，设两点A（x1，0），B（x2，0），设圆Q的方程为x2+y2+Dx+Ey+F＝0，取y＝0，可得x2+Dx+F＝0．则方程x2+Dx+F＝0与方程x2+mx﹣2＝0等价，则D＝m，F＝﹣2，则圆的方程为x2+y2+mx+Ey﹣2＝0．∵圆Q过C（3，1），∴10+3m+E﹣2＝0，即E＝﹣8﹣3m，得圆Q的方程为x2+y2+mx﹣（8+3m）y﹣2＝0，即x2+y2﹣8y﹣2+m（x﹣3y）＝0，由圆系方程可知，圆x2+y2﹣8y﹣2+m（x﹣3y）＝0经过圆x2+y2﹣8y﹣2＝0与直线x﹣3y＝0的交点，则圆Q被直线x﹣3y＝0所截弦长为定值．故选：A．+alnx+e2≥ax恒成立（e为自然对数的底数），则正实数a的取值范围是13．对任意x＞0，若不等式e xx（）A．（0，e]B．（0，e2]C．[2e ，e]D．[2e，e2]【解答】解：不等式e xx +alnx+e2≥ax可化为e xx−a（x﹣lnx）+e2≥0，即e xx−aln e xx+e2≥0；设t=e xx，其中x＞0；由e x≥ex知t≥e，所以f（t）＝t﹣alnt+e2（t≥e），只需证明f（t）的最小值f（t）min≥0即可；对函数f（t）求导数，得f′（t）＝1−at =t−at（t≥e），①当0＜a≤e时，f′（t）≥0恒成立，f（t）是[e，+∞）上的单调增函数，所以f（t）的最小值是f（t）min＝f（e）＝e﹣alne+e2≥0，解得a≤e2+e；又0＜a≤e，所以a的取值范围是（0，e]．②当a＞e时，f（t）在[e，a）上单调递减，在（a，+∞）上单调递增，所以f（t）的最小值是f（t）min＝f（a）＝a﹣alna+e2≥0；设g（a）＝a﹣alna+e2，其中a＞e，则g′（a）＝1﹣lna﹣1＝﹣lna＜0，所以g（a）在（e，+∞）上是单调减函数；g（e2）＝e2﹣e2lne2+e2＝0，所以g（a）≥0时，a≤e2；由a＞e知，a的取值范围是（e，e2]；综上知，正实数a的取值范围是（0，e2]．故选：B．14．已知双曲线x2a2−y2b2=1(a＞0，b＞0)的左、右焦点分别为F1，F2，O为坐标原点，点P是其右支上第一象限内的一点，直线PO，PF2分别交该双曲线左、右支于另两点A，B，若|PF1|＝2|PF2|，且∠AF2B＝60°，则该双曲线的离心率是（）A．√3B．√2C．2√33D．√52【解答】解：由双曲线的定义可得|PF1|﹣|PF2|＝2a，由|PF1|＝2|PF2|，可得|PF2|＝2a，|PF1|＝4a，结合双曲线性质可以得到|PO|＝|AO|，而|F1O|＝|F2O|，结合四边形对角线平分，可得四边形PF1AF2为平行四边形，结合∠AF2B＝60°，得∠F1AF2＝60°，对三角形F1AF2，用余弦定理，得到|AF1|2+|AF2|2﹣|F1F2|2＝2|AF1|•|AF2|•cos∠F1PF2，由|PF1|＝2|PF2|，可得|AF1|＝2a，|AF2|＝4a，|F1F2|＝2c，代入上式子中，得到3a2＝c2，∴e=ca=√3，故选：A．15．如图，双曲线F：x2a2−y2b2=1（a＞0，b＞0）以梯形ABCD的顶点A，D为焦点，且经过点B，C，其中AB∥CD，∠BAD＝60°，|CD|＝4|AB|，则F的离心率为（）A．3√34B．√3C．65D．5√36【解答】解：如图，不妨设|AB|＝1，|CD|＝4，则|BD|＝1+2a，|AC|＝4+2a，在△ABD中，由余弦定理得1+4c2﹣2•1•2c•cos60°＝（1+2a）2，①在△ACD中，由余弦定理得16+4c2﹣2•4•2c•cos120°＝（4+2a）2，②②﹣①得，15+10c＝12a+15，则e=ca =65．故选：C．16．已知定义R在上的函数f（x），其导函数为f'（x），若f（x）＝f（﹣x）﹣2sin x．且当x≥0时，f'（x）+cos x＞0，则不等式f（x+π2）＞f（x）+sin x﹣cos x的解集为（）A．（﹣∞，π2）B．（π2，+∞）C．（﹣∞，﹣π4）D．（﹣π4，+∞）【解答】解:令g(x)＝f(x)+sin x,则g(﹣x)＝f(﹣x)+sin(﹣x)＝f(﹣x)﹣sin x,又f(x)＝f(﹣x)﹣2sin x,∴f(x)+sin x＝f(﹣x)﹣sin x,故g(﹣x)＝g(x),∴g(x)为定义在R上的偶函数；当x≥0时,g′(x)＝f′(x)+cos x＞0,∴g(x)在[0,+∞)上单调递增,又∵g(x)为偶函数,故g(x)在(﹣∞,0]上单调递减,由f(x+π2)+cosx=f(x+π2)+sin(x+π2)＞f(x)+sinx得g(x+π2)＞g(x),∴|x+π2|＞|x|,解得x＞−π4,∴不等式的解集为(−π4,+∞)．故选：D．17．已知双曲线C：x2a2−y2b2=1（a＞0，b＞0），过C的右焦点F作垂直于渐近线的直线l交两渐近线于A，B两点，A，B两点分别在一、四象限，若|AF||BF|=513，则双曲线C的离心率为（）A．1312B．√133C．√135D．√13【解答】解：由题意知：双曲线的右焦点F（c，0），渐近线方程为y=±bax，即bx±ay＝0，如下图所示：由点到直线距离公式可知：|F A |=√a 2+b 2=b ，又∵c 2＝a 2+b 2，∴|OA |＝a ，∵|AF||BF|=513，∴|BF |=135b ，设∠AOF ＝α，由双曲线对称性可知∠AOB ＝2α， 而tan α=ba ，tan2α=|AB||OA|=18b 5a，由正切二倍角公式可知：tan2α=2tanα1−tan 2α=2×b a 1−(b a)2=2ab a 2−b 2，即2ab a 2−b2=18b 5a，化简可得：4a 2＝9b 2， 由双曲线离心率公式可知：e =c a=√1+b 2a2=√1+49=√133． 故选：B ．18．数学中一般用min {a ，b }表示a ，b 中的较小值．关于函数f(x)=min{sinx +√3cosx ，sinx −√3cosx}有如下四个命题：①f （x ）的最小正周期为π； ②f （x ）的图象关于直线x =3π2对称；③f （x ）的值域为[﹣2，2]；④f （x ）在区间(−π6，π4)上单调递增． 其中是真命题的是（ ） A ．②④B ．①②C ．①③D ．③④【解答】解：令g(x)=sinx +√3cosx =2sin(x +π3)，ℎ(x)=sinx −√3cosx =2sin(x −π3)， 则f （x ）＝min {g （x ），h （x ）}={g(x)，g(x)⩽ℎ(x)ℎ(x)，g(x)＞ℎ(x)={2sin(x +π3)，π2+2kπ⩽x ⩽3π2+2kπ2sin(x −π3)，−π2+2kπ＜x ＜π2+2kπ，(k ∈Z)，如图所示：由图知：则f （x ）的最小正周期为2π，故①错误； f （x ）的图象关于直线x =3π2对称，故②正确；f （x ）的值域为[﹣2，1]，故③错误；f （x ）在区间(−π6，π4)上单调递增，故④正确． 故选：A ．19．四棱锥P ﹣ABCD 中，底面ABCD 为矩形，体积为163，若P A ⊥平面ABCD ，且P A ＝2，则四棱锥P ﹣ABCD的外接球体积的最小值是（ ） A ．160√53π B ．256πC ．125πD ．20√53π【解答】解：底面为矩形的四棱锥P ﹣ABCD 的体积为163，若P A ⊥平面ABCD ，且P A ＝2， 可得底面面积为：8，设AB ＝a ，BC ＝b ，则ab ＝8，四棱锥的外接球就是扩展的长方体的外接球，PC 就是外接球的直径，可得：2R =√a 2+b 2+22≥√4+2ab =√4+2×8=2√5，当且仅当a ＝b ＝2√2，取等号，R ≥√5． 外接球的体积的最小值为：4π3×（√5）3=20√5π3．故选：D ．20．已知函数f （x ）={|log 2x|(x ＞0)2x 2+4x +1(x ≤0)，若函数F （x ）＝f （x ）﹣b 有四个不同的零点x 1，x 2，x 3，x 4，且满足：x 1＜x 2＜x 3＜x 4，则x 1+x 2﹣x 3x 4的值是（ ） A ．﹣4B ．﹣3C ．﹣2D ．﹣1【解答】解：作出f （x ）的函数图象如图所示：因为函数F （x ）＝f （x ）﹣b 有四个不同的零点x 1，x 2，x 3，x 4， 即y ＝f （x ）与y ＝b 有四个不同的交点， 由图象知 x 1+x 2＝﹣2×42×2=−2，由﹣log 2x 3＝log 2x 4，得：log 2x 3+log 2x 4＝0，得：x 3x 4＝1， ∴x 1+x 2﹣x 3x 4＝﹣3， 故选：B ．21．农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽籺，俗称“粽子”，古称“角黍”，是端午节大家都会品尝的食品，传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原．小明在和家人一起包粽子时，想将一丸子（近似为球）包入其中，如图，将粽叶展开后得到由六个边长为4的等边三角形所构成的平行四边形，将粽叶沿虚线折起来，可以得到如图所示的粽子形状的六面体，则放入丸子的体积最大值为（ ）A ．512√6729π B ．16√23π C ．32√627π D ．128√281π【解答】解：由题意可得每个三角形面积为S =12×4×2√3=4√3，由对称性可知该六面体是由两个正四面体合成的，可得该四面体的高为√16−(4√33)2=4√63，故四面体的体积为13×4√3×4√63=16√23，∵该六面体的体积是正四面体的2倍， ∴六面体的体积是32√23， 由图形的对称性得，内部的丸子要是体积最大，就是丸子要和六个面相切，连接球心和五个顶点，把六面体分成了六个三棱锥， 设丸子的半径为R ，则32√23=6×13×4√3×R ，解得R =4√69，∴丸子的体积的最大值为V max =4π3R 3=4π3×(4√69)3=512√6729π． 故选：A ．22．已知函数f （x ）＝e x ﹣aln （ax ﹣a ）+a （a ＞0），若关于x 的不等式f （x ）＞0恒成立，则实数a 的取值范围为（ ） A ．（0，e 2]B ．（0，e 2）C ．[1，e 2]D ．（1，e 2）【解答】解：∵f （x ）＝e x ﹣aln （ax ﹣a ）+a ＞0（a ＞0）恒成立， ∴e xa ＞ln(x −1)+lna −1， ∴e x ﹣lna+x ﹣lna ＞ln （x ﹣1）+x ﹣1， ∴e x﹣lna+x ﹣lna ＞e ln（x ﹣1）+ln （x ﹣1）．令g （x ）＝e x +x ，易得g （x ）在（1，+∞）上单调递增， ∴x ﹣lna ＞ln （x ﹣1），∴﹣lna ＞ln （x ﹣1）﹣x ． ∵ln （x ﹣1）﹣x ≤x ﹣2﹣x ＝﹣2， ∴﹣lna ＞﹣2，∴0＜a ＜e 2， ∴实数a 的取值范围为（0，e 2）． 故选：B ．23．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，若c cos A +a cos C ＝2，AC 边上的高为√3，则∠ABC 的最大值为（ ） A ．π6B ．π3C ．π2D ．2π3【解答】解：因为c cos A +a cos C ＝2， 所以由余弦定理可得c •b 2+c 2−a 22bc+a •a 2+b 2−c 22ab=2，整理可得b ＝2，因为AC 边上的高为√3， 所以12×2×√3=12acsinB ， 所以ac =2√3sinB， 因为cos B =a 2+c 2−b 22ac≥2ac−b 22ac=1−2ac，当且仅当a ＝c 时取等号，所以cos B ≥1−√33sinB ， 即3cos B +√3sin B ≥3， 所以2√3sin （B +π3）≥3，所以sin （B +π3）≥√32， 因为B ∈（0，π），所以B +π3∈（π3，4π3）， 所以B +π3∈（π3，2π3]，所以B ∈（0，π3]， 则∠ABC 的最大值为π3． 故选：B ．24．在平面直角坐标系xOy 中，若抛物线C ：y 2＝2px （p ＞0）的焦点为F ，直线x ＝3与抛物线C 交于A ，B 两点，|AF |＝4，圆E 为△F AB 的外接圆，直线OM 与圆E 切于点M ，点N 在圆E 上，则OM →⋅ON →的取值范围是（ ） A ．[−6325，9]B ．[﹣3，21]C ．[6325，21]D ．[3，27]【解答】解：抛物线C ：y 2＝2px （p ＞0）的焦点F （p2，0），准线方程为x =−p2， 设A （3，√6p ），所以|AF |＝3+p2=4，解得p ＝2， 所以抛物线的方程为y 2＝4x ，A （3，2√3），B （3，﹣2√3），F （1，0）， 所以直线AF 的方程为y =√3（x ﹣1）， 设圆心坐标为（x 0，0）， 所以（x 0﹣1）2＝（3﹣x 0）2+12， 解得x 0＝5，即E （5，0）， ∴圆的方程为（x ﹣5）2+y 2＝16，不妨设y M ＞0，设直线OM 的方程为y ＝kx ，则k ＞0， 根据√1+k2=4，解得k =43， 由{y =43x(x −5)2+y 2=16，解得M （95，125）， 设N （4cos θ+5，4sin θ）， 所以OM →•ON →=365cos θ+485sin θ+9=125（3cos θ+4sin θ）+9，因为3cos θ+4sin θ＝5sin （θ+φ）∈[﹣5，5]， 所以OM →•ON →∈[﹣3，21]． 故选：B ．25．已知双曲线x 24−y 25=1的右焦点为F ，点M 在双曲线上且在第一象限，若线段MF 的中点在以原点O为圆心，|OF |为半径的圆上，则直线MF 的斜率是（ ） A ．−√35B ．−5√117C ．5√117D ．√35【解答】解：如图所示，设线段MF 的中点为H ，连接OH ，设双曲线的右焦点为F，连接MF．双曲线的左焦点为F′，连接MF′，则OH∥MF′．又|OH|＝|OF|＝c＝3，|FH|=12|MF|=12（2a﹣2c）＝a﹣c＝1．设∠HFO＝α，在△OHF中，tanα=√32−(12)212=√35，∴直线MF的斜率是−√35．故选：A．二．多选题（共7小题）26．下列结论正确的是（）A．存在这样的四面体ABCD，四个面都是直角三角形B．存在这样的四面体ABCD，∠BAC＝∠CAD＝∠DAB＝∠BCD＝90°C．存在不共面的四点A、B、C、D，使∠ABC＝∠BCD＝∠CDA＝90°D．存在不共面的四点A、B、C、D，使∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°【解答】解：对于A，在长方体ABCD﹣A1B1C1D1中，四面体A1﹣ABC的四个面都是直角三角形，所以选项A正确；对于B ，三个直角均以A 为顶点，那么△BCD 为锐角三角形，故选项B 错误；对于C ，存在不共面的四点A 、B 、C 、D ，使∠ABC ＝∠BCD ＝∠CDA ＝90°，如图所示，故选项C 正确；对于D ，若∠ABC ＝∠BCD ＝∠CDA ＝∠DAB ＝90°，则A ，B ，C ，D 四点共面，故选项D 错误． 故选：AC ．27．已知函数f （x ）＝x 2﹣ax ﹣lnx （a ∈R ），则下列说法正确的是（ ） A ．若a ＝﹣1，则f （x ）是（0，12）上的减函数B ．若0＜a ＜1，则f （x ）有两个零点C ．若a ＝1，则f （x ）≥0D ．若a ＞1，则曲线y ＝f （x ）上存在相异两点M ，N 处的切线平行 【解答】解：函数f （x ）＝x 2﹣ax ﹣lnx （a ∈R ），对于A ，当a ＝﹣1，f （x ）＝x 2+x ﹣lnx （x ＞0），f ′（x ）＝2x +1−1x在（0，+∞）上单调递增，又f ′（12）＝0，故当x ∈（0，12）时，f ′（x ）＜0，则f （x ）是（0，12）上的减函数，故A 正确； 对于B ，若f （x ）＝0，则x 2﹣ax ﹣lnx ＝0，故a ＝x −lnx x（x ＞0），令g （x ）＝x −lnx x（x ＞0），则g ′（x ）＝1−1−lnx x 2=x 2+lnx−1x 2，再令h （x ）＝x 2+lnx ﹣1（x ＞0），显然，h （x ）在（0，+∞）上单调递增，又h （1）＝0，所以，当x ∈（0，1）时，h （x ）＜0，即g ′（x ）＜0，则g （x ）在（0，1）上单调递减， 当x ∈（1，+∞）时，h （x ）＞0，即g ′（x ）＞0，则g （x ）在（1，+∞）上单调递增， 故g （x ）min ＝g （1）＝1，要使f （x ）有零点，则a ≥1，故B 错误；对于C ，当a ＝1时，f （x ）＝x 2﹣x ﹣lnx （x ＞0），f ′（x ）＝2x ﹣1−1x 在（0，+∞）上单调递增，又f ′（1）＝0，故当x ∈（0，1）时，f ′（x ）＜0，则f （x ）是在（0，1）上单调递减；当x ∈（1，+∞）时，f ′（x ）＞0，则f （x ）在（1，+∞）上单调递增，故f （x ）≥f （1）＝0，故C 正确；对于D ，由于f ′（x ）＝2x ﹣a −1x （x ＞0），若曲线y ＝f （x ）上存在相异两点M （x 1，f （x 1）），N （x 2，f （x 2））处的切线平行， 则f ′（x 1）＝f ′（x 2）（x 1，x 2＞0，且x 1≠x 2）， 即2x 1﹣a −1x 1=2x 2﹣a −1x 2，即2x 1−1x 1=2x 2−1x 2，也就是f ′（x ）＝2x ﹣a −1x =0有两异根，即a ＝2x −1x （x ＞0）有两个交点．令t （x ）＝2x −1x （x ＞0），则t （x ）在（0，+∞）上单调递增，当t →0+时，t （x ）→﹣∞；当t →+∞时，t （x ）→+∞，故y ＝a 与t （x ）＝2x −1x （x ＞0）只有一个交点，故D 错误． 综上所述，AC 正确， 故选：AC ．28．已知无穷等差数列{a n }的公差d ∈N *，且5，17，23是{a n }中的三项，则下列结论正确的是（ ） A ．d 的最大值是6 B ．2a 2≤a 8C ．a n 一定是奇数D ．137一定是数列{a n }中的项【解答】解：∵无穷等差数列{a n }的公差d ∈N *，且5，17，23是{a n }中的三项， ∴设{17−5=12=md 23−17=6=nd ，解得d =6m−n ，∴d 的最大值为6，故A 正确； ∵a 1≤5，d ∈N *，∴2a 2﹣a 8＝a 1﹣5d ≤0，故B 正确；∵d =6m−n ，∴当m ﹣n ＝2时，d ＝3，数列可能为5，8，11，14，17，20，23，…，故C 错误； ∵137＝23+19×6，∴137一定是等差数列{a n }中的项，故D 正确． 故选：ABD ．29．已知函数f （x ）＝（sin x +cos x ）|sin x ﹣cos x |，下列说法正确的是（ ） A ．f （x ）是周期函数B ．f （x ）在区间[−π2，π2]上是增函数 C ．若|f （x 1）|+|f （x 2）|＝2，则x 1+x 2=kπ2（k ∈Z ）D ．函数g （x ）＝f （x ）+1在区间[0，2π]上有且仅有1个零点【解答】解：f （x ）＝（sin x +cos x ）|sin x ﹣cos x |={cos 2x −sin 2x ，sinx ＜cosx sin 2x −cos 2x ，sinx ≥cosx ={cos2x ，sinx ＜cosx−cos2x ，sinx ≥cosx ．其图象如图：由图可知，f （x ）是周期为2π的周期函数，故A 正确； f （x ）在区间[−π2，π2]上不是单调函数，故B 错误；若|f （x 1）|+|f （x 2）|＝2，由|f （x 1）|≤1，|f （x 2）|≤1，则只有|f （x 1）|＝|f （x 2）|＝1，即x 1，x 2只能是函数的最值点的横坐标， 可得x 1+x 2=kπ2（k ∈Z ），故C 正确；函数g （x ）＝f （x ）+1的图象是把y ＝f （x ）的图象向上平移1个单位得到的，则在区间[0，2π]上有且仅有2个零点，故D 错误． ∴说法正确的是AC ． 故选：AC ．30．已知F 1，F 2是双曲线E ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）的左、右焦点，过F 1作倾斜角为π3的直线分别交y 轴、双曲线右支于点M 、点P ，且|PM |＝|MF 1|，下列判断正确的是（ ）A．E的渐近线方程为y＝±√2x B．|MF2|=12|PF1|C．E的离心率等于2+√3D．∠F1PF2=π6【解答】解：如右图，由|PM|＝|MF1|，可得M为PF1的中点，又O为F1F2的中点，可得OM∥PF2，∠PF2F1＝90°，∠PF1F2＝60°，∠F1PF2＝30°，|MF2|=12|PF1|，故B正确，D正确；设|F1F2|＝2c，则|PF1|=2ccos60°=4c，|PF2|＝2c tan60°＝2√3c，则2a＝|PF1|﹣|PF2|＝（4﹣2√3）c，可得e=ca =(4−2√3)c=2+√3，ba=√c2a2−1=√6+4√3，则双曲线的渐近线方程为y＝±bax即为y＝±√6+4√3x．故C正确，A错误．故选：BCD．31．已知函数f（x）＝e x﹣cos x，x∈R，下列判断正确的是（）A．f（x）在（﹣2π，−32π）单调递增B．f（x）在（﹣π，0）有2个极值点C．f（x）在（﹣2π，−π2）仅有1个极小值D．当﹣4π≤x≤﹣2π时，f（x）≤1【解答】解：函数f（x）＝e x﹣cos x，则f′（x）＝e x+sin x，对于A，当x∈（﹣2π，−32π）时，f′（x）＞0，所以f（x）单调递增，故A正确；对于B，函数f′（x）＝e x+sin x的零点，即为方程f′（x）＝0的根，作出函数y＝﹣sin x与函数y＝e x的大致图象，如图所示：由图象可知，当x∈（﹣π，0）时，函数y＝﹣sin x与函数y＝e x有两个交点，则方程f′（x）＝0有两个实根，所以f（x）在（﹣π，0）有2个极值点，故B正确；对于C，由图象可得，函数y＝﹣sin x与函数y＝e x在（﹣2π，−π2）上只有一个交点，则方程f′（x）＝0只有一个实数根x0，且在（﹣2π，x0）上，f′（x）＞0，f（x）单调递增，在（x0，−π2）上，f′（x）＜0，f（x）单调递减，所以f（x）在x＝x0处取得极大值，故C错误；对于D，当x＝﹣3π时，f（x）＝e﹣3π+1＞1，故D错误．故选：AB．32．随着高三毕业日期的逐渐临近，有n（n≥2）个同学组成的学习小组，每人写了一个祝福的卡片准备送给其他同学，小组长收齐所有卡片后让每个人从中随机抽一张作为祝福卡片，则（）A．当n＝4时，每个人抽到的卡片都不是自己的概率为38B．当n＝5时，恰有一人抽到自己的卡片的概率为340C．甲和乙恰好互换了卡片的概率为1n−1−1nD．记n个同学都拿到其他同学的卡片的抽法数为a n，则a n+2＝（n+1）（a n+a n+1）n∈N*【解答】解：考虑n+1个同学时的情况，若n+1个同学都拿到其他同学的卡片，则第n+2个同学可以与其中任何一个交换卡片，若n+1个同学只有一个拿到自己的卡片，则第n+2个同学必须与该同学交换卡片，∴a n+2＝（n+1）a n+1+（n+1）a n，故D正确；a n+2﹣（n+2）a n+1＝﹣[a n+1﹣（n+1）a n]，∵a1＝0，a2＝1，∴a n﹣na n﹣1＝（﹣1）n，∴a n=n!⋅∑n i=2(−1)ii!，代入数据可得a4＝9，∴当n＝4时，每个人抽到的卡片都不是自己的概率为a44!=38，故A正确；当n＝5时，恰有一人抽到自己的卡片的概率为5a45!=38，故B错误；甲和乙恰好互换了卡片的概率为(n−2)!n!=1n−1−1n，故C正确．故选：ACD．三．填空题（共18小题）33．已知矩形ABCD中，AB=2，BC=√3，E是CD边的中点．现以AE为折痕将△ADE折起，当三棱锥D﹣ABE的体积最大时，该三棱锥外接球的表面积为16π3．【解答】解：由题意，当平面ADE⊥平面ABE时，三棱锥D﹣ABE的高最大值，此时体积最大．∵△ADE是直角三角形，∴三棱锥D﹣ABE换成B﹣ADE∴底面△ADE外接圆半径r=12AE＝1，垂直面△ABE是边长为2等边三角形，可得AE边上的高h=√3；设球心与圆心距离为d，球半径为R，R2＝r2+d2……①√3−d=R⋯⋯②由①②解得R=√3；三棱锥外接球的表面积S＝4πR2=16π3；故答案为：16π3．34．由正三棱锥S﹣ABC截得的三棱台ABC﹣A1B1C1的各顶点都在球O的球面上，若AB＝6，三棱台ABC ﹣A1B1C1的高为2，且球心O在平面ABC与平面A1B1C1之间（不在两平面上），则AB1的取值范围为(2√6，6)．【解答】解：该三棱台的横截面如图所示，因为△ABC为正三角形，且AB＝6，=2√3，则AH=√3又GH＝2，球心O在GH上，A，A1都在球面上，故OA＝OA1，设OH＝h，A1G＝m，则由△A1GO和△AOH均为直角三角形，所以m2+（2﹣h）2＝h2+12，解得m2＝8+4h，由图可知，h∈（0，2），m∈(0，2√3)，综上可得，m∈(2√2，2√3)，又A1B1=√3A1G，所以A1B1∈(2√6，6)，即AB1的取值范围为(2√6，6)．故答案为：(2√6，6)．35．设数列a1，a2，a3，a4各项互不相同，且a i∈{1，2，3，4}（i＝1，2，3，4）．若下列四个关系①a1＝1；②a2≠1；③a3＝2；④a4≠4中恰有一个正确，则（10a1+a2）﹣（10a3+a4）的最大值是18．【解答】解：若①正确，则②一定正确，因此不符合题意；若②正确，此时令a4＝4，a3＝1，a1＝3，a2＝2，则有（10a1+a2）﹣（10a3+a4）的最大值为18；若③正确，此时a4＝4，a2＝1，a1＝3，a3＝2，则有（10a1+a2）﹣（10a3+a4）的最大值为7；若④正确，此时a4＝2，a3＝3，a1＝4，a2＝1，则有（10a1+a2）﹣（10a3+a4）的最大值为9．综上可得，（10a1+a2）﹣（10a3+a4）的最大值为18．故答案为：1836．设抛物线C1：y＝x2﹣2x+2和C2：y＝﹣x2+ax+b在它们的一个交点处的切线互相垂直，则C2过定点（1，3）．2【解答】解：∵y＝x2﹣2x+2，∴y'＝2x﹣2，∵y＝﹣x2+ax+b，∴y'＝﹣2x+a，设交点为（x0，y0），∵它们在一个交点处切线互相垂直，∴（2x0﹣2）（﹣2x0+a）＝﹣1，即4x02﹣（2a+4）x0+2a﹣1＝0，①由交点分别代入二次函数式，整理得，2x02﹣（2+a）x0+2﹣b＝0，即4x02﹣（4+2a）x0+4﹣2b＝0，②由①②整理得2a﹣1﹣4+2b＝0，即a+b=52，所以C2：y＝﹣x2+ax+52−a，令x＝1，可得y=32，则C2过定点（1，32），故答案为：（1，32），37．在三棱锥A﹣BCD中，AB＝AC＝BC＝BD＝CD＝6，AD＝9，则三棱锥A﹣BCD外接球O的表面积为84π．【解答】解：如图所示：取BC的中点E，连接AE，DE，取AD的中点F，连接EF，因为AB＝AC＝BC＝BD＝CD＝6，所以AE⊥BC，DE⊥BC，且三角形ABC和三角形BCD都是正三角形，所以AE＝DE＝3√3，即三角形ADE为等腰三角形，所以EF⊥AD，且EF平分∠AED，不妨设三角形BCD的外接圆圆心为O′，且O′在DE上，所以EO′=13ED=√3，设外接球的球心为O，半径为R，则OA＝OD＝R，利用面面垂直可证得平面AED⊥平面BCD，又平面AED∩平面BCD＝ED，则球心O必在三角形AED中，又OA＝OD＝R，所以O在∠AED的角平分线EF上，连接OO′，则OO′⊥平面BCD，即OO′⊥ED，在三角形AED中，由余弦定理可得：cos∠AED=AE2+ED2−AD22AE⋅ED =−12，所以∠AED＝120°，所以∠FED=12∠AED＝60°，在Rt△EOO′中，tan∠FED=OO′EO′=√3=√3，所以OO′＝3，在Rt△OO′D中，OD＝R，O′D＝2√3，所以R2＝OO′2+O′D2＝21，所以球O的表面积为S＝4πR2＝84π，故答案为：84π．38．如图，在三棱锥A﹣BCD中，BC＝CD＝BD＝2√2，AB＝AC＝AD＝2a，若该三棱锥的侧面积是底面积的√3倍，则该三棱锥外接球的表面积为12π．【解答】解：取BC边的中点E，连结AE，如图所示，△BCD外接圆的圆心为F，三棱锥A﹣BCD外接球的球心为O，因为AB＝AC且点E为BC的中点，所以AE=√4a2−2，=3√2×√4a2−2=6√2a2−1，由此可知该三棱锥的侧面积S侧底面△BCD的面积为2√3，所以6√2a2−1=√3×2√3，解得a＝1，设三棱锥A﹣BCD外接球半径为R，OF＝x，因为AB＝AC＝AD＝2，所以点A在底面BCD上的射影为点F，因为AB＜BC，故三棱锥外接球球心O在直线AF的延长线上，BF为△BCD外接圆的半径，所以BF=2√6，3)2=4①，在Rt△ABF中，由勾股定理可得(R−x)2+(2√63)=R2②，在Rt△OBF中，由勾股定理可得x2+(2√63，由①②解得R=√3，x=√33所以外接球的表面积S ＝4πR 2＝12π． 故答案为：12π．39．在△ABC 中，点M ，N 是线段BC 上的两点，|MA →|＝|MB →|＝|MC →|＝1，MA →⋅MN →=12，则MA →⋅NA →= 12 ，|NA →|的取值范围是 （12，1] ．【解答】解：根据题意，画出大致图形如下：结合题意及图形， 可知MA →•MN →+MA →•NA →=MA →•（MN →+NA →） =MA →•MA →＝|MA →|2 ＝1，∵MA →⋅MN →=12， ∴MA →⋅NA →=1−12=12，又∵12=MA →⋅NA →=|MA →|•|NA →|•cos ＜MA →，NA →＞=|NA →|•cos ＜MA →，NA →＞， ∴|NA →|=12cos ＜MA →，NA →＞，由题意可知点N 在线段BC 上，假设点N 与点B 重合，则12=MA →⋅MN →=MA →•MB →=|MA →|•|MB →|•cos ＜MA →，MB →＞=cos ＜MA →，MB →＞， 即cos ∠BMA =12，∴∠BMA =π3或2π3，∴∠BAM =π3或π6，即cos ＜MA →，NA →＞=12或√32， 假设点N 与点C 重合，则12=MA →⋅MN →=MA →•MC →=|MA →|•|MC →|•cos ＜MA →，MC →＞=cos ＜MA →，MC →＞，此时cos ＜MA →，NA →＞=12或√32， 综合可得，12≤cos ＜MA →，NA →＞＜1， ∴1≤2cos ＜MA →，NA →＞＜2， ∴12＜12cos ＜MA →，NA →＞≤1，即12＜|NA →|≤1， 故答案为：12；（12，1]．40．已知一圆锥纸盒母线长为6，其轴截面为正三角形，在纸盒内放置一个棱长为a 的正方体，若正方体可在纸盒内任意转动，则a 的最大值为 2 ．【解答】解：由于正方体可在圆锥内任意转动，故当正方体棱长a 最大时，正方体外接球为圆锥内切球， 设圆心为P ，半径为r ，轴截面上球与圆锥母线切点为Q ，SO ⊥AB ，SO 平分AB ， 由△SAB 为正三角形，SA ＝SB ＝AB ＝6，OA ＝OB ＝3， 因为PB 为∠SAB 的角平分线，所以∠PBA ＝30°，PO ＝OB tan30°=√3=r ，由正方体外接球直径与正方体之间的关系可得，2R =√3a ， 又正方体外接球为圆锥内切球，所以√3a =2r =2√3，故a ＝2， 所以a 的最大值为2． 故答案为：2．41．若数列{a n}满足递推公式a n+2＝a n+1+a n（n∈N*），且a1＝a2，a2020＝2021，则a1+a3+a5+…+a2019＝2021．【解答】解：∵a1＝a2，a n+2＝a n+1+a n（n∈N*），且a2020＝2021，∴a1+a3+a5+…+a2019＝a2+a3+a5+…+a2019＝a4+a5+…+a2019＝…＝a2018+a2019＝a2020＝2021，故答案为：2021．42．法国著名的军事家拿破仑．波拿巴最早提出的一个几何定理：“以任意三角形的三条边为边向外构造三个等边三角形，则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点”．在三角形ABC中，角A ＝60°，以AB、BC、AC为边向外作三个等边三角形，其外接圆圆心依次为O1、O2、O3，若三角形O1O2O3的面积为√32，则三角形ABC的周长最小值为3√2．【解答】解：由题意知△O1O2O3为等边三角形，设边长为m，则S△O1O2O3=12m2sin60°=√34m2=√32，解得|O1O2|＝m=√2；设BC＝a，AC＝b，AB＝c，如图所示：在△O1AO2中，∠O1AB＝∠O1BA＝30°，由∠BAC ＝60°，所以∠O 1AO 2＝120°， 在等腰△BO 1A 中，ABO 1A=sin120°sin30°，解得O 1A =√3，同理得O 3A =√3，在△O 1AO 2中，由余弦定理得O 1O 32=O 1A 2+O 3A 2﹣2O 1A •O 3A •cos120°， 即2=c 23+b 23−2•bc 3•（−12），即b 2+c 2+bc ＝6，在△ABC 中，由余弦定理知， a 2＝b 2+c 2﹣2bc cos A ＝b 2+c 2﹣bc ， ∴a =√(b 2+c 2+bc)−2bc =√6−2bc ， 又∵（b +c ）2＝b 2+c 2+bc +bc ＝6+bc ， ∴b +c =√6+bc ，∴△ABC 的周长为a +b +c =√6−2bc +√6+bc ， 又∵b 2+c 2≥2bc ， ∴b 2+c 2+bc ＝6≥3bc ， ∴bc ≤2．令f （x ）=√6−2x +√6+x （0＜x ≤2）， 则f ′（x ）=√6−2x2√6+x ，当f ′（x ）＜0时，有√6−2x2√6+x0，解得x ＞3，∴f （x ）在（0，2]上单调递减， ∴当x ＝2时取得最小值，f （2）＝3√2． ∴a +b +c ≥3√2，即△ABC 的周长最小值为3√2． 故答案为：3√2．43．设函数f （x ）的定义域为D ，若存在x 0∈D ，使得f （x 0+1）＝f （x 0）+f （1），则称x 0为函数f （x ）的“可拆点”．若函数f(x)=log 2a1+x 2在（0，+∞）上存在“可拆点”，则正实数a 的取值范围为 [3−√5，2) ． 【解答】解：由已知可得函数f （x ）有“可拆点”， 则log 2（a1+x 2）+log 2（a2）＝log 2（a1+(1+x)2）成立，即a1+(1+x)2=a1+x2⋅a2，整理可得：（2﹣a）x2﹣2ax+2﹣2a＝0，从而问题转化为方程（2﹣a）x2﹣2ax+2﹣2a＝0在区间（0，+∞）上有解，设h（x）＝（2﹣a）x2﹣2ax+2﹣2a，由已知可得a＞0，则当a＞2且x＞0时，h（x）＜0，方程h（x）＝0无解，不满足题意，当a＝2时，方程h（x）＝0的根为−12，不满足题意，当0＜a＜2时，函数h（x）的图象的对称轴为x=a2−a＞0，要使方程h（x）＝0在区间（0，+∞）上有解，只需△＝4a2﹣4（2﹣a）（2﹣2a）≥0，解得3−√5≤a≤3+√5，所以3−√5≤a＜2，故实数a的取值范围为：[3−√5，2）．故答案为：[3−√5，2）．44．在棱长为√2的正方体ABCD﹣A1B1C1D1中，棱BB1，B1C1的中点分别为E，F，点P在平面BCC1B1内，作PQ⊥平面ACD1，垂足为Q．当点P在△EFB1内（包含边界）运动时，点Q的轨迹所组成的图形的面积等于√312．【解答】解：连结BD交AC于点O，连结OD1，B1D交于点H，设G为CD1的中点，因为AC⊥BD，AC⊥BB1，BB1∩BD＝B，BB1，BD⊂平面BB1D，所以AC⊥平面BB1D，因为B1D⊂平面BB1D，所以B1D⊥AC，同理可证B1D⊥AD1，又AC∩AD1＝A，AC，AD1⊂平面ACD1，所以B1D⊥平面ACD1，即点B1在平面ACD1的投影为H，且D1H＝2HO，同理，点E，F在面ACD1的投影分别为O，G，所以△EFB1在平面ACD1的投影为△OGH，又AC=√2AB=2，所以HC=HG=13D1C=13AC⋅√32=√33，所以点Q的轨迹所组成的图形的面积S=12CH⋅HG⋅sin120°=√312．故答案为：√312．45．已知F1，F2分别为双曲线x2a2−y2b2=1（a＞0，b＞0）的左、右焦点，过点F2作圆x2+y2＝a2的切线交双曲线左支于点M，且∠F1MF2＝60°，则该双曲线的渐近线方程为y＝±（1+√33）x．【解答】解：设切点为A，过F1作F1B⊥MF2，垂足为B，由题意可得|OA|＝a，|OF2|＝c，|AF2|=√c2−a2=b，由OA为△BF1F2的中位线，可得|BF1|＝2a，|BF2|＝2b，又∠F1MF2＝60°，可得|MF1|=|BF1|sin60°=√3，|MB|=√3|MF2|＝|MB|+|BF2|=√32b，又|MF2|﹣|MF1|=√3+2b√3=2a，所以b＝（1+√33）a，所以双曲线的渐近线方程为y＝±（1+√33）x．故答案为：y＝±（1+√33）x．46．已知函数f（x）＝xe x，g（x）=xe x，h（x）＝xlnx，现有以下四个命题：①f（x）﹣g（x）是奇函数；②函数f（x）的图象与函数g（x）的图象关于原点中心对称；③对任意x∈R，恒有f（x）≥g（x）；④函数f（x）与函数h（x）的最小值相同其中正确命题的序号是③④．【解答】解：函数f（x）＝xe x，g（x）=xe x，h（x）＝xlnx，对于①，令F（x）＝f（x）﹣g（x）＝x•e x﹣x•e﹣x，由于F（﹣x）＝F（x）故函数F（x）为偶函数，故①错误；对于②，函数f（﹣x）＝﹣x•e﹣x≠﹣f（x），所以函数f（x）不为奇函数，函数g（﹣x）=−xe−x=−x⋅e x≠−g(x)，所以函数g（x）不为奇函数，故②错误；对于③，当x＝0时，f（x）＝g（x）＝0，当x＞0时，e2x＞1，得到e x＞1e x，两边同乘以x得到x⋅e x＞xe x，即f（x）＞g（x），当x＜0时，e2x＜1，整理得e x＜1e x ，两边同乘以x得到x⋅e x＞xe x，即f（x）＞g（x），故③正确；对于④，f′（x）＝（1+x）•e x，令f′（x）＜0，得到x＜﹣1，f′（x）＞0，得到x＞﹣1，所以函数f（x）的最小值为f（﹣1）=−e−1=−1e．h′（x）＝1+lnx（x＞0），令h ′（x ）＜0，解得0＜x ＜1e ， 令h ′（x ）＞0，解得x ＞1e ，所以函数h （x ）的最小值为h （1e ）=1e ⋅ln 1e =−1e =f(−1)，故④正确； 故选：③④．47．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，已知sin A +2sin B ＝2cos A sin C ，a +b ＝3√2，△ABC 的面积是√3，则边长c ＝ √14 ． 【解答】解：∵sin A +2sin B ＝2cos A sin C ， ∴sin A +2sin （A +C ）＝2cos A sin C ， 即sin A +2sin A cos C +2cos A sin C ＝2cos A sin C ， 即sin A +2sin A cos C ＝0， ∵sin A ≠0，∴cos C =−12，则C ＝120°， ∵△ABC 的面积是S =12ab ×√32=√3，∴ab ＝4，则c 2＝a 2+b 2﹣2ab ×（−12）＝（a +b ）2﹣ab ＝18﹣4＝14， 则c =√14， 故答案为：√14．48．抛物线C ：y 2＝2px （p ＞0）的焦点为F ，其准线与x 轴的交点为A ，如果在直线x +y +4＝0上存在点M ，使得∠FMA ＝90°，则实数p 的取值范围是 [4√2，+∞） ． 【解答】解：由题意可得F （p2，0），A （−p2，0），∵M 在直线x +y +4＝0上，设点M （x ，﹣x ﹣4）， ∴AM →=（x +p2，﹣x ﹣4），FM →=（x −p2，﹣x ﹣4），又∠FMA ＝90°，∴AM →•FM →=（x +p 2）（x −p2）+（﹣x ﹣4）2＝0， 即2x 2+8x +16−p24=0，∴△＝82﹣4×2×（16−p24）＝2p2﹣64≥0，解得p ≤﹣4√2或p ≥4√2， 又p ＞0，∴p 的取值范围是[4√2，+∞）． 故答案为：[4√2，+∞）． 49．已知F 1，F 2是双曲线C 1：x 2a2−y 2b 2=1(a ＞0，b ＞0)与椭圆C 2：x 225+y 29=1的公共焦点，点P ，Q 分别是曲线C 1，C 2在第一、第三象限的交点，四边形PF 1QF 2的面积为6√6，设双曲线C 1与椭圆C 2的离心率依次为e 1，e 2，则e 1+e 2＝2√10+45．【解答】解：由题意可得a 2+b 2＝16，根据双曲线C 1与椭圆C 2的对称性可得△PF 1F 2的面积为3√6， 设P （x 0，y 0），（x 0，y 0＞0），则{12⋅8⋅y 0=3√6x 0225+y 029=1，解得x 0=5√104，y 0=3√64， 代入双曲线的方程结合b 2＝16﹣a 2，可得a 4﹣35a 2+250＝0，结合0＜a ＜c ＝4，解得a =√10， 双曲线的离心率为e 1=c a=√10=2√105， 而椭圆的离心率e 2=45， ∴e 1+e 2=2√10+45． 故答案为：2√10+45．50．一个球被平面截下的一部分叫做球缺，截面叫做球缺的底面，垂直于截面的直径被截下的线段长叫做球缺的高，球缺的体积公式为V =π3(3R −ℎ)ℎ2，其中R 为球的半径，h 为球缺的高．若一球与一棱长为。
2024全国数学高考压轴题(数列选择题)附答案
2024全国数学高考压轴题(数列)一、单选题1．若数列{b n }、{c n }均为严格增数列 且对任意正整数n 都存在正整数m 使得b m ∈[c n ，c n+1] 则称数列{b n }为数列{c n }的“M 数列”．已知数列{a n }的前n 项和为S n 则下列选项中为假命题的是（ ）A ．存在等差数列{a n } 使得{a n }是{S n }的“M 数列”B ．存在等比数列{a n } 使得{a n }是{S n }的“M 数列”C ．存在等差数列{a n } 使得{S n }是{a n }的“M 数列”D ．存在等比数列{a n } 使得{S n }是{a n }的“M 数列”2．已知函数f(x)及其导函数f ′(x)的定义域均为R 记g(x)=f ′(x)．若f(x +3)为奇函数 g(32+2x)为偶函数 且g(0)=−3 g(1)=2 则∑g 2023i=1(i)=（ ） A ．670B ．672C ．674D ．6763．我们知道按照一定顺序排列的数字可以构成数列 那么按照一定顺序排列的函数可以构成函数列.设无穷函数列{f n (x)}（n ∈N +）的通项公式为f n (x)=n 2+2nx+x 2+1(n+x)(n+1)x ∈(0，1) 记E n 为f n (x)的值域 E =U n=1+∞E n 为所有E n 的并集 则E 为（ ）A ．(56，109)B ．(1，109)C ．(56，54)D ．(1，54)4．已知等比数列{x n }的公比q >−12则（ ）A ．若|x 1+x 2+⋅⋅⋅+x 100|<1 则√|x 1|+√|x 2|+⋅⋅⋅+√|x 100|<10B ．若|x 1+x 2+⋅⋅⋅+x 100|>1 则√|x 1|+√|x 2|+⋅⋅⋅+√|x 100|>10C ．若|x 1+x 2+⋅⋅⋅+x 101|<1 则√|x 1|+√|x 2|+⋅⋅⋅+√|x 101|<10D ．若|x 1+x 2+⋅⋅⋅+x 101|>1 则√|x 1|+√|x 2|+⋅⋅⋅+√|x 101|>105．已知数列{a n } {b n }满足a 1=2 b 1=12 {a n+1=b n +1an b n+1=a n +1bn,，,n ,∈,N ∗ 则下列选项错误的是（ ） A ．a 2b 2=14B ．a 50⋅b 50<112C ．a 50+b 50=52√a 50⋅b 50D ．|a 50−b 50|≤156．已知数列{a n }满足：a 1=2 a n+1=13(√a n +2a n )(n ∈N ∗)．记数列{a n }的前n 项和为S n 则（ ）A ．12<S 10<14B ．14<S 10<16C ．16<S 10<18D ．18<S 10<207．已知数列 {a n } 满足： a 1=100，a n+1=a n +1an则（ ）A ．√200+10000<a 101<√200.01+10000B ．√200.01+10000<a 101<√200.1+10000C ．√200.1+10000<a 101<√201+10000D ．√201+10000<a 101<√210+100008．已知数列 {a n } 满足 a 1=a(a >0) √a n+1a n =a n +1 给出下列三个结论：①不存在 a 使得数列 {a n } 单调递减；②对任意的a 不等式 a n+2+a n <2a n+1 对所有的 n ∈N ∗ 恒成立；③当 a =1 时 存在常数 C 使得 a n <2n +C 对所有的 n ∈N ∗ 都成立.其中正确的是（ ） A ．①②B ．②③C ．①③D ．①②③9．已知F 为抛物线y 2=4x 的焦点 点P n (x n ，y n )(n =1，2，3，⋯)在抛物线上.若|P n+1F|−|P n F|=1 则（ ） A ．{x n }是等差数列 B ．{x n }是等比数列 C ．{y n }是等差数列D ．{y n }是等比数列10．已知数列 11 21 12 31 22 13 41 32 23 14… 其中每一项的分子和分母均为正整数.第一项是分子与分母之和为2的有理数；接下来两项是分子与分母之和为3的有理数 并且从大到小排列；再接下来的三项是分子与分母之和为4的有理数 并且从大到小排列 依次类推.此数列第n 项记为 a n 则满足 a n =5 且 n ≥20 的n 的最小值为（ ） A ．47B ．48C ．57D ．5811．已知△A n B n C n (n =1，2，3，⋯)是直角三角形 A n 是直角 内角A n ，B n ，C n 所对的边分别为a n ，b n ，c n 面积为S n ．若b 1=4，c 1=3，b n+12=a n+12+c n 23，c n+12=a n+12+b n 23则下列选项错误的是（ ）A ．{S 2n }是递增数列B ．{S 2n−1}是递减数列C ．数列{b n −c n }存在最大项D ．数列{b n −c n }存在最小项12．已知数列{a n }的各项都是正数 a n+12−a n+1=a n (n ∈N ∗)．记b n =(−1)n−1a n −1数列{b n }的前n 项和为S n 给出下列四个命题：①若数列{a n }各项单调递增 则首项a 1∈(0，2)②若数列{a n }各项单调递减 则首项a 1∈(2，+∞)③若数列{a n }各项单调递增 当a 1=32时 S 2022>2④若数列{a n }各项单调递增 当a 1=23时S2022<−5则以下说法正确的个数（）A．4B．3C．2D．113．已知正项数列{a n}对任意的正整数m、n都有2a m+n≤a2m+a2n则下列结论可能成立的是（）A．a nm+a mn=a mn B．na m+ma n=a m+n C．a m+a n+2=a mn D．2a m⋅a n=a m+n14．古希腊哲学家芝诺提出了如下悖论：一个人以恒定的速度径直从A点走向B点要先走完总路程的三分之一再走完剩下路程的三分之一如此下去会产生无限个“剩下的路程” 因此他有无限个“剩下路程的三分之一”要走这个人永远走不到终点．另一方面我们可以从上述第一段“三分之一的路程”开始通过分别计算他在每一个“三分之一距离”上行进的时间并将它们逐个累加不难推理出这个人行进的总时间不会超过一个恒定的实数．记等比数列{a n}的首项a1=13公比为q 前n项和为S n则造成上述悖论的原理是（）A．q=16，∃t∈R，∀n∈N ∗，Sn<t B．q=13，∃t∈R，∀n∈N∗，S n<tC．q=12，∃t∈R，∀n∈N ∗，Sn<t D．q=23，∃t∈R，∀n∈N∗，S n<t15．已知sinx，siny，sinz依次组成严格递增的等差数列则下列结论错误的是（）A．tanx，tany，tanz依次可组成等差数列B．cosx，cosy，cosz依次可组成等差数列C．cosx，cosz，cosy依次可组成等差数列D．cosz，cosx，cosy依次可组成等差数列16．记U={1，2，⋯，100}．对数列{a n}(n∈N∗)和U的子集T 若T=∅定义S T=0；若T={t1，t2，⋯，t k}定义S T=a t1+a t2+⋯+a tk．则以下结论正确的是（）A．若{a n}(n∈N∗)满足a n=2n−1，T={1，2，4，8}则S T=15B．若{a n}(n∈N∗)满足a n=2n−1则对任意正整数k(1≤k≤100)，T⊆{1，2，⋯，k}，S T< a kC．若{a n}(n∈N∗)满足a n=3n−1则对任意正整数k(1≤k≤100)，T⊆{1，2，⋯，k}，S T≥a k+1D ．若{a n }(n ∈N ∗)满足a n =3n−1 且C ⊆U ，D ⊆U ，S C ≥S D 则S C +S C∩D ≥2S D17．已知数列 {a n }、{b n }、{c n } 满足 a 1=b 1=c 1=1，c n =a n+1−a n ，c n+2=bn+1b n ⋅c n (n ∈N ∗)，S n =1b 2+1b 3+⋯+1b n （n ≥2），T n =1a 3−3+1a 4−4+⋯+1a n −n （n ≥3） 则下列有可能成立的是（ ）A ．若 {a n } 为等比数列 则 a 20222>b 2022B ．若 {c n } 为递增的等差数列 则 S 2022<T 2022C ．若 {a n } 为等比数列 则 a 20222<b 2022D ．若 {c n } 为递增的等差数列 则 S 2022>T 202218．已知数列{a n }满足a 1=1 a n =a n−1+4(√a n−1+1√an−1)(n ∈N ∗，n ≥2) S n 为数列{1a n }的前n 项和 则（ ） A ．73<S 2022<83B ．2<S 2022<73C ．53<S 2022<2 D ．1<S 2022<5319．已知数列{a n }满足a n ⋅a n+1⋅a n+2=−1(n ∈N ∗)，a 1=−3 若{a n }的前n 项积的最大值为3 则a 2的取值范围为（ ） A ．[−1，0)∪(0，1] B ．[−1，0)C ．(0，1]D ．(−∞，−1)∪(1，+∞)20．已知正项数列{a n }的前n 项和为S n (a n +1)2=4S n 记b n =S n ⋅sin nπ2+S n+1⋅sin (n+1)π2若数列{b n }的前n 项和为T n 则T 100=（ ） A ．-400B ．-200C ．200D ．40021．设S n 是等差数列{a n }的前n 项和 a 2=−7 S 5=2a 1 当|S n |取得最小值时 n =（ ）A ．10B ．9C ．8D ．722．已知数列{a n }中 a 2+a 4+a 6=285 na n =(n −1)a n+1+101(n ∈N ∗) 当数列{a n a n+1a n+2}(n ∈N ∗)的前n 项和取得最大值时 n 的值为（ ） A ．53B ．49C ．49或53D ．49或5123．定义在R 上的函数序列{f n (x)}满足f n (x)<1nf n ′(x)（f n ′(x)为f n (x)的导函数） 且∀x ∈N ∗ 都有f n (0)=n ．若存在x 0>0 使得数列{f n (x 0)}是首项和公比均为q 的等比数列 则下列关系式一定成立的是（ ）．A ．0<q <2√2e x 0B ．0<q <√33e x 0C ．q >2√2e x 0D ．q >√33e x 024．已知数列{a n }的前n 项和为S n 满足a 1=1 a 2=2 a n =a n−1⋅a n+1(n ≥2) 则（ ）A ．a 1：a 2：a 3=a 6：a 7：a 8B ．a n ：a n+1：a n+2=1：2：2C ．S 6 S 12 S 18成等差数列D ．S 6n S 12n S 18n 成等比数列25．已知S n 为数列{a n }的前n 项和 且a 1=1 a n+1+a n =3×2n 则S 100=（ ）A ．2100−3B ．2100−2C ．2101−3D ．2101−226．已知 {a n } 为等比数列 {a n } 的前n 项和为 S n 前n 项积为 T n 则下列选项中正确的是（ ）A ．若 S 2022>S 2021 则数列 {a n } 单调递增B ．若 T 2022>T 2021 则数列 {a n } 单调递增C ．若数列 {S n } 单调递增 则 a 2022≥a 2021D ．若数列 {T n } 单调递增 则 a 2022≥a 2021二、多选题27．“冰雹猜想”也称为“角谷猜想” 是指对于任意一个正整数x 如果x 是奇数㩆乘以3再加1 如果x 是偶数就除以2 这样经过若干次操作后的结果必为1 犹如冰雹掉落的过程.参照“冰雹猜想” 提出了如下问题：设k ∈N ∗ 各项均为正整数的数列{a n }满足a 1=1 a n+1={a n2，a n 为偶数，a n +k ，a n 为奇数，则（ ）A ．当k =5时 a 5=4B ．当n >5时 a n ≠1C ．当k 为奇数时 a n ≤2kD ．当k 为偶数时 {a n }是递增数列28．已知数列{a n } a 2=12且满足a n+1a n 2=a n −a n+1 n ∈N ∗ 则（ ） A ．a 4−a 1=1929B ．a n 的最大值为1C ．a n+1≥1n+1D ．√a 1+√a 2+√a 3+⋅⋅⋅+√a 35>1029．已知数列{a n }的前n 项和为S n a 1=1 且4a n ⋅a n+1=a n −3a n+1（n =1 2 …） 则（ ）A ．3a n+1<a nB ．a 5=1243C ．ln(1an )<n +1D ．1≤S n <171430．如图 已知正方体ABCD −A 1B 1C 1D 1顶点处有一质点Q 点Q 每次会随机地沿一条棱向相邻的某个顶点移动 且向每个顶点移动的概率相同．从一个顶点沿一条棱移动到相邻顶点称为移动一次．若质点Q 的初始位置位于点A 处 记点Q 移动n 次后仍在底面ABCD 上的概率为P n 则下列说法正确的是（ ）A ．P 2=59B ．P n+1=23P n +13C ．点Q 移动4次后恰好位于点C 1的概率为0D ．点Q 移动10次后仍在底面ABCD 上的概率为12(13)10+1231．已知数列{a n } {b n } 有a n+1=a n −b n b n+1=b n −a n n ∈N ∗ 则（ ）A ．若存在m >1 a m =b m 则a 1=b 1B ．若a 1≠b 1 则存在大于2的正整数n 使得a n =0C ．若a 1=a a 2=b 且a ≠b 则b 2022=−b ×22020D ．若a 1=−1 a 2=−3 则关于x 的方程2a 3+(2a 3+1)cosx +2cos2x +cos3x =0的所有实数根可构成一个等差数列32．已知△A n B n C n (n =1，2，3，⋯)是直角三角形 A n 是直角 内角A n 、B n 、C n 所对的边分别为a n 、b n 、c n 面积为S n 若b 1=4 c 1=3 b n+12=a n+12+c n 23 c n+12=a n+12+b n 23则（ ） A ．{S 2n }是递增数列 B ．{S 2n−1}是递减数列 C ．{b n −c n }存在最大项D ．{b n −c n }存在最小项33．已知S n 是数列{a n }的前n 项和 且S n+1=−S n +n 2 则下列选项中正确的是（ ）.A ．a n +a n+1=2n −1（n ≥2）B ．a n+2−a n =2C ．若a 1=0 则S 100=4950D ．若数列{a n }单调递增 则a 1的取值范围是(−14，13)三、填空题34．已知n ∈N ∗ 将数列{2n −1}与数列{n 2−1}的公共项从小到大排列得到新数列{a n } 则1a 1+1a 2+⋯+1a 10= .35．若函数f(x)的定义域为(0，+∞) 且f(x)+f(y)=f(xy) f(a n )=n +f(n) 则∑f ni=1(a i i )= ．36．在数列{a n }中 a 1=1 a n+1=a n +1an（n∈N ∗） 若t ∈Z 则当|a 7−t|取得最小值时 整数t 的值为 .37．已知函数f(x)满足f(x −2)=f(x +2)，0≤x <4时 f(x)=√4−(x −2)2 g(x)=f(x)−k n x(n ∈N ∗，k n >0)．若函数g(x)的图像与x 轴恰好有2n +1个不同的交点 则k 12+k 22+⋅⋅⋅+k n 2= ．38．已知复数z =1+i 对于数列{a n } 定义P n =a 1+2a 2+⋅⋅⋅+2n−1a n n为{a n }的“优值”．若某数列{a n}的“优值”P n =|z|2n 则数列{a n }的通项公式a n = ；若不等式a n 2−a n +4≥(−1)nkn 对于∀n ∈N ∗恒成立 则k 的取值范围是 ．39．数列{a n }是公比为q(q ≠1)的等比数列 S n 为其前n 项和. 已知a 1⋅a 3=16 S3q=12 给出下列四个结论： ①q <0 ；②若存在m 使得a 1，a 2，⋅⋅⋅，a m 的乘积最大 则m 的一个可能值是3； ③若存在m 使得a 1，a 2，⋅⋅⋅，a m 的乘积最大 则m 的一个可能值是4； ④若存在m 使得a 1，a 2，⋅⋅⋅，a m 的乘积最小 则m 的值只能是2． 其中所有正确结论的序号是 .40．如图 某荷塘里浮萍的面积y （单位：m 2）与时间t （单位：月）满足关系式：y =a t lna （a 为常数） 记y =f(t)（t ≥0）．给出下列四个结论：①设a n=f(n)(n∈N∗)则数列{a n}是等比数列；②存在唯一的实数t0∈(1，2)使得f(2)−f(1)=f′(t0)成立其中f′(t)是f(t)的导函数；③常数a∈(1，2)；④记浮萍蔓延到2m23m26m2所经过的时间分别为t1t2t3则t1+t2>t3．其中所有正确结论的序号是．41．在现实世界很多信息的传播演化是相互影响的.选用正实数数列{a n}{b n}分别表示两组信息的传输链上每个节点处的信息强度数列模型：a n+1=2a n+b n，b n+1=a n+2b n(n=1，2⋯)描述了这两组信息在互相影响之下的传播演化过程.若两组信息的初始信息强度满足a1>b1则在该模型中关于两组信息给出如下结论：①∀n∈N∗，a n>b n；②∀n∈N∗，a n+1>a n，b n+1>b n；③∃k∈N∗使得当n>k时总有|a nb n−1|<10−10④∃k∈N∗使得当n>k时总有|a n+1a n−2|<10−10．其中所有正确结论的序号是答案解析部分1．【答案】C2．【答案】D3．【答案】C4．【答案】A5．【答案】D6．【答案】B7．【答案】A8．【答案】A9．【答案】A10．【答案】C11．【答案】B12．【答案】B13．【答案】D14．【答案】D15．【答案】B16．【答案】D17．【答案】B18．【答案】D19．【答案】A20．【答案】C21．【答案】C22．【答案】D23．【答案】D24．【答案】C25．【答案】D26．【答案】D27．【答案】A,C,D28．【答案】B,C,D29．【答案】A,D30．【答案】A,C,D 31．【答案】A,C,D 32．【答案】A,C,D 33．【答案】A,C 34．【答案】102135．【答案】n(n+1)236．【答案】4 37．【答案】n 4(n+1) 38．【答案】n+1；[−163，5] 39．【答案】①②③ 40．【答案】①②④ 41．【答案】①②③。
高考数学压轴题100题汇总(含答案)
高考数学压轴题100题汇总(含答案)1. 设函数f(x) = x^3 3x + 1，求f(x)的极值点和极值。
答案：f(x)的极值点为x = 1和x = 1，极值分别为f(1) = 1和f(1) = 3。
2. 已知等差数列{an}的前n项和为Sn = n^2 + n，求该数列的通项公式。
答案：an = 2n + 1。
3. 已知三角形ABC中，AB = AC = 5，BC = 8，求三角形ABC的面积。
答案：三角形ABC的面积为12。
4. 设直线y = kx + b与圆x^2 + y^2 = 1相切，求k和b的值。
答案：k = ±√3/3，b = ±√6/3。
5. 已知函数f(x) = log2(x^2 + 1)，求f(x)的导数。
答案：f'(x) = 2x/(x^2 + 1)ln2。
6. 已知向量a = (2, 3)，向量b = (1, 4)，求向量a和向量b的夹角。
答案：向量a和向量b的夹角为arccos(1/√5)。
7. 已知矩阵A = [1 2; 3 4]，求矩阵A的逆矩阵。
答案：矩阵A的逆矩阵为[4 2; 3 1]。
8. 已知函数f(x) = x^3 6x^2 + 9x + 1，求f(x)的零点。
答案：f(x)的零点为x = 1和x = 3。
9. 已知函数f(x) = sin(x) cos(x)，求f(x)在区间[0, π/2]上的最大值。
答案：f(x)在区间[0, π/2]上的最大值为√2。
10. 已知函数f(x) = x^2 + 4x + 4，求f(x)的顶点坐标。
答案：f(x)的顶点坐标为(2, 0)。
高考数学压轴题100题汇总(含答案)11. 已知函数f(x) = e^x 2x，求f(x)的导数。
答案：f'(x) = e^x 2。
12. 已知函数f(x) = x^2 4x + 4，求f(x)的极值点和极值。
答案：f(x)的极值点为x = 2，极值为f(2) = 0。
高考数学压轴题大全
高考数学压轴题大全高考数学压轴题大全1.(本小题满分14分)如图，设抛物线的焦点为F，动点P在直线上运动，过P作抛物线C 的两条切线PA、PB，且与抛物线C分别相切于A、B两点.(1)求△APB的重心G的轨迹方程.(2)证明PFA=PFB.解：(1)设切点A、B坐标分别为，切线AP的方程为：切线BP的方程为：解得P点的坐标为：因此△APB的重心G的坐标为，因此，由点P在直线l上运动，从而得到重心G的轨迹方程为：(2)方法1：因为由于P点在抛物线外，则同理有AFP=PFB.方法2：①当因此P点坐标为，则P点到直线AF的距离为：即因此P点到直线BF的距离为：因此d1=d2，即得AFP=PFB.②当时，直线AF的方程：直线BF的方程：因此P点到直线AF的距离为：，同理可得到P点到直线BF的距离，因此由d1=d2，可得到AFP=PF B.2.(本小题满分12分)设A、B是椭圆上的两点，点N(1，3)是线段AB的中点，线段AB的垂直平分线与椭圆相交于C、D两点.(Ⅰ)确定的取值范畴，并求直线AB的方程;(Ⅱ)试判定是否存在如此的，使得A、B、C、D四点在同一个圆上?并说明理由.(此题不要求在答题卡上画图)本小题要紧考查直线、圆和椭圆等平面解析几何的基础知识以及推理运算能力和综合解决问题的能力.(Ⅰ)解法1：依题意，可设直线AB的方程为，整理得①设是方程①的两个不同的根，且由N(1，3)是线段AB的中点，得解得k=-1，代入②得，的取值范畴是(12，+).因此，直线AB的方程为解法2：设则有依题意，∵N(1，3)是AB的中点，又由N(1，3)在椭圆内，的取值范畴是(12，+).直线AB的方程为y-3=-(x-1)，即x+y-4=0.(Ⅱ)解法1：∵CD垂直平分AB，直线CD的方程为y-3=x-1，即x-y+ 2=0，代入椭圆方程，整理得又设CD的中点为是方程③的两根，因此由弦长公式可得④将直线AB的方程x+y-4=0，代入椭圆方程得⑤同理可得⑥∵当时，假设存在12，使得A、B、C、D四点共圆，则CD必为圆的直径，点M为圆心.点M到直线AB的距离为⑦因此，由④、⑥、⑦式和勾股定理可得故当12时，A、B、C、D四点匀在以M为圆心，为半径的圆上.(注：上述解法中最后一步可按如下解法获得：)A、B、C、D共圆△ACD为直角三角形，A为直角|AN|2=|CN||DN|，即⑧由⑥式知，⑧式左边由④和⑦知，⑧式右边⑧式成立，即A、B、C、D四点共圆.解法2：由(Ⅱ)解法1及12,∵CD垂直平分AB，直线CD方程为，代入椭圆方程，整理得将直线AB的方程x+y-4=0，代入椭圆方程，整理得解③和⑤式可得不妨设运算可得，A在以CD为直径的圆上.又B为A关于CD的对称点，A、B、C、D四点共圆.(注：也可用勾股定理证明ACAD)3.(本小题满分14分)已知不等式为大于2的整数，表示不超过的最大整数. 设数列的各项为正，且满足(Ⅰ)证明(Ⅱ)推测数列是否有极限?假如有，写出极限的值(不必证明);(Ⅲ)试确定一个正整数N，使得当时，对任意b0，都有本小题要紧考查数列、极限及不等式的综合应用以及归纳递推的思想.(Ⅰ)证法1：∵当即因此有所有不等式两边相加可得由已知不等式知，当n3时有，证法2：设，第一利用数学归纳法证不等式(i)当n=3时，由知不等式成立.(ii)假设当n=k(k3)时，不等式成立，即则即当n=k+1时，不等式也成立.由(i)、(ii)知，又由已知不等式得(Ⅱ)有极限，且则有故取N=1024，可使当nN时，都有4.如图，已知椭圆的中心在坐标原点，焦点F1，F2在x轴上，长轴A 1A2的长为4，左准线l与x轴的交点为M，|MA1|∶|A1F1|=2∶1.(Ⅰ)求椭圆的方程;(Ⅱ)若点P为l上的动点，求F1PF2最大值.本题要紧考查椭圆的几何性质、椭圆方程、两条直线的夹角等基础知识，考查解析几何的差不多思想方法和综合解题能力.满分14分.解：(Ⅰ)设椭圆方程为，半焦距为，则5.已知函数和的图象关于原点对称，且.(Ⅰ)求函数的解析式;(Ⅱ)解不等式;(Ⅲ)若在上是增函数，求实数的取值范畴.本题要紧考查函数图象的对称、二次函数的差不多性质与不等式的应用等基础知识，以及综合运用所学知识分析和解决问题的能力.满分14分.解：(Ⅰ)设函数的图象上任意一点关于原点的对称点为，则∵点在函数的图象上(Ⅱ)由当时，，现在不等式无解.当时，，解得.因此，原不等式的解集为.6.(本题满分16分)本题共有3个小题,第1小题满分4分, 第2小题满分6分, 第3小题满分6分.对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),f(x)g(x) 当xDf且xDg规定: 函数h(x)= f(x) 当xDf且xDgg(x) 当xDf且xDg若函数f(x)=,g(x)=x2,xR,写出函数h(x)的解析式;求问题(1)中函数h(x)的值域;(3)若g(x)=f(x+), 其中是常数,且[0,],请设计一个定义域为R的函数y=f (x),及一个的值,使得h(x)=cos4x,并予以证明.[解] (1)h(x)= x(-,1)(1,+)1 x=1(2) 当x1时, h(x)= =x-1++2,若x1时, 则h(x)4,其中等号当x=2时成立若x1时, 则h(x) 0,其中等号当x=0时成立函数h(x)的值域是(-,0] {1}[4,+)(3)令f(x)=sin2x+cos2x,=则g(x)=f(x+)= sin2(x+)+cos2(x+)=cos2x-sin2x,因此h(x)= f(x)f(x+)= (sin2x+co2sx)( cos2x-sin2x)=cos4x.另解令f(x)=1+sin2x, =,g(x)=f(x+)= 1+sin2(x+)=1-sin2x,因此h(x)= f(x)f(x+)= (1+sin2x)( 1-sin2x)=cos4x..(本题满分18分)本题共有3个小题,第1小题满分4分, 第2小题满分8分, 第3小题满分6分.在直角坐标平面中,已知点P1(1,2),P2(2,22),,Pn(n,2n),其中n是正整数.对平面上任一点A0,记A1为A0关于点P1的对称点, A2为A1关于点P2的对称点, , AN为AN-1关于点PN的对称点.(1)求向量的坐标;(2)当点A0在曲线C上移动时, 点A2的轨迹是函数y=f(x)的图象,其中f(x)是以3为周期的周期函数,且当x(0,3]时,f(x)=lgx.求以曲线C为图象的函数在(1,4]上的解析式;(3)对任意偶数n,用n表示向量的坐标.[解](1)设点A0(x,y), A0为P1关于点的对称点A0的坐标为(2-x,4-y), A1为P2关于点的对称点A2的坐标为(2+x,4+y),={2,4}.(2) ∵={2,4},f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到.因此, 曲线C是函数y=g(x)的图象,其中g(x)是以3为周期的周期函数,且当x(-2,1]时,g(x)=lg(x+2)-4.因此,当x(1,4]时,g(x)=lg(x-1)-4.另解设点A0(x,y), A2(x2,y2),因此x2-x=2,y2-y=4,若36,则0 x2-33,因此f(x2)=f(x2-3)=lg(x2-3).当14时, 则36,y+4=lg(x-1).当x(1,4]时,g(x)=lg(x-1)-4.(3) =,由于,得13分)如图，已知双曲线C：的右准线与一条渐近线交于点M，F是双曲线C 的右焦点，O为坐标原点.(I)求证：;(II)若且双曲线C的离心率，求双曲线C的方程;(III)在(II)的条件下，直线过点A(0，1)与双曲线C右支交于不同的两点P、Q且P在A、Q之间，满足，试判定的范畴，并用代数方法给出证明.解：(I)右准线，渐近线3分(II)双曲线C的方程为：7分(III)由题意可得8分证明：设，点由得与双曲线C右支交于不同的两点P、Q11分，得的取值范畴是(0，1)13分2.(本小题满分13分)已知函数，数列满足(I)求数列的通项公式;(II)设x轴、直线与函数的图象所围成的封闭图形的面积为，求;(III)在集合，且中，是否存在正整数N，使得不等式对一切恒成立?若存在，则如此的正整数N共有多少个?并求出满足条件的最小的正整数N;若不存在，请说明理由.(IV)请构造一个与有关的数列，使得存在，并求出那个极限值.解：(I)1分将这n个式子相加，得3分(II)为一直角梯形(时为直角三角形)的面积，该梯形的两底边的长分别为，高为16分(III)设满足条件的正整数N存在，则又均满足条件它们构成首项为2021，公差为2的等差数列.设共有m个满足条件的正整数N，则，解得中满足条件的正整数N存在，共有495个，9分(IV)设，即则明显，其极限存在，同时10分注：(c为非零常数)，等都能使存在.19. (本小题满分14分)设双曲线的两个焦点分别为，离心率为2.(I)求此双曲线的渐近线的方程;(II)若A、B分别为上的点，且，求线段AB的中点M的轨迹方程，并说明轨迹是什么曲线;(III)过点能否作出直线，使与双曲线交于P、Q两点，且.若存在，求出直线的方程;若不存在，说明理由.解：(I)，渐近线方程为4分(II)设，AB的中点则M的轨迹是中心在原点，焦点在x轴上，长轴长为，短轴长为的椭圆.(9分)(III)假设存在满足条件的直线设由(i)(ii)得k不存在，即不存在满足条件的直线.14分3. (本小题满分13分)已知数列的前n项和为，且对任意自然数都成立，其中m为常数，且.(I)求证数列是等比数列;(II)设数列的公比，数列满足：，试问当m为何值时，成立?解：(I)由已知(2)由得：，即对任意都成立事实上,任何一门学科都离不开死记硬背,关键是经历有技巧,“死记”之后会“活用”。
【压轴题】高考数学试卷带答案
【压轴题】高考数学试卷带答案一、选择题1．已知在ABC 中，::3:2:4sinA sinB sinC =，那么cosC 的值为（ ） A ．14- B ．14 C ．23- D ．23 2．已知集合{}{}x -1<x 1Q=x 0x 2P =<<<，，那么P Q=⋃A ．（-1,2）B ．（0，1）C ．（-1,0）D ．（1,2） 3．若以连续掷两颗骰子分别得到的点数m ，n 作为点P 的横、纵坐标，则点P 落在圆229x y +=内的概率为（ ）A ．536B ．29C ．16D ．194．已知向量a ，b 满足2a =，||1b =，且2b a +=，则向量a 与b 的夹角的余弦值为（ ）A ．22B ．23C ．28D ．245．函数()ln f x x x =的大致图像为 （ ）A ．B ．C ．D ．6．若干年前，某教师刚退休的月退休金为6000元，月退休金各种用途占比统计图如下面的条形图.该教师退休后加强了体育锻炼，目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元，则目前该教师的月退休金为（ ）.A ．6500元B ．7000元C ．7500元D ．8000元7．在ABC 中，若 13,3,120AB BC C ==∠=，则AC =（ ）A ．1B ．2C ．3D ．48．已知向量()1,1m λ=+，()2,2n λ=+，若()()m n m n +⊥-，则λ=（ ） A ．4- B ．3- C ．2- D ．1-9．设F 为双曲线C ：22221x y a b-=（a >0，b >0）的右焦点，O 为坐标原点，以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点．若|PQ |=|OF |，则C 的离心率为A ．2B ．3C ．2D ．5 10．由a 2，2﹣a ，4组成一个集合A ，A 中含有3个元素，则实数a 的取值可以是（ ）A ．1B ．﹣2C ．6D ．2 11．如图，中心均为原点O 的双曲线与椭圆有公共焦点，M ，N 是双曲线的两顶点.若M ，O ，N 将椭圆长轴四等分，则双曲线与椭圆的离心率的比值是A ．3B ．2C 3D 212．设双曲线22221x y a b-=（0a >，0b >）的渐近线与抛物线21y x =+相切，则该双曲线的离心率等于（ ）A 3B ．2C 6D 5二、填空题13．若三点1(2,3),(3,2),(,)2A B C m --共线，则m 的值为 ． 14．函数()22,026,0x x f x x lnx x ⎧-≤=⎨-+>⎩的零点个数是________．15．复数()1i i +的实部为 ．16．设a R ∈，直线20ax y -+=和圆22cos ,12sin x y θθ=+⎧⎨=+⎩（θ为参数）相切，则a 的值为____. 17．在极坐标系中，直线cos sin (0)a a ρθρθ+=>与圆2cos ρθ=相切，则a =__________．18．能说明“若f （x ）>f （0）对任意的x ∈（0，2］都成立，则f （x ）在［0，2］上是增函数”为假命题的一个函数是__________．19．已知集合P 中含有0,2,5三个元素,集合Q 中含有1,2,6三个元素,定义集合P+Q 中的元素为a+b ,其中a ∈P ,b ∈Q ,则集合P+Q 中元素的个数是_____.20．函数()lg 12sin y x =-的定义域是________．三、解答题21．已知曲线C 的参数方程为32cos 12sin x y αα=+⎧⎨=-⎩（a 参数），以直角坐标系的原点为极点，x 正半轴为极轴建立极坐标系.（Ⅰ）求曲线C 的极坐标方程；（Ⅱ）若直线l 极坐标方程为1sin 2cos θθρ-=，求曲线C 上的点到直线l 最大距离. 22．为评估设备生产某种零件的性能，从设备生产该零件的流水线上随机抽取100个零件为样本，测量其直径后，整理得到下表：经计算，样本的平均值，标准差，以频率值作为概率的估计值.（I ）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为，并根据以下不等式进行判定（表示相应事件的概率）：①； ②； ③.判定规则为：若同时满足上述三个式子，则设备等级为甲；若仅满足其中两个，则等级为乙，若仅满足其中一个，则等级为丙；若全部都不满足，则等级为了.试判断设备的性能等级.（Ⅱ）将直径尺寸在之外的零件认定为是“次品”.①从设备的生产流水线上随机抽取2个零件，求其中次品个数的数学期望；②从样本中随意抽取2个零件，求其中次品个数的数学期望.23．如图，在直四棱柱1111ABCD A B C D -中，底面ABCD 是矩形，1A D 与1AD 交于点E .124AA AB AD ===.（1）证明：AE ⊥平面ECD ；（2）求直线1A C 与平面EAC 所成角的正弦值.24．如图：在ABC ∆中，10a =，4c =，5cos C =-.（1）求角A ；（2）设D 为AB 的中点，求中线CD 的长.25．已知菱形ABCD 的顶点A ，C 在椭圆2234x y +=上，对角线BD 所在直线的斜率为1．（1）当直线BD 过点(0,1)时，求直线AC 的方程．（2）当60ABC ∠=︒时，求菱形ABCD 面积的最大值．26．△ABC 在内角A 、B 、C 的对边分别为a ，b ，c ，已知a=bcosC+csinB ．（Ⅰ）求B ；（Ⅱ）若b=2，求△ABC 面积的最大值.【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【解析】【分析】【详解】::sin :sin :sin 3:2:4a b c A B C == ，不妨设3,2,4a k b k c k ===，,则()()()2223241cos 2324k k k C k k+-==-⨯⨯ ，选A. 2．A解析：A【解析】 利用数轴，取,P Q 所有元素，得PQ =(1,2)-． 【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理． 3．D解析：D【解析】掷骰子共有36个结果,而落在圆x 2+y 2=9内的情况有(1,1),(1,2),(2,1),(2,2)这4种,∴P=41369=. 故选D 4．D解析：D【解析】【分析】 根据平方运算可求得12a b ⋅=，利用cos ,a b a b a b ⋅<>=求得结果. 【详解】由题意可知：2222324b a b a b a a b +=+⋅+=+⋅=，解得：12a b ⋅=cos ,22a ba b a b ⋅∴<>===本题正确选项：D【点睛】本题考查向量夹角的求解问题，关键是能够通过平方运算求得向量的数量积.5．A解析：A【解析】【分析】【详解】∵函数f （x ）=xlnx 只有一个零点，∴可以排除CD 答案又∵当x ∈（0，1）时，lnx ＜0，∴f （x ）=xlnx ＜0，其图象在x 轴下方∴可以排除B 答案考点：函数图像．6．D解析：D【解析】【分析】设目前该教师的退休金为x 元，利用条形图和折线图列出方程，求出结果即可．【详解】设目前该教师的退休金为x 元，则由题意得：6000×15%﹣x×10%＝100．解得x ＝8000． 故选D ．【点睛】本题考查由条形图和折线图等基础知识解决实际问题，属于基础题．7．A解析：A【解析】余弦定理2222?cos AB BC AC BC AC C =+-将各值代入得2340AC AC +-=解得1AC =或4AC =-(舍去)选A.8．B解析：B【解析】【分析】【详解】∵()()m n m n +⊥-，∴()()0m n m n +⋅-=. ∴，即22(1)1[(2)4]0λλ++-++=， ∴3λ=-,，故选B.【考点定位】向量的坐标运算9．A解析：A【解析】【分析】准确画图，由图形对称性得出P 点坐标，代入圆的方程得到c 与a 关系，可求双曲线的离心率．【详解】设PQ 与x 轴交于点A ，由对称性可知PQ x ⊥轴，又||PQ OF c ==，||,2c PA PA ∴=∴为以OF 为直径的圆的半径， A ∴为圆心||2c OA =． ,22c c P ⎛⎫∴ ⎪⎝⎭，又P 点在圆222x y a +=上， 22244c c a ∴+=，即22222,22c c a e a=∴==． 2e ∴=，故选A ．【点睛】本题为圆锥曲线离心率的求解，难度适中，审题时注意半径还是直径，优先考虑几何法，避免代数法从头至尾，运算繁琐，准确率大大降低，双曲线离心率问题是圆锥曲线中的重点问题，需强化练习，才能在解决此类问题时事半功倍，信手拈来．10．C解析：C【解析】试题分析：通过选项a 的值回代验证，判断集合中有3个元素即可．解：当a=1时，由a 2=1，2﹣a=1，4组成一个集合A ，A 中含有2个元素，当a=﹣2时，由a 2=4，2﹣a=4，4组成一个集合A ，A 中含有1个元素，当a=6时，由a 2=36，2﹣a=﹣4，4组成一个集合A ，A 中含有3个元素，当a=2时，由a 2=4，2﹣a=0，4组成一个集合A ，A 中含有2个元素，故选C ．点评：本题考查元素与集合的关系，基本知识的考查．11．B解析：B【解析】【分析】【详解】M N ，是双曲线的两顶点，M O N ，，将椭圆长轴四等分∴椭圆的长轴长是双曲线实轴长的2倍双曲线与椭圆有公共焦点，∴双曲线与椭圆的离心率的比值是2故答案选B12．D解析：D【解析】 由题意可知双曲线的渐近线一条方程为b y x a =，与抛物线方程组成方程组2,1b y x a y x ⎧=⎪⎨⎪=+⎩消y 得，2210,()40b b x x a a -+=∆=-=，即2()4b a =，所以e == D. 【点睛】 双曲线22221x y a b-=（0a >，0b >）的渐近线方程为b y x a =±． 直线与抛物线交点问题，直线与抛物线方程组方程组，当直线与抛物线对称轴平行时，直线与抛物线相交，只有一个交点．当直线与抛物线对称轴不平行时，当>0∆时，直线与抛物线相交，有两个交点． 当0∆=时，直线与抛物线相切，只有一个交点．当∆<0时，直线与抛物线相离，没有交点．二、填空题13．【解析】试题分析：依题意有即解得考点：三点共线 解析：12【解析】 试题分析：依题意有AB AC k k =，即531522m --=+，解得12m =. 考点：三点共线．14．2【解析】【详解】当x≤0时由f （x ）=x2﹣2=0解得x=有1个零点；当x ＞0函数f （x ）=2x ﹣6+lnx 单调递增则f （1）＜0f （3）＞0此时函数f （x ）只有一个零点所以共有2个零点故答案为：解析：2【解析】【详解】当x≤0时，由f （x ）=x 2﹣2=0，解得x=1个零点；当x ＞0，函数f （x ）=2x ﹣6+lnx ，单调递增，则f （1）＜0，f （3）＞0，此时函数f （x ）只有一个零点，所以共有2个零点．故答案为：2．【点睛】判断函数零点个数的方法直接法（直接求零点）：令f (x )＝0，如果能求出解，则有几个不同的解就有几个零点， 定理法（零点存在性定理）：利用定理不仅要求函数的图象在区间[a ，b ]上是连续不断的曲线，且f (a )·f (b )<0，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点，图象法（利用图象交点的个数）：画出函数f (x )的图象，函数f (x )的图象与x 轴交点的个数就是函数f (x )的零点个数；将函数f (x )拆成两个函数h (x )和g (x )的差，根据f (x )＝0⇔h (x )＝g (x )，则函数f (x )的零点个数就是函数y ＝h (x )和y ＝g (x )的图象的交点个数，性质法（利用函数性质）：若能确定函数的单调性，则其零点个数不难得到；若所考查的函数是周期函数，则只需解决在一个周期内的零点的个数15．【解析】复数其实部为考点：复数的乘法运算实部解析：1-【解析】复数(1)11i i i i +=-=-+，其实部为1-.考点：复数的乘法运算、实部.16．【解析】【分析】根据圆的参数方程确定圆的半径和圆心坐标再根据直线与圆相切的条件得出满足的方程解之解得【详解】圆化为普通方程为圆心坐标为圆的半径为由直线与圆相切则有解得【点睛】直线与圆的位置关系可以使 解析：34【解析】【分析】根据圆的参数方程确定圆的半径和圆心坐标，再根据直线与圆相切的条件得出a 满足的方程，解之解得。
高考数学压轴题精选100题汇总(含答案)
7. 已知动圆过定点 P（1，0），且与定直线 L:x=-1 相切，点 C 在 l 上. (1)求动圆圆心的轨迹 M 的方 程； (2)设过点 P,且斜率为 3 的直线与曲线 M 相交于 A, B 两点. （i）问：△ABC 能否为正三角形？若能，求点 C 的坐标；若不能，说明理由 （ii）当△ABC 为钝角三角形时，求这种点 C 的纵坐标的取值范围.
1
1
n 1 1
（Ⅱ）已知各项不为零的数列an 满足 4Sn f ( ) 1 ，求证： ln
；
an
an1
n
an
（Ⅲ）设 bn 1 ， Tn 为数列bn 的前 n 项和，求证： T2008 1 ln 2008 T2007 ．
ba b a
2
（1）求椭圆的方程；
（2）若直线 AB 过椭圆的焦点 F（0，c），（c 为半焦距），求直线 AB 的斜率 k 的值；
（3）试问：△AOB 的面积是否为定值？如果是，请给予证明；如果不是，请说明理由.
5．已知数列{an}中各项为： 12、1122、111222、……、111 22 2 ……
n
T 2n 1 ．
n
3
26. 对于函数 f (x) ，若存在 x0 R ，使 f (x0 ) x0 成立，则称 x0 为 f (x) 的不动点．如果函数
f (x) x2 a (b, c N*) 有且仅有两个不动点 0 、 2 ，且 f (2) 1 ．
bx c
2
（Ⅰ）试求函数 f (x) 的单调区间；
a2 a3
an1 3
14．已知函数gx a2 x3 a x 2 cxa 0,
32
（I）当a 1 时，若函数 gx在区间1,1上是增函数，求实数c的取值范围；
2023届高考数学压轴题(函数整数解问题)专题练习(附答案)
2023届高考数学压轴题（函数整数解问题）专题练习1．已知函数1()()22x f x kx e x =+-，若()0f x <的解集中有且只有一个正整数，则实数k 的取值范围为() A．221[4e -，21)2e - B．221(4e -，21]2e - C．322121[,64e e -- D．32121[,62e e -- 【名师解析】解：()0f x <，即1(202x kx e x +-<，也就是1()22x kx e x +<，即122x xkx e +<，令2()x xg x e =，则2222(1)()x x x xe xe x g x e e --'==， 当(,1)x ∈-∞时，()0g x '>，当(1,)x ∈+∞时，()0g x '<． ()g x ∴在(,1)-∞上单调递增，在(1,)+∞上单调递减． 作出函数()g x 与12y kx =+的图象如图： 12y kx =+的图象过定点1(0,2P ，2(1,A e ，24(2,B e， 21212102PAe k e -==--，2241212204PB e k e -==--． ∴实数k 的取值范围为221[4e -，21)2e -． 故选：A ．2．已知函数()(2)(0)x f x kx e x x =-->，若()0f x <的解集为(,)s t ，且(,)s t 中恰有两个整数，则实数k 的取值范围为( )A．211[1,2)e e++ B．431112[,)23e e ++ C．21(,1)e -∞+ D．32121[,1)3e e ++ 【名师解析】解：由()(2)0x f x kx e x =--<，得(2)x kx e x -<， 即2xxkx e -<，(0)x >， 设()xxh x e =，(0)x >， 21()()x x x x e xe xh x e e--'==，由()0h x '>得01x <<，函数()h x 为增函数， 由()0h x '<得1x >，函数()h x 为减函数， 即当1x =时，()h x 取得极大值，极大值为h （1）1e=， 要使2x xkx e-<，(0)x >，在s ，)t 中恰有两个整数，则0k …时，不满足条件． 则0k >，当2x =时，h （2）22e =，当3x =时，h （3）33e =，即22(2,)A e ，33(3,)B e， 则当直线()2g x kx =-在A ，B 之间满足条件，此时两个整数解为1，2， 此时满足232(2)3(3)g e g e ⎧<⎪⎪⎨⎪⎪⎩…，即23222332k e k e ⎧-<⎪⎪⎨⎪-⎪⎩…得2311213k e k e ⎧<+⎪⎪⎨⎪+⎪⎩…，即3212113k e e +<+…， 即k 的取值范围是312[3e +，211)e+， 故选：D ．3．已知函数()x f x xe mx m =-+，若()0f x <的解集为(,)a b ，其中0b <；不等式在(,)a b中有且只有一个整数解，则实数m 的取值范围是( ) A．221(,)32e eB．221(,)3e eC．221[,)32e eD．221[,3e e【名师解析】解：设()x g x xe =，y mx m =-， 由题设原不等式有唯一整数解， 即()x g x xe =在直线y mx m =-下方，()(1)x g x x e '=+，()g x 在(,1)-∞-递减，在(1,)-+∞递增，故1()(1)min g x g e=-=-，y mx m =-恒过定点(1,0)P ，结合函数图象得PA PB K m K <…， 即22132m e e<…， ，故选：C ．4．已知函数()(2)(0)x f x x kx e x =+->，若()0f x >的解集为(,)a b ，且(,)a b 中恰有两个整数，则 实数k 的取值范围为( ) A．21(,)e -∞ B．411[2e +，312)3e +C．312[3e +，211)e + D．21[1e +，12)e+ 【名师解析】解：设()xxg x e =， 则1()xxg x e -'=当01x <<时，()0g x '>，当1x >时，()0g x '<，所以函数()g x 在(0,1)为增函数，在(1,)+∞为减函数，()0f x >的解集为(,)a b 等价于(2)xxkx e >-的解集为(,)a b ， 即当且仅当在区间(,)a b 上函数()xxg x e =的图象在直线2y kx =-的上方， 函数()xxg x e =的图象与直线2y kx =-的位置关系如图所示， 由图可知：(1)2(2)22(3)32g k g k g k >-⎧⎪>-⎨⎪-⎩…，解得：3221113k e e+<+…， 故选：C ．5．已知函数2()(1)x f x mx e x =--，若不等式()0f x <的解集中恰有两个不同的正整数解，则实数m 的取值范围( ) A．221(2e +，11)e + B．221[2e +，11)e + C．331[3e +，2212e + D．331(3e +，2212e + 【名师解析】解：函数2()(1)xf x mx e x =--，不等式()0f x <化为：21x x mx e -<．分别令()1f x mx =-，2()x x g x e =．(2)()xx x g x e -'=． 可得：函数()g x 在(,0)-∞上单调递减，在(0,2)上单调递增，在(2,)+∞上单调递减．(0)0g =，g （2）24e =．如图所示．不等式()0f x <的解集中恰有两个不同的正整数解，∴正整数解为1，2，∴(2)(2)(3)(3)f g f g <⎧⎨⎩…，即23421931m e m e ⎧-<⎪⎪⎨⎪-⎪⎩…． 解得：32312132m e e +<+…． ∴数m 的取值范围是331[3e +，221)2e +． 故选：C ．6．已知函数()()x f x x a e alnx =--，若恰有三个正整数0x ，使得0()0f x <，则实数a 的取值范围是( ) A．333(3e e ln +，444]22e e ln +B．412[42ln e +，313)33ln e +C．222(2e e ln +，444]22e e ln +D．313[33ln e +，212)22ln e+【名师解析】解：()f x 的定义域为(0,)+∞， 由()0f x <可得xalnxx a e -<， （1）显然0a =时，不等式在(0,)+∞上无解，不符合题意； （2）当0a <时，不等式为11x lnx x a e->， 令1()1f x x a =-，()x lnxg x e =，则当1x …时，()1f x <-，()0g x …，故不等式11x lnxx a e->没有正整数解，不符合题意；（3）当0a >时，不等式为11x lnx x a e-<， 显然1()1f x x a=-为增函数， 1()x xlnxg x xe -'=，令()1h x xlnx =-，则()(1)h x lnx '=-+， ∴当1x e >时，()0h x '<，故()h x 在1(e，)+∞上单调递减， 而h （1）10=>，h （2）12204eln ln =-=<， ∴存在0(1,2)x ∈使得0()0h x =，∴当[1x ∈，0)x 时，()0h x >，当0x x >时，()0h x <，即当[1x ∈，0)x 时，()0g x '>，当0x x >时，()0g x '<，()g x ∴在[1，0)x 上单调递增，在0(x ．)+∞上单调递减， 又g （1）0=，且1x >时，()0g x >， 故不等式11x lnxx a e-<的三个正整数解为1，2，3， ∴(1)(1)(3)(3)(4)(4)0f g f g f g a <⎧⎪<⎪⎨⎪⎪>⎩…，即34110331441a ln a e ln a e ⎧-<⎪⎪⎪-<⎨⎪⎪-⎪⎩…，解得：343434322e e a e ln e ln <++…． 故选：A ．7．已知函数若1()(34x f x kx e x =+-，若()0f x <的解集中恰有两个正整数，则k 的取值范围为( )A．331(12e -，231]8e - B．331[12e -，231)8e -C．231(8e -，314e - D．231[8e -，31)4e - 【名师解析】解：由()0f x <得1()()304x f x kx e x =+-<，即1()34x kx e x +<，即13(4x xkx e +<的解集中恰有两个正整数，设3()x x h x e =，则23333()()x x x xe xe xh x e e--'==， 由()0h x '>得330x ->得1x <，由()0h x '<得330x -<得1x >，即当1x =时函数()h x 取得极大值h （1）3e=， 设函数1()4g x kx =+， 作出函数()h x 的图象如图，由图象知当0k …，13()4x xkx e +<的解集中有很多整数解，不满足条件．则当0k >时，要使，13()4x xkx e+<的解集中有两个整数解，则这两个整数解为1x =和2x =， h （2）26e =，h（3）39e =，(2A ∴，26(3B e ，39)e ， 当直线()g x 过(2A ，26(3B e ，39)e 时，对应的斜率满足 21624A k e +=，31934B k e +=，得2318A k e =-，33112B k e =-， 要使，13()4x xkx e+<的解集中有两个整数解，则B A k k k <…，即323131128k e e -<-…， 即实数k 的取值范围是331[12e -，231)8e -， 故选：B ．8．已知()f x '是函数()f x 的导函数，且对任意的实数x 都有1()()(xf x f x e e '=-是自然对数的底数），(0)0f =，若不等式()0f x k ->的解集中恰有两个整数，则实数k 的取值范围是( )A．221[,)e eB．3232(,e e C．3232(,e e D．3232[,e e 【名师解析】解：设()()x g x e f x =， 则()[()()]1x g x e f x f x '='+=， 可设()g x x c=+，(0)(0)00g f c ==+= ． 0c ∴=，()g x x ∴=， ()xx f x e ∴=， 1()xxf x e -∴'=， 当1x <时，()0f x '>，函数()f x 单调递增， 当1x >时，()0f x '<，函数()f x 单调递减， ()max f x f ∴=（1）1e=， 当x →+∞时，()0f x →，不等式()0f x k ->的解集中恰有两个整数，结合图形可知，整数为1，2f ∴（3）k f <…（2）， ∴3232k e e <… 故选：D ．9．已知函数(2)()ln x f x x=，关于x 的不等式2()()0f x af x +>只有两个整数解，则实数a 的取值范围是( )A．1(2,6]3ln ln -- B．16(,3ln e --C．1[6,2)3ln lnD．62[,3ln e【名师解析】解：21(2)()ln x f x x -'=，令()0f x '=得2ex =， ∴当02ex <<时，()0f x '>，()f x 单调递增， 当2ex >时，()0f x '<，()f x 单调递减， 由当12x <时，()0f x <，当12x >时，()0f x >， 作出()f x 的大致函数图象如图所示：2()()0f x af x +> ，（1）若0a =，即2()0f x >，显然不等式有无穷多整数解，不符合题意； （2）若0a >，则()f x a <-或()0f x >，由图象可知()0f x >有无穷多整数解，不符合题意； （3）若0a <，则()0f x <或()f x a >-，由图象可知()0f x <无整数解，故()f x a >-有两个整数解， f （1）f =（2）2ln =，且()f x 在(2e，)+∞上单调递减，()f x a ∴>-的两个整数解必为1x =，2x =， 又f （3）63ln =， ∴623ln a ln -<…，解得623ln ln a -<-…． 故选：A ．10．函数()(4)(1)f x kx lnx x x =+->，若()0f x >的解集为(,)s t ，且(,)s t 中只有一个整数，则实数k 的取值范围为( ) A．1(22ln -，1433ln - B．1(22ln -，14)33ln - C．14(33ln -，11]22ln - D．14(33ln -，11)22ln - 【名师解析】解：令()0f x >，得：4xkx lnx+>， 令()xg x lnx =，则21()()lnx g x lnx -'=， 令()0g x '>，解得：x e >，令()0g x '<，解得：1x e <<， 故()g x 在(1,)e 递减，在(,)e +∞递增， 结合函数的单调性得：24(2)34(3)k g k g +>⎧⎨+⎩…，即22423343k ln k ln ⎧+>⎪⎪⎨⎪+⎪⎩…，解得：1142233k ln ln -<-…， 故选：A ． 11．已知函数()xxf x e =，若不等式()(1)0f x a x -+>的解集中有且仅有一个整数，则实数a 的取值范围是( ) A．211[,]e eB．211[,)e eC．221[,]32e eD．221[,)32e e【名师解析】解：1()xxf x e -'=， ∴当1x <时，()0f x '>，当1x >时，()0f x '<，()f x ∴在(,1)-∞上单调递增，在(1,)+∞上单调递减， 作出()y f x =的函数图象如图所示：由()(1)0f x a x -+>仅有一个整数解得()(1)f x a x >+只有一整数解， 设()(1)g x a x =+，由图象可知：当0a …时，()()f x g x >在(0,)+∞上恒成立，不符合题意， 当0a >时，若()()f x g x >只有1个整数解，则此整数解必为1， ∴(1)(1)(2)(2)f g f g >⎧⎨⎩…，即21223a eae ⎧>⎪⎪⎨⎪⎪⎩…，解得22132a e e <…． 故选：D ．12．已知函数2()(31)x f x x x e k =++-有三个不同的零点，则实数k 的取值范围是( )A．415(,)e e-B．45(0,)e C．451(,e e -D．1(,)e-+∞【名师解析】解：函数2()(31)x f x x x e k =++-， 可得：2()(54)(1)(4)x x f x x x e x x e '=++=++，()f x 在(,4)-∞-和(1,)-+∞上是增函数；在(4,1)--上是减函数， 当x →-∞时()f x k →-，当x →+∞时()f x →+∞， 所以函数2()(31)x f x x x e k =++-有三个不同的零点， 只需：满足0k -<，45(4)0f k e -=->，1(1)0f k e-=--<，解得45(0,)k e∈ 故选：B．13．已知函数()(2)x f x x e ax a =---，若不等式()0f x >恰有两个正整数解，则a 的取值范围是( ) A．31[4e -，0)B．1[2e -，0)C．31[4e -，)2eD．31[4e -，2)【名师解析】解：令()(2)x g x x e =-，()h x ax a =+， 由题意知，存在2个正整数，使()g x 在直线()h x 的上方，()(1)x g x x e '=- ，∴当1x >时，()0g x '<，当1x <时，()0g x '>，()max g x g ∴=（1）e =，且(0)2g =，g （2）0=，g （3）3e =-， 直线()h x 恒过点(1,0)-，且斜率为a ， 由题意可知，3(1)(2)0(3)h e h h e <⎧⎪<⎨⎪-⎩…，故实数a 的取值范围是31[4e -，0)，故选：A ．14．已知函数2,0(),0x x x f x e x <⎧=⎨⎩…，且()||f x a x …有且只有一个整数解，则a 的取值范围是( )A．(2，]eB．(2，2]e C．(2，8]D．[e ，21)2e【名师解析】解：0a …时，||y a x =的图象在x 轴下方，不符题意； 0a >时，()||f x a x …有且只有一个整数解，即为x e ax …有且只有一个整数解， 由y ax =与x y e =相切，设切点为(,)m m e ， 可得mme e a m==，解得1m =，a e =， 由题意可得x e ax …有且只有一个整数解，且为1， 可得22e a >，即212a e <，且a e …，即212e a e <…，故选：D ．15．函数()(4)(1)f x kx lnx x x =+->，若()0f x >的解集为(,)s t ，且(,)s t 中恰有两个整数，则实数k 的取值范围为( ) A．11(2,1)222ln ln -- B．11(2,1]222ln ln -- C．141(,1)3322ln ln -- D．141(,1]3322ln ln -- 【名师解析】解：令()0f x >，得：4xkx lnx+>， 令()xg x lnx=，则21()()lnx g x lnx -'=，令()0g x '>，解得：x e >，令()0g x '<，解得：1x e <<， 故()g x 在(1,)e 递增，在(,)e +∞递减， 结合函数的单调性得44(4)34(3)k g k g +⎧⎨+>⎩…，即44443343k ln k ln ⎧+⎪⎪⎨⎪+>⎪⎩…，解得：14113322k ln ln -<-…， 故选：D ．16．已知函数1()()23x f x kx e x =+-，若()0f x <的解集中有且只有一个正整数，则实数k 的取值范围为22121[,63e e -- ． 【名师解析】解： 且()0f x <的解集中有且只有一个正整数， ∴有且只有一个正整数使123xx kx e +<，令1()3g x kx =+，2()x xh x e =，易得()h x 的图象如图()g x 的图象恒过1(0,3，∴结合()g x 和()h x 的图象特点可知0k >．且()()()()212113221423k g h e g h k e ⎧+<⎪<⎧⎪⎪⎨⎨⎪⎩⎪+⎪⎩即……． 故答案为：22121[,)63e e --． 17．已知函数()(1)(2)xf x m x x e e =----，若关于x 的不等式()0f x >有且只有一个正整数解，则实数m 的取值范围是 3(,2e e e + ．【名师解析】解：()0f x >即为(1)(2)x m x x e e ->-+，设(1)y m x =-，()(2)x g x x e e =-+，()(1)x g x x e ∴'=-，当1x >时，()0g x '>，()g x 单增，当1x <时，()0g x '<，()g x 单减，()g x g ∴…（1）0=，当x →+∞时，()g x →+∞，当x →-∞时，()g x e →，函数(1)y m x =-恒过(1,0)， 分别画出函数(1)y m x =-及函数()g x的图象如图所示，由图可知，要使不等式()0f x >有且仅有一个正整数解，则(1)y m x =-的图象在函数()y g x =图象的上方只有一个正整数值2，2m g ∴…（3）3e e =+且m g >（2）e =， ∴32e ee m +<…． 故答案为：3(,]2e ee +．。
高考数学高考数学压轴题 多选题分类精编含答案
一、函数的概念与基本初等函数多选题1．对于函数()9f x x x=+，则下列判断正确的是（ ）A ．()f x 在定义域内是奇函数B ．函数()f x 的值域是(][),66,-∞-⋃+∞ C ．()12,0,3x x ∀∈，12x x ≠，有()()12120f x f x x x ->-D ．对任意()12,0,x x ∈+∞且12x x ≠，有()()1212122x x f f x f x +⎛⎫<+⎡⎤ ⎪⎣⎦⎝⎭【答案】ABD 【分析】根据函数奇偶性定义判断()f x 的奇偶性，利用基本不等式求()f x 的值域，设1203x x <<<，根据解析式判断()()12,f x f x 的大小，进而确定()()1212,0f x f x x x --的大小关系，应用作差、作商法判断12122,2()()f x f x x x f +⎛⎫⎪+⎝⎭大小关系，进而确定各项的正误. 【详解】A ：由解析式知：定义域为0x ≠，99()()()f x x x f x x x-=-+=-+=--，即()f x 在定义域内是奇函数，正确； B ：当0x >时，()96f x x x =+≥=当且仅当3x =时等号成立；当0x <时有0x ->，()9[()()]6f x x x=--+-≤-=-当且仅当3x =-时等号成立；故其值域(][),66,-∞-⋃+∞，正确；C ：当1203x x <<<时，()()1212121212999()(1)f x f x x x x x x x x x -=-+-=--，而120x x -<，12910x x -<，则()()120f x f x ->，所以()()12120f x f x x x -<-，错误；D ：若120x x >>，1212123622x x f x x x x +⎛⎫=++⎪+⎝⎭，12121299()()f x f x x x x x +=+++，所以121212123699()()]2[()2f x f x x x x x x x f +⎛⎫- ⎪⎝+=-++⎭，而121221212364199()x x x x x x x x +=<++，即()()1212122x x f f x f x +⎛⎫<+⎡⎤ ⎪⎣⎦⎝⎭，正确； 故选：ABD 【点睛】关键点点睛：综合应用函数奇偶性的证明、对勾函数值域的求法、作差(作商)法比较大小，判断各选项的正误.2．设函数ln(2),2()1,2x x f x x x ->⎧=⎨+≤⎩，g （x ）＝x 2-（m ＋1）x ＋m 2-2，下列选项正确的有（ ）A ．当m ＞3时，f [f （x ）]＝m 有5个不相等的实根B ．当m ＝0时，g [g （x ）]＝m 有4个不相等的实根C ．当0＜m ＜1时，f [g （x ）]＝m 有6个不相等的实根D ．当m ＝2时，g [f （x ）]＝m 有5个不相等的实根 【答案】BCD 【分析】作出函数()f x 的图象，利用函数()f x 的图象和函数()g x 的图象分析可解得结果.【详解】作出函数()f x 的图象：令()f x t =，得[()]()f f x f t m ==；当3m >时，()f x m =有两个根：31242e t t <->+，，方程1()f x t =有1个根，方程2()f x t =有2个根，所以A 错误；②当0m =时，2 ()2g x x x =--，[()]0g g x =，令()g x t =，由()0g t =，得1221t t ==-，， 由2122t x x ==--12117117x x -+⇒=由2234151512t x x x x -+=-=--⇒==所以B 正确；③令()g x t =，()f t m =∴，因为01m <<，所以()f t m =有3个实根根123,,t t t ，设123t t t <<，所以12311ln(2)t m t m t m --=+=-=，，， 22()(1)2g x x m x m =-++-221329()24m m m x +--=-+23294m m --≥， 221329329144m m m m t m -----=---23254m m --+=， 因为2325m m --+在(0,1)上递减，所以23253250m m --+>--+=， 所以2132504m m t --+->，所以213254m m t --+>， 即方程()f t m =的最小根1t 大于()g x 的最小值，所以1()g x t =、2()g x t =、3()g x t =都有2个不等实根，且这6个实根互不相等， 所以当0＜m ＜1时，f [g （x ）]＝m 有6个不相等的实根，所以C 正确； ④令()f x t =，则()g t m =，当2m =时，方程()2g t =化为230t t -=，得1230t t ==，；当20()t f x ==，得1213x x =-=，； 当13()t f x ==，得3442x x =-=，，352e x =+符合题意，所以D 正确. 故选：BCD. 【点睛】关键点点睛：作出函数的图象，利用数形结合法求解是解题关键.3．已知53a =，85b =，则（ ） A ．a b < B ．112a b+> C ．11a b a b+<+ D ．b a a a b b +<+【答案】ABD 【分析】根据条件求得,a b 表达式，根据对数性质结合放缩法得A 正确，根据不等式性质得B 正确，通过作差法判断C 错，结合指数函数单调性与放缩法可得D 正确． 【详解】解：∵53a =，85b =， ∴35log a =，58log b =，因为3344435533535log 3log 54<⇒<⇒<=， 又由3344438835858log 5log 84>⇒>⇒>=，所以a b <，选项A 正确； 35lo 01g a <=<，580log 1b <=<，则11a >，11b >，所以112a b+>，选项B 正确；因为a b <，01a b <<<，则0b a ->，11ab>，此时111()()10b a a b a b b a a b ab ab -⎛⎫⎛⎫+-+=-+=--> ⎪ ⎪⎝⎭⎝⎭， 所以11a b a b+>+，故选项C 不正确； 由1324a <<和314b <<知()x f x a =与()x g x b =均递减， 再由a ，b 的大小关系知b b a b a b a a b b a b a a b b <<⇒<⇒+<+，故选项D 正确. 故选：ABD 【点睛】本题考查了数值大小比较，关键运用了指对数运算性质，作差法和放缩法．4．已知()f x 是定义域为(,)-∞+∞的奇函数，(1)f x +是偶函数，且当(]0,1x ∈时，()(2)f x x x =--，则（ ）A ．()f x 是周期为2的函数B ．()()201920201f f +=-C ．()f x 的值域为[]1,1-D ．()y f x =在[]0,2π上有4个零点【答案】BCD 【分析】对于A ，由()f x 为R 上的奇函数，()1f x +为偶函数，得(4)()f x f x +=，则()f x 是周期为4的周期函数，可判断A.对于B ，由()f x 是周期为4的周期函数，则()()202000f f ==，()()()2019111f f f =-=-=-，可判断B ．对于C ，当(]01x ∈，时，()()2f x x x =--，有()01f x ≤＜，又由()f x 为R 上的奇函数，则[)10x ∈-，时，()10f x -≤＜，可判断C ． 对于D ，根据函数的周期性和对称性，可以求出函数在各段上的解析式，从而求出函数的零点，可判断D ． 【详解】 解：对于A ，()1f x +为偶函数，其图像关于x 轴对称，把()1f x +的图像向右平移1个单位得到()f x 的图像，所以()f x 图象关于1x =对称， 即(1)(1)f x f x +=-，所以(2)()f x f x +=-，()f x 为R 上的奇函数，所以()()f x f x -=-，所以(2)()f x f x +=-，用2x +替换上式中的x 得， (4)(2)f x f x +=-+，所以，(4)()f x f x +=，则()f x 是周期为4的周期函数.故A 错误.对于B ，()f x 定义域为R 的奇函数，则()00f =，()f x 是周期为4的周期函数，则()()202000f f ==；当(]0,1x ∈时，()()2f x x x =--，则()()11121f =-⨯-=，则()()()()201912020111f f f f =-+=-=-=-， 则()()201920201f f +=-.故B 正确.对于C ，当(]01x ∈，时，()()2f x x x =--，此时有()01f x <≤，又由()f x 为R 上的奇函数，则[)1,0x ∈-时，()10f x -≤<，(0)0f =，函数关于1x =对称，所以函数()f x 的值域[]1,1-.故C 正确.对于D ，(0)0f =，且(]0,1x ∈时，()()2f x x x =--，[0,1]x ∴∈，()(2)f x x x =--，[1,2]x ∴∈，2[0,1]x -∈，()(2)(2)f x f x x x =-=--①[0,2]x ∴∈时，()(2)f x x x =--，此时函数的零点为0，2；()f x 是奇函数，[2,0],()(2)x f x x x ∴∈-=+，②(]2,4x ∴∈时，()f x 的周期为4，[]42,0x ∴-∈-，()()()()424f x f x x x =-=--，此时函数零点为4；③(]4,6x ∴∈时，[]40,2x ∴-∈，()()4(4)(6)f x f x x x =-=---，此时函数零点为6；④(]6,2x π∴∈时，(]42,4x ∴-∈，()()()()468f x f x x x =-=--，此时函数无零点；综合以上有，在(0,2)π上有4个零点.故D 正确； 故选：BCD 【点睛】关键点点睛：由(1)f x +是偶函数，通过平移得到()f x 关于1x =对称，再根据()f x 是奇函数，由此得到函数的周期，进一步把待求问题转化到函数的已知区间上，本题综合考查抽象函数的奇偶性、周期性.5．函数()f x 的定义域为D ，若存在区间[],m n D ⊆使()f x 在区间[],m n 上的值域也是[],m n ，则称区间[],m n 为函数()f x 的“和谐区间”，则下列函数存在“和谐区间”的是（ ）A ．()f x =B ．()222f x x x =-+C ．()1f x x x=+D ．()1f x x=【答案】ABD 【分析】根据题意，可知若()f x 在区间[],m n 上的值域也是[],m n ，则()f x 存在“和谐区间”[],m n ，且m n <，则()()f m m f n n ⎧=⎪⎨=⎪⎩或()()f m nf n m ⎧=⎪⎨=⎪⎩，再对各个选项进行运算求解,m n ，即可判断该函数是否存在“和谐区间”.【详解】解：由题得，若()f x 在区间[],m n 上的值域也是[],m n ，则()f x 存在“和谐区间”[],m n ，可知，m n <，则()()f m m f n n ⎧=⎪⎨=⎪⎩或()()f m nf n m ⎧=⎪⎨=⎪⎩，A ：())0f x x =≥，若()()f m mf n n⎧==⎪⎨==⎪⎩，解得：01m n =⎧⎨=⎩，所以()f x =“和谐区间”[]0,1；B ：()()222f x x x x R =-+∈，若 ()()222222f m m m m f n n n n ⎧=-+=⎪⎨=-+=⎪⎩，解得：12m n =⎧⎨=⎩， 所以()222f x x x =-+存在“和谐区间” []1,2；C ：()()10f x x x x =+≠，若()()11f m m m m f n n n n ⎧=+=⎪⎪⎨⎪=+=⎪⎩，得1010mn ⎧=⎪⎪⎨⎪=⎪⎩，故无解；若()()11f m m nmf n n mn⎧=+=⎪⎪⎨⎪=+=⎪⎩，即 21111m n m m m n n m n ⎧+=⎪⎪⎪=⎨+⎪⎪+=⎪⎩，化简得：2210(1)m m m m ++=+， 即210m m ++=，由于2141130∆=-⨯⨯=-<，故无解； 若()0112,m n f m m <<<∴=∴= 不成立 所以()1f x x x=+不存在“和谐区间”； D ：()()10f x x x =≠，函数在()()0+-0∞∞，，，单调递减，则 ()()11f m n mf n mn ⎧==⎪⎪⎨⎪==⎪⎩， 不妨令122m n ⎧=⎪⎨⎪=⎩， 所以()1f x x =存在“和谐区间”1,22⎡⎤⎢⎥⎣⎦； 综上得：存在“和谐区间”的是ABD. 故选：ABD. 【点睛】关键点点睛：本题以函数的新定义为载体，考查函数的定义域、值域以及零点等知识，解题的关键是理解“和谐区间”的定义，考查运算能力以及函数与方程的思想.6．已知当0x >时，2()24f x x x =-+；0x ≤时(2)y f x =+，以下结论正确的是（ ）A ．()f x 在区间[]6,4--上是增函数；B ．()()220212f f -+-=；C ．函数()y f x =周期函数，且最小正周期为2；D ．若方程()1f x kx =+恰有3个实根，则142k <<-4k =； 【答案】BD 【分析】利用函数的性质，依次对选项加以判断，ABC 考查函数的周期性及函数的单调性，重点理解函数周期性的应用，是解题的关键，D 选项考查方程的根的个数，需要转化为两个函数的交点个数，在同一图像中分别研究两个函数，临界条件是直线与函数()f x 相切，结合图像将问题简单化. 【详解】对于A ，0x ≤时(2)y f x =+，即()f x 在区间[]6,4--上的单调性与()f x 在区间[]0,2上单调性一致， 所以()f x 在[]6,5--上是增函数，在[]5,4--上是减函数，故A 错误； 对于B ，当0x ≤时，()2()f x f x +=，()()22=22242=0f f -=-⨯+⨯，()()()()20211=1+2=1=2+42f f f f -=---=，故B 正确；对于C ，当0x ≤时，()2()f x f x +=， 当0x >时，()f x 不是周期函数，故C 错误； 对于D ，由0x >时，2()24f x x x =-+；0x ≤时(2)y f x =+，可求得当20x -<<时，2()24f x x x =--；直线1y kx =+恒过点(0,1)，方程()1f x kx =+恰有3个实根， 即函数()f x 和函数1y kx =+的图像有三个交点，当0k >时，直线1y kx =+与函数()f x （0x >）相切于点00(,)x y ，则020001244124k k x kx xx⎧>⎪⎪=-+⎨⎪+=-+⎪⎩，解得04222=2k x ⎧=-⎪⎨⎪⎩，要函数()f x 和函数1y kx =+的图像有三个交点， 则k 的取值范围为：14222k <<-； 当0k <时，当0x >时，直线1y kx =+与函数()f x 有两个交点， 设直线1y kx =+与函数()f x （0x ≤）相切于点00(,)x y ''，则0200044124k x kx x x =-'-⎧⎨'+=-'-'⎩，解得02242=2k x ⎧=-⎪⎨'-⎪⎩综上，方程()1f x kx =+有3个实根， 则14222k <<-或224k =-,故D 正确.故选：BD. 【点睛】本题考查函数的性质，单调性，及函数零点个数的判断，主要考查学生的逻辑推理能力，数形结合能力，属于较难题.7．已知直线2y x =-+分别与函数x y e =和ln y x =的图象交于点()()1122,,,A x y B x y ，则下列结论正确的是( ) A ．122x x +=B ．122x x e e e +>C ．1221ln ln 0x x x x +<D ．12e x x >【答案】ABC 【分析】根据互为反函数的性质可得()()1122,,,A x y B x y 的中点坐标为()1,1，从而可判断A ；利用基本不等式可判断B 、D ；利用零点存在性定理以及对数的运算性质可判断C. 【详解】函数xy e =与ln y x =互为反函数， 则xy e =与ln y x =的图象关于y x =对称，将2y x =-+与y x =联立，则1,1x y ==，由直线2y x =-+分别与函数xy e =和ln y x =的图象交于点()()1122,,,A x y B x y ，作出函数图像：则()()1122,,,A x y B x y 的中点坐标为()1,1， 对于A ，由1212x x +=，解得122x x +=，故A 正确； 对于B ，12121222222x x x x x x e e e e e e e +≥=+⋅==， 因为12x x ≠，即等号不成立，所以122x x e e e +>，故B 正确；对于C ，将2y x =-+与xy e =联立可得2x x e -+=，即20x e x +-=，设()2xf x e x =+-，且函数为单调递增函数，()010210f =+-=-<，112211320222f e e ⎛⎫=+-=-> ⎪⎝⎭，故函数的零点在10,2⎛⎫ ⎪⎝⎭上，即1102x <<，由122x x +=，则212x <<， 122112211ln ln ln lnx x x x x x x x +=- ()1222122ln ln ln 0x x x x x x x <-=-<，故C 正确；对于D，由12x x +≥，解得121x x ≤， 由于12x x ≠，则121x x <，故D 错误； 故选：ABC 【点睛】本题考查了互为反函数的性质、基本不等式的应用、零点存在性定理以及对数的运算性质，考查了数形结合的思想，属于难题.8．定义在R 上的函数()(),()22(2)f x x g x g x x g x =+=--+--,若()f x 在区间[1,)-+∞上为增函数,且存在20t -<<,使得(0)()0f f t ⋅<.则下列不等式一定成立的是( )A ．21(1)()2f t t f ++> B ．(2)0()f f t ->> C ．(2)(1)f t f t +>+D ．(1)()f t f t +>【答案】ABC 【分析】先由()(),()22(2)f x x g x g x x g x =+=--+--推出()f x 关于1x =-对称，然后可得出B 答案成立，对于答案ACD ，要比较函数值的大小，只需分别看自变量到对称轴的距离的大小即可 【详解】因为()(),()22(2)f x x g x g x x g x =+=--+--所以(2)2(2)2()22()()f x x g x x g x x g x x f x --=--+--=--+++=+= 所以()f x 关于1x =-对称，所以(0)(2)f f =- 又因为()f x 在区间[1,)-+∞上为增函数，20t -<< 所以(0)(2)()f f f t =-> 因为(0)()0f f t ⋅<所以()0,(2)(0)0f t f f <-=> 所以选项B 成立因为2231120224t t t ⎛⎫++-=++> ⎪⎝⎭所以21t t ++比12离对称轴远所以21(1)()2f t t f ++>，所以选项A 成立 因为()()2232250t t t +-+=+>所以32t t +>+，所以2t +比1t +离对称轴远 所以(2)(1)f t f t +>+，即C 答案成立因为20t -<<，所以()()222123t t t +-+=+符号不定 所以2t +，1t +无法比较大小，所以(1)()f t f t +>不一定成立 所以D 答案不一定成立 故选：ABC 【点睛】本题考查的是函数的性质，由条件得出()f x 关于1x =-对称是解题的关键.9．已知21,1,()ln ,1,x x f x x x ⎧-≤⎪=⎨>⎪⎩，则关于x 的方程2[()]()210f x f x k -+-=，下列正确的是（ ）A ．存在实数k ，使得方程恰有1个不同的实数解；B ．存在实数k ，使得方程恰有2个不同的实数解；C ．存在实数k ，使得方程恰有3个不同的实数解；D ．存在实数k ，使得方程恰有6个不同的实数解； 【答案】ACD 【分析】令()0f x t =≥，根据判别式确定方程2210t t k -+-=根的个数，作出()f x 的大致图象，根据根的取值，数形结合即可求解. 【详解】令()0f x t =≥，则关于x 的方程2[()]()210f x f x k -+-=，可得2210t t k -+-=， 当58k =时，()14210k ∆=--=，此时方程仅有一个根12t =； 当58k <时，()14210k ∆=-->，此时方程有两个根12,t t ， 且121t t +=，此时至少有一个正根； 当58k >时，()14210k ∆=--<，此时方程无根； 作出()f x 的大致图象，如下：当58k =时，此时12t =，由图可知()f x t =，有3个不同的交点，C 正确； 当58k <时，此时方程有两个根12,t t ，且121t t +=，此时至少有一个正根， 当()10,1t ∈、()20,1∈t ，且12t t ≠时，()f x t =，有6个不同的交点，D 正确； 当方程有两个根12,t t ，一个大于1，另一个小于0， 此时()f x t =，仅有1个交点，故A 正确；当方程有两个根12,t t ，一个等于1，另一个等于0，()f x t =，有3个不同的交点，当58k >时，()14210k ∆=--<，此时方程无根. 故选：ACD 【点睛】关键点点睛：本题考查了根的个数求参数的取值范围，解题的关键是利用换元法将方程化为2210t t k -+-=，根据方程根的分布求解，考查了数形结合的思想，分类讨论的思想.10．已知函数12()123x x x f x x x x ++=+++++，下列关于函数()f x 的结论正确的为（ ） A ．()f x 在定义域内有三个零点 B ．函数()f x 的值域为R C ．()f x 在定义域内为周期函数 D ．()f x 图象是中心对称图象【答案】ABD 【分析】将函数变形为111()3123f x x x x ⎛⎫=-++ ⎪+++⎝⎭，求出定义域，结合导数求函数的单调性即可判断BC ，由零点存在定理结合单调性可判断A ，由()()46f x f x --=+可求出函数的对称点，即可判断D. 【详解】解：由题意知，1111()111312311123f x x x x x x x ⎛⎫=-+-+-=-++ ⎪++++++⎝⎭， 定义域为()()()(),33,22,11,-∞-⋃--⋃--⋃-+∞，()()()22211()01213f x x x x '=++>+++，所以函数在()()()(),3,3,2,2,1,1,-∞------+∞定义域上单调递增，C 不正确； 当1x >-时，()3371230,004111523f f ⎛⎫-=-++<=+> ⎪⎝⎭，则()1,-+∞上有一个零点， 当()2,1x ∈--时，750,044f f ⎛⎫⎛⎫-<-> ⎪ ⎪⎝⎭⎝⎭，所以在()2,1x ∈--上有一个零点， 当()3,2x ∈--时，1450,052f f ⎛⎫⎛⎫-<-> ⎪ ⎪⎝⎭⎝⎭，所以在()3,2x ∈--上有一个零点， 当3x <-，()0f x >，所以在定义域内函数有三个零点，A 正确； 当0x <，1x +→-时，()f x →-∞，当x →+∞时，()f x →+∞， 又函数在()1,-+∞递增，且在()1,-+∞上有一个零点，则值域为R ，B 正确；()1111(4)363612311123f x f x x x x x x x ⎡⎤⎛⎫⎛⎫--=+++=--++=- ⎪ ⎪⎢⎥++++++⎝⎭⎝⎭⎣⎦， 所以()()46f x f x --=+，所以函数图象关于()2,3-对称，D 正确； 故选:ABD. 【点睛】 结论点睛:1、()y f x =与()y f x =-图象关于x 轴对称；2、()y f x =与()y f x =-图象关于y 轴对称；3、()y f x =与()2y f a x =-图象关于x a =轴对称；4、()y f x =与()2y a f x =-图象关于y a =轴对称；5、()y f x =与()22y b f a x =--图象关于(),a b 轴对称.二、导数及其应用多选题11．关于函数()e cos xf x a x =-，()π,πx ∈-下列说法正确的是（ ）A ．当1a =时，()f x 在0x =处的切线方程为y x =B ．若函数()f x 在()π,π-上恰有一个极值，则0a =C ．对任意0a >，()0f x ≥恒成立D ．当1a =时，()f x 在()π,π-上恰有2个零点 【答案】ABD 【分析】直接逐一验证选项，利用导数的几何意义求切线方程，即可判断A 选项；利用分离参数法，构造新函数和利用导数研究函数的单调性和极值、最值，即可判断BC 选项；通过构造新函数，转化为两函数的交点个数来解决零点个数问题，即可判断D 选项. 【详解】解：对于A ，当1a =时，()e cos xf x x =-，()π,πx ∈-，所以()00e cos00f =-=，故切点为（0，0），则()e sin xf x x '=+，所以()00e sin01f '=+=，故切线斜率为1，所以()f x 在0x =处的切线方程为：()010y x -=⨯-，即y x =，故A 正确； 对于B ，()e cos xf x a x =-，()π,πx ∈-，则()e sin xf x a x '=+，若函数()f x 在()π,π-上恰有一个极值，即()0f x '=在()π,π-上恰有一个解， 令()0f x '=，即e sin 0x a x +=在()π,π-上恰有一个解， 则sin xxa e -=在()π,π-上恰有一个解， 即y a =与()sin xxg x e -=的图象在()π,π-上恰有一个交点， ()sin cos xx xg x e -'=，()π,πx ∈-，令()0g x '=，解得：134x π=-，24x π=， 当3,,44x ππππ⎛⎫⎛⎫∈--⎪ ⎪⎝⎭⎝⎭时，()0g x '>，当3,44x ππ⎛⎫∈-⎪⎝⎭时，()0g x '<， ()g x ∴在3,4ππ⎛⎫--⎪⎝⎭上单调递增，在443,ππ⎛⎫-⎪⎝⎭上单调递减，在,4ππ⎛⎫ ⎪⎝⎭上单调递增， 所以极大值为343204g e ππ-⎛⎫-=> ⎪⎝⎭，极小值为4204g e ππ-⎛⎫=< ⎪⎝⎭， 而()()()0,0,00g g g ππ-===， 作出()sinx g x e-=，()π,πx ∈-的大致图象，如下：由图可知，当0a =时，y a =与()sinx g x e-=的图象在()π,π-上恰有一个交点， 即函数()f x 在()π,π-上恰有一个极值，则0a =，故B 正确； 对于C ，要使得()0f x ≥恒成立，即在()π,πx ∈-上，()e cos 0xf x a x =-≥恒成立，即在()π,πx ∈-上，cos x xa e ≥恒成立，即maxcos x x a e ⎛⎫≥ ⎪⎝⎭，设()cos x x h x e =，()π,πx ∈-，则()sin cos xx xh x e--'=，()π,πx ∈-， 令()0h x '=，解得：14x π=-，234x π=， 当3,,44x ππππ⎛⎫⎛⎫∈--⎪ ⎪⎝⎭⎝⎭时，()0h x '>，当3,44x ππ⎛⎫∈- ⎪⎝⎭时，()0h x '<， ()h x ∴在,4ππ⎛⎫--⎪⎝⎭上单调递增，在3,44ππ⎛⎫-⎪⎝⎭上单调递减，在3,4ππ⎛⎫⎪⎝⎭上单调递增， 所以极大值为42204h eππ-⎛⎫-=> ⎪⎝⎭，()()11,h h e e ππππ--==，所以()cos x xh x e =在()π,πx ∈-上的最大值为42204h e ππ-⎛⎫-=> ⎪⎝⎭， 所以422a e π-≥时，在()π,πx ∈-上，()e cos 0xf x a x =-≥恒成立，即当422a e π-≥时，()0f x ≥才恒成立，所以对任意0a >，()0f x ≥不恒成立，故C 不正确； 对于D ，当1a =时，()e cos xf x x =-，()π,πx ∈-，令()0f x =，则()e cos 0xf x x =-=，即e cos x x =，作出函数xy e =和cos y x =的图象，可知在()π,πx ∈-内，两个图象恰有两个交点，则()f x 在()π,π-上恰有2个零点，故D 正确.故选：ABD. 【点睛】本题考查函数和导数的综合应用，考查利用导数的几何意义求切线方程，考查分离参数法的应用和构造新函数，以及利用导数研究函数的单调性、极值最值、零点等，考查化简运算能力和数形结合思想.12．已知函数1(),()122x x f x e g x n ==+的图象与直线y =m 分别交于A ､B 两点，则（ ）A ．f (x )图像上任一点与曲线g (x )上任一点连线线段的最小值为2+ln 2B ．∃m 使得曲线g (x )在B 处的切线平行于曲线f (x )在A 处的切线C ．函数f (x )-g (x )+m 不存在零点D ．∃m 使得曲线g (x )在点B 处的切线也是曲线f (x )的切线 【答案】BCD 【分析】利用特值法，在f (x )与g (x )取两点求距离，即可判断出A 选项的正误；解方程12()(2)m f lnm g e-''=，可判断出B 选项的正误；利用导数判断函数()()y f x g x m =-+的单调性，结合极值的符号可判断出C 选项的正误；设切线与曲线()y g x =相切于点(C n ，())g n ，求出两切线的方程，得出方程组，判断方程组是否有公共解，即可判断出D 选项的正误．进而得出结论． 【详解】在函数1(),()122xx f x e g x n ==+上分别取点1(0,1),(2,)2P Q，则||2PQ =，而2ln 2<+（注ln 20.7≈），故A 选项不正确； ()x f x e =，1()22x g x ln =+，则()x f x e '=，1()g x x'=，曲线()y f x =在点A 处的切线斜率为()f lnm m '=， 曲线()y g x =在点B 处的切线斜率为12121(2)2m m g ee--'=，令12()(2)m f lnm g e-''=，即1212m m e-=，即1221m me -=，则12m =满足方程1221m me -=，m ∴∃使得曲线()y f x =在A 处的切线平行于曲线()y g x =在B 处的切线，B 选项正确；构造函数1()()()22xx F x f x g x m e ln m =-+=-+-，可得1()x F x e x'=-，函数1()xF x e x'=-在(0,)+∞上为增函数，由于1()20F e '<，F '（1）10e =->，则存在1(,1)2t ∈，使得1()0tF t e t'=-=，可得t lnt =-，当0x t <<时，()0F x '<；当x t >时，()0F x '>．∴11()()2222t t min t F x F t e ln m e lnt m ln ==-+-=-++-11132220222t m ln m ln ln m t =+++->+-=++>， ∴函数()()()F x f x g x m =-+没有零点，C 选项正确；设曲线()y f x =在点A 处的切线与曲线()y g x =相切于点(C n ，())g n ，则曲线()y f x =在点A 处的切线方程为()lnm y m e x lnm -=-，即(1)y mx m lnm =+-，同理可得曲线()y g x =在点C 处的切线方程为1122n y x ln n =+-， ∴11(1)22m n n m lnm ln ⎧=⎪⎪⎨⎪-=-⎪⎩，消去n 得1(1)202m m lnm ln --++=，令1()(1)22G x x x lnx ln =--++，则11()1x G x lnx lnx x x-'=--=-， 函数()y G x '=在(0,)+∞上为减函数，G '（1）10=>，1(2)202G ln '=-<， 则存在(1,2)s ∈，使得1()0G s lns s'=-=，且1s s e =．当0x s <<时，()0G x '>，当x s >时，()0G x '<．∴函数()y G x =在(2,)+∞上为减函数，5(2)02G =>，17(8)20202G ln =-<， 由零点存 定理知，函数()y G x =在(2,)+∞上有零点， 即方程1(1)202m m lnm ln --++=有解． m ∴∃使得曲线()y f x =在点A 处的切线也是曲线()y g x =的切线．故选：BCD ． 【点睛】本题考查导数的综合应用，涉及函数的最值、零点以及切线问题，计算量较大，考查了转化思想和数形结合思想，属难题．13．已知函数()f x 对于任意x ∈R ，均满足()()2f x f x =-.当1x ≤时()ln ,01,0x x x f x e x <≤⎧=⎨≤⎩，若函数()()2g x m x f x =--，下列结论正确的为（ ）A ．若0m <，则()g x 恰有两个零点B ．若32m e <<，则()g x 有三个零点 C ．若302m <≤，则()g x 恰有四个零点 D ．不存在m 使得()g x 恰有四个零点 【答案】ABC 【分析】设()2h x m x =-，作出函数()g x 的图象，求出直线2y mx =-与曲线()ln 01y x x =<<相切以及直线2y mx =-过点()2,1A 时对应的实数m 的值，数形结合可判断各选项的正误. 【详解】由()()2f x f x =-可知函数()f x 的图象关于直线1x =对称. 令()0g x =，即()2mx f x -=，作出函数()f x 的图象如下图所示：令()2h x m x =-，则函数()g x 的零点个数为函数()f x 、()h x 的图象的交点个数，()h x 的定义域为R ，且()()22h x m x m x h x -=--=-=，则函数()h x 为偶函数，且函数()h x 的图象恒过定点()0,2-，当函数()h x 的图象过点()2,1A 时，有()2221h m =-=，解得32m =. 过点()0,2-作函数()ln 01y x x =<<的图象的切线， 设切点为()00,ln x x ，对函数ln y x =求导得1y x'=， 所以，函数ln y x =的图象在点()00,ln x x 处的切线方程为()0001ln y x x x x -=-， 切线过点()0,2-，所以，02ln 1x --=-，解得01x e=，则切线斜率为e ， 即当m e =时，函数()y h x =的图象与函数()ln 01y x x =<<的图象相切. 若函数()g x 恰有两个零点，由图可得0m ≤或m e =，A 选项正确； 若函数()g x 恰有三个零点，由图可得32m e <<，B 选项正确； 若函数()g x 恰有四个零点，由图可得302m <≤，C 选项正确，D 选项错误. 故选：ABC.【点睛】方法点睛：利用导数解决函数零点问题的方法：（1）直接法：先对函数求导，根据导数的方法求出函数的单调区间与极值，根据函数的基本性质作出图象，然后将问题转化为函数图象与x 轴的交点问题，突出导数的工具作用，体现了转化与化归思想、数形结合思想和分类讨论思想的应用； （2）构造新函数法：将问题转化为研究两函数图象的交点问题；（3）参变量分离法：由()0f x =分离变量得出()a g x =，将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.14．（多选）已知函数()ln ()f x ax x a =-∈R ，则下列说法正确的是（ ） A ．若0a ≤，则函数()f x 没有极值 B ．若0a >，则函数()f x 有极值C ．若函数()f x 有且只有两个零点，则实数a 的取值范围是1,e ⎛⎫-∞ ⎪⎝⎭D ．若函数()f x 有且只有一个零点，则实数a 的取值范围是1(,0]e ⎧⎫-∞⋃⎨⎬⎩⎭【答案】ABD 【分析】先对()f x 进行求导，再对a 进行分类讨论，根据极值的定义以及零点的定义即可判断. 【详解】解：由题意得，函数()f x 的定义域为(0,)+∞，且11()ax f x a x x'-=-=， 当0a ≤时，()0f x '<恒成立，此时()f x 单调递减，没有极值， 又当x 趋近于0时，()f x 趋近于+∞，当x 趋近于+∞时，()f x 趋近于-∞， ∴()f x 有且只有一个零点， 当0a >时，在10,a ⎛⎫⎪⎝⎭上，()0f x '<，()f x 单调递减， 在1,a ⎛⎫+∞⎪⎝⎭上，()0f x '>，()f x 单调递增， ∴当1x a=时，()f x 取得极小值，同时也是最小值， ∴min 1()1ln f x f a a ⎛⎫==+⎪⎝⎭， 当x 趋近于0时，ln x 趋近于-∞，()f x 趋近于+∞，当x 趋近于+∞时，()f x 趋近于+∞， 当1ln 0a +=，即1a e=时，()f x 有且只有一个零点；当1ln 0a +<，即10a e<<时，()f x 有且仅有两个零点， 综上可知ABD 正确，C 错误． 故选：ABD ． 【点睛】方法点睛：函数零点的求解与判断方法：(1)直接求零点：令()0f x ＝，如果能求出解，则有几个解就有几个零点； (2)零点存在性定理：利用定理不仅要函数在区间[]a b ，上是连续不断的曲线，且()()·0f a f b ＜，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点；(3)利用图象交点的个数：将函数变形为两个函数的差，画两个函数的图象，看其交点的横坐标有几个不同的值，就有几个不同的零点．15．已知函数()1ln f x x x x=-+，给出下列四个结论，其中正确的是（ ） A ．曲线()y f x =在1x =-处的切线方程为10x y ++= B ．()f x 恰有2个零点C ．()f x 既有最大值，又有最小值D ．若120x x >且()()120f x f x +=，则121=x x 【答案】BD 【分析】本题首先可根据()10f -=以及13f判断出A 错误，然后根据当0x >时的函数单调性、当0x <时的函数单调性、()10f -=以及()10f =判断出B 正确和C 错误，最后根据()()120f x f x +=得出()121f x f x ⎛⎫=⎪⎝⎭，根据函数单调性即可证得121=x x ，D 正确. 【详解】函数()1ln f x x x x=-+的定义域为()(),00,-∞⋃+∞， 当0x >时，()1ln f x x x x=-+，()2221111x x f x x x x -+-'=--=；当0x <时，1ln f x x x x，()2221111x x f x x x x -+-'=--=， A 项：1ln 1110f，22111131f，则曲线()y f x =在1x =-处的切线方程为031y x ，即33y x =--，A 错误；B 项：当0x >时，222215124x x x f xx x ，函数()f x 是减函数，当0x <时，222215124x x x f xx x ，函数()f x 是减函数，因为()10f -=，()10f =，所以函数()f x 恰有2个零点，B 正确； C 项：由函数()f x 的单调性易知，C 错误； D 项：当1>0x 、20x >时， 因为()()120f x f x +=， 所以1222222221111ln lnf x f x x x x fx x x x ， 因为()f x 在()0,∞+上为减函数，所以121x x =，120x x >， 同理可证得当10x <、20x <时命题也成立，D 正确， 故选：BD. 【点睛】本题考查函数在某点处的切线求法以及函数单调性的应用，考查根据导函数求函数在某点处的切线以及函数单调性，导函数值即切线斜率，若导函数值大于0，则函数是增函数，若导函数值小于0，则函数是减函数，考查函数方程思想，考查运算能力，是难题.16．已知函数()()2214sin 2x xe xf x e -=+，则下列说法正确的是（ ） A ．函数()y f x =是偶函数，且在(),-∞+∞上不单调 B ．函数()y f x '=是奇函数，且在(),-∞+∞上不单调递增 C ．函数()y f x =在π,02⎛⎫-⎪⎝⎭上单调递增 D ．对任意m ∈R ，都有()()f m f m =，且()0f m ≥【答案】AD 【分析】由函数的奇偶性以及函数的单调性即可判断A 、B 、C 、D. 【详解】 解：对A ，()()222114sin =2cos 2x x xx e x e f x x e e-+=+-，定义域为R ，关于原点对称，()2211=2cos()2cos()()x x x xe ef x x x f x e e--++---=-=， ()y f x ∴=是偶函数，其图像关于y 轴对称，()f x ∴在(),-∞+∞上不单调，故A 正确；对B ，1()2sin xx f x e x e'=-+， 11()2sin()=(2sin )()x xx x f x e x e x f x e e--''-=-+---+=-， ()f x '∴是奇函数，令1()2sin xx g x e x e=-+， 则1()+2cos 2+2cos 0x x g x e x x e'=+≥≥， ()f x '∴在(),-∞+∞上单调递增，故B 错误；对C ，1()2sin x x f x e x e'=-+，且()'f x 在(),-∞+∞上单调递增， 又(0)0f '=，π,02x ⎛⎫∴∈- ⎪⎝⎭时，()0f x '<，()y f x ∴=在π,02⎛⎫- ⎪⎝⎭上单调递减，故C 错误；对D ，()y f x =是偶函数，且在(0,)+∞上单调递增，()()f m f m ∴=，且()(0)0f m f ≥=，故D 正确.故选：AD. 【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面： (1)在利用导数讨论函数的单调区间时，首先要确定函数的定义域； (2)不能随意将函数的2个独立的单调递增（或递减）区间写成并集形式；(3)利用导数解决含参函数的单调性问题时，一般将其转化为不等式恒成立问题，解题过程中要注意分类讨论和数形结合思想的应用.17．已知函数()()()221x f x x e a x =-+-有两个零点，则a 的可能取值是（ ） A ．1- B ．0C ．1D ．2【答案】CD 【分析】求出()f x 的导数，讨论a 的范围，结合函数的单调性和零点存在性定理可判断求出.【详解】解：∵函数()()()221x f x x e a x =-+-， ∴()()()()()12112xx f x x e a x x e a '=-+-=-+，①若0a =，那么()()0202xf x x e x =⇔-=⇔=，函数()f x 只有唯一的零点2，不合题意； ②若0a >，那么20x e a +>恒成立， 当1x <时，()0f x '<，此时函数为减函数； 当1x >时，()0f x '>，此时函数为增函数； 此时当1x =时，函数()f x 取极小值e -，由()20f a =>，可得：函数()f x 在1x >存在一个零点； 当1x <时，x e e <，210x -<-<，∴()()()()()222121x f x x e a x x e a x =-+->-+-()()211a x e x e =-+--，令()()2110a x e x e -+--=的两根为1t ，2t ，且12t t <， 则当1x t <，或2x t >时，()()()2110f x a x e x e >-+-->， 故函数()f x 在1x <存在一个零点；即函数()f x 在R 上存在两个零点，满足题意； ③若02ea -<<，则()ln 2ln 1a e -<=， 当()ln 2x a <-时，()1ln 21ln 10x a e -<--<-=，()ln 2220a x e a e a -+<+=，即()()()120xf x x e a '=-+>恒成立，故()f x 单调递增，当()ln 21a x -<<时，10x -<，()ln 2220a x e a e a -+>+=， 即()()()120xf x x e a '=-+<恒成立，故()f x 单调递减，当1x >时，10x ->，()ln 2220a x e a e a -+>+=，即()()(1)20xf x x e a '=-+>恒成立，故()f x 单调递增，故当()ln 2x a =-时，函数取极大值，由()()()()()2ln 2ln 222ln 21f a a a a a ⎡⎤⎡⎤-=---+--⎣⎦⎣⎦(){}2ln 2210a a ⎡⎤⎣⎦=--+<得：函数()f x 在R 上至多存在一个零点，不合题意； ④若2ea =-，则()ln 21a -=， 当()1ln 2x a <=-时，10x -<，()ln 2220a x e a e a -+<+=，即()()()120xf x x e a '=-+>恒成立，故()f x 单调递增，当1x >时，10x ->，()ln 2220a x e a e a -+>+=， 即()()()120xf x x e a '=-+>恒成立，故()f x 单调递增，故函数()f x 在R 上单调递增，函数()f x 在R 上至多存在一个零点，不合题意；⑤若2ea <-，则()ln 2ln 1a e ->=， 当1x <时，10x -<，()ln 2220a x e a e a -+<+=， 即()()()120xf x x e a '=-+>恒成立，故()f x 单调递增，当()1ln 2x a <<-时，10x ->，()ln 2220a x e a e a -+<+=， 即()()()120xf x x e a '=-+<恒成立，故()f x 单调递减，当()ln 2x a >-时，10x ->，()ln 2220a x e a e a -+>+=， 即()()()120xf x x e a '=-+>恒成立，故()f x 单调递增，故当1x =时，函数取极大值，由()10f e =-<得：函数()f x 在R 上至多存在一个零点，不合题意； 综上所述，a 的取值范围为()0,∞+， 故选：CD. 【点睛】本题考查利用导数研究函数的零点问题，属于较难题.18．函数()ln f x x x =、()()f x g x x'=，下列命题中正确的是（ ）.A ．不等式()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭B ．函数()f x 在()0,e 上单调递增，在(,)e +∞上单调递减C ．若函数()()2F x f x ax =-有两个极值点，则()0,1a ∈D ．若120x x >>时，总有()()()2212122m x x f x f x ->-恒成立，则m 1≥ 【答案】AD【分析】对A ，根据()ln f x x x =，得到()()ln 1f x xg x x x'+==，然后用导数画出其图象判断；对B ，()1ln f x x '=+，当x e >时，()0f x '>，当0x e <<时，()0f x '<判断；对C ，将函数()()2F x f x ax =-有两个极值点，()ln 120x a x+=+∞在，有两根判断；对D ，将问题转化为22111222ln ln 22m m x x x x x x ->-恒成立，再构造函数()2ln 2m g x x x x =-，用导数研究单调性. 【详解】对A ，因为()()()ln 1ln f x x f x x x g x x x'+===、， ()2ln xg x x -'=， 令()0g x '>，得()0,1x ∈，故()g x 在该区间上单调递增；令()0g x '<，得()1x ∈+∞，，故()g x 在该区间上单调递减. 又当1x >时，()0g x >，()10,11g g e ⎛⎫== ⎪⎝⎭， 故()g x 的图象如下所示：数形结合可知，()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭，故正确；对B ，()1ln f x x '=+，当x e >时，()0f x '>，当0x e <<时，()0f x '<，所以函数()f x 在()0,e 上单调递减，在(,)e +∞上单调递增，错误；对C ，若函数()()2F x f x ax =-有两个极值点，即()2ln F x x x ax =-有两个极值点，又()ln 21F x x ax '=-+，要满足题意，则需()ln 2100x ax -+=+∞在，有两根， 也即()ln 120x a x+=+∞在，有两根，也即直线()2y a y g x ==与的图象有两个交点. 数形结合则021a <<，解得102a <<. 故要满足题意，则102a <<，故错误； 对D ，若120x x >>时，总有()()()2212122m x x f x f x ->-恒成立， 即22111222ln ln 22m m x x x x x x ->-恒成立， 构造函数()2ln 2m g x x x x =-，()()12g x g x >，对任意的120x x >>恒成立， 故()g x ()0+∞，单调递增，则()ln 10g x mx x '=--≥()0+∞， 恒成立， 也即ln 1x m x+≤，在区间()0,∞+恒成立，则()max 1g x m =≤，故正确. 故选：AD. 【点睛】本题主要考查导数在函数图象和性质中的综合应用，还考查了数形结合的思想、转化化归思想和运算求解的能力，属于较难题.19．（多选题）已知函数31()1x x xe x f x e x x⎧<⎪=⎨≥⎪⎩，，，函数()()g x xf x =，下列选项正确的是（ ）A ．点(0,0)是函数()f x 的零点B ．12(0,1),(1,3)x x ∃∈∈，使12()()f x f x >C ．函数()f x 的值域为)1e ,-⎡-+∞⎣D ．若关于x 的方程[]2()2()0-=g x ag x 有两个不相等的实数根，则实数a 的取值范围是222e e,(,)e 82⎛⎤+∞ ⎥⎝⎦ 【答案】BC【分析】根据零点的定义可判断A ；利用导数判断出函数在()0,1、()1,3上的单调性性，求出各段上的值域即可判断B ；利用导数求出函数的最值即可判断C ；利用导数求出函数的最值即可判断D. 【详解】对于选项A ，0是函数()f x 的零点，零点不是一个点，所以A 错误. 对于选项B ，当1x <时，()(1)xf x x e '=+，可得， 当1x <-时，()f x 单调递减； 当11x -<<时，()f x 单调递增； 所以，当01x <<时， 0()<<f x e ，当1x >时，4(3)()x e x f x x -'=，当13x <<时，()f x 单调递减； 当3x >时，()f x 单调递增；()y f x =图像所以，当13x <<时， 3()27e f x e << ，综上可得，选项B 正确；对于选项C ，min 1()(1)f x f e=-=-，选项C 正确. 对于选项D ，关于x 的方程[]2()2()0-=g x ag x 有两个不相等的实数根⇔关于x 的方程()[()2]0-=g x g x a 有两个不相等的实数根 ⇔关于x 的方程()20-=g x a 有一个非零的实数根⇔函数()y g x =与2y a =有一个交点，且0x ≠，22,1(),1x xx e x g x e x x⎧<⎪=⎨≥⎪⎩当1x <时，/2()(2)=+xg x e x x ，当x 变化时，'()g x ，()g x 的变化情况如下：x2x <-2-20x -<<0 01x << /()g x +-+()g x极大值 极小值极大值2(2)g e -=，极小值(0)0g =，当1≥x 时，3(2)'()e x g x x -=当x 变化时，'()g x ，()g x 的变化情况如下： x 112x <<2 2x >/()g x-+()g xe极小值极小值(2)4e g =，()y g x =图像综上可得，22424<<e a e 或2a e >，a 的取值范围是222e e,(,)e 82⎛⎫+∞ ⎪⎝⎭，D 不正确.故选：BC 【点睛】本题考查了利用导数求函数的最值，利用导数研究方程的根，考查了转化与化归的思想，属于难题.20．已知实数a ，b ，c ，d 满足2111a a e cb d --==-，其中e 是自然对数的底数，则()()22a cb d -+-的值可能是（ ） A ．7 B ．8C ．9D ．10【答案】BCD 【分析】由题中所给的等式，分别构造函数()2xf x x e =-和()2g x x =-+，则()()22a cb d -+-的表示()y f x =上一点(),M a b 与()y g x =上一点(),Ncd 的距离的平方，利用导数的几何意义可知当()01f x '=-时，切点到直线的距离最小，再比较选项.【详解】由212a a a e b a e b-=⇒=-，令()2x f x x e =-，()12xf x e '∴=-由1121cd c d -=⇒=-+-，令()2g x x =-+ 则()()22a cb d -+-的表示()y f x =上一点(),M a b 与()y g x =上一点(),Ncd 的距离的平方，设()y f x =上与()y g x =平行的切线的切点为()000,M x y 由()0001210xf x e x '=-=-⇒=，∴切点为()00,2M -所以切点为()00,2M -到()y g x =的距离的平方为28=的距离为(),M a b 与(),N c d 的距离的平方的最小值.故选：BCD. 【点睛】本题考查构造函数，利用导数的几何意义求两点间距离的最小值，重点考查转化思想，构造函数，利用几何意义求最值，属于偏难题型.三、三角函数与解三角形多选题21．在ABC 中，角,,A B C 所对的边分别为,,a b c ，下列命题正确的是（ ） A ．若::4:5:6a b c =，ABC 的最大内角是最小内角的2倍 B ．若cos cos a B b A c -=，则ABC 一定为直角三角形C ．若4,5,6a b c ===，则ABCD ．若()()()cos cos cos 1A B B C C A ---=，则ABC 一定是等边三角形 【答案】ABD 【分析】。
高考数学高三模拟考试试卷压轴题普通高等学校招生全国统一考试理科数学
高考数学高三模拟考试试卷压轴题普通高等学校招生全国统一考试理科数学一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是复合题目要求的。
1．1212ii+=-（） A ．4355i --B ．4355i -+C ．3455i --D ．3455i -+2．已知集合(){}223A x y xy x y =+∈∈Z Z ，≤，，，则A 中元素的个数为（）A ．9B ．8C ．5D ．43．函数()2x xe ef x x --=的图象大致是（）4．已知向量a b ，满足，1a =，1a b ⋅=-，则()2a a b ⋅-=（）A ．4B ．3C ．2D ．05．双曲线()2222100x y a b a b-=＞，＞的离心力为3，则其渐近线方程为（）A ．2y x =±B ．3y x =±C ．2y x =±D ．3y x =± 6．在ABC △中，5cos2C =，1BC =，5AC =，则AB =（） A ．42B ．30 C ．29 D ．257．为计算11111123499100S =-+-+⋅⋅⋅+-，设计了右侧的程序框图，则在空白框中应填入（）A ．1i i =+B ．2i i =+C ．3i i =+D ．4i i =+8．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30723=+．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是（） A ．112B ．114C ．115D ．1189．在长方体1111ABCD A B C D -中，1AB BC ==，1AA =1AD 与1DB 所成角的余弦值为（）A ．15BCD10．若()cos sin f x x x =-在[]a a -，是减函数，则a 的最大值是（）A ．4πB ．2πC ．43πD ．π 11．已知()f x 是定义域为()-∞+∞，的奇函数，满足()()11f x f x -=+．若()12f =，则()()()()12350f f f f +++⋅⋅⋅+=（）A ．50-B ．0C ．2D ．5012．已知1F ，2F 是椭圆()2222:10x y C a b a b+=＞＞的左、右焦点交点，A 是C 的左顶点，点P 在过A 且的直线上，12PF F △为等腰三角形，12120F F P ∠=︒，则C 的离心率为（） A ．23B ．12C ．13D ．14 二、填空题，本题共4小题，每小题5分，共20分．13．曲线()2ln 1y x =+在点()00，处的切线方程为__________．14．若x y ，满足约束条件25023050x y x y x +-⎧⎪-+⎨⎪-⎩≥≥≤，则z x y =+的最大值为_________．15．已知sin cos 1αβ+=，cos sin 0αβ+=，则()sin αβ+=__________． 16．已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45︒．若SAB △的面积为_________．三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤。
数学高考压轴题含答案
数学高考压轴题学校:___________姓名：___________班级：___________考号：___________评卷人得分一、解答题1．已知函数()x f x e ax =-和()ln g x ax x =-有相同的最小值．(1)求a ；(2)证明：存在直线y b =，其与两条曲线()y f x =和()y g x =共有三个不同的交点，并且从左到右的三个交点的横坐标成等差数列．2．已知点(2,1)A 在双曲线2222:1(1)1x y C a a a -=>-上，直线l 交C 于P ，Q 两点，直线,AP AQ 的斜率之和为0．(1)求l 的斜率；(2)若tan PAQ ∠=PAQ △的面积．3．已知函数()e e ax x f x x =-．(1)当1a =时，讨论()f x 的单调性；(2)当0x >时，()1f x <-，求a 的取值范围；(3)设n *∈Nln(1)n ++>+ ．4．已知双曲线2222:1(0,0)x y C a b a b -=>>的右焦点为(2,0)F ，渐近线方程为y =．(1)求C 的方程；(2)过F 的直线与C 的两条渐近线分别交于A ，B 两点，点()()1122,,,P x y Q x y 在C 上，且1210,0x x y >>>．过P 且斜率为Q M .从下面①②③中选取两个作为条件，证明另外一个成立：①M 在AB 上；②PQ AB ∥；③||||MA MB =．注：若选择不同的组合分别解答，则按第一个解答计分.5．已知函数()e ln(1)x f x x =+．(1)求曲线()y f x =在点(0,(0))f 处的切线方程；(2)设()()g x f x '=，讨论函数()g x 在[0,)+∞上的单调性；(3)证明：对任意的,(0,)s t ∈+∞，有()()()f s t f s f t +>+．6．如图，已知椭圆22112x y +=．设A ，B 是椭圆上异于(0,1)P 的两点，且点0,21Q ⎛⎫ ⎪⎝⎭在线段AB 上，直线,PA PB 分别交直线132y x =-+于C ，D两点．(1)求点P 到椭圆上点的距离的最大值；(2)求||CD 的最小值．7．设函数e()ln (0)2f x x x x=+>．(1)求()f x 的单调区间；(2)已知,a b ∈R ，曲线()y f x =上不同的三点()()()()()()112233,,,,,x f x x f x x f x 处的切线都经过点(,)a b ．证明：（ⅰ）若e a >，则10()12e a b f a ⎛⎫<-<- ⎪⎝⎭；（ⅱ）若1230e,a x x x <<<<，则22132e 112e e 6e 6ea ax x a --+<+<-．（注：e 2.71828= 是自然对数的底数）参考答案：1．(1)1a =(2)见解析【解析】【分析】（1）根据导数可得函数的单调性，从而可得相应的最小值，根据最小值相等可求a.注意分类讨论.（2）根据（1）可得当1b >时，e x x b -=的解的个数、ln x x b -=的解的个数均为2，构建新函数()e ln 2x h x x x =+-，利用导数可得该函数只有一个零点且可得()(),f x g x 的大小关系，根据存在直线y b =与曲线()y f x =、()y g x =有三个不同的交点可得b 的取值，再根据两类方程的根的关系可证明三根成等差数列.(1)()e x f x ax =-的定义域为R ，而()e '=-x f x a ，若0a ≤，则()0f x '>，此时()f x 无最小值，故0a >.()ln g x ax x =-的定义域为()0,∞+，而11()ax g x a x x'-=-=.当ln x a <时，()0f x '<，故()f x 在(),ln a -∞上为减函数，当ln x a >时，()0f x '>，故()f x 在()ln ,a +∞上为增函数，故()min ()ln ln f x f a a a a ==-.当10x a <<时，()0g x '<，故()g x 在10,a ⎛⎫⎪⎝⎭上为减函数，当1x a >时，()0g x '>，故()g x 在1,a ⎛⎫+∞ ⎪⎝⎭上为增函数，故min 11()1ln g x g a a ⎛⎫==- ⎪⎝⎭.因为()e x f x ax =-和()ln g x ax x =-有相同的最小值，故11lnln a a a a-=-，整理得到1ln 1a a a -=+，其中0a >，设()1ln ,01a g a a a a -=->+，则()()()222211011a g a a a a a --'=-=≤++，故()g a 为()0,∞+上的减函数，而()10g =，故()0g a =的唯一解为1a =，故1ln 1aa a-=+的解为1a =.综上，1a =.(2)由（1）可得e ()x x f x =-和()ln g x x x =-的最小值为11ln11ln 11-=-=.当1b >时，考虑e x x b -=的解的个数、ln x x b -=的解的个数.设()e xS x x b =--，()e 1x S x '=-，当0x <时，()0S x '<，当0x >时，()0S x '>，故()S x 在(),0∞-上为减函数，在()0,∞+上为增函数，所以()()min 010S x S b ==-<，而()e0bS b --=>，()e 2b S b b =-，设()e 2b u b b =-，其中1b >，则()e 20bu b '=->，故()u b 在()1,+∞上为增函数，故()()1e 20u b u >=->，故()0S b >，故()e xS x x b =--有两个不同的零点，即e x x b -=的解的个数为2.设()ln T x x x b =--，()1x T x x-'=，当01x <<时，()0T x '<，当1x >时，()0T x '>，故()T x 在()0,1上为减函数，在()1,+∞上为增函数，所以()()min 110T x T b ==-<，而()ee0bbT --=>，()e e 20b b T b =->，()ln T x x x b =--有两个不同的零点即ln x x b -=的解的个数为2.当1b =，由（1）讨论可得ln x x b -=、e x x b -=仅有一个零点，当1b <时，由（1）讨论可得ln x x b -=、e x x b -=均无零点，故若存在直线y b =与曲线()y f x =、()y g x =有三个不同的交点，则1b >.设()e ln 2x h x x x =+-，其中0x >，故1()e 2xh x x'=+-，设()e 1x s x x =--，0x >，则()e 10xs x '=->，故()s x 在()0,∞+上为增函数，故()()00s x s >=即e 1x x >+，所以1()1210h x x x'>+-≥->，所以()h x 在()0,∞+上为增函数，而(1)e 20h =->，31e 333122(e 3e 30e e eh =--<--<，故()h x 在()0,∞+上有且只有一个零点0x ，0311ex <<且：当00x x <<时，()0h x <即e ln x x x x -<-即()()f x g x <，当0x x >时，()0h x >即e ln x x x x ->-即()()f x g x >，因此若存在直线y b =与曲线()y f x =、()y g x =有三个不同的交点，故()()001b f x g x ==>，此时e x x b -=有两个不同的零点1010,(0)x x x x <<，此时ln x x b -=有两个不同的零点0404,(01)x x x x <<<，故11e xx b -=，00e x x b -=，44ln 0x x b --=，00ln 0x x b --=所以44ln x b x -=即44ex bx -=即()44e0x bx b b ----=，故4x b -为方程e x x b -=的解，同理0x b -也为方程e x x b -=的解又11e x x b -=可化为11e xx b =+即()11ln 0x x b -+=即()()11ln 0x b x b b +-+-=，故1x b +为方程ln x x b -=的解，同理0x b +也为方程ln x x b -=的解，所以{}{}1004,,x x x b x b =--，而1b >，故0410x x b x x b =-⎧⎨=-⎩即1402x x x +=.【点睛】思路点睛：函数的最值问题，往往需要利用导数讨论函数的单调性，此时注意对参数的分类讨论，而不同方程的根的性质，注意利用方程的特征找到两类根之间的关系.2．(1)1-；(2)9．【解析】【分析】（1）由点(2,1)A 在双曲线上可求出a ，易知直线l 的斜率存在，设:l y kx m =+，()()1122,,,P x y Q x y ，再根据0AP BP k k +=，即可解出l 的斜率；（2）根据直线,AP AQ 的斜率之和为0可知直线,AP AQ的倾斜角互补，再根据tan PAQ ∠=,AP AQ 的斜率，再分别联立直线,AP AQ 与双曲线方程求出点,P Q 的坐标，即可得到直线PQ 的方程以及PQ 的长，由点到直线的距离公式求出点A 到直线PQ 的距离，即可得出PAQ △的面积．(1)因为点(2,1)A 在双曲线2222:1(1)1x yC a a a -=>-上，所以224111a a -=-，解得22a =，即双曲线22:12x C y -=易知直线l 的斜率存在，设:l y kx m =+，()()1122,,,P x y Q x y ，联立2212y kx m x y =+⎧⎪⎨-=⎪⎩可得，()222124220k x mkx m ----=，所以，2121222422,2121mk m x x x x k k ++=-=--，()()22222216422210120m k m k m k ∆=++->⇒-+>．所以由0AP BP k k +=可得，212111022y y x x --+=--，即()()()()122121210x kx m x kx m -+-+-+-=，即()()()1212212410kx x m k x x m +--+--=，所以()()2222242124102121m mk k m k m k k +⎛⎫⨯+-----= ⎪--⎝⎭，化简得，()2844410k k m k +-++=，即()()1210k k m +-+=，所以1k =-或12m k =-，当12m k =-时，直线():21l y kx m k x =+=-+过点()2,1A ，与题意不符，舍去，故1k =-．(2)不妨设直线,PA PB 的倾斜角为(),αβαβ<，因为0AP BP k k +=，所以παβ+=，因为tan PAQ ∠=，所以()tan βα-=，即tan 2α=-，2tan 0αα-=，解得tan α，于是，直线):21PA y x =-+，直线):21PB y x =-+，联立)222112y x x y ⎧=-+⎪⎨-=⎪⎩可得，(23211002x x +-+-=，因为方程有一个根为2，所以103P x -=，P y=53，同理可得，103Q x +=，Q y=53-．所以5:03PQ x y +-=，163PQ =，点A 到直线PQ的距离3d =，故PAQ △的面积为11623⨯=3．(1)()f x 的减区间为(),0-∞，增区间为()0,+∞.(2)12a ≤(3)见解析【解析】【分析】（1）求出()f x ¢，讨论其符号后可得()f x 的单调性.（2）设()e e 1ax xh x x =-+，求出()h x ''，先讨论12a >时题设中的不等式不成立，再就102a <≤结合放缩法讨论()h x '符号，最后就0a ≤结合放缩法讨论()h x 的范围后可得参数的取值范围.（3）由（2）可得12ln t t t<-对任意的1t >恒成立，从而可得()ln 1ln n n +-的*n N ∈恒成立，结合裂项相消法可证题设中的不等式.(1)当1a =时，()()1e x f x x =-，则()e xf x x '=，当0x <时，()0f x ¢<，当0x >时，()0f x ¢>，故()f x 的减区间为(),0-∞，增区间为()0,+∞.(2)设()e e 1ax xh x x =-+，则()00h =，又()()1e e ax x h x ax '=+-，设()()1e e ax xg x ax =+-，则()()22e e ax xg x a a x '=+-，若12a >，则()0210g a '=->，因为()g x '为连续不间断函数，故存在()00,x ∈+∞，使得()00,x x ∀∈，总有()0g x ¢>，故()g x 在()00,x 为增函数，故()()00g x g >=，故()h x 在()00,x 为增函数，故()()01h x h >=-，与题设矛盾.若102a <≤，则()()()ln 11e e ee ax ax ax xx h x ax ++'=+-=-，下证：对任意0x >，总有()ln 1x x +<成立，证明：设()()ln 1S x x x =+-，故()11011x S x x x-'=-=<++，故()S x 在()0,+∞上为减函数，故()()00S x S <=即()ln 1x x +<成立.由上述不等式有()ln 12e e e e e e 0ax ax x ax ax x ax x +++-<-=-≤，故()0h x '≤总成立，即()h x 在()0,+∞上为减函数，所以()()01h x h <=-.当0a ≤时，有()e e e 1100ax x axh x ax '=-+<-+=，所以()h x 在()0,+∞上为减函数，所以()()01h x h <=-.综上，12a ≤.(3)取12a =，则0x ∀>，总有12e e 10x x x -+<成立，令12e x t =，则21,e ,2ln x t t x t >==，故22ln 1t t t <-即12ln t t t<-对任意的1t >恒成立.所以对任意的*n N ∈，有<整理得到：()ln 1ln n n +-()ln 2ln1ln 3ln 2ln 1ln n n +-+-+++- ()ln 1n =+，故不等式成立.【点睛】思路点睛：函数参数的不等式的恒成立问题，应该利用导数讨论函数的单调性，注意结合端点处导数的符号合理分类讨论，导数背景下数列不等式的证明，应根据已有的函数不等式合理构建数列不等式.4．(1)2213y x -=(2)见解析【解析】【分析】（1）利用焦点坐标求得c 的值，利用渐近线方程求得,a b 的关系，进而利用,,a b c 的平方关系求得,a b 的值，得到双曲线的方程；（2）先分析得到直线AB 的斜率存在且不为零，设直线AB 的斜率为k ,M (x 0,y 0),由③|AM |=|BM |等价分析得到200283k x ky k +=-；由直线PM 和QM 的斜率得到直线方程，结合双曲线的方程，两点间距离公式得到直线PQ 的斜率03x m y =，由②//PQ AB 等价转化为003ky x =，由①M在直线AB 上等价于()2002ky k x =-，然后选择两个作为已知条件一个作为结论，进行证明即可.(1)右焦点为(2,0)F ，∴2c =,∵渐近线方程为y =，∴ba=b ，∴222244c a b a =+==，∴1a =，∴b =∴C 的方程为：2213y x -=；(2)由已知得直线PQ 的斜率存在且不为零，直线AB 的斜率不为零，若选由①②推③或选由②③推①：由②成立可知直线AB 的斜率存在且不为零；若选①③推②，则M 为线段AB 的中点，假若直线AB 的斜率不存在，则由双曲线的对称性可知M 在x 轴上，即为焦点F ,此时由对称性可知P 、Q 关于x 轴对称，与从而12x x =，已知不符；总之，直线AB 的斜率存在且不为零.设直线AB 的斜率为k ,直线AB 方程为()2y k x =-,则条件①M 在AB 上，等价于()()2000022y k x ky k x =-⇔=-；两渐近线的方程合并为2230x y -=,联立消去y 并化简整理得：()22223440k x k x k --+=设()()3334,,,A x y B x y ,线段中点为(),N N N x y ,则()2342226,2233N N N x x k kx y k x k k +===-=--,设()00,M x y ,则条件③AM BM =等价于()()()()222203030404x x y y x x y y -+-=-+-,移项并利用平方差公式整理得：()()()()3403434034220x x x x x y y y y y ⎡⎤⎡⎤--++--+=⎣⎦⎣⎦，()()3403403434220y y x x x y y y x x -⎡⎤⎡⎤-++-+=⎣⎦⎣⎦-,即()000N N x x k y y -+-=,即200283k x ky k +=-；由题意知直线PM 的斜率为直线QM ,∴由))10102020,y y x x y y x x -=--=-,∴)121202y y x x x -=+-,所以直线PQ的斜率)1201212122x x x y y m x x x x +--==--,直线)00:PM y x x y =-+,即00y y =,代入双曲线的方程22330x y --=,即)3yy +-=中，得：()()00003y y ⎡⎤-=⎣⎦,解得P的横坐标：100x y ⎛⎫=+⎪⎪⎭,同理：200x y ⎛⎫=⎪⎪⎭，∴0012012002222000033,2,33y x x x y x x x x y x y x ⎛⎫-=++-=--⎪--⎭∴03x m y =,∴条件②//PQ AB 等价于003m k ky x =⇔=，综上所述：条件①M 在AB 上，等价于()2002ky k x =-；条件②//PQ AB 等价于003ky x =；条件③AM BM =等价于200283kx ky k +=-；选①②推③:由①②解得：2200002228,433k k x x ky x k k =∴+==--,∴③成立；选①③推②：由①③解得：20223k x k =-，20263k ky k =-，∴003ky x =，∴②成立；选②③推①：由②③解得：20223k x k =-，20263k ky k =-，∴02623x k -=-，∴()2002ky k x =-，∴①成立.5．(1)y x=(2)()g x 在[0,)+∞上单调递增.(3)证明见解析【解析】【分析】（1）先求出切点坐标，在由导数求得切线斜率，即得切线方程；（2）在求一次导数无法判断的情况下，构造新的函数，再求一次导数，问题即得解；（3）令()()()m x f x t f x =+-，(,0)x t >，即证()(0)m x m >，由第二问结论可知()m x 在[0,+∞）上单调递增，即得证.(1)解：因为()e ln(1)x f x x =+，所以()00f =，即切点坐标为()0,0，又1()e (ln(1))1xf x x x=+++'，∴切线斜率(0)1k f '==∴切线方程为：y x =(2)解：因为1()()e (ln(1))1xg x f x x x=++'=+，所以221()e (ln(1))1(1)xg x x x x =++++'，令221()ln(1)1(1)h x x x x =++-++，则22331221()01(1)(1)(1)x h x x x x x +=-+=>++++'，∴()h x 在[0,)+∞上单调递增，∴()(0)10h x h ≥=>∴()0g x '>在[0,)+∞上恒成立，∴()g x 在[0,)+∞上单调递增.(3)解：原不等式等价于()()()(0)f s t f s f t f +->-，令()()()m x f x t f x =+-，(,0)x t >，即证()(0)m x m >，∵()()()e ln(1)e ln(1)x t x m x f x t f x x t x +=+-=++-+，e e ()e ln(1)e ln(1)()()11x t x x tx m x x t x g x t g x x t x++=++++-=+-++'+，由（2）知1()()e (ln(1))1xg x f x x x=++'=+在[)0,∞+上单调递增，∴()()g x t g x +>，∴()0m x '>∴()m x 在()0,∞+上单调递增，又因为,0x t >，∴()(0)m x m >，所以命题得证.6．(1)11；(2)5．【解析】【分析】（1）设,sin )Q θθ是椭圆上任意一点,再根据两点间的距离公式求出2||PQ ，再根据二次函数的性质即可求出；（2）设直线1:2AB y kx =+与椭圆方程联立可得1212,x x x x +，再将直线132y x =-+方程与PA PB 、的方程分别联立，可解得点,C D 的坐标，再根据两点间的距离公式求出CD ，最后代入化简可得231CD k =⋅+，由柯西不等式即可求出最小值．(1)设,sin )Q θθ是椭圆上任意一点,(0,1)P ,则222221144144||12cos (1sin )1311sin 2sin 11sin 111111PQ θθθθθ⎛⎫=+-=--=-+≤⎭+⎪⎝，当且仅当1sin 11θ=-时取等号，故||PQ (2)设直线1:2AB y kx =+,直线AB 方程与椭圆22112x y +=联立,可得22130124k x kx ⎛⎫++-= ⎪⎝⎭,设()()1122,,,A x y B x y ，所以12212211231412k x x k x x k ⎧+=-⎪+⎪⎪⎨⎪=-⎛⎫⎪+ ⎪⎪⎝⎭⎩，因为直线111:1y PA y x x -=+与直线132y x =-+交于C ,则111114422(21)1C x x x x y k x ==+-+-,同理可得,222224422(21)1D x x x x y k x ==+-+-.则224||(21)1C D x CD x k x =-=+-2=35161656565231555k =⋅=≥=+，当且仅当316k =时取等号，故CD 的最小值为5.【点睛】本题主要考查最值的计算，第一问利用椭圆的参数方程以及二次函数的性质较好解决，第二问思路简单，运算量较大，求最值的过程中还使用到柯西不等式求最值，对学生的综合能力要求较高，属于较难题．7．(1)()f x 的减区间为e 02⎛⎫⎪⎝⎭,，增区间为e ,2⎛⎫+∞ ⎪⎝⎭.(2)（ⅰ）见解析；（ⅱ）见解析.【解析】【分析】（1）求出函数的导数，讨论其符号后可得函数的单调性.（2）（ⅰ）由题设构造关于切点横坐标的方程，根据方程有3个不同的解可证明不等式成立，（ⅱ）31x k x =，1e a m =<，则题设不等式可转化为()()()2131313122236m m m t t m m t t --++--<+，结合零点满足的方程进一步转化为()()()()211312ln 0721m m m m m m ---++<+，利用导数可证该不等式成立.(1)()22e 12e 22xf x x x x -'=-+=，当e02x <<，()0f x ¢<；当e 2x >，()0f x ¢>，故()f x 的减区间为e 02⎛⎫⎪⎝⎭,，()f x 的增区间为e ,2⎛⎫+∞ ⎪⎝⎭.(2)（ⅰ）因为过(),a b 有三条不同的切线，设切点为()(),,1,2,3i i x f x i =，故()()()i i i f x b f x x a '-=-，故方程()()()f x b f x x a '-=-有3个不同的根，该方程可整理为()21e e ln 022x a x b x x x ⎛⎫----+= ⎪⎝⎭，设()()21e e ln 22g x x a x b x x x ⎛⎫=---+ ⎪⎝⎭，则()()22321e 1e 1e22g x x a x x x x x x⎛⎫'=-+-+--+ ⎪⎝⎭()()31e x x a x =---，当0e x <<或x a >时，()0g x ¢<；当e x a <<时，()0g x ¢>，故()g x 在()()0,e ,,a +∞上为减函数，在()e,a 上为增函数，因为()g x 有3个不同的零点，故()e 0g <且()0>g a ，故()21e e e ln e 0e 2e 2e a b ⎛⎫----+< ⎪⎝⎭且()21e e ln 022a a a b a a a ⎛⎫---+> ⎪⎝⎭，整理得到：12e a b <+且()e ln 2b a f a a >+=，此时()1e 13e11ln ln 2e 2e 22e 222a a a b f a a a a a ⎛⎫⎛⎫---<-+-+=-- ⎪ ⎪⎝⎭⎝⎭，设()3e ln 22u a a a =--，则()2e-202au a a '=<，故()u a 为()e,+∞上的减函数，故()3eln e 022eu a <--=，故()1012e a b f a ⎛⎫<-<- ⎪⎝⎭.（ⅱ）当0e a <<时，同（ⅰ）中讨论可得：故()g x 在()()0,,e,a +∞上为减函数，在(),e a 上为增函数，不妨设123x x x <<，则1230e x a x x <<<<<，因为()g x 有3个不同的零点，故()0g a <且()e 0g >，故()21e e e ln e 0e 2e 2e a b ⎛⎫----+> ⎪⎝⎭且()21e e ln 022a a a b a a a ⎛⎫---+< ⎪⎝⎭，整理得到：1ln 2e 2ea ab a +<<+，因为123x x x <<，故1230e x a x x <<<<<，又()2e e 1ln 2a ag x x b x x+=-+-+，设e t x =，()0,1e a m =∈，则方程2e e 1ln 02a ax b x x+-+-+=即为：2e ln 0e 2ea at t t b +-+++=即为()21ln 02m m t t t b -++++=，记123123e e e ,,,t t t x x x ===则113,,t t t 为()21ln 02m m t t t b -++++=有三个不同的根，设3131e 1x t k t x a ==>>，1eam =<，要证：22122e 112e e 6e 6e a a x x a --+<+<-，即证13e 2e e 26e 6ea at t a --+<+<-，即证：13132166m mt t m --<+<-，即证：131********m m t t t t m --⎛⎫⎛⎫+-+-+< ⎪⎝⎭⎝⎭，即证：()()()2131313122236m m m t t m m t t --++--<+，而()21111ln 02m m t t t b -++++=且()23331ln 02mm t t t b -++++=，故()()()22131313ln ln 102m t t t t m t t -+--+-=，故131313ln ln 222t t t t m m t t -+--=-⨯-，故即证：()()()21313131312ln ln 236m m m t t m t t m t t --+--⨯<-+，即证：()()()1213313ln1312072t t t m m m t t t +--++>-即证：()()()213121ln 0172m m m k k k --+++>-，记()()1ln ,11k k k k k ϕ+=>-，则()()2112ln 01k k k kk ϕ⎛⎫'=--> ⎪⎝⎭-，设()12ln u k k k k =--，则()2122210u k k k k k'=+->-=即()0k ϕ'>，故()k ϕ在()1,+∞上为增函数，故()()k m ϕϕ>，所以()()()()()()22131213121ln 1ln 172172m m m m m m k k m m k m --+--++++>+--，记()()()()()211312ln ,01721m m m m m m m m ω---+=+<<+，则()()()()()()()2232322132049721330721721m mm m m mm m m m m ω---+-+'=>>++，所以()m ω在()0,1为增函数，故()()10m ωω<=，故()()()()211312ln 0721m m m m m m ---++<+即()()()213121ln 0172m m m m m m --+++>-，故原不等式得证：【点睛】思路点睛：导数背景下的切线条数问题，一般转化为关于切点方程的解的个数问题，而复杂方程的零点性质的讨论，应该根据零点的性质合理转化需求证的不等式，常用的方法有比值代换等.。
【压轴题】高考数学试卷带答案
【压轴题】高考数学试卷带答案一、选择题1．设1i2i 1iz -=++，则||z =A ．0B ．12 C ．1 D2．设5sin7a π=，2cos 7b π=，2tan 7c π=，则（ ） A ．a b c <<B ．a c b <<C ．b c a <<D ．b a c <<3．为美化环境，从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中，余下的2种花种在另一个花坛中，则红色和紫色的花不在同一花坛的概率是A ．13B ．12C ．23D ．564．函数()()2ln 1f x x x=+-的一个零点所在的区间是( )A ．()0,1B ．()1,2C ．()2,3D ．()3,45．在等比数列{}n a 中，44a =，则26a a ⋅=（ ） A ．4B ．16C ．8D ．326．甲、乙两人玩猜数字游戏，先由甲心中想一个数字，记为a ，再由乙猜甲刚才所想的数字，把乙猜的数字记为b ，其中a ，b ∈{1，2，3，4，5，6}，若|a-b|≤1，就称甲乙“心有灵犀”．现任意找两人玩这个游戏，则他们“心有灵犀”的概率为（ ） A ．19B ．29C ．49D ．7187．已知向量a ，b 满足2a =，||1b =，且2b a +=，则向量a 与b 的夹角的余弦值为（ ）A ．2B ．3C ．8D ．48．设双曲线2222:1x y C a b-=(00a b >>，)的左、右焦点分别为12F F ，，过1F 的直线分别交双曲线左右两支于点M N ，，连结22MF NF ，，若220MF NF ⋅=，22MF NF =，则双曲线C 的离心率为( ).ABCD ．69．抛掷一枚质地均匀的硬币两次,在第一次正面向上的条件下,第二次反面向上的概率为( ) A ．14B ．13C ．12D ．2310．已知平面向量a ,b 是非零向量,|a |=2,a ⊥(a +2b ),则向量b 在向量a 方向上的投影为( )A ．1B ．-1C ．2D ．-211．某单位有职工100人，不到35岁的有45人，35岁到49岁的有25人，剩下的为50岁以上（包括50岁）的人，用分层抽样的方法从中抽取20人，各年龄段分别抽取的人数为（ ） A ．7，5，8B ．9，5，6C ．7，5，9D ．8，5，712．已知a 与b 均为单位向量，它们的夹角为60︒，那么3a b -等于（ ） A ．7B ．10C ．13D ．4二、填空题13．已知曲线ln y x x =+在点()1,1处的切线与曲线()221y ax a x =+++相切,则a= ．14．某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200,400,300,100件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取________ 件. 15．事件,,A B C 为独立事件，若()()()111,,688P A B P B C P A B C ⋅=⋅=⋅⋅=，则()P B =_____．16．函数log (1)1(01)a y x a a =-+>≠且的图象恒过定点A ，若点A 在一次函数y mx n =+的图象上，其中,0,m n >则12m n+的最小值为 17．若9()ax x-的展开式中3x 的系数是84-，则a = ．18．如图，用6种不同的颜色给图中的4个格子涂色，每个格子涂一种颜色，要求最多使用3种颜色且相邻的两个格子颜色不同，则不同的涂色方法共有 种（用数字作答）．19．34331654+log log 8145-⎛⎫+= ⎪⎝⎭________. 20．已知集合P 中含有0,2,5三个元素,集合Q 中含有1,2,6三个元素,定义集合P+Q 中的元素为a+b ,其中a ∈P ,b ∈Q ,则集合P+Q 中元素的个数是_____.三、解答题21．在平面直角坐标系中，直线l 的参数方程为cos sin x t y t αα=⎧⎨=⎩（t 为参数，0≤α<π）．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为244cos 2sin ρρθρθ-=-．(Ⅰ)写出曲线C 的直角坐标方程；(Ⅱ)若直线l 与曲线C 交于A ，B 两点，且AB 的长度为25，求直线l 的普通方程． 22．某农场有一块农田，如图所示，它的边界由圆O 的一段圆弧MPN （P 为此圆弧的中点）和线段MN 构成．已知圆O 的半径为40米，点P 到MN 的距离为50米．现规划在此农田上修建两个温室大棚，大棚I 内的地块形状为矩形ABCD ，大棚II 内的地块形状为CDP ，要求,A B 均在线段MN 上，,C D 均在圆弧上．设OC 与MN 所成的角为θ．（1）用θ分别表示矩形ABCD 和CDP 的面积，并确定sin θ的取值范围；（2）若大棚I 内种植甲种蔬菜，大棚II 内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4:3．求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大． 23．已知数列{}n a 与{}n b 满足：*1232()n n a a a a b n N ++++=∈，且{}n a 为正项等比数列，12a =，324b b =+. （1）求数列{}n a 与{}n b 的通项公式； （2）若数列{}n c 满足*2211()log log n n n c n N a a +=∈，n T 为数列{}n c 的前n 项和，证明：1n T <.24．选修4-5：不等式选讲 设函数()|2||1|f x x x =-++.（1）求()f x 的最小值及取得最小值时x 的取值范围； （2）若集合{|()10}x f x ax +->=R ，求实数a 的取值范围.25．随着“互联网+交通”模式的迅猛发展，“共享自行车”在很多城市相继出现。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高考数学综合题系列训练（一）【例1】已知函数241)(+=xx f )(R x ∈ （1）试证函数)(x f 的图象关于点)41,21(对称；（2）若数列}{n a 的通项公式为), ,2 ,1 ,( )(m n N m mnf a n =∈=+，求数列}{n a 的前m 项和m S（3）设数列}{n b 满足： 311=b ，n n n b b b +=+21， 设11111121++++++=n n b b b T ，若（2）中的n S 满足对任意不小于2的正整数n ，n n T S <恒成立, 试求m 的最大值解: (1)设点)y ,x (P 000 是函数)x (f 的图象上任意一点, 其关于点)41,21( 的对称点为)y ,x (P .由⎪⎪⎩⎪⎪⎨⎧=+=+412y y 212x x 00 得⎪⎩⎪⎨⎧-=-=.y 21y ,x 1x 00 所以, 点P 的坐标为P )y 21,x 1(00-- .………………(2分) 由点)y ,x (P 000 在函数)x (f 的图象上, 得241y 0x 0+=. ∵,)24(244244241)x 1(f 0000x x x x x 10+=⋅+=+=-- =+-=-24121y 210x 0,)24(2400x x + ∴点P )y 21,x 1(00-- 在函数)x (f 的图象上. ∴函数)x (f 的图象关于点)41,21( 对称. ………………(4分) (2)由(1)可知, 21)x 1(f )x (f =-+, 所以)1m k 1(21)m k 1(f )m k (f -≤≤=-+ ,即,21a a , 21)m k m (f )m k (f k m k =+∴=-+- ………………(6分)由m 1m 321m a a a a a S +++++=- , ……………… ① 得,a a a a a S m 13m 2m 1m m +++++=--- ………………② 由①＋②, 得,612m 61221m a 221)1m (S 2m m -=⨯+-=+⨯-= ∴).1m 3(121S m -=………………(8分)(3) ∵,31b 1=)1b (b b b b n n n 2n 1n +=+=+, ………………③ ∴对任意的0b ,N n n >∈+ . ………………④ 由③、④, 得,1b 1b 1)1b (b 1b 1n n n n 1n +-=+=+即1n n n b 1b 11b 1+-=+.∴1n 1n 11n n 3221n b 13b 1b 1)b 1b 1()b 1b 1()b 1b 1(T +++-=-=-++-+-= .……………(10分) ∵,b b ,0b b b n 1n 2n n 1n >∴>=-++ ∴数列}b {n 是单调递增数列. ∴n T 关于n 递增. 当2n ≥, 且+∈N n 时, 2n T T ≥. ∵,8152)194(94b ,94)131(31b ,31b 321=+==+==∴.5275b 13T T 12n =-=≥………………(12分) ∴,5275S m <即,5275)1m 3(121<-∴,394639238m =< ∴m 的最大值为6. ……………(14分) 【例2】将圆:O 422=+y x 上各点的纵坐标变为原来的一半（横坐标不变）得到曲线C（1）求曲线C 的方程;（2）设O 为坐标原点， 过点)0 ,3(F 的直线l 与C 交于B A 、两点，N 为线段AB 的中点，延长线段ON 交C 于点E ，求证：ON OE 2=的充要条件是3=AB解：（1）设点),(y x P ''，点),(y x M ，由题意⎩⎨⎧='='y y xx 2，又∵422='+'y x ∴14442222=+⇒=+y x y x ，故曲线C 的方程为1422=+y x （2）设点) ,(11y x A ， ) ,(22y x B ， 点N 的坐标为) ,(00y x当直线l 与x 轴重合时，线段AB 的中点N 就是原点O ，不合题意，舍去；设直线 3:+=my x l ，将直线l 的方程代入方程1422=+y x 整理得：0132)4(22=-++my y m ∴4320+-=m m y ，4343200+=+=m my x ，即点N )43 ,434(22+-+m mm ○1若ON OE 2=, 则点)432 ,438(22+-+m mm E , 由题意得1)4(12)4(4822222=+++m m m , 即032424=--m m ∴ 82=m （42-=m 舍去） ∴2121 y y m AB -+=34)1(44164121222222=++=+++⋅+=m m m m m m ○2若3=AB , 由○1得34)1(422=++m m ，∴82=m ∴点N 的坐标为)66 ,33(±, 射线ON 方程为)0( 22>±=x x y , 由⎪⎩⎪⎨⎧=+>±=44)0( 2222y x x x y 解得⎪⎪⎩⎪⎪⎨⎧±==36332y x ∴点E 的坐标为)36 ,332(±，故2= 综上，2=的充要条件是3=AB【例3】E 、F 是椭圆2224x y +=的左、右焦点，l 是椭圆的右准线，点P l ∈，过点E 的直线交椭圆于A 、B 两点.（1） 当AE AF ⊥时，求AEF ∆的面积； （2） 当3AB =时，求AF BF +的大小；（3） 求EPF ∠的最大值. 解：（1）2241282AEF m n S mn m n ∆+=⎧⇒==⎨+=⎩（2）因484AE AF AB AF BF BE BF ⎧+=⎪⇒++=⎨+=⎪⎩，则 5.AF BF +=（1）设)(0)P t t > ()tan EPF tan EPM FPM ∠=∠-∠221((1)663t t t t t t -=-÷+==≤++，当t =30tan EPF EPF ∠=⇒∠=【例1】已知焦点在x 轴上的抛物线C 点)2,1(M ，动直线l 过点)0,3(P ，交抛物线于B A 、两点，是否存在垂直于x 轴的直线l '被以AP 为直径的圆截得的弦长为定值？若存在，求出l '的方程；若不存在，说明理由.解：设抛物线方程为)0(22>=p px y ，将)2,1(M 代入方程得2=p ， ∴抛物线方程为x y 42=（Ⅱ）设AP 的中点为C ，l '的方程为：x a =，以AP 为直径的圆交l '于,D E 两点，DE 中点为H令()11113,,,22x y A x y +⎛⎫∴ ⎪⎝⎭ C ………………………………………………（7分）()1112312322DC AP x CH a x a ∴==+=-=-+()()()2222221112121132344-23246222DH DC CH x y x a a x a aa DH DE DH l x ⎡⎤⎡⎤∴=-=-+--+⎣⎦⎣⎦=-+==-+=∴=='= 当时,为定值; 此时的方程为： …………（12分）【例4】已知正项数列{}n a 中，16a =，点(n n A a 在抛物线21y x =+上；数列{}n b 中，点(),n n B n b 在过点()0,1，以方向向量为()1,2的直线上.（Ⅰ）求数列{}{},n n a b 的通项公式；（Ⅱ）若()()()n n a f n b ⎧⎪=⎨⎪⎩, n 为奇数, n 为偶数，问是否存在k N ∈，使()()274f k f k +=成立，若存在，求出k 值；若不存在，说明理由；（Ⅲ）对任意正整数n，不等式1120111111n n n ab b b +≤⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭成立，求正数a 的取值范围.解：（Ⅰ）将点(n n A a 代入21y x =+中得()11111115:21,21n n n n n n a a a a d a a n n l y x b n ++=+∴-==∴=+-⋅=+=+∴=+ 直线 …………………………………………（4分）（Ⅱ）()()()521n f n n ⎧+⎪=⎨+⎪⎩, n 为奇数, n 为偶数………………………………（5分）()()()()()()27274275421,42735227145,24k k f k f k k k k k k k k k k ++=∴++=+∴=+∴++=+∴==当为偶数时，为奇数， 当为奇数时，为偶数， 舍去综上，存在唯一的符合条件。
……………………（8分）（Ⅲ）由1120111111n n n a b b b +≤⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭()()()()121212111111111111111111111111124123n n nn n a b b bf n b b bf n b b b b f n n f n b n ++⎛⎫⎫⎛⎫+++ ⎪⎪⎪⎭⎝⎭⎝⎭⎛⎫⎫⎛⎫=+++⎪⎪⎪⎭⎝⎭⎝⎭⎛⎫⎛⎫⎫⎛⎫∴+=++++ ⎪⎪⎪⎪⎭⎝⎭⎝⎭⎝⎭+⎛⎫+∴=+== ⎪+⎝⎭即记 ()()()()()min 11,4130f n f n f n f n f a =>∴+>∴===∴<≤即递增， ………………………………（14分）6．（14分）已知数列{}n a 中，113a =，当2n ≥时，其前n 项和n S 满足2221n n n S a S =-，（2） 求n S 的表达式及2limnn na S →∞的值；（3） 求数列{}n a 的通项公式； （4） 设n b =n N ∈且2n ≥时，n n a b <.解：（1）2111121122(2)21n n n n n n n n n n n S a S S S S S S n S S S ----=-=⇒-=⇒-=≥-所以1n S ⎧⎫⎨⎬⎩⎭是等差数列.则121nS n =+. 222limlim 2212lim 1n n n n n nn a S S S →∞→∞→∞===---.（2）当2n ≥时，12112212141n n n a S S n n n --=-=-=+--，综上，()()21132214n n a n n⎧=⎪⎪=⎨⎪≥⎪-⎩.（3）令a b ==，当2n ≥时，有0b a <<≤ （1） 法1：等价于求证112121n n >-+.当2n ≥时，0<≤令()23,0f x x x x =-<≤ ()233232(1)2(12(1022f x x x x x x x '=-=-≥-=>，则()fx 在递增.又0<<≤所以g g <即n n a b <.法（2）223311()2121n n a b b a b a n n -=--=---+- 22()()a b a b ab a b =-++-- （2）22()[()()]22ab ab a b a a b b =-+-++- ()[(1)(1)]22b a a b a a b b =-+-++- （3）因31111102222a b a b a +-<+-<-<=-<，所以(1)(1)022b a a a b b +-++-<由（1）（3）（4）知n n a b <.法3：令()22g b a b ab a b =++--，则()12102ag b b a b -'=+-=⇒=所以()()(){}{}220,,32g b max g g a max a a a a ≤=--因0a <≤则()210a a a a -=-<，22323()303a a a a a -=-≤<所以()220g b a b ab a b =++--< （5） 由（1）（2）（5）知n n a b <2009年高考数学压轴题系列训练含答案及解析详解二1. (本小题满分12分)已知常数a > 0, n 为正整数，f n ( x ) = x n – ( x + a)n ( x > 0 )是关于x 的函数. (1) 判定函数f n ( x )的单调性，并证明你的结论. (2) 对任意n ≥ a , 证明f `n + 1 ( n + 1 ) < ( n + 1 )f n `(n) 解: (1) f n `( x ) = nx n – 1 – n ( x + a)n – 1 = n [x n – 1 – ( x + a)n – 1 ] ,∵a > 0 , x > 0, ∴ f n `( x ) < 0 , ∴ f n ( x )在（0，+∞）单调递减. 4分 （2）由上知：当x > a>0时, f n ( x ) = x n – ( x + a)n 是关于x 的减函数,∴ 当n ≥ a 时, 有：(n + 1 )n – ( n + 1 + a)n ≤ n n – ( n + a)n . 2分又 ∴f `n + 1 (x ) = ( n + 1 ) [x n –( x+ a )n ] ,∴f `n + 1 ( n + 1 ) = ( n + 1 ) [(n + 1 )n –( n + 1 + a )n ] < ( n + 1 )[ n n – ( n + a)n ] = ( n + 1 )[ n n – ( n + a )( n + a)n – 1 ] 2分( n + 1 )f n `(n) = ( n + 1 )n[n n – 1 – ( n + a)n – 1 ] = ( n + 1 )[n n – n( n + a)n – 1 ], 2分 ∵( n + a ) > n ,∴f `n + 1 ( n + 1 ) < ( n + 1 )f n `(n) . 2分 2. (本小题满分12分)已知：y = f (x) 定义域为［–1，1］，且满足：f (–1) = f (1) = 0 ，对任意u ,v ∈[–1，1］，都有|f (u) – f (v) | ≤ | u –v | .(1) 判断函数p ( x ) = x 2 – 1 是否满足题设条件？ (2) 判断函数g(x)=1,[1,0]1,[0,1]x x x x +∈-⎧⎨-∈⎩，是否满足题设条件？解： (1) 若u ,v ∈ [–1，1]， |p(u) – p (v)| = | u 2 – v 2 |=| (u + v )(u – v) |，取u =43∈[–1，1]，v = 21∈[–1，1],则 |p (u) – p (v)| = | (u + v )(u – v) | = 45| u – v | > | u – v |， 所以p( x)不满足题设条件. （2）分三种情况讨论：10. 若u ,v ∈ [–1，0]，则|g(u) – g (v)| = |(1+u) – (1 + v)|=|u – v |，满足题设条件； 20. 若u ,v ∈ [0，1]， 则|g(u) – g(v)| = |(1 – u) – (1 – v)|= |v –u|，满足题设条件； 30. 若u ∈[–1，0]，v ∈[0，1]，则：|g (u) –g(v)|=|(1 – u) – (1 + v)| = | –u – v| = |v + u | ≤| v – u| = | u –v|，满足题设条件; 40 若u ∈[0，1]，v ∈[–1，0], 同理可证满足题设条件.综合上述得g(x)满足条件. 3. (本小题满分14分)已知点P ( t , y )在函数f ( x ) = 1x x+(x ≠ –1)的图象上，且有t 2 – c 2at + 4c 2 = 0 ( c ≠ 0 ). (1) 求证：| ac | ≥ 4;(2) 求证：在(–1，+∞）上f ( x )单调递增. (3) (仅理科做)求证：f ( | a | ) + f ( | c | ) > 1. 证：(1) ∵ t ∈R, t ≠ –1,∴ ⊿ = (–c 2a)2 – 16c 2 = c 4a 2 – 16c 2 ≥ 0 ， ∵ c ≠ 0, ∴c 2a 2 ≥ 16 , ∴| ac | ≥ 4. (2) 由 f ( x ) = 1 –1x 1+, 法1. 设–1 < x 1 < x 2, 则f (x 2) – f ( x 1) = 1–1x 12+–1 + 1x 11+= )1x )(1x (x x 1221++-. ∵ –1 < x 1 < x 2, ∴ x 1 – x 2 < 0, x 1 + 1 > 0, x 2 + 1 > 0 ,∴f (x 2) – f ( x 1) < 0 , 即f (x 2) < f ( x 1) , ∴x ≥ 0时，f ( x )单调递增. 法2. 由f ` ( x ) =2)1x (1+> 0 得x ≠ –1, ∴x > –1时，f ( x )单调递增.（3）（仅理科做）∵f ( x )在x > –1时单调递增，| c | ≥|a |4> 0 ,∴f (| c | ) ≥ f (|a |4) = 1|a |4|a |4+= 4|a |4+f ( | a | ) + f ( | c | ) =1|a ||a |++ 4|a |4+> 4|a ||a |++4|a |4+=1. 即f ( | a | ) + f ( | c | ) > 1. 4．（本小题满分15分）设定义在R 上的函数43201234()f x a x a x a x a x a =++++（其中i a ∈R ，i=0,1,2,3,4），当x= －1时，f (x)取得极大值23，并且函数y=f (x+1)的图象关于点（－1，0）对称． （1） 求f (x)的表达式；（2） 试在函数f (x)的图象上求两点，使这两点为切点的切线互相垂直，且切点的横坐标都在区间⎡⎣上；（3）若+213),(N )23n n n n n n x y n --==∈，求证：4()().3n n f x f y -< 解：（1）31().3f x x x =-…………………………5分 （2）()0,0,⎭或()0,0,.⎛ ⎝⎭…………10分 （3）用导数求最值，可证得4()()(1)(1).3n n f x f y f f -<--<……15分 5．（本小题满分13分）设M 是椭圆22:1124x y C +=上的一点，P 、Q 、T 分别为M 关于y 轴、原点、x 轴的对称点，N 为椭圆C 上异于M 的另一点，且MN ⊥MQ ，QN 与PT 的交点为E ，当M 沿椭圆C 运动时，求动点E 的轨迹方程．解：设点的坐标112211(,),(,)(0),(,),M x y N x y x y E x y ≠则111111(,),(,),(,),P x y Q x y T x y ----……1分221122221,(1)124 1.(2)124x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩………………………………………………………3分由（1）－（2）可得1.3MN QN k k •=-………………………………6分 又MN ⊥MQ ，111,,MN MQ MN x k k k y ⋅=-=-所以11.3QN y k x = 直线QN 的方程为1111()3y y x x y x =+-，又直线PT 的方程为11.xy x y =-……10分 从而得1111,.22x x y y ==-所以112,2.x x y y ==- 代入（1）可得221(0),3x y xy +=≠此即为所求的轨迹方程.………………13分 6．（本小题满分12分）过抛物线y x 42=上不同两点A 、B 分别作抛物线的切线相交于P 点，.0=⋅PB PA（1）求点P 的轨迹方程；（2）已知点F （0，1），是否存在实数λ使得0)(2=+⋅FP FB FA λ？若存在，求出λ的值，若不存在，请说明理由.解法（一）：（1）设)(),4,(),4,(21222211x x x x B x x A ≠由,42y x =得：2'x y =2,221x k x k PB PA ==∴ 4,,021-=∴⊥∴=⋅x x PB PA PB PA ………………………………3分直线PA 的方程是：)(241121x x x x y -=-即42211x x x y -= ① 同理，直线PB 的方程是：42222x x x y -= ② 由①②得：⎪⎩⎪⎨⎧∈-==+=),(,142212121R x x x x y x x x ∴点P 的轨迹方程是).(1R x y ∈-=……………………………………6分（2）由（1）得：),14,(211-=x x ),14,(222-=x x )1,2(21-+xx P 4),2,2(2121-=-+=x x x x FP 42)14)(14(2221222121x x x x x x FB FA +--=--+=⋅ …………………………10分2444)()(22212212++=++=x x x x所以0)(2=+⋅故存在λ=1使得0)(2=+⋅λ…………………………………………12分 解法（二）：（1）∵直线PA 、PB 与抛物线相切，且,0=⋅ ∴直线PA 、PB 的斜率均存在且不为0，且,PB PA ⊥ 设PA 的直线方程是)0,,(≠∈+=k R m k m kx y由⎩⎨⎧=+=yx m kx y 42得：0442=--m kx x 016162=+=∆∴m k 即2k m -=…………………………3分即直线PA 的方程是：2k kx y -= 同理可得直线PB 的方程是：211kx k y --= 由⎪⎩⎪⎨⎧--=-=2211k x k y k kx y 得：⎪⎩⎪⎨⎧-=∈-=11y R k k x 故点P 的轨迹方程是).(1R x y ∈-=……………………………………6分 （2）由（1）得：)1,1(),1,2(),,2(22---kk P k k B k k A )11,2(),1,2(22--=-=kk FB k k FA)2,1(--=kk FP)1(2)11)(1(42222kk k k +--=--+-=⋅………………………………10分 )1(24)1()(2222k k k k ++=+-=故存在λ=1使得0)(2=+⋅λ…………………………………………12分 7．（本小题满分14分）设函数x axxx f ln 1)(+-=在),1[+∞上是增函数. （1） 求正实数a 的取值范围；（2） 设1,0>>a b ，求证：.ln 1bba b b a b a +<+<+ 解：（1）01)(2'≥-=axax x f 对),1[+∞∈x 恒成立， xa 1≥∴对),1[+∞∈x 恒成立 又11≤x1≥∴a 为所求.…………………………4分 （2）取b b a x +=，1,0,1>+∴>>bba b a ，一方面，由（1）知x axxx f ln 1)(+-=在),1[+∞上是增函数，0)1()(=>+∴f b b a f0ln 1>+++⋅+-∴b b a b b a a b b a 即ba b b a +>+1ln ……………………………………8分 另一方面，设函数)1(ln )(>-=x x x x G)1(0111)('>>-=-=x xx x x G ∴)(x G 在),1(+∞上是增函数且在0x x =处连续，又01)1(>=G ∴当1>x 时，0)1()(>>G x G∴x x ln > 即bba b b a +>+ln 综上所述，.ln 1bba b b a b a +<+<+………………………………………………14分8．(本小题满分12分)如图，直角坐标系xOy 中，一直角三角形ABC ，90C ∠=，B 、C 在x 轴上且关于原点O 对称，D 在边BC 上，3BD DC =，ABC 的周长为12．若一双曲线E 以B 、C 为焦点，且经过A 、D 两点．(1) 求双曲线E 的方程；(2) 若一过点(,0)P m （m 为非零常数）的直线l 与双曲线E相交于不同于双曲线顶点的两点M 、N ，且MP PN λ=，问在x 轴上是否存在定点G ，使()BC GM GN λ⊥-？若存在，求出所有这样定点G 的坐标；若不存在，请说明理由．解：(1) 设双曲线E 的方程为22221(0,0)x y a b a b-=>>，则(,0),(,0),(,0)B c D a C c -．由3BD DC =，得3()c a c a +=-，即2c a =．∴222||||16,||||124,||||2.AB AC a AB AC a AB AC a ⎧-=⎪+=-⎨⎪-=⎩（3分）解之得1a =，∴2,c b ==∴双曲线E 的方程为2213y x -=．（5分）(2) 设在x 轴上存在定点(,0)G t ，使()BC GM GN λ⊥-．设直线l 的方程为x m ky -=，1122(,),(,)M x y N x y ． 由MP PN λ=，得120y y λ+=． 即12yy λ=-① （6分）∵(4,0)BC =，1212(,)GM GN x t x t y y λλλλ-=--+-，∴()BC GM GN λ⊥-12()x t x t λ⇔-=-． 即12()ky m t ky m t λ+-=+-． ②（8分）xxx把①代入②，得12122()()0ky y m t y y +-+=③ （9分）把x m ky -=代入2213y x -=并整理得222(31)63(1)0k y kmy m -++-=其中2310k -≠且0∆>，即213k ≠且2231k m +>． 212122263(1),3131km m y y y y k k --+==--．（10分）代入③，得2226(1)6()03131k m km m t k k ---=--， 化简得 kmt k =． 当1t m=时，上式恒成立． 因此，在x 轴上存在定点1(,0)G m，使()BC GM GN λ⊥-．（12分）9．(本小题满分14分)已知数列{}n a 各项均不为0，其前n 项和为n S ，且对任意*n ∈N 都有(1)n n p S p pa -=-（p 为大于1的常数），记12121C C C ()2n n n n nn na a a f n S ++++=．(1) 求n a ；(2) 试比较(1)f n +与1()2p f n p+的大小（*n ∈N ）； (3) 求证：2111(21)()(1)(2)(21)112n p p n f n f f f n p p -⎡⎤⎛⎫++-+++--⎢⎥ ⎪-⎢⎥⎝⎭⎣⎦，（*n ∈N ）． 解：(1) ∵(1)n n p S p pa -=-，① ∴11(1)n n p S p pa ++-=-．②②－①，得11(1)n n n p a pa pa ++-=-+，即1n n a pa +=．（3分）在①中令1n =，可得1a p =．∴{}n a 是首项为1a p =，公比为p 的等比数列，n n a p =． （4分）(2) 由(1)可得(1)(1)11n n n p p p p S p p --==--． 12121C C C nn n n n a a a ++++1221C C C (1)(1)n nn n n n n p p p p p =++++=+=+．∴12121C C C ()2n n n n nn na a a f n S ++++=1(1)2(1)nn n p p p p -+=⋅-， （5分）(1)f n +1111(1)2(1)n n n p p p p +++-+=⋅-． 而1()2p f n p+1111(1)2()n n n p p p p p +++-+=⋅-，且1p >， ∴1110n n p p p ++->->，10p ->． ∴(1)f n +<1()2p f n p+，（*n ∈N ）． （8分）(3) 由(2)知 1(1)2p f p +=，(1)f n +<1()2p f n p+，（*n ∈N ）． ∴当2n时，211111()(1)()(2)()(1)()2222n np p p p f n f n f n f p pp p-++++<-<-<<=． ∴221111(1)(2)(21)222n p p p f f f n p p p -⎛⎫⎛⎫++++++-+++ ⎪ ⎪⎝⎭⎝⎭2111112n p p p p -⎡⎤⎛⎫++=-⎢⎥ ⎪-⎢⎥⎝⎭⎣⎦， （10分）（当且仅当1n =时取等号）． 另一方面，当2n，1,2,,21k n =-时，2221(1)(1)()(2)2(1)2(1)k n k k k n k n k p p p f k f n k p p p ---⎡⎤-+++-=+⎢⎥--⎣⎦1p p -⋅1p p -=1p p -=∵22k n k n p p p -+，∴2222121(1)n k n k n n n p p p p p p ---+-+=-．∴12(1)()(2)2()2(1)nn n p p f k f n k f n p p -++-⋅=-，（当且仅当k n =时取等号）．（13分） ∴2121211111()[()(2)]()(21)()2n n n k k k f k f k f n k f n n f n ---====+-=-∑∑∑．（当且仅当1n =时取等号）． 综上所述，2121111(21)()()112n n k p p n f n f k p p --=⎡⎤⎛⎫++--⎢⎥∑ ⎪-⎢⎥⎝⎭⎣⎦，（*n ∈N ）．（14分）2009年高考数学压轴题系列训练含答案及解析详解三1．（本小题满分13分）如图，已知双曲线C ：x a y ba b 2222100-=>>()，的右准线l 1与一条渐近线l 2交于点M ，F 是双曲线C 的右焦点，O 为坐标原点.（I ）求证：OM MF →⊥→；（II ）若||MF →=1且双曲线C 的离心率e =62，求双曲线C 的方程；（III ）在（II ）的条件下，直线l 3过点A （0，1）与双曲线C 右支交于不同的两点P 、Q 且P 在A 、Q 之间，满足AP AQ →=→λ，试判断λ的范围，并用代数方法给出证明. 解：（I ） 右准线l 12：x a c =，渐近线l 2：y bax =∴=+M a c ab c F c c a b ()()22220，，，， ，∴→=OM a c ab c ()2， MF c a c ab c b c abc →=--=-()()22，， OM MF a b c a b cOM MF →⋅→=-=∴→⊥→2222220……3分（II ） e b a e a b =∴=-=∴=621222222，， ||()MF b c a b c b b a c b a →=∴+=∴+=∴==1111142222222222，，， ∴双曲线C 的方程为：x y 2221-=……7分 （III ）由题意可得01<<λ……8分证明：设l 31：y kx =+，点P x y Q x y ()()1122，，，由x y y kx 22221-==+⎧⎨⎩得()1244022--+=k x kxl 3与双曲线C 右支交于不同的两点P 、Q∴-≠=+->+=->=-->⎧⎨⎪⎪⎪⎩⎪⎪⎪∴≠±<<-<⎧⎨⎪⎪⎪⎩⎪⎪⎪120161612041204120221012022212212222k k k x x k k x x k k k k k ∆() ∴-<<-122k……11分AP AQ x y x y →=→∴-=-λλ，，，()()112211，得x x 12=λ∴+=-=--∴+=--=-=+-()()()1412412116412421222122222222222λλλλx k k x k k k k k k ， -<<-∴<-<∴+>12202111422k k ，，()λλ∴+>∴-+>()1421022λλλλ∴λ的取值范围是（0，1）……13分2．（本小题满分13分）已知函数f x x n x n f n n x n n N ()()[()]()(*)=≤--+--<≤∈⎧⎨⎩00111，，数列{}a n 满足a f n n N n =∈()(*) （I ）求数列{}a n 的通项公式；（II ）设x 轴、直线x a =与函数y f x =()的图象所围成的封闭图形的面积为S a a ()()≥0，求S n S n n N ()()(*)--∈1；（III ）在集合M N N k k Z ==∈{|2，，且10001500≤<k }中，是否存在正整数N ，使得不等式a S n S n n ->--10051()()对一切n N >恒成立？若存在，则这样的正整数N 共有多少个？并求出满足条件的最小的正整数N ；若不存在，请说明理由.（IV ）请构造一个与{}a n 有关的数列{}b n ，使得lim()n n b b b →∞+++12 存在，并求出这个极限值.解：（I ） n N ∈*∴=--+-=+-f n n n n f n n f n ()[()]()()111 ∴--=f n f n n ()()1……1分∴-=-=-=f f f f f f ()()()()()()101212323……f n f n n ()()--=1 将这n 个式子相加，得 f n f n n n ()()()-=++++=+012312f f n n n ()()()0012=∴=+ ∴=+∈a n n n N n ()(*)12……3分 （II ）S n S n ()()--1为一直角梯形（n =1时为直角三角形）的面积，该梯形的两底边的长分别为f n f n ()()-1，，高为1∴--=-+⨯=+-S n S n f n f n a a n n ()()()()112121=-++=12121222[()()]n n n n n……6分（III ）设满足条件的正整数N 存在，则n n n nn ()+->⇔>⇔>12100522100520102 又M ={}200020022008201020122998，，，，，，， ∴=N 201020122998，，……，均满足条件 它们构成首项为2010，公差为2的等差数列.设共有m 个满足条件的正整数N ，则2010212998+-=()m ，解得m =495 ∴M 中满足条件的正整数N 存在，共有495个，N min =2010 ……9分（IV ）设b a n n =1，即b n n n n n =+=-+212111()() 则b b b n n n n 122112121313141112111+++=-+-+-++-+=-+ [()()()()]() 显然，其极限存在，并且lim()lim[]n n n b b b n →∞→∞+++=-+=122112 ……10分注：b c a n n=（c 为非零常数），b b q q n a n n an n n==<<++()(||)12012121，等都能使lim()n n b b b →∞+++12 存在.19. （本小题满分14分）设双曲线y ax 22231-=的两个焦点分别为F F 12、，离心率为2. （I ）求此双曲线的渐近线l l 12、的方程；（II ）若A 、B 分别为l l 12、上的点，且2512||||AB F F =，求线段AB 的中点M 的轨迹方程，并说明轨迹是什么曲线；（III ）过点N ()10，能否作出直线l ，使l 与双曲线交于P 、Q 两点，且OP OQ →→=·0.若存在，求出直线l 的方程；若不存在，说明理由.解：（I ） e c a =∴=2422， c a a c 22312=+∴==，，∴-=双曲线方程为y x 2231，渐近线方程为y x =±33 4分（II ）设A x y B x y ()()1122，，，，AB 的中点()M x y ，[]2552522101033332233333331012121221221122121212121212122122||||||||()()()()()()AB F F AB F F c x x y y y x y x x x x y y y y y x x y y x x y y x x =∴==⨯=∴-+-===-=+=+∴+=--=+∴+++⎡⎣⎢⎤⎦⎥=又，，，， ∴+=+=321321007532512222()()y x x y ，即则M 的轨迹是中心在原点，焦点在x 轴上，长轴长为103，短轴长为1033的椭圆.（9分） （III ）假设存在满足条件的直线l设l y k x l P x y Q x y ：，与双曲线交于，、，=-()()()11122[] OP OQ x x y y x x k x x x x k x x x x i →→=∴+=∴+--=∴+-++=·0110101212122121221212()()()()由得则，y k x y x k x k x k x x k k x x k k ii =--=⎧⎨⎪⎩⎪--+-=+=-=--()()()13131633063133312222212221222 由（i ）（ii ）得k 230+=∴k 不存在，即不存在满足条件的直线l .14分3. （本小题满分13分）已知数列{}a n 的前n 项和为S n N n ()*∈，且S m ma n n =+-()1对任意自然数都成立，其中m 为常数，且m <-1.（I ）求证数列{}a n 是等比数列；（II ）设数列{}a n 的公比q f m =()，数列{}b n 满足：b a b f b n n 11113==-，() ()*n n N ≥∈2，，试问当m 为何值时，lim (lg )lim (n b a n b b b b b b n n →∞=→∞+++3122334…+-b b n n 1)成立？解：（I ）由已知S m ma n n ++=+-1111()()S m ma n n =+-()1 （2）由()()12-得：a ma ma n n n ++=-11，即()m a ma n n +=+11对任意n N ∈*都成立{} m m a a m m a n n n 为常数，且即为等比数列分<-∴=++1151（II ）当n =1时，a m ma 111=+-()∴====+∴==+≥∈---a b I q f m m m b f b b b n n N n n n n 11111113112，从而由（）知，()()()*∴=+-=∴⎧⎨⎩⎫⎬⎭∴=+-=+=+∈--1111111131212911b b b b b b n n b n n N n n n n n n n ，即为等差数列，分()()*a m m n n =+⎛⎝ ⎫⎭⎪-11∴→∞=→∞-++=+→∞+++=→∞-+-+++-+⎛⎝ ⎫⎭⎪=-lim (lg )lim lg lg lim ()lim n b a n n n m m mm n b b b b b b n n n n n n n 121133131414151112112231·……由题意知lgm m +=11，∴+=∴=-m m m 110109， 13分4．（本小题满分12分）设椭圆)0(12222>>=+b a by a x 的左焦点为F ，上顶点为A ，过点A 与AF 垂直的直线分别交椭圆和x 轴正半轴于P ，Q 两点，且P 分向量所成的比为8∶5．（1）求椭圆的离心率；（2）若过F Q A ,,三点的圆恰好与直线l ：033=++y x 相切，求椭圆方程． 解：（1）设点),0,(),0,(0c F x Q -其中),0(,22b A b a c -=．由P 分所成的比为8∶5，得)135,138(0b x P ， 2分 ∴a x a x 231)135()138(022202=⇒=+．①， 4分而b x b c ⊥-==),,(),,(0，∴0=⋅．cb x b cx 2020,0==-∴．②， 5分由①②知0232,32222=-+∴=a ac c ac b ． ∴21.02322=∴=-+e e e ． 6分 （2）满足条件的圆心为)0,2(22cc b O -'， )0,(,2222222c O c cc c a c c b '∴=--=-， 8分 圆半径a ca cb r ==+=22222． 10分由圆与直线l ：033=++y x 相切得，a c =+2|3|， 又3,2,1,2===∴=b a c c a ．∴椭圆方程为13422=+y x ． 12分 5．（本小题满分14分）（理）给定正整数n 和正数b ，对于满足条件b a a n ≥-+211的所有无穷等差数列{}n a ，试求1221++++++=n n n a a a y 的最大值，并求出y 取最大值时{}n a 的首项和公差．（文）给定正整数n 和正数b ，对于满足条件b a a n =-+211的所有无穷等差数列{}n a ，试求1221++++++=n n n a a a y 的最大值，并求出y 取最大值时{}n a 的首项和公差．（理）解：设{}n a 公差为d ，则1111,a a nd nd a a n n -=+=++． 3分dn a n nd a d a a a a a y n n n n n n n )21()1()()(11111221+++++=+++++=+++=+++++++ d n n a n n 2)1()1(1+++=+ 4分 )2)(1()2)(1(1111a a a n nda n n n n -++=++=+++ )3(2111a a n n -+=+． 7分 又211211,++--≤-∴≥-n n a b a b a a ．∴449449)23(332112111b b a b a a a a n n n n -≤-+--=-+-≤-++++，当且仅当231=+n a 时，等号成立． 11分∴8)49)(1()3(2111b n a a n y n -+≤-+=+． 13分 当数列{}n a 首项491+=b a ，公差n b d 434+-=时，8)49)(1(b n y -+=，∴y 的最大值为8)49)(1(b n -+． 14分（文）解：设{}n a 公差为d ，则1111,a a nd nd a a n n -=+=++． 3分)2)(1(2)1()1()21()1()()(1111111221nda n d n n a n d n a n nd a d a a a a a y n n n n n n n n n ++=+++=+++++=++++=+++=+++++++++)3(21)2)(1(11111a a n a a a n n n n -+=-++=+++， 6分 又211211,++--=-∴=-n n a b a b a a ．∴449449)23(332112111bb a b a a a a n n n n -≤-+--=-+-=-++++． 当且仅当231=+n a 时，等号成立． 11分 ∴8)49)(1()3(2111b n a a n y n -+=-+=+． 13分 当数列{}n a 首项491+=b a ，公差n b d 434+-=时，8)49)(1(b n y -+=．∴y 的最大值为8)49)(1(b n -+． 14分6．（本小题满分12分）垂直于x 轴的直线交双曲线2222=-y x 于M 、N 不同两点，A 1、A 2分别为双曲线的左顶点和右顶点，设直线A 1M 与A 2N 交于点P （x 0，y 0）（Ⅰ）证明：;22020为定值y x +（Ⅱ）过P 作斜率为02y x -的直线l ，原点到直线l 的距离为d ，求d 的最小值. 解（Ⅰ）证明：)0,2(),0,2(),,(),,(211111A A y x N y x M --- 则设)2(2111++=∴x x y y M A 的方程为直线 ①直线A 2N 的方程为)2(211---=x x y y ②……4分①×②，得)2(2221212---=x x y y分为定值的交点与是直线即822),(22),2(21,222020210022222121 =+∴=+--=∴=-y x N A M A y x P y x x y y x（Ⅱ）02222),(20020200000=-+=+--=-y y x x y x x x y x y y l 整理得结合的方程为 2220201222242y y y x d +=+=+=于是……10分 11221122220202020≥+=∴≤+∴≤∴=+y d y y y x 当1,1,1200取最小值时d y y =±=……12分7．（本小题满分14分） 已知函数x x x f sin )(-= （Ⅰ）若;)(],,0[的值域试求函数x f x π∈（Ⅱ）若);32(3)()(2:),,0(],,0[xf x f f x +≥+∈∈θθπθπ求证（Ⅲ）若)32(3)()(2,),)1(,(],)1(,[xf x f f Z k k k k k x ++∈+∈+∈θθππθππ与猜想的大小关系（不必写出比较过程）.解：（Ⅰ）为增函数时当)(,0cos 1)(,),0(x f x x f x ∴>-='∈π分的值域为即求得所以上连续在区间又4],0[)()(0),()()0(],0[)( ππππx f x f f x f f x f ≤≤≤≤（Ⅱ）设)32(3)()(2)(x f x f f x g +-+-=θθ，32sin3sin )(2)(xx f x g +++-=θθ即 )32cos cos (31)(xx x g ++-='θ……6分θπθπθπ=='∈+∴∈∈x x g x x 得由,0)(),0(32),0(],,0[.)(,0)(,),0(为减函数时当x g x g x <'∈∴θ分为增函数时当8)(,0)(,),( x g x g x >'∈πθ分因而有对的最小值为则上连续在区间10)32(3)()(20)()(],0[)()(],0[)( x f x f f g x g x x g g x g +≥+=≥∈θθθπθπ （Ⅲ）在题设条件下，当k 为偶数时)32(3)()(2xf x f f +≥+θθ当k 为奇数时)32(3)()(2xf x f f +≤+θθ……14分2009年高考数学压轴题系列训练含答案及解析详解四1．（本小题满分14分） 已知f(x)=222+-x ax (x ∈R)在区间[－1，1]上是增函数. （Ⅰ）求实数a 的值组成的集合A ； （Ⅱ）设关于x 的方程f(x)=x1的两个非零实根为x 1、x 2.试问：是否存在实数m ，使得不等式m 2+tm+1≥|x 1－x 2|对任意a ∈A 及t ∈[－1，1]恒成立？若存在，求m 的取值范围；若不存在，请说明理由. 本小题主要考查函数的单调性，导数的应用和不等式等有关知识，考查数形结合及分类讨论思想和灵活运用数学知识分析问题和解决问题的能力.满分14分.解：（Ⅰ）f ＇(x)=222)2(224+-+x x ax = 222)2()2(2+---x ax x ， ∵f(x)在[－1，1]上是增函数， ∴f ＇(x)≥0对x ∈[－1，1]恒成立，即x 2－ax －2≤0对x ∈[－1，1]恒成立. ① 设ϕ(x)=x 2－ax －2， 方法一：ϕ(1)=1－a －2≤0，① ⇔ ⇔－1≤a ≤1，ϕ(－1)=1+a －2≤0.∵对x ∈[－1，1]，f(x)是连续函数，且只有当a=1时，f ＇(-1)=0以及当a=－1时，f ＇(1)=0 ∴A={a|－1≤a ≤1}. 方法二：2a ≥0， 2a<0，①⇔ 或ϕ(－1)=1+a －2≤0 ϕ(1)=1－a －2≤0⇔ 0≤a ≤1 或 －1≤a ≤0 ⇔ －1≤a ≤1.∵对x ∈[－1，1]，f(x)是连续函数，且只有当a=1时，f ＇(－1)=0以及当a=-1时，f ＇(1)=0 ∴A={a|－1≤a ≤1}. （Ⅱ）由222+-x a x =x1，得x 2－ax －2=0， ∵△=a 2+8>0 ∴x 1，x 2是方程x 2－ax －2=0的两非零实根， x 1+x 2=a ，∴ 从而|x 1－x 2|=212214)(x x x x -+=82+a .x 1x 2=－2，∵－1≤a ≤1，∴|x 1-x 2|=82+a ≤3.要使不等式m 2+tm+1≥|x 1－x 2|对任意a ∈A 及t ∈[－1，1]恒成立， 当且仅当m 2+tm+1≥3对任意t ∈[－1，1]恒成立， 即m 2+tm －2≥0对任意t ∈[－1，1]恒成立. ② 设g(t)=m 2+tm －2=mt+(m 2－2)， 方法一：g(－1)=m 2－m －2≥0， ② ⇔g(1)=m 2+m －2≥0，⇔m ≥2或m ≤－2.所以，存在实数m ，使不等式m 2+tm+1≥|x 1－x 2|对任意a ∈A 及t ∈[－1，1]恒成立，其取值范围是{m|m ≥2，或m ≤－2}. 方法二：当m=0时，②显然不成立； 当m ≠0时，m>0， m<0， ②⇔ 或g(－1)=m 2－m －2≥0 g(1)=m 2+m －2≥0⇔ m ≥2或m ≤－2.所以，存在实数m ，使不等式m 2+tm+1≥|x 1－x 2|对任意a ∈A 及t ∈[-1，1]恒成立，其取值范围是{m|m ≥2，或m ≤－2}.2．（本小题满分12分）如图，P 是抛物线C ：y=21x 2上一点，直线l 过点P 且与抛物线C 交于另一点Q.（Ⅰ）若直线l 与过点P 的切线垂直，求线段PQ 中点M 的轨迹方程；（Ⅱ）若直线l 不过原点且与x 轴交于点S ，与y 轴交于点T ，试求||||||||SQ ST SP ST +的取值范围. 本题主要考查直线、抛物线、不等式等基础知识，求轨迹方程的方法，解析几何的基本思想和综合解题能力.满分12分.解：（Ⅰ）设P(x 1，y 1)，Q(x 2，y 2)，M(x 0，y 0)，依题意x 1≠0，y 1>0，y 2>0. 由y=21x 2， ① 得y ＇=x.∴过点P 的切线的斜率k 切= x 1， ∴直线l 的斜率k l =－切k 1=-11x ，∴直线l 的方程为y －21x 12=－11x (x －x 1)，方法一：联立①②消去y ，得x 2+12x x －x 12－2=0. ∵M 是PQ 的中点 x 0=221x x +=-11x ， ∴y 0=21x 12－11x (x 0－x 1).消去x 1，得y 0=x 02+221x +1(x 0≠0)，∴PQ 中点M 的轨迹方程为y=x 2+221x +1(x ≠0).方法二： 由y 1=21x 12，y 2=21x 22，x 0=221x x +，得y 1－y 2=21x 12－21x 22=21(x 1+x 2)(x 1－x 2)=x 0(x 1－x 2)， 则x 0=2121x x y y --=k l =-11x ，∴x 1=－1x ， 将上式代入②并整理，得 y 0=x 02+221x +1(x 0≠0)，∴PQ 中点M 的轨迹方程为y=x 2+221x +1(x ≠0).（Ⅱ）设直线l:y=kx+b ，依题意k ≠0，b ≠0，则T(0，b).分别过P 、Q 作PP ＇⊥x 轴，QQ ＇⊥y 轴，垂足分别为P ＇、Q ＇，则=+||||||||SQ ST SP ST ||||||||||||||||21y b y b Q Q OT P P OT +='+'.y=21x 2 由 消去x ，得y 2－2(k 2+b)y+b 2=0. ③ y=kx+b y 1+y 2=2(k 2+b)，则y 1y 2=b 2.方法一： ∴=+||||||||SQ ST SP ST |b|(2111y y +)≥2|b|211y y =2|b|21b=2. ∵y 1、y 2可取一切不相等的正数， ∴||||||||SQ ST SP ST +的取值范围是（2，+∞）. 方法二：∴||||||||SQ ST SP ST +=|b|2121y y y y +=|b|22)(2bb k +. 当b>0时，||||||||SQ ST SP ST +=b 22)(2b b k +=b b k )(22+=b k 22+2>2； 当b<0时，||||||||SQ ST SP ST +=－b 22)(2b b k +=b b k -+)(22.又由方程③有两个相异实根，得△=4(k 2+b)2-4b 2=4k 2(k 2+2b)>0， 于是k 2+2b>0，即k 2>－2b. 所以||||||||SQ ST SP ST +>bb b -+-)2(2=2. ∵当b>0时，bk 22可取一切正数，∴||||||||SQ ST SP ST +的取值范围是（2，+∞）. 方法三：由P 、Q 、T 三点共线得k TQ =K TP ， 即22x b y -=11x by -.则x 1y 2－bx 1=x 2y 1－bx 2，即b(x 2－x 1)=(x 2y 1－x 1y 2).于是b=122212122121x x x x x x -⋅-⋅=－21x 1x 2.∴||||||||SQ ST SP ST +=||||||||21y b y b +|1|21x x -|1|21x x -=||12x x +||21x x ≥2. ∵||12x x 可取一切不等于1的正数， ∴||||||||SQ ST SP ST +的取值范围是（2，+∞）. 3．（本小题满分12分）某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成400万元的损失. 现有甲、乙两种相互独立的预防措施可供采用. 单独采用甲、乙预防措施所需的费用分别为45万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9和0.85. 若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用，请确定预防方案使总费用最少.（总费用．．．=采取预防措施的费用+发生突发事件损失的期望值.） 本小题考查概率的基本知识和数学期望概念及应用概率知识解决实际问题的能力，满分12分. 解：①不采取预防措施时，总费用即损失期望为400×0.3=120（万元）；②若单独采取措施甲，则预防措施费用为45万元，发生突发事件的概率为1－0.9=0.1，损失期望值为400×0.1=40（万元），所以总费用为45+40=85（万元）③若单独采取预防措施乙，则预防措施费用为30万元，发生突发事件的概率为1－0.85=0.15，损失期望值为400×0.15=60（万元），所以总费用为30+60=90（万元）；④若联合采取甲、乙两种预防措施，则预防措施费用为45+30=75（万元），发生突发事件的概率为（1－0.9）（1－0.85）=0.015，损失期望值为400×0.015=6（万元），所以总费用为75+6=81（万元）.综合①、②、③、④，比较其总费用可知，应选择联合采取甲、乙两种预防措施，可使总费用最少.4．（本小题满分14分）已知.,2,1,1,}{,011 =+==>+n a a a a a a a nn n 满足数列 （I ）已知数列}{n a 极限存在且大于零，求n n a A ∞→=lim （将A 用a 表示）；（II ）设;)(:,,2,1,1A b A b b n A a b n nn n n +-==-=+证明。