第9章管内流体流动
流体在管内的流动阻力

2.2 流体在管内的流动阻力本节重点:牛顿粘性定律、层流与湍流的比较。
难点: 边界层与层流内层。
2.2.1 牛顿粘性定律与流体的粘度 1. 流体的粘性流体的典型特征是具有流动性,但不同流体的流动性能不同,这主要是因为流体内部质点间作相对运动时存在不同的内摩擦力。
这种表明流体流动时产生内摩擦力的特性称为粘性。
粘性是流动性的反面,流体的粘性越大,其流动性越小。
流体的粘性是流体产生流动阻力的根源。
2. 牛顿粘性定律与流体的粘度如图2-3所示,设有上、下两块面积很大且相距很近的平行平板,板间充满某种静止液体。
若将下板固定,而对上板施加一个恒定的外力,上板就以恒定速度u 沿x 方向运动。
若u 较小,则两板间的液体就会分成无数平行的薄层而运动,粘附在上板底面下的一薄层流体以速度u 随上板运动,其下各层液体的速度依次降低,紧贴在下板表面的一层液体,因粘附在静止的下板上, 其速度为零,两平板间流速呈线性变化。
对任意相邻两层流体来说,上层速度较大,下层速度较小,前者对后者起带动作用,而后者对前者起拖曳作用,流体层之间的这种相互作用,产生内摩擦,而流体的粘性正是这种内摩擦的表现。
平行平板间的流体,流速分布为直线,而流体在圆管内流动时,速度分布呈抛物线形,如图2-4所示。
实验证明,对于一定的流体,内摩擦力F 与两流体层的速度差.u d 成正比,与两层之间的垂直距离dy 成反比,与两层间的接触面积A 成正比,即图2-4 实际流体在管内的速度分布图2-3 平板间液体速度变化dyud AF .μ= (2-16) 式中:F ——内摩擦力,N ;dyud .——法向速度梯度,即在与流体流动方向相垂直的y 方向流体速度的变化率,1/s ; μ——比例系数,称为流体的粘度或动力粘度,Pa ·s 。
一般,单位面积上的内摩擦力称为剪应力,以τ表示,单位为Pa ,则式(1-26)变为dyud .μτ= (2-17) 式(2-16)、(2-17)称为牛顿粘性定律,表明流体层间的内摩擦力或剪应力与法向速度梯度成正比。
第七章 管内流体流动分析

第九章 管内流体流动
§9.1 粘性流体的两种流动状态(内部结构) §9.2 圆管中充分发展的层流流动 §9.3 湍流(紊流)的半经验公式 §9.4 圆管中充分发展的湍流流动 §9.5 管道入口段中的流动
§9.1 粘性流体的两种流动状态
一、层流与湍流
1.流动形态 雷诺试验揭示出粘性流体有两种性
层流 过渡状态
紊流
§9.1 粘性流体的两种流动状态
雷诺实验(续)
实验现象(续)
§9.1 粘性流体的两种流动状态
2.两种流动状态的判定
a、实验发现
v vcr v vcr
流动较稳定 流动不稳定
b、临界流速
vcr ——下临界流速
vcr ——上临界流速
层 流: v vcr
不稳定流: vcr v vcr
§9.2 圆管中充分发展的层流流动
4. 阻力系数与 流动损失
定义式
p
L D
um2 2
um
p L
R2
8
p L
D2
32
阻力系数
64
Re
水平管:
hf
p
gL uΒιβλιοθήκη 2 D 2gRe Dum
雷诺数
结论:层流流动的沿程损失与平均流速的一次方成正比。
§9.3 湍流的半经验理论
一、湍流假说---普朗特混合长度理论
紊 流: v vcr
§9.1 粘性流体的两种流动状态
2、两种流动状态的判定(续)
c、临界雷诺数 雷诺数
Re ud
Recr 2300 ——下临界雷诺数
Recr 4000 ——上临界雷诺数
工程上常用的圆管临界雷诺数
流体流动
第一章.流体流动1.计算空气在-40℃和310mmHg真空度下的密度和重度(用SI制和工程单位制表示)。
2.在大气压为760[毫米汞柱]的地区,某真空蒸馏塔塔顶真空表的读数为738[毫米汞柱]。
若在大气压为655[毫米汞柱]的地区使塔内绝对压力维持相同的数值,则真空度读数应为多少。
3.敞口容器底部有一层深0.52m的水,(ρ=1000kg/m3),其上为深3.46m的油(ρ=916kg/m3)。
求器底的压力,以Pa,atm及mH2O三种单位表示。
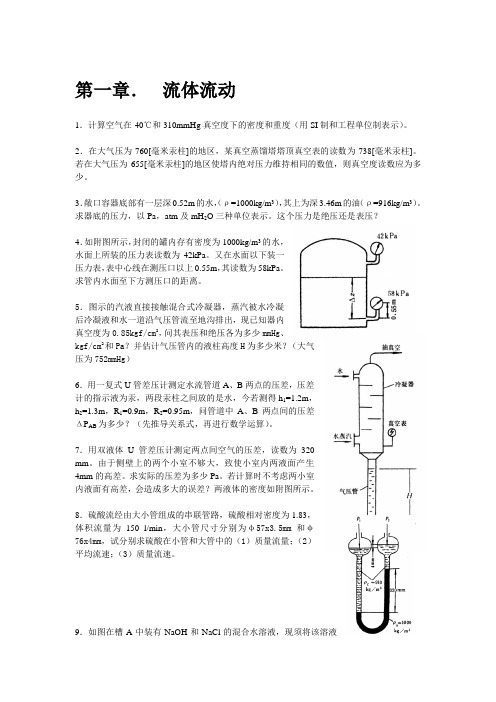
这个压力是绝压还是表压?4.如附图所示,封闭的罐内存有密度为1000kg/m3的水,水面上所装的压力表读数为42kPa。
又在水面以下装一压力表,表中心线在测压口以上0.55m,其读数为58kPa。
求管内水面至下方测压口的距离。
5.图示的汽液直接接触混合式冷凝器,蒸汽被水冷凝后冷凝液和水一道沿气压管流至地沟排出,现已知器内真空度为0.85kgf/cm2,问其表压和绝压各为多少mmHg、kgf/cm2和Pa?并估计气压管内的液柱高度H为多少米?(大气压为752mmHg)6.用一复式U管差压计测定水流管道A、B两点的压差,压差计的指示液为汞,两段汞柱之间放的是水,今若测得h1=1.2m,h2=1.3m,R1=0.9m,R2=0.95m,问管道中A、B两点间的压差ΔP AB为多少?(先推导关系式,再进行数学运算)。
7.用双液体U管差压计测定两点间空气的压差,读数为320mm。
由于侧壁上的两个小室不够大,致使小室内两液面产生4mm的高差。
求实际的压差为多少Pa。
若计算时不考虑两小室内液面有高差,会造成多大的误差?两液体的密度如附图所示。
8.硫酸流经由大小管组成的串联管路,硫酸相对密度为1.83,体积流量为150 l/min,大小管尺寸分别为φ57x3.5mm和φ76x4mm,试分别求硫酸在小管和大管中的(1)质量流量;(2)平均流速;(3)质量流速。
9.如图在槽A中装有NaOH和NaCl的混合水溶液,现须将该溶液放入反应槽B 中,阀C 和D 同时打开。
水力学第九章讲义

第九章 孔口、管嘴出流和有压管道 本章在定量分析沿程水头损失和局部水头损失的基础上,对工程实际中最常见的有压管道恒定流动和孔口、管嘴出流进行水力计算。
§9—1 孔口与管嘴的恒定出流液体从孔口以射流状态流出,流线不能在孔口处急剧改变方向,而会在流出孔口后在孔口附近形成收缩断面,此断面可视为处在渐变流段中,其上压强均匀。
● 孔口出流的分类:小孔口出流、大孔口出流(按H /D 是否大于10来判定);恒定出流、非恒定出流;淹没出流、非淹没出流;薄壁出流、厚壁出流。
薄壁出流确切地讲就是锐缘孔口出流,流体与孔壁只有周线上接触,孔壁厚度不影响射流形态,否则就是厚壁出流,如孔边修圆的情况,此时孔壁参与了出流的收缩,但收缩断面还是在流出孔口后形成。
如果壁厚达到3~4D ,孔口就可以称为管嘴,收缩断面将会在管嘴内形成,而后再扩展成满流流出管嘴。
管嘴出流的能量损失只考虑局部损失,如果管嘴再长,以致必须考虑沿程损失时就是短管了。
一. 薄壁孔口出流● 非淹没出流的收缩断面上相对压强均为零。
对上游断面O 和收缩断面C 运用能量方程即可得到小孔口非淹没出流公式:00221gH gH v C C ϕζα≡+=,0022gH A gH A A v Q C C μϕε≡==. 其中H 0是作用总水头;ϕ称为孔口的流速系数,主要取决于水头损失系数;μ是孔口的流量系数,它是流速系数ϕ与小孔口断面收缩系数A A C /=ε的乘积。
● 由于边壁的整流作用,它的存在会影响收缩系数,故有完全收缩与非完全收缩之分,视孔口边缘与容器边壁距离与孔口尺寸之比的大小而定,大于3则可认为完全收缩。
● 小孔口淹没出流的相应公式只需将作用总水头改成孔口上下游水位差即可。
● 大孔口出流的流量公式形式不变,只是相应的水头应为孔口形心处的值,具体的流量系数也与小孔口出流不同。
二. 厚壁孔口出流厚壁孔口出流与薄壁孔口出流的差别在于收缩系数和边壁性质有关,注意到收缩系数定义中的A 为孔口外侧面积,容易看出孔边修圆后,收缩减小,收缩系数和流量系数都增大。
传热学(第9章--对流换热)

— —
横向节距 纵向节距
23
9-3 流体有相变时的对流换热
一、凝结换热
1.特点:
——蒸汽和低于饱和温度的冷壁面相接触时会发 生凝结换热,放出凝结潜热。(如电厂中:凝汽 器和回热加热器内,管外蒸汽与管外壁的换热)
➢两种凝结方式:根据凝结液体依附在壁面上的形
态不同分.
tw ts
1)膜状凝结:凝结液体能润湿壁面,
腾换热设备安全经济的工作区为泡态沸腾区。
34
炉内高热负荷区水冷壁沸腾换热的强化
35
各种对流换热比较
液体对流换热比气体强;
对同一种流体,强制对流换热比自然对流换热强;
紊流换热比层流换热强;横向冲刷比纵向冲刷强;
有相变的对流换热比无相变换热强。
表9-5 各种对流换热平均换热系数的大致范围
换热系数 α[w/(m2.K)]
二是在蒸汽中混入油类或脂类物质。对紫铜管进行表面改 性处理,能在实验室条件下实现连续的珠状凝结,但在工 业换热器上应用,尚待时日。
26
2.影响蒸汽膜状凝结换热的因素:
(1)蒸汽中含有不凝结气体的影响 ➢ 蒸汽中含有不凝结气体(如空气)时,即使含量极微,
也会对凝结换热产生十分有害的影响。不凝结气体将会在 液膜外侧聚集而形成一层气膜,使热阻大大增加,从而恶 化传热。
21
(1)管束排列方式的影响
s1
s1
s2
顺排
s2
叉排
叉排:换热系数大,但流动阻力大. 顺排:换热系数小,但流动阻力小.
22
s1
s1
s2
s2
顺排
叉排
(2)流动方向上管排数的影响
后排管受前排管尾流的扰动作用对平均换热系 数的影响直到20排以上的管子才能消失。
第9章管内流体流动

9.1.2 湍流基本特征
稳态层流: 速度不随时间变化,只随空间位置变化。 湍流: 流体质点在随主流流动过程中还有随机脉动.
在稳态湍流流场中,虽然速度u的瞬时变化无规律可循,但 瞬时速度的时间平均值 u是常量。 u u u
在非稳态湍流流场中,时均 速度u也随时间变化但这种变化
是因为非稳态流场中主体流动本身是随时间变化的,与随机 脉动无关。
k2)
1 ln k
切应力与速度分布:
C2
p L
R2 4
1
(1
k2)
ln R ln k
rz
p L
R 2
r R
1k2 2ln(1/ k)
R r
u
R2
4
p L
1
r
2
R
1 k2 ln(1/ k)
ln
r R
套管内层流流动
最大速度: 对于套管内流动,在套管间某一半径r0处速度取得最大值。
Re
套管内层流流动
圆形套管内的层流流动
微元体的选取及受力和圆管相同
切应力分布方程:
yx
p L
度分布方程:
u
p L
r2 4
C1
ln
r
C2
z
r
圆形管套内的层流流动
边界条件: u 0,u 0
rkR
rR
将边界条件代入方程有:
套管内层流流动
C1
p L
R2 4
(1
(
du dy
)
0
引入两个特征参数: 特征速度:
壁面摩擦速度
u 0
摩擦长度
特征长度: y u 0
粘性底层速度分布:
化工原理流体流动

化工原理流体流动
化工原理中的流体流动是一个重要的研究领域,它涉及到各种物质在化工过程中的传输、混合、分离等关键过程。
在化工流体流动中,流体的性质和流动行为对化工过程的效率和产品质量具有重要影响。
在流体流动的研究中,我们通常会涉及到不同的流动模式,如层流、湍流等。
层流是指流体在管道中以规则的、层次分明的方式流动,其粘滞作用较强,流速均匀。
湍流则是一种不规则的、紊乱的流动方式,其粘滞作用较弱,流速不均匀。
在化工过程中,通常会通过控制流体的流动模式来达到更好的传输效果。
另外,在化工流体流动中,物质的输送也是一个重要的问题。
液体在管道中的流动主要通过压力差和重力来实现,而气体的流动则主要受到压力差和浓度差的影响。
我们可以通过调节管道的形状和尺寸,以及控制流体的流速和粘度来实现物质的有效输送。
此外,在化工过程中,流体的混合和分离也是一个重要的问题。
混合是指将不同的物质进行均匀混合,以达到一定的反应效果或产品质量。
分离则是将混合物中的不同组分分离出来,以达到对应的目的。
在化工过程中,我们通常会使用各种设备和技术来实现流体的混合和分离,如搅拌器、离心机等。
总之,化工原理中的流体流动是一个复杂而重要的研究领域。
通过深入了解流体的性质和流动行为,我们可以更好地控制化
工过程中的传输、混合和分离等关键环节,以提高生产效率和产品质量。
第9章 气体和蒸汽的流动

第9章气体和蒸汽的流动9.1 基本要求1.深入理解喷管和扩压管流动中的基本关系式和滞止参数的物理意义,熟练运用热力学理论分析亚音速、超音速和临界流动的特点。
2.对于工质无论是理想气体或蒸汽,都要熟练掌握渐缩、渐缩渐扩喷管的选型和出口参数、流量等的计算。
理解扩压管的流动特点,会进行热力参数的计算。
3.能应用有摩擦流动计算公式,进行喷管的热力计算。
4.熟练掌握绝热节流的特性,参数的变化规律。
9.2 本章难点450℃的蒸熵膨胀至℃在水蒸1,查得2,查因此,节流前后熵变量为Δs=s2-s1=7.94-7.1=0.84kJ/(kg·K)Δs>0,可见绝热节流过程是个不可逆过程。
若节流流汽定熵膨胀至0.1bar,由1h =2250kJ/kg,可作技术功为图kJ/kg 11002250335011=-='-h h若节流后的蒸汽定熵膨胀至相同压力0.1bar ,由图查得2h '=2512kJ/kg ,可作技术功为kJ/kg 83825123350=-='-h h 应用等熵过程参数间的关系式得:11010-⎪⎪⎭⎫⎝⎛=k k T T p pbar 0525.1110011151136.136.111010=⎪⎭⎫⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛=--k k T T p p喷管出口状态参数也可根据等熵过程参数之间的关系求得:11010-⎪⎪⎭⎫⎝⎛=k k T T p p即:136.136.121115343.00525.1-⎪⎪⎭⎫⎝⎛=T即喷管出口截面处气体的温度为828.67K 。
22220c h h +=m/s67.789)67.8281115(089.172.44)(72.44)(10002)(100022020202=-=-=-⨯⨯=-⨯=T T c T T c h h c p p因为喷管效率η=0.8822288.0c c ⨯='所以 m/s 740)67.789(88.022=⨯='c喷管出口处气体的温度 )(2112T T T T --='η=861K 喷管出口处气体的密度: 由R =287J/kg ·K139.086128710343.052=⨯⨯='ρkg/m 3由质量流量222v f c m =出口截面积:438.0740139.0452=⨯=f m 2喉部截面处的温度(候部的参数为临界参数):1010)12(,)12(--+=+=k kc k kc k p p k p p∴ 5632.0)136.12(0525.1136.136.1=+=-c p bar847.0)0525.15632.0()(36.136.0100===-k k c C p p T TK T T 8.944847.01115847.000=⨯=⨯=喉部截面处的密度:8.944287105632.05000⨯⨯==RT p ρ = 0.2077 kg/m 2喉部截面处的流速: )8.9441115(089.172.44)(72.4400-=-=C p T T c c=608.8 m/s流量系数 c c =0.96200370.08.6082077.096.045m c c m f c f c mc d c c c d=⨯⨯===ρρ求得喷管喉部截面321.0=c f m 2例3 空气流经一断面为0.1m 2的等截面管道,且在点1处测得c 1=100m/s 、p 1=1.5bar 、t 1=100℃;在点2测得p 2=1.4bar 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微元体的受力按Z轴正方向投影相加,则有:
rz
2
rdz
( rz
rz
r
dr)2
(r
dr)dz
p2
rdr
( p p dz)2 rdr g cos 2 rdrdz
z
管内层流流动
切应力方程:
(r rz
r
)
r
p z
g
cos
r
p z
其中: p p gz cos
对于Z方向充分发展的一维流动有: p const z
9.1.2 湍流基本特征
稳态层流: 速度不随时间变化,只随空间位置变化。 湍流: 流体质点在随主流流动过程中还有随机脉动.
在稳态湍流流场中,虽然速度u的瞬时变化无规律可循,但 瞬时速度的时间平均值 u是常量。 u u u
在非稳态湍流流场中,时均 速度u也随时间变化但这种变化
是因为非稳态流场中主体流动本身是随时间变化的,与随机 脉动无关。
充分发展的层流流动: u x 0
管内层流流动
圆管内的层流流动
r P0 z R
g
β
u
L
pl
p
rz
rz r
dr
u
rz
dr
gβ dz
r p p dz z
u
圆管内的层流流动分析
管内层流流动
输入微元体的动量流量: u2 2 rdr 输出微元体的动量流量: u2 2 rdr
注:对充分发展的 一维层流流动,输 入输出微元体的动
基本思想:湍流中流体微团的不规则运动与气体分子的 热运动相似,因此可借用分子运动论中建立粘性应力与 速度梯度之间关系的方法来研究湍流中雷诺应力与时均 速度之间的关系。
r0 R
1 k2 2ln(1/ k)
umax
R2
4
p L
1
1 k2 2ln(1/ k)
1
ln
1 k 2
2
ln(1/
k)
平均速度:
1
um z R2 (1 k 2 )
R kR
ug2
rdr
p L
R2
8
(1
k
2
)
1 k2 ln(1/ k)
体积流量:
qV
R2 (1 k 2 )um
p R4 L 8
切应力 分布方程:
rz
p L
r 2
C1 r
应用条件:圆管与圆形套管;牛 顿流体和非牛顿流体均适用。
rz
du dr
du p r C1
dr L 2 r
速度 分布方程:
u p r2
L 4
C1
ln
r
C2
应用条件:圆管与圆形套管; 牛顿流体均适用
管内层流流动
边界条件:
du 0,u 0
流体在管道中流动要克服管壁的摩擦阻力,因管壁摩擦阻力 产生的压降称为流动阻力损失,用hf表示。
hf
p
g
8 LqV R4g
λ
用平均速度表示:
hf
8 Lum R2 g
64 Dum
L um2 D 2g
阻力系数:
达西-怀斯巴赫公式:
(Darcy-Weisbach)
hf
L um2
D 2g
D 2R
阻力系数: 64
(1 k4 )
(1 k 2 )2
ln(1/
k)
应用条件:对于套管,层流流动的条件是雷诺数
Re um D(1 k) / 2000
9.3 湍流的半经验理论
9.3.1 湍流假说--普朗特混合长度理论
雷诺应力:
流体作湍流流动时,流体层之间除了存在着由于流体粘性作用引起的 切应力外,还存在着由于湍流脉动引起的附加切应力,这种附加的切 应力称为湍流切应力或雷诺应力。
时均 速度 u为:
1 tt
u(x, y, z,t)
u(x, y, z,t)dt
t t
u
u
u
u
u
u
u
t 稳态层流流动
t 稳态湍流流动
t 非稳态湍流流动
湍流强度: I u2
相对湍流强度:
Ir
u2 u
9.2 圆管内充分发展层流流动
管内流动 管内流动包括圆管和圆形套管内的流动。
管内流动简化
不可压缩流体在圆管内作层流流动时,在距管道入口相 对远处,流体的速度分布将不再随流动距离发生变化,这种 流动称为充分发展的层流流动。
湍流流动时流体内部的切应力可表示为:
yx e yx yx T
有效切应力
粘性切应力
雷诺应力
将湍流瞬时速度代入N-S方程并作简化处理有:
yx T uv 其中: u, v 分别为x、y方向脉动速度
粘性切应力是由流体层间分子扩散产生动量横向传递引起的。
对牛顿流体:粘性应力可通过牛顿剪切定理与速度联系起来。
雷诺应力是由流体微团的脉动产生动量横向传递引起的。
雷诺应力因影响因素较多,目前只能通过假设将其与时均速度联系起来。
布辛聂斯克涡粘性假设:
流体作一维稳态湍流流动时,雷诺应力仿牛顿切应力可表示为:
yx
T
T
du dy
du dy
其中:μT为涡粘系数(湍流粘性系数);
定义: T
ε为运动涡粘系数
普朗特混合长度理论(1952)
Re
套管内层流流动
圆形套管内的层流流动
微元体的选取及受力和圆管相同
切应力分布方程:
yx
p L
r 2
C1 r
kR r0
R
速度分布方程:
u
p L
r2 4
C1
ln
r
C2
z
r
圆形管套内的层流流动
边界条件: u 0,u 0
rkR
rR
将边界条件代入方程有:
套管内层流流动
C1
p L
R2 4
(1
um
1
z R2
R
ug2 rdr
p
R2
umax
0
L 8 2
层流平均速度等于管轴上最大流速的一半。
体积流量:
qV
R2um
R4 8
p L
哈根-泊谡叶方程(Hagen-Poiseuille)
阻力系数:
64 64 um D / Re
应用条件:
圆管; 牛顿流体; 层流流动。
管内层流流动
阻力损失:
dr r0
rR
切应力与速度分布:
将边界条件代入方程有:
rz
p L
r 2
应用条件:圆管; 牛顿流体;层流流 动。
u
R2 4
p L
1
r R
2
r zR
u
rz
圆管层流速度分布 和切应力分布
•速度为抛物线分布; •切应力为线性分布;
管内层流流动
最大速度:
umax
R2 4
p L
平均速度:
k2)
1 ln k
切应力与速度分布:
C2
p L
R2 4
1
(1
k2)
ln R ln k
rz
p L
R 2
r R
1k2 2ln(1/ k)
R r
u
R2
4
p L
1 Biblioteka r2R 1 k2 ln(1/ k)
ln
r R
套管内层流流动
最大速度: 对于套管内流动,在套管间某一半径r0处速度取得最大值。
雷诺实验 Reynolds (1883)
染料示踪剂
染料示踪 剂喷头
层流
水 阀门
过渡状态
湍流
流态判定:
流动从层流型态过渡到湍流型态的过程是一个流动失稳的过 程,称为流动型态的转换,其判定指标为雷诺数Re. (Re=ρuD/μ)
通常:
•Re<2300, 层流; •Re>4000, 湍流; •Re=2300~4000, 过渡区,与流动环境有关
