第二章 线性时不变系统的时域分析
信号与系统第二章_线性时不变系统

x(k)h(n k) ku(k)u(n k)
k
k
n k 1 n1 u(n)
k 0
1
11
例2:
x(n)
1 0
0n4 otherwise
n
h(n) 0
1,0 n 6
otherwise
h(t) h(n)
x(t)
y(t) y(n)
结论:
一个单位冲激响应是 h(t) 的LTI系统对输入 信号 x(t) 所产生的响应,与一个单位冲激响应 是x(t)的LTI系统对输入信号 h(t) 所产生的响应
相同。
25
2. 分配律: x(n) [h1(n) h2 (n)] x(n) h1(n) x(n) h2(n) x(t) [h1(t) h2 (t)] x(t) h1(t) x(t) h2(t)
1
本章主要内容:
• 信号的时域分解——用 (n) 表示离散时间信号; 用 (t) 表示连续时间信号。
• LTI系统的时域分析——卷积积分与卷积和。
• LTI系统的微分方程及差分方程表示。 • LTI系统的框图结构表示。 • 奇异函数。
2
2.0 引言 ( Introduction )
由于LTI系统满足齐次性和可加性,并且具有 时不变性的特点,因而为建立信号与系统分析的 理论与方法奠定了基础。
缺点:①只适用于两个有限长序列的卷积和; ②一般情况下,无法写出 y(n)的封闭表达式。
15
2.2 连续时间LTI系统:卷积积分
(Continuous-Time LTI Systems:The convolution integral)
控制工程基础第二章控制系统的时域分析

2.2线性系统的时域性能指标
为了评价线性系统的时间响应的性能,需要研究其在典型输入信号 作用下的时间响应过程。在典型输入信号的作用下,控制系统的时间响 应分为动态过程和稳态过程两部分。
动态过程又称为过渡过程或瞬态过程,是指系统在典型输入信号作 用下,其输出量从初始状态到最终状态的响应过程。根据系统结构和参 数的选择情况,动态过程表现为衰减、发散或等幅振荡的形式。显然, 一个实际运行的系统其动态过程必须是衰减的,也就是说,系统必须是 稳定的。动态过程除提供系统稳定的信息外,还可以提供其相应速度和 阻尼情况等信息,这些特性用动态性能指标描述。
控制系统的单位阶跃响应常用h(t)表示,单位阶跃响应曲线及 时域性能指标如图2-2所示。
图2-2 单位阶跃响应曲线及时域性能指标
(1)延迟时间 td。响应曲线第一次达到稳态值的一半所需的时间 称为延迟时间。 (2)上升时间 tr。上升时间是响应曲线从稳态值的10%上升到90%所 需的时间;或从0上升到100%所需的时间。对于欠阻尼二阶系统,通 常采用0~100%的上升时间;对于过阻尼系统,通常采用10%~90%的 上升时间。上升时间越短,响应速度越快。 (3)峰值时间tp。响应曲线达到超调量的第一个峰值所需要的时间称 为峰值时间。 (4)调节时间ts。调节时间是在响应曲线的稳态线上,用稳态值的百 分数(通常Δ取5%或2%)做一个允许误差范围,响应曲线达到并永远 保持在这一允许误差范围内所需的时间。 (5)最大超调量Mp。最大超调量指响应的最大偏离量h(tp)与终值h(∞ )之差的百分比,用σ%表示:
所谓时域分析法,就是在时域内通过拉氏变换求解系统的微分方 程,得到系统的时间响应,根据相应表达式和相应曲线分析系统的稳 定性、稳态误差等指标。
本章主要介绍时域响应及典型的输入信号;一阶、二阶系统的时 间响应;高阶系统的时间响应及主导极点、偶极子及高阶系统的降阶 方法;稳态误差的概念和计算方法,以及提高系统稳态精度的方法。
系统的时域分析 线性时不变系统的描述及特点 连续时间LTI系统的响应

y x (t ) K1e 2t K 2 e 3t
y(0)=yx(0)=K1+K2=1 y' (0)= y'x(0)= 2K13K2 =3
解得 K1= 6,K2= 5
y x (t ) 6e 2t 5e 3t , t 0
18
[例] 已知某线性时不变系统的动态方程式为: y" (t)+4y ' (t) +4y (t) = 2f ' (t )+3f(t), t>0 系统的初始状态为y(0) = 2,y'(0) = 1, 求系统的零输入响应yx(t)。 解: 系统的特征方程为 系统的特征根为
2t
Be
4t
1 y (0) A B 1 3 解得 A=5/2,B= 11/6 1 y ' (0) 2 A 4 B 2 3
5 2t 11 4t 1 t y(t ) e e e , t 0 2 6 3
12
1 t e 3
系统的几个概念:
9
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et u(t), 求系统的完全响应y(t)。
解:
(1) 求齐次方程y''(t)+6y'(t)+8y(t) = 0的齐次解yh(t)
11
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
信号与系统王明泉版本~第二章习题解答
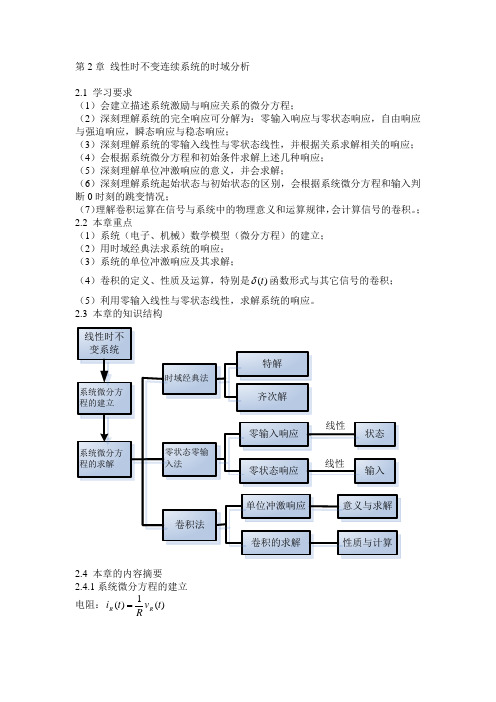
第2章 线性时不变连续系统的时域分析2.1 学习要求(1)会建立描述系统激励与响应关系的微分方程;(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解;(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。
; 2.2 本章重点(1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积; (5)利用零输入线性与零状态线性,求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻:)(1)(t v Rt i R R =电感:dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容:dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
§2-1 LTI系统的零状态响应

1 2
x(τ)
1 −1 0 1
τ
τ2 t2 1 当1<t<2 y (t ) = ∫ (t − τ + 1)dτ = (tτ − + τ) t −1 = 2 − 2 2 t −1
∞
h(t − τ)
1
t − 10 t
1
t +1
τ
当t>2
y (t ) =
−∞
∫ x(τ)h(t − τ)dτ = 0
h(t − τ)
−∞
u (t − τ ) d τ
1
0
1
u (−τ)
以上积分式的积分的上下限为(1~t),积 分结果的定义区间为(1~∞),所以后面要乘 分结果的定义区间为(1~ (1~∞ 以u(t-1)。
t t
1
0
t =0
τ
u (t − τ)
1 t <1 0 t
y 2 (t ) = − ∫ e − ( t − τ ) d τ = − e − t ∫ e τ d τ
大连海事大学信息科学技术学院
《信号与系统》 信号与系统》
∞ ∞
第二章
LTI系统的时域分析 LTI系统的时域分析
y (t ) =
=
−∞ ∞
∫ x ( τ ) h (t − τ ) d τ =
−(t − τ)
−∞
u ( τ ) e − ( t − τ ) u (t − τ ) d τ ∫
u (τ)
1
0
x (t ) = u (t )
,
h (t ) = e − t u (t )
求系统的零状态响应 解:
y (t ) = x (t ) ∗ h (t )
信号与系统第二章小结

信号与系统第二章 连续时不变系统的时域分析小结一、系统的初始条件)()()(t y t y t y zs zi +=,令-=0t 和+=0t ,可得)0()0()0(---+=zs zi y y y)0()0()0(++++=zs zi y y y对于因果系统,由于激励在0=t 时接入,故有0)0(=-zs y ;对于时不变系统,内部参数不随时间变化,故有)0()0(+-=zi zi y y 。
因此)0()0()0(+--==zi zi y y y)0()0()0(+-++=zs y y y同理)0()0()0()()()(+--==zi j zi j j y y y)0()0()0()()()(+-++=zs j j j y y y对于n 阶系统,分别称)1,,1,0)(0()(-=-n j y j 和)1,,1,0)(0()(-=+n j y j 为系统的-0和+0初始条件。
二、零输入响应)()()()()(01110111p D p N a p a p a p b p b p b p b t f t y p H n n n m m m m =++++++++==---- )(t y zi 满足算子方程0)()(=t y p D zi ,0≥t即零输入响应)(t y zi 是齐次算子方程满足-0初始条件的解。
)(t y zi 的函数形式与齐次解的形式相同。
简单系统的零输入响应1、)()()(t ce t y p p D t zi ελλ-=⇒+=2、)()()()()(102t e t c c t y p p D t zi ελλ-+=⇒+=三、单位冲激响应)()()(t ke t h p k p H t ελλ-=⇒+= )()()(t k t h kp p H δ'=⇒=)()()(t k t h k p H δ=⇒=)()()()(t kte t h p k p H t ελλ-=⇒+= 四、零状态响应)()()(t h t f t y zs *=五、完全响应)()()(t y t y t y zs zi +=六、卷积1、定义:⎰∞∞--⋅=*τττd t f f t f t f )()()()(21212、性质:交换律:)()()()(1221t f t f t f t f *=*结合律:)()]()([)]()([)(321321t f t f t f t f t f t f **=**分配律:)()()()()]()([)(3121321t f t f t f t f t f t f t f *+*=+*时移性质:)()()(21t y t f t f =*,则)()()()()(0201021t t y t f t t f t t f t f -=*-=-*3、常用信号的卷积公式 )()()(t f t t f =*δ)()()(t f t t f '='*δ)()()()1(t f t t f -=*ε)()()(t t t t εεε=*)()1(1)()(t e at e t at at εεε---=* 七、例题例1已知某连续系统的微分方程为)(3)(2)(2)(3)(t f t f t y t y t y +'=+'+''若系统的初始条件1)0()0(='=--y y ,输入)()(t e t f t ε-=,求)(t y zi ,)(t y zs ,)(t y 。
信号与系统课件

u[n] d [m]
mn
d [m]
n
n-k=m
7
离散LTI系统的时域分析—单位脉冲响应与卷积和(1)
利用单位脉冲响应h[n]求离散系统对输入信号x[n]的响应y[n]
(1)单位脉冲响应
x[n]
δ[n]
δ[n-n0]
LTI x[n] y[n]
x[n]
LTI
y[n]
(4) n>6, n–46, 即6<n 10
k
n-4
n
a n4 a 7 y[n] a 1 a k n4
6
k
注:也可以将x[n]分解成d[n]的5项移位线性组合,输出就变成了h[n]的移位线性组合
n 例2-4 x[n] u[n] u[n 5] h[n] a {u[n] u[n 7]}, a 1 求 y[n] x[n] h[n]
10
离散LTI系统的时域分析—单位脉冲响应与卷积和(4)
(4)卷积和的图示求解 1)自变量变换及翻转
x[n] * h[n]
k
x[k ]h[n k ]
x[n] x[k ]
h[n] h[k ] h[k ]
2)平移:将h[-k]随自变量n平移得h[n-k] n>0时,h[-k]向右平移n ; 3)相乘(同一k) :x[k]h[n-k] 4)求和:将相乘后的x[k]h[n-k]各点相加,即
3
本章主要内容
(1) 离散时间LTI系统的时域分析:卷积和,卷积性质 (2) 连续时间LTI系统的时域分析:卷积积分,卷积性质
(3) 单位冲激/脉冲响应与LTI系统的基本性质
(4) LTI系统的微分、差分方程描述 (5) 系统的响应分解:零输入、零状态响应 (6) 用微分方程、差分方程表征的LTI系统的框图表示
第二章 线性时不变系统

9
例5 y[n] 6,5,24,13,22,10,n 0,1,2,3,4,5 h[n] 3,1,4,2 n 0,1,2,3
y[n] x[n]h[n] 求 x[n]
2 t 5t2 x(t)
x[n] x[k] [n k] 离散的信号分解成脉冲
k
信号的 线性组合的形式
把任意一个序列表示成一串移位的单位脉冲序列 [n k]
的线性组合,而这个线性组合式中的权因子就是 x[k]
4
二. 离散时间线性时不变系统卷积和表示
[n] h[n]
[n k] h[n k]
时不变
x[k] [n k] x[k]h[n k] 齐次性
11
二. 连续时间线性时不变系统的卷积积分表示
(t) h (t)
(t k)
x(k) (t k)
x(k) (t k)
k
h (t k)
时不变
x(k
)h
(t
k
)
齐次性
x(k)h (t k) 可加性
k
xˆ(t)
yˆ (t )
y(t) x( )h(t )d x(t) h(t)
12
卷积的计算
(1)由定义计算卷积积分
例:设某一线性时不变系统的输入为x(t),其单位冲
激响应为h(t) x(t) eatu(t) , a 0 h(t) u(t)
试求 x(t) h(t)
x(t) h(t) ea u( )u(t )d
t ea d ,
0
t0
0,
t0
1 1 eat u(t) a
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下图是一个简单的离散系统,它由一个延时器、 下图是一个简单的离散系统,它由一个延时器、 是一个简单的离散系统 一个相加器和一个倍乘器组成。 一个相加器和一个倍乘器组成。根据图中各个 部件的连接关系和各个部件的基本功能, 部件的连接关系和各个部件的基本功能,写出 该系统输入 x[n] 和输出 y[n] 之间的关系为: 之间的关系为:
重要意义: (1)零状态响应能够真实地反映系统特性; (2)系统的零状态响应可以用卷积的方法 求解。
2.零输入响应和零状态响应的求解 .
零输入响应的求解 零输入响应的解的形式应和微分方程齐次解的 形式相同,它应是微分方程齐次解中的一部分。 如果一个 N 阶微分方程的 N 个特征根 αi 都是单 根,则零输入响应 yzi(t) 可写为:
例1-17-例1-20
2.时不变性 时不变性
时不变性的含义是,如果系统的输入在 时间上有一个平移 t0,则由其引起的响 应也产生一个同样的平移.
例1-14-例1-16
3.因果性 因果性
如果一个系统在任何时刻的输出只与系 统当前时刻的输入和过去的输入有关, 而与系统未来的输入无关,则这个系统 就是因果系统。 例1-12
1.冲激响应的特点 冲激响应的特点
y zi (t ) =
N
∑
i =1
Ci e α i t
待定系数 Ci 完全由系统的起始状态 y(k)(0-) 确定
零状态响应的求解 齐次解中剩下的一部分将和特解一起组 成系统的零状态响应 。 零状态响应有3种求解方法 (1)零状态响应=完全响应-零输入响应; (2)利用系统从起始状态 y(k)(0-) 到初始 状态 y(k)(0+) 的跳变量y(k)(0) 来求解系 统的零状态响应 ; (3)卷积法
第二章 线性时不变系统的时域分析
学习目标: 学习目标: (1) 正确理解零输入响应、零状态响应、冲激 正确理解零输入响应、零状态响应、 响应和阶跃响应的基本概念; 响应和阶跃响应的基本概念; (2)能应用不同的方法求解零状态响应和冲激 能应用不同的方法求解零状态响应和冲激 响应; 响应; (3)掌握用冲激响应卷积求解零状态响应的原 掌握用冲激响应卷积求解零状态响应的原 理和方法 (4) 掌握用冲激响应表征系统的基本特性。 掌握用冲激响应表征系统的基本特性。
框图法就是用一个方框来表示一个系统 或子系统,而方框中的符号表示输入和 输出之间的关系 :
系统分类
线性系统和非线性系统 时不变系统和时变系统 因果系统和非因果系统 稳定系统和不稳定系统 我们主要讨论线性时不变系统。 我们主要讨论线性时不变系统。
二、系统的基本性质
系统的基本特性包括有线性、时不变性、 因果性和稳定性等 。 1.线性 1.线性 如果系统的输入和输出之间满足叠加性 和比例性,则该系统就是线性系统。 叠加性 比例性 线性系统
n
∑C e
k k =1
αkt
⑵ 如果在特征根中, 是 k 重特征根 am , 则与 am 相对应的齐次解为:
k
∑C t
i i =1
k i
e
ai t
=0
⑶ 如果特征根中有共轭复根 α ± jβ ,则 共轭复根所对应的齐次解为:
e (C1 cos β t + C 2 sin β t )
αt
在上述三种齐次解中,Ci 是待定系数, 它的确定与特解有关。 举例2.14
一、系统的定义及表示
系统:具有特定功能的总体, 系统:具有特定功能的总体,可以看作信号 的变换器、处理器。 的变换器、处理器。 系统模型:系统物理特性的数学抽象。 系统模型:系统物理特性的数学抽象。 系统的表示方法 (1)数学表达式:系统物理特性的数学抽象。 )数学表达式:系统物理特性的数学抽象。 (2)系统框图:形象地表示其功能。 )系统框图:形象地表示其功能。
在特征根都是单根的情况下,零状态响 应的形式为:
y zs (t ) =
N
∑
i =1
Ai eαit + B(t )
零输入响应和零状态响应的概念同样适 用于离散系统,而且,它们的求解方法 也相同。
dy(t ) + 3 y (t ) = 3u (t ) 举例:已知 dt
y(0-)=3/2,求自由响应、强迫响应、零
如果系统的起始状态y(0-)≠0,则系统的 输出 y(t) 和系统的输入 x(t) 之间就不满 足线性和时不变性。然而,只要 y(0-)=0, y(t) 和 x(t) 之间就能够满足 线性和时不变的关系。
完全响应等于零输入响应加上零状态响 应:
零输入响应:在激励信号 x(t) 为0,或者 不考虑激励信号的作用时,由系统起始 状态 y(k)(0-) 产生的响应; 零状态响应:当系统起始状态 y(k)(0-) 为 0,或者不考虑系统的起始状态时,由激 励信号 x(t) 产生的响应。
y(t)与y[n]计算结果的比较
四、零输入响应和零状态响应
1.起始状态对系统的影响 . 用线性方程 y ( t ) = a x ( t ) + b 来描 述的系统可能不是一个线性系统!为什 么? 如果方程中没有常数项 b ,则 y(t)=ax(t) 所描述的系统就是一个线性系统 。
将系统的响应分为两部分: (1)与激励信号无关,完全由某些“常数” 决定; (2)完全由激励信号确定。 结论:完全由激励信号确定的响应与激励 信号之间就可能满足线性关系了。 举例说明
常见激励信号的特解形式
微分方程的特解与激励信号有关,根据 不同的激励信号,特解也有不同的形式。 几种常见的激励信号,特解的形式见表 2.1所示。 特解的求解过程一般是将表2.1中和激励 信号相对应、并具有待定系数 B 的特解 代入微分方程后求出待定系数 B,这样 也就求出了特解。
微分方程的齐次解和特解求出以后, 微分方程的齐次解和特解求出以后 , 其完全解的 形式也就确定下来了。 但是, 形式也就确定下来了 。 但是 , 完全解中的待定系 数则需要由方程给定的初值来确定。 数则需要由方程给定的初值来确定。 为求得这些初值, 为求得这些初值 , 我们将系统在激励信号加入前 瞬间的状态定义为系统的起始状态, 瞬间的状态定义为系统的起始状态,记为 y(k)(0-); ; 而将系统在激励信号加入后瞬间的状态定义为系 统的初始状态, 记为y 统的初始状态 , 记为 (k)(0+) , 确定系统完全响应 所需要的初值是初始状态 y(k)(0+), ( 系统的初始 , 时刻的响应) 状态就是系统在 t=0+ 时刻的响应)。
这个常系数线性微分方程, 这个常系数线性微分方程,其完全解由 齐次解和特解两部分组成 。 齐次解是微分方程在输入为0时的齐次 齐次解是微分方程在输入为 时的齐次 方程的解( 方程的解(式2.111) ) 而特解则是在输入的作用下满足微分方 程式(2.109) 的解。 的解。 程式
对于式(2.109)的微分方程,相应的齐次 方程为
1.连续时间 连续时间LTI系统的微分方程及其求解 连续时间 系统的微分方程及其求解 对连续时间LTI系统,如果 x(t) 为输入, y(t) 为输出,则描述输入和输出之间的 微分方程为:
∑
d y (t ) ak = k dt k =0
N
k
∑
d x(t ) bk dt k k =0
N
k
(2.109)
求解差分方程的方法有两种: (1)迭代法,也叫做递归法,这种方法易 于用计算机求解,但不易给出一个闭式 的解答。 (2)经典法,这种方法完全可以按照微 分方程的求解方式进行,其完全解也分 为齐次解和特解两部分。 例2.15
根据特征根的性质, 根据特征根的性质,差分方程的齐次解也 有以下三种形式: 有以下三种形式: ⑴ 如果特征根 α1、α2 、αn 都是单根, 则齐次解的形式为 ⑵ 如果在特征根中, αm 是 K 重特征根, 则齐次解中与 αm 相对应的有 K 项,其 形式为
数学表达式: 数学表达式:微分方程和差分方程
常用的系统描述方法是数学方程,包括 有用于连续系统的微分方程和用于离散 系统的从差分方程。 列写系统的数学方程有两条基本依据: (1)系统内部元器件或子系统的连接关系 (拓扑约束); (2)另一条是元器件或子系统的电气特性 (性能约束)。
系统的框图表示法
y[n] ay[n 1] = x[n]
一阶差分方程
N 阶离散系统的差分方程为: 阶离散系统的差分方程为:
∑ a y[n k ] = ∑ b x[n k ]
k k k =0 k =0
N
M
(2.113)
离散系统差分方程的形式类似于连续系统的微分方 程,只不过这里用差分信号替代了微分方程中的微 分信号而已。 分信号而已。 (2)差分方程的求解 ) 对于一阶差分方程式, 对于一阶差分方程式,如果输入信号 x[n]=δ[n] , 将如何求得呢? 则输出信号 y[n] 将如何求得呢?
输入响应、零状态响应和完全响应。
解: 自由响应:1/2e-3t 强迫响应 :1 3 3 t 零输入响应:y zi (t ) = e
2
y zs (t ) = 1 e 3t 零状态响应:
1 3 t y 完全响应 : (t ) = e + 1 2
t >0
t >0
五、单位冲激响应
单位冲激响应也简称为冲激响应,常用 符号 h ( t ) 或 h [ n ] 表示 。 单位冲激响应是系统在单位冲激信号激 励下的零状态响应; 或者说,是系统在零状态的条件下对单 位冲激信号激励时的响应。
⑶ 如果特征根中有共轭复 根 α ± jβ ,则共轭复根所 对应的齐次解为
