第二章补充习题
第二章补充习题及答案普通化学

第二章补充习题及答案普通化学概念、习题与解答化学反应基本原理——判断题1、指定单质的fGm、fHm、Sm皆为零。
(错:指定单质S不为零,)θmθθθ(错:升高温度正逆反应速率都增大,不会减小)10、反应活化能越大,反应速率也越大。
(错:相同温度下,活化能越大,速率常数越小,一般讲速率也越小)11、若反应速率方程式中浓度的指数等于反应方程式中反应物的系数,则该反应使基元反2、ΔrSm>0的反应都能自发进行。
(错:该条件只能判断对应温度孤立系统、标准状态下自发)3、rGm<0的反应必能自发进行。
(错:该条件只能判断对应温度标准状态4、若生成物的分子数比反应物的分子数多,则该反应的ΔrSm>0(错:主要看气体分子数)5、CaCO3在高温下可以发生分解反应,故该反应为吸热熵增。
(对:)6、根据能量最低原理,放热反应是自发进行的。
(错:影响自发性因素还有混乱度)7、冰在室温下自动融化成水,是熵增起了重要作用的结果。
(对:)8、化学反应的熵变与温度有关,但随温度变化不明显。
(对:温度变化没有引起状态变化的前提下)9、对于可逆反应C()+H2O(g)=CO(g)+H2(g),rHm0,升高温度使正增大,逆减小,故平衡向右移动。
应。
(错:例如H2(g)+I2(g)=2HI的反应就不是基元反应)12、反应级数取决于反应方程式中反应物的计量系数。
(错:非基元反应必须以试验为依据)13、根据分子碰撞理论,具有一定能量的分子在一定方位上发生有效碰撞,才可能生成产物。
(对)14、根据质量作用定律,反应物浓度增大,则反应速率加快,所以反应速率常数增大。
(错:速率常数与浓度无关)15、反应速率常数与温度有关,而与反应物浓度无关。
(对)二、选择题1热力学函数的定义与性质1-1下列各热力学函数中,哪一个为零:(B)(A)fGm(I2,g.298K)(B)fHm(Br2,l.298K)概念、习题与解答(C)Sm(H2,g.298K)(D)fGm(O3,g.298K)(E)fHm(CO2,g.298K)(C)对孤立体系而言,rSm>0的反应总是自发进行的。
初级会计资格考试·经济法基础第二章会计法律制度 补充练习_习题

➢补充习题第二章会计法律制度一、单选题1. 下列各项中,不属于会计工作岗位的是()。
A.出纳岗位B.会计机构中的会计档案保管岗位C.财产物资核算岗位D.仓库保管员岗位2. 下列各项中,不属于会计专业职务的是()。
A.高级会计师B.助理会计师C.会计师D.总会计师3. 中级会计师资格的取得实行()。
A.全国统一考试制度B.考试和评审相结合制度C.地方统一考试制度D.评审制度4. 根据会计法律制度的规定,现金日记账的保管时间应达到法定最低保管期限。
该期限为()。
A.5年B.30年C.10年D.20年5. 在我国,单位内部会计监督的对象是()。
A.本单位的单位负责人B.本单位的会计人员C.本单位的会计机构D.本单位的经济活动6. 在对外报出的财务会计报告上签名并盖章的人员不包括( )。
A.注册会计师B.会计主管人员C.总会计师D.单位负责人7. 根据会计法律制度的规定,下列行为中,属于会计工作政府监督的是()。
A.个人检举会计违法行为B.会计师事务所对单位经济活动进行审计C.单位内部会计机构审核本单位会计账簿D.财政部门对各单位的会计工作进行监督检查8. 根据会计法律制度的规定,对于尚不构成犯罪的伪造、变造会计凭证行为,需要承担的行政罚款,下列说法正确的是()。
A.对单位罚款3 000元以上50 000元以下B.对个人罚款3 000元以上50 000元以下C.对单位罚款5 000元以上50 000元以下D.对个人罚款5 000元以上100 000万元以下9. 伪造、变造会计凭证、会计账簿,尚不构成犯罪的,会计人员()内不得从事会计工作。
A.5年B.10年C.15年D.20年10. 下列有关会计职业道德与会计法律制度关系的表述中,不正确的是()。
A.在作用上相互补充,相互协调B.违反会计法律制度,一定违反会计职业道德C.在内容上相互渗透,互相吸收D.违反会计职业道德,一定违反会计法律制度11. 根据会计法律制度的规定,注册会计师已经获取被审计单位充分、适当的审计证据作为形成审计意见的基础。
第二章 蛋白质补充习题及答案

第二章蛋白质一、填空题1. 组成蛋白质分子的碱性氨基酸有________________、________________和________________。
酸性氨基酸有________________和________________。
2. 在下列空格中填入合适的氨基酸名称。
(1)________________是带芳香族侧链的极性氨基酸。
(2)________________和________________是带芳香族侧链的非极性氨基酸。
(3)________________是含硫的极性氨基酸。
(4)________________或________________是相对分子质量小且不含硫的氨基酸,在一个肽链折叠的蛋白质中它能形成内部氢键。
(5)在一些酶的活性中心中起作用并含羟基的极性较小的氨基酸是________________。
3. 氨基酸的等电点(pI)是指________________。
4. 脯氨酸与茚三酮反应产生________________色的物质,而其它氨基酸与茚三酮反应产生________________色的物质。
5. 实验室常用的甲醛滴定是利用氨基酸的氨基与中性甲醛反应,然后用碱(NaOH)来滴定________________上放出的________________。
6.通常可用紫外分光光度法测定蛋白质的含量,这是因为蛋白质分子中的________________、________________和________________三种氨基酸的共轭双键有紫外吸收能力。
7. 在α-螺旋中C=O和N-H基之间形成的氢键最稳定,因为这三个原子以________________排列。
8. 维持蛋白质构象的化学键有________________、________________、________________、________________、________________和________________。
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解
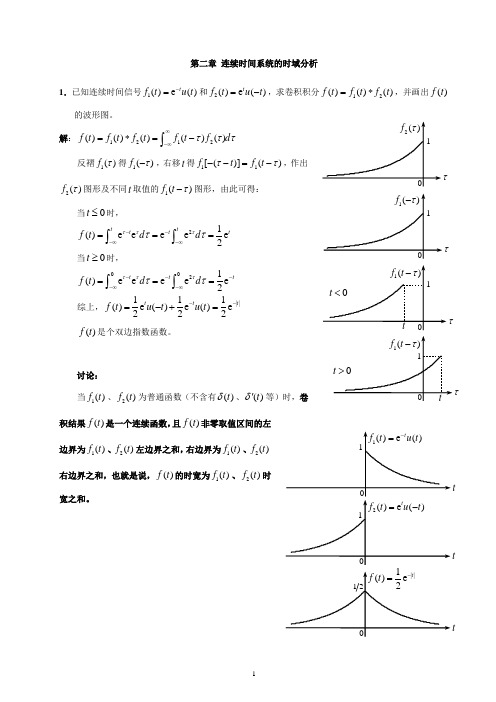
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
财务管理第二章课后补充习题及课堂例题(学生版)

财务管理第二章课后补充习题及课堂例题(学生版)第二章财务管理的价值观念课后补充计算题:1、某人希望以8%的年利率,按每半年付款一次的方式,在3年内等额偿还现有的6 000元债务,问每次应偿还多少?PV A6=6000 P/A4%,6 A=PV A6/(P/A4%,6)一农户购置了一台新收割机,他估2、计新机器头两年不需要维修,从第3年末开始的10年中,每年需支付200元维修费,若折现率为3%,问10年维修费的现值为多少? A=200P=A*(P/A3%,12-P/A3%,2)3、某人在2000年1月1日存入银行1000元,年利率为10%。
要求计算:(1)每年复利一次,2003年1月1日存款账户余额是多少?FV3=1000*(1+10%)^3=1000*F/P10%,3(2)每季度复利一次,2003年1月1日存款账户余额是多少?1000*(1+2.5%)^12=1000*F/P2.5%,12(3)若1000元,分别在2000年、2001年、2002年和2003年1月1日存入250元,仍按10%利率,每年复利一次,求2003年1月1日余额?FV A4=250*F/A10%,4 (4)假定分4年存入相等金额,为了达到第一问所得到的账户余额,每期应存入多少金额?FV3/(F/A10%,4)(5)假定第三问为每季度复利一次,2003年1月1日余额是多少?250*(F/P2.5%,12+F/P2.5%,8+F/P2.5%,4+1)(6)假定第四问改为每季度复利一次,每年应存入多少金额?FV3/(F/P2.5%,12+F/P2.5%,8+F/P2.5%,4+1)4、某人拟明年年初借款42000元,从明年年末开始,每年年末还本付息6000元,连续10年还清,设预定最低借款利率为8%,问此人是否能按计划借到款项?A=6000 P/A8%,10最多能借:PV A10=A*(P/A8%,10) 420005、有人在今后五年中每年末借给你2 500元,要求你在随后的10年中,每年末归还2 500元于他,若年利率为5%,问你是否接受这笔借款?2500*(P/A5%,5)2500*(P/A5%,15-P/A5%,5)6、某工商管理研究生计划从银行借款10 000元,利率12%,半年计息一次。
生物统计第二章 补充习题及答案

第二章习题及答案(来源:《生物统计学学习指导》李春喜等,科学出版社,2008:p14-15)一、填空1.变量的分布有两个明显的基本特征,即和。
二、判断1.计数资料也称为连续性变异资料。
计量资料也称为不连续性变异资料或间断性变异资料。
()三、选择题(《生物统计学题解及练习》杜荣赛高等教育出版社。
2003.p164)1.下面的变量属于非连续性变量的是( )。
A. 身高B. 体重C. 血型D. 血压2.身高、体重、年龄这一类数据属于()。
A. 离散性数据B. 计数数据C. 连续性数据D. 质量性状资料3.身高、体重、年龄这一类数据属于()。
A. 离散性数据B. 计数数据C. 计量资料D. 质量性状资料4.每十人中男性人数,每一万人中得H1N1流感人数,每亩麦田中杂草株数等,这一类数据属于()。
A. 离散性数据B. 连续性数据C. 计量资料D. 质量性状资料5.每十人中男性人数,每一万人中得H1N1流感人数,每亩麦田中杂草株数等,这一类数据属于()。
A. 计数数据B. 连续性数据C. 计量资料D. 质量性状资料6.频数按其组值的次序排列起来,称为()。
A. 频数排列B. 频数分布C. 组值排列D. 二项分布四、计算题1. 现以50枚受精种蛋孵化出雏鸡的天数为例,说明计数资料的整理。
21 20 20 21 23 22 22 22 21 22 20 23 22 23 22 19 22 2324 22 19 22 21 21 21 22 22 24 22 21 21 22 22 23 22 22小鸡出壳天数在19─24天范围内变动,有6个不同的观察值。
用各个不同观察值进行分组,共分为6组,可得表2-3形式的次数分布表。
表2-3 50枚受精种蛋出雏天数的次数分布表孵化天数划线计数次数(f)19 ║ 220 ║│ 321 ╫╫╫╫1022 ╫╫╫╫╫╫╫╫║║2423 ╫╫║║924 ║ 2合计50从表2-3可以看出:种蛋孵化出雏天数大多集中在21−23天,以22 天的最多,孵化天数较短(19−20天)和较长(24天)的都较少。
第二章补充习题
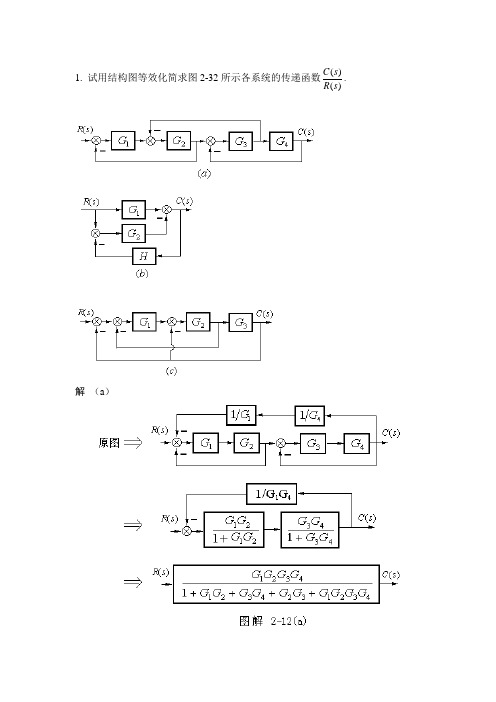
1. 试用结构图等效化简求图2-32所示各系统的传递函数)()(s R s C .解 (a )所以: 432132432143211)()(G G G G G G G G G G G G G G s R s C ++++= (b )所以: HG G G s R s C 2211)()(--=(c )2. 试用梅逊增益公式求上题中各结构图对应的闭环传递函数。
解 (a )图中有1条前向通路,3个回路,有1对互不接触回路,,,2111432111G G L G G G G P -==∆=,,,21321323432)(1L L L L L G G L G G L +++-=∆-=-=43213243214321111)()(G G G G G G G G G G G G G G P s R s C ++++=∆∆=(b )图中有2条前向通路,1个回路,,,,,H G L G P G P 2122211111==∆-==∆= 11L -=∆HG G G P P s R s C 22122111)()(--=∆∆+∆=(c )图中有1条前向通路,3个回路,,,211132111G G L G G G P -==∆=,,,)(132********L L L G G G L G G L ++-=∆-=-=3213221321111)()(G G G G G G G G G G P s R s C +++=∆∆=3. 求图中系统从v 到y的传递函数。
解:4. 已知系统方程组如下:⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111s X s G s C s G s G s C s X s X s X s G s X s G s X s C s G s G s G s R s G s X 试绘制系统结构图,并求闭环传递函数)()(s R s C 。
《随机过程》第二章补充习题

1、 设有状态空间为}4,3,2,1,0{=S 的齐次Markov 链}0;{≥n X n ,其初始分布为),,,,()0(43210p p p p p =π一步转移矩阵为 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1000000000000000001p q p q p qP 试回答以下问题: (1) 求出该马氏链进入各常返类的概率;(2) 求出该马氏链平均多长时间进入常返类集;(3) 计算:nn P ∞→lim 。
2、 (网球比赛):网球一局比赛在两个选手(发球者和接发球者)之间进行,网球的记分制是:15、30、40、和60分。
平分是指第五球后双方分数相同。
平分后,从第六球开始,如果发球者得分/失分,则此时发球者占先/接发球者占先。
如果发球者在发球占先后再得分,则发球者赢得该局。
如果接发球者在接发球后占先后再得分,则接发球者赢得该局。
若发球者发一球获胜的概率为p ,输的概率为q ,1=+q p ,试回答以下问题:(1) 试用马氏链建模网球一局比赛过程,确定其状态,画出状态转移图;(2) 分析各状态的性质;(3) 试确定一局网球比赛发球者获胜的概率;(4) 试确定一局比赛平均需要发几个球才能结束。
3、 设有状态空间为}4,3,2,1,0{=S 的齐次Markov 链}0;{≥n X n ,其一步转移概率为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=2/12/10004/14/104/14/1002/12/10004/34/1000001P 试回答以下问题:(1) 研究此马氏链的状态性质,并对各状态进行分类;(2) 针对状态1和2,确定其平稳分布;(3) 若i 和j 是非常返状态,试求ii f 、ij f 、ji f 和jj f ;(4) 假设该链起始的时候等概率处于非常返状态,试求该链进入常返状态集的期望步数;(5) 假设该链起始的时候等概率处于非常返状态,求出该马氏链进入各常返类的概率;(6) 计算:}12{35==X X P ;(7) 计算:nn P ∞→lim 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、桌上有一只盘子,最多可容纳两个水果,每次只能放入或取出一个水果。
爸爸专向盘中放苹果,妈妈放专向盘中放桔子;两个儿子专等吃盘子中的桔子,两个女儿专等吃盘子中的苹果。
请用P、V操作来实现爸爸、妈妈、儿子、女儿之间的同步与互斥关系。
答:本题中需设置4个信号量,其中empty表示还可以向盘中放几个水果,其初值为2;apple对应已放入盘中的苹果,orange对应已放入盘中的桔子,它们的初值均为0;mutex 用来实现对盘子的互斥访问(包括放和取),其初值为1。
相应的进程可描述为:
father(){
while(1){
P(empty);
P(mutex);
向盘中放苹果;
V(mutex);
V(apple);
}
{
}
mother(){
while(1){
P(empty);
P(mutex);
向盘中放桔子;
V(mutex);
V(orange);
}
}
<
son (){ /* 两个儿子对应同一段代码*/
while(1){
P(orange);
P(mutex);
从盘中取桔子;
V(mutex);
V(empty);
吃桔子;
}
}
^
daughter(){ /* 两个女儿对应同一段代码*/
while(1){
P(apple);
P(mutex);
从盘中取苹果;
V(mutex);
V(empty);
吃苹果;
}
}
]
2、某招待所有100个床位,住宿者住入要先登记(在登记表上填写姓名及床位号),离去时要撤消登记(在登记表上删去姓名和床位号)。
请给出住宿登记及撤消登记过程的算法描述。
答:本题中,被住宿者竞争的资源主要有床位和住宿登记表两种,可分别为它们设置初值为100的信号量bed及初值为1的信号量mutex。
住宿登记过程的算法描述如下:P(bed);
P(mutex);
在登记表上填写姓名及床位号;
v(mutex);
撤消登记过程的算法描述如下:
P(mutex);
在登记表上删去姓名和床位号;
V(mutex);
|
V(bed);
3、一阅览室,读者进入阅览室必须先在一张登记表(TB)上登记,该表为每一座位设一个表目,读者离开时要消掉其登记信息,阅览室共有100个座位。
为了描述读者的动作,请用Pascal语言和P、V操作写出进程间的同步算法。
约定:
(1)flag的值:0座位空闲,1座位被占用。
(2)用语句i=getflag(0)可搜索到一个空座位i,用语句=0或1可给标志位赋值。
(3)用i=getname(readername)可搜索到某读者所登记的座位号i;用=0或=readername 可给姓名字段赋值,0表示消除读者姓名。
(4)计数信号量用count,互斥信号量用mutex。
答:本题中,读者要竞争座位、登记表两种资源,故可分别为它们设置初值为100的信号量count,以及初值为1的信号量mutex。
读者的动作可描述为:
reader(){
while(1){
¥
P(count); /* 申请一个座位*/
P(mutex); /* 申请登记表*/
i=getflag(0); /* 在登记表上搜索一个空座位*/
=1; /* 登记该座位已被占用*/
=readername; /* 登记读者姓名*/
V(mutex);/* 释放登记表*/
进入阅览室,坐下并开始阅览;
P(mutex); /* 申请登记表*/
i=getname(readername); /* 在登记表上搜索读者登记的座位号*/
=0; /* 撤消登记信息*/
》
=0;
P(mutex); /* 释放登记表*/
V(count); /* 释放座位*/
离开阅览室;
}
}
4、某寺庙,有小和尚、老和尚若干。
有一水缸,有小和尚提水入缸供老和尚饮用。
水缸可容10桶水,水取自同一井中。
水井径窄,每次只能容一个桶取水。
水桶总数为3个。
每次入、取缸水仅为1桶,且不可同时进行。
试给出有关取水、入水的算法描述。
答:本题中需设置5个信号量:bucket对应临界资源水桶,初值为3;jar用来对水缸进行互斥操作,初值为1;full表示水缸中可以使用的水,初值为0;empty表示缸中还可入水的容量,初值为10;well用来保证互斥地使用水井,初值为1。
有关取水、入水的算法描述如下:
semaphore bucket=3,jar=1,full=0,empty=10,well=1;
%
little_monk(){ /* 小和尚入水算法*/
while(1){
P(empty);
P(bucket);
P(well);
从水井中打水;
V(well);
P(jar);
倒水入缸;
V(jar);
.
V(full);
V(bucket);
}
}
old_monk(){ /* 老和尚取水算法*/
while(1){
P(full);
P(bucket);
P(jar);
[
从缸中取水;
V(jar);
V(empty);
从桶中倒水饮用;
V(bucket);
}
}
5. 如图所示,三个合作进程P1、P2、P3,它们都需通过同一输入设备输入各自的数据a 、b 、c ,该输入设备必须互斥地使用,而且其第一个数据必须由P1进程读取,第二个数据必须由P2进程读取,第三个数据则必须由P3进程读取。
然后,三个进程分别对输入数据进行下列计算:
P1: x = a + b
P2: y = a * b
,
P3: z = y + c – a
最后,P1进程通过所连的打印机将计算结果x 、y 、z 的值打印出来。
请用信号量实现它们的同步。
图 P1、P2、P3的工作示意图
答:为了控制三个进程依次使用输入设备进行输入,需分别设置三个信号量S1、S2、S3,其中S1的初值为1,S2和S3的初值为0。
使用上述信号量后,三个进程不会同时使用输入设备,故不必再为输入设备设置互斥信号量。
另外,还需设置信号量Sb 、Sy 、Sz 来分别表示数据b 是否已经输入,以及y 、z 是否已计算完成,它们的初值均为0。
三个进程的动作可描述为:
P1:
P(S1);
从输入设备输入数据a ;
,
V(S2);
P(Sb);
x=a+b;
P(Sy);
P(Sz);
使用打印机打印出x 、y 、z 的结果;
P2:
P(S2);
从输入设备输入数据b ;
V(S3);
V(Sb);
y=a*b;
V(Sy);
P3:
P(S3);
P1 P2 P3
Non-preemptive input device Input(a)
Input(c) |
从输入设备输入数据c;P(Sy);
Z=y+c-a;
V(Sz);。
