数学建模实验作业参考例子
数学建模作业实验线性规划实验模板

数学建模作业(实验3线性规划实验)基本实验1.生产计划安排某公司使用三种操作装配三种玩具——玩具火车、玩具卡车和玩具汽车。
对于三种操作可用时间限制分别是每天430分钟、460分钟和420分钟, 玩具火车、玩具卡车和玩具汽车的单位收入分别是3美元、2美元和5美元。
每辆玩具火车在三种操作的装配时间分别是1分钟, 3分钟和1分钟。
每辆玩具卡车和每辆玩具汽车相应的时间是( 2, 0, 4) 和( 1, 2, 0) 分钟( 零时间表示不使用该项操作) 。
( 1) 将问题建立成一个线性规划模型, 确定最优的生产方案。
( 2) 对于操作1, 假定超过它当前每天430分钟能力的任何附加时间必须依靠每小时50美元的加班获得。
每小时成本包括劳动力和机器运行费两个方面。
对于操作1, 使用加班在经济上有利吗? 如果有利, 最多加多少时间?( 3) 假定操作2的操作员已同意每天加班工作两小时, 加班费是45美元一小时。
还有, 操作自身的成本是一小时10美元。
这项活动对于每天收入的实际结果是什么?( 4) 操作3需要加班时间吗?解答解:设生产玩具火车、玩具卡车和玩具汽车的数量分别为X1, X2, X3, 则目标函数为:3X1+2X2+5X3约束条件:X1+2X2+X3<=4303X1+2X3<=460X1+4X2<=420X1>=0; X2>=0; X3>=0最优值为目标函数取得最大。
LINGO程序max=3*x1+2*x2+5*x3;x1+2*x2+x3<=430;3*x1+2*x3<=460;x1+4*x2<=420;运行结果Globaloptimalsolutionfound.Objectivevalue:1350.000Infeasibilities:0.000000Totalsolveriterations:2ModelClass:LPTotalvariables:3Nonlinearvariables:0Integervariables:0Totalconstraints:4Nonlinearconstraints:0Totalnonzeros:10Nonlinearnonzeros:0VariableValueReducedCostX10.0000004.000000X2100.00000.000000X3230.00000.000000RowSlackorSurplusDualPrice11350.0001.00000020.0000001.00000030.0000002.000000420.000000.000000( 1) 由运行结果可得, 最优的生产方案为:玩具火车、玩具卡车和玩具汽车的生产数量分别为: 0、100、230; 收入为1350.( 2) 由DualPrice第二行可知, 当操作1每增加1分钟收入增加1美元, 因此50/60<1, 使用加班在经济上是有利的; Rangesinwhichthebasisisunchanged: ObjectiveCoefficientRanges:CurrentAllowableAllowable VariableCoefficientIncreaseDecreaseX13.0000004.000000INFINITYX22.0000008.0000002.000000X35.000000INFINITY2.666667RighthandSideRanges:CurrentAllowableAllowableRowRHSIncreaseDecrease2430.000010.00000200.00003460.0000400.000020.000004420.0000INFINITY20.00000分析可知, 最多增加10分钟。
数学建模与应用案例练习题

数学建模与应用案例练习题数学建模是将实际问题转化为数学问题,并通过数学方法和计算机技术求解的过程。
它在各个领域都有着广泛的应用,能够帮助我们更好地理解和解决现实中的复杂问题。
下面我们将通过一些具体的案例练习题来深入了解数学建模的方法和应用。
案例一:生产计划优化问题某工厂生产 A、B 两种产品,生产 A 产品每件需要消耗 2 个单位的原材料和 3 个单位的工时,生产 B 产品每件需要消耗 3 个单位的原材料和 2 个单位的工时。
工厂现有 100 个单位的原材料和 80 个单位的工时,A 产品的单位利润为 5 元,B 产品的单位利润为 4 元。
问如何安排生产计划,才能使工厂获得最大利润?首先,我们设生产 A 产品 x 件,生产 B 产品 y 件。
那么,目标函数就是利润最大化,即 Z = 5x + 4y。
然后,我们需要考虑约束条件。
原材料的限制为 2x +3y ≤ 100,工时的限制为 3x +2y ≤ 80,同时 x、y 都应该是非负整数。
接下来,我们可以使用线性规划的方法来求解这个问题。
通过绘制可行域,找到目标函数在可行域上的最大值点。
经过计算,我们可以得出当 x = 20,y = 20 时,工厂能够获得最大利润 180 元。
这个案例展示了数学建模在生产决策中的应用,通过合理地安排生产计划,能够有效地提高企业的经济效益。
案例二:交通流量预测问题在一个城市的某个十字路口,每天不同时间段的车流量不同。
我们收集了过去一段时间内每天各个时间段的车流量数据,希望建立一个数学模型来预测未来某一天的车流量。
首先,我们对收集到的数据进行分析,发现车流量具有一定的周期性和季节性变化。
然后,我们可以选择使用时间序列分析的方法来建立模型。
比如,可以使用 ARIMA 模型(自回归移动平均模型)。
在建立模型之前,需要对数据进行预处理,包括平稳性检验、差分处理等。
通过建立合适的 ARIMA 模型,并进行参数估计和检验,我们就可以利用这个模型对未来的车流量进行预测。
数学建模简单13个例子 ppt课件

1、从包汤圆(饺子)
通常,1公斤面, 1公斤馅,包100个汤圆(饺子)
今天,1公斤面不变,馅比 1公斤多了,问应多包几 个(小一些),还是少包几个(大一些)?
问题
圆面积为S的一个皮,包成体积为V的汤圆。若 分成n个皮,每个圆面积为s,包成体积为v。
S
s s … s (共n个)
某航空母舰派其护卫舰去搜寻其跳伞的飞 行员, 护卫舰找到飞行员后,航母通知它尽快返回与其汇 合并通报了航母当前的航速与方向,问护卫舰应怎 样航行,才能与航母汇合。
数学建模简单13个例子
Y
P(x,y)
记v2/ v1=a通常a>1
航母
则 |BP|2a2|AP|2 即:
A(0,b)
θ1
x2 (y b )2 a 2[x2 (y-b )2]
v 也是交管部门早已定好的,目的是使交通流量最大,可
另建模型研究,从而L1=v*t1。刹车距离 L2既可用曲线
拟合方法得出,也可利用牛顿第二定律计算出来
黄灯究竟应当亮多久现在已经变得清楚多了。
第一步,先计算出L应多大才能使看见黄灯的司机停
得住车。
第二步,黄灯亮的时间应当让已过线
的车顺利穿过马路,DFra bibliotek即T 至少应当达到 (L数+学建D模)简单/13v个。例子
数学建模简单13个例子
4、爬山问题
某人早8时从山下旅店出发沿一条路径上山,下午5 时到达山顶并留宿,次日早8时沿同一路径下山,下午5 时回到旅店,则这人在两天中的同一时刻经过途中的 同—地点,为什么?
解法一: 将两天看作一天,一人两天的运动看作一天两人 同时分别从山下和山顶沿同一路径相反运功,因为两 人同时出发,同时到达目的地,又沿向一路径反向运 动,所以必在中间某一时刻t两人相遇,这说明某人在 两天中的同一时刻经过路途中的同一地点。
数学建模小实例

1、司乘人员配备问题某昼夜服务的公交路线每天各时间区段内需司机和乘务人员如下:设司机和乘务人员分别在各时间区段一开始上班,并连续工作八小时,问该公交线路至少配备多少名司机和乘务人员?解: 设i x为第i班应报到的人员i,建立线性模型如下:)6,(,2,1LINGO程序如下:MODEL:min=x1+x2+x3+x4+x5+x6;x1+x6>=60;x1+x2>=70;x2+x3>=60;x3+x4>=50;x4+x5>=20;x5+x6>=30;END得到的解为:x1=60,x2=10,x3=50,x4=0,x5=30,x6=0 ;配备的司机和乘务人员最少为150人。
2、铺瓷砖问题要用40块方形瓷砖铺下图所示形状的地面,但当时市场上只有长方形瓷砖,每块大小等于方形的两块。
一人买了20块长方形瓷砖,试着铺地面,结果无法铺好。
试问是这人的功夫不到家还是这个问题根本无解呢?3、 棋子颜色问题在任意拿出黑白两种颜色的棋子共n 个,随机排成一个圆圈。
然后在两颗颜色相同的棋子中间放一颗黑色棋子,在两颗颜色不同的棋子中间放一颗白色棋子,放完后撤掉原来所放的棋子,再重复以上的过程,这样放下一圈后就拿走前次的一圈棋子,问这样重复进行下去各棋子的颜色会怎样变化呢?分析与求解:由于在两颗同色棋子中放一颗黑色棋子,两颗不同色的棋子中间放一颗白色棋子,故可将黑色棋子用1表示,白色棋子用-1表示。
这是因为-1×(-1)=1,1×1=1,这代表两颗同色棋子中放一颗黑色棋子;1×(-1)= -1,这代表两颗不同色的棋子中间放一颗白色棋子。
设棋子数为n ,12,,,n a a a 为初始状态。
当n=3时步数 状态(舍掉偶次项) 0 1a 2a 3a1 21a a 32a a 13a a231a a 21a a 32a a3 32a a 31a a21a a412a a 23a a 31a a说明当n=3时,经过3步进入初始状态。
数学建模简单13个例子

另建模型研究,从而L1=v*t1。刹车距离 L2既可用曲线
拟合方法得出,也可利用牛顿第二定律计算出来
黄灯究竟应当亮多久现在已经变得清楚多了。
第一步,先计算出L应多大才能使看见黄灯的司机停
得住车。
第二步,黄灯亮的时间应当让已过线
的车顺利穿过马路,
D
即T 至少应当达到 (L+D)/v。
L
返回
9、砖块延伸
出,黄灯起的是警告的作用,意思是马上
要转红灯了,假如你能停住,请立即停车。
停车是需要时间的,在这段时间内,车辆
仍将向前行驶一段距离 L。这就是说,在
离街口距离为 L处存在着一条停车线(尽
管它没被画在地上),见图。对于那些黄
D
灯亮时已过线的车辆,则应当保证它们仍 能穿过马路。
L
马路的宽度D是容易测得的,问题的关键在于L的确
总距离为 n 1 ,
故有砖点n块 出向人右意可料时 叠。k1至, 2knk任1 2意1k远,n这1 一21n结果多少返回
10、寻找黑匣子
飞机失事时,黑匣子会自动打开,发射出某种 射线。为了搞清失事原因,人们必须尽快找回匣子。 确定黑匣子的位置,必须确定其所在的方向和距离, 试设计一些寻找黑匣子的方法。由于要确定两个参 数,至少要用仪器检测两次,除非你事先知道黑匣 子发射射线的强度。
I2 I1
1
方法二
A
在方法一中,两检测点与黑匣子
位于β一α a
直线上,这一点比较容易 点是结果对照度测
量的精C做度到要, 求主 较要 高缺 ,B
很少的误差会造成结果的很大变化,即敏感性很
强,现提出另一方法,在 A点测得黑匣子方向后 ,
到B点再测方向 ,AB 距离为a ,∠BAC=α,
数学建模举例
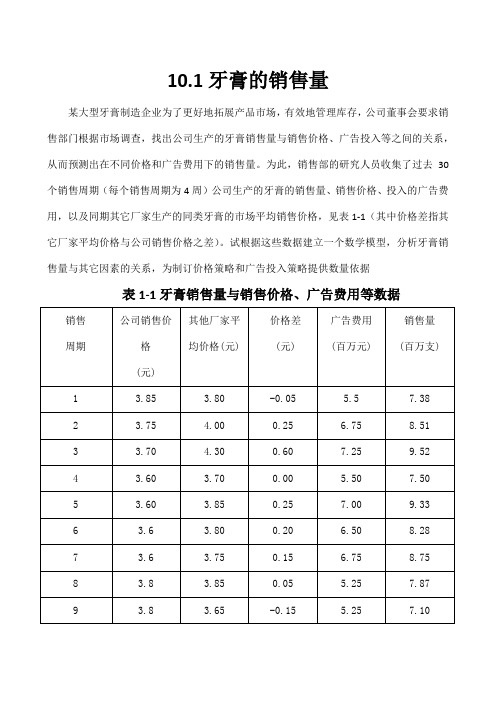
10.1牙膏的销售量某大型牙膏制造企业为了更好地拓展产品市场,有效地管理库存,公司董事会要求销售部门根据市场调查,找出公司生产的牙膏销售量与销售价格、广告投入等之间的关系,从而预测出在不同价格和广告费用下的销售量。
为此,销售部的研究人员收集了过去30个销售周期(每个销售周期为4周)公司生产的牙膏的销售量、销售价格、投入的广告费用,以及同期其它厂家生产的同类牙膏的市场平均销售价格,见表1-1(其中价格差指其它厂家平均价格与公司销售价格之差)。
试根据这些数据建立一个数学模型,分析牙膏销售量与其它因素的关系,为制订价格策略和广告投入策略提供数量依据表1-1牙膏销售量与销售价格、广告费用等数据一、问题重述根据过去30个销售周期(每个销售周期为4周)公司生产的牙膏的销售量、销售价格、投入的广告费用,以及同期其它厂家生产的同类牙膏的市场平均销售价格,见表1-1。
根据这些数据建立一个数学模型,分析牙膏销售量与其它因素的关系,为制订价格策略和广告投入策略提供数量依据二、问题分析由于牙膏是生活必需品,对大多属顾客来说,在购买同类产品的牙膏是更多地会在意不同品牌之间的价格差异,而不是它们的价格本身。
因此,在研究各个因素对销量的影响时,用价格差代替公司销售价格和其他厂家平均价格更为合适。
三、模型假设1.画出牙膏销售量与价格差,公司投入的广告费用的散点图2.由散点图确定两个函数模型,再由这两个函数模型解出回归模型3.对模型进行改进,添加新的条件确定更好的回归模型系数,得到新的回归模型4.对模型进一步改进,确定最终的模型四、符号约定牙膏销售量为y,其他厂家平均价格和公司销售价格之差(价格差)为x1,公司投入的广告费用为x2,其他厂家平均价格和公司销售价格分别为x3和x4,x1=x3-x4。
基于上面的分析,我们仅利用1x和2x来建立y的预测模型。
五、模型的建立和求解1.基本模型利用表1-1的数据用matlab 作出y 与x1的散点图(图1-1),y 与x2的散点图(图1-2) 代码如下:x1=[-0.05 0.25 0.6 0 0.25 0.2 0.15 0.05 -0.15 0.15 0.2 0.1 0.4 0.45 0.35 0.3 0.5 0.5 0.4 -0.05 -0.05 -0.1 0.2 0.1 0.5 0.6 -0.05 0 0.05 0.55];x2=[5.5 6.75 7.25 5.5 7 6.5 6.75 5.25 5.25 6 6.5 6.25 7 6.9 6.8 6.8 7.1 7 6.8 6.5 6.25 6 6.5 7 6.8 6.8 6.5 5.75 5.8 6.8];y=[7.38 8.51 9.52 7.5 9.33 8.28 8.75 7.87 7.1 8 7.89 8.15 9.1 8.86 8.9 8.87 9.26 9 8.75 7.95 7.65 7.27 8 8.5 8.75 9.21 8.27 7.67 7.93 9.26];A1=polyfit(x1,y,1); yy1=polyval(A1,x1); A2=polyfit(x2,y,2); x5=5:0.05:7.25; yy2=polyval(A2,x5);subplot(1,2,1);plot(x1,y,'o',x1,yy1); title('图1 y 对x1的散点图'); subplot(1,2,2);plot(x2,y,'o',x5,yy2); title('图2 y 对x2的散点图');图(1-1)与图(1-2)从图1可以发现,随着1x 的增加,y 的值有比较明显的线性增长趋势,图中的直线是用线性模型:011y x ββε=++(1)拟合的(其中ε是随机误差)。
数学建模有趣的例子

数学建模有趣的例子
1. 嘿,你知道吗?数学建模能帮我们规划最优的快递配送路线呢!就像给快递小哥设计一条超级捷径,让包裹能最快到达我们手中。
这是不是很有趣呀?
2. 哇塞,数学建模还可以用来模拟传染病的传播呢!就如同解开一个神秘疾病扩散的谜团,太奇妙了吧。
3. 哎呀,想想看,用数学建模来优化城市交通信号灯的时间安排,这不就像是给城市的交通脉络做了一次精心梳理嘛,多有意思啊!
4. 嘿,数学建模甚至能帮助农民伯伯确定最佳的种植布局呢!是不是感觉像给田地施了一次神奇的魔法呀。
5. 哇哦,通过数学建模来分析股票的走势,那不就像是在股海里找到正确的航向嘛,这可太引人入胜啦!
6. 天哪,数学建模可以帮助消防员确定最佳的救援路线,这简直就是给生命开辟快速通道啊,太厉害了吧!
7. 哈哈,数学建模能用来给超市设计最合理的货架摆放呢!这不就像是给商品们找到了最舒适的家嘛。
8. 你想想,利用数学建模来预测天气变化,岂不是像拥有了提前知晓大自然秘密的超能力,有趣极了呀!
我觉得数学建模真的是充满了无限可能和乐趣,它在各个领域都能发挥出神奇的作用,让我们的生活变得更加美好和高效。
数学建模解决实际问题的实践案例

数学建模解决实际问题的实践案例数学建模是一种将实际问题进行抽象、建模、求解、验证的一种方法,可以解决各种各样的实际问题。
实践中,数学建模已经发展成为一门独立的学科,吸引着越来越多的学生和专业人士关注和参与。
本文将介绍数学建模解决实际问题的一些实践案例,以期为学习和实践的人提供一些启示和借鉴。
1. 预测疫情发展趋势随着全球新冠疫情的爆发,各国政府和公众非常关注疫情的发展趋势。
数学建模可以帮助预测疫情的传播和爆发趋势,为政府制定应对措施提供参考和依据。
一个成功的例子是2020年初,中国各大高校和研究机构联合开展的“新冠疫情数学建模竞赛”,其中多个团队使用了数学模型预测了疫情的发展趋势,并对实际情况进行调整和优化,取得了很好的成果。
2. 优化交通运输系统交通拥堵是城市发展的一大难题,为了解决这个问题,可以使用数学模型优化交通运输系统。
例如,瑞典斯德哥尔摩的交通问题比较突出,瑞典皇家理工学院的研究人员使用数学模型建立了一个交通仿真系统,可以模拟不同的交通场景,优化交通路线和信号灯的配时,从而减少拥堵和排放污染物。
3. 改善医疗服务质量医疗服务是人民生活的重要组成部分,如何优化医疗服务质量是医疗行业面临的重要问题。
数学模型可以帮助医疗机构优化医疗流程和资源配置,提高医疗服务效率和质量。
例如,美国佛罗里达州的一家医疗中心就使用了数学模型对医生的看诊时间进行优化,从而减少了等待时间和排队人数,提高了医疗服务质量和满意度。
4. 提高金融风险管理能力金融风险管理是金融机构必须面对的问题之一,如何预测和管理风险是保证金融行业稳定发展的关键。
数学模型可以帮助金融机构进行风险评估和预测,制定风险管理策略。
例如,中国银监会就使用了数学模型对风险指标进行监测和预测,从而提高了银行业的风险管理能力和金融稳定性。
总的来说,数学建模可以解决各种各样的实际问题,这些案例只是冰山一角。
数学建模不仅有理论上的重要性,更有实践上的应用价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1.1 求解线性方程组命令如下:>> a=[2,3,-1;8,2,3;45,3,9];>> b=[2;4;23];>> x=inv(a)*bx =0.55310.2051-0.2784例1.2 绘制正弦曲线和余弦曲线。
命令如下:>> x=[0:0.5:360]*pi/180;>> plot(x,sin(x),x,cos(x)) ;例1.3 输入10个学生的成绩并对成绩按升序排序。
>>g=[45 56 34 24 76 89 32];>>f=sort(g)f =24 32 34 45 56 76 89例1.4 设有常微分方程初值问题,试求其数值解,并与精确解相比较。
(1)建立函数文件funt.m:function yp=funt(t,y)yp=(y^2-t-2)/4/(t+1);(2)求解微分方程:t0=0;tf=10;y0=2;[t,y]=ode23('funt',[t0,tf],y0);y1=sqrt(t+1)+1;t'例2.1 计算表达式的值,并将结果赋给变量x,然后显示出结果。
在MA TLAB命令窗口输入命令:>>x=(5+cos(47*pi/180))/(1+sqrt(7)-2*i) %计算表达式的值2.2 A=[1 2 3;4 5 6;7 8 9]A =1 2 34 5 67 8 9例2.3 分别建立3×3、3×2和与矩阵A同样大小的零矩阵。
(1)建立一个3×3零矩阵:zeros(3)>> zeros(3)ans =0 0 00 0 00 0 0)建立一个3×2零矩阵:zeros(3,2)>> zeros(3,2)ans =0 00 00 0(3)建立与矩阵A同样大小零矩阵:zeros(size(A))>> A=[2 4 7 5;7 8 9 10];zeros(size(A))ans =0 0 0 00 0 0 0例2.4 产生5阶随机方阵A,其元素为[10,90]区间的随机整数,然后判断A的元素是否能被3整除。
(1) 生成5阶随机方阵A。
>> A=fix((90-10+1)*rand(5)+10)A =86 71 59 42 1428 46 74 85 3859 11 84 84 7549 76 69 43 1082 46 24 82 21(2) 判断A的元素是否可以被3整除。
>> P=rem(A,3)==0P =0 0 0 1 00 0 0 0 00 0 1 1 10 0 1 0 00 0 1 0 1例3.1 建立一个命令文件将变量a,b的值互换,然后运行该命令文件。
首先建立命令文件并以文件名exch.m存盘:clear;a=1:10; b=[11,12,13,14;15,16,17,18];c=a;a=b;b=c;abanta =11 12 13 1415 16 17 18b =1 2 3 4 5 6 7 8 9 10例3.2 建立一个函数文件将变量a,b的值互换,然后在命令窗口调用该函数文件。
首先建立函数文件fexch.m:function [a,b]=fexch(a,b) % exchc=a;a=b;b=c;clear;x=1:10; y=[11,12,13,14;15,16,17,18];[x,y]=fexch(x,y)例3.5 输入一个字符,若为大写字母,则输出其后继字符,若为小写字母,则输出其前导字符,若为数字字符则输出其对应的数值,若为其他字符则原样输出。
c=input('请输入一个字符','s');if c>='A' & c<='Z'disp(setstr(abs(c)+1));elseif c>='a'& c<='z'disp(setstr(abs(c)-1));elseif c>='0'& c<='9'disp(abs(c)-abs('0'));elsedisp(c);end例3.6 某商场对顾客所购买的商品实行打折销售,已知打折标准为:商品价格小于200元时,折扣率为0;商品价格大于或等于200元且小于500时,折扣率为0.03;商品价格大于或等于500且小于1000元时,折扣率为0.05;商品价格大于或等于1000且小于2500元时,折扣率为0.08;商品价格大于或等于2500且小于5000元时,折扣率为0.1;商品价格大于或等于5000元时,折扣率为0.14;求所售商品的实际销售价格。
>>price=input('请输入商品价格');switch fix(price/100)case {0,1}rate=0;case {2,3,4}rate=3/100;case num2cell(5:9)rate=5/100;case num2cell(10:24)rate=8/100;case num2cell(25:49)rate=10/100;otherwiserate=14/100;endprice=price*(1-rate)请输入商品价格890price =845.5000例3.7 矩阵乘法运算要求两矩阵的维数相容,否则会出错。
先求两矩阵的乘积,若出错,则自动转去求两矩阵的点乘。
程序如下:A=[1,2,3;4,5,6]; B=[7,8,9;10,11,12];tryC=A*B;catchC=A.*B;endClasterr %显示出错原因C =7 16 2740 55 72ans =Error using ==> *Inner matrix dimensions must agree.例3.8 已知求y 的表达式,当n=100时,求y 的值。
程序如下y=0;n=100;for i=1:ny=y+1/i/i;endy补充知识: 在实际MATLAB 编程中,为提高程序的执行速度,常用向量运算来代替循环操作:n=100; i=1:n;f=1./i.^2;y=sum(f)例3.9 求定积分程序如下:a=0;b=3*pi;n=1000; h=(b-a)/n;x=a:h:b; f=exp(-0.5*x).*sin(x+pi/6);for i=1:ns(i)= (f(i)+f(i+1))*h/2;ends=sum(s) 补充知识:事实上,MATLAB 提供了有关数值积分的标准函数,实际应用中可直接调用这些函数求数值积分例3.10 已知5个学生4门功课的成绩,求每名学生的总成绩。
程序如下:1320()sin()6x e x dx ππ-+⎰s=0;a=[65,76,56,78;98,83,74,85;76,67,78,79;98,58,42,73;67,89,76,87]for k=as=s+k;enddisp(s');结果为:a =65 76 56 7898 83 74 8576 67 78 7998 58 42 7367 89 76 87275 340 300 271 319 例3.11 产生一个长度为6的调和数列。
程序如下:X=zeros(1,6);i=1;while i<=6X(i)=1/i;i=i+1;endformat rat %使用分数表示数值disp(X例3.12 用while语句实现例3.8。
程序如下:y=0; i=1;while 1f=1/i/i;y=y+f;if i==100break;endi=i+1;endy例3.13 用筛选法求某自然数范围内的全部素数。
程序如下:m=input('m=');p=2:m;for i=2:sqrt(m)n=find(rem(p,i)==0&p~=i);p(n)=[];endp输入一个值为:m=100p =Columns 1 through 52 3 5 7 11Columns 6 through 1013 17 19 23 29Columns 11 through 1531 37 41 43 47Columns 16 through 2053 59 61 67 71Columns 21 through 2573 79 83 89 97例3.14 编写函数文件求半径为r的圆的面积和周长。
函数文件如下:function [s,p]=fcircle(r)%CIRCLE calculate the area and perimeter of a circle of radii r%r 圆半径%s 圆面积%p 圆周长%2001年7月30日编s=pi*r*r;p=2*pi*r;将以上函数文件以文件名fcircle.m存入c:\matlabr11\work下,然后在MA TLAB命令窗口调用该函数:[s,p]=fcircle(10)s =13823/44p =7100/113例3.15 利用函数文件,实现直角坐标(x,y)与极坐标(ρ,θ)之间的转换。
函数文件tran.m:function [rho,theta]=tran(x,y)rho=sqrt(x*x+y*y);theta=atan(y/x);调用tran.m的命令文件main1.m:x=input('Please input x=:');y=input('Please input y=:');[rho,the]=tran(x,y);rhothe例3.17 nargin用法示例。
函数文件examp.m:function fout=examp(a,b,c)if nargin==1fout=a;elseif nargin==2fout=a+b;elseif nargin==3fout=(a*b*c)/2;end命令文件mydemo.m:x=[1:3];y=[1;2;3];examp(x)examp(x,y')examp(x,y,3)例3.18 全局变量应用示例。
先建立函数文件wadd.m,该函数将输入的参数加权相加。
function f=wadd(x,y)global ALPHA BETAf=ALPHA*x+BETA*y;在命令窗口中输入:global ALPHA BETAALPHA=1;BETA=2;s=wadd(1,2)。
