河北省2019届中考数学系统复习第一单元数与式第1讲实数及其运算课件
2019届冀教版中考《第一单元数与式第1讲实数》知识梳理
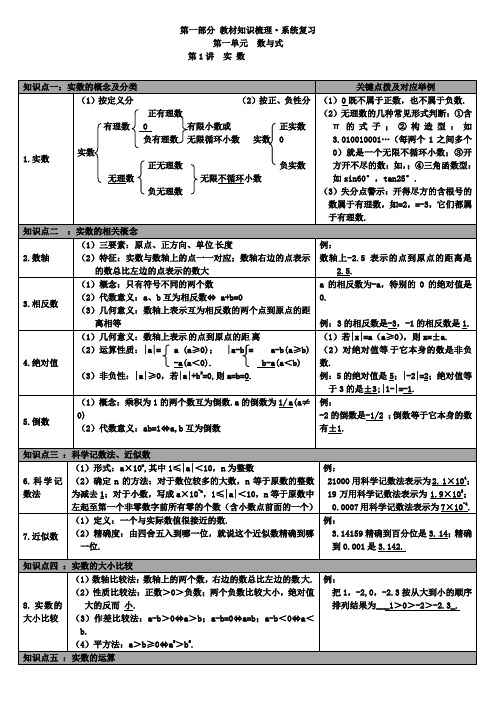
第一部分教材知识梳理·系统复习第一单元数与式第1讲实数:实数的相关概念)三要素:原点、正方向、单位的点到原点的距离)对绝对值等a(a用科学记数法表示为2.13.14右边的数总比左边的数大算术平方根2019-2020学年数学中考模拟试卷一、选择题1.实数a ,b ,c 在数轴上的对应点的位置如图所示,则正确的结论是( )A .a >bB .a =b >0C .ac >0D .|a|>|c|2.不等式组111324(1)2()x x x x a -⎧-<-⎪⎨⎪--⎩…有3个整数解,则a 的取值范围是( ) A .﹣6≤a<﹣5B .﹣6<a≤﹣5C .﹣6<a <﹣5D .﹣6≤a≤﹣53.已知a 是方程x 2﹣3x ﹣2=0的根,则代数式﹣2a 2+6a+2019的值为( ) A .2014B .2015C .2016D .20174.如图,AB AC 、都是圆O 的弦,OM AB ON AC ⊥⊥,,垂足分别为M N 、,如果MN =,那么BC =( )A .3BC.D.5.如图,在锐角ABC 中,延长BC 到点D ,点O 是AC 边上的一个动点,过点O 作直线MNBC ,MN 分别交ACB ∠、ACD ∠的平分线于E ,F 两点,连接AE 、AF .在下列结论中.①OE OF =;②CE CF =;③若12CE =,5CF =,则OC 的长为6;④当AO CO =时,四边形AECF 是矩形.其中正确的是( )A .①④B .①②C .①②③D .②③④6.如图,直线AB :y =12x +1分别与x 轴、y 轴交于点A 、B ,直线CD : y =x +b 分别与x 轴、y 轴交于点C 、D .直线AB 与CD 相交于点P ,已知S △ABD =4,则点P 的坐标是 ( )A .(3,4)B .(8,5)C .(4,3)D .(12,54) 7.在正方形、矩形、菱形、平行四边形中,其中是中心对称图形的个数为( ) A .1B .2C .3D .48.下列二次根式中是最简二次根式的是( ) ABCD9.我国古代数学著作《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余4.5尺,将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”,设绳子长x 尺,木条长y 尺,根据题意所列方程组正确的是( )A .x y 4.51x y 12-=⎧⎪⎨-=⎪⎩B .x y 4.51y x 12-=⎧⎪⎨-=⎪⎩C .x y 4.51y x 12+=⎧⎪⎨-=⎪⎩D .x y 4.51x y 12-=⎧⎪⎨-=⎪⎩10.若2(2)a -+0,则(a+b )2011的值是( ) A .﹣2011B .2011C .﹣1D .111.下列图形中,可以看作是中心对称图形的是( )A. B .C. D .12.已知命题A :“若aa =”.在下列选项中,可以作为“命题A 是假命题”的反例的是( ) A .a =1 B .a =0C .a =﹣1﹣k (k 为实数)D .a =﹣1﹣k 2(k 为实数)二、填空题13.若22116,10,22x y xy x y xy +==+=则_____. 14.分解因式:ax 2﹣ax =_____.15.关于x 的一元二次方程(a-1)x 2+x+(a 2-1)=0的一个根是0,则a 的值是________.16.某学校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元,至少买一个排球,在购买资金恰好用尽的情况下,购买方案有_____种.17.如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是_____.18.因式分解__________.三、解答题19.图①、图②均是3×2的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上.在图①、图②给定的网格中各画一个△APC,使点P在线段AB上,点C为格点,且∠APC的正切值为2.要求:(1)图①中的△APC为直角三角形,图②中的△APC为锐角三角形.(2)只用无刻度的直尺,保留适当的作图痕迹.20.某校为了解本校九年级学生的数学作业完成情况,将完成情况分为四个等级:随机对该年级若干名学生进行了调查,然后把调查结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:(1)补全条形统计图;(2)该年级共有700人,估计该年级数学作业完成等级为D等的人数;(3)在此次调查中,有甲、乙、丙、丁四个班的学生数学作业完成表现出色,现决定从这四个班中随机选取两个班在全校举行一次数学作业展览,请用画树状图或列表的方法,求恰好选到甲、乙两个班的概率.21.如图,OA、OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连接AC并延长交⊙O于D,过点D 作圆的切线交OB的延长线于E,已知OA=6.(1)求证:∠ECD=∠EDC;(2)若BC=2OC,求DE长;(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.22.已知:如图,在矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交AD、BC于点E,F,求证:BE=DF.23.乒乓球是我国的国球,比赛采用单局11分制,是一种世界流行的球类体育项目,比赛分团体、单打、双打等数种在某站公开赛中,某直播平台同时直播4场男单四分之一比赛,四场比赛的球桌号分别为“T1”、“T2”、“T3”、“T4”(假设4场比赛同时开始),小宁和父亲准备一同观看其中的某一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“1、“2”、“3”、“4”的四张卡片(除数字不同外,其余均相同,数字“1”、“2”、“3”、“4”分别对应球桌号(“T1”、“T2”、“T3”、“T4”(背面朝上洗匀,父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛(1)下列事件中属于必然事件的是A.抽到的是小宁最终想要看的一场比赛的球桌号B.抽到的是父亲最终想要看的一场比赛的球桌号C.小宁和父亲抽到同一个球桌号D.小宁和父亲抽到的球桌号不一样(2)用列表法或树状图法求小宁和父亲最终观看“T4”球桌比赛的概率24.如图,在△ABC中,E为BC边上一点,以BE为直径的AR半圆D与AC相切于点F,且EF∥AD,AD交半圆D于点G.(1)求证:AB是半圆D的切线;(2)若EF=2,AD=5,求切线长AB.25.企业举行“爱心一日捐”活动,捐款金额分为五个档次,分别是50元,100元,150元,200元,300元.宣传小组随机抽取部分捐款职工并统计了他们的捐款金额,绘制成两个不完整的统计图,请结合图表中的信息解答下列问题:(1)宣传小组抽取的捐款人数为人,请补全条形统计图;(2)统计的捐款金额的中位数是元;(3)在扇形统计图中,求100元所对应扇形的圆心角的度数;(4)已知该企业共有500人参与本次捐款,请你估计捐款总额大约为多少元?【参考答案】***一、选择题二、填空题13.3014.ax(x﹣1).15.-116.317.1618.三、解答题19.见解析.【解析】【分析】根据正切函数的定义,结合网格特点作图即可.【详解】解:如图所示,图①中的△APC为直角三角形,图②中的△APC为锐角三角形.由题意可知,是DE,AB 的中点,∴AP=2 ,PE=2, ∴由勾股定理的逆定理可知,∠AEP=90°,且tan ∠APC=2. 【点睛】本题主要考查作图﹣应用与设计作图,解题的关键是掌握正切函数的定义. 20.(1)详见解析;(2)56;(3)16【解析】 【分析】(1)根据A 等学生人数除以它所占的百分比求得总人数,然后乘以B 等所占的百分比求得B 等人数,从而补全条形图;(2)用该年级学生总数乘以足球测试成绩为D 等的人数所占百分比即可求解; (3)利用树状图法,将所有等可能的结果列举出来,利用概率公式求解即可. 【详解】(1)总人数为14÷28%=50人, B 等人数为50×40%=20人. 条形图补充如下:(2)该年级足球测试成绩为D 等的人数为700×450=56(人). 故答案为56; (3)画树状图:共有12种等可能的结果数,其中选取的两个班恰好是甲、乙两个班的情况占2种,所以恰好选到甲、乙两个班的概率是16.【点睛】本题考查了列表法与树状图法:通过列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.也考查了样本估计总体、扇形统计图和条形统计图.21.(1)证明见解析;(2)8;(3)39π+ .【解析】【分析】(1)连接OD,由切线的性质得出∠EDC+∠ODA=90°,由等腰三角形的性质得出∠ODA=∠OAC,得出∠EDC=∠ACO,即可得出结论;(2)设DE=x,则CE=DE=x,OE=2+x,在Rt△ODE中,由勾股定理得出方程,解法长即可;(3)过点D作DF⊥AO交AO的延长线于F,当∠A=15°时,∠DOF=30°,得出DF=12OD=12OA=3,∠DOA=150°,S弓形ABD=S扇形ODA-S△AOD=15π-9,当∠A=30°时,∠DOF=60°,S弓形ABD=S扇形ODA-S△AOD=12π果.【详解】(1)证明:连接OD,如图1所示:∵DE是⊙O的切线,∴∠EDC+∠ODA=90°,∵OA⊥OB,∴∠ACO+∠OAC=90°,∵OA、OB是⊙O的两条半径,∴OA=OB,∴∠ODA=∠OAC,∴∠EDC=∠ACO,∵∠ECD=∠ACO,∴∠ECD=∠EDC;(2)∵BC=2OC,OB=OA=6,∴OC=2,设DE=x,∵∠ECD=∠EDC,∴CE =DE =x , ∴OE =2+x , ∵∠ODE =90°, ∴OD 2+DE 2=OE 2, 即:62+x 2=(2+x )2, 解得:x =8, ∴DE =8;(3)解:过点D 作DF ⊥AO 交AO 的延长线于F ,如图2所示:当∠A =15°时,∠DOF =30°, ∴DF =12OD =12OA =3,∠DOA =150°, S 弓形ABD =S 扇形ODA ﹣S △AOD =21506360π⋅﹣12OA•DF=15π﹣12×6×3=15π﹣9,当∠A =30°时,∠DOF =60°,∴DF OA =DOA =120°,S 弓形ABD =S 扇形ODA ﹣S △AOD =21206360π⋅﹣12OA•DF=12π﹣1212π﹣,∴当∠A 从15°增大到30°的过程中,AD 在圆内扫过的面积=(15π﹣9)﹣(12π﹣)=3π﹣9. 【点睛】本题考查了切线的性质、圆周角定理、直角三角形的性质、等腰三角形的性质、扇形面积的计算、勾股定理等知识;本题综合性强,熟练掌握切线的性质和勾股定理是解题的关键. 22.见解析. 【解析】 【分析】由矩形可得∠ABD=∠CDB ,结合BE 平分∠ABD,DF 平分∠BDC 得∠EBD=∠FDB,即可知道BF ∥DF ,根据AD ∥BC 即可证明 【详解】证明:∵四边形ABCD 是矩形, ∴AB ∥DC 、AD ∥BC ,∴∠ABD=∠CDB,∵BE平分∠ABD、DF平分∠BDC,∴∠EBD=12∠ABD,∠FDB=12∠BDC,∴∠EBD=∠FDB,∴BE∥DF,又∵AD∥BC,∴四边形BEDF是平行四边形,∴BE=DF.【点睛】此题考查了矩形的性质和平行四边形的判断与性质,解题关键在于利用好矩形性质证明BE∥DF23.(1)D;(2)1 3【解析】【分析】(1)根据随机随机和必然事件的定义进行判断;(2)画树状图展示所有12种等可能的结果数,找出小宁和父亲最终观看“T4”球桌比赛的结果数,然后根据概率公式求解.【详解】(1)因为父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,所以小宁和父亲抽到的球桌号不一样,它为必然事件.故选D;(2)画树状图为:共有12种等可能的结果数,其中小宁和父亲最终观看“T4”球桌比赛的结果数为4,所以小宁和父亲最终观看“T4”球桌比赛的概率41 123 ==.【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A 或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.24.(1)详见解析;(2)【解析】【分析】(1)连接DF,根据切线的性质得到DF⊥AC,根据平行线的性质得到∠EFD=∠ADF,∠FED=∠ADB,由等腰三角形的性质得到∠EFD=∠FED,求得∠ADF=∠ADB,根据全等三角形的性质得到∠ABD=∠AFD=90°,于是得到结论;(2)根据相似三角形的判定和性质定理得到25CE CF EFCD CA AD===,设CE=2x,于是得到CD=5x,DF=DE=3x,根据勾股定理得到CF=4x,于是得到AF=6x,在Rt△ADF中根据勾股定理即可得到结论.【详解】(1)证明:连接DF,∵AC与半圆D相切于点F,∴DF⊥AC,∴∠AFD=90°,∵EF∥AD,∴∠EFD=∠ADF,∠FED=∠ADB,又∵DF=DE,∴∠EFD=∠FED,∴∠ADF=∠ADB,在△ABD与△AFD中DB DFADB ADF AD AD=⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△AFD (SAS),∴∠ABD=∠AFD=90°,∴AB是半圆D的切线;(2)解:∵EF∥AD,∴△CFE∽△CAD,∴25 CE CF EFCD CA AD===,设CE=2x,∴CD=5x,DF=DE=3x,∴在Rt△DFC中,由勾股定理得CF=4x,∴AF=6x,在Rt△ADF中,(6x)2+(3x)2=52,解得x∴AB=AF=6x=【点睛】本题考查了切线的判定和性质,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理,平行线的性质,熟练正确切线的判定定理是解题的关键.25.(1)50,见解析;(2)150;(3)72°;(4)84000(元).【解析】【分析】(1)根据题意即可得到结论;求得捐款200元的人数即可补全条形统计图;(2)根据中位数的定义即可得到结论;(3)用周角乘以100元所占的百分比即可求得圆心角;(4)根据题意即可得到结论.【详解】(1)12÷24%=50(人),捐款200元的人数为:50-4-10-12-6=18(人),补全条形统计图,(2)第25,26名捐款均为150元,故中位数为:150元;(3)1050×360°=72°.(4)150(50×4+100×10+150×12+200×18+300×6)×500=84000(元).【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.2019-2020学年数学中考模拟试卷一、选择题1.如图,点A、B、C、D在⊙O上,∠AOC=120°,点B是弧AC的中点,则∠D的度数是( )A.60°B.35°C.30.5°D.30°BD=,将AOB绕其对称中心旋转180︒. 2.如图,已知平行四边形的对角线交于点.2cm则点所转过的路径长为( )km.A.B.C.D.3.如图,抛物线y=ax2+bx+c(a>0)过原点O,与x轴另一交点为A,顶点为B,若△AOB为等边三角形,则b的值为()A. B.﹣ C.﹣ D.﹣4.下列计算结果正确的是()A.(﹣a)2•a6=﹣a8B.(m﹣n)(m2+mn+n2)=m3﹣n3C.(﹣2b2)3=﹣6b6D.5.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,C.现有下面四个推断:①抛物线开口向下;②当x=-2时,y取最大值;③当m<4时,关于x的一元二次方程ax2+bx+c=m必有两个不相等的实数根;④直线y=kx+c(k≠0)经过点A,C,当kx+c> ax2+bx+c时,x的取值范围是-4<x<0;其中推断正确的是()A .①②B .①③C .①③④D .②③④6.在数轴上表示不等式组10420x x +>⎧⎨-≥⎩的解集,正确的是A .B .C .D .7.如图,在ABC ∆中,8AB =,6AC =,O 为ABC ∆角平分线的交点,若ABO ∆的面积为20,则ACO ∆的面积为是( )A .12B .15C .16D .188.对于平面图形上的任意两点P ,Q ,如果经过某种变换得到新图形上的对应点P′,Q′,保持PQ=P′Q′,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是( )A .平移B .旋转C .轴对称D .位似 9.扇形的弧长为20πcm ,面积为240πcm 2,那么扇形的半径是( )A .6cmB .12cmC .24cmD .28cm10.在平面直角坐标系中,已知点A (﹣4,2),B (﹣6,﹣4),以原点O 为位似中心,相似比为12,把△ABO 缩小,则点A 的对应点A′的坐标是( )A .(﹣2,1)B .(﹣8,4)C .(﹣8,4)或(8,﹣4)D .(﹣2,1)或(2,﹣1) 11.方程24222x x x x =-+-- 的解为( ) A .2 B .2或4 C .4 D .无解12.方程kx 2﹣2x ﹣1=0有实数根,则k 的取值范围是( )A.k≠0且k≥﹣1B.k≥﹣1C.k≠0且k≤﹣1D.k≠0或k≥﹣1 二、填空题13.当x 为_____时,312x -的值为﹣1. 14.一个不透明的盒子中装有6个红球,3个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,则摸到的不是红球的概率为__________15.如图,▱ABCD 中,点E 是边BC 上一点,AE 交BD 于点F ,若BE =2,EC =3,△BEF 的面积是1,则▱ABCD 的面积为_____.16.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为_____.17.分式方程的解是_____.18.如图,A ,B 是反比例函数y=在第一象限内的图象上的两点,且A ,B 两点的横坐标分别是2和4,则△OAB 的面积是_____.三、解答题19.如图,直线l :33y x =-+与x 轴、y 轴分别相交于A 、B 两点,抛物线22+4(0)y ax ax a a =-+<经过点B.(1)求该抛物线的函数表达式;(2)已知点M 是抛物线上一动点,并且点M 在第一象限内,连接AM 、BM.设点M 的横坐标为m ,△ABM 的面积为S ,求S 与m 的函数表达式,并求出S 的最大值;(3)在(2)的条件下,,以MA 、MB 为邻边作平行四边形MBNA①当平行四边形MBNA 面积最大时,点N 的坐标为____②当平行四边形MBNA 面积为整数时,点M 的个数为___20.如图,直线y =﹣x+4分别交x 轴、y 轴于A 、C 两点,抛物线y =﹣x 2+mx+4经过点A ,且与x 轴的另一个交点为点B .连接BC ,过点C 作CD ∥x 轴交抛物线于点D(1)求抛物线的函数表达式;(2)若点E是抛物线上的点,求满足∠ECD=∠BCO的点E的坐标;(3)点M在y轴上且位于点C上方,点N在直线AC上,点P为第一象限内的抛物线上一点,若以点C、M、N、P为顶点的四边形是菱形,求菱形的边长.211tan602|︒-+-.22.如图1,是小明荡秋千的侧面示意图,秋千链长AB=5m(秋千踏板视作一个点),静止时秋千位于铅垂线BC上,此时秋千踏板A到地面的距离为0.5m.(1)当摆角为37°时,求秋千踏板A与地面的距离AH;(参考数据:si n37°≈0.6,cos37°≈0.8,tan37°≈0.75)(2)如图2,当秋千踏板摆动到点D时,点D到BC的距离DE=4m;当他从D处摆动到D'处时,恰好D'B ⊥DB,求点D'到BC的距离.23.在平面直角坐标系中,点O为原点,点A的坐标为(﹣8,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.(1)如图2,若α=45°,OE=OA,求直线EF的函数表达式;(2)如图3,若α为锐角,且tanα=12,当EA⊥x轴时,正方形对角线EG与OF相交于点M,求线段AM的长;(3)当正方形OEFG的顶点F落在y轴正半轴上时,直线AE与直线FG相交于点P,是否存在△OEP的两:1?若存在,求出点P的坐标;若不存在,试说明理由.24.解不等式组31112x xx+≥-⎧⎨-≤⎩①②,请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得_________;(Ⅱ)解不等式②,得_________;(Ⅲ)把不等式①和②的解集在数轴上表示出来:(Ⅳ)原不等式组的解集为_________.25.为响应国家的一带一路经济发展战略,树立品牌意识,我市质检部分别对A 、B 、C 、D 四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C 厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图:(1)抽查D 厂家的零件为 件,扇形统计图中D 厂家对应的圆心角为 度;(2)抽查C 厂家的合格率零件为 件,并将图1补充完整;(3)通过计算说明A 、C 两厂家谁的合格率更高?【参考答案】***一、选择题二、填空题13.﹣13 14.2515.35216.120°17.x=18.3三、解答题19.(1)223y x x =-++;(2)21522s m m =-+ ,254;(3)①(35-,24 )②12 【解析】【分析】(1)求出A 、B 两点坐标,把B 点坐标代入抛物线的解析式即可解決问题.(2)如图1中,连接OM,设M(m,-m 2+2m+3),根据S=S △BOM+ S △AOM-S △AOB 计算即可.再利用次函数的性质求出最大值(3)①如图2中,设N(x,y),根据中点坐标公式列出方程组即可解决问题.②如图3中,平行四边形AMBN 的面积为S=2 S △ABM=-m 2+5m,求出S 的范围,画出图象即可解决问题【详解】(1):直线:y=-3x+3与x 轴、y 轴分别相交于A,B 两点,∴A(1,0),B(0,3),把点B(0,3)代入y=ax 2-2ax+a+4得a=-1∴抛物线的解析式为y=-x 2+2x+3(2)如图1中,连接OM,设M(m,-m 2+2m+3)・∴S=S △BOM+S △AOM- S △AOB=221131531(23).(022222m m m m m +-++-=-+<m <3) ∵S=22151525()22224m m m -+=--+∵-12<0 ∴m=52 时,S 有最大值为254(3)①如图2中,设N(x,y)∵当△MAB 面积最大时,平行四边形MBNA 面积最大,由(2)可知,M (5724, ),A(1,0),B(0,3)∵四边形AMBN 是平行四边形,∴AB 与MN 互相平分510222703422x y ⎧+⎪+=⎪⎪⎨⎪++⎪=⎪⎩ ,解得3254x y ⎧=-⎪⎪⎨⎪=⎪⎩ , ∴点N 坐标(-3524,)故答案为(-3524,)②如图3中∵平行四边形AMBN 的面积为S=2· S△ABM=-m 2+5m∵a=-1<0∴S 有最大值=254 ∴0<S<254∵S 是整数,∴S=1或2或3或4或5或6由图象可知对应的m 的值有12个故答案为12【点睛】此题为二次函数综合题,考查了三角形面积,平行四边形面积,解题关键在于把已知点代入到方程求参数20.(1)y =﹣x 2+3x+4;(2)E 的坐标为E 1175,416⎛⎫⎪⎝⎭或1351,416⎛⎫ ⎪⎝⎭;(3)﹣2. 【解析】【分析】(1)利用直线方程求得点A 、C 的坐标,根据点A 、C 坐标求得抛物线解析式;(2)分点E 在CD 上方、点E 在CD 下方两种情况,分别求解即可;(3)分CM 为菱形的一条边、CM 为菱形的对角线两种情况,分别求解即可.【详解】解:(1)y =﹣x+4,令x =0,则y =4,令y =0,则x =4,则点A、C的坐标分别为(4,0)、(0,4),将点A的坐标代入抛物线的表达式并解得:m=3,故抛物线的表达式为:y=﹣x2+3x+4①,令y=0,则x=﹣1或4,故点B(﹣1,0);(2)①当点E在CD上方时,tan∠BCO=14 OBOC,则直线CE的表达式为:y=14x+4②,联立①②并解得:x=0或114(舍去0),则点E(114,7516);②当点E在CD下方时,同理可得:点E′(134,5116);故点E的坐标为E(114,7516)或(134,5116);(3)①如图2,当CM为菱形的一条边时,过点P作PQ∥x轴,∵OA=OC=4,∴∠PMQ=∠CAO=45°,设点P(x,﹣x2+3x+4),则PM PQ x,C、M、N、P为顶点的四边形是菱形,则PM=PN,x=﹣x2+3x+4,解得:x=0或4(舍去0),x=﹣2;②如图3,当CM 为菱形的对角线时,同理可得:菱形边长为;故:菱形边长为﹣2.【点睛】本题考查的是二次函数综合运用,涉及到一次函数、菱形基本性质等,要注意分类求解、避免遗漏. 21.12【解析】【分析】根据负整数指数幂和12【详解】原式=+12=12. 【点睛】本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,然后进行加减运算.也考查了负整数指数幂以及特殊角的三角函数值.22.(1)AH =1.5m ;(2)点D'到BC 的距离D′F=3m .【解析】【分析】(1)作AD ⊥BC ,在Rt △ABD 中,根据三角函数得到BD ,再根据线段的和差关系得到CD ,根据矩形的性质可求AH ;(2)作D′F⊥BC ,在Rt △BDE 中,根据勾股定理得到BE ,再根据全等三角形的判定和性质解答即可.【详解】(1)作AD ⊥BC 于D ,在Rt △ABD 中,BD =AB•cos37°=5×0.8=4(m ),CD =A′B+A′C﹣BD =5+0.5﹣5×0.8=1.5(m ),在矩形ADCH 中,AH =CD =1.5(m );(2)作D′F⊥BC 于E ,在Rt △BDE 中,BE3(m ),∵∠BD′F+∠FBD′=90°=∠FBD′+∠DBE ,∴∠BD′F=∠DBE ,在△BD′F 与△DBE 中,BFD DEB BD F DBE BD DB '''⎧∠=∠⎪∠=∠⎨⎪=⎩,∴△BD′F≌△DBE ,∴点D'到BC 的距离:D′F=BE =3(m ).【点睛】本题考查解直角三角形的应用、全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.23.(1)直线EF 的解析式为y =;(2)AM =(3)满足条件的点P 的坐标为(0,8),(﹣8,24),(﹣24,48).【解析】【分析】(1)过点E 作EH ⊥OA 于点H,进而求出点E 的坐标,再根据勾股定理求出OF 的值,然后利用待定系数法,即可求出直线EF 的解析式(2)作MN ⊥AM 交x 轴于点N,此时△AEM ≌△NOM,得到AE=ON=4,△AMN 是等腰直角三角形,即可求出AM 的长;(3)根据点F 落在y 轴正半轴上,通过改变正方形的边长,画出直线AE 与直线FG 相交的点P,并判断△OEP的其中两边之比能否为2:1,当△OEP :1时,再通过分类讨论确定出图形,根据图形性质,利用勾股定理、相似三角形、三角函数等知识求得点P 的坐标【详解】(1)∵OE =OA =8,α=45°,∴E(﹣,F(0,),设直线EF 的解析式为y =kx+b ,则有b b ⎧=⎪⎨-+=⎪⎩, 解得1k b =⎧⎪⎨=⎪⎩∴直线EF 的解析式为y =.(2)如图3中,作MH ⊥OA 于H ,MK ⊥AE 交AE 的延长线于K .在Rt△AEO中,tan∠AOE=12AEOA=,OA=8,∴AE=4,∵四边形EOGF是正方形,∴∠EMO=90°,∵∠EAO=∠EMO=90°,∴E、A、O、M四点共圆,∴∠EAM=∠EOM=45°,∴∠MAK=∠MAH=45°,∵MK⊥AE,MH⊥OA,∴MK=MH,四边形KAOM是正方形,∵EM=OM,∴△MKE≌△MHO,∴EK=OH,∴AK+AH=2AH=AE+EK+OA﹣OH=12,∴AH=6,∴AM=.(3)如图2中,设F(0,2a),则E(﹣a,a).∵A(﹣8,0),E(﹣a,a),∴直线AP的解析式为y=888a axa a+--,直线FG的解析式为y=﹣x+2a,由22424,84884a ay x a xa ay x a aa a y⎧-=-+=⎧⎪⎪⎪⎨⎨=++⎪⎪--⎩=⎪⎩解得,∴P(2244,44a a a a-+).①当POOE时,∴PO2=2OE2,则有:2222(4)(4)1616a a a a-++=4a2,解得a=4或﹣4(舍弃)或0(舍弃),此时P(0,8).②当POPE时,则有:2222(4)(4)1616a a a a-++=2[(22244+)44a a a aa a-++-()2],解得:a=4或12,此时P(0,8)或(﹣24,48),③当PE EO 时,[(22244+)44a a a a a a -++-()2]=4a 2, 解得a =8或0(舍弃),∴P(﹣8,24)综上所述,满足条件的点P 的坐标为(0,8),(﹣8,24),(﹣24,48).【点睛】本题考査了正方形的性质、等腰三角形的性质、勾股定理、待定系数法求函数解析式、解直角三角形、相似三角形的判定与性质,解题关键在于做辅助线24.(Ⅰ)1x ≥-;(Ⅱ)3x ≤;(Ⅲ)数轴见解析;(Ⅳ)13x -≤≤【解析】【分析】(Ⅰ)先移项,两边同时除以2即可得答案;(Ⅱ)移项,即可得答案;(Ⅲ)根据不等式解集的表示方法解答即可;(Ⅳ)根据数轴,找出不等式①②的公共解集即可.【详解】(Ⅰ)3x 1x 1+≥- 移项得:2x≥-2系数化为1得:x≥-1.故答案为:x≥-1(Ⅱ) x 12-≤移项得:x≤3.故答案为:x≤3(Ⅲ)不等式①和②的解集在数轴上表示如图所示:(Ⅳ)由数轴可得①和②的解集的公共解集为-1≤x≤3,∴原不等式组的解集为-1≤x≤3,故答案为:-1≤x≤3【点睛】本题考查了解一元一次不等式,解一元一次不等式组,在数轴上表示不等式的解集的应用,能根据不等式的解集求出不等式组的解集是解此题的关键.25.(1)500,90;(2)380;(3)C 厂家.【解析】【分析】(1)先计算D 占的百分比,与总人数的积得抽查D 厂家的零件数,与360°的积得扇形统计图中D 厂家对应的圆心角的度数;(2)百分比×总数×合格率可得结果;(3)分别计算其合格率,并作比较.【详解】解:(1)(1﹣35%﹣20%﹣20%)×2000=25%×2000=500,(1﹣35%﹣20%﹣20%)×360°=90°,故答案为:500,90;(2)20%×2000×95%=380;故答案为:380,如图所示;(3)A厂家合格率=630÷(2000×35%)=90%,C厂家合格率=95%,合格率更高的是C厂家.【点睛】本题考查了利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题。
2019版河北省中考数学一轮复习《课题1实数》课件

5
中考题型突破 栏目索引
题型三
题型.
考查实数的大小比较和估算
答案 C
∵ 4 =2,∴ 4 是有理数,①不正确;∵π是无限不循环小数,是无理
数,∴②不正确,而④⑤正确;∵开方开不尽的数都是无限不循环小数,是无理 数,∴③不正确,故选C.
中考题型突破 栏目索引
题型二
考查科学记数法
该题型主要考查用科学记数法表示较大或较小的数,以及用科学记数法表示 的数与原数的关系. 典例2 (2018邢台模拟)PM2.5是指大气中直径小于或等于0.000 000 25 m的
×4=80分,故选B. 名师点拨 解决本题的关键是熟练掌握绝对值、相反数、倒数、方根等基 本概念,并能利用相关概念解决实际问题,由此也提醒我们,熟练掌握有关概 念、定义等是解题的重要基石.
中考题型突破 栏目索引
变式训练1 (2018沧州模拟)下列说法:①带根号的数是无理数;②不含根号
的数一定是有理数;③无理数是开方开不尽的数;④无限不循环小数是无理 数;⑤π是无理数.其中正确的有 ( C ) A.4个 C.2个 B.3个 D.1个
1.一个近似数
2.科学记数法就是把一个数表示成
a×10n 的形式,其中1≤|a|<10,n为整
整数
数.若原数的绝对值大于或等于10,则n为正整数,其值等于原数的
位数减1;若原数的绝对值小于1,则n为负整数,其绝对值等于原数从左边起第
2019版中考数学第一部分基础知识过关第一章数与式第1讲实数及其运算课件

(ab)c a(bc) a(b c) ab
ac
3.实数范围内的运算顺序:先算乘方、开方,再算 乘除 ,最 后算 加减 ;有括号的,先算括号内的,按小括号、中括号、 大括号依次进行;同级运算要从左到右依次进行.
4.非负数性质的应用:若n个非负数的和为0,则这n个非负数同时
为
0 .如|a|+b2+ =c 0,则
方法技巧 (1)科学记数法的表示形式为a×10n,其中1≤|a|<10, n为整数,表示时要正确确定a的值以及n的值;(2)对于含有计数单
位的数,需要先利用1亿=1×108,1万=1×104,1千=1×103等将计数单 位转换,然后用科学记数法表示.
考点五 实数的运算
中考解题指导 实数的混合运算要综合运用绝对值、算术平方 根、立方根、三角函数、零指数幂和负整数指数幂等知识,同时 要注意运算顺序. 考向1 实数的混合运算
(2)2
解析
原式=4-(2-
3 )+1-3×
-3 2=4-2+
3
+31-
-23=1.
考向2 非负数性质的应用
例7 已知|x-y+2|+ x y 2 =0,则x2-y2的值为 -4 .
x y 2 0,
解析 根据非负数的性质可得 所 x以 xy –2 y0,= -2,x+y=2,所以 x2-y2=(x-y)(x+y)=-4,故答案为-4.
4.绝对值等于它本身的数是非负数,在数轴上,绝对值越大的数 所对应的点离原点越远.
5.若|a|=a,则a≥0;若|a|= -a,则a≤0.
6.相反数等于它本身的数是0,倒数等于它本身的数是±1,平方等 于它本身的数是1和0.
河北中考复习方案第一单元数与式PPT课件

冀考解读
课前热身
考点聚焦
冀考探究
第1课时┃ 实数的有关概念与大小比较
探究二 实数的有关概念及性质
命题角度:
1.会用实数表示具有相反意义的量; 2.求实数的相反数、倒数、绝对值;
3.数轴的概念、用数轴上的点表示数.
例 2 (1)[2014·福州] -5 的相反数是
A.-5
B.5
1 C.5
D.-15
解 析 因为-(-5)=5,所以应选 B.
年份 2012 2012 2013 2014 2013 2014
2012 2013 2014
2015 热度预测 ☆☆
☆☆☆☆☆
☆☆☆☆☆ ☆☆ ☆☆☆ ☆☆☆ ☆☆
冀考解读
课前热身
考点聚焦
冀考探究
第1课时┃ 实数的有关概念与大小比较
课前热身
1.下列各数中,为负数的是
A.0
B.-2
C.1
D.12
(B)
D.|b|<|a|
解 析 因为 a<-1,0<b<1,所以 b>a,a+b <0,ab<0,又|a|>1,|b|<1,所以仅 D 正确.故选 D.
冀考解读
课前热身
考点聚焦
冀考探究
第1课时┃ 实数的有关概念与大小比较
探究三 科学记数法与近似数
命题角度: 1.用科学记数法表示数; 2.指出近似数的精确度或按精确度取近似数.
例 3 [2014·唐山市路北区一模] 北京故宫的占地面积达
到 720000 平方米,这个数据用科学记数法表示为 ( D )
A.0.72×106 平方米 B.7.2×106 平方米
C.72×104 平方米
D.7.2×105 平方米
解 析 用科学记数法表示数时,a 和 n 的确定方法 是解题的关键.
通用2019中考数学总复习第一章数与式第1节实数的有关概念及运算课件新人教版_153

◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
河北省2019年中考数学一轮复习第一章数与式第一节实数课件20181222256

A.M或R
B .N或P
C .M或N
D.P或R
【分析】 分别假设M,N,P,R为原点,再逐一确定
|a|+|b|=3是否满足即可.
【自主解答】当M为原点,则a为0.5,b为2.5,此时满足条
件;当N为原点,a为-0.5,b为1.5,此时
|a|+|b|=2≠3,不满足题意;当P为原点,同理可知不满
足题意;当点R为原点可知,满足题意,故选A.
第一章 第一节
数与式 实 数
考点一
实数的分类 ) D.
例1 (2018·沈阳)下列各数中是有理数的是( A.π B.0 C.
【分析】 由有理数的概念直接进行判断. 【自主解答】 ∵有理数包括:整数和分数,0是整数,故0 是有理数.故选B.
判断有理数和无理数的方法 判断一个数是有理数还是无理数,注意不能简单的从形式上 进行判断,而要化简成最终结果后,看结果是否满足有理数 或无理数的定义.一般的,可从以下几种方式进行判断: (1)所有的整数、分数都是有理数;但分式型的数不一定全是 有理数,如 不是分数,是无理数;
解:根据题意得该快递员一共骑行的路程为
2+3+9+(9-5)=18 km.
内部文件,请勿外传
确;1的倒数是1不是-1,故B错误;1的立方根是1不是±1, 故C错误,-1是有理数不是无理数,故D错误.故选A.
1.(2018·江西)-2的绝对值是( B
A.-2 B .2
1 C.- 2
)
1 D. 2
2.(2014·河北)-2是2的( B
)
A.倒数
B.相反数
C.绝对值
D.平方根
3.(2017·河北)如图是张小亮的答卷,他的得分应是( B ) A.100分 B.80分 C.60分 D.40分
