平面向量与三角形三心
2016高考数学 常见题型 平面向量与三角形的“心”课件

A.重心、外心、垂心 B.重心、外心、内心 C.外心、重心、垂心 D.外心、重心、内心
答案 C
→ |=|OB → |=|OC → |知,O是三角形的外心,排除 解析 由 |OA 答案A,B. → +NB → +NC → =0得出N必然为重心. 由NA →· → =PB →· → ,∴(PA → -PC → )· → =0. ∵PA PB PC PB →· → =0,∴CA⊥PB,同理,AP⊥BC. ∴CA PB ∴P为△ABC的垂心,故选C.
平面向量与三角形的“心”
三角形的“心”的向量表示及应用 1.三角形各心的概念介绍
Hale Waihona Puke 重心:三角形的三条中线的交点;
垂心:三角形的三条高线的交点; 内心:三角形的三个内角角平分线的交点(三角形内切圆 的圆心); 外心:三角形的三条边的垂直平分线的交点(三角形外接 圆的圆心).
根据概念,可知各心的特征条件.比如:重心将中线长 度分成 2∶1 ;垂线与对应边垂直;角平分线上的任意点到角 两边的距离相等;外心到三角形各顶点的距离相等.
→ → → → AB AC BA BC →· →· (4)O 是△ABC 的内心⇔OA ( - )=OB ( - ) → | |AC →| → | |BC →| |AB |BA → → CA CB →· =OC ( - )=0. → | |CB →| |CA → → AB AC 注意 向量 λ( + )(λ≠0)所在直线过△ABC 的内 → | |AC →| |AB 心(是∠BAC 的角平分线所在直线)
零,则两向量所在直线垂直 ” 、三角形的垂心的定义等相关 知识.将三角形的垂心的定义与平面向量有关运算及 “ 数量 积为零,则两向量所在直线垂直”等相关知识巧妙结合.
专题:平面向量与三角形四心问题

专题:平面向量与三角形四心问题三角形四心指的是三角形的垂心、重心、内心和外心,在高考中常常结合平面向量的知识进行考察,是高中数学的一个难点.很多学生对三角形四心总是产生混淆,面对与四心有关的问题也常常束手无策,为了解决广大学子的困扰,本文以四心的常见结论出发,借助几道经典的例题,对三角形四心问题进行系统梳理,希望能够为读者提供帮助.如果读者是在校高中生,则标注了星号的内容可作为拓展知识. 一、三角形的内心(1)定义:三角形内切圆的圆心,即三角形三条角平分线的交点(如图1). (2)向量表示:若O 为△ABC 的内心→→→→=⋅+⋅+⋅⇔0OC c OB b OA a . (注:本文中的边a ,b ,c 分别表示BC ,AC ,AB .角A ,B ,C 分别表示BAC ∠,ABC ∠,ACB ∠.)证明:→→→→→→→→→→=+⋅++⋅+⋅⇔=⋅+⋅+⋅0)()(0AC OA c AB OA b OA a OC c OB b OA a→→→→=⋅+⋅+⋅++⇔0)(AC c AB b OA c b a →→→⋅+⋅=⋅++⇔AC c AB b AO c b a )(||||||||)(→→→→→→→⋅⋅+⋅⋅=⋅++⇔AC AC AC c AB AB AB b AO c b a)||||()(→→→→→+⋅=⋅++⇔AC ACAB ABbc AO c b a)||||(→→→→→+⋅++=⇔AC ACAB AB c b a bc AO (图1)⇔点O 在角A 的角平分线上,同理点O 也在角B 、C 的角平分线上. ⇔O 为△ABC 的内心.(3)常用性质性质1:))(||||(R AC ACAB AB∈+⋅→→→→λλ所在的直线与A ∠的角平分线重合(经过内心).证明:如图所示,||→→AB AB 表示→AB 上的单位向量,不妨记作→AD ,||→→AC AC 表示→AC 上的单位向量,不妨记作→AE .设→→→+=AE AD AP ,由平行四边形法则知,四边形ADPE 为菱形, 故直线AP 为A ∠的角平分线.))(||||(RAC ACAB AB∈+⋅∴→→→→λλ所在的直线与A ∠的角平分线重合(经过内心).性质2:r c b a S ABC ⋅++=∆)(21(r △ABC 内切圆的半径). 证明:由等面积法易证.性质3:O 为△ABC 的内心c b a S S S OAB OAC OBC ::::=⇔∆∆∆. 证明:由面积公式易证. (4)典例剖析例1-1:在△ABC 中,O 为平面内一个定点,动点P 满足)||||(→→→→→→++=AC ACAB ABOA OP λ,),0(+∞∈λ.则动点P 的轨迹经过△ABC 的( )A .内心B .外心C .垂心D .重心 解析:由性质1知,答案为A .例1-2:已知O 是△ABC 所在平面上的一点,若cb a PCc PB b PA a PO ++++=→→→→(其中P 是△ABC 所在平面内任意一点),则O 是△ABC 的( )A .内心B .外心C .垂心D .重心 解析:由题意知→→→→→→++=++PC c PB b PA a PO c PO b aPO ,即+-→→)(PO PA a→→→→→=-+-0)()(PO PC c PO PB b ,化简得→→→→=⋅+⋅+⋅0OC c OB b OA a .根据内心的向量表示知,O 是△ABC 的内心,答案为A .例1-3:已知O 是△ABC 内的一点,且满足0)||||(=-⋅→→→→→AC ACAB ABOA ,则OA 所在的直线一定经过三角形的( )A .内心B .外心C .垂心D .重心解析:||→→AB AB 表示→AB 上的单位向量,不妨记作→1e ,||→→AC AC 表示→AC 上的单位向量,不妨记作→2e .故0)(21=-⋅→→→e e OA ,即→→→→⋅=⋅21e OA e OA ,即>>=<<→→→→21,,e OA e OA .∴直线OA 与A ∠的角平分线重合,故OA 所在的直线一定经过三角形的内心,答案A .二、三角形的外心(1)定义:三角形外接圆的圆心,即三角形三边中垂线的交点(如图2). (2)向量表示:若O 为△ABC 的外心||||||→→→==⇔OC OB OA . (3)常用性质:奔驰定理*:已知O 为△ABC 内的一点(不一定为外心), 则→→∆→∆→∆=⋅+⋅+⋅0OC S OB S OA S OAB OAC OBC .(该定理反之也成立)证明:不妨延长AO 到D (如下图),则 (图2)=++===∆∆∆∆∆∆∆∆ACD ABD OAC OAB ACD OAC ABD OAB S S S S S S S S AD AO ABC OACOAB S S S ∆∆∆+, 即→∆∆∆→+=AD S S S AO ABCOAC OAB .且根据B ,D ,C 三点共线知,→∆∆∆→∆∆∆→+++=AB S S S AC S S S AD OAC OAB OACOAC OAB OAB ,故→∆∆→∆∆→+=AB S S AC S S AO ABC OAC ABC OAB ,即)()(→→∆∆→→∆∆→-+-=-OA OB S S OA OC S S OA ABCOAC ABC OAB . →→∆→∆→∆=⋅+⋅+⋅∴0OC S OB S OA S OAB OAC OBC (反之易证)性质1*:O 为△ABC 的外心C B A S S S OAB OAC OBC 2sin :2sin :2sin ::=⇔∆.证明:如图2所示,O 为△ABC 的外心A R BOC R S OBC 2sin 212sin 2122=∠=⇔∆,B R AOC R S OAC 2sin 212sin 2122=∠=∆,C R AOB R S OAB 2sin 212sin 2122=∠=∆ C B A S S S OAB OAC OBC 2sin :2sin :2sin ::=⇔∆(R 为△ABC 外接圆半径).性质2*:O 为△ABC 的外心→→→→=⋅+⋅+⋅⇔0)2(sin )2(sin )2(sin OC C OB B OA A . 证明:结合性质1与奔驰定理易证.(4)典例剖析例2-1:在△ABC 中,O 为平面内一个定点,动点P 满足++=→→→2OCOB OP )cos ||cos ||(CAC AC BAB AB →→→→+λ,),0(+∞∈λ.则动点P 的轨迹一定经过△ABC 的( )A .内心B .外心C .垂心D .重心 解析:设线段BC 的中点为D ,故)cos ||cos ||(C AC AC BAB AB OD OP →→→→→→++=λ,即)cos ||cos ||(CAC AC BAB AB DP →→→→→+=λ,而)cos ||cos ||(CAC BC AC BAB BC AB BC DP →→→→→→→→⋅+⋅=⋅λ,即)cos ||cos ||||cos ||)cos(||||(CAC CBC AC B AB B BC AB BC DP →→→→→→→→⋅+-⋅=⋅πλ0|)|||(=+-=→→BC BC λ 即→→⊥BC DP ,故点P 在线段BC 的垂直平分线上. ∴动点P 的轨迹一定经过△ABC 的外心,答案B .例2-2:在△ABC 中,动点O 满足→→→→⋅=-BC AO AB AC 222,则点O 一定经过△ABC 的( )A .内心B .外心C .垂心D .重心解析:由题知→→→→→→⋅=+-BC AO AB AC AB AC 2))((,设D 为BC 的中点,则=⋅→→AD BC 2→→⋅BC AO 2,故0=⋅→→OD BC ,即→→⊥OD BC ,O ∴在BC 的垂直平分线上,故点O 一定经过△ABC 的外心,答案B .例2-3:已知O 为△ABC 所在平面内的一点,满足→→→→⋅=⋅BA OB AB OA ,=⋅→→BC OB→→⋅CB OC ,则O 为△ABC 的( )A .内心B .外心C .垂心D .重心解析:由→→→→⋅=⋅BA OB AB OA 知0)(=+⋅→→→OA OB AB ,即0)()(=+⋅-→→→→OA OB OA OB ,即||||→→=OA OB ,同理可得:||||→→=OC OB ,O ∴为△ABC 的外心,答案B .三、三角形的垂心(1)定义:三角形三条高的交点(如图3).(2)向量表示:若O 为△ABC 的垂心→→→→→→⋅=⋅=⋅⇔OC OB OC OA OB OA . 证明:→→→→→→→→→→→⊥⇔=⋅=-⋅⇔⋅=⋅BC OA BC OA OB OC OA OC OA OB OA 0)(.同理→→⊥AC OB ,O AB OC ⇔⊥→→为△ABC 的垂心.(3)常用性质性质1*:O 为锐角△ABC 的垂心⇔=∆∆∆OAB OAC OBC S S S ::C B A tan :tan :tan . (图3)证明:ACDOC b BCDOC a OF b OE a S S OAC OBC ∠⋅⋅∠⋅⋅=⋅⋅=∆∆sin sin ,且在直角△BCD 和直角△ACD 中有 B BCD cos sin =∠,A ACD cos sin =∠.故BAA B B A A b B a S S OAC OBC tan tan cos sin cos sin cos cos =⋅⋅=⋅⋅=∆∆. 同理,CBS S OAB OAC tan tan =∆∆. C B A S S S OAB OAC OBC tan :tan :tan ::=∴∆∆∆,反之易证.性质2*:当O 为锐角△ABC 的垂心→→→→=⋅+⋅+⋅⇔0tan tan tan C OC B OB A OA .证明:利用性质1和“奔驰定理”易证. (4)典例剖析例3-1:在△ABC 中,O 为平面内一个定点,动点P 满足)cos ||cos ||(CAC AC BAB AB OA OP →→→→→→++=λ,),0(+∞∈λ,则动点P 的轨迹一定经过△ABC 的( )A .内心B .外心C .垂心D .重心 解析:由题知)cos ||cos ||(CAC AC BAB AB AP →→→→→+=λ,得=⋅+-⋅=⋅+⋅=⋅→→→→→→→→→→→→→→)cos ||cos ||||cos ||)cos(||||()cos ||cos ||(CAC CBC AC B AB B BC AB CAC BC AC BAB BC AB BC AP πλλ0|)|||(=+-→→BC BC λ,即→→⊥BC AP .P ∴在BC 边上的高上,过垂心,答案C .例3-2:已知O 为△ABC 所在平面内的一点,且满足=+=+→→→→2222||||||||AC OB BC OA22||||→→+AB OC ,则O 是△ABC 的( )A .内心B .外心C .垂心D .重心 解析:由题知2222||||||||→→→→-=-BC AC OB OA ,即=+⋅-→→→→)()(OB OA OB OA)()(→→→→+⋅-BC AC BC AC ,即0)()(=+⋅++⋅→→→→→→OB OA AB BC AC AB ,即02=⋅→→OC AB ,故→→⊥OC AB ,同理→→⊥OB AC ,→→⊥OA BC∴O 是△ABC 的垂心,答案C .例3-3:设O 是△ABC 的外心,点P 满足→→→→=++OP OC OB OA ,则P 是△ABC 的( )A .内心B .任意一点C .垂心D .重心 解析:由题知→→→→→=-=+CP OC OP OB OA ,由于O 是△ABC 的外心,故→→→=+OD OB OA 2(D 为线段AB 的中点)且→→⊥AB OD ,即→→=OD CP 2,→→⊥∴AB CP ,同理→→⊥AC BP ,→→⊥BC AP ,故P 是△ABC 的垂心,答案C .四、三角形的重心(1)定义:三角形三条中线的交点(如图4).(2)向量表示:若O 为△ABC 的重心→→→→=++⇔0OC OB OA . (3)常用性质 ( 图4 )性质1:若O 为△ABC 的重心ABC OBC OAC OAB S S S S ∆∆∆∆===⇔31性质2:若O 为△ABC 的重心→→=⇔AF AO 32,→→=BD BO 32,→→=CF CO 32性质3:已知),(11y x A ,),(22y x B ,),(33y x C .若O 为△ABC 的重心)3,3(321321y y y x x x O ++++⇔.(4)典例剖析例4-1:在△ABC 中,O 为平面内一个定点,动点P 满足)sin ||sin ||(CAC AC BAB AB OA OP →→→→→→++=λ,),0(+∞∈λ,则动点P 的轨迹一定经过△ABC的( )A .内心B .外心C .垂心D .重心 解析:由题知)sin ||sin ||(CAC AC BAB AB AP →→→→→+=λ,其中hC AC B AB ==→→sin ||sin ||(h 表示BC 边上的高),故)(hACh AB AP →→→+=λ→=AF h λ2(F 为线段BC 的中点). P ∴在BC 边上的中线上,故动点P 的轨迹一定经过△ABC 的重心,答案D .例4-2:在△ABC 中,O 为平面内一个定点,动点P 满足])21()1()1[(31→→→→++-+-=OC OB OA OP λλλ,R ∈λ,则动点P 的轨迹一定经过△ABC 的( )A .内心B .外心C .垂心D .重心解析:设AB 的中点为D ,故])21()1(2[31→→→++-=OC OD OP λλ,由于+-3)1(2λ1321=+λ,即点P ,C ,D 三点共线. P ∴在AB 边上的中线上,故动点P 的轨迹一定经过△ABC 的重心,答案D .例4-3:已知O 在△ABC 内,且满足→→→→=++0432OC OB OA ,现在到△ABC 内随机取一点,次点取自△OAB ,△OAC ,△OBC 的概率分别记为1P 、2P 、3P ,则( )A .321P P P ==B .123P P P >>C .321P P P >>D .312P P P >> 解析:法一:如图,延长OA ,OB ,OC 使得OA OD 2=,OB OE 3=,OC OF 4=, 故→→→→=++0OF OE OD ,即O 是△DEF 的重心,即△OED 、△ODF 、 △OEF 的面积相等,不妨令它们的面积都为1. 61=∴∆OAB S ,81=∆OAC S ,121=∆OBC S ,故321P P P >>,答案C . 法二:由“奔驰定理”知,k S OBC 2=∆,k S OAC 3=∆,kS OAB 4=∆(k 为比例系数),故321P P P >>,答案C .法三:根据三角形内心的向量表示,不妨设O 是以2k ,3k ,4k (k 为比例系数)为边长的三角形的内心,所以OBC OAC OAB S S S ∆∆∆>>,即321P P P >>,答案C .五、等腰(边)三角形的四心 (1)等腰三角形等腰三角形只有顶角的角平分线与中线、高三线重合,其余的线不重合.另外,等腰三角形的四心不重合. (2)等边三角形性质1:若△ABC 为等边三角形⇔△ABC 四心合一. 性质2:若△ABC 为等边三角形⇔△ABC 三线合一. 六、欧拉线*瑞士数学家欧拉(1707~1783)于1765年在他的著作《三角形 的几何学》中首次提出:(如图5)任意△ABC (非等边三角形)的垂心D 、重心E 、外心F 三点共线,即欧拉线. (图5)特别地,(如图6)当△ABC 为直角三角形时(A 为直角),垂心D 与A 重合,外心F 在BC 的中点上,欧拉线为直角△ABC 的外接圆半径(或BC 边上的中线).(图6)性质1:在任意三角形中,垂心与重心的距离是重心与外心距离的2倍,即EF DE 2=.。
三角形重心、外心、垂心、内心的向量表示及其性质

三角形“四心”向量形式的充要条件应用1.O 是ABC ∆的重心⇔=++; 若O 是ABC ∆的重心,则A BC A OB A OC BOC S 31S S S ∆∆∆∆===故0OC OB OA =++;1()3PG PA PB PC =++uu u r uu r uu r uu u r⇔G 为ABC ∆的重心. 2.O 是ABC ∆的垂心⇔OA OC OC OB OB OA ⋅=⋅=⋅;若O 是ABC ∆(非直角三角形)的垂心,则C tan B tan A tan S S S A OB A OC BOC ::::=∆∆∆ 故0OC C tan OB B tan OA A tan =++3.O 是ABC ∆的外心⇔||||||==(或222O C O B O A ==)若O 是ABC ∆的外心则C 2sin :B 2sin :A 2sin AOB sin AOC sin BOCsin S S S AOB AOC BOC =∠∠∠=∆∆∆:::: 故0OC C 2sin OB B 2sin OA A 2sin =++ 4.O 是内心ABC ∆的充要条件是|CB ||CA ||BC ||BA |AC|AB |=-⋅=-⋅=-⋅引进单位向量,使条件变得更简洁。
如果记CA ,BC ,AB 的单位向量为321e ,e ,e ,则刚才O 是ABC ∆内心的充要条件可以写成 0)e e (O )e e (O )e e (O 322131=+⋅=+⋅=+⋅ ,O 是ABC ∆内心的充要条件也可以是c b a =++。
若O 是ABC ∆的内心,则c b a S S S A O B A O C B O C ::::=∆∆∆故 0OC C sin OB B sin OA A sin 0OC c OB b OA a =++=++或;||||||0AB PC BC PA CA PB P ++=⇔u u u r u u u r u u u r u u r u u r u u r r是ABC ∆的内心;向量()(0)||||AC AB AB AC λλ+≠uu u r uu u ruu u r uu u r 所在直线过ABC ∆的内心(是BAC ∠的角平分线所在直线);(一)将平面向量与三角形内心结合考查例1.O 是平面上的一定点,A,B,C 是平面上不共线的三个点,动点P 满足++=λ,[)+∞∈,0λ则P 点的轨迹一定通过ABC ∆的( )(A )外心(B )内心(C )重心(D )垂心解析:因为是向量AB 的单位向量设AB 与AC 方向上的单位向量分别为21e e 和, 又=-,则原式可化为)(21e e +=λ,由菱形的基本性质知AP 平分BAC ∠,那么在ABC ∆中,AP 平分BAC ∠,则知选B.(二)将平面向量与三角形垂心结合考查“垂心定理”例2. H 是△ABC 所在平面内任一点,HA HC HC HB HB HA ⋅=⋅=⋅⇔点H 是△ABC 的垂心. 由AC HB AC HB HA HC HB HC HB HB HA ⊥⇔=⋅⇔=-⋅⇔⋅=⋅00)(,同理⊥,⊥.故H 是△ABC 的垂心. (反之亦然(证略))例3.(湖南)P 是△ABC 所在平面上一点,若⋅=⋅=⋅,则P 是△ABC 的(D )A .外心B .内心C .重心D .垂心解析:由0=⋅-⋅⋅=⋅得.即0,0)(=⋅=-⋅即 则AB PC BC PA CA PB ⊥⊥⊥,,同理 所以P 为ABC ∆的垂心. 故选D. (三)将平面向量与三角形重心结合考查“重心定理”例4. G 是△ABC 所在平面内一点,++=0⇔点G 是△ABC 的重心.证明 作图如右,图中=+连结BE 和CE ,则CE=GB ,BE=GC ⇔BGCE 为平行四边形⇒D 是BC 的中点,AD 为BC 边上的中线.将GE GC GB =+代入GC GB GA ++=0,得EG GA +=0⇒GD GE GA 2-=-=,故G 是△ABC 的重心.(反之亦然(证略)) 例5. P 是△ABC 所在平面内任一点.G 是△ABC 的重心⇔)(31++=. 证明 +=+=+=⇒)()(3PC PB PA CG BG AG PG +++++= ∵G 是△ABC 的重心 ∴++=0⇒++=0,即++=3 由此可得)(31PC PB PA PG ++=.(反之亦然(证略))例6 若O 为ABC ∆内一点,0OA OB OC ++= ,则O 是ABC ∆ 的( ) A .内心 B .外心 C .垂心 D .重心解析:由0OA OB OC ++=uu r uu u r uuu r r 得OB OC OA +=-u u u r u u u r u u r,如图以OB 、OC 为相邻两边构作平行四边形,则OB OC OD +=uu u r uu u r uuu r,由平行四边形性质知12OE OD =uu u r uuu r ,2OA OE =,同理可证其它两边上的这个性质,所以是重心,选D 。
向量与三心

向量与三角形内心、外心、重心、垂心知识的交汇一、四心的概念介绍(1)重心——中线的交点:重心将中线长度分成2:1; (2)垂心——高线的交点:高线与对应边垂直; (3)内心——角平分线的交点(内切圆的圆心):角平分线上的任意点到角两边的距离相等; (4)外心——中垂线的交点(外接圆的圆心):外心到三角形各顶点的距离相等。
二、四心与向量的结合(1)⇔=++0OC OB OA O 是ABC ∆的重心.证法1:设),(),,(),,(),,(332211y x C y x B y x A y x O⇔=++0OC OB OA ⎩⎨⎧=-+-+-=-+-+-0)()()(0)()()(321321y y y y y y x x x x x x ⎪⎪⎩⎪⎪⎨⎧++=++=⇔33321321y y y y x x x x ⇔O 是ABC ∆的重心.证法2:如图++ 02=+=OD OA ∴OD AO 2=∴D O A 、、三点共线,且O 分AD为2:1∴O 是ABC ∆的重心(2)⇔⋅=⋅=⋅OA OC OC OB OB OA O 为ABC ∆的垂心.证明:如图所示O 是三角形ABC 的垂心,BE 垂直AC ,AD 垂直BC , D 、E 是垂足.0)(=⋅=-⇔⋅=⋅ AC OB ⊥⇔同理BC OA ⊥,AB OC ⊥⇔O 为ABC ∆的垂心(3)设a ,b ,c 是三角形的三条边长,O 是∆ABC 的内心O OC c OB b OA a ⇔=++0为ABC ∆的内心.证明:b ACc AB 、分别为AC AB 、方向上的单位向量, ∴bAC c AB +平分BAC ∠,(λ=∴AO bACc AB +),令c b a bc ++=λ∴c b a bcAO ++=(bAC c AB +)化简得0)(=++++AC c AB b OA c b a∴0=++OC c OB b OA a(4==⇔O 为ABC ∆的外心。
三角形重心、外心、垂心、内心的向量表示及其性质

三角形“四心”向量形式的充要条件应用1.O 是ABC ∆的重心⇔=++; 若O 是ABC ∆的重心,则A BC A OB A OC BOC S 31S S S ∆∆∆∆===故0OC OB OA =++;1()3PG PA PB PC =++uu u r uu r uu r uu u r⇔G 为ABC ∆的重心. 2.O 是ABC ∆的垂心⇔OA OC OC OB OB OA ⋅=⋅=⋅;若O 是ABC ∆(非直角三角形)的垂心,则C tan B tan A tan S S S A OB A OC BOC ::::=∆∆∆ 故0OC C tan OB B tan OA A tan =++3.O 是ABC ∆的外心⇔||||||==(或222O C O B O A ==)若O 是ABC ∆的外心则C 2sin :B 2sin :A 2sin AOB sin AOC sin BOCsin S S S AOB AOC BOC =∠∠∠=∆∆∆:::: 故0OC C 2sin OB B 2sin OA A 2sin =++ 4.O 是内心ABC ∆的充要条件是|CB ||CA ||BC ||BA |AC|AB |=-⋅=-⋅=-⋅引进单位向量,使条件变得更简洁。
如果记CA ,BC ,AB 的单位向量为321e ,e ,e ,则刚才O 是ABC ∆内心的充要条件可以写成 0)e e (O )e e (O )e e (O 322131=+⋅=+⋅=+⋅ ,O 是ABC ∆内心的充要条件也可以是c b a =++。
若O 是ABC ∆的内心,则c b a S S S A O B A O C B O C ::::=∆∆∆故 0OC C sin OB B sin OA A sin 0OC c OB b OA a =++=++或;||||||0AB PC BC PA CA PB P ++=⇔u u u r u u u r u u u r u u r u u r u u r r是ABC ∆的内心;向量()(0)||||AC AB AB AC λλ+≠uu u r uu u ruu u r uu u r 所在直线过ABC ∆的内心(是BAC ∠的角平分线所在直线);(一)将平面向量与三角形内心结合考查例1.O 是平面上的一定点,A,B,C 是平面上不共线的三个点,动点P 满足++=λ,[)+∞∈,0λ则P 点的轨迹一定通过ABC ∆的( )(A )外心(B )内心(C )重心(D )垂心解析:因为是向量AB 的单位向量设AB 与AC 方向上的单位向量分别为21e e 和, 又=-,则原式可化为)(21e e +=λ,由菱形的基本性质知AP 平分BAC ∠,那么在ABC ∆中,AP 平分BAC ∠,则知选B.(二)将平面向量与三角形垂心结合考查“垂心定理”例2. H 是△ABC 所在平面内任一点,HA HC HC HB HB HA ⋅=⋅=⋅⇔点H 是△ABC 的垂心. 由AC HB AC HB HA HC HB HC HB HB HA ⊥⇔=⋅⇔=-⋅⇔⋅=⋅00)(,同理⊥,⊥.故H 是△ABC 的垂心. (反之亦然(证略))例3.(湖南)P 是△ABC 所在平面上一点,若⋅=⋅=⋅,则P 是△ABC 的(D )A .外心B .内心C .重心D .垂心解析:由0=⋅-⋅⋅=⋅得.即0,0)(=⋅=-⋅即 则AB PC BC PA CA PB ⊥⊥⊥,,同理 所以P 为ABC ∆的垂心. 故选D. (三)将平面向量与三角形重心结合考查“重心定理”例4. G 是△ABC 所在平面内一点,++=0⇔点G 是△ABC 的重心.证明 作图如右,图中=+连结BE 和CE ,则CE=GB ,BE=GC ⇔BGCE 为平行四边形⇒D 是BC 的中点,AD 为BC 边上的中线.将GE GC GB =+代入GC GB GA ++=0,得EG GA +=0⇒GD GE GA 2-=-=,故G 是△ABC 的重心.(反之亦然(证略)) 例5. P 是△ABC 所在平面内任一点.G 是△ABC 的重心⇔)(31++=. 证明 +=+=+=⇒)()(3PC PB PA CG BG AG PG +++++= ∵G 是△ABC 的重心 ∴++=0⇒++=0,即++=3 由此可得)(31PC PB PA PG ++=.(反之亦然(证略))例6 若O 为ABC ∆内一点,0OA OB OC ++= ,则O 是ABC ∆ 的( ) A .内心 B .外心 C .垂心 D .重心解析:由0OA OB OC ++=uu r uu u r uuu r r 得OB OC OA +=-u u u r u u u r u u r,如图以OB 、OC 为相邻两边构作平行四边形,则OB OC OD +=uu u r uu u r uuu r,由平行四边形性质知12OE OD =uu u r uuu r ,2OA OE =,同理可证其它两边上的这个性质,所以是重心,选D 。
平面向量与三角形三心

向量与三角形内心、外心、重心、垂心知识的交汇、四心的概念介绍(1) 重心——中线的交点:重心将中线长度分成 2 : 1 ;(2) 垂心一一高线的交点:高线与对应边垂直;(3) 内心一一角平分线的交点(内切圆的圆心):角平分线上的任意点到角两边的距离相等;(4) 外心一一中垂线的交点(外接圆的圆心) :外心到三角形各顶点的距离相等。
二、四心与向量的结合证法1设0(x, y), A(x i, yj B(X2, y2),C(X3, y3)(1) OA OB 0C =0:二0是:ABC的重心.OA OB OC = 0 二(X i _X)+(X2 _X)+(X3 _ X) =0(y i -y) (y2 - y) 仏- y) =o % y 2 y33 O是ABC的重心•证法2:如图OA OB OC=OA 2OD =0.AO =2OD.A、O、D三点共线,且O分AD为2:1.O是ABC的重心(2) OA OB = OB OC = OC OA:= O为ABC 的垂心.证明:如图所示O是三角形ABC的垂心,BE垂直AC,AD垂直BC,OA OB =OB OC 二OB(OA -OC) =OB CA = 0二OB _ AC同理OA _ BC,OC _ AB=O为-ABC的垂心(3)设a, b , c是三角形的三条边长,O是厶ABC的内心▼faOA bOB cOC = 0 = O 为ABC 的内心.AB AC ——-——-证明:... AB、AC分别为AB、AC方向上的单位向量,ABcAC+ 平分N BAC, bX1X2X3y二D、E是垂足.AB AC),令一be a b cbe AB ACAO()a b c c b化简得(a b c)OA bAB eAC =0 aOA bOB cOC = 0(4) OA=OB=OC 二 O 为占ABC 的外心。
典型例题分析[例题]已知点G 是丁ABC 内任意一点,点M 是丁ABC 所在平面内一点•试根据下列条件判断G 点可能通过VABC 的 _______ 心.(填“内心”或“外心”或“重心”或“垂心”).[提出问题]⑵ 若点D 是丁 ABC 的底边BC 上的中点,满足GDGB 二GDGC ,则点G 可能通过VABC 的 __________.⑶若存在常数 上,满足MG = MA + 珥一-AB — +™AC —)仏丰0),则点G 可能 AB 廉i nB AC 隔 nC 通过VABC 的 ___________通过VABC 的 __________ .[思路分析]以上四个问题的解决要求不同,除了熟悉三角形的“四心”的性质 同时更要熟悉平面向量的性质,对于平面向量与三角函数的结合也要相当熟悉形或三角形法则知,点G 是角平分线上的点,故应填内心. (2) 简单的变形后发现点G 是BC 边中垂线上的点,故应填外心. (3) 叮 ABVin B =|AC 蹩i nC/.记 ABVin B=| AC^i nC = h ,则AG =「(AB AC)('').由平面向量的平行四边形或三角形法则知,点G 是hBC 边的中线上的点,故应填重心.(4) 分析后发现,本题学生难以找到解决问题的突破口 ,主要在于平面向量的数量(1)若存在常数 ———A丸,满足MG = MA +九(—〜AB ACG 可能通过丁 ABCAC(4)若存在常数 ABAC■a^s a^s丸,满足MG = MA + k (—飞ABVosB ACPosC)(■ =0),则点G 可能[解答过程](1)记 AB AB AC〜,一~■ (ej e 2).由平面向量的平行四边)(=0),第3页共4页积的充分利用•由MG =MA …(AB AB£osBAC AC \cosC得 AG = ■( 一 一+ —)(丸丰 0),AB Vos B AC \cosC (关键点)AGB^ (一亠—T )x BC (“o ) AB^cosB AC^CosC于是AG BC = ■( IAB A 啤乞+ AC 乎)(+) YosB〔ACpCosC =■( BC cos( -:-B) BC cosB)从而AG _ BC ,点G 是高线上的点,故应填垂心.[点评]以上四个问题处理的方法各不相同,注意到平面向量及三角形的“四心” 的性质在解答问题时的作用•特别注意第四问两边同乘以某个表达式的技巧•总结:(1) OA OB OC =0 = O 是 ABC 的重心.(2) OA OB =OB OC =OC OA := O 为 ABC 的垂心.(3) 设a , b , c 是三角形的三条边长, O 是厶ABC 的内心aOA bOB cOC = 0 = O 为 ABC 的内心.(4) OA=OB=OC= O 为 AABC 的外心。
平面向量中的三角形四心问题

平面向量中的三角形四心问题(一)向量是高中数学中引入的重要概念,是解决几何问题的重要工具。
本文就平面向量与三角形四心的联系做一个归纳总结。
在给出结论及证明结论的过程中,可以体现数学的对称性与推论的相互关系。
一、重心(barycenter) 三角形重心是三角形三边中线的交点。
重心到顶点的距离与重心到对边中点的距离之比为2:1。
在重心确定上,有著名的帕普斯定理。
结论1:是三角形的重心所在平面内一点,则为若G GC GB GA ABC G ⇔=++∆0的重心为故上在中线同理可得上在中线这表明,,则中点为证明:设ABC G CF BE G AD G GD GA GCGB GA GC GB GA GCGB GD D BC ∆=-∴+=-⇔=+++=,,202结论2:的重心是证明:的重心是所在平面内一点,则为若ABC G GC GB GA PC PG PB PG PA PG PC PB PA PG ABC G PC PB PA PG ABC ∆⇔=++⇔=-+-+-⇔++=∆⇔++=∆00)()()()(31)(31P二、垂心(orthocenter)三角形的三条高线的交点叫做三角形的垂心。
结论3:的垂心是所在平面内一点,则为若ABC H HA HC HC HB HB HA ABC ∆⇔⋅=⋅=⋅∆H 为三角形垂心故同理,有证明:H ABHC CB HA ACHB AC HB HC HA HB HC HB HB HA ⊥⊥⊥⇔=⋅⇔=-⋅⇔⋅=⋅,00)(结论4:可知命题成立由结论同理可证得,得,证明:由的垂心是所在平面内一点,则为若3)()(H 22222222222222HAHC HC HB HB HA HAHC HC HB HA HC HB HC HB HA CA HB BC HA ABC H AB HC AC HB BC HA ABC ⋅=⋅=⋅⋅=⋅⇔-+=-++=+∆⇔+=+=+∆三、外心(circumcenter)三角形三条边的垂直平分线(中垂线)的相交点。
高中数学平面向量与三角形的“四心”
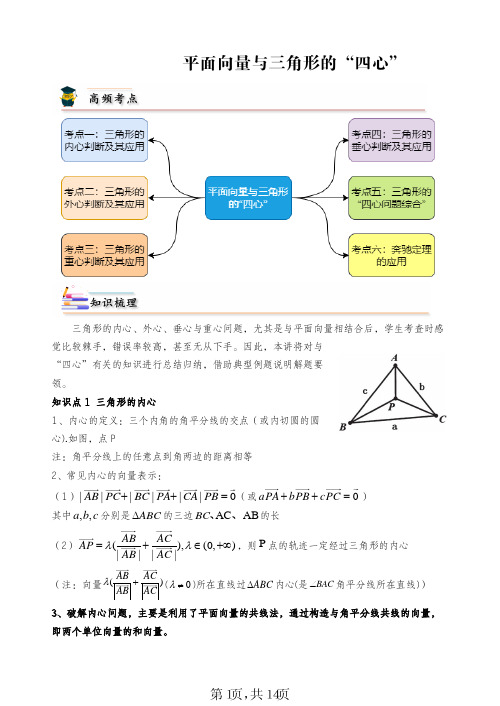
培优专题1 平面向量与三角形的“四心”三角形的内心、外心、垂心与重心问题,尤其是与平面向量相结合后,学生考查时感觉比较棘手,错误率较高,甚至无从下手。
因此,本讲将对与“四心”有关的知识进行总结归纳,借助典型例题说明解题要领。
知识点1 三角形的内心1、内心的定义:三个内角的角平分线的交点(或内切圆的圆心).如图,点P注:角平分线上的任意点到角两边的距离相等 2、常见内心的向量表示:(1)||||||0AB PC BC PA CA PB ++=(或0aPA bPB cPC ++=)其中,,a b c 分别是ABC ∆的三边AC AB BC 、、的长 (2)(),(0,)||||AB ACAP AB AC λλ=+∈+∞,则P 点的轨迹一定经过三角形的内心 (注:向量()AB AC ABACλ+(0λ≠)所在直线过ABC ∆内心(是BAC ∠角平分线所在直线))3、破解内心问题,主要是利用了平面向量的共线法,通过构造与角平分线共线的向量,即两个单位向量的和向量。
拓展:是平面上一定点,,,是平面上不共线的三个点,动点满足,证明的轨迹一定通过的内心. 【解析】证明:、分别表示与、方向相同的单位向量, 的方向与的角平分线方向一致; 又,; 的方向与的角平分线方向一致, 点的轨迹一定通过的内心.知识点2 三角形的外心1、外心的定义:三角形三边的垂直平分线的交点(或外接圆的圆心)注:外心到三角形各顶点的距离相等. 2、常用外心的向量表示:(1)222||||||OA OB OC OA OB OC ==⇔==(2)()()()0OA OB AB OB OC BC OA OC AC +⋅=+⋅=+⋅= 变形:P 为平面ABC 内一动点,若()()()()()()0OA OB PB PA OB OC PC PB OA OC PC PA +⋅−=+⋅−=+⋅−=,则O 为三角形的外心3、破解外心问题,关键是运用平面向量的加减法和数量积的运算,结合数量积的运算律从而得到三角形的外心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向量与三角形内心、外心、重心、垂心知识的交汇一、四心的概念介绍(1)重心——中线的交点:重心将中线长度分成2:1; (2)垂心——高线的交点:高线与对应边垂直; (3)内心——角平分线的交点(内切圆的圆心):角平分线上的任意点到角两边的距离相等; (4)外心——中垂线的交点(外接圆的圆心):外心到三角形各顶点的距离相等。
二、四心与向量的结合(1)⇔=++0OC OB OA O 是ABC ∆的重心.证法1:设),(),,(),,(),,(332211y x C y x B y x A y x O⇔=++0OC OB OA ⎩⎨⎧=-+-+-=-+-+-0)()()(0)()()(321321y y y y y y x x x x x x ⎪⎪⎩⎪⎪⎨⎧++=++=⇔33321321y y y y x x x x ⇔O 是ABC ∆的重心.证法2:如图OC OB OA ++02=+=OD OA∴OD AO 2=∴D O A 、、三点共线,且O 分AD为2:1∴O 是ABC ∆的重心(2)⇔⋅=⋅=⋅OA OC OC OB OB OA O 为ABC ∆的垂心.证明:如图所示O 是三角形ABC 的垂心,BE 垂直AC ,AD 垂直BC , D 、E 是垂足.0)(=⋅=-⇔⋅=⋅CA OB OC OA OB OC OB OB OAAC OB ⊥⇔同理BC OA ⊥,AB OC ⊥⇔O 为ABC ∆的垂心(3)设a ,b ,c 是三角形的三条边长,O 是∆ABC 的内心O OC c OB b OA a ⇔=++0为ABC ∆的内心.证明:b ACc AB 、分别为AC AB 、方向上的单位向量, ∴bAC c AB +平分BAC ∠, (λ=∴AO bACc AB +),令c b a bc ++=λB CDBCD∴c b a bc AO ++=(bACc AB +) 化简得0)(=++++AC c AB b OA c b a∴0=++OC c OB b OA a(4)==⇔O 为ABC ∆的外心。
典型例题分析[例题]已知点G 是ABC 内任意一点,点 M 是ABC 所在平面内一点.试根据下列条件判断G 点可能通过ABC 的_______心.(填“内心”或“外心”或“重心”或“垂心”).[提出问题](1)若存在常数λ,满足()(0)AB AC MG MA ABACλλ=++≠,则点G 可能通过ABC的__________.(2)若点D 是ABC 的底边BC 上的中点,满足GD GB GD GC =,则点G 可能通过ABC 的__________.(3)若存在常数λ,满足()(0)sin sin AB AC MG MA AB BAC Cλλ=++≠,则点G 可能通过ABC 的__________.(4)若存在常数λ,满足()(0)cos cos AB AC MG MA AB BAC Cλλ=++≠,则点G 可能通过ABC 的__________.[思路分析]以上四个问题的解决要求不同,除了熟悉三角形的“四心”的性质,同时更要熟悉平面向量的性质,对于平面向量与三角函数的结合也要相当熟悉. [解答过程](1)记12,AB AC e e ABAC==,则12()AG e e λ=+.由平面向量的平行四边形或三角形法则知,点G 是角平分线上的点,故应填内心.(2)简单的变形后发现点G 是BC 边中垂线上的点,故应填外心. (3)sin sin ,AB B AC C =∴记sin sin AB B AC C h ==,则''()()AG AB AC hλλλ=+=.由平面向量的平行四边形或三角形法则知,点G 是BC 边的中线上的点,故应填重心.(4)分析后发现,本题学生难以找到解决问题的突破口,主要在于平面向量的数量积的充分利用.由()(0)cos cos AB AC MG MA AB BAC Cλλ=++≠,得()(0)cos cos AB ACAG AB BAC C λλ=+≠,(关键点) ()(0)cos cos AB AC AG BC BC AB BAC Cλλ=+≠于是()(0)cos cos )()0AB BC AC BC AG BC AB BAC CBC B BC B BC BC λλλπλ=+≠=+-+=(cos(-cos )=.从而AG BC ⊥,点G 是高线上的点,故应填垂心.[点评]以上四个问题处理的方法各不相同,注意到平面向量及三角形的“四心”的性质在解答问题时的作用.特别注意第四问两边同乘以某个表达式的技巧.总结:(1)⇔=++0OC OB OA O 是ABC ∆的重心.(2)⇔⋅=⋅=⋅OAOC OCOB OB OAO 为ABC ∆的垂心. (3)设a ,b ,c 是三角形的三条边长,O 是∆ABC 的内心O OC c OB b OA a ⇔=++0为ABC ∆的内心.(4)==⇔O 为ABC ∆的外心。
或者若P 点为ABC 内任意一点,若P 点满足:1.(),0()0AB ACAP AB AC P ABC BA BC BP t t BA BC λλ⎧=+>⎪⎪⎪⇒⎨⎪=+>⎪⎪⎩为的内心,; 2.D E 、两点分别是ABC 的边BC CA 、上的中点,且DP PB DP PCP ABC EP PC EP PA⎧=⎪⇒⎨=⎪⎩为的外心; 3. 1(),31()3AP AB AC P ABC BP BA BC ⎧=+⎪⎪⇒⎨⎪=+⎪⎩为的重心,;4. 0AP BC P ABC BP AC ⎧=⎪⇒⎨=⎪⎩为的垂心.结合运用:例1:O 是平面上一定点,C B A 、、是平面上不共线的三个点,动点P 满足)(AC AB OA OP ++=λ,[)+∞∈,0λ ,则点P 的轨迹一定通过ABC ∆的( )A .外心B .内心C .重心D .垂心 分析:如图所示ABC ∆,E D 、分别为边AC BC 、的中点.AD AC AB 2=+∴AD OA OP λ2+=AP OA OP += AD AP λ2=∴AP ∴//AD∴点P 的轨迹一定通过ABC ∆的重心,即选C .例2:O 是平面上一定点,C B A 、、是平面上不共线的三个点,动点P满足OA OP ++=λ,[)+∞∈,0λ ,则点P 的轨迹一定通过ABC ∆的( B )A .外心B .内心C .重心D .垂心分析:ACAB分别为AC AB 、方向上的单位向量,∴AC AB +BAC ∠,∴点P 的轨迹一定通过ABC ∆的内心,即选B .例3:O 是平面上一定点,C B A 、、是平面上不共线的三个点,动点P满足OA OP ++=λ,[)+∞∈,0λ ,则点P 的轨迹一定通过ABC ∆的( )A .外心B .内心C .重心D .垂心B CD分析:如图所示AD 垂直BC ,BE 垂直AC , D 、E 是垂足.+BC ⋅++=-=0∴点P 的轨迹一定通过ABC ∆的垂心,即选D .练习:1.已知ABC ∆三个顶点C B A 、、及平面内一点P ,满足0=++PC PB PA ,若实数λ满足:AP AC AB λ=+,则λ的值为( )A .2B .23C .3D .6 2.若ABC ∆的外接圆的圆心为O ,半径为1,0=++OC OB OA ,则=⋅OB OA ( ) A .21 B .0 C .1 D .21- 3.点O 在ABC ∆内部且满足022=++OC OB OA ,则ABC ∆面积与凹四边形ABOC 面积之比是( )A .0B .23 C .45 D .344.ABC ∆的外接圆的圆心为O ,若OC OB OA OH ++=,则H 是ABC ∆的( )A .外心B .内心C .重心D .垂心5.O 是平面上一定点,C B A 、、是平面上不共线的三个点,若222OB BC OA =+222AB OC CA +=+,则O 是ABC ∆的( )A .外心B .内心C .重心D .垂心6.ABC ∆的外接圆的圆心为O ,两条边上的高的交点为H ,)(OC OB OA m OH ++=, 则实数m =C7.已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC →| =12 , 则△ABC 为( )A .三边均不相等的三角形B .直角三角形C .等腰非等边三角形D .等边三角形8.已知ABC ∆三个顶点C B A 、、,若CA BC CB AB AC AB AB ⋅+⋅+⋅=2,则ABC ∆为( )A .等腰三角形B .等腰直角三角形C .直角三角形D .既非等腰又非直角三角形练习答案:C 、D 、C 、D 、D 、1、D 、C。
