《机械振动》考试试题
(完整版)机械振动试题(参考答案)
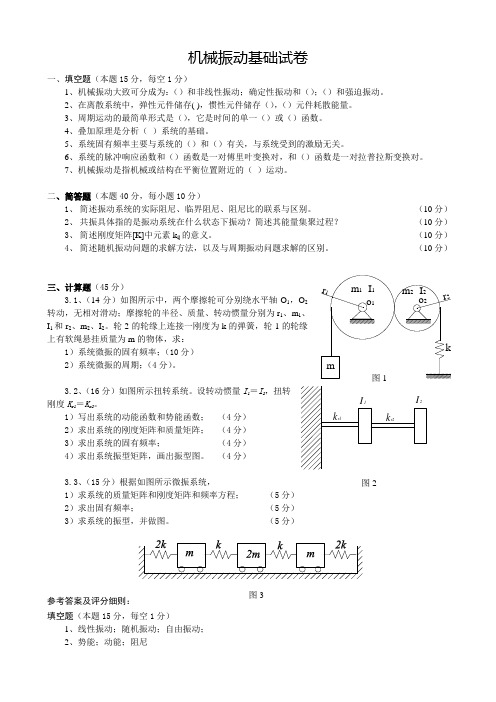
机械振动基础试卷一、填空题(本题15分,每空1分)1、机械振动大致可分成为:()和非线性振动;确定性振动和();()和强迫振动。
2、在离散系统中,弹性元件储存( ),惯性元件储存(),()元件耗散能量。
3、周期运动的最简单形式是(),它是时间的单一()或()函数。
4、叠加原理是分析( )系统的基础。
5、系统固有频率主要与系统的()和()有关,与系统受到的激励无关。
6、系统的脉冲响应函数和()函数是一对傅里叶变换对,和()函数是一对拉普拉斯变换对。
7、机械振动是指机械或结构在平衡位置附近的( )运动。
二、简答题(本题40分,每小题10分)1、 简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
(10分)2、 共振具体指的是振动系统在什么状态下振动?简述其能量集聚过程? (10分)3、 简述刚度矩阵[K]中元素k ij 的意义。
(10分)4、 简述随机振动问题的求解方法,以及与周期振动问题求解的区别。
(10分)三、计算题(45分) 3.1、(14分)如图所示中,两个摩擦轮可分别绕水平轴O 1,转动,无相对滑动;摩擦轮的半径、质量、转动惯量分别为r 1、m I 1和r 2、m 2、I 2。
轮2的轮缘上连接一刚度为k 的弹簧,轮1上有软绳悬挂质量为m 的物体,求: 1)系统微振的固有频率;(10分)2)系统微振的周期;(4分)。
3.2、(16分)如图所示扭转系统。
设转动惯量I 1=I 2,扭转刚度K r1=K r2。
1)写出系统的动能函数和势能函数; (4分) 2)求出系统的刚度矩阵和质量矩阵; (4分)3)求出系统的固有频率; (4分)4)求出系统振型矩阵,画出振型图。
(4分)3.3、(15分)根据如图所示微振系统, 1)求系统的质量矩阵和刚度矩阵和频率方程; (5分)2)求出固有频率; (5分)3)求系统的振型,并做图。
(5分)参考答案及评分细则:填空题(本题15分,每空1分)1、线性振动;随机振动;自由振动;2、势能;动能;阻尼图2图33、简谐运动;正弦;余弦4、线性5、刚度;质量6、频响函数;传递函数7、往复弹性简答题(本题40分,每小题10分)5、 简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
机械振动试题及答案

一、填空题1、机械振动按不同情况进行分类大致可分成(线性振动)和非线性振动;确定性振动和(随机振动);(自由振动)和强迫振动,连续振动和离散系统。
2、(弹性元件)元件、(惯性元件)元件、(阻尼元件)元件是离散振动系统的三个最基本元素。
3、在振动系统中,弹性元件存储(势能)、惯性元件存储(动能)、(阻尼元件)元件耗散能量。
4、系统固有频率主要与系统的(质量)和(刚度)有关,与系统受到的激励无关。
5、研究随机振动的方法是(数理统计),工程上常见的随机过程的数字特征有:(均值)(方差)(自相关函数)和(互相关函数)。
6、周期运动的最简单形式是(简谐运动),它是时间的单一(正弦)或(余弦)函数。
7、单自由度系统无阻尼自由振动的频率只与(质量)和(刚度)有关,与系统受到的激励无关。
8、简谐激励下单自由度系统的响应由(瞬态响应)和(稳态响应)组成。
9、工程上分析随机振动用(数学统计)方法,描述随机过程的最基本的数字特征包括均值、方差、(自相关函数)和(互相关函数)。
10、机械振动是指机械或结构在(静平衡)附近的(弹性往复)运动。
11、单位脉冲力激励下,系统的脉冲响应函数和系统的(频响函数)函数是一对傅里叶变换对,和系统的(传递函数)函数是一对拉普拉斯变换对。
12、叠加原理是分析(线性振动系统)和(振动性质)的基础。
二、简答题1、什么是机械振动?振动发生的内在原因是什么?外在原因是什么?答:机械振动是指机械或结构在它的静平衡位置附近的往复弹性运动。
振动发生的内在原因是机械或结构具有在振动时储存动能和势能,而且释放动能和势能并能使动能和势能相互转换的能力。
外在原因是由于外界对系统的激励或者作用。
2、机械振动系统的固有频率与哪些因素有关?关系如何?答:机械振动系统的固有频率与系统的质量矩阵、刚度矩阵和阻尼有关。
质量越大,固有频率越低;刚度越大,固有频率越高;阻尼越大,固有频率越低。
3、从能量、运动、共振等角度简述阻尼对单自由度系统振动的影响。
机械振动期末考试题及答案

机械振动期末考试题及答案一、选择题(每题2分,共20分)1. 简谐振动的周期与振幅无关,这是由哪个定律决定的?A. 牛顿第二定律B. 牛顿第三定律C. 胡克定律D. 能量守恒定律答案:C2. 下列哪个不是阻尼振动的特点?A. 振幅逐渐减小B. 频率逐渐增大C. 能量逐渐减少D. 振幅随时间呈指数衰减答案:B3. 一个物体做自由振动,若其振幅逐渐减小,这表明振动受到了:A. 阻尼B. 共振C. 强迫振动D. 非线性振动答案:A4. 质点的振动方程为 \( y = A \sin(\omega t + \phi) \),其中\( \omega \) 表示:A. 振幅B. 频率C. 角频率D. 相位答案:C5. 弹簧振子的振动周期与下列哪个参数无关?A. 弹簧的劲度系数B. 振子的质量C. 振子的振幅D. 振子的初始相位答案:C6. 阻尼振动的振幅随时间呈指数衰减,其衰减速率与什么有关?A. 振幅大小B. 阻尼系数C. 振动频率D. 振动周期答案:B7. 以下哪个不是振动系统的自由度?A. 1B. 2C. 3D. 无穷大答案:D8. 共振现象发生在以下哪种情况下?A. 系统固有频率等于外部激励频率B. 系统阻尼系数最大C. 系统振幅最小D. 系统能量最大答案:A9. 以下哪个是简谐振动的特有现象?A. 振幅不变B. 频率不变C. 能量不变D. 周期不变答案:A10. 一个物体在水平面上做简谐振动,其振动能量主要由以下哪两个因素决定?A. 振幅和频率B. 振幅和阻尼系数C. 阻尼系数和频率D. 振幅和劲度系数答案:A二、填空题(每空2分,共20分)11. 简谐振动的周期公式为 \( T = \frac{2\pi}{\omega} \),其中\( \omega \) 为________。
答案:角频率12. 当外部激励频率接近系统的________时,系统将产生共振现象。
答案:固有频率13. 阻尼振动的振幅随时间的变化规律可表示为 \( A(t) = A_0 e^{-\beta t} \),其中 \( \beta \) 为________。
大学机械振动考试题目及答案

大学机械振动考试题目及答案一、选择题(每题2分,共10分)1. 在简谐振动中,振幅与振动的能量关系是()。
A. 无关B. 成正比C. 成反比D. 振幅越大,能量越小答案:B2. 下列哪个不是机械振动系统的自由度?()。
A. 转动B. 平动C. 振动D. 形变答案:C3. 一个单自由度系统在受到初始条件激励后,其振动形式是()。
A. 简谐振动B. 阻尼振动C. 受迫振动D. 自由振动答案:D4. 在阻尼振动中,如果阻尼系数增加,振动的振幅将()。
A. 增加B. 不变C. 减小D. 先增加后减小答案:C5. 对于一个二自由度振动系统,其振动模态数量是()。
A. 1B. 2C. 3D. 4答案:B二、填空题(每题2分,共10分)6. 一个物体做自由振动时,其频率称为______。
答案:固有频率7. 当外力的频率与系统的固有频率相等时,系统发生的振动称为______。
答案:共振8. 阻尼力与速度成正比的阻尼称为______阻尼。
答案:线性9. 振动系统的动态响应可以通过______分析法求解。
答案:傅里叶10. 在转子动力学中,临界转速是指转子发生______振动的转速。
答案:自激三、简答题(每题5分,共20分)11. 简述什么是简谐振动,并说明其运动方程的形式。
答案:简谐振动是一种周期性的振动,其加速度与位移成正比,且方向相反。
在数学上,简谐振动的运动方程可以表示为:x(t) = A * cos(ωt + φ)其中,A 是振幅,ω 是角频率,t 是时间,φ 是初相位。
12. 解释什么是阻尼振动,并说明其特点。
答案:阻尼振动是指在振动系统中存在能量耗散,导致振幅随时间逐渐减小的振动。
其特点包括振幅逐渐衰减,振动频率可能会随着振幅的减小而发生变化,且阻尼力通常与振动速度成正比。
13. 描述什么是受迫振动,并给出其稳态响应的条件。
答案:受迫振动是指系统在周期性外力作用下的振动。
当外力的频率接近系统的固有频率时,系统将发生共振,此时振幅会显著增大。
机械振动期末试题及答案

机械振动期末试题及答案1. 选择题1.1 哪种情况下,系统的振动是简谐振动?A. 有耗尽能量的情况B. 存在非线性的力恢复系统中C. 无外部干扰D. 系统的振幅随时间而增长答案:C1.2 振动系统达到稳态的条件是:A. 初始位移为零B. 扰动力为零C. 初始速度为零D. 振幅随时间减小答案:B1.3 一个简谐振动的周期与振幅的关系是:A. 周期与振幅无关B. 周期与振幅成正比C. 周期与振幅成反比D. 周期与振幅正弦相关答案:A2. 判断题2.1 简谐振动的周期和角频率之间满足正比关系。
A. 对B. 错答案:B2.2 简谐振动的中心力是恒力。
A. 对B. 错答案:A2.3 当振动系统有阻尼情况时,振幅会随时间增大。
A. 对B. 错答案:B3. 简答题3.1 什么是简谐振动?它的特点是什么?答案:简谐振动是指振动系统在没有外力干扰的情况下,其平衡位置附近以某一频率固定幅度上下振动的现象。
它的特点包括振动周期与振幅无关,且系统的振动可由正弦或余弦函数进行描述。
3.2 请简要说明受迫振动的原理。
答案:受迫振动是指振动系统在外力作用下的振动。
外力的频率与系统的固有频率相近或相等时,会发生共振现象。
在共振时,外力的能量会以最大幅度传递给振动系统,导致振动幅度增大。
4. 计算题4.1 一个弹簧振子平衡位置附近的势能函数为U(x) = 4x^2 + 3,求振子的振动周期。
答案:根据简谐振动的势能函数表达式,势能函数为U(x) =1/2kx^2,其中k为弹簧的劲度系数。
将已知的势能函数与标准表达式进行比较,可得4x^2 = 1/2kx^2,解得k = 8。
由振动周期公式T =2π√(m/k),代入m和k的值,可计算出振子的振动周期。
5. 算法题设计一个程序,计算一个简谐振动系统的振动频率和振幅,并将结果打印输出。
// 输入参数float k; // 弹簧的劲度系数float m; // 系统的质量// 计算振动频率float omega = sqrt(k / m);// 计算振幅float A = 1; // 假设振幅为1// 打印输出结果print("振动频率:", omega);print("振幅:", A);经过以上计算,我们可以得到一个简谐振动系统的振动频率和振幅。
机械振动试题(含答案)

D.t=2s时,甲的速度为零,乙的加速度达到最大值
6.下列叙述中符合物理学史实的是( )
A.伽利略发现了单摆的周期公式
B.奥斯特发现了电流的磁效应
C.库仑通过扭秤实验得出了万有引力定律
D.牛顿通过斜面理想实验得出了维持运动不需要力的结论
7.如图所示,质量为m的物块放置在质量为M的木板上,木板与弹簧相连,它们一起在光滑水平面上做简谐振动,周期为T,振动过程中m、M之间无相对运动,设弹簧的劲度系数为k、物块和木板之间滑动摩擦因数为μ,
A. B. C. D.
9.如图所示,在一条张紧的绳子上悬挂A、B、C三个单摆,摆长分别为L1、L2、L3,且L1<L2<L3,现将A拉起一较小角度后释放,已知当地重力加速度为g,对释放A之后较短时间内的运动,以下说法正确的是( )
A.C的振幅比B的大B.B和C的振幅相等
C.B的周期为2π D.C的周期为2π
A.物体B从P向O运动的过程中,A、B之间的摩擦力对A做正功
B.物体B处于PO之间某位置时开始计时,经 时间,物体B通过的路程一定为L
C.当物体B的加速度为a时开始计时,每经过T时间,物体B的加速度仍为a
D.当物体B相对平衡位置的位移为x时,A、B间摩擦力的大小等于
13.如图所示是两个理想单摆的振动图象,纵轴表示摆球偏离平衡位置的位移,以向右为正方向.下列法中正确的是___________(填入正确选项前的字母.选对1个给2分,选对2个给4分,选对3个给5分,每选错一个扣3分,得分为0分)
A.6sB.4sC.22sD.8s
16.如图甲为竖直弹簧振子,物体在A、B之间做简谐运动,O点为平衡位置,A点为弹簧的原长位置,从振子经过A点时开始计时,振动图象如图乙所示,下列说法正确的是
物理机械振动考试题及答案

物理机械振动考试题及答案一、单项选择题(每题3分,共30分)1. 简谐运动的振动周期与振幅无关,与以下哪个因素有关?A. 质量B. 弹簧常数C. 初始位移D. 初始速度答案:B2. 阻尼振动中,振幅逐渐减小的原因是:A. 摩擦力B. 重力C. 弹力D. 空气阻力答案:A3. 以下哪个量描述了简谐运动的振动快慢?A. 振幅B. 周期C. 频率D. 相位答案:C4. 两个简谐运动的合成,以下哪个条件可以产生拍现象?A. 频率相同B. 频率不同C. 振幅相同D. 相位相反答案:B5. 以下哪个量是矢量?A. 位移B. 速度C. 加速度D. 以上都是答案:D6. 单摆的周期与以下哪个因素无关?A. 摆长B. 摆球质量C. 重力加速度D. 摆角答案:B7. 以下哪个量描述了简谐运动的能量?A. 振幅C. 频率D. 相位答案:A8. 以下哪个因素会影响单摆的周期?A. 摆长B. 摆球质量C. 摆角D. 重力加速度答案:A9. 阻尼振动中,振幅减小到原来的1/e时,经过的时间为:A. 1/2TB. TC. 2T答案:C10. 以下哪个现象不是简谐运动?A. 弹簧振子B. 单摆C. 弹簧振子的振幅逐渐减小D. 单摆的振幅逐渐减小答案:C二、填空题(每题4分,共20分)11. 简谐运动的周期公式为:T = 2π√(____/k),其中m为质量,k为弹簧常数。
答案:m12. 单摆的周期公式为:T = 2π√(L/g),其中L为摆长,g为重力加速度。
答案:L13. 阻尼振动的振幅公式为:A(t) = A0 * e^(-γt),其中A0为初始振幅,γ为阻尼系数,t为时间。
答案:A014. 简谐运动的频率公式为:f = 1/T,其中T为周期。
答案:1/T15. 简谐运动的相位公式为:φ = ωt + φ0,其中ω为角频率,t 为时间,φ0为初始相位。
答案:ωt + φ0三、计算题(每题10分,共50分)16. 一个质量为2kg的物体,通过弹簧连接在墙上,弹簧的弹簧常数为100N/m。
机械振动试题

机械振动试题一、选择题1. 下列关于机械振动的说法中,正确的是:A. 机械振动只存在于弹簧系统中B. 机械振动只存在于质点系统中C. 机械振动既存在于弹簧系统中,也存在于质点系统中D. 机械振动只存在于液体中2. 以下哪个现象不属于机械振动的特征:A. 周期性B. 振动幅度相等C. 能量交换D. 机械振动的振幅随时间变化3. 关于自由振动和受迫振动的说法,正确的是:A. 自由振动需要外力驱动B. 受迫振动不需要外力驱动C. 自由振动和受迫振动都需要外力驱动D. 自由振动和受迫振动都不需要外力驱动4. 振动系统的自然频率与以下哪个因素无关:A. 系统的刚度B. 系统的阻尼C. 系统的质量D. 系统所受的外力5. 下面哪种振动现象是产生共振的原因:A. 外力频率与振动系统自然频率相同B. 外力频率与振动系统自然频率不同C. 外力频率与振动系统自然频率较大差异D. 外力频率与振动系统自然频率较小差异二、简答题1. 什么是机械振动?机械振动是物体围绕平衡位置做周期性的往复运动。
它有着特定的振动频率和振幅,是一种具有周期性和能量交换的运动形式。
2. 机械振动有哪些特征?机械振动具有周期性、振幅相等、能量交换和振幅随时间变化等特征。
周期性表示机械振动运动形式的重复性;振幅相等表示振动系统在每个周期内的振动幅度相等;能量交换表示振动系统的能量在正、反向振动过程中的转化与交换;振幅随时间变化表示振动幅度随着时间的推移而发生变化。
3. 什么是自由振动和受迫振动?自由振动是指机械振动系统受到初位移或初速度激发后,在无外力驱动的情况下进行的振动。
受迫振动是指机械振动系统受到外力周期性激励后产生的振动。
4. 什么是共振现象?共振现象是指当外力的频率与振动系统的自然频率相同时,产生的振幅迅速增大的现象。
在共振状态下,系统振幅可能会无限增大,从而引起系统的损坏甚至破坏。
5. 如何减小机械振动的共振现象?减小机械振动的共振现象可以通过以下几种方法来实现:- 调整外力的频率,使其与振动系统的自然频率有所偏离,避免共振;- 增加阻尼,通过增加振动系统的阻尼来消耗振动能量,减小共振现象;- 改变振动系统的刚度和质量,使其自然频率与外力频率有所偏离,从而减少共振。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009--2011中南大学考试试卷一、填空题(本题15分,每空1分)1、按不同情况进行分类,振动系统大致可分成,线性振动和(非线性振动);(确定性振动)和随机振动;自由振动和(强迫振动);周期振动和(瞬态振动);(连续系统)和离散系统。
2、(惯性)元件、(弹性)元件、(阻尼)元件是离散振动系统的三个最基本元素。
3、系统固有频率主要与系统的(质量)和(刚度)有关,与系统受到的激励无关。
4、研究随机振动的方法是(概率统计),工程上常见的随机过程的数字特征有:(均值),(方差),(自相关函数)和(互相关函数)。
二、简答题(本题40分,每小题8分)1、简述机械振动的定义和系统发生振动的原因。
(10分)答:机械振动是指机械或结构在它的静平衡位置附近往复弹性运动。
振动系统发生振动的原因是由于外界对系统运动状态的影响,即外界对系统的激励或作用。
2、简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
答:实际阻尼是度量系统消耗能量的能力的物理量,阻尼系数c是度量阻尼的量;临界阻尼是c2enm ω=;阻尼比是/eccξ=(8分)3、共振具体指的是振动系统在什么状态下振动?简述其能量集聚过程?答:共振是指振动系统在激励频率约等于系统的固有频率时的振动状态。
在此过程中,激励力与阻尼力平衡,弹性力与惯性力平衡。
即动能与势能相互转化,激励力提供阻尼消耗。
4、简述线性系统在振动过程中动能和势能之间的关系。
(8分)5、简述刚度矩阵[K]中元素k ij的意义。
答:如果系统的第j个自由度沿其坐标正方向有一个单位位移,其余各个自由度的位移保持为零,为保持系统这种变形状态需要在各个自由度施加外力,其中在第i个自由度上施加的外力就是kij(8分)三、计算题(45分)3.1、(10分)求如图1所示的扭转系统的固有频率。
图13.2、(15分)如图2所示系统,轮子可绕水平轴转动,对转轴的转动惯量为I,轮缘绕有软绳,下端挂有重量为P的物体,绳与轮缘之间无滑动。
在图示位置,由水平弹簧维持平衡。
半径R与a均已知。
1)写出系统的动能函数和势能函数;(5分)2) 求系统的运动方程;(5分)2)求出系统的固有频率。
(5分)3.3、求如图3所示的弹簧质量系统的固有频率和振型。
(设13;m m m==22;m m=14;k k k==232;k k k==563;k k k==)(20分)图2P koIRa图32009—2010年参考答案3.1 解:1)串联刚度k t1与k t2的总刚度:1212K K K K K =+2) 系统总刚度:12312K K K K K K =++3) 系统固有频率:ω==也可用能量法,求得系统运动方程,即可得其固有频率)3.2解:取轮的转角θ为坐标,顺时针为正,系统平衡时0θ=,则当轮子有θ转角时,系统有:θθθ=+=+2222111()()222T P P E I R I R g gθ=21()2U k a由()0T d E U +=可知:θθ++=222()0P I R ka g即:ω=n (rad/s ),故πω==22n T (s )3.3 解:1)以静平衡位置为原点,设123,,I I I 的位移123,,θθθ为广义坐标,画出123,,I I I 隔离体,根据牛顿第二定律得到运动微分方程:1111212222213233333243()0()()0()0θθθθθθθθθθθθθ⎧++-=⎪+-+-=⎨⎪+-+=⎩t t t t t t I k k I k k I k k所以:[][]12312222333340010000040;0000102101210012t t t t t t t t t t I M I I I k k k K k k k k k k k k ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦+--⎡⎤⎡⎤⎢⎥⎢⎥=-+-=--⎢⎥⎢⎥⎢⎥⎢⎥-+-⎣⎦⎣⎦系统运动微分方程可写为:[][]1122330θθθθθθ⎧⎫⎧⎫⎪⎪⎪⎪+=⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭M K ………… (a)或者采用能量法:系统的动能和势能分别为222112233111222T E I I I θθθ=++ 222211212323431111()()2222t t t t U k k k k θθθθθθ=+-+-+222121232343212323111()()()222t t t t t t t t k k k k k k k k θθθθθθθ=+++++--求偏导也可以得到[][],M K 。
2)设系统固有振动的解为:112233cos θθωθ⎧⎫⎧⎫⎪⎪⎪⎪=⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭u u t u ,代入(a )可得:[][]1223()0u K M u u ω⎧⎫⎪⎪-=⎨⎬⎪⎪⎩⎭………… (b)得到频率方程:222220()24002k I k k k I k kk Iωωωω--=---=--即:222422()(2)(4102)0k I I kI k ωωωω=--+=解得:2k I ω=和22ω=kI所以:123ωωω=<=<=………… (c)将(c )代入(b )可得:1-1 -0.281111.781112352(0452(404502(4k k I kI u kk k I k u I u k kk I I ⎡⎤±--⎢⎥⎢⎥⎧⎫⎢⎥±⎪⎪---=⎢⎥⎨⎬⎢⎥⎪⎪⎩⎭⎢⎥±--⎢⎥⎢⎥⎣⎦和1232202240022k k I k I u kk k I ku Iu k kk II ⎡⎤--⎢⎥⎧⎫⎢⎥⎪⎪⎢⎥---=⎨⎬⎢⎥⎪⎪⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦解得: 112131::1:1.78:1u u u ≈;(or 112131:::1u u u ≈) 122232::1:0:1u u u ≈-; 132333::1:0.28:1u u u ≈-;(or 1121313::1::14u u u +≈)令31u =,得到系统的三阶振型如图:2011- 2012中南大学考试试卷一、填空题(本题15分,每空1分)1、图1为线性系统,根据图1填空:1)图1所示的系统中,如果C=0,则系统固有频率ωn=(),当C≠0时,系统的阻尼比ζ=(),当阻尼比ζ小于1时,系统的阻尼固有频率为();2)如果F(t)为简谐函数,则系统的响应由()响应和()响应两部分组成;3)如果F(t)=0,C=0,系统的振动称为()其表达式为x(t)=()。
图22、图2是一个线性系统,根据图2填空:1)该系统有()个自由度,系统中的惯性元件包括(),弹性元件包括(),阻尼元件是();2)如果F(t)为周期函数,则系统的激励向量是(),对应的响应向量是();系统微分方程通式为()3)如果系统的刚度矩阵为非对角矩阵,则微分方程存在()耦合,求解微分方程需要解耦。
二、简答题(本题40分,每小题10分)6、在图1中,若F(t)=k Acosωt,写出系统响应x(t)通式,根据放大因子分析抑制系统共振的方法;(8分)7、在图1中,如果F(t)为非周期函数且其傅里叶积分存在,有哪些求解系统响应的方式,并简述一种以上具体求解方法;(8分)8、在图2中,如果已求出x1、x2、x3,分析该系统作用在基础上的弹簧力,阻尼力及合力;(8分)9、分析多自由度系统的线性变换矩阵[u]包含有哪些信息;(8分)10、线性系统中,平稳随机激励与随机响应有哪些相互关联的数字特征,表述一个以上关联关系;(8分)三、计算题(共45分)1、求图3所示系统的等效刚度(5分)。
图32、 求图4所示系统的固有频率(5分)。
图42、 在图5所示系统中,摆锤质量为m ;摆杆长l ,摆杆质量可以忽略;在距离铰链O 距离为a 的地方,两侧都安装刚度为k 的弹簧。
假设系统做微幅摆动,求系统的固有频率(10分)。
提示:242kcos =1-+-......(-1)24(2)k k θθθθ!!!图53、 求图6所示系统的固有频率和固有振型(10分)。
4、 求图7所示系统的固有频率及振型,并画出振型图 (15分)。
其中:132;2m m m m m === ;123456k k k k k k k ======。
图7《机械振动基础》答案和评分细则:一、填空题(本题15分,每空1分)1、1)(m/k )1/2;C/2(mk )1/2;ωn /(1-ζ2)1/2; 2)瞬态; 稳态3)自由振动;x(t)=Acos(ωt -φ) 2、1)3; m 1,m 2,m 3; k 1,k 2,k 3; C 1,C 2,C 3;2){0,0,F(t)}T ;{x 1,x 2,x 3}T ;[M]{x} +[C]{x ’}+[K]{x ”}={F(t)} 3) 弹性二、 简答题(本题40分,,5小题,每小题8分)1、写出x 通式x=AH(ω)co s (ωt -φ)(3分),写出放大因子表达式(2分),222)/2(])/(1[1)(n n H ωζωωωω+-=根据H (ω)正确分析(3分); 2、写出“脉冲积分法,傅里叶变换法、拉普拉斯变换法”中的两个(3分),分别写出对应求解公式[⎰-=t d F t h t x 0)()()(τττ)()()(ωωωF H X =)()()(s F s H s X =]中的两个(2分),用文字表述公式含义(3分);3、分析并写出弹簧力公式 11x k F s -=(3分),分析并写出阻尼力公式11x c F d -=(3分),以矢量和写出合力211211)()(•+==x c x k F N tr (2分); 4、[u]中的n 个列向量构成变换后的主坐标系(3分),每一列向量表示一种振型(2分),列向量数值反映同一振型下各坐标振幅比值和相位关系(3分); 5、答出“均值、方差、相关函数(自相关、互相关)、功率谱(自谱、互谱)”得6分,写出一种以上关联关系(fH μμ)0(x =)()()(2ωωωf x S H S •=)(/)()(ωωωf fx S S H =…)得2分三、 计算题1、 (5分)。
计算过程正确2分,结果正确给3分。
答案: 1212t t eq t t k k k k k =+2、 (5分)。
写出动势能方程2分,推出微分方程2分,写出结果1分答案:取圆柱体的转角θ为坐标,逆时针为正,静平衡位置时θ=0,则当m 有θ转角时,系统的动能和势能函数为:22222111()()2221()2T E I m r I mr U k r θθθθ⎧=+=+⎪⎪⎨⎪=⎪⎩ 由()0T d E U +=可知: 22()0I mr kr θθ++=即:22n kr I mrω=+3、 (10分)。
