桂林电子科技大学静力学试卷
桂林电子科技大学2016年考研试题801机械设计(2016-A)
桂林电子科技大学2016年研究生统一入学考试试题科目代码：801 科目名称：机械设计（A）请注意：答案必须写在答题纸上（写在试题上无效）。
答题纸请注明页码与总页数。
一、选择题（20分，每小题2分）1. 下列零件的失效形式中，不属于强度问题。
A 螺栓断裂B 齿轮的齿面发生疲劳点蚀C 蜗杆轴产生过大的弯曲变形D 滚动轴承套圈的滚道上被压出的深的凹坑2. 在齿轮传动中从动轮的齿面接触应力按变化。
rA. 对称循环B. 脉动循环C. 循环特性=-0.5循环D. 循环特性r=+1循环3. 在常用的螺纹连接中，自锁性能最好的螺纹是。
A. 三角形螺纹B.梯形螺纹C.锯齿形螺纹D.矩形螺纹4. 对轴的削弱最大。
A.平键B.半圆键C.楔键D.花键5. 平带和V带传动主要依靠来传递运动和动力。
A. 带的紧边拉力B. 带的松边拉力C. 带的预紧力D. 带和带轮接触面间的摩擦力6. 设计V带传动时发现V带根数过多，可采用来解决。
A. 增大传动比B. 加大传动中心距C. 选用更大截面型号的V带D. 无法确定7. 下列措施中，不利于提高齿轮轮齿抗弯疲劳折断能力。
A．减轻加工损伤 B. 减小齿面粗糙度 C. 表面强化处理 D. 减小齿根过渡曲线半径8. 选择齿轮毛坯的形式（锻造、铸造或轧制圆钢）的主要依据是。
A. 齿轮精度B. 齿面宽度C. 齿轮直径D. 齿轮在轴上的布置位置9. 在以下四点中，是不属于轮胎联轴器的特点。
A. 富有弹性B. 结构紧凑C. 扭转刚度小D. 缓冲性能好10. 不能做轴向定位。
A. 平键B. 螺钉C. 圆柱销D. 轴肩二、填空题（14分，每空1分）1. 静应力的应力比r= ，对称循环应力的应力比r= ，脉动循环应力的应力比r= 。
2. 螺纹连接拧紧的目的是增强连接的、和能力。
3. 当带有打滑趋势时．带传功的有效拉力达到，而带传动的最大有效拉力决定于，，三个因素。
4. 当链节数为偶数时，接口处可用或来固定。
2017年广西桂林电子科技大学机械设计考研真题A卷
2017年广西桂林电子科技大学机械设计考研真题A卷一、单项选择题（在空格里填上正确答案前的符号，每小题2分，共20分）。
1、一钢制零件材料的疲劳强度极限σr=152 MPa,取寿命指数m=9，应力循环基数N0=5×106，当应力循环次数N=8×106时,材料的疲劳强度极限σrN = MPa。
A. 144B. 152C. 155D. 1602、双线螺纹的直径为：大径d=20mm，小径d1=17.294mm，中径d2=18.376mm，螺距p=2.5mm，则螺纹升角φ为。
A．2.48° B．4.55° C．4.95° D．5.26°3、楔键联接与平键联接相比较，其主要缺点是。
A．楔键的斜面加工困难 B．安装时易损坏C．楔键装入键槽后，在轮毂中产生初应力 D．轴与轮毂的对中性差4、普通V带截面的楔角为40°，V带轮相应的槽角应是 40°。
A. 大于B. 小于C. 等于D. 大于或等于5、链号为08A的滚子链，其节距值是。
A. 8mmB. 16mmC. 12.70mm D．25.4mm6、在圆柱齿轮传动中，常使小轮齿宽b1略大于大轮齿宽b2，是为了。
A.提高小齿轮齿面接触疲劳强度B.提高小齿轮根弯曲疲劳强度C.补偿安装误差，以保证全齿宽接触D.减少小齿轮载荷分布不均。
7、在非液体摩擦滑动轴承设计中，限制比压P的主要目的是。
A．防止出现过大的摩擦阻力矩 B．防止轴承的压力过大而过度发热C．防止轴承过度磨损 D．防止轴承因压力过大而发生塑性变形。
8、万向联轴器的主要缺点是。
A．结构复杂 B．能传递的转矩很小C．从动轴角速度有周期性变化 D．不允许两轴间有较小的位移9、某厂运输带由转速1440 r/min 的电机通过三套减速装置（a、b、c）来驱动，其中 a.双级直齿圆柱齿轮减速器；b.套筒滚子链传动；c.V带传动;这三套减速装置的较为合理的排列次序是。
桂林电子科技大学材料力学试卷
桂林电子科技大学应用科技学院试卷课程名称工程力学(闭卷）题号一二三四五六七八九十成绩满分30 15 55 100 得分（注：请将答案直接写在试卷上，写在其它纸上无效。
）一、填空题（30分，每空1分）1、低碳钢拉伸时的变形过程可分为————、————、————、————四个阶段。
2、提高梁强度的措施有————————、———————、———————等。
3、杆件受力变形的基本形式有—————、—————、—————、————。
4、材料力学中关于材料的基本假定有—————、—————、—————、—————。
5、杆件的基本变形是_____________、______________、_____________、_____________。
6、延伸率δ≥______的材料为____________。
7、轴向拉压横截面上的正应力为σ0，则斜截面上的应力在α=______时正应力最大且等于_____；α=______时切应力最大且等于______。
8、应力集中容易发生在_______、_______、_______、_______等截面尺寸发生变化的部位。
1.直径为D的圆截面其极惯性矩为____________；惯性矩为____________；抗扭截面系数为____________。
二、判断题判断题判断题判断题（本题共10小题，1.5分共15分）1.泊松比是材料纵向线应变和横向线应变的绝对值之比。
（）2.胡克（Hooke）定律的适用范围是构件的应力不超过材料的比例极限。
（）3.塑性材料试件拉伸试验时，在强化阶段只发生塑性变形。
（）4.中性轴一定是横截面的对称轴。
（）5.梁的挠曲线近似微分方程(''EIwM=)对线弹性小变形总是成立。
（）6.梁发生弯曲变形时，挠度越大的截面，其转角也越大。
（）7.主应力一定是正应力。
（）8.受力构件某点处，在正应力为零的方向上线应变也一定为零。
（）9.杆件发生的组合变形是线弹性小变形时，一般可应用叠加原理。
电子科技大学《理论力学》20春期末考试.doc
1.三力平衡定理是（）A.共面不平行的三个力相互平衡必汇交于一点B.共面三力若平衡，必汇交于一点C.三力汇交于一点，则这三个力必互相平衡【参考答案】: A2.如果两个力系满足下列哪个条件，则该两个力系为等效力系（）A.两个力系的主矢相等B.两个力系的主矩相等C.两个力系的主矢和主矩分别对应相等 D.两个力系作用在同一刚体上【参考答案】: C3.若一平面任意力系分别向A.B 两点简化，所得的主矢和主矩都不为零，则两者的（）。
A.主矢相等，主矩相等B.主矢相等，主矩不等C.主矢不等，主矩相等 D.主矢不等，主矩不等【参考答案】: B4.两个力，它们的大小相等、方向相反和作用线沿同一直线。
这是( )。
A.它们作用在物体系统上，使之处于平衡的必要和充分条件B.它们作用在刚体系统上，使之处于平衡的必要和充分条件C.它们作用在刚体上，使之处于平衡的必要条件，但不是充分条件D.它们作用在变形体上，使之处于平衡的必要条件，但不是充分条件【参考答案】: D5.时钟上分针转动的角速度是（）A. B. C.【参考答案】: B6.平面运动刚体相对其上任意两点的( ）。
A.角速度相等,角加速度相等B.角速度相等,角加速度不相等C.角速度不相等,角加速度相等 D.角速度不相等,角加速度不相等【参考答案】: A7.下列属于二力构件的是( )A.杆件 ACB.杆件 BCC.杆件 DED.杆件 AE.BC和 DE均是二力构件【参考答案】: C8.作用在刚体上两个力平衡的充要条件是：两个力的大小( )，方向（），作用在（）上。
A.相等，相反,同一条直线B.相等，相同,同一条直线C.相等，相同,同一条曲线D.相等，相反,同一条曲线【参考答案】: A9.已知F1、F2、F3为作用于刚体上的一个平面汇交力系，其各力矢的关系如下图所示，则该力系?（）。
A.有合力 R = F1B.有合力 R = F3C.有合力 R = 2F3D.无合力。
【参考答案】: C10.某瞬时定轴转动刚体的角速度ω和角加速度ε都是一代数量（）。
2014桂林电子科技大学硕士研究生入学考试复试试卷工程力学试题A卷
2014桂林电子科技大学硕士研究生入学考试复试试卷工程力
学试题A卷
桂林电子科技大学2014年硕士研究生入学考试复试试卷
考试科目代码：201考试科目名称：工程力学（A卷）请注意：答案必须写在答题纸上（写在试卷上无效）。
一、杆AB、轮C和绳子AC组成的物体系统如图所示。
作用在杆上的力偶，其力矩为m
，
设AC＝2R，R为轮C的半径，各物体重量均忽略不计，各接触处均为光滑的，试求铰链
A对AB杆的约束反力。
（16分）
题一图题二图
二、组合梁由AC和CE用铰链联接而成，结构的尺寸和载荷如图所示，已知 F 5kN，q4kN/m，力偶矩M10kN·m，试求梁的支座反力。
（24分）
三、某桥式起重机，电动机通过变速箱带动传动轴如图示。
已知传动轴转速n=27转/分，传递功率P=3kW，轴的许用剪应力[]=40MPa，剪切弹性模量G=80GPa，轴单位长度的许
可扭角[θ]=1/m，试按强度条件和刚度条件选择轴径d。
（20分）题三图题四图
四、悬臂梁受载荷如图所示，试求B处的支反力，并画出梁的剪力图和弯矩图。
（14分）
共2页第1页
请注意：答案必须写在答题纸上（写在试卷上无效）。
五、截面为No20a的工字钢梁受力如图所示，已知[ ] 160MPa，W z237cm3，F 30KN，试校核梁的强度。
（12分）
题五图题六图
六、试用解析法求图示单元体斜截面上的正应力和切应力。
(14分)
共2页第2页。
桂林电子科技大学大学物理复习资料2学期
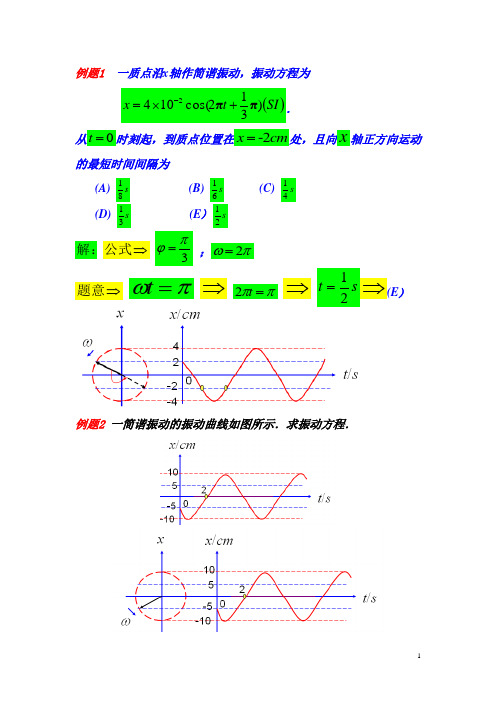
例题1 一质点沿x 轴作简谐振动，振动方程为 ()SI t x )312cos(1042ππ+⨯=-． 从0=t 时刻起，到质点位置在cm x 2-=处，且向x 轴正方向运动的最短时间间隔为(A) s 81 (B) s 61(C) s 41(D) s 31(E ) s 21解： ⇒公式 3πϕ= ；πω2=⇒题意 πω=t ⇒ ππ=t 2 ⇒ s t 21=⇒(E )例题2 一简谐振动的振动曲线如图所示．求振动方程．解： ⇒由图 m 1.0A = ；s t 2=⇒由图 旋转矢量 ⇒ 3262πππϕ=+= 旋转矢量 ⇒ 65πω=t ⇒ 125πω= ⇒ ())(32125cos 1.0cos SI t t A x ⎪⎭⎫ ⎝⎛+=+=ππϕω 例题3 一质点作简谐振动．其运动速度与时间的曲线如图所示．若质点的振动规律用余弦函数描述，则其初相应为(A) π/6． (B) 5π/6． (C) -5π/6． (D) -π/6． (E) -2π/3．答案：(C) -5π/6()SI t x )22.22cos(05.0+=π()ϕω+=t A x cos ；()'cos ϕωυυ+=t m23'πϕπϕ+=-= ⇒ πϕ65-= 例题4 一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，（如图所示），作成一复摆．已知细棒绕通过其一端的轴的转动惯量231ml J =，此摆作微小振动的周期为 A g l π2；B g l 22π；C √g l 322π；D g l 3π；练习题1. 一物体同时参与两个同方向的简谐振动：()SI t x )212cos(04.01π+π= , ()SI t x )2cos(03.02π+π= 求此物体的振动方程．解：设合成运动（简谐振动）的振动方程为)cos(φω+=t A x 则)cos(2122122212φφ-++=A A A A A ① 以 A 1 = 4 cm ，A 2 = 3 cm ，π=π-π=-212112φφ代入①式，得cm A 5cm 3422=+= 2分又rad A A A A 22.2127cos cos sin sin arctg 22112211≈≈++= φφφφφ ② O l∴ 1分练习题2. 两个同方向简谐振动的振动方程分别为 ()SI )4310cos(10521π+⨯=-t x ；()SI )4110cos(10622π+⨯=-t x 求合振动方程．解：依合振动的振幅及初相公式可得 φ∆++=cos 2212221A A A A Am 2-2221081.710)4143cos(65265⨯=⨯-⨯⨯⨯++=-ππ rad 48.18.84)4/cos(6)4/3cos(5)4/sin(6)4/3sin(5arctg ==++= ππππφ 2分 则所求的合成振动方程为()SI )48.110cos(1081.72+⨯=-t x 1分练习题3. 两个同方向的简谐振动的振动方程分别为 x 1 = 4×10-2cos2π)81(+t (SI), x 2 = 3×10-2cos2π)41(+t (SI) 求合振动方程．解：由题意 x 1 = 4×10-2cos )42(ππ+t (SI) x 2 =3×10-2cos )22(ππ+t (SI) 按合成振动公式代入已知量，可得合振幅及初相为 m A -22221048.610)4/2/cos(2434⨯=⨯-++=-ππrad 12.1)2/cos(3)4/cos(4)2/sin(3)4/sin(4arctg =++=ππππφ 合振动方程为x = 6.48×10-2 cos(2πt+1.12)(SI)练习题4. 一质点同时参与两个同方向的简谐振动，其振动方程分别为 x 1 =5×10-2cos(4t + π/3) (SI) , x 2 =3×10-2sin(4t - π/6） (SI) 画出两振动的旋转矢量图，并求合振动的振动方程．解：x 2 = 3×10-2 sin(4t - π/6) = 3×10-2cos(4t - π/6- π/2)= 3×10-2cos(4t - 2π/3)．作两振动的旋转矢量图，如图所示由图得：合振动的振幅和初相分别为A = (5-3)cm = 2 cm ，φ = π/3合振动方程为 x = 2×10-2cos(4t + π/3) (SI)第九章例题1. 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则(A) 其振幅为3 m ． (B) 其周期为s 31(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播． 答案：ππω6T2== ⇒ s 31T = ⇒ （B ） mm A 3= ；波沿x 轴负向传播；s m u /100=例题2：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则(A) 波速为C ． (B)周期为1/B ． (C) 波长为 2π /C ． (D) 角频率为2π /B ． 答案：(A) 波速为C u ω= ；(B) 周期B T π2= ；(C ) 波长为Cπλ2= ；(D)角频率为Cu =ω 例题3：一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为： A =_________；ω =_____ __；φ =_______________．答案：m A 1.0= ；s T 12= ；s rad /6T 2ππω== ；3πφ= 例题4. 图为t = T / 4 时一平面简谐波的波形曲线，则其波的表达式为 ______________________________________________．答案：m A 1.0= ；m 4=λ ；s m u /330= ⇒ s rad uv /16522===λππω由t = T / 4时刻的波形图⇒t=0时刻的波形图，利用旋转矢量法求ϕ，在利用三步法求出波函数。
大学物理复习资料桂林电子科技大学
一、力学答案习题1：一质点从静止开始作直线运动，开始时加速度为a 0，此后加速度随时间均匀增加，经过时间t 后，加速度为2a 0，经过时间2t 后，加速度为3 a 0 ,…求经过时间nt 后，该质点的速度和走过的距离． 已知：初始时加速度为a 0，当τ=t 时，012a a =;当τ2=t 时，023a a =; ;当τn t =时，()01a n a n +=。
求：经过τn t =后，该质点的速度()τυn 和走过的距离()τn s 。
解：设质点的加速度为 a = a 0+a t ∵ t = t 时， a =2 a 0 ∴ a = a 0 /t即 a = a 0+ a 0 t /t ，1分由 a = dv /dt ， 得 dv = adt∴2002ta t a τ+=v1分由 v = ds /dt ， ds = v dtt t a t a t s ttsd )2(d d 2000τ+==⎰⎰⎰v302062t a t a s τ+=1分t = nt 时，质点的速度 ττ0)2(21a n n n +=v1分质点走过的距离202)3(61ττa n n s n +=1分2. 有一质点沿x 轴作直线运动，t 时刻的坐标为x = 4.5 t 2 - 2 t 3 (SI) ．试求：(1)第2秒内的平均速度；(2)第2秒末的瞬时速度；(3) 第2秒内的路程．已知：x = 4.5 t2 - 2 t3求：⑴υ；⑵υ；⑶S解：(1)()()5.012-=∆-=∆∆=txxtxvm/s 1分(2) v = d x/d t = 9t - 6t21分v(2) =-6 m/s1分(3) S = |x(1.5)-x(1)| + |x(2)-x(1.5)| = 2.25 m2分3.已知：求：解：（A）4. B2分(A2/R)+4pB3分5. 已知：求：解：v212分1分v212分6. 已知：求：解：j t i t 2323+ (SI)3分7. 已知：求：解：0 2分2 g 2分8. 已知：求：解：l/cos 2θ3分9. 已知：求：解：θcos /mg1分θθcos sin gl2分10. 已知：求：解：解：(1) 子弹进入沙土后受力为－Ｋv ，由牛顿定律tmK d d v v =- 3分∴⎰⎰=-=-vv v vvv 0d d ,d d 0tt m K t m K 1分∴mKt /0e -=v v1分(2) 求最大深度 解法一： t x d d =vtx m Kt d e d /0-=v 2分∴)e 1()/(/0m Kt K m x --=v2分Km x /0max v =1分解法二：x m t x x m t mK d d )d d )(d d (d d vv v v v ===-∴v d K mdx -=3分 ∴Km x /0max v =2分11. 解： (1) 设同步卫星距地面的高度为h ，距地心的距离r=R+h ，由牛顿定律 22/ωmr r GMm = ①2分又由mg R GMm =2/得2gR GM =，1分代入①式得3/122)/(ωgR r =②1分同步卫星的角速度w 与地球自转角速度相同，其值为51027.7-⨯=ω rad/s1分解得=r 71022.4⨯m ， 41058.3⨯=-=R r h km2分(2) 由题设可知卫星角速度w 的误差限度为10105.5-⨯=∆ω rad/s1分由②式得 223/ωgR r =取对数ωln 2ln ln 32-=）（gR r取微分并令 dr =Dr, dw =Dw 且取绝对值 3D r/r =2Dw/w∴ Dr=2rDw /(3w) =213 m2分12. (B) 13. (B) 14. (A) 15. (C)16. (C) 17. (C)参考解： 挂重物时，mg －T= ma = mR β , TR =Jb由此解出 J mR mgR+=2β而用拉力时， 2mgR = J β' β'=2mgR / J故有β'＞2b18. (C) 19.31ω3分20. 3v 0 / (2l)3分21.()R m M m 22+v3分22. 8 rad ·s -13分23. 3.77 rad ·s -13分24. 0.2prad ·s -13分25. 解：体系所做的运动是匀速→匀加速→匀减速定轴转动．其中w 1是匀加速阶段的末角速度，也是匀减速阶段的初角速度，由此可得t ＝8 s 时， w 1＝w 0＋9＝27 rad /s3分当w ＝0时，得 t ＝(w 1＋24）/ 3＝17s所以，体系在17s 时角速度为零． 2分26. 解：R = 0.5 m ，w 0 = 900 rev/min = 30p rad/s ，根据转动定律 M = -Jb ①1分这里 M = -mNR ②1分m 为摩擦系数，N 为正压力，221mR J =． ③设在时刻t 砂轮开始停转，则有：从而得 b ＝-w 0 / t ④1分将②、③、④式代入①式，得)/(2102t mR NR ωμ-=-1分∴ m =μRw 0 / (2Nt)≈0.51分27. 解：根据转动定律 M ＝Jdw / dt1分即 dw ＝(M / J) dt1分其中 M ＝Fr ， r ＝0.1 m ， F ＝0.5 t ，J ＝1×10-3 kg ·m 2, 分别代入上式，得dw ＝50t dt 1分则1 s 末的角速度 w 1＝⎰1050t dt ＝25 rad / s2分28.T a解：撤去外加力矩后受力分析如图所示． 2分 m 1g －T = m 1a 1分Tr ＝Jb1分a ＝rb 1分 a = m 1gr / ( m 1r + J / r)代入J ＝221mr , a =mm gm 2111+= 6.32 ms -2 2分 ∵ v 0－at ＝02分∴ t ＝v 0 / a ＝0.095 s1分29. 解：由人和转台系统的角动量守恒J 1w 1 + J 2w 2 = 02分其中 J 1＝300 kg ·m 2，w 1=v/r =0.5 rad / s ， J 2＝3000 kg?m 2∴ w 2＝－J 1w 1/J 2＝－0.05 rad/s1分人相对于转台的角速度 w r ＝w 1－w 2＝0.55 rad/s1分∴ t ＝2p /r ω＝11.4 s1分四、电磁感应 电磁场习题1.t O (A)t O(C)t O (B)t O(D)如图所示，矩形区域为均匀稳恒磁场，半圆形闭合导线回路在纸面内绕轴O 作逆时针方向匀角速转动，O 点是圆心且恰好落在磁场的边缘上，半圆形闭合导线完全在磁场外时开始计时．图(A)-(D)的E--t 函数图象中哪一条属于半圆形导线回路中产生的感应电动势？［］2. 一块铜板垂直于磁场方向放在磁感强度正在增大的磁场中时，铜板中出现的涡流(感应电流)将(A) 加速铜板中磁场的增加．(B) 减缓铜板中磁场的增加．(C) 对磁场不起作用．(D) 使铜板中磁场反向．［］3. 半径为a的圆线圈置于磁感强度为B 的均匀磁场中，线圈平面与磁场方向垂直，线圈电阻为R；当把线圈转动使其法向与B 的夹角a =60°时，线圈中通过的电荷与线圈面积及转动所用的时间的关系是(A) 与线圈面积成正比，与时间无关．(B) 与线圈面积成正比，与时间成正比．(C) 与线圈面积成反比，与时间成正比．(D) 与线圈面积成反比，与时间无关．［］4.一个圆形线环，它的一半放在一分布在方形区域的匀强磁场B 中，另一半位于磁场之外，如图所示．磁场B 的方向垂直指向纸内．欲使圆线环中产生逆时针方向的感应电流，应使(A) 线环向右平移．(B) 线环向上平移．(C) 线环向左平移．(D) 磁场强度减弱．［］5.O O ′Babω一矩形线框长为a 宽为b ，置于均匀磁场中，线框绕OO ′轴，以匀角速度w 旋转(如图所示)．设t =0时，线框平面处于纸面内，则任一时刻感应电动势的大小为(A) 2abB | cosw t |． (B) w abB (C)t abB ωωcos 21． (D) w abB | cosw t |．(E) w abB | sinw t |． ［ ］6.H 磁极磁极条形磁铁N N S A B E F G在如图所示的装置中，把静止的条形磁铁从螺线管中按图示情况抽出时(A) 螺线管线圈中感生电流方向如A 点处箭头所示． (B) 螺线管右端感应呈S 极． (C) 线框EFGH 从图下方粗箭头方向看去将逆时针旋转． (D) 线框EFGH 从图下方粗箭头方向看去将顺时针旋转． ［ ］7.如图所示，导体棒AB 在均匀磁场B 中 绕通过C 点的垂直于棒长且沿磁场方向的轴OO? 转动（角速度ω与B同方向），BC 的长度为棒长的31，则(A) A 点比B 点电势高． (B) A 点与B 点电势相等． (B) A 点比B 点电势低． (D) 有稳恒电流从A 点流向B 点．8.如图所示，闭合电路由带铁芯的螺线管，电源，滑线变阻器组成．问在下列哪一种情况下可使线圈中产生的感应电动势与原电流Ｉ的方向相反．(A) 滑线变阻器的触点A 向左滑动． (B) 滑线变阻器的触点A 向右滑动． (C) 螺线管上接点B 向左移动(忽略长螺线管的电阻)． (D) 把铁芯从螺线管中抽出． ［ ］9. 用导线制成一半径为r =10 cm 的闭合圆形线圈，其电阻R =10 W ，均匀磁场垂直于线圈平面．欲使电路中有一稳定的感应电流i = 0.01 A ，B 的变化率应为dB /dt =_______________________________．10.x一段导线被弯成圆心在O 点、半径为R 的三段圆弧ab 、bc 、ca ，它们构成了一个闭合回路，ab 位于xOy 平面内，bc 和ca 分别位于另两个坐标面中(如图)．均匀磁场B沿x 轴正方向穿过圆弧bc 与坐标轴所围成的平面．设磁感强度随时间的变化率为K (K >0)，则闭合回路abca 中感应电动势的数值为______________；圆弧bc 中感应电流的方向是 _________________．11.×××磁换能器常用来检测微小的振动．如图，在振动杆的一端固接一个N 匝的矩形线圈，线圈的一部分在匀强磁场B中，设杆的微小振动规律为x =Acos w t ,线圈随杆振动时，线圈中 的感应电动势为_______________________． 12.在国际单位制中，磁场强度的单位是__________．磁感强度的单位是______，用H B 21表示的单位体积内储存的磁能的单位是__________．13.半径为r的小绝缘圆环，置于半径为R的大导线圆环中心，二者在同一平面内，且r <<R．在大导线环中通有正弦电流（取逆时针方向为正）I =I0sinwt，其中w、I0为常数，t为时间，则任一时刻小线环中感应电动势（取逆时针方向为正）为_________________________________．14. 在一马蹄形磁铁下面放一铜盘，铜盘可自由绕轴转动，如图所示．当上面的磁铁迅速旋转时，下面的铜盘也跟着以相同转向转动起来．这是因为________________________________________________________________________________．15.x×××××如图所示，aOc为一折成∠形的金属导线(aO =Oc =L)，位于xy平面中；磁感强度为B 的匀强磁场垂直于xy平面．当aOc以速度v 沿x轴正向运动时，导线上a、c两点间电势差U ac =____________；当aOc以速度v 沿y轴正向运动时，a、c两点的电势相比较,是____________点电势高．16.B金属杆AB以匀速v =2 m/s平行于长直载流导线运动，导线与AB共面且相互垂直，如图所示．已知导线载有电流I = 40 A，则此金属杆中的感应电动势E i =____________，电势较高端为______．(ln2 = 0.69)17.两个半径分别为R和r的同轴圆形线圈相距x，且R >>r，x >>R．若大线圈通有电流I而小线圈沿x轴方向以速率v运动，试求x =NR时(N为正数)小线圈回路中产生的感应电动势的大小．18.I (t)v如图所示，真空中一长直导线通有电流I (t) =I0e-lt (式中I0、l为常量，t为时间)，有一带滑动边的矩形导线框与长直导线平行共面，二者相距a．矩形线框的滑动边与长直导线垂直，它的长度为b，并且以匀速v (方向平行长直导线)滑动．若忽略线框中的自感电动势，并设开始时滑动边与对边重合，试求任意时刻t在矩形线框内的感应电动势Ei并讨论E i方向．19.B一导线弯成如图形状，放在均匀磁场B 中，B 的方向垂直图面向里．∠bcd =60°，bc =cd =a．使导线绕轴OO＇旋转，如图，转速为每分钟n转．计算E OO＇．20. 一球形电容器, 内导体半径为R1，外导体半径为R2．两球间充有相对介电常数为e r的介质. 在电容器上加电压，内球对外球的电压为U = U0sinwt．假设w不太大，以致电容器电场分布与静态场情形近似相同，求介质中各处的位移电流密度，再计算通过半径为r (R1 < r < R2) 的球面的总位移电流．a21.如图所示，一电荷线密度为l的长直带电线(与一正方形线圈共面并与其一对边平行)以变速率v =v(t)沿着其长度方向运动，正方形线圈中的总电阻为R，求t时刻方形线圈中感应电流i(t)的大小(不计线圈自身的自感)．22.如图所示，一长直导线通有电流I，其旁共面地放置一匀质金属梯形线框abcda，已知：da =ab =bc =L，两斜边与下底边夹角均为60°，d 点与导线相距l．今线框从静止开始自由下落H高度，且保持线框平面与长直导线始终共面，求：(1) 下落高度为H的瞬间，线框中的感应电流为多少？(2) 该瞬时线框中电势最高处与电势最低处之间的电势差为多少？23.I如图所示，一长直导线中通有电流I，有一垂直于导线、长度为l的金属棒AB在包含导线的平面内，以恒定的速度v 沿与棒成q角的方向移动．开始时，棒的A端到导线的距离为a，求任意时刻金属棒中的动生电动势，并指出棒哪端的电势高．24.a b如图所示，在竖直面内有一矩形导体回路abcd置于均匀磁场B 中，B的方向垂直于回路平面，abcd回路中的ab边的长为l，质量为m，可以在保持良好接触的情况下下滑，且摩擦力不计．ab边的初速度为零，回路电阻R集中在ab边上．(1) 求任一时刻ab边的速率v和t的关系；(2) 设两竖直边足够长，最后达到稳定的速率为若干？四、电磁感应电磁场答案1. (A)2. (B)3. (C)4. (C)5. (D)6. (C)7. (A)8. (A)9. 3.18 T/s3分10.4/2K R π=4分从c 流至b1分11. E=)2/cos(/d d π+==t A NbB t x NbB ωω 或E t NBbA ωωsin =3分12. A/m2分T 1分J/m 32分13.tI Rr ωωμcos 2020π-3分14. 铜盘内产生感生电流，磁场对电流作用所致． 3分15. vBLsinq2分a 2分16. 1.11×10-5 V3分A 端2分17. 解：由题意，大线圈中的电流Ｉ在小线圈回路处产生的磁场可视为均匀的．2/322202/3222)(2)(24x R IR x R IR B +=+ππ=μμ 3分故穿过小回路的磁通量为22/32220)(2r x R IR S B π+==⋅μΦ 32202x RI r π≈μ2分由于小线圈的运动，小线圈中的感应电动势为t x x IR r t i d d 23d d 4220π=Φ=μ v422023x I R r π=μ2分当x =NR 时，小线圈回路中的感应电动势为)2/(32420R N I r i v π=μ1分18.x (t )解：线框内既有感生又有动生电动势．设顺时针绕向为 E i 的正方向．由 E i = -dF /d t 出发，先求任意时刻t 的F (t)yt x yt I ba ad )(2)(0⎰+π=μ 2分a ba t x t I +π=ln)()(20μ2分再求F (t)对t 的导数：∴E ia ba t I t t +-π=-=-ln )1(e 2d d 00λμΦλv 4分E i 方向：l t <1时，逆时针；l t >1时，顺时针． 2分19. 解：4/32/32122a a S ==t BS ωΦcos =， 60/2n π=ω2分)60/2sin()120/3(2nt B na ππ=3分20. 解：由静电学计算： 0r 代表r 方向单位矢量∴012221)(r R R r R UR E -=012221sin )(r t U R R r R R⋅-=ω5分位移电流密度为t E t D J r∂∂=∂∂= εε000122210cos )(r t U R R r R R r⋅-=ωωεε4分过球面的总位移电流24d r J S J I π⋅==⎰⋅ t U R R R R r ωωεεcos 4012210-π=3分21. 解：长直带电线运动相当于电流λ⋅=)(t I v ．2分正方形线圈内的磁通量可如下求出x a x a I d 2d 0+⋅π=μΦ 2分2ln 2d 2000⋅π=+π=⎰Ia x a x Ia aμμΦ2分2ln d d 2d d 0t I a t i π=-=μΦ 2ln d )(d 20t t a v λμπ=2分2ln d )(d 2)(0t t aRRt i iv λμπ==2分22. 解：(1)由于线框垂直下落，线框所包围面积内的磁通量无变化，故感应电流I i = 02分(2) 设dc 边长为l ′，则由图可见 l '= L + 2Lcos60°= 2L 取d →c 的方向为dc 边内感应电动势的正向，则l l l gH I+'π=ln220μlLl gH I2ln220+π=μ 3分0>dc ，说明cd 段内电动势的方向由d →c2分由于回路内无电流 dcd c cdU U V =-=ll L gH I+π=2ln220μ2分因为c 点电势最高，d 点电势最低，故：cd V 为电势最高处与电势最低处之间的电势差． 1分23. 解： θsin v v =⊥θcos //v v =1分E i x x Ix x i d sin 2d 210θμv ⎰⎰π-== (i 指向以A 到B 为正) 3分式中：θcos v 2t l a x ++= θcos v 1t a x +=θθθμcos v cos vt lnsin v 20t a l a Ii +++π-= 2分A 端的电势高． 2分24. 解∶(1) 由l BI mg t m-=d d v ，R BlI v = 3分得v v mR l B g t 22d d -=积分⎰⎰=-vv v0d d t22t mR l B g得)ex p(2222t mR l B lB Rmg --=v 4分其中Lre3ult$Øltrch^lingnp2052^pict鸤*Lpacpsop0ãx635etavile8_45010009000003080100_0024015000000000050000000902000000000400000002010100050000000102ffffff00040000082e011<0085000000310201000000050000000b0200800000050000000c024*********2000026060f001a00ffffffff000010000002c0ffffffb7ffffvf_0070002f70q00000`00800_26060f000c004d617068547970610000501015000000fB0220ff000000000000900101000000002001054694d6573204e657'20526f6d616e000083040040002d0100p008000000320af400930601000000780015400000fb0280fe0_00000000009001010000000402007054696d6573204u6u7720526f 6d616e000083P60000002d01010044000000f00100000x000000320qa001f8020100000680015000000fb0280fe0002000000009001_00000000402001054696d6573204e6577205?6f6d616 e0000?3040000002d01000004000000f001010008000p00320ai001c10501000000650008000000320aa 001ac03010_0020290009040000320aa001340004_000006578702810000000fb0280fe0000000000009 001000000020002001053796d636f6c00020400_000d010********?00f001000008000000220aa0019204010000003d000a000_0026060&010a00ffff ffff01000000040010p00q0fb021000070000000010bc_2000p008>010_0222537973746?6d0086040004802d01000004000000f00 10100?70000000000Lrtlch|zchè\`f1#]hich£®«¥ôlch´\kesning0$(_li0"Üaf0 ´\kerfing0 _ (2)trcht tlch|kerning0_7×_¹»´óÔòòch~och\srsid_6336317 ± Laf13 \ltrchãs0 :õ2^sv750cAley100010009000003370100000300150000000000050000 000902000000000400000002010100050000000102ffffff0004000 0002e01180005000000310201000000050000000b020********* 0000000c02200480081200000026060f001a00ffffffff00001000000 0c0ffffffa9ffffff40080000c90300000b00000026060f000c004d6174 68547970650000c00009000000fa0200001000000000000000220 0040000002d0100000500000014024002f4030500000013024002 020*********fb0280fe000000000000900100000000040200105 4696d6573204e657720526f6d616e000016040000002d01010008 000000320aa002bc0701000000290009000000320aa0023400040 000006578702815000000fb0220ff0000000000009001000000000 402001054696d6573204e657720526f6d616e000016040000002d 01020004000000f001010008000000320a02014d0601000000320 008000000320a02012b0501000000320015000000fb0280fe0000 000000009001010000000402001054696d6573204e657720526f6 d616e000016040000002d01010004000000f001020008000000320aa002380701000000740008000000320acc037c04020000006d5208000000320aae01ae05010000006c0008000000320aae011a0401000000420010000000fb0280fe0000000000009001000000020002001053796d626f6c0002040000002d01020004000000f001010008000000320aa002e602010000002d000a00000026060f000a00f fffffff01000000000010000000fb021000070000000000bc02000000860102022253797374656d0086040000002d01010004000000f0010200030000000000 二、静电场习题1. 如图所示，两个同心球壳．内球壳半径为R 1，均匀带有电荷Q ；外球壳半径为R 2，壳的厚度忽略，原先不带电，但与地相连接．设地为电势零点，则在两球之间、距离球心为r 的P 点处电场强度的大小与电势分别为：(A) E ＝204r Q επ，U ＝r Q04επ．(B) E ＝204r Qεπ，U ＝⎪⎪⎭⎫ ⎝⎛-πr R Q 11410ε． (C) E ＝204r Qεπ，U ＝⎪⎪⎭⎫ ⎝⎛-π20114R r Q ε．(D) E ＝0，U ＝204R Qεπ． ［ ］2.如图所示，两个同心的均匀带电球面，内球面半径为R 1、带电荷Q 1，外球面半径为R 2、带有电荷Q 2．设无穷远处为电势零点，则在内球面之内、距离球心为r 处的P 点的电势U 为： (A)rQ Q 0214επ+． (B)20210144R Q R Q εεπ+π．(C) 0． (D)1014R Q επ．3.在一个带有正电荷的均匀带电球面外，放置一个电偶极子，其电矩p的方向如图所示．当释放后，该电偶极子的运动主要是A) 沿逆时针方向旋转，直至电矩p 沿径向指向球面而停止． B) 沿顺时针方向旋转，直至电矩p 沿径向朝外而停止． C) 沿顺时针方向旋转至电矩p 沿径向朝外，同时沿电场线远离球面移动． D) 沿顺时针方向旋转至电矩p 沿径向朝外，同时逆电场线方向向着球面移动．4. 一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的： (A) 2倍． (B) 22倍． (C) 4倍． (D) 42倍． ［ ］5. 一平行板电容器，板间距离为d ，两板间电势差为U 12,一个质量为m 、电荷为－e 的电子，从负极板由静止开始飞向正极板．它飞行的时间是：(A) 122eU md ． (B) 122eU md ． (C)122eU m d(D)meU d212［ ］6.E图示为一具有球对称性分布的静电场的E~r 关系曲线．请指出该静电场是由下列哪种带电体产生的． (A) 半径为R 的均匀带电球面．(B) 半径为R 的均匀带电球体． (C) 半径为R 、电荷体密度r ＝Ar (A 为常数）的非均匀带电球体．(D) 半径为R 、电荷体密度r ＝A/r (A 为常数)的非均匀带电球体．7.在点电荷+q 的电场中，若取图中P 点处为电势零点 ， 则M 点的电势为(A) Xresult Üafs18 "ö 75~ gFlipHÜsn fFlipV$0Xsp °\seatdefaultcl Üfcs1 # ãs0_fs24<]loch Tìangfe2052`1046:885¸8885．(`;cs0 ]kerning0Linsrsid45888858B) ]parä\plai. •wIdctlparTitap0fs18*Üloch _2ãt%mbXobjh673a q08επ．(C)a q04επ-． (D)a q08επ-．［ ］8.如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于： (A)06εq． (B) 012εq ． (C)24εq ． (D)48εq ． ［ ］9. 有一个球形的橡皮膜气球，电荷q 均匀地分布在表面上，在此气球被吹大的过程中，被气球表面掠过的点(该点与球中心距离为r )，其电场强度的大小将由___________________变为_________________．10.E图中曲线表示一种轴对称性静电场的场强大小E 的 分布，r 表示离对称轴的距离，这是由______________ ______________________产生的电场．11. 一闭合面包围着一个电偶极子，则通过此闭合面的电场强度通量F e ＝_________________．12. 一面积为S的平面，放在场强为E 的均匀电场中，已知E 与平面间的夹角为q(＜p/2)，则通过该平面的电场强度通量的数值F e＝______________________．13. 真空中一半径为R的均匀带电球面，总电荷为Q．今在球面上挖去很小一块面积△S (连同其上电荷)，若电荷分布不改变，则挖去小块后球心处电势(设无穷远处电势为零)为________________．14. 一半径为R的均匀带电球面，其电荷面密度为s．若规定无穷远处为电势零点，则该球面上的电势U＝____________________．15. 一半径为R的绝缘实心球体，非均匀带电，电荷体密度为r＝r 0 r (r为离球心的距离，r0为常量)．设无限远处为电势零点．则球外(r＞R)各点的电势分布为U＝__________________．16.E图中所示曲线表示球对称或轴对称静电场的某一物理量随径向距离r成反比关系，该曲线可描述_______________的电场的E~r关系，也可描述_____________ 的电场的U~r关系．(E为电场强度的大小，U为电势)17. LP如图所示，真空中一长为L的均匀带电细直杆，总电荷为q，试求在直杆延长线上距杆的一端距离为d的P点的电场强度．18. 电荷线密度为l的?无限长?均匀带电细线，弯成图示形状．若半圆弧AB的半径为R，试求圆心O点的场强．19.半径为R的带电细圆环，其电荷线密度为l=l0sinf，式中l0为一常数，f为半径R与x轴所成的夹角，如图所示．试求环心O处的电场强度．20. “无限长”均匀带电的半圆柱面，半径为R，设半圆柱面沿轴线OO'单位长度上的电荷为l，试求轴线上一点的电场强度．21.真空中两条平行的“无限长”均匀带电直线相距为a，其电荷线密度分别为－l和＋l．试求：(1) 在两直线构成的平面上，两线间任一点的电场强度(选Ox轴如图所示，两线的中点为原点)．(2) 两带电直线上单位长度之间的相互吸引力．22. 实验表明，在靠近地面处有相当强的电场，电场强度E 垂直于地面向下，大小约为100 N/C；在离地面1.5 km高的地方，E 也是垂直于地面向下的，大小约为25 N/C．(1) 假设地面上各处E 都是垂直于地面向下，试计算从地面到此高度大气中电荷的平均体密度；(2) 假设地表面内电场强度为零，且地球表面处的电场强度完全是由均匀分布在地表面的电荷产生，求地面上的电荷面密度．(已知：真空介电常量0ε＝8.85×10-12 C2·N-1·m-2)23.x电荷面密度分别为+s和－s的两块?无限大?均匀带电平行平面，分别与x轴垂直相交于x1＝a，x2＝－a 两点．设坐标原点O处电势为零，试求空间的电势分布表示式并画出其曲线．24.qP有一带正电荷的大导体，欲测其附近P点处的场强，将一电荷量为q0 (q0 >0 )的点电荷放在P点，如图所示，测得它所受的电场力为F．若电荷量q0不是足够小，则(A) F/ q0比P点处场强的数值大．(B) F/ q0比P点处场强的数值小．(C) F/ q0与P点处场强的数值相等．(D) F/ q0与P点处场强的数值哪个大无法确定．［］25. A+σ2一“无限大”均匀带电平面A，其附近放一与它平行的有一定厚度的“无限大”平面导体板B ，如图所示．已知A 上的电荷面密度为+s ，则在导体板B 的两个表面1和2上的感生电荷面密度为： (A) s 1 = - s ， s 2 = + s ． (B) s 1 = σ21-， s 2 =σ21+．(C) s 1 = σ21-， s 1 = σ21-．(D)s 1= - s ，s 2=0． ［ ］26. 选无穷远处为电势零点，半径为R 的导体球带电后，其电势为U 0，则球外离球心距离为r 处的电场强度的大小为 (A)302r U R ． (B) RU 0．(C)20r RU ． (D)rU 0． ［ ］27.如图所示，一厚度为d 的“无限大”均匀带电导体板，电荷面密度为s ，则板的两侧离板面距离均为h 的两点a 、b 之间的电势差为：(A) 0． (B) 02εσ．(C) 0εσh ． (D) 02εσh． ［ ］28. 关于高斯定理，下列说法中哪一个是正确的？(A) 高斯面内不包围自由电荷，则面上各点电位移矢量D 为零．(B) 高斯面上处处D 为零，则面内必不存在自由电荷．(C) 高斯面的D 通量仅与面内自由电荷有关．(D) 以上说法都不正确．［］29. 一导体球外充满相对介电常量为e r的均匀电介质，若测得导体表面附近场强为E，则导体球面上的自由电荷面密度s为(A) e 0 E．(B) e 0 e r E．(C) e r E．(D) (e0e r- e )E．［］30. +Q一个大平行板电容器水平放置，两极板间的一半空间充有各向同性均匀电介质，另一半为空气，如图．当两极板带上恒定的等量异号电荷时，有一个质量为m、带电荷为+q的质点，在极板间的空气区域中处于平衡．此后，若把电介质抽去，则该质点(A) 保持不动．(B) 向上运动．(C) 向下运动．(D) 是否运动不能确定．［］31. 如果某带电体其电荷分布的体密度r 增大为原来的2倍，则其电场的能量变为原来的(A) 2倍．(B) 1/2倍．(C) 4倍．(D) 1/4倍．［］32. q一空心导体球壳，其内、外半径分别为R 1和R 2，带电荷q ，如图所示．当球壳中心处再放一电荷为q 的点电荷时，则导体球壳的电势(设无穷远处为电势零点)为(A)104R q επ ． (B) 204R qεπ ．(C) 102R qεπ . (D) 20R q ε2π ． ［ ］ 33. 一空气平行板电容器，两极板间距为d ，充电后板间电压为U ．然后将电源断开，在两板间平行地插入一厚度为d/3的金属板，则板间电压变成U' =________________ ．34. S S如图所示，把一块原来不带电的金属板B ，移近一块已带有正电荷Q的金属板A ，平行放置．设两板面积都是S ，板间距离是d ，忽略边缘效应．当B 板不接地时，两板间电势差U AB =___________________ ；B 板接地时两板间电势差='AB U __________ ．35. 如图所示，将一负电荷从无穷远处移到一个不带电的导体附近，则导体内的电场强度______________，导体的电势______________．(填增大、不变、减小)36. 一金属球壳的内、外半径分别为R1和R2，带电荷为Q．在球心处有一电荷为q的点电荷，则球壳内表面上的电荷面密度s =______________．37. 空气的击穿电场强度为2×106 V·m-1，直径为0.10 m的导体球在空气中时最多能带的电荷为______________．(真空介电常量e 0 = 8.85×10-12 C2·N-1·m-2 )38. 地球表面附近的电场强度为100 N/C．如果把地球看作半径为6.4×105 m的导体球，则地球表面的电荷Q=___________________．(2/CmN1094129⋅⨯=πε)39. 一任意形状的带电导体，其电荷面密度分布为s (x，y，z)，则在导体表面外附近任意点处的电场强度的大小E(x，y，z) =______________________，其方向______________________．40. 地球表面附近的电场强度约为100 N /C，方向垂直地面向下，假设地球上的电荷都均匀分布在地表面上，则地面带_____电，电荷面密度s =__________．(真空介电常量e 0 = 8.85×10-12 C2/(N·m2) )41. 1σda厚度为d的“无限大”均匀带电导体板两表面单位面积上电荷之和为s ．试求图示离左板面距离为a的一点与离右板面距离为b的一点之间的电势差．42. 半径分别为1.0 cm与2.0 cm的两个球形导体，各带电荷1.0×10-8 C，两球相距很远．若用细导线将两球相连接．求(1) 每个球所带电荷；(2) 每球的电势．(22/CmN109419⋅⨯=πε)43.半径分别为R1和R2 (R2 > R1 )的两个同心导体薄球壳，分别带有电荷Q1和Q2，今将内球壳用细导线与远处半径为r的导体球相联，如图所示, 导体球原来不带电，试求相联后导体球所带电荷q．44. 一圆柱形电容器，外柱的直径为4 cm，内柱的直径可以适当选择，若其间充满各向同性的均匀电介质，该介质的击穿电场强度的大小为E0= 200 KV/cm．试求该电容器可能承受的最高电压．(自然对数的底e = 2.7183)45. 两金属球的半径之比为1∶4，带等量的同号电荷．当两者的距离远大于两球半径时，有一定的电势能．若将两球接触一下再移回原处，则电势能变为原来的多少倍？46. 一绝缘金属物体，在真空中充电达某一电势值，其电场总能量为W0．若断开电源，使其上所带电荷保持不变，并把它浸没在相对介电常量为e r的无限大的各向同性均匀液态电介质中，问这时电场总能量有多大？一、力学习题1. 一质点从静止开始作直线运动，开始时加速度为a0，此后加速度随时间均匀增加，经过时间t后，加速度为2a0，经过时间2t后，加速度为3 a 0 ,…求经过时间nt 后，该质点的速度和走过的距离．2. 有一质点沿x 轴作直线运动，t 时刻的坐标为x = 4.5 t 2 - 2 t 3(SI) ．试求：(3) 第2秒内的平均速度；(4) 第2秒末的瞬时速度；(3) 第2秒内的路程．3. 在以加速度a 向上运动的电梯内，挂着一根劲度系数为k 、质量不计的弹簧．弹簧下面挂着一质量为M 的物体，物体相对于电梯的速度为零．当电梯的加速度突然变为零后，电梯内的观测者看到物体的最大速度为(A)k M a /． (B) M k a /． (C) k M a /2． (D) k M a /21． ［ ］4. 一质点沿半径为R 的圆周运动，在t = 0时经过P 点，此后它的速率v 按Bt A +=v (A ，B 为正的已知常量)变化．则质点沿圆周运动一周再经过P 点时的切向加速度a t = ___________ ，法向加速度a n = _____________．5. 如图，两个用轻弹簧连着的滑块A 和B ，滑块A 的质量为m 21，B 的质量为m ，弹簧的劲度系数为k ，A 、B 静止在光滑的水平面上（弹簧为原长）．若滑块A 被水平方向射来的质量为m 21、速度为v 的子弹射中，则在射中后，滑块A 及嵌在其中的子弹共同运动的速度v A =________________，此时刻滑块B 的速度v B =__________，在以后的运动过程中，滑块B 的最大速度v max=__________．6. 质量为0.25 kg 的质点，受力it F = (SI)的作用，式中t 为时间．t= 0时该质点以j 2=v (SI)的速度通过坐标原点，则该质点任意时刻的位置矢量是______________．7. 质量相等的两物体A 和B ，分别固定在弹簧的两端，竖直放在光滑水平面C 上，如图所示．弹簧的质量与物体A 、B 的质量相比，可以忽略不计．若把支持面C 迅速移走，则在移开的一瞬间，A 的加速度大小a A ＝_______，B 的加速度的大小a B ＝_______． 8.A 质量为m 的小球，用轻绳AB 、BC 连接，如图，其中AB 水平．剪断绳AB 前后的瞬间，绳BC 中的张力比T : T ′＝____________________．9.一圆锥摆摆长为l 、摆锤质量为m ，在水平面上作匀速圆周运动，摆线与铅直线夹角q ，则(1) 摆线的张力T ＝_____________________；(2) 摆锤的速率v ＝_____________________．10. 质量为m 的子弹以速度v 0水平射入沙土中，设子弹所受阻力与速度反向，大小与速度成正比，比例系数为Ｋ，忽略子弹的重力，求：(1) 子弹射入沙土后，速度随时间变化的函数式；(2) 子弹进入沙土的最大深度．11. (1) 试求赤道正上方的地球同步卫星距地面的高度．(2) 若10年内允许这个卫星从初位置向东或向西漂移10°，求它的轨道半径的误差限度是多少？已知地球半径R＝6.37×106 m，地面上重力加速度g＝9.8 m/s2．12.一光滑的内表面半径为10 cm的半球形碗，以匀角速度ω绕其对称OC旋转．已知放在碗内表面上的一个小球P相对于碗静止，其位置高于碗底4 cm，则由此可推知碗旋转的角速度约为(A) 10 rad/s．(B) 13 rad/s．(C) 17 rad/s (D) 18 rad/s．［］13.质量为m的小球，放在光滑的木板和光滑的墙壁之间，并保持平衡，如图所示．设木板和墙壁之间的夹角为a，当a逐渐增大时，小球对木板的压力将(A) 增加．(B) 减少．(C) 不变．(D) 先是增加，后又减小．压力增减的分界角为a ＝45°．14. 质量为m 的物体自空中落下，它除受重力外，还受到一个与速度平方成正比的阻力的作用，比例系数为k ，k 为正值常量．该下落物体的收尾速度(即最后物体作匀速运动时的速度)将是 (A) k mg. (B) k g 2 .(C) gk . (D) gk .［ ］15.mm一圆盘正绕垂直于盘面的水平光滑固定轴O 转动，如图射来两个质量相同，速度大小相同，方向相反并在一条直线上的子弹，子弹射入圆盘并且留在盘内，则子弹射入后的瞬间，圆盘的角速度w(A) 增大． (B) 不变．(C) 减小． (D) 不能确定． ［ ］16. 如图所示，A 、B 为两个相同的绕着轻绳的定滑轮．A 滑轮挂一质量为M 的物体，B 滑轮受拉力F ，而且F ＝Mg ．设A 、B 两滑轮的角加速度分别为b A 和b B ，不计滑轮轴的摩擦，则有(A) b A ＝b B ． (B) b A ＞b B ．(C) b A ＜b B ． (D) 开始时b A ＝b B ，以后b A ＜b B ． ［ ］。
电子科大理论力学期末考试试题A卷答案
电子科技大学2006〜2007学年第2学期理论力学期末考试试卷A答案及评分标准一、判断题(每题1.5分，共9分)1、错误；2、错误；3、错误；4、正确；5、正确；6、正确。
二、填空题(每题3分，共15分)T T 呻彳 T T T1、F R - -200k(N)，M o =400i 200k(N m)；力螺旋，F R - -200k(N)，M =200(N m)。
2、，= . 2 rad ： s ； = 1 rad s2 a C = 6 cm 's2。
3、mv，0.5v。
2 2 24、P = 3mr ，L o = 28.5mr ‘，T = 6.75mr ，。
1 1 25、(m1 3m2)l ；, (5m2 -m1)l ；2 6三、选择题(每题2分，共10 分)1、B ；2、A;3、D ；4、D；5、A四、(12分)解：以直梁CD为研究对象，受力分析如图(a)所示。
、F x = 0 F Cx-Pcos： -0 F Cx二5.2kN( > )X M D(F) =0 F ey 3-Psinn 1=0 F Cy=1kN()' Fy =0 F D£-P S in”0 F^2kN()以折梁AC为研究对象，受力分析如图(b)所示。
、F x=0 F AX-F CX" F AX =F CX =5.2N( TM A二 12.9kN m (逆时针) 、F y =0 F Ay - F ey -q 3 = 0 F A『=4kN()3、M A(F"0M A q 33 F ey 3-F ex 2亠"评分细则：(1)绘制研究对象受力图，共5分。
正确绘制图(a)―― 2分；正确绘制图(b)―― 3分。
(2)列写平衡方程，共5分。
包含待求约束力的5个平衡方程，每个方程1分。
(3)正确计算全部约束力，共2分。
五、(12分)解：AD杆作平动，其上各点的速度和加速度与A点或B 点的速度和加速度相同。
电子科技大学智慧树知到“机电一体化技术”《工程力学》网课测试题答案卷4
电子科技大学智慧树知到“机电一体化技术”《工程力学》网课测试题答案（图片大小可自由调整）第1卷一.综合考核(共10题)1.不管是低碳钢还是铸铁，不管受单向拉伸还是单向压缩，强度条件都是σ≤[σ]，所以它们的弹性失效也有共同的力学原因。
()A.正确B.错误2.若二梁的材料、轴向与截面形状尺寸均相同，且在外载荷作用下具有相同的弯矩方程，则此二梁的弯曲变形和位移完全相同。
()A.正确B.错误3.作用在刚体上的四个力偶，若各力偶矩矢自行封闭，则一定是平衡力系。
()A.正确B.错误4.空间任意力系向两个不同的点简化，试问下述情况中可能的有：()A.主矩相等，主矢不相等B.主矢相等，主矩不相等C.主矢和主矩均相等D.主矢和主矩均不相等5.两个大小为5N、3N的力合成一个力时，此合力最大值为()。
A.2NB.4NC.6ND.8N6.在下列有关压杆临界应力σcr的结论中，()是正确的。
A.细长杆的σcr值与杆的材料无关B.粗短杆的σcr值与杆的柔度无关C.中长杆的σcr值与杆的柔度无关D.中长杆的σcr值与杆的材料无关7.以下说法中正确的是()。
A.理论力学中主要研究力对物体的外效应B.物体在两个力作用下平衡的充分必要条件是这二力等值、反向、共线C.力是滑移矢量，力沿其作用线滑移不会改变对物体的作用效应D.凡是受到两个力作用的刚体都是二力构件8.平面应力状态下的两个正应力极值与剪应力极值必定分别是空间意义上的主应力σ1，σ2与τmax。
()A.正确B.错误9.力是物体之间的相互机械作用。
()A.正确B.错误10.在材料相同的条件下，随着柔度的增大()。
A.细长杆的临界应力是减小的，中长杆不变B.细长杆和中长杆的临界应力均是减小的C.细长杆和中长杆的临界应力均不是减小的D.中长杆的临界应力是减小的，细长杆不变第1卷参考答案一.综合考核1.参考答案：B2.参考答案：B3.参考答案：A4.参考答案：BC5.参考答案：D6.参考答案：A7.参考答案：A8.参考答案：B9.参考答案：B10.参考答案：B。
电磁场期末考试试卷_桂林电子科技大学(详细答案)
∂D _， 并说明它的物理意义 ∂t
磁场的旋 场，
；时变电磁场中，随时间变化的磁场可以产生 电 K K ∂B 请写出微分形式麦克斯韦方程的第二式__ ∇ × E = − __。 ∂t
2、在 无 源 静 电 场 中 ， 两 种 介 质 交 界 面 上 的 边 界 条 件 为
K K K ___ n ×( E1 − E2 ) = 0 ____。
ρa 3
3r 2
ρa 3 3ε 0 r 2
(3 分)
P = D − ε 0 E = (ε r − 1)ε 0 E ＝
(ε r − 1) ρ r ρr er = er 3ε r 6
(3 分)
球内极化体电荷密度 极化面电荷密度
−∇i P = −
(ε r − 1) ρ
εr
=−
ρ
2
(3 分) (3 分)
n i P r = a = er i P =
则电场的瞬时值：
(2 分)
π E = e zηH m sin 1010 πt − 66.7πy − 4 π = e z 30π sin 1010 πt − 66.7πy − V / m 4
3）空气中的本征阻抗：η0 = 120π
反射系数 ρ =
大一静力学试题及答案
大一静力学试题及答案一、选择题（每题2分，共20分）1. 静力学中，力的三要素不包括以下哪一项？A. 大小B. 方向C. 作用点D. 作用效果答案：D2. 静力学中，一个物体处于平衡状态的条件是：A. 受到的合力为零B. 受到的合力不为零C. 受到的合力和合力矩都为零D. 受到的合力为零，合力矩不为零答案：C3. 以下哪个力不是保守力？A. 重力B. 弹簧力C. 摩擦力D. 电场力答案：C4. 一个质量为m的物体在水平面上受到一个大小为F的力，若物体与水平面之间的摩擦系数为μ，则物体受到的摩擦力为：A. FB. μFC. μmgD. F - μmg答案：D5. 以下哪个选项不是静力学平衡方程？A. ΣFx = 0B. ΣFy = 0C. ΣM = 0D. ΣI = 0答案：D6. 一个物体在斜面上保持静止，以下哪个说法是正确的？A. 物体受到的重力分量与斜面的支持力平衡B. 物体受到的重力分量与斜面的摩擦力平衡C. 物体受到的重力分量与斜面的支持力和摩擦力的合力平衡D. 物体受到的重力分量与斜面的支持力和摩擦力的合力不平衡答案：C7. 以下哪个选项不是静力学中常见的约束类型？A. 铰链约束B. 滑动摩擦约束C. 固定约束D. 弹性约束答案：B8. 一个物体在水平面上受到一个大小为F的力，若物体与水平面之间的摩擦系数为μ，且μ < tan(θ)，则物体：A. 静止不动B. 沿斜面向上滑动C. 沿斜面向下滑动D. 沿斜面做匀速直线运动答案：C9. 以下哪个选项不是静力学平衡条件？A. 合力为零B. 合力矩为零C. 合力和合力矩都为零D. 合力不为零，合力矩为零答案：D10. 一个质量为m的物体在竖直方向上受到两个大小相等、方向相反的力，这两个力的合力为：A. 0B. 2mC. -mD. m答案：A二、填空题（每题2分，共20分）1. 静力学中，一个物体处于平衡状态时，其合力为______。
答案：02. 静力学中，一个物体处于平衡状态时，其合力矩为______。
工程力学(桂林电子科技大学)智慧树知到答案章节测试2023年
绪论单元测试1.《工程力学》通常被专业要求支撑毕业要求指标点1-2“能针对具体工程领域的实际问题建立数学模型并求解”。
A:对B:错答案:A第一章测试1.在外力作用下，体内任意两点距离保持不变的物体称为刚体。
( )A:对B:错答案:A2.物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。
( )A:对B:错答案:B3.加减平衡力系公理不但适用于刚体，而且也适用于变形体。
( )A:对B:错答案:B4.力的可传性只适用于刚体，不适用于变形体。
( )A:错B:对答案:A5.作用与反作用公理的适用范围是（）A:对任何宏观物体和物体系统都适用；B:只适用于平衡刚体的内部；C:只适用于刚体的内部；答案:A6.作用在刚体的同平面上的三个互不平行的力，它们的作用线汇交于一点，这是刚体平衡的（）A:必要条件和充分条件；B:充分条件，但不是必要条件；C:必要条件，但不是充分条件；答案:C7.刚化公理适用于（）A:处于平衡状态下的物体和物体系统都适用。
B:任何受力情况下的变形体；C:只适用于处于平衡状态下的变形体；D:任何受力情况下的物体系统；答案:A8.两点受力的构件都是二力杆。
A:错B:对答案:A9.图示A、B两物体，自重不计，分别以光滑面相靠或用铰链C相联接，受两等值、反向且共线的力F1、F2的作用。
以下四种由A、B所组成的系统中，哪些是平衡的？A:B:C:D:答案:BC10.图示各杆自重不计，以下四种情况中，哪一种情况的BD杆不是二力构件？A:B:C:D:答案:C第二章测试1.当刚体受三个不平行的力作用时，只要这三个力的作用线汇交于同一点，则刚体一定处于平衡状态。
（）A:对B:错答案:B2.已知力F的大小及其与x轴的夹角，能确定力F在x轴方向上的分力。
（）A:错B:对答案:A3.凡是力偶都不能用一个力来平衡。
（）A:错B:对答案:B4.只要平面力偶的力偶矩保持不变，可将力偶的力和臂作相应的改变，而不影响其对刚体的效应。
桂电大学物理试题和答案
三、计算题(共8道小题，每道5分，共40分）
17.
月球质量是地球质量的1/81，直径为地球直径的3/11，计算一个质量为65 kg的人在月球上所受的月球引力大小．
18.
边长为b的立方盒子的六个面，分别平行于xOy、yOz和xOz平面．盒子的一角在坐标原点处．在此区域有一静电场，场强为 .试求穿过各面的电通量．
(A)R．(B) ．
(C) ．(D) ．［］
4.
用细导线均匀密绕成长为l、半径为a(l>>a)、总匝数为N的螺线管，管内充满相对磁导率为r的均匀磁介质．若线圈中载有稳恒电流I，则管中任意一点的
(A)磁感强度大小为B=0rNI．
(B)磁感强度大小为B=rNI / l．
(C)磁场强度大小为H=0NI / l．
______________；圆弧bc中感应电流的方向是
_________________．
15.
.分别画出下面二种情况下，物体A的受力图．
(1)物体A放在木板B上，被一起抛出作斜上抛运动，A始终位于B的上面，不计空气阻力；
(2)物体A的形状是一楔形棱柱体，横截面为直角三角形，放在桌面C上．把物体B轻轻地放在A的斜面上，设A、B间和A与桌面C间的摩擦系数皆不为零，A、B系统静止．．
13.
一平行板电容器，充电后与电源保持联接，然后使两极板间充满相对介电常
量为r的各向同性均匀电介质，这时两极板上的电荷是原来的______倍；电场强
度是原来的_________倍；电场能量是原来的_________倍．
14.
一段导线被弯成圆心在O点、半径为R的三段圆弧ab、bc、ca，它们构成了一个闭合回路，ab位于xOy平面内，bc和ca分别位于另两个坐标面中(如图)．均匀磁场 沿x轴正方向穿过圆弧bc与坐标轴所围成的平面．设磁感强度随时间的变化率为K(K>0)，则闭合回路abca中感应电动势的数值为
桂林电子科技大学2011年考研真题803工程力学
桂林电子科技大学2011年硕士研究生入学考试试卷
考试科目代码：803 考试科目名称：工程力学 二、如图所示，已知123150,300,'200,F N F F N F F N =====求力系向点O 并求力系合力的大小及其与原点O 的距离10分）。
三、图示组合梁由AC 和DC 两段铰接构成，起重机放在梁上，已知起重机重150kN,P =四、图示凸轮机构，已知推杆（不计自重）与滑道之间的静摩擦系数为s f ，滑道宽度为杆接触处的摩擦忽略不计，问a 为多大，推杆才不致被卡住（15分）。
第一题图 第二题图 第三题图 第四题图
B 和D ，若10kN F =
第二部分（材料力学）变截面直杆的受力如图，已知2128cm ,A A =
八、铸铁梁的载荷及横截面尺寸如图，许用拉应力[]40MPa t σ=，许用压应力[]160MPa c σ=。
试画出其弯矩图，并按正应力强度条件校核梁的强度。
若载荷不变，但将第五题图 第六题图
第七题图 第八题图
第十题图。
电子科技大学智慧树知到“机械设计制造及其自动化”《理论力学》网课测试题答案卷4
电子科技大学智慧树知到“机械设计制造及其自动化”《理论力学》网课测试题答案（图片大小可自由调整）第1卷一.综合考核(共10题)1.质点系的动量的方向，就是外力主矢的方向。
()A.正确B.错误2.力偶矩的三要素是()。
A.力偶矩的大小B.力偶的转向C.力偶的大小D.力偶的作用面方位3.一刚体在多个力系作用下保持静止状态，若加上或减去任意个平衡力系，该刚体将继续保持静止状态。
()A.正确B.错误4.平面汇交力系平衡的充分且必要的解析条件是()。
A.Y方向合力为零B.X方向合力为零C.X、Y两个方向的合力同时为零5.只适用于刚体的公理是()。
A.加减平衡力系公理B.力的平行四边形公理C.作用与反作用公理D.二力平衡公理6.动静法使动力学问题变成了静力学问题。
()A.正确B.错误7.甲乙两人质量相同，沿绕过无重滑轮的细绳的两端，由静止起同时向上爬，如果甲比乙更努力上爬，则()。
A.甲先到达上端B.甲乙两人同时到达C.乙先到达上端8.内力不改变质点系的动量，但是可改变质点系内质点的动量。
()A.正确B.错误9.点的复合运动和刚体的平面运动两种分析方法中，动坐标系的运动可以是任何一种刚体运动。
()A.正确B.错误10.刚体作平面运动时，某瞬时，若取图形上A点为基点，求得图形的角加速度为w₁；若用瞬心法求得的图形的角速度为w₂。
则w₁与w₂的关系是()。
A.w₁＞w₂B.w₁＝w₂C.w₁＜w₂第1卷参考答案一.综合考核1.参考答案：B2.参考答案：ABD3.参考答案：A4.参考答案：C5.参考答案：AD6.参考答案：B7.参考答案：B8.参考答案：A9.参考答案：B10.参考答案：B。
桂林电子科技大学《机械设计A》2012年考研专业课真题试卷
桂林电子科技大学2012年硕士研究生入学考试试卷考试科目代码：801 考试科目名称：机械设计（A）请注意：答案必须写在答题纸上（写在试卷上无效）。
一、选择题（20分，每小题2分）1、变应力特性可用σmax、σmin、σm、σa和r五个参数中的任意来描述。
A．一个B．两个C．三个D．四个2、受横向载荷的螺栓组连接中，用铰制孔螺栓时，靠来承受横向载荷。
A. 螺杆的挤压B. 螺纹的挤压C. 结合面间的摩擦力D. 无法判定3、对轴的削弱最大。
A.平键B.半圆键C.楔键D.花键4、带传动主动轮直径d1=180mm，转速n=940 r/min，从动轮直径d2＝710mm，转速n=233 r/min，则传动的滑差率ε=。
A. 1.2％B. 1.5％C. 1.8％D. 2.2％5、设计链传动时，链长（节数）最好取。
A．偶数B．奇数C．5的倍数D．链轮齿数的整数倍6、一对标准圆柱齿轮，已知m=2，z1=z2=50，它们的齿形系数是。
A. Y F1<Y F2B. Y F1>Y F2C.Y F1=Y F2D. 可能相等，也可能不等7、提高蜗杆传动效率的有效措施是。
A.增加蜗轮齿数z2B.增加蜗杆头数z1C.减小模数mD.增大蜗杆直径系数q8、温度升高时，润滑油的粘度。
A. 随之升高B. 保持不变C. 随之降低D. 可能升高也可能降低9、滚动轴承寿命计算公式为L=(C/P)ε，ε为寿命指数，对于球轴承，ε= 。
A. 1B. 3C. 1/3D. 10/310、用联轴器联接的两轴，若主动轴直径为d1，从动轴直径为d2，则。
A. d1≥d2B. d1≤d2C. d1=d2D.d1和d2可以不相等二、判断题（20分，每小题2分）1、静载荷作用下的零件，不仅可以产生静应力，也可能产生变应力。
( )2、紧螺栓连接在按拉伸强度计算时，将拉伸载荷增加到原来的1．3倍．这是考虑螺纹应力集中的影响。
( )3、花键联接通常用于要求轴与轮毂严格对中的场合。
(完整word版)桂林电子科技大学2007理论力学试卷B
桂林电子科技大学试卷学年第学期课号课程名称（A、 B 卷，开、闭卷）适用班级（或年级、专业）考试时间分钟班级学号姓名题号一二三四五六七八九十成绩满分20202040得分评卷人注意：所有解题答案请写在答题纸上，写在试卷上将会被视为未答题并不能得分。
一、判断题1. 当平面力系的主矢为零时，其主矩一定与简化中心的位置无关。
（）2.只要平面力偶的力偶矩保持不变，可将力偶的力和臂作相应的改变，而不影响其对刚体的效应。
（）3. 两端用光滑铰链连接的构件是二力构件。
（）4.转动惯量是刚体转动惯性的度量，如为获得较好的灵敏度，千分计的指针制作应将质量分布尽量远离转轴。
（）5.作平面运动的刚体，在某一时刻一定有且只有一个确定的瞬心。
（）v v v6. 不论牵连运动为何种运动，点的速度合成定理v a v r v e 皆成立。
（）7.刚体作平面运动时，若某一时刻其角速度为零，则刚体作瞬时平移，其上各点的速度大小和方向均相同。
（）8.作平面运动的刚体，其绕基点转动的角速度和角加速度与基点的选择无关。
（）9.某圆轮沿水平面作既滚又滑的直线运动，则在某一时刻其速度瞬心为与地面相接触的那一点。
（）10.作用在质点系的内力总是成对出现，大小相等，方向相反，所以作用在质点系的内力所作功之和为零。
（）二、选择题1.如图 1，四本相同的书，每本重 G，设书与书间的摩擦系数为 0.1 ，书与手间的摩擦系数为0.25 ，欲将四本书一起提起，则两侧应加之P 力应至少大于。
A. 10GB. 8GC. 4GD. 12.5G图12．如图 2，直角刚杆（即 AOB 为一整体） AO = 2m，BO = 3m，已知某瞬时 A 点的速度v A= 6m/s ；而 B 点的加速度与BO 成 = 60°角。
则该瞬时刚杆的角速度和角加速度的大小分别为: .A.3，3 3B. 2 3，12C. 3，5 3D. 3，9 33. 如图 3，杆 AB 的两端可分别沿水平、铅直滑道运动，已知 B 端的速度为v B，则图示瞬时B 点相对于 A 点的速度为。
电子科技大学22春“机械设计制造及其自动化”《理论力学》作业考核题库高频考点版(参考答案)试题号3
电子科技大学22春“机械设计制造及其自动化”《理论力学》作业考核题库高频考点版（参考答案）一.综合考核(共50题)1.一刚体在多个力系作用下保持静止状态，若加上或减去任意个平衡力系，该刚体将继续保持静止状态。
()A.正确B.错误参考答案：A2.甲乙两人质量相同，沿绕过无重滑轮的细绳的两端，由静止起同时向上爬，如果甲比乙更努力上爬，则()。
A.甲先到达上端B.甲乙两人同时到达C.乙先到达上端参考答案：B3.动点在平面内运动，已知其运动轨迹y=f(x)及其速度在x轴方向的分量vx，下述说法中正确的有：()。
A.当vx≠0时，动点的切向加速度at和法相加速度an可完全确定B.动点的速度v和加速度a均可完全确定C.动点的速度v可完全确定D.动点的加速度在x轴方向的分量ax可完全确定参考答案：ACD4.三个质量相同的质点，在同一点A以大小相同的初速度V抛出，其方向各不相同。
如不记空气阻力，三个质点落到水平面时，下面物理量相等的是()。
A.重力的冲量B.重力所做的功C.质点的速度参考答案：BCD5.作用在刚体上的四个力偶，若其力偶矩矢都位于同一平面内，则一定是平面力偶系。
()A.正确B.错误参考答案：B6.质点系的动量的方向，就是外力主矢的方向。
()A.正确B.错误参考答案：B7.车厢内悬挂一质量为m的小球，当车厢以加速度a₀在水平直线轨道上行驶时，小球相对于车厢处于静止状态，此时悬线与铅垂线成B角，此时B角等于()。
A.tanB=a₀/gB.tanB=a₀/2gC.tanB=2a₀/g参考答案：A8.刚体作平面运动时，若某瞬时其平面图形上有两点的加速度的大小和方向均相同，则该瞬时此刚体上各点的加速度都相同。
()A.正确B.错误参考答案：A9.点以匀速率沿阿基米德螺旋线(曲率半径越来越小)自外向内运动时，点的加速度()。
C.保持不变参考答案：B10.三个质量相同的质点，一个作自由落体运动，一个作垂直上抛运动，第三个作斜抛运动，这三个质点的惯性力大小、方向均相同。
2017年广西桂林电子科技大学工程力学考研真题A卷
2021年广西桂林电子科技大学工程力学考研真题A 卷1. 如题1图所示，将两个一样的光滑圆柱放在矩形槽内，各圆柱的半径为r=200mm,重P 1=P 2=600N 。
试求接触点 A 、B 、C 的约束力。
(15分)题1图2. 如题2图所示,机构OABO 1在图示位置平衡。
OA=400mm,O 1B=600mm,作用在OA 上的力偶矩大小m N M e .11 。
试求力偶矩2e M 的大小和杆AB 所受的力。
各杆的重量及各处摩擦均不计。
〔10分〕题2图3. 试求题3图中1、2、3、4杆的内力。
〔20分〕C A B m 1，r 1 m 2，r 2 3题3图4. 如题4图，均质正方形板重P=100N ，在O 处用球形铰链固定在墙上，B 处用两活动铰支座支撑，通过绳CD 将板保持在水平位置。
试求绳CD 的拉力、支座O 和B 处的约束力。
〔20分〕题4图5. 两均质滑轮如题5图所示，在重物C 的作用下，轮A 与地面只滚不滑，求重物C 由静止开场下降高度h 时轮A 质心的加速度A a 。
〔20分〕题5图6. 一根等直圆杆如题6图所示，其直径为d=30mm.F=20kN,l =0.9m ，E=5101.2⨯MPa 。
试作轴力图，并求杆端D 的水平位移D ∆以及B 、C 两截面的相对纵向位移BC ∆。
〔15分〕题6图7. 题7图示一根两端固定的阶梯形圆轴。
它在截面突变处受一大小为e M 的外力偶作用。
假设212d d =,试求固定端的约束力偶矩A M 和B M ，并作扭矩图。
〔15分〕题7图8.题8图所示双跨等截面连续梁。
〔1〕试求支座约束反力；〔2〕绘剪力图和弯矩图。
(20分)提示:跨中集中荷载F 作用下跨度为l 的简支梁跨中挠度为EI Fl 48/3题8图9.在一处于平面应力状态下的受力物体中，用三个相互成60o截面取出一个正三角形单元体，其受力状态如题图9所示.试求其主应力及其截面位置。
〔15分〕题9图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
桂林电子科技大学应用科技学院试卷
课程名称工程力学(闭卷）
题号一二三四五六七八九十成绩满分30 10 30 30 100 得分
（注：请将答案直接写在试卷上，写在其它纸上无效。
）
一、填空题（30分，每空1.5分）
1. 作用于刚体上的二力，使刚体保持平衡状态的必要与充分条件是：此二
力大小______、方向______、且在________；
2. 力偶对刚体的（平动或旋转）______运动不会产生任何影响，力与力偶相互(能或不能)______平衡；
3. 力偶的三要素是______、______、______；
4. 平面汇交力系平衡的几何条件是_____________________________；
5. 二矩式方程∑Y=0，∑M A（F）=0，∑M B（F）=0 的使用补充条件为
__________________________；
6. 静不定指的是____________________________________；
7. 平面三力汇交定理是指________________________________________；
8. 约束基本类型为______、______、______、______；
9. 摩擦按运动类型可分为______、______、______；
10. 倾角为α的斜面，其最大静摩擦系数为fs，则其自锁条件为______；
二、是非题（10分，每题1分）
1. 二力杆指的是直杆（）；
2. 约束反力总是与其所能阻碍的物体的运动方向相反（）；
3. 力系平衡的几何条件是具有封闭的力的多边形（）；
4. 力偶是一对平行力（）；
5. 力对点的矩在某轴上的投影就是力对该轴的矩（）；
6. 桁架分析时其中所有杆件都是二力杆（）；
7.一般情况下，摩擦系数排序为fs≥fd≥δ（）；
8. 分力就是投影（）；
9. 作用与反作用力是一对平衡力（）；
10. 柔性体约束的约束反力总是指向受力体（）。
三、作图题（30分，每题10分）
1.作下图所示各构件的受力图，并用几何法求解约束反力。
2. 用负面积法求解如图所示图形形心。
3. 作各个构件以及节点B 的受力图。
四、计算题（30分，每题10分）
1. 组合梁AC 与CE 铰接，受力情况如图所示，已知a=1m ，Q=4KN ，载荷集度
q=2KN/m ，力偶矩M=4KN ·m ，求约束A 、B 、C 、D 的约束反力。
(8分）
图2
2.如图所示,求A、B约束的约束反力。
3.梯子AB靠在墙壁上，其重为P=200N，如图所示，梯子长为L，并与水平面夹角为θ=60°。
已知接触面间的静摩擦因子为0.25.今有一重为650N的人往上爬，问人所能达到的最高点C到A点的距离S是多少？。