一次函数应用题常见类型
一次函数必考题型

一次函数必考题型
一次函数是初中数学中一个重要的概念,它在中考中也常常出现。
以下是一些一次函数的必考题型:
1. 求函数解析式:中考中最重要的一次函数题型之一,要求通
过已知条件求函数的解析式。
通常需要利用函数的单调性、极值等性质进行求解。
2. 求函数值域:一次函数的值域是它的定义域的扩大,也是中
考中常见的题型之一。
通常需要利用函数的单调性、端点值等性质进行求解。
3. 绘制函数图像:一次函数的图像在中考中也常常出现。
绘制
函数图像通常需要利用函数的解析式和定义域、值域等条件进行求解。
4. 求函数的最值:一次函数的最值通常是通过求导的方法进行
求解的。
在中考中,要求求函数的最值通常需要利用函数的单调性、极值等性质进行求解。
5. 与函数相关的应用题:一次函数在中考中也常常出现在应用
题中。
通常需要利用函数的思想和方法进行求解。
总之,一次函数是初中数学中一个重要的概念,它在中考中也常常出现。
考生需要熟练掌握一次函数的基本概念和性质,并能够利用这些性质进行求解。
一次函数的应用

(3)设货车从甲地出发 x 小时后再与轿车相遇,根据轿车(x-4.5)小时 行驶的路程+货车 x 小时行驶的路程=300 千米列出方程,解方程即可.
考点聚焦
归类探究
回归教材
例 1 [2013·山西] 某校实行学案式教学,需印制若干份数学 学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外, 甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用 y(元)与印刷份数 x(份)之间的关系如图 11-1 所示:
考点聚焦
归类探究
回归教材
(1)填空:甲种收费方式的函数关系式是__y_甲__=__0_.1_x_+___6; 乙种收费方式的函数关系式是___y_乙_=__0_._1_2_x.
段函数是解决问题的关键,一般应从如下几方面入手:(1)寻找分段 函数的分界点;(2)针对每一段函数关系,求解相应的函数解析式; (3)利用条件求未知问题.
考点聚焦
归类探究
回归教材
探究三 利用一次函数解决其他生活实际问题
命题角度: 函数图象在实际生活中的应用.
例 3 甲、乙两地相距 300 千米,一辆货车和一辆轿车先后 从甲地出发向乙地,如图 11-3,线段 OA 表示货车离甲地距 离 y(千米)与时间 x(小时)之间的函数关系;折线 BCD 表示轿车 离甲地距离 y(千米)与 x(小时)之间的函数关系.请根据图象解 答下列问题:
度上升和下降阶段 y 与 x 之间的函数关 系式.
图 11-4
考点聚焦
归类探究
回归教材
解:(1)由图象知,服药后 3 小时血液中药物浓度最高. (2)当 0≤t≤3 时,函数为正比例函数,设关系式为 y=kx(k≠0),
一次函数经典题型+习题(精华-含答案)

一次函数题型一、点的坐标方法: x 轴上的点纵坐标为0,y 轴上的点横坐标为0;若两个点关于x 轴对称,则他们的横坐标相同,纵坐标互为相反数; 若两个点关于y 轴对称,则它们的纵坐标相同,横坐标互为相反数; 若两个点关于原点对称,则它们的横坐标互为相反数,纵坐标也互为相反数;1、 若点A (m,n )在第二象限,则点(|m|,-n )在第____象限;2、 若点P (2a-1,2-3b )是第二象限的点,则a,b 的范围为______________________;3、 已知A (4,b ),B (a,-2),若A ,B 关于x 轴对称,则a=_______,b=_________;若A,B 关于y 轴对称,则a=_______,b=__________;若若A ,B 关于原点对称,则a=_______,b=_________;4、 若点M (1-x,1-y )在第二象限,那么点N (1-x,y-1)关于原点的对称点在第______象限。
题型二、关于点的距离的问题方法:点到x 轴的距离用纵坐标的绝对值表示,点到y 轴的距离用横坐标的绝对值表示;若AB ∥x 轴,则(,0),(,0)A B A x B x 的距离为A B x x -; 若AB ∥y 轴,则(0,),(0,)A B A y B y 的距离为A B y y -;点B (2,-2)到x 轴的距离是_________;到y 轴的距离是____________; 1、 点C (0,-5)到x 轴的距离是_________;到y 轴的距离是____________;到原点的距离是____________;2、 点D (a,b )到x 轴的距离是_________;到y 轴的距离是____________;到原点的距离是____________; 3、 已知点P (3,0),Q(-2,0),则PQ=__________,已知点110,,0,22M N ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭,则MQ=________; ()()2,1,2,8E F --,则EF 两点之间的距离是__________;已知点G (2,-3)、H (3,4),则G 、H 两点之间的距离是_________;4、 两点(3,-4)、(5,a )间的距离是2,则a 的值为__________;5、 已知点A (0,2)、B (-3,-2)、C (a,b ),若C 点在x 轴上,且∠ACB=90°,则C 点坐标为___________.题型三、一次函数与正比例函数的识别方法:若y=kx+b(k,b 是常数,k ≠0),那么y 叫做x 的一次函数,特别的,当b=0时,一次函数就成为y=kx(k 是常数,k ≠0),这时,y 叫做x 的正比例函数,当k=0时,一次函数就成为若y=b ,这时,y 叫做常函数。
一次函数应用题知识点总结

一次函数应用题知识点总结一次函数是数学中的基础函数之一,其形式为y = kx + b,其中k和b为常数,x为自变量,y为因变量。
一次函数的图像是一条直线,其特点是斜率为k,截距为b。
在生活中,一次函数具有丰富的应用场景,例如经济学中的成本和收益分析、物理学中的速度和加速度问题、工程学中的线性规划问题等。
因此,掌握一次函数的知识对于解决实际问题具有重要意义。
本文将对一次函数的应用进行详细总结,包括经济学、物理学、工程学等方面的具体应用案例和解题方法。
经济学中的应用1. 成本和收益分析在经济学中,企业通常需要对生产成本和收益进行分析,以便制定合理的生产策略。
一次函数可以用来描述成本和收益的关系,其中斜率代表每单位产量的成本变化率,截距代表固定成本。
假设某企业生产某种产品,设生产成本C与产量x之间的关系为C = kx + b,其中k为单位产量成本,b为固定成本。
企业的总成本可以表示为C = kx + b,总收益可以表示为R = px,其中p为产品的售价。
则企业的利润为P = R - C = px - (kx + b) = (p - k)x - b,由于p - k为单位产量利润,因此利润与产量的关系是一次函数。
企业如果要最大化利润,可以通过求解一次函数的最大值来确定最优产量。
假设一次函数P = (p - k)x - b,当x达到最大值时,利润P也达到最大值。
2. 税收和福利分析在宏观经济学中,政府税收政策对社会福利的影响是一个重要的研究课题。
一次函数可以用来描述税收和福利之间的关系,其中斜率代表福利变化率,截距代表固定福利。
假设政府对某种商品征税,税收收入T与商品销量x之间的关系为T = kx + b,其中k为单位销量税收,b为固定税收。
利用一次函数可以进行福利分析,例如探讨税收调整对社会福利的影响。
物理学中的应用1. 速度和加速度问题在物理学中,一次函数可以描述物体的运动情况。
假设某物体在t时刻的位移为s(t),速度为v(t),加速度为a(t),则s(t)、v(t)和a(t)之间的关系可以用一次函数来描述。
一次函数的应用题【图象型】
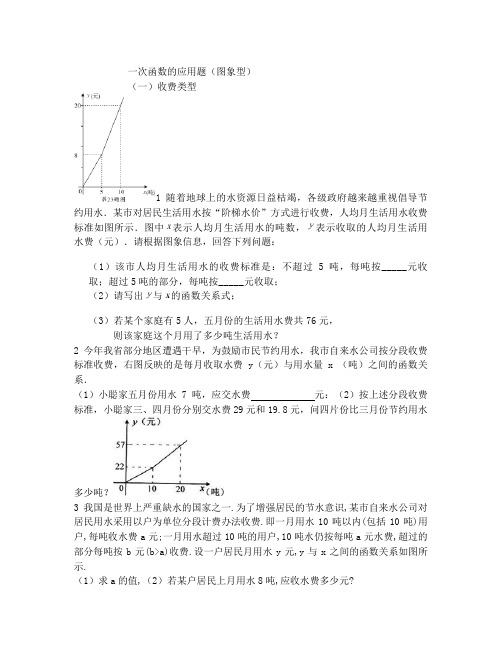
一次函数的应用题(图象型)(一)收费类型1随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市对居民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示.图中表示人均月生活用水的吨数,表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:(1)该市人均月生活用水的收费标准是:不超过5吨,每吨按_____元收取;超过5吨的部分,每吨按_____元收取;(2)请写出与的函数关系式;(3)若某个家庭有5人,五月份的生活用水费共76元,则该家庭这个月用了多少吨生活用水?2今年我省部分地区遭遇干早,为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是毎月收取水费y(元)与用水量x (吨)之间的函数关系.(1)小聪家五月份用水7吨,应交水费元:(2)按上述分段收费标准,小聪家三、四月份分别交水费29元和19.8元,问四片份比三月份节约用水多少吨?3我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元水费,超过的部分每吨按b元(b>a)收费.设一户居民月用水y元,y与x之间的函数关系如图所示.(1)求a的值,(2)若某户居民上月用水8吨,应收水费多少元?求b的值,并写出当x大于10时,y与x之间的函数关系;(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?4为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:每月用气量单价(元/m3)不超出75m3的部分 2.5超出75m3不超出125m3的部分a超出125m3的部分a+0.25(1)若甲用户3月份的用气量为60m3,则应缴费元;(2)若调价后每月支出的燃气费为y(元),每月的用气量为x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;(3)在(2)的条件下,若乙用户2、3月份共用1气175m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?5某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.(二)行程类型1甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:(1)轿车到达乙地后,货车距乙地多少千米?(2)求线段CD对应的函数解析式.(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).2设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设秒后两车间的距离为千米,关于的函数关系如图所示,则甲车的速度是米/秒.3早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:①打电话时,小刚和妈妈的距离为1250米;②打完电话后,经过23分钟小刚到达学校;③小刚和妈妈相遇后,妈妈回家的速度为150米/分;④小刚家与学校的距离为2550米.其中正确的个数是()个4一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是()A.客车比出租车晚4小时到达目的地B.客车速度为60千米/时,出租车速度为100千米/时C.两车出发后3.75小时相遇D.两车相遇时客车距乙地还有225千米【4的变式题】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为千米,出租车离甲地的距离为千米,两车行驶的时间为小时,、关于的函数图像如右图所示:(1)根据图像,直接写出、关于的函数关系式;(2)若两车之间的距离为千米,请写出关于的函数关系式;(3)甲、乙两地间有、两个加油站,相距200千米,若客车进入加油站时,出租车恰好进入加油站,求加油站离甲地的距离.5甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是()6甲乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.(1)A、B两地的距离----- 千米;乙车速度是;a= .(2)乙出发多长时间后两车相距330千米?7“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离(千米)与汽车行驶时间(小时)之间的函数图像,当他们离目的地还有20千米时,汽车一共行驶的时间是8在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B 地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:(1)写出A、B两地直接的距离;(2)求出点M的坐标,并解释该点坐标所表示的实际意义;(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.9周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.(1)求小明骑车的速度和在甲地游玩的时间;(2)小明从家出发多少小时后被妈妈追上?此时离家多远?(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.(三)接水问题出水放水问题类型1一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图10所示. 当容器内的水量大于5升时,求时间x的取值范围.2一个装有进水管和出水管的容器,单位时间内进出的水量都是一定的.设从某刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到时间(分)与容器内存水量(升)之间的关系如图所示.(1)求进水管和出水管每分钟进水多少升?出水多少升?(2)当4≤x≤12时,求y关于的函数解析式(3)若12分钟过后只放水不进水,求y与x之间的函数关系及何时放完水?3教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?(3)按(2)的放法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?4课间休息时,同学们到饮水机旁依次每人接水0.25升,他们先打开了一个饮水管,后来又打开了第二个饮水管.假设接水的过程中每根饮水管出水的速度是匀速的,在不关闭饮水管的情况下,饮水机水桶内的存水量y(升)与接水时间x(分)的函数关系图象如图所示.请结合图象回答下列问题:(1)存水量y(升)与接水时间x(分)的函数关系式;(2)如果接水的同学有28名,那么他们都接完水需要几分钟?(3)如果有若干名同学按上述方法接水,他们接水所用时间要比只开第一个饮水管接水的时间少用2分钟,那么有多少名学生接完水?(四)工程类型1甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC-CD-DE,如图所示,从甲队开始工作时计时.(1)分别求线段BC、DE所在直线对应的函数关系式.(2)当甲队清理完路面时,求乙队铺设完的路面长.2如图是某工程队在"村村通"工程中,修筑的公路长度y (米)与时间x (天)之间的关系图象,根据图象提供的信息,可知修筑该公路的时间是_________天.【变式题】如图是某工程队在"村村通"工程中,修筑的公路长度y (米)与时间x (天)之间的关系图象.根据图象提供的信息,可知该公路的长度是_________米.3某路桥公司承包了一段路基工程,进入施工场地后,所挖筑路基的长度y(m)与挖筑时间x(天)之间的函数关系如图所示,请根据提供的信息解答下列问题.(1)求y与x的函数关系式.(2)用所求的函数解析式预测完成1620m的路基工程,需要挖筑多少天?4.甲,乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)·与挖掘时间x小时之间的关系如图所示,请根据图象所提供的信息解答下列问题: (1)乙队开挖到30米时,用了_________.小时。
一次函数经典例题大全

一. 定义型例1. 已知函数是一次函数,求其解析式。
解:由一次函数定义知,,故一次函数的解析式为y=-6x+3。
注意:利用定义求一次函数y=kx+b解析式时,要保证k≠0。
如本例中应保证m-3≠0。
二. 点斜型例2. 已知一次函数y=kx-3的图像过点(2, -1),求这个函数的解析式。
解:一次函数的图像过点(2, -1),,即k=1。
故这个一次函数的解析式为y=x-3。
变式问法:已知一次函数y=kx-3 ,当x=2时,y=-1,求这个函数的解析式。
三. 两点型例3.已知某个一次函数的图像与x轴、y轴的交点坐标分别是(-2, 0)、(0, 4),则这个函数的解析式为_____。
解:设一次函数解析式为y=kx+b,由题意得,故这个一次函数的解析式为y=2x+4四. 图像型例4. 已知某个一次函数的图像如图所示,则该函数的解析式为__________。
解:设一次函数解析式为y=kx+b由图可知一次函数的图像过点(1, 0)、(0, 2)有故这个一次函数的解析式为y=-2x+2五. 斜截型例5. 已知直线y=kx+b与直线y=-2x平行,且在y轴上的截距为2,则直线的解析式为___________。
解析:两条直线;。
当k1=k2,b1≠b2时,直线y=kx+b与直线y=-2x平行,。
又直线y=kx+b在y轴上的截距为2,故直线的解析式为y=-2x+2六. 平移型例6. 把直线y=2x+1向下平移2个单位得到的图像解析式为___________。
解析:设函数解析式为y=kx+b,直线y=2x+1向下平移2个单位得到的直线y=kx+b与直线y=2x+1平行直线y=kx+b在y轴上的截距为b=1-2=-1,故图像解析式为七. 实际应用型例7. 某油箱中存油20升,油从管道中匀速流出,流速为0.2升/分钟,则油箱中剩油量Q (升)与流出时间t(分钟)的函数关系式为___________。
解:由题意得Q=20-0.2t ,即Q=-0.2t+20故所求函数的解析式为Q=-0.2t+20()注意:求实际应用型问题的函数关系式要写出自变量的取值范围。
一次函数的应用题分类总结整理剖析

一次函数的应用题分类总结整理剖析一次函数应用一、确定解析式的几种方法:1.直接写出一次函数表达式,根据实际意义解决相应问题;(直接法)2.利用待定系数法构建函数表达式,已经明确函数类型;(待定系数法)3.利用问题中各个量之间的关系,变形推导所求两个变量之间的函数关系式;(等式变形法)二、重点题型1.根据各类信息猜测函数类型为一次函数,并验证猜想;2.运用函数思想,构建函数模型解决(最值、决策)问题。
一)根据实际意义直接写出一次函数表达式,然后解决相应问题特点:当所给问题中的两个变量间的关系非常明了时,可以根据二者之间的关系直接写出关系式,然后解决问题。
例1:某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠。
书包每个定价20元,水性笔每支定价5元。
XXX和同学需买4个书包,水性笔若干支(不少于4支)。
1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;直接法:对于第一种优惠方法,每个书包都赠送1支水性笔,所以购买4个书包需要买4支水性笔,总共需要花费4×20+4×5=100元。
因此,y=100.对于第二种优惠方法,购买4个书包和4支水性笔需要花费4×20×0.9+4×5×0.9=82.8元。
因此,y=82.8-0.9x。
2)对x的取值情况进行分析,说明按哪种优惠方法购买比较便宜;当0≤x≤4时,第一种优惠方法更便宜;当x>4时,第二种优惠方法更便宜。
3)XXX和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济。
由于第一种优惠方法总共需要花费100元,而第二种优惠方法的费用函数为y=82.8-0.9x,因此需要求解当x=12时,y 的值为多少。
代入公式得到y=71.4元。
因此,购买4个书包和12支水性笔的最经济方法是选择第二种优惠方法。
例2:某实验中学组织学生到距学校6千米的XXX去参观,学生XXX因事没能乘上学校的校车,于是准备在学校门口改乘出租车去XXX,出租车的收费标准为:3千米以下(含3千米)收费8元,3千米以上,每增加1千米,收费1.8元。
一次函数知识点总结和常见题型归类

一次函数知识点总结与常见题型基本概念1、变量:在一个变化过程中可以取不同数值的量。
常量:在一个变化过程中只能取同一数值的量。
例题:在匀速运动公式vt s =中,v 表示速度,t 表示时间,s 表示在时间t 内所走的路程,则变量是________,常量是_______。
在圆的周长公式C =2πr 中,变量是________,常量是_________.2、函数:一般的,在一个变化过程中,如果有两个变量x 和y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就把x 称为自变量,把y 称为因变量,y 是x 的函数。
*判断Y 是否为X 的函数,只要看X 取值确定的时候,Y 是否有唯一确定的值与之对应例题:下列函数(1)y =πx (2)y =2x -1 (3)y =1x (4)y =21-3x (5)y =x 2-1中,是一次函数的有( )(A )4个 (B )3个 (C )2个 (D )1个P116 1 P87 23、定义域:一般的,一个函数的自变量允许取值的范围,叫做这个函数的定义域。
4、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数;(2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零;(4)关系式中含有指数为零的式子时,底数不等于零; (5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
例题:下列函数中,自变量x 的取值范围是x ≥2的是( )A .y =2x -B .y =12x - C .y =24x - D .y =2x +·2x - 函数5y x =-中自变量x 的取值范围是___________.已知函数221+-=x y ,当11≤<-x 时,y 的取值范围是 ( ) A .2325≤<-y B .2523<<y C .2523<≤y D .2523≤<y5、函数的图像一般来说,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.例题:P117 56、函数解析式:用含有表示自变量的字母的代数式表示因变量的式子叫做解析式。
