卢瑟福散射公式的实验验证
卢瑟福散射实验报告
陈杨PB05210097 物理二班实验题目:卢瑟福散射实验实验目的:1.通过卢瑟福核式模型，说明α粒子散射实验，验证卢瑟福散射理论；2.并学习应用散射实验研究物质结构的方法。
实验原理:现从卢瑟福核式模型出发，先求α粒子散射中的偏转角公式，再求α粒子散射公式。
1.α粒子散射理论（1）库仑散射偏转角公式设原子核的质量为M，具有正电荷+Ze，并处于点O，而质量为m，能量为E，电荷为2e的α粒子以速度ν入射，在原子核的质量比α粒子的质量大得多的情况下，可以认为前者不会被推动，α粒子则受库仑力的作用而改变了运动的方向，偏转θ角，如图所示。
图中ν是α粒子原来的速度，b是原子核离α粒子原运动径的延长线的垂直距离，即入射粒子与原子核无作用时的最小直线距离，称为瞄准距离。
图α粒子在原子核的库仑场中路径的偏转当α粒子进入原子核库仑场时，一部分动能将改变为库仑势能。
设α粒子最初的的动能和角动量分别为E和L，由能量和动量守恒定律可知：⎪⎪⎭⎫⎝⎛++⋅=••222202241ϕπεr r m r Ze E （1）L b m mr ==••νϕ2 （2）由（1）式和（2）式可以证明α粒子的路线是双曲线，偏转角θ与瞄准距离b 有如下关系：202242Ze Ebctgπεθ= （3）设E Ze a 0242πε=，则 a bctg22=θ（4）这就是库仑散射偏转角公式。
（2）卢瑟福散射公式在上述库仑散射偏转公式中有一个实验中无法测量的参数b ，因此必须设法寻找一个可测量的量代替参数b 的测量。
事实上，某个α粒子与原子散射的瞄准距离可大，可小，但是大量α粒子散射都具有一定的统计规律。
由散射公式（4）可见，θ与b 有对应关系，b 大，θ就小，如图所示。
那些瞄准距离在b 到db b +之间的α粒子，经散射后必定向θ到θθd -之间的角度散出。
因此，凡通过图中所示以b 为内半径，以db b +为外半径的那个环形ds 的α粒子，必定散射到角θ到θθd -之间的一个空间圆锥体内。
实验报告
实验报告
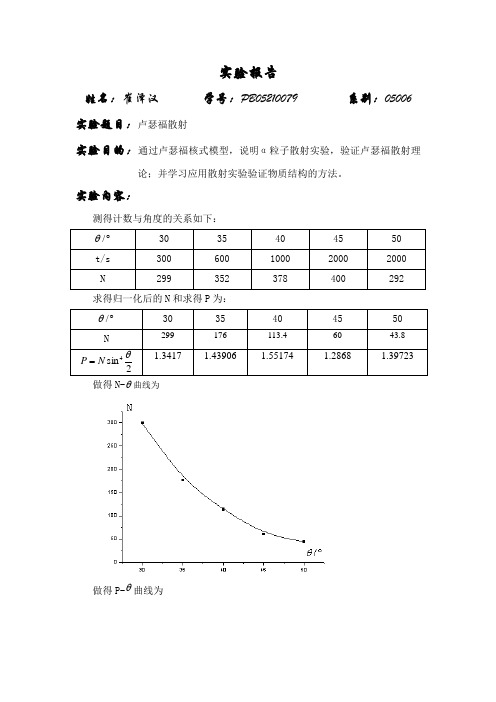
姓名：崔泽汉 学号：PB05210079 系别：05006 实验题目：卢瑟福散射
实验目的：通过卢瑟福核式模型，说明α粒子散射实验，验证卢瑟福散射理
论；并学习应用散射实验验证物质结构的方法。
实验内容：
测得计数与角度的关系如下：
︒/θ
30 35 40 45 50 t/s 300 600 1000 2000 2000 N
299
352
378
400
292
求得归一化后的N 和求得P 为：
︒/θ
30
35
40
45
50
N
299
176
113.4
60
43.8
2
sin 4
θ
N P =
1.3417 1.43906 1.55174 1.2868 1.39723
做得N-θ曲线为
做得P-θ曲线为
思考题:
根据卢瑟福散射公式2
sin 4
N 应为常数，本实验的结果有偏差吗？试分析其
原因。
答： 1.散射真空室处于低真空状态，离真正的真空还差很远。
2.α粒子源辐射离子具有随机性，因此即使在同一角度同一时间段里所测的粒子数也会不同。
所测的时间段太短，因此由随机性带来的误差太大，延长测量时间可以减小误差。
卢瑟福散射_实验报告
一、实验目的1. 验证卢瑟福散射理论，理解原子核式结构模型；2. 掌握实验装置的使用方法，学会数据处理和误差分析；3. 培养科学实验技能和团队协作能力。
二、实验原理卢瑟福散射实验是通过α粒子轰击金箔，观察α粒子在金箔后的散射情况，从而验证原子核式结构模型。
根据卢瑟福散射理论，当α粒子穿过原子时，只有当α粒子与原子核的距离小于某一特定值时，α粒子才会发生散射。
该特定值与原子核的半径有关，即r = (ke^2)/(p^2)，其中k为库仑常数，e为电子电荷，p为α粒子的动量。
三、实验仪器与材料1. 实验仪器：卢瑟福散射实验装置、α粒子源、金箔、计数器、显微镜、计算机等；2. 实验材料：金箔、α粒子源、电源、真空泵等。
四、实验步骤1. 安装实验装置，确保所有仪器连接正确；2. 将金箔固定在实验装置上，调整显微镜位置，使其与金箔垂直；3. 打开α粒子源，调整电流，使α粒子流稳定；4. 打开计数器，记录α粒子在金箔后的散射情况；5. 调整显微镜位置，观察不同角度的散射情况，记录散射角度及计数；6. 重复步骤4和5，记录多组数据；7. 关闭α粒子源，关闭电源，整理实验器材。
五、实验数据与处理1. 记录实验数据，包括散射角度、计数等；2. 利用计算机软件处理数据，计算散射角度与计数的关系；3. 对比实验数据与理论计算值，分析误差来源。
六、实验结果与分析1. 实验结果显示，绝大多数α粒子穿过金箔后仍沿原来的方向前进，偏转角度很小；2. 少数α粒子发生了较大的偏转，偏转角度超过90度；3. 极少数α粒子的偏转角度超过180度，甚至被反弹回来。
根据实验结果，可以得出以下结论：1. 原子内部存在一个带正电的核，核的半径远小于原子半径；2. 原子核的质量远大于电子的质量；3. 原子核的正电荷集中在原子内部，电子围绕原子核运动。
七、误差分析1. α粒子源电流不稳定，导致α粒子流不稳定；2. 金箔厚度不均匀，导致α粒子散射角度不准确；3. 实验装置存在一定误差，如显微镜的读数误差等；4. 数据处理过程中存在舍入误差。
卢瑟福的α粒子散射实验观察和结论
卢瑟福的α粒子散射实验观察和结论卢瑟福的α粒子散射实验观察和结论导言卢瑟福的α粒子散射实验是物理学史上具有里程碑意义的实验之一。
通过此实验，卢瑟福成功地证实了原子结构的基本概念，并揭示了原子核的存在。
本文将探讨卢瑟福的α粒子散射实验的观察结果和结论，并分享我对此实验的观点和理解。
1. 实验背景卢瑟福的α粒子散射实验于1911年进行，当时科学界对原子结构的理解还较为模糊。
卢瑟福希望通过实验来验证当时流行的“杜尔文模型”，即认为原子是由带正电的球体（原子核）和带负电的电子云组成的。
他选择使用α粒子（带有两个负电荷的氦离子）作为入射粒子，通过散射角度的观察来揭示原子的内部结构。
2. 实验过程卢瑟福将一束经过加速的α粒子照射到薄金属箔上，并在周围布置了一个荧光屏。
通过观察荧光屏上出现的散射点和角度，卢瑟福记录下了大量实验数据。
3. 实验观察结果卢瑟福的实验观察结果出人意料，与当时的预期相去甚远：(1) 大多数α粒子出射角度很小，接近与入射方向一致；(2) 一小部分α粒子发生明显的偏转，出射角度远离入射方向；(3) 极少数α粒子甚至发生180度的反向散射，返回入射方向。
4. 实验结论基于上述观察结果，卢瑟福得出了以下结论：(1) 原子具有较大的空隙，大部分α粒子可以直接穿过原子而不发生散射；(2) 原子中存在带正电的原子核，同时带负电的电子云位于其周围；(3) 发生明显偏转的α粒子与正电荷较大的原子核发生了相互作用；(4) 散射角度与入射粒子的能量和散射物质的原子核正电荷有关。
5. 对实验的观点和理解卢瑟福的α粒子散射实验提供了直接证据，证明了历史上首次提出的原子核模型。
此模型认为原子核位于原子的中心，其中带有正电荷，并且占据了大部分原子的质量。
这个实验打破了当时流行的汤姆孙模型，即认为原子是由均匀分布的正负电荷所组成。
对于实验的观察结果，我认为其中最令人震惊的是极少数α粒子的180度反向散射。
这意味着原子核的大小远远小于原子的整体大小，同时具有较大的正电荷。
第一章5-卢瑟福公式验证
§4 卢瑟福公式的实验验证
一．盖革-马斯顿的α散射实验
分四种情况验证：
1．dN'∝1/Sin4θ/2;
2．dN'∝t;
3．dN'∝1/E2;
4．dN'∝Z22;
1、2、3情况，与实验结果符合很好，而4情况与实验有偏差。
后查德维克改进了实验，也证明了第4情况与实验符合。
并由实验第一次测出了一些原子的电荷数Z，纠正了历史上有关原子电荷数Z的一些错误。
问题：在散射公式中，当θ→0时，
dN'/N→∞,不合理。
原因？
二．原子核大小估计
α粒子最接近原子核的距离，应是原子核大小的上限。
能量守恒， mV2/2=mV'2/2+Z1Z2e2/r m
角动量守恒， mVb=mV’r m
消去V’，取+号，得：
r m=a(1+cscθ/2)/2
取E=5.3Mev,29C u，θ=180，得r m~15,8×10-15m~10-4Å.
若采用对头碰撞, 得r m更简单：
mV2/2=z1z2e2/r m, 得
r m= 2z1z2e2 /mV2
§5 行星模型的意义与困难
一．困难---在经典理论下行星模型是不稳定的，原子核外电子会很快掉到原子核
上。
二．意义
1．有核模型仍是正确的，但电子不能作轨道运动，而是以‘电子云’弥散在
原子核外。
2．卢瑟福散射公式至今仍是正确的。
卢瑟福散射是当今研究物质结构、材料
分析的一种有效方法与手段。
卢瑟福散射公式的实验验证
卢瑟福散射公式的实验验证
一、实验简介
卢瑟福散射公式（Rutherford scattering formula）是1911年英国
科学家阿尔弗雷德·卢瑟福提出的，它是用来解释热核反应的微观动力学
模型，根据该公式，当重粒子（如α粒子）抵达质量集中的区域（原子核）时，其有几率发生Scattering过程，进而使得粒子的方向改变。
为
了验证卢瑟福散射公式，本实验采用重粒子（铯粒子），在特定的重粒子
浓度下，观察重粒子运动的方向，检测是否与卢瑟福散射公式所预期相同。
二、实验环境及设备
本实验使用半导体α质量分析仪设备，它是一种能够通过测定散射
冲击中核的质量来测量粒子能量的装备。
本实验使用的核物质是6种称为“原子核供体”的晶体，用化学方法制备成椭圆形状的晶体，晶体表面由
一层石英薄膜覆盖，用作放射性核反应探测器。
晶体板两端设有灯，用来
提供实验散射图形的阴影效果。
三、实验实施
1.首先在实验室中放入所需的晶体和灯，将晶体板放在室内的两端，
并在晶体板的表面上以固定间距制作放射线路径，以便观察粒子在穿过该
晶体板的过程中的变化情况。
2.然后向晶体板注入适量的铯粒子，将晶体板放置在射线源（用于发
射α粒子的装置）上方，调节粒子浓度。
卢瑟福散射
卢瑟福散射卢瑟福散射实验是近代物理科学发展史中最具有影响力的重要实验之一。
本世纪初，人们虽然知道了物质由原子构成，并且由气体性质和热力学理论也知道了原子的大概尺寸，约为10-8cm 。
1897年，汤姆生（J.J.Thomson ）发现了电子，而且知道了电子是原子的组成部分，但原子的内部结构却仍处于假想阶段。
由于原子是中性的，电子带有负电荷，所以原子中还应有带正电的部分。
汤姆生提出一种原子模型，认为正电荷均匀地分布在整个原子球内，一定数目的电子“镶嵌”在这个球内或球面上。
电子可以在它们的平衡位置附近振动，从而发出特定频率的电磁波，这就是汤姆生的原子模型。
这似乎可以解释当时已观察到的原子光谱，但事实很快否定了这一模型。
1909年，卢瑟福（Lord Ernest Rutherford ）和其合作者盖革（H.Geiger ）与马斯顿（E.Marsden ）所进行的α粒子散射实验则为另一种原子模型，即原子的核式模型（又称“行星模型”）的建立奠定了基础。
卢瑟福散射实验最重要的结果是发现大约有1/8000的α粒子散射角大于900，甚至接近1800，即发现存在大角度散射。
当卢瑟福试图用汤姆生模型解释这个实验结果时，他发现大角度上的散射截面是不能被解释的。
在汤姆生模型中，正电荷分布于整个原子，因而在原子内部的任何位置上都不可能有足够强的电场使α粒子发生大角度散射。
为了证实该实验结果，卢瑟福认为原子中的正电荷不得不更紧密地集中在一起。
通过他对物理现象深刻的洞察力，最终提出了原子的核式模型。
在核式模型中，原子核的半径近似为10-13cm ，约为原子半径的1/105。
卢瑟福散射实验给了我们正确的有关原子结构的图像，是现代核物理的基石。
一、原理1. 瞄准距离与散射角的关系卢瑟福把α粒子和原子都当做点电荷，并且假设两者之间的静电斥力是唯一的相互作用力。
设一个α粒子以速度v 0沿AT 方向入射，由于受到核电荷的库仑作用，α粒子将沿轨道ABC 出射。
卢瑟福的a粒子散射实验结论原理计算
卢瑟福的a粒子散射实验结论原理计算卢瑟福的α粒子散射实验是一个具有重要意义的物理实验。
该实验是由新西兰物理学家欧内斯特·卢瑟福于20世纪初进行的，实验中使用了α粒子（即氦离子或称α粒子）射向一个金属薄膜，并对散射角度和散射强度进行了观察和测量。
根据经典的电磁理论，当一个α粒子入射到坚硬物体上时，它会受到库仑力的相互作用。
根据库仑定律，这个作用力具有反比于距离的平方的关系，因此入射到金属薄膜的α粒子将会受到金属原子核的库仑力作用，与之发生散射。
卢瑟福实验的重要结论如下：1.大部分的α粒子直线穿过金属薄膜，只发生微小的散射。
这表明原子的大部分空间是由空隙构成的，因为α粒子直径比原子小得多。
2.少数的α粒子经过散射后，发现其散射角度很大。
这暗示了原子具有一个高度集中的、具有正电荷的中心区域，即原子核。
3.α粒子散射的散射角度与入射粒子的能量有关。
这表明散射的短距离库仑相互作用，与α粒子的能量相关。
根据以上结论，卢瑟福提出了最早的原子核模型，即卢瑟福散射模型。
根据该模型，原子由一个带正电荷的原子核和围绕核的负电荷电子云组成。
原子的大部分体积为空隙，几乎所有的质量都集中在原子核中。
卢瑟福散射实验结论的原理可以通过经典的库仑力和动量守恒定律来解释。
在实验中，当α粒子与金属原子核发生相互作用时，它们之间的库仑力导致了散射。
根据电磁力的方向，α粒子将会受到一个向外的力，从而发生向后的散射。
根据动量守恒定律，散射后的α粒子的动量也会改变，从而使其散射角度发生偏转。
根据电磁力的定性描述和动量守恒定律可以计算散射角度和散射强度。
实际上，卢瑟福通过对散射后α粒子的观察和测量，得出了散射角度与入射粒子能量之间的关系，并从而确定了原子核的存在。
总结起来，卢瑟福的α粒子散射实验结论揭示了原子内部结构的重要特征，尤其是原子核的存在。
这项实验在现代原子物理学的发展中具有深远意义，为原子核物理学的诞生奠定了基础，也为后来的量子力学的发展提供了重要线索。
使用卢瑟福散射公式探究原子结构
使用卢瑟福散射公式探究原子结构在物理学的发展史上，探究原子结构一直是一个重要的课题。
而卢瑟福散射实验则是揭示原子内部结构的重要里程碑。
本文将介绍卢瑟福散射实验的原理及其应用，以及对原子结构的深入认识。
卢瑟福散射实验是由英国物理学家欧内斯特·卢瑟福于20世纪初进行的。
实验的原理是通过将高能粒子（通常是α粒子）轰击金属箔，观察粒子的散射情况，从而推断出原子的结构。
卢瑟福散射公式是在实验数据的基础上，由卢瑟福提出的。
该公式描述了散射粒子的散射角度与原子核的位置关系。
公式的推导基于库仑定律和牛顿第二定律，并假设原子核是一个点电荷。
通过卢瑟福散射公式，我们可以推断出原子核的位置和电荷分布。
实验结果显示，大部分α粒子都经过了轻微的散射，但有少部分α粒子发生了巨大的散射角度，这表明原子内部存在着极小但带正电的核。
根据散射角度的大小，我们可以计算出原子核的半径和电荷数。
卢瑟福散射实验的结果颠覆了当时对原子结构的认识。
传统的“布丹模型”认为原子是一个均匀带负电的球体，而卢瑟福实验表明原子内部存在着带正电的核。
这一发现对于后来量子力学的发展产生了深远的影响。
通过卢瑟福散射实验和公式，我们不仅可以了解原子核的性质，还可以进一步研究原子的电子结构。
根据卢瑟福散射实验的结果，我们可以推断出电子围绕原子核运动的轨道和能级。
除了卢瑟福散射实验，现代科学家还利用其他方法来探究原子结构。
例如，X射线衍射技术可以通过测量X射线的散射模式来确定晶体的结构。
这些实验方法的发展使我们对原子结构有了更深入的认识。
然而，卢瑟福散射实验仍然是研究原子结构的重要工具之一。
虽然现代科学已经发展出更精确的实验方法和理论模型，但卢瑟福散射实验的意义不可忽视。
它为我们提供了一个最初的窗口，让我们能够窥探原子内部的奥秘。
总之，卢瑟福散射实验及其公式的发现对于我们认识原子结构产生了深远的影响。
通过实验数据和公式的分析，我们可以推断出原子核的位置和电荷分布，进一步研究原子的电子结构。
卢瑟福散射实验报告
卢瑟福散射实验报告实验步骤：1.测量α粒子在空气中的射程，计算α粒子的能量Ea) 将空靶插入卡槽，测量靶到探头的距离l 1 和源到探头的距离l 2 ，并记录室温Tb) 盖上真空室上盖，开启机械泵电源将真空室抽真空。
c) 打开测量软件，从-5°测到5°,以1°为步长测α粒子能谱峰区计数，每个角度测60s，确定物理0°角；d) 靶台转至物理0°角，测ROI 计数120s；e) 关闭电磁阀2，缓慢放气至6.0kPa 左右后停止放气。
f) 在6~30kPa 范围测气压对计数的影响，测4 个点（连同气压为0 的点共至少5 个点），每点测120s。
g) 绘制P-N曲线，得到α粒子的平均射程及能量2.验证关系a) 缓慢放完气后，打开真空室盖子，换上金靶，合上盖子抽真空。
b) 在-5°~5°范围以1°为步长测α粒子能谱峰区计数，每个角度测90s，确定物理0°角；c) 在10°~25°范围选5 个角度测散射计数，每个角度根据计数率调整测量时间。
d）绘制N-θ曲线，并与理论值比较。
数据分析：1.α粒子射程及能量确定物理零度角：角度/°-5-4-3-2-1选区计数7362573675698316199151905改变真空室气压，记录120s内探测器计数，绘制P-N关系图对曲线进行线性拟合，得到N = -2750.3P + 150823 ，相关系数R² = 0.988由解析式可推得，P=0时N0=150823，N=N0/2时P=27.42kPa。
此时源到探测器距离l2即平均射程。
由，得到室温24.3℃，P=27.42kPa时空气密度∴由可解出E=2.323MeV2.验证关系角度/°-3-2-10选区计数6628693767876437改变散射角，测散射计数，绘制N-θ图散射角/°1013161922时间/s2001503006001000选区计数57682173197919541453，对曲线进行线性拟合，斜率即K=0.0016.做图像，与理论计算值比较121416182022th eta d eg ree0.0050.0100.015K K theta relation相对误差思考题2. 有偏差，而且在θ较大时更加明显，主要原因在于卢瑟福散射公式本身所推论的是一个概率，只有当实验时间趋于无穷时才会完全相符，但由于客观原因的限制我们无法利用更长的时间来获得更加准确的数据，因此随机性的因素便会较大的影响实验的结果。
卢瑟福的α粒子散射实验结论
卢瑟福的α粒子散射实验结论1. 实验背景说起卢瑟福，那可真是个了不起的科学家，咱们今天要聊的就是他那经典的α粒子散射实验。
大约在1911年，这位大名鼎鼎的物理学家在研究原子结构时，做了个大胆的实验。
想象一下，那个时候，科学界对原子内部的构造可谓是一头雾水，搞得像是在摸黑走路。
卢瑟福和他的团队决定用α粒子，也就是一种带正电的粒子，来探探原子里到底藏了些什么东西。
真是敢为人先啊！实验的过程其实挺简单的。
他们把α粒子从放射性元素发射出来，然后让这些粒子撞击一层极薄的金箔。
金箔薄得就像是纸一样，几乎可以用手指捅破。
接着，卢瑟福用荧光屏观察这些α粒子是怎么散射的。
这里面可有不少戏剧性的时刻，就像一场精彩的表演。
2. 实验结果2.1 意外的发现好吧，结果真是让人瞠目结舌！大部分的α粒子都是笔直穿过金箔的，仿佛金箔根本就不存在。
但有一小部分的粒子却偏偏改变了方向，有的甚至反弹回来，简直像是看见了鬼。
卢瑟福当时一定觉得，哎呀，怎么回事呢？难道原子内部隐藏着什么秘密？这可真是让人百思不得其解。
2.2 原子模型的重构经过一番深入思考，卢瑟福得出一个惊人的结论：原子并不是一团糟的“梅花”，而是有着明确结构的。
他提出，原子里有一个非常小且密集的“原子核”，而α粒子反弹就是因为碰到了这个“核”。
这个核是正电的，周围则是负电的电子在转啊转，真是一个小宇宙！这不禁让人想起一句话：外表光鲜，内里却是别有洞天。
3. 实验的意义3.1 对科学界的影响卢瑟福的发现简直就是科学界的一场地震，彻底颠覆了之前的“汤姆逊的葡萄干布丁模型”。
他这一理论，不但让大家看到了原子的真实结构，还为后来的科学研究铺平了道路。
原子核的概念后来成了核物理学的基石，简直是功德无量。
3.2 对日常生活的启示你可能会问，这跟我们日常生活有什么关系呢？其实，卢瑟福的实验提醒我们，很多时候，表象并不代表真相。
就像我们看到的一个人，可能外表光鲜亮丽，内心却藏着故事。
所以，别轻易下结论，要多观察，多思考！另外，卢瑟福的好奇心也是我们每个人都应该学习的。
卢瑟福散射公式结论
卢瑟福散射公式结论卢瑟福散射实验是一种通过射入粒子束到金属箔上来研究原子核结构的方法。
实验中，卢瑟福用射电性物质铀的放射性衰变得到的α粒子作为探针粒子，通过一个小孔射向非常薄的金属箔。
借助于一块放射性屏前后的闪烁屏，科学家可以观察到α粒子在金属箔上的散射情况。
基于大量的实验数据，卢瑟福总结出以下几个重要的结论：1.大部分α粒子直线通过了金属箔。
根据经验关系，粒子的质量越大，其运动惯性越大，使得α粒子在经过金属箔的碰撞中更倾向于直线通过。
2.一小部分α粒子被金属箔散射了。
尽管只有少数几个，但卢瑟福发现这些散射事件是非常重要的。
这些散射事件表明了一种新的粒子之间的相互作用，这种相互作用是通过原子核所发生的。
3.α粒子的散射角度不均匀。
卢瑟福发现散射角度的分布是一个连续的函数，这是相对于传统的“洛雷恩兹定律”的破坏。
洛雷恩兹定律是经典物理学中与射线光学紧密相关的定律。
基于这些实验结果，卢瑟福提出了著名的卢瑟福散射公式：θ = (2πNAZze² / Kmv²) * (1 / (4πε₀)) * (1/sin²(2θ/2))其中，θ是散射角度，NA是阿伏伽德罗常数，Z是目标原子的原子序数，z是入射粒子的电荷数，e是元电荷，K是库仑电荷常数，m是入射粒子的质量，v是入射粒子的速度，ε₀是真空介电常数。
卢瑟福散射公式的推导基于一个假设：入射的α粒子与目标原子核之间的相互作用是一个库仑散射过程，这种相互作用力是一个中心力，与入射粒子和靶粒子间的距离成反比。
根据这个假设，卢瑟福运用了库仑定律、动能守恒和动量守恒等基本物理原理，得出了这一公式。
1.相对于其他轻原子核而言，重原子核对α粒子的散射更明显。
这是因为重原子核所产生的库仑散射力比较大，使得α粒子更容易改变方向而散射。
2.根据散射角度的分布情况，可以推断出目标原子核的质量和电荷分布。
这为原子核物理学的发展提供了重要线索和依据。
3.卢瑟福散射公式的推导过程中，还考虑到了散射角度与入射粒子速度的关系。
卢瑟福散射实验报告
一、实验目的1. 了解卢瑟福散射实验的基本原理和实验方法；2. 掌握实验仪器和实验步骤；3. 通过实验观察和分析，验证卢瑟福散射实验的结论，即原子具有核式结构。
二、实验原理卢瑟福散射实验是英国物理学家卢瑟福在1909年设计的一种实验，旨在验证原子结构的模型。
实验中，卢瑟福使用了一束α粒子轰击薄金属箔，通过观察α粒子的散射情况，推断出原子具有核式结构。
根据经典电磁理论，当α粒子与原子核发生碰撞时，会发生库仑散射。
根据库仑定律，散射角θ与入射角φ、α粒子的能量E和原子核的电荷量q有关。
实验中，通过改变入射角和α粒子的能量，可以观察不同角度下的散射情况，从而验证原子核的存在。
三、实验仪器与材料1. 实验仪器：α粒子源、金箔、显微镜、计数器、实验装置等；2. 实验材料：α粒子源、金箔、实验装置等。
四、实验步骤1. 将α粒子源与金箔固定在实验装置上；2. 将实验装置放入真空容器中，确保容器内无空气；3. 打开α粒子源，调整入射角φ，观察散射情况；4. 记录不同入射角下的散射数据，包括散射角度、散射强度等；5. 改变α粒子的能量E，重复步骤3和4；6. 对实验数据进行处理和分析，验证卢瑟福散射实验的结论。
五、实验结果与分析1. 实验结果显示，大部分α粒子穿过金箔，未发生偏转，表明原子内部存在较大的空间；2. 部分α粒子发生散射，且散射角度较小，表明原子内部存在微粒；3. 极少数α粒子发生大角度散射，甚至反弹回来，表明原子内部存在质量较大、带正电的微粒，即原子核。
根据实验结果，可以得出以下结论：1. 原子具有核式结构，即原子由一个重而带正电的核心和围绕其周围的带负电子的电子云组成；2. 原子核的存在是导致α粒子散射的主要原因；3. 原子核的质量和电荷量远大于电子，因此α粒子在碰撞过程中主要受到原子核的影响。
六、实验讨论1. 实验过程中，α粒子的能量和入射角对散射结果有较大影响。
能量越高、入射角越小，散射角度越小；2. 实验过程中，实验装置的真空度对实验结果有一定影响。
卢瑟福的a粒子散射实验现象及结论
卢瑟福的a粒子散射实验现象及结论一、实验介绍二、实验现象1. α粒子的发射与散射2. α粒子的反跳现象三、实验结论1. 原子具有空心结构2. 原子核具有正电荷3. 原子核与电子的比例关系四、实验意义及影响一、实验介绍卢瑟福的a粒子散射实验是物理学中非常重要的一个经典实验，它是对原子结构和性质进行研究的基础。
该实验于1910年由英国物理学家欧内斯特·卢瑟福（Ernest Rutherford）领导完成，是一项利用α粒子对原子核进行探测的实验。
二、实验现象1. α粒子的发射与散射在卢瑟福的a粒子散射实验中，首先将α放射源放置在一个铅盒中，使其向外发出α粒子。
然后将α粒子引入真空玻璃管中，通过调节电压和电流来使α粒子加速，并通过一个小孔射向金箔靶。
在金箔靶后面设立一个荧光屏，用来观察α粒子的散射情况。
实验结果表明，大多数α粒子直线穿过金箔靶，只有极少数α粒子被散射。
这说明原子具有空心结构，其中正电荷集中在原子核内。
2. α粒子的反跳现象在实验中，还观察到了α粒子的反跳现象。
即有些α粒子经过金箔靶后会发生反弹，回到射线源处。
这说明原子核具有正电荷，并且与电子相比非常小。
三、实验结论1. 原子具有空心结构卢瑟福的a粒子散射实验表明，大多数α粒子直线穿过金箔靶，只有极少数α粒子被散射。
这说明原子具有空心结构，其中正电荷集中在原子核内。
2. 原子核具有正电荷实验还观察到了α粒子的反跳现象。
即有些α粒子经过金箔靶后会发生反弹，回到射线源处。
这说明原子核具有正电荷，并且与电子相比非常小。
3. 原子核与电子的比例关系通过对实验数据的分析，卢瑟福得出了一个重要的结论：原子核的质量与电子的质量相比非常大，而原子核的直径只有原子直径的万分之一。
这说明原子核与电子的比例关系是非常不同的。
四、实验意义及影响卢瑟福的a粒子散射实验是对原子结构和性质进行研究的基础。
它揭示了原子具有空心结构，其中正电荷集中在原子核内；同时也证明了原子核具有正电荷，并且与电子相比非常小。
卢瑟福的a粒子散射实验结论原理计算
卢瑟福的a粒子散射实验结论原理计算卢瑟福的α粒子散射实验被认为是原子物理学的里程碑之一，它为原子结构的理论奠定了基础。
实验中，卢瑟福将带有正电荷的α粒子轰击薄薄的金属箔，观察散射后α粒子的轨迹和能量分布情况。
根据实验结果，卢瑟福提出了以下结论：1.原子有一个小而重的核心：卢瑟福发现大部分α粒子穿过金箔而不受到偏转，只有极少数粒子会发生大角度的散射。
这表明原子中存在一个小而重的核心，α粒子必须以足够大的角度接近核心才能发生散射。
2.原子核带有正电荷：由于α粒子带有正电荷，而且只有很少的粒子角度发生大的散射，可推断出核内带有与α粒子电荷相反的正电荷。
3.原子是空旷的：由于几乎所有的α粒子都能穿过金箔而不受到偏转，推断出原子的体积主要是由空旷的空间构成，α粒子只有在靠近核心时才会发生散射。
4.原子中电子的位置和分布：卢瑟福的实验结果无法解释电子分布的精确位置，但可以推测出电子主要处于与核心固定位置的轨道上，并且占据大部分原子体积。
卢瑟福的实验结论可以得出以下原理：1.核内带正电荷：由于α粒子在金箔中的大角度散射，推测出核内带有正电荷。
瑟福的实验结果与电子云模型中的平均电荷情况不符，进而证实了带正电荷的原子核的存在。
2.原子是空旷的：由于大部分α粒子穿过了金箔而不受到偏转，推测原子主要是由空旷的空间构成。
这与传统的布尔理论，即原子由电子环绕的核心构成的观点不同，从而推动了后来的量子力学的发展。
计算原理：卢瑟福实验的计算原理基于库伦定律和动量守恒定律。
根据库仑定律，两个带电体之间的作用力与它们电荷之间的乘积成正比，与它们之间距离的平方成反比。
在实际计算中，我们可以假设α粒子和原子核为点电荷，并且α粒子的质量远大于电子和原子核的质量。
由于其中一个电荷为正电荷，而另一个电荷为负电荷，通过库伦定律可以计算出粒子受到的作用力大小。
此外，卢瑟福实验还考虑了动量守恒定律。
在碰撞前后，α粒子和原子核之间的总动量矢量在大小和方向上都保持不变。
卢瑟福散射实验(262)
卢瑟福散射实验 5-04级06系 姓名：薛林林 学号：PB04210262 实验题目：卢瑟福散射实验实验目的：通过卢瑟福核式模型，说明α粒子散射实验，验证卢瑟福散射理论；并学习应用散射实验研究物质结构的方法。
实验原理：1、α粒子散射理论（1）库仑散射偏转角公式偏转角θ与瞄准距离b 有如下关系：22242Ze Eb ctgπεθ=设EZe a 0242πε=，则a b ctg 22=θ这就是库仑散射偏转角公式。
（2）卢瑟福散射公式2sin 14241)(422200θπεθσ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=Ω=ΩE Ze td nN dnd d （8）这就是著名的卢瑟福散射公式。
代入各常数值，以E 代表入射α粒子的能量，得到公式：()2sin 12296.142θσ⎪⎭⎫⎝⎛=ΩE Z d d （9）其中，Ωd d σ的单位为sr mb /，E 的单位为Mev 。
2、卢瑟福理论的实验验证方法在本实验中，只是改变散射角，验证散射计数率与散射角的关系2sin14θ∝N 。
这是对卢瑟福散射理论最有力的验证。
实验仪器：散射真空室、电子学系统、步进电机及其控制系 数据处理：（1）确定仪器的物理零度。
（2）原始数据：（3）数据处理：A:将实验中的计数测量按同一测量时间归一按t=100s 进行归一得:2、以散射角θ为横坐标，散射计数N 为纵坐标，作θ-N 关系图如下：Y A x i s T i t l eX Axis Title3、以散射角θ为横坐标，P 为纵坐标，作θ-P 关系图，如下图所示：由p=)2(sin 4θN 得：Linear Regression for ccc_y:Y = A + B * XParameter Value Error------------------------------------------------------------A 0.37370.11165B 0.00230.00258------------------------------------------------------------R SD N P------------------------------------------------------------0.407290.0538760.42285Pθ35度的点可认为奇点,实验结果就好多了由图知，P-θ是一条斜率较小的直线。
卢瑟福散射 实验报告
卢瑟福散射实验报告卢瑟福散射实验报告引言：卢瑟福散射实验是20世纪初物理学家欧内斯特·卢瑟福进行的一项重要实验，通过观察α粒子在金属箔上的散射现象，揭示了原子结构中的核心概念。
本文将对卢瑟福散射实验进行详细介绍，并探讨其对原子理论的贡献。
实验装置与方法：卢瑟福散射实验主要使用了阻挡放射性α粒子的金属箔和荧光屏。
实验时，α粒子从放射源发射出来，经过一系列的准直装置后，射到金属箔上。
箔片上的α粒子会发生散射，一部分散射到荧光屏上，形成亮点。
通过观察亮点的分布情况，可以推断出α粒子在金属箔中的散射规律。
实验结果与讨论：卢瑟福实验的最重要结果之一是发现了一个非常小而密集的正电荷核心，即原子核。
通过对散射角度的测量和分析，卢瑟福得出结论：α粒子在经过金属箔时，与核心发生散射的概率与散射角度的平方成反比。
这一结论被称为卢瑟福散射公式。
卢瑟福散射公式的推导与解释：卢瑟福散射公式的推导基于库仑力的作用。
当α粒子靠近原子核时，它受到核心的正电荷吸引，同时也受到库仑斥力的作用。
根据库仑定律，这两个力与距离的平方成反比。
因此，当α粒子靠近核心时，它的散射角度会增大。
卢瑟福散射公式的解释也揭示了原子的空间结构。
根据公式，α粒子在经过金属箔时，只有极小的一部分发生散射，而大部分直线通过。
这表明原子内部存在着大量的空隙，α粒子可以穿过这些空隙而不与核心发生碰撞。
而当α粒子与核心发生碰撞时，它们的散射角度较大，说明核心的大小相对较小。
卢瑟福散射实验对原子理论的贡献：卢瑟福散射实验的结果对于原子理论的发展产生了深远的影响。
首先，实验结果证实了汤姆逊提出的“杏仁布丁模型”是错误的。
根据杏仁布丁模型，原子是由均匀分布的正电荷和电子组成的，而卢瑟福实验的结果表明，原子核的正电荷集中在一个非常小的区域内，而电子则分布在核外的轨道上。
其次，卢瑟福散射实验为后来的量子力学理论奠定了基础。
实验结果揭示了原子内部的空隙结构，这启发了后来量子力学理论中的波粒二象性概念。
卢瑟福_散射实验报告
一、实验目的1. 验证汤姆孙原子模型的正确性；2. 探究原子内部结构，寻找原子核的位置；3. 通过实验结果，推导出原子核的半径和电荷分布。
二、实验原理卢瑟福散射实验是利用α粒子轰击金箔，观察α粒子在穿过金箔后的散射情况，以此来研究原子内部结构。
根据经典电磁学理论，α粒子在穿过金箔时，会发生库仑散射，散射角度与金箔原子核的电荷量和距离有关。
通过实验测量散射角度和散射强度，可以推导出原子核的位置、半径和电荷分布。
三、实验器材1. α粒子源：用于产生α粒子束；2. 金箔：用于实验，厚度约为0.01微米；3. 电磁场发生器：用于产生磁场，使α粒子束发生偏转；4. 观察屏：用于观察α粒子散射后的轨迹；5. 数据采集系统：用于采集散射数据；6. 计算机软件：用于数据处理和分析。
四、实验步骤1. 准备实验器材，将α粒子源、金箔、电磁场发生器、观察屏和计算机软件连接好；2. 打开α粒子源，调节α粒子束的强度和方向；3. 调节电磁场发生器的磁场强度，使α粒子束发生偏转；4. 观察α粒子散射后的轨迹，记录散射角度和散射强度；5. 利用计算机软件对数据进行处理和分析，推导出原子核的位置、半径和电荷分布。
五、实验结果与分析1. 实验数据：（1）α粒子束穿过金箔后的散射角度分布；（2）α粒子束穿过金箔后的散射强度分布。
2. 分析：（1）根据散射角度分布，可以发现大部分α粒子几乎沿原方向前进，说明原子内部大部分空间是空的；（2）少数α粒子发生了较大偏转，说明原子内部存在一个质量较大、体积较小的正电荷集中区域，即原子核；（3）极少数α粒子被反弹回来，说明原子核的电荷量较大，且与α粒子的碰撞过程中，α粒子损失了大部分能量。
根据以上实验结果，可以推导出以下结论：1. 原子的核式结构模型：原子由一个质量较大、体积较小的正电荷集中区域（原子核）和围绕原子核运动的电子组成；2. 原子核的半径：根据散射角度分布，可以推导出原子核的半径约为10^-15米；3. 原子核的电荷分布：根据散射强度分布，可以推导出原子核的电荷分布近似为一个点电荷。
卢瑟福实验证明了
卢瑟福实验证明了：这一装置的成本极为低廉，但用显微镜观察屏上闪烁的工作极为艰苦!这一实验的成功引起了一场热烈争论，最后以云室照片证明了卢瑟福的正确而告终。
这标志着人类第一次实现了改变化学元素的人工核反应。
古代炼金术士转化元素的梦想终于变成了现实!此外，他还预言了重氢和中子的存在，这在后来都得到了证实。
他同查德威克和艾利斯合作，于1930年出版了巨著《从放射性物质发出的辐射》，这部著作是早期核物理学的总结并具有当代水平。
在20世纪初叶物理学革命迅速发展时期，为什么卢瑟福能取得其他人难以取得的一连串巨大成功，成为第一个深入原子宇宙的成功探索者?大体可以从以下几方面来考察：(1)紧紧抓住关键问题扎扎实实地进行一系列准确而简单的实验。
卢瑟福一生的许多重大成就贯穿着一条红线：透彻地研究α粒子的本质，并利用其巨大的能量与动量作为“炮弹”去轰击原子和原子核，揭开原子组成与变化的奥秘。
他极其热爱实验，允许助手和学生们大胆提出设想，但实验时必须一丝不苟，提倡自制和利用最简单的仪器，实验结果必须绝对可靠。
在19QS年诺贝尔化学奖受奖演说中，他描述了他和盖革长时间利用低倍显微镜在暗室中“枯燥地”计数a粒子击中硫化锌屏上的闪烁次数，并与其他方法比较。
结果使最顽固的怀疑者不得不心悦诚服。
这样的工作精神也导致大角度散射即原子有核结构的发现。
正是在这些目的明确、烦琐、单调的常规工作中，实验者的耐心和毅力导致了辉煌的成就。
(2)理论与实验的紧密结合。
卢瑟福在1929年皇家学会曾以“理论与实验”为题说过：“每一个新的实验观察立即被抓住，以检验它是否能被现有的理论所解释。
如果不能，就要寻求理论图式中的改正……过去十年中物理学明显的迅速发展，主要是由于理论与实验的密切结合”。
卢瑟福的c粒子散射公式的推导及有核模型的提出，就是一个光辉例证。
(3)特殊的勤奋、敏锐的洞察力和丰富伪科学直觉。
他能在最易于被人们忽视的新一现象出现时洞在它的本质，分辨某些假说的正误。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§2.4 类氢离子光谱类氢离子：类似氢原子那样的离子氢原子的结构：原子核带一个单位的正电荷，核外有一个电子绕核运动。
类氢离子：原子核带Z个单位的正电荷，核外有一个电子绕核运动。
相同处：核外有一个电子不同处：Z不同，核质量不同氦离子He+、锂离子Li++、铍离子Be+++……，目前利用加速器技术已能产生O7+、Cl16+、Ar17+那样的高Z的类氢离子。
类氢离子与氢原子的区别在于核电荷数和质量数不同，类氢离子核电荷数为Ze（Z=2，3，4等）。
一．氦离子(He+)光谱1897年，天文学家毕克林（Pickering）在星光谱中发现有一系列谱线非常类似氢光谱中的巴耳未线系的线系，称为毕克林线系，图2.4.1为两线系的比较图，图中较长的线代表巴耳末系的谱线，较短线代表毕克林线系的谱线。
图2.10 毕克林线系和巴耳末线系的比较图从图中我们可见，毕克林系可以分为两组：一组几乎与巴耳末线系的谱线相重合，但显然波长稍有差别（短）。
一组大约分布在两条相邻的巴耳末线系的谱线之间。
毕克林认为：毕克林线系也是氢光谱，是星体上一种特殊的氢所发的谱线。
里德伯根据毕克林系谱线，得到如下公式：)121(~22n R -=ν （ 27,4,25,3,25=n ） 此式与巴耳末公式相似，仅量子数n 中含有半整数。
当 5,4,3=n 等整数时，得到与巴耳末线系重合的那组谱线；当 5.4,5.3,5.2=n 等半整数时，得到夹在中间的那组谱线。
里德伯认为这些谱线都属于氢的，但在实验室中总是观察不到这类谱线，而只存在于宇宙星体光谱中，因此他认为这是星体特殊条件下存在的一种不同于地球上的氢，把它叫做宇宙氢。
但如果真的有宇宙氢存在，把毕克林线系当作氢的一个线系的话，玻尔理论是无法解释的。
二．玻尔理论对He +光谱的解释玻尔认为：毕克林线系属于氦离子He +。
氦离子He +与氢原子十分相似，不同之处仅仅是核的质量较大（4M H ），核电荷比氢大一倍。
若在玻尔有关氢原子的公式中，以Z=2代入，则玻尔理论完全适用于氦离子He +：244212122220n a Z n a Zn me h r n ⋅⇒⋅=⋅=ππε 2222222042/4)4(2n Rhc nZ Rhc n Z h me E n -⇒⋅-=⋅-=πεπ 2222232042/4)4(2n R nZ R n Z c h me T n -⇒⋅=⋅=πεπ )11(4)11(~22222nm R n m RZ hc E E He m n -⇒-=-=ν式中He R 表示He 的里德伯常数，对每一个m ，均有n =m +1、m +2、m +3……，代表He +的一个线系，当然其中也应包括毕克林线系。
若取m =4，则n =5、6、7……，则由玻尔理论可知：)121(~22kR He -=ν 29,4,27,3,252==n k ，毕克林线系。
由于m =4，n >4都是较高的激发态，所以在高温的星体中易于激发它们，这就是最先在星体光谱中发现它们的原因。
1912年，有人在氢中掺杂一些氦的实验中，发现了这些谱线，后来又在纯氦的实验装置中发现了这些谱线，而在纯氢的装置中始终找不到它们，这就完全证明了玻尔的观点。
由此可见，玻尔不仅成功地解释了类氢离子光谱，而且还正确地解释了曾经为实验家们所误解的事实。
当m 等于不同的整数时，将代表氦离子的各种谱线系，它们也陆续被发现： 1=m ， 4,3,2=n 远紫外区，1916年由赖曼发现；2=m ， 5,4,3=n 远紫外区，1916年由赖曼发现；3=m ， 6,5,4=n 4686λ系，1916年由福勒(Fowler)发现；4=m ， 7,6,5=n 毕克林系，1897年由毕克林发现；…………Li ++（Z=3）：)11(9~22n m R lI -=ν Be +++（Z=4）：)11(16~22n m R Be -=ν 一般：)11(~222n m Z R A -=ν比较H 的巴耳末线系：)121(~22n R H -=ν 和He+的毕克林线系：))2(121(~22n R He -=ν 发现当 10,8,6=n 等偶数时，毕克林线系与巴耳末线系几乎重合，但波长稍有差别。
这是由于两种原子的里德伯常数略有差别而引起的。
三．里德伯常数的变化不同的原子，R 值不同是由于原子核质量不同。
在前面曾假定原子核固定不动，这只有在原子核的质量与电子的质量相比可视为无限大时，才是正确的。
实际上，原子核的质量虽然远大于电子的质量，但不能把它视为无限大，它仍有运动，其运动引起的一些效应还是可以观察到的，毕克林线系和巴耳末线系的差别。
考虑到原子核的运动，原子中的运动就不再是电子绕核的圆周运动而是电子和原子核绕它们的质心运动，如图所示。
mM Mm +=μ ⇒ 折合质量 考虑到原子核的运动，只需将氢原子理论中的电子质量m 换为折合质量μ，则全部公式都是适用的。
原子的能量：rZe E 2402⋅-=πε 角动量角子化条件：πμω22h n r =牛顿第二定律：20224r Ze r πεωμ= 可见在以上三式中，只要用μ代替m ，就从原子核不动的情况过渡到了原子核运动的情况。
Z n me h r n 2222044⋅=ππε Zn e h r n 2222044⋅=⇒μππε c h me R R 32042)4(2πεπ==∞ ch e R R A 32042)4(2πεμπ==⇒ 22n Z hc R E n ⋅-=∞ 22nZ hc R E A n ⋅-=⇒ 22nZ R T n ⋅=∞ 22n Z R T A n ⋅=⇒ )()4(2)4(23204232042m M c h Mme c h e R A +==πεππεμπMm R M m c h me /1)/1()4(232042+=+=∞πεπ 当∞→M 时，可以认为核不动，这时17100973731.1-∞⨯=→m R R A ；若考虑核的运动，则)/1/(M m R R A +=∞，随原子核的质量而变。
例如：17100967758.1-⨯=m R H ，17100972227.1-⨯=m R HeHe R >H R ⇒ He ν~>H ν~，He λ<Hλ 故毕克林线系中相近于巴耳末线系的那一组谱线都比氢原子相应的谱线波长稍短些。
四、氢的同位素——氘的证实玻尔理论的成功，还有一个出色的例子，这就是证实了氘的存在。
1932年，美国化学家尤雷发现所摄赖曼线系的头四条谱线都是双线，并利用里德伯常数与原子核质量的相关性，肯定了氢的同位素——氘的存在。
例1：如果氘和氢各自的αH 线的波长分别是656.101nm 和656.280nm ,试确定氘和氢的质量比。
解：αH 线即巴耳末线系的第一条谱线365)9141(~H H H R R =-=ν H H H R 536~1==⇒νλ 其中HH M m R R +=∞1 365)9141(~D D D R R =-=ν D D D R 536~1==⇒νλ 其中D D M m R R +=∞1 )1(-=-D H H H H D M M M m λλλ 将18401=H M m 及D λ、H λ数字代入得：H D M M 2= 玻尔理论在解释氢原子光谱和类氢离子光谱等方面获得了令人信服的成功，也即是说氢原子光谱和类氢离子光谱对玻尔理论进行了很好的实验验证。
例2：已知一对正负电子绕其共同的质心转动会暂时形成类似于氢原子结构的“正电子素”或“电子偶素”。
试计算“正电子素”的（1）第一玻尔轨道半径，（2）基态能量，（3）电离电势和第一激发电势，（4）赖曼线系中的最长波长。
解：m mm mm 5.0=+=μ （1）2122220244n a Zn e h r n ==μππε nm a r 106.0211==⇒ （2）∞==R ch e R A 5.0)4(232042πεμπ222/5.0n hc R nZ hc R E A n ∞-=⋅-=eV hc R E 8.65.01-=-=⇒∞ （3）V eE E U 8.61=-=∞∞ eV eV hc R E 7.14/8.64/5.02-=-=-=∞V V V eE E U 1.57.18.6121=-=-= （4）8343)411(~1∞==-=R R R A A ν nm R 24338~111===⇒∞νλ§2.5 夫兰克-赫兹实验1913年，玻尔提出了一个氢原子模型，这已被氢原子光谱和其它原子光谱的实验规律所证实。
此外，还可以用其它方法来证实玻尔理论。
1914年，德国物理学家夫兰克和赫兹采取慢电子（几个到几十个电子伏特）与单元素气体原子碰撞的方法，观察测量到了汞的激发电位和电离电位，这就是著名的F-H 实验。
通过实验观测，直接证明了原子发生跃迁时吸收和发射的能量是分立的、不连续的；证明了原子能级的存在；为玻尔的原子结构理论的假说提供了有力的实验证据；为此他们分享了1925年的诺贝尔物理学奖。
他们的实验方法至今仍是探索原子结构的重要手段之一。
研究原子结构的主要途径有两个，一是利用光谱推测原子结构；二是利用碰撞研究原子的结构。
一、设计思想⎩⎨⎧--→)(,,,12211E E E E E E E E e e e ⎩⎨⎧->-<1212E E E E E E e e 原子能量不连续 ⇔ 原子吸收的能量不连续 ⇔ 电子失去的能量不连续 ⇔ 电子能量的变化不连续二、第一激发电势（共振电势、中肯电势）（1914）1．实验装置图2.11 夫兰克－赫兹实验示意图电压KG U ↑ ⇒ 电子的能量（KG e eU m E ==221υ）增加↑ ⇒ 电流A I ↑ 2．实验结果实验时，调节电位器，KG U 变⇒e E 变⇒A I 变。
记录A I 随KG U 的变化关系，如图2.5.2所示，横坐标是加速电压KG U ，纵坐标是板极电流A I 。
开始时，电流A I 随电压KG U 的增加而增加。
当KG U 增加到4.9V 时，A I 突然下降，不久又上升。
当KG U 增加到9.8V 时，A I 又突然下降，然后再上升。
当KG U 增加到14.7V 时，A I 又突然下降……请注意：电流突然下降时的电压相差都是4.9V ，即，KG 间的电压为4.9V 的整数倍时，电流突然下降。
3．分析和结论电子：受到加速电压的作用而加速⇒能量增加。
与Hg 原子相碰撞，有可能把能量传递给原子⇒能量减少。
原子：多数原子是处于基态的，在获得能量后就有可能跃迁到激发态上。
设原子基态能量为1E ，第一激发态能量为2E ，电子的能量为e E ，则⎩⎨⎧--→)(,,,12211E E E E E E E E e e e ⎩⎨⎧->-<1212E E E E E E e e 当KG U ＜4.9V 时，e E ＜4.9eV ，A I 随KG U 的增加而增加，说明电子的能量未损失，即汞原子不接受低于4.9eV 的能量。