2020年成人高考专升本高等数学复习资料
2020成人高考专升本高等数学二知识点汇总复习(自编)
2020年成人高考专升本高等数学二知识点复习第一章：极限与连续1-1、极限的运算1、极限的概念(1)设函数y=f(x)在点x0的某个邻域内有定义，如果当x无限趋于x0时函数f(x)无限地趋于f(x)=A一个常数A，则称A为函数f(x)当x→x0时的极限，记作limx→x0(2)左极限、右极限；在某点极限存在，左右极限存在且唯一。
limf(x)=Ax→x0−f(x)=Alimx→x0+2、无穷小量与无穷大量无穷小量定义：对于函数y=f(x)，如果当x在某个变化过程中，函数f(x)的极限为0，则f(x)=0称在该变化过程中， f(x)为无穷小量，记作limx→x0无穷大量定义：对于函数y=f(x)，如果当x在某个变化过程中，函数f(x)的极限值越来越f(x)=∞大，则称在该变化过程中， f(x)为无穷大量，记作limx→x03、无穷小量与无穷大量的关系为无穷小量；在同一变化过程中，如果f(x)为无穷大量，且f(x)≠0，则1f(x)为无穷大量；在同一变化过程中，如果f(x)为无穷小量，且f(x)≠0，则1f(x)4、无穷小量的性质性质1：有限个无穷小量的代数和仍是无穷小量★性质2：无穷小量与有界函数的积仍是无穷小量5、无穷小量的比较与替换定义：设α，β是同一变化过程中的无穷小量，即limα=0，limβ=0=0，则称β是α比较高阶的无穷小量（1）如果limβα（2）如果limβα=∞，则称β是α比较低阶的无穷小量（3）如果lim βα=c ≠0，则称β是与α同阶的无穷小量（4）如果lim βα=1，则称β与α是等价的无穷小量★常见的等价无穷小量：当x →0时，x ~sin x ~tan x ~ arc sin x ~ arc tan x ~ e x −1 ~ ln (1+x) 1−cos x ~12x 2★★6、两个重要极限 （1）limx→0sin x x=1（2）lim x→∞(1+1x )x=e 或lim x→0(1+x)1x=e★★7、求极限的方法 （1）直接代入法：分母不为零 （2）分子分母消去为0公因子 （3）分子分母同除以最高次幂（4）利用等价代换法求极限（等价无穷小） （5）利用两个重要极限求极限 （6）洛必达求导法则（见第二章）1-2、函数的连续性1、函数在某一点上的连续性定义1：设函数y =f(x)在点x 0的某个邻域内有定义，如果有自变量∆x 趋近于0时，相应的函数改变量∆y 也趋近于0，即lim ∆x→0[f (x 0+∆x )−f (x 0)]=0，则称函数y =f(x)在x 0处连续。
成人高考(专升本)高等数学(一)知识点复习资料
它们是作为相应三角函数的反函数定义出来的，由于
[答]
.
，y=cosx在定义域内不单调，所以对于
2.初等函数
1.直线的倾角和斜率：
当
2.直线的斜截式方程： 3.两 直 线 的 平 行 与 垂 直 ： 己 知 两 条 直 线
时，函数
的左极限是 A，记作
或
所谓初等函数是指由基本初等函数经过有限次的四则
，只考虑
母 y换成 x得
（1）各组函数中，两个函数相等的是
3）对分段函数求函数值时，不同点的函数值应代入相 结论：
应范围的公式中去求；
这就是
的反函数。
A.
4）分段函数的定义域是各段定义域的并集。
（1）直接函数
与它的反函数 y=
的
例 4.分段函数
图形，必定对称于直线 y=x（一般地，二者是不同的函
B.
数，其图形是不同的曲线）；
（2）
是微积分中常用的指数函数。 4.对数函数
例如，匀速直线运动路程公式 示速度）
（其中 v表 内自变量 x的不同值，函数不能用一个统一的公式表示， 是 一 个 函 数 ， 则 称 它 为 而是要用两个或两个以上的公式来表示。这类函数称为
的反函数，记为
自由落体运动
（其中 g为重力加速度）
“分段函数”。
3.了解函数
与其反函数
之间的关
系（定义域、值域、图像），会求单调函数的反函数。
4.熟练掌握函数的四则运算与复合运算。
5.掌握基本初等函数的性质及其图像。
6.了解初等函数的概念。
7.会建立简单实际问题的函数关系式。
（4）设
，则
例 5．函数的性质
它的定义域是
2020年最新成人高考高升专数学资料
概率和初步统计1、平均数和方差（1）平均数，假设三个数字1,2,3，平均数是所有数字相加除以数字个数，（2）方差，假设三个数字1,2,3，平均数是所有相加除以数字个数，，方差是用每一个数字减去平均数得到的差的平方相加，再除以数字个数，。
这部分需要先计算平均数，再根据平均数计算得出方差。
应试指导：每年都会出一道平均数或方差的填空题4分，平均数简单而容易理解，而且出题概率最高，同学们要尽量认真仔细计算核对，要用计算器验算两遍答案都相同才可以，确保拿到这4分。
2、概率（1）等可能事件的概率：抛硬币哪一面朝上的概率是一样的，我们又把这样的两个事件叫做等可能事件。
等可能事件概率的公式就是基本事件个数/基本事件总数。
如：抛硬币，要么字面朝上，要么花面朝上，这有两种可能，而每种可能的都是相同的1/2；掷骰子，只有6个数字，每种可能都是相同的1/6.（2）互斥事件概率：两件事不能同时发生，我们叫互斥事件，相互排斥不会同时发生，互斥事件概率我们用两个事件的自己发生概率相加计算。
如：掷骰子得到5点的概率是1/6，得到6点的概率也是1/6，那么得到5点或者6点的概率就是1/6+1/6=1/3.（3）独立事件：事件A概率的发生对事件B概率的发生没有影响。
独立事件概率我们用两个事件的自己发生概率相乘计算。
如：我们第一次掷骰子5点的概率是1/6，第二次5点的概率也是1/6，那么两次掷骰子都是5点的概率就是1/36。
（4）条件事件（非独立）：在发生事件B的条件下发生事件A的概率称为事件A关于事件B的条件概率。
如：一个箱子里面有3个红球和2个黑球，我们要知道先抓到1红球，在抓到1黑球的概率，在先抓到一个红球的前提下再抓到一个黑球就是条件事件，先抓到红球是2个球中抓到一个红球，概率是3/5，我们再抓黑球的时候要减去已经发生的部分，5个球抓走了一个红球还有4个球，那么再抓到一个黑球的概率就是2/4(4个球中2个黑球），所以先抓到1红球，在抓到1黑球的概率，是3/5×2/4=3/10.应试指导：每年至少出一道概率的选择题，2016年出了两道，每题五分，相当于5-10分，这个部分也比较简单，等可能事件概率出题率最高，其次是独立事件，只要能理解，计算都是简单的计算，选择题还有选项可以参考，还是很容易拿分的，同学们一定要好好把握。
专升本资料成人高考(专科起点升本科)《高等数学(一)》
2020年全国各类成人高考（专科起点升本科）《高等数学（一）》考点精讲及典型题（含历年真题）详解
完整版>精研学习䋞>免费试用20％资料
全国547所院校视频及题库资料
考研全套>视频资料>课后答案>往年真题>职称考试
目录
第1章极限与连续
1.1考点精讲
1.2典型题（含历年真题）详解
第2章一元函数微分学
2.1考点精讲
2.2典型题（含历年真题）详解
第3章一元函数积分学
3.1考点精讲
3.2典型题（含历年真题）详解第4章空间解析几何
4.1考点精讲
4.2典型题（含历年真题）详解第5章多元函数微积分学
5.1考点精讲
5.2典型题（含历年真题）详解第6章无穷级数
6.1考点精讲
6.2典型题（含历年真题）详解第7章常微分方程
7.1考点精讲
7.2典型题（含历年真题）详解。
2020年成人高等学校招生全国统一考试专升本 高等数学(一)
6.设函数y =x +2s i n x ,则d y =( )A .(1+c o s x )dx B .(1+2c o s x )dx C .(1-c o s x )dx D .(1-2c o s x )d x 7.设函数z =x 2-4y 2,则d z =( )A .x d x -4y d yB .x d x -y d yC .2x d x -4y d yD .2x d x -8y d y8.方程x 2+y 2-z 2=0表示的二次曲面是( )A .圆锥面B .球面C .旋转抛物面D .柱面9.l i m x ң1x 2+x +1x 2-x +2=( )A .2B .1C .32D .1210.微分方程y '+y =0的通解为y =( )A .C x e xB .C x e -x C .C exD .C e-x 第Ⅱ卷(非选择题,共110分)得分评卷人二、填空题(11~20小题,每小题4分,共40分)11.ʏ1-ɕe xd x =.12.设函数y =e 2x,则d y =.13.l i m x ң0s i n x2x2=.14.ʏ(3x +2s i n x )dx =.15.曲线y =a r c t a n (3x +1)在点0,π4处切线的斜率为.16.若函数f (x )x 2-2,x ɤ0,a +s i n x ,x >0在x =0处连续,则a =.17.过点(-1,2,3)且与直线x -12=y +23=z -24垂直的平面方程为.18.函数f (x )=x 3-6x 的单调递减区间为.19.区域D ={(x ,y )|1ɤx ɤ2,1ɤy ɤx 2}的面积为.20.方程y 3+l n y -x 2=0在点(1,1)的某邻域确定隐函数y =y (x ),则d y d xx =1=.得分评卷人三、解答题(21~28题,共70分.解答应写出推理㊁演算步骤) 21.(本题满分8分)计算ʏx s i n x d x .22.(本题满分8分)已知函数f (x )=e xc o s x ,求f ᵡπ2.23.(本题满分8分)计算l i m x ң01-c o s x -x 22s i n 2x.24.(本题满分8分)计算ʏ1031+x dx.参考答案一㊁选择题1.ʌ答案ʏʌ解析ɔʏ1-ɕex d x =ex1-ɕ=e -0=e.12.ʌ答案ɔ2e 2xdx ʌ解析ɔy '=(e 2x )'=2e 2x ,故d y =y'd x =2e 2xd x .13.ʌ答案ɔ1ʌ解析ɔx ң0时,x 2ң0,故有l i m x ң0s i n x 2x2=1.14.ʌ答案ɔ32x 2-2c o s x +C ʌ解析ɔʏ(3x +2s i n x )dx =32x 2-2c o s x +C .15.ʌ答案ɔ32ʌ解析ɔy '=[a r c t a n (3x +1)]'=31+(3x +1)2,故曲线在点0,π4处的切线斜率为y'x =031+(3x +1)2x =0=32.16.ʌ答案ɔ-2ʌ解析ɔ由于f (x )在x =0处连续,故有l i m x ң0-f (x )=l i m x ң0+f (x )=f (0),而f (0)=-2,l i m x ң0-f (x )=l i m x ң0-(x 2-2)=-2,l i m x ң0+f (x )=l i m x ң0+(a +s i n x )=a ,因此a =-2.17.ʌ答案ɔ2x +3y +4z =16ʌ解析ɔ已知直线与所求平面垂直,故所求平面的法向量为n =(2,3,4),因此所求平面的方程为2(x +1)+3(y -2)+4(z -3)=0,即2x +3y +4z =16.18.ʌ答案ɔ(-2,2)ʌ解析ɔ易知f '(x )=3x 2-6,令f '(x )<0,则有-2<x <2,故f (x )的单调递减区间为(-2,2).19.ʌ答案ɔ43ʌ解析ɔ区城D 的面积为ʏ21(x 2-1)d x =13x 3-x21=43.20.ʌ答案ɔ12ʌ解析ɔ方程两边对x 求导,得3y 2㊃d y d x +1y ㊃d y d x -2x =0,即d y d x =2x y 3y 3+1,故有d y d x x =1=2x y 3y 3+1x =1=2ˑ1ˑ13ˑ13+1=12.三、解答题21.ʏxs i n x d x =-ʏx d (c o s x )=-(x c o s x -ʏc o s xd x )=-xc o s x +ʏc o s xd x =-xc o s x +s i n x +C .22.f'(x )=e x c o s x +e x ㊃(c o s x )'=e xco s x -e xs i n x =e x(c o s x -s i n x ),fᵡ(x )=e x (c o s x -s i n x )+e x (c o s x -s i n x )'=e x(c o s x -s i n x )+e x(-s i n x -c o s x )=-2e xs i n x ,故有f ᵡπ2=-2e π2s i n π2=-2e π2.23.l i m x ң01-c o s x -x 22s i n 2x =l i m x ң01-c o s x 2s i n 2x -l i m x ң0x 22s i n 2x=l i m x ң012x 22x 2-12l i m x ң0x 2x 2=14-12=-14.24.ʏ1031+x d x =ʏ10(1+x )13d (x +1)=11+13(1+x )13+110=34(1+x )4310=34(243-1).25.原方程对应的特征方程为r 2-r -2=0,。
2020成人高考专升本高数一复习题
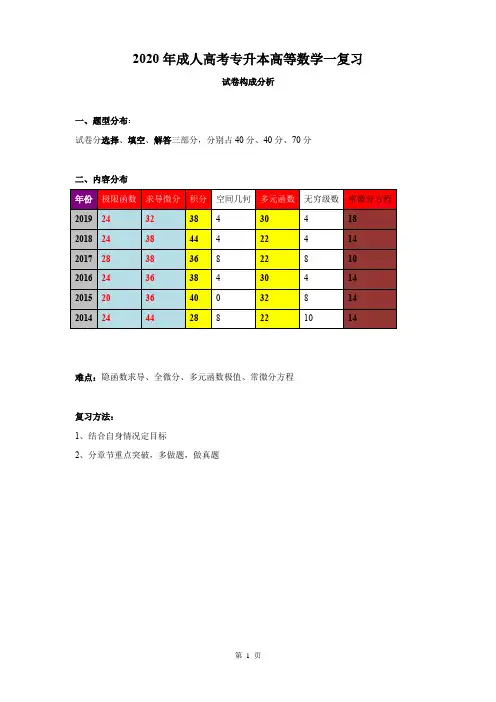
2020年成人高考专升本高等数学一复习试卷构成分析一、题型分布：试卷分选择、填空、解答三部分，分别占40分、40分、70分二、内容分布难点：隐函数求导、全微分、多元函数极值、常微分方程复习方法：1、结合自身情况定目标2、分章节重点突破，多做题，做真题第一部分 极限与连续题型一：求极限方法一：直接代入法（代入后分母不为0都可以用） 练习：1. 2limπ→x xx sin 12-＝_______ 2. x x x sin lim 1→＝______方法二：约去为零公因子法练习1. 12lim 221--+→x x x x ＝______ 练习2、lim x→1x 4−1x 3−1=练习3. lim x→1√5x−4−√xx−1 =方法三：分子分母同时除以最高次项（∞∞） 练习1. ∞→x lim1132-+x x ＝_______ 2. 112lim 55-+-∞→x x x x ＝______ 练习3.lim x→+∞(√x 2+2x −√x 2−1)方法四：等价代换法（x →0时，sinx~x tanx~x arcsinx~x arctanx~x ln(1+x)~x 1−cos x~12x 2）（等价代换只能用于乘除，不能用于加减）练习1. 1lim →x 1)1sin(2--x x ＝练习2. 0lim →x x x x sin cos 1-＝___ ____ 3. 1)1arcsin(lim 31--→x x x ＝______方法五：洛必达法则（分子分母求导）（∞∞）型 或（00）型 或 其他变形形式练习1. ∞→x lim 353-+x x ＝_______ 2. 112lim 22-+-∞→n n n n ＝______练习：3. 1lim →x 1ln --+x e e x x ＝_______ 4. 12lim 221--+→x x x x ＝______两个重要极限（背2个重要极限）练习1.1lim→x 22)22sin(--x x ＝__ ____ 2. xxx 42sin lim 0→＝____ __练习3.0lim →x x x 4sin 2sin ＝__ _ 4. xxx 2tan lim 0→＝____ __(练习1-4也可以用等价无穷小法)练习5.∞→x lim x x 2)11(+＝__ ____ 6.∞→x lim x x )211(+＝__ ____练习7.∞→x lim x x )231(+＝__ ____ 8. ∞→x lim x x3)211(-＝__ ____练习9.0lim →x xx 1)21(+ ＝__ ____ 10. 0lim →x xx 21)1(-＝__ ____无穷小量乘以有界函数 ＝ 无穷小量 练习1. 0lim →x xsinx1=________ 2. ∞→x lim x 1sinx=________(什么是无穷小量？高阶无穷小，低阶无穷小，等阶无穷小，等价无穷小？)题型二：连续性问题（可导/练习1. 函数⎩⎨⎧<+≥+=1,1,1ln )(2x x ax x x x f 在x=1处连续，则a=______练习2. 函数⎪⎩⎪⎨⎧<+≥+=0,0,)1()(1x x a x x x f x 在x=0处有极限，则a=______练习3. 函数⎩⎨⎧<+≥+=2,2,1)(2x x b x ax x f 在x=2处可导，则a=______， b=______第二部分 一元函数微分学题型一：求导（背导数公式、导数的四则运算，复合函数求导公式）(y’=f’(x)=dxdy这三种是一个意思, 如果求微分dy ，就是dy= y’dx) 练习1. f(x)=sinx+2cosx , 则f’(2π)=__ ____练习2. y=xlnx , 则dy=___ ___练习3. y=x x cos 12+ , 则dxdy=___ ___练习4. y=x 4cosx +x1+ e x, 则y’=__ ____ 练习5. y=cos 4x, 则y’=___ 6. y=sin （x 3+1）, 则dy=___ ___ 练习7. y=x x +2, 则y’=__ ____ 8. y=)ln(x x +, 则dy=___ ___题型三中，一定要注意运算率 (kv)’=______ (uv)’=______ )'(vu=_____ f(g)’=_____ 一定要背好导数公式，在考试中占40分左右题型二：高阶导数与隐函数的求导练习1. y=x 3+lnx, 则y”=______ 2. y=cos2x, 则y (4)=______ 练习3. y=ln （2x+1）, 则y”=______ 4. y=xe 2x , 则y”(1)=______ 练习5. 2x 3+xy++y+y 2=0, 则dx dy =______ 6. e x +y=sinxy, 则dxdy =______题型三. 在某点处的切线或法线（斜率或方程）练习1.曲线y=2x 3在点（1，2）处的切线的斜率为_______, 切线方程为___________ 练习2. 曲线y=sin(x+1)在x=-1处的切线方程为___________ 练习3. 若y=ax 2+2x 在x=1处的切线与y=4x+3平行，则a=________ 练习4.双曲线y =1x 在点（12,2）处的法线方程为题型四：求驻点、极值点（极值）、拐点、单调区间、凹凸区间1.求驻点、拐点、极值点练习1. 曲线 y=x 3－3x 的驻点为___________ 极值点为__________ 拐点为_______2.求单调区间与极值（大题） 练习2.求1431)(3+-=x x x f 的单调区间、极值、凹凸区间和拐点（答案见11年高考）练习3. 若f(x)=ax 3+bx 2+x 在x=1处取得极大值5，求a,b第三部分 一元函数积分学题型一：求不定积分基础计算（背好公式：原函数、不定积分的性质、基本积分公式 ） 练习1：f(x)=3e 2x 则⎰dx x f)('＝___ ___练习2：f(x) 的一个原函数是x 3，则f’(x)=_ __ 练习3：x 2是f(x)的一个原函数，则f(x)=__ ___ 练习4：⎰+）21(dx d x dx=__ 练习5：⎰+dx x x )(＝______练习6：⎰dx x )1(2＝______练习7：⎰++++dx e xx x x )11cos 2(＝______题型二：凑微分法求积分 练习1：⎰2x xe dx=_ __ 练习2：⎰+12x e dx=_ __练习3：⎰+x 321dx=__ 练习4：⎰+22x xdx=__ 练习5：⎰+)2cos(2x x dx=___ 练习6：⎰xxln dx=___ 练习7：⎰xx )sin(ln dx=___ 练习8：⎰+12x x dx=__ _题型三：分部积分法求积分 公式：______________________ 练习1：⎰x ln dx=___ 练习2：⎰x x ln dx=___练习3：⎰x e x 2dx=___ 练习4：⎰x x sin dx=___练习5：⎰x x sin 2dx=___题型四： 求定积分基础计算练习1：⎰-22sin ππx dx=_ __ 练习2：⎰+121(）x dx=__ _练习3：⎰+1021(dxd ）x dx=__ _ 练习4：⎰e dx x11=_ __练习5：＝则⎰⎩⎨⎧≤<≤≤=202f(x)dy ,21,210,)(x x x x x f _________ 练习6：⎰ex x 1ln dx=___题型五：广义积分 练习1：⎰+∞12x e dx=___ 练习2：⎰∞-+0211x dx=___题型六：平面图形的面积与旋转体的体积（有可能大题）练习1. 设D 为曲线y=1-x 2， 直线y=x+1及x 轴所围成的平面区域，如图 （1）求平面图形的面积（2）求平面图形D 绕x 轴旋转一周所成旋转体的体积V x还有一道2013年26题见课本第四部分 空间解析几何题型一： 求直线方程或法向量练习1、一平面过点（1,-1,0）且与向量{2,1,3}垂直，则该平面方程应为= 练习2、一平面过点（1,0,2）且与平面2x −y +4z −1=0平行，则该平面方程为 练习3、已知两平面π1:kx −2y +3z −2=0与平面：π2:3x −2y −z +5=0垂直；则k= 练习4、过两点A （1,2,1）,B （-1,3,0）的直线方程为 练习5、直线x−13=y+1−1=z−21与平面x+2y -z+3=0位置关系是（ ）A 、直线垂直于平面B 、直线平行于平面，但不在平面上C 、直线与平面斜交D 、直线在平面内题型二：二次曲面练习1、试确定球面x 2+y 2+z 2−2x +2y +4z +2=0的球心与半径。
2020成人高考专升本高等数学二知识点汇总复习(自编)
2020成人高考专升本高等数学二知识点汇总复习(自编)本文介绍了成人高考专升本高等数学二的第一章：极限与连续，其中包括极限的概念、无穷小量与无穷大量、无穷小量与无穷大量的关系、无穷小量的性质、无穷小量的比较与替换、两个重要极限和求极限的方法。
另外，还介绍了函数在某一点上的连续性。
极限的概念是指当自变量趋近于某一值时，函数值趋近于某一常数。
左极限、右极限存在且唯一时，称该点极限存在。
无穷小量和无穷大量是指在某一变化过程中，函数值趋近于零或无穷大的量。
它们之间有一定的关系，比如同阶无穷小量可以相互替换，等价无穷小量的极限相等。
函数的连续性是指函数在某一点上的极限等于函数在该点的函数值。
如果函数在某一点上连续，则该点的左右极限存在且等于该点的函数值。
求极限的方法包括直接代入法、分子分母消去公因子、分子分母同除最高次幂、利用等价代换法、利用两个重要极限和洛必达求导法则等。
最后，需要注意的是，文章中存在一些格式错误和明显有问题的段落，需要删除和改写。
第二章一元函数微分学2-1 导数与微分1.导数概念在函数y=f(x)的某个邻域内，当自变量x在点x处的改变量为Δx时，相应的函数改变量Δy=f(x+Δx)-f(x)。
如果极限lim(Δy/Δx)存在，则称此极限为函数y=f(x)在x处的导数，表示形式如下：lim(Δy/Δx) Δx→0存在，则称此极限为函数y=f(x)在x处连续。
2.常见的求导公式1) (c)'=02) (xa)'=ax^(a-1)3) (log_a x)'=xlna4) (ln x)'=1/x5) (ax)'=a^xlna6) (e^x)'=e^x7) (sin x)'=cos x8) (cos x)'=-sin x 3.导数的运算法则1) (u±v)'=u'±v'2) (uv)'=u'v+uv'3) (cu)'=cu'4) (v/u)'=(u'v-uv')/u^24.复合函数求导如果函数u=φ(x)在点x处可导，函数y=f(u)在对应点u处也可导，则复合函数y=f[φ(x)]在点x处可导，且有：dy/dx)=(dy/du)(du/dx)5.隐函数求导隐函数：x与y之间的函数关系是由一个方程F(x,y)=0来确定。
成人高考专升本高等数学(一)复习资料
第一阶段（3月初）主要任务是全面复习，夯实基础。
这个阶段，要按照考试大纲所列复习考试内容，全面系统地复习基础知识，对基本概念与基本原理狠下功夫，对两者的理解要深、透、不留死角。
复习基础知识时要讲究方法，注意各种知识点的归纳与类比、分析与综合，注意各知识点之间纵向与横向的联系，建立基础知识框架，总体把握基础知识的脉络。
第二阶段（8月初）主要任务是重点复习，强化练习。
这个阶段，要抓住复习重点，加强考试热点、常考知识点的复习，同时强化练习，掌握基本方法、基本技能，提高解题能力。
第三阶段（9月底10月初）主要任务是冲刺复习，模拟测试。
这个阶段，在重点复习的同时，要进行模拟测试。
通过模拟测试能发现自己的薄弱环节，从而拾遗补缺，针对薄弱环节重点复习。
同时，通过模拟测试，有利于熟悉考试情景，合理安排答题时间，调整应考心里，从而提高应试能力。
第一章极限和连续第一节极限[复习考试要求]1.理解极限的概念（对极限定义、、等形式的描述不作要求）。
会求函数在一点处的左极限与右极限，了解函数在一点处极限存在的充分必要条件。
2.了解极限的有关性质，掌握极限的四则运算法则。
3.理解无穷小量、无穷大量的概念，掌握无穷小量的性质、无穷小量与无穷大量的关系。
会进行无穷小量阶的比较（高阶、低阶、同阶和等价）。
会运用等价无穷小量代换求极限。
4.熟练掌握用两个重要极限求极限的方法。
第二节函数的连续性（1）理解函数在一点处连续与间断的概念，理解函数在一点处连续与极限存在的关系，掌握判断函数（含分段函数）在一点处连续性的方法 （2）会求函数的间断点。
（3）掌握在闭区间上连续函数的性质，会用介值定理推证一些简单的命题。
（4）理解初等函数在其定义区间上的连续性，会利用连续性求极限 精选考题例题1 设,0≠b 当0→x 时，bx sin 是2x 的（ ） 高阶无穷小量 等阶无穷小量 同阶但不等价无穷小量 低阶无穷小量 【答案】 D【考点】 本题考查了无穷小量的比较的知识点. 【解析】 因为,1lim 1lim sin lim sin lim 00020∞==⋅⋅=→→→→x b x b bxbx x bx x x x x 故bx sin 是比2x 低阶的无穷小量，即bx sin 是2x 的低阶无穷小量.例题2 函数22)(-+=x x x f 的间断点为=x _______________. 【答案】 2【考点】 本题考查了函数的间断点的知识点. 【解析】 函数22)(-+=x x x f 在2=x 处无定义，故2=x 为)(x f 的间断 点.例题3 计算.1)1sin(lim 21--→x x x 解：.2111lim 1)1(lim 1)1sin(lim 12121=+=--=--→→→x x x x x x x x 第二章 一元函数微分学第一节 导数与微分（一）导数与微分（1）理解导数的概念及其几何意义，了解可导性与连续性的关系，掌握用定义要求函数在一点处的导数的方法。
成人高考专升本高等数学(一)考试辅导复习资料【全】
成人高等学校招生考试专升本高等数学（一）（适合2022年及往后的成考复习）函数、极限与连续本章内容一、函数二、极限三、连续本章约13%，20分选择题、填空题、解答题第一节函数知识点归纳●函数的概念、性质●反函数●复合函数●基本初等函数●初等函数考试要求1、理解概念会求函数包括分段函数的定义域、表达式及函数值，并会作出简单的分段函数图象。
2、掌握判断掌握函数的单调性、奇偶性、有界性和周期性定义，会判断所给函数的相关性质。
3、理解函数理解函数与它的反函数之间的关系，会求单调函数的反函数。
4、掌握过程掌握函数四则运算与复合运算，熟练掌握复合函数的复合过程。
5、掌握性质掌握基本初等函数的简单性质及其图象。
6、掌握概念掌握初等函数的概念。
第一节函数一、函数的概念定理设x和y是两个变量，D是一个给定的数集，如果对于每个数x∈D，变量y按照一定法则总有确定的数值和它对应，则称y是x的函数，记作y=f(x).y是因变量，x是自变量。
函数值全体组成的数集W={y|y=f(x),x∈D} 称为函数的值域。
函数概念的两个基本要素对于给定的函数y=f(x)，当函数的定义域D确定后，按照对应法则f，因变量的变化范围也随之确定，所以定义域和对应法则就是确定一个函数的两个要素。
两个函数只有在它们的定义域和对应法则都相同时，才是相同的。
例：研究函数y=x和y=2是不是表示相同的函数。
解：y=x是定义在(−∞,+∞)上的函数关系，y=2是定义在(−∞,0)∪(0,+∞)上的函数关系，它们定义域不同，所以这两个函数是不同的函数关系。
例：研究下面这两个函数是不是相同的函数关系f(x)=x,g(x)=2解：f(x)=x和g(x)=2是定义在(−∞,+∞)上的函数关系，f(x)的值域在(−∞,+∞)上的函数，g(x)的值域在[0,+∞)，它们定义域相同，值域不同函数。
函数的定义域（1）在分式中，分母不能为零；（2）在根式中，负数不能开偶次方根；（3）在对数式中，真数必须大于零，底数大于零且不等于１；（4）在反三角函数式中，应满足反三角函数的定义要求；（5）如果函数的解析式中含有分式、根式、对数式和反三角函数式中的两者或两者以上的，求定义域时应取各部分定义域的交集。
2020成人高考专升本数学复习(高数一)复习题及答案
2020年成人高考专升本高等数学一复习试卷构成分析一、题型分布：试卷分选择、填空、解答三部分，分别占40分、40分、70分二、内容分布难点：隐函数求导、全微分、多元函数极值、常微分方程复习方法：1、结合自身情况定目标2、分章节重点突破，多做题，做真题第一部分 极限与连续题型一：求极限方法一：直接代入法（代入后分母不为0都可以用） 练习：1. 2limπ→x xx sin 12-＝_______ 2. x x x sin lim 1→＝______方法二：约去为零公因子法练习1. 12lim 221--+→x x x x ＝______ 练习2、lim x→1x 4−1x 3−1=练习3. lim x→1√5x−4−√xx−1 =方法三：分子分母同时除以最高次项（∞∞） 练习1. ∞→x lim1132-+x x ＝_______ 2. 112lim 55-+-∞→x x x x ＝______ 练习3.lim x→+∞(√x 2+2x −√x 2−1)方法四：等价代换法（x →0时，sinx~x tanx~x arcsinx~x arctanx~x ln(1+x)~x 1−cos x~12x 2）（等价代换只能用于乘除，不能用于加减）练习1. 1lim →x 1)1sin(2--x x ＝练习2. 0lim →x x x x sin cos 1-＝___ ____ 3. 1)1arcsin(lim 31--→x x x ＝______方法五：洛必达法则（分子分母求导）（∞∞）型 或（00）型 或 其他变形形式练习1. ∞→x lim 353-+x x ＝_______ 2. 112lim 22-+-∞→n n n n ＝______练习：3. 1lim →x 1ln --+x e e x x ＝_______ 4. 12lim 221--+→x x x x ＝______两个重要极限（背2个重要极限）练习1.1lim→x 22)22sin(--x x ＝__ ____ 2. xxx 42sin lim 0→＝____ __练习3.0lim →x x x 4sin 2sin ＝__ _ 4. xxx 2tan lim 0→＝____ __(练习1-4也可以用等价无穷小法)练习5.∞→x lim x x 2)11(+＝__ ____ 6.∞→x lim x x )211(+＝__ ____练习7.∞→x lim x x )231(+＝__ ____ 8. ∞→x lim x x3)211(-＝__ ____练习9.0lim →x xx 1)21(+ ＝__ ____ 10. 0lim →x xx 21)1(-＝__ ____无穷小量乘以有界函数 ＝ 无穷小量 练习1. 0lim →x xsinx1=________ 2. ∞→x lim x 1sinx=________(什么是无穷小量？高阶无穷小，低阶无穷小，等阶无穷小，等价无穷小？)题型二：连续性问题（可导/练习1. 函数⎩⎨⎧<+≥+=1,1,1ln )(2x x ax x x x f 在x=1处连续，则a=______练习2. 函数⎪⎩⎪⎨⎧<+≥+=0,0,)1()(1x x a x x x f x 在x=0处有极限，则a=______练习3. 函数⎩⎨⎧<+≥+=2,2,1)(2x x b x ax x f 在x=2处可导，则a=______， b=______第二部分 一元函数微分学题型一：求导（背导数公式、导数的四则运算，复合函数求导公式）(y’=f’(x)=dxdy这三种是一个意思, 如果求微分dy ，就是dy= y’dx) 练习1. f(x)=sinx+2cosx , 则f’(2π)=__ ____练习2. y=xlnx , 则dy=___ ___练习3. y=x x cos 12+ , 则dxdy=___ ___练习4. y=x 4cosx +x1+ e x, 则y’=__ ____ 练习5. y=cos 4x, 则y’=___ 6. y=sin （x 3+1）, 则dy=___ ___ 练习7. y=x x +2, 则y’=__ ____ 8. y=)ln(x x +, 则dy=___ ___题型三中，一定要注意运算率 (kv)’=______ (uv)’=______ )'(vu=_____ f(g)’=_____ 一定要背好导数公式，在考试中占40分左右题型二：高阶导数与隐函数的求导练习1. y=x 3+lnx, 则y”=______ 2. y=cos2x, 则y (4)=______ 练习3. y=ln （2x+1）, 则y”=______ 4. y=xe 2x , 则y”(1)=______ 练习5. 2x 3+xy++y+y 2=0, 则dx dy =______ 6. e x +y=sinxy, 则dxdy =______题型三. 在某点处的切线或法线（斜率或方程）练习1.曲线y=2x 3在点（1，2）处的切线的斜率为_______, 切线方程为___________ 练习2. 曲线y=sin(x+1)在x=-1处的切线方程为___________ 练习3. 若y=ax 2+2x 在x=1处的切线与y=4x+3平行，则a=________ 练习4.双曲线y =1x 在点（12,2）处的法线方程为题型四：求驻点、极值点（极值）、拐点、单调区间、凹凸区间1.求驻点、拐点、极值点练习1. 曲线 y=x 3－3x 的驻点为___________ 极值点为__________ 拐点为_______2.求单调区间与极值（大题） 练习2.求1431)(3+-=x x x f 的单调区间、极值、凹凸区间和拐点（答案见11年高考）练习3. 若f(x)=ax 3+bx 2+x 在x=1处取得极大值5，求a,b第三部分 一元函数积分学题型一：求不定积分基础计算（背好公式：原函数、不定积分的性质、基本积分公式 ） 练习1：f(x)=3e 2x 则⎰dx x f)('＝___ ___练习2：f(x) 的一个原函数是x 3，则f’(x)=_ __ 练习3：x 2是f(x)的一个原函数，则f(x)=__ ___ 练习4：⎰+）21(dx d x dx=__ 练习5：⎰+dx x x )(＝______练习6：⎰dx x )1(2＝______练习7：⎰++++dx e xx x x )11cos 2(＝______题型二：凑微分法求积分 练习1：⎰2x xe dx=_ __ 练习2：⎰+12x e dx=_ __练习3：⎰+x 321dx=__ 练习4：⎰+22x xdx=__ 练习5：⎰+)2cos(2x x dx=___ 练习6：⎰xxln dx=___ 练习7：⎰xx )sin(ln dx=___ 练习8：⎰+12x x dx=__ _题型三：分部积分法求积分 公式：______________________ 练习1：⎰x ln dx=___ 练习2：⎰x x ln dx=___练习3：⎰x e x 2dx=___ 练习4：⎰x x sin dx=___练习5：⎰x x sin 2dx=___题型四： 求定积分基础计算练习1：⎰-22sin ππx dx=_ __ 练习2：⎰+121(）x dx=__ _练习3：⎰+1021(dxd ）x dx=__ _ 练习4：⎰e dx x11=_ __练习5：＝则⎰⎩⎨⎧≤<≤≤=202f(x)dy ,21,210,)(x x x x x f _________ 练习6：⎰ex x 1ln dx=___题型五：广义积分 练习1：⎰+∞12x e dx=___ 练习2：⎰∞-+0211x dx=___题型六：平面图形的面积与旋转体的体积（有可能大题）练习1. 设D 为曲线y=1-x 2， 直线y=x+1及x 轴所围成的平面区域，如图 （1）求平面图形的面积（2）求平面图形D 绕x 轴旋转一周所成旋转体的体积V x还有一道2013年26题见课本第四部分 空间解析几何题型一： 求直线方程或法向量练习1、一平面过点（1,-1,0）且与向量{2,1,3}垂直，则该平面方程应为= 练习2、一平面过点（1,0,2）且与平面2x −y +4z −1=0平行，则该平面方程为 练习3、已知两平面π1:kx −2y +3z −2=0与平面：π2:3x −2y −z +5=0垂直；则k= 练习4、过两点A （1,2,1）,B （-1,3,0）的直线方程为 练习5、直线x−13=y+1−1=z−21与平面x+2y -z+3=0位置关系是（ ）A 、直线垂直于平面B 、直线平行于平面，但不在平面上C 、直线与平面斜交D 、直线在平面内题型二：二次曲面练习1、试确定球面x 2+y 2+z 2−2x +2y +4z +2=0的球心与半径。
成人高考专升本高数一复习资料
精品文档. 成人高考高数一复习资料第一章极限和连续第一节极限[复习考试要求]1.理解极限的概念（对极限定义、、等形式的描述不作要求）。
会求函数在一点处的左极限与右极限，了解函数在一点处极限存在的充分必要条件。
2.了解极限的有关性质，掌握极限的四则运算法则。
3.理解无穷小量、无穷大量的概念，掌握无穷小量的性质、无穷小量与无穷大量的关系。
会进行无穷小量阶的比较（高阶、低阶、同阶和等价）。
会运用等价无穷小量代换求极限。
4.熟练掌握用两个重要极限求极限的方法。
[主要知识内容]（一）数列的极限1.数列按一定顺序排列的无穷多个数称为数列，记作，其中每一个数称为数列的项，第n项。
为数列的一般项或通项，例如（1）1，3，5，…，，…（2）（3）（4）1，0，1，0，…，…都是数列。
在几何上，数列可看作数轴上的一个动点，它依次取数轴上的点。
2.数列的极限定义对于数列，如果当时，无限地趋于一个常数A，则称当n 趋于无穷大时，数列以常数A为极限，或称数列收敛于A，记作否则称数列没有极限，如果数列没有极限，就称数列是发散的。
数列极限的几何意义：将常数A及数列的项依次用数轴上的点表示，若数列以A为极限，就表示当n趋于无穷大时，点可以无限靠近点A。
（二）数列极限的性质定理1.1（惟一性）若数列收敛，则其极限值必定惟一。
定理1.2（有界性）若数列收敛，则它必定有界。
注意：这个定理反过来不成立，也就是说，有界数列不一定收敛。
定理 1.3（两面夹定理）若数列，，满足不等式且。
定理1.4若数列单调有界，则它必有极限。
下面我们给出数列极限的四则运算定理。
定理1.5（1）（2）（3）当时，（三）函数极限的概念1.当时函数的极限（1）当时的极限定义对于函数，如果当x无限地趋于时，函数无限地趋于一个常数A，则称当时，函数的极限是A，记作或（当时）（2）当时的左极限定义对于函数，如果当x从的左边无限地趋于时，函数无限地趋于一个常数A，则称当时，函数的左极限是A，记作或例如函数当x从0的左边无限地趋于0时，无限地趋于一个常数1.我们称：当时，的左极限是1，即有（3）当时，的右极限定义对于函数，如果当x从的右边无限地趋于时，函数无限地趋于一个常数A，则称当时，函数的右极限是A，记作或又如函数当x从0的右边无限地趋于0时，无限地趋于一个常数-1 。
成人高考高等数学二复习资料汇总
成考专升本高数(二)复习资料汇总第一部分考点⅛解第一章极限和连续一.常见的考试知识点L ftffi(1)√Λtt的左扱阳与右极用以決函数在一点处极限"在的允分必箜茶件.(2)根浪的性JliM的四則运算+(3)无穷小啟的槪念、性质从无穷小秋阶的比较.辛价无穷小故代除及Jt应用・(4)MtIStt限及其应用.2» ⅛⅛(1)⅛JSft-AttS续与间断的槪念及连续的fl⅛+(2)闭KfHl I：连续甯故的性厳.3.试卷内容比例本就内容约占试总总分的∣5%t ft计22分左右・二、常用的解题方法与技巧(_) IftlKj R⅛ft(或數列)极限的席用方½1⅛⅛:(1)H用极限的四則运WffiNl(2)利用函数的违续性：«/(*)在*处O t MlInlΛt)√(χj.• ■苇⑶帖瑞r他式•町加呗"解消左讪子法无穷小【唯快⑷故利Jeit奥极限lim—^=I等方法*∙→fl X(4)⅛τ-"tt⅛不定式•可考Igifi去Je穷因子比对于4∙∣"9⅛i****11的不定式•还可以用洛必½ifeW∣求解.V ∞0 X(5)叶…”叭…为的不定式■应先化叫r或的梯式血泌方法求悴(6)利用两个Mft限:IinI 1 Jim( I+—) ≡c( ⅛lim( l+x)τ≡e) t∙∙∙o X ∙-*∙∖ XI∙-∙o注盘関个亀要极限的结构式分别为：Iim 迦口≡≡∣∙Iim(I÷□)r^c to∙*t O OY其中方块“口”内可以为*•也可以为*的甬数・只要涡足上述结构形式•公式都止堀• 特別菱记住下列常用的公式：lim( 1÷αx其中的a.b.d为4数・(7)利用无穷小■的性质•主刻r无穷小*与有界变■之积为无穷小Ir以及*无穷大It 的倒数为无穷小ιr∙(8)利用等价无穷小缺代换•利用等价无穷小備代换常能简化运算•但是等价无穷小:It 代换能在秦除法中便FlLRiTnliH面的廉因不聽在加减法中使用•常用的等价无穷小肚代换幻：当*->0时.Bin 1 * X t tan X -X t arCMIl X ^X t arCtan X -X t In( l+x) -XJ -COb X上述各式也应该理解为：当χ→χ0( × )时•口→0∙則有SinC□ J O ■ IanO * 口等■其中口内可以为Z •也可以为*的由败•(9)求分段师在分段点处的极IR时.•定要分别求左段限与右极限•然后押判定极限是否IimzU)=M的允分必要条件是Iim /(x)≡ Hm /(χ)≡ Λ.—6 ∙→∙∣(二)连续1.判定/(#)在点*•处连续性的方法先考察/(*)是否为初第⅞tt.χφ点是否为/("的宦义区间内的点•如果给定魚数为分段函ft.IL>∙又是分段点•则需利用连续性定义来判定•特别是在分段点两制甬数衣达式不同的时候,应该用左连续•右连续判定.2.n r s,f{×)何斯点的方法连续性的三个耍素之Ty不到満足的点•即为两数的间断点•因此押定两敌间斯点的步驟通tft：(1)⅝⅛∕(χ)在点*•处科无定义.ft∕(χβ)X定义•则"为“的间断点.(2)to∣jβ∕(x.)存在.再⅛Λlim∕(Jr)⅛⅛存在.如果Iim/(x)不存在•則*■必为/("的何∙∙∙∙ f ∙→∙⅜断点.第二章一元函数微分学一、常见的考试知识点1.导数与微分(1)导数的槪念及几何恿义•用定义求隕数在一点处的导数值.(2)曲线上一点的切线方程和法线方程.(3)导数的四则运算及复合隕数的求导.(4)隐丙数的求导及对数求导法.(5)高阶导数的求法.(6)微分法则.2.洛必达法则及导数的应用(1)用洛必达法则求各类不定式的极限•(2)用导数求函数的单调区间.(3)函数的极值、最fit(4)曲线的凹凸性、拐点及曲线的水平渐近线与铅直渐近线.(5)证明不等式.3.试卷内容比例本腹内容约占试卷总分的30% •共计45分左右.二、常用的解题方法与技巧(-)⅛tt⅛at分L#數的定义/≡∕(χ)在点X。
成人高考专升本高等数学(二)复习资料
第一阶段（3月初）主要任务是全面复习，夯实基础。
这个阶段，要按照考试大纲所列复习考试内容，全面系统地复习基础知识，对基本概念与基本原理狠下功夫，对两者的理解要深、透、不留死角。
复习基础知识时要讲究方法，注意各种知识点的归纳与类比、分析与综合，注意各知识点之间纵向与横向的联系，建立基础知识框架，总体把握基础知识的脉络。
第二阶段（8月初）主要任务是重点复习，强化练习。
这个阶段，要抓住复习重点，加强考试热点、常考知识点的复习，同时强化练习，掌握基本方法、基本技能，提高解题能力。
第三阶段（9月底10月初） 主要任务是冲刺复习，模拟测试。
这个阶段，在重点复习的同时，要进行模拟测试。
通过模拟测试能发现自己的薄弱环节，从而拾遗补缺，针对薄弱环节重点复习。
同时，通过模拟测试，有利于熟悉考试情景，合理安排答题时间，调整应考心里，从而提高应试能力。
第一节、函数（不单独考，了解即可）一、复合函数：要会判断一个复合函数是由哪几个简单函数复合而成的。
2ln sin y x =是由ln y u =，2u v =和sin v x =这三个简单函数复合而成.3arctan x y e =是由arctan y u =，v u e =和3v x =这三个简单函数复合而成. 该部分是后面求导的关键！ 二、基本初等函数：（1）常值函数：y c = （2）幂函数：y x μ= （3）指数函数：x y a =(a 〉0,1)a ≠且 （4）对数函数：log a y x =(a 〉0,1)a ≠且（5）三角函数：sin y x =，cos y x =，tan y x =，cot y x =，sec y x =，csc y x =（6）反三角函数：arcsin y x =，arccos y x =，arctan y x =，cot y arc x = 其中： （正割函数）1sec cos x x =， （余割函数）1csc sin x x= 三、初等函数：由基本初等函数经过有限次的四则运算和复合运算，并能用一个解析式表示的函数称为初等函数。
成人高考专升本《高等数学(一)》通关资料
(特殊情况：对数求导法时，先两边同时取对数， 再求解）
一、求导方法
（七）对数函数求导法
利用对数函数的运算性质可以将原来的函数两边同时取对数后化简 然后利用隐函数求导法或复合求导法求导，因此称为对数求导法 通常解决函数类型为：
y u( x)v( x) 步骤为： （1）两边同时取对数得 ln y vx.lnu( x)
0,则函数f (x)在区间(a, b)内是递增的 0,则函数f (x)在区间(a, b)内是递减的 0不影响f (x)的单调性.
五、导数的应用
（四）函数的极值
1.极值的第一充分条件
设f (x)在x0的某领域内可导.
1 若x x0 时，f"(x) 0，x 0 x ，" f (x) 0时则0 称x 为极大值点，0f (x )为极大
在连续的曲线上的凹弧与凸弧之间的分界点称为曲线的拐点。
五、导数的应用
（六）曲线的水平渐近线与铅直渐近线
定义：
若 lim f (x) A或 lim f (x) A或 lim f (x) A，
dt
三、导数
（六）隐函数的求导
解析法表示函数通常有两种： （1）.y f（x）来表示的，称之为显函数。
如y sinwx，y xe ln（x 1 2 x ） （2）.x与y之间的函数关系是由一 个方程F（x，y）
这种称之为隐函数，
0来确定
如2x y3 -1 0，xy -x e y e 0 对于隐函数的求导通常做法： 可直接在方程F（x，y） 0的两端同时对x求导，而把y 视为中间变量，利用复合函数求导法即可。
M (x0，f (x0 ))的切线方程为：
y - f (x ) "f (x )(x x )
2020成人高考专升本高数冲刺班复习资料
高等数学冲刺班复习资料知识点一、极限求法1、代入法（分母不为0）2、分子分母消去为零公因子（00）3、分子分母除以最高次幂（∞∞） 4、等价代换法当x →0时，x ~sin x ~tan x ~ arc sin x ~ arc tan x ~ e x −1 ~ ln (1+x) 1−cos x ~12x 25、洛必达法则求法：（1）先判定是否符合00 或∞∞型（2）分别对分子分母求导，如果求导完还是00 或∞∞型那么再对分子分母求导 （3）当出现分母不为0时，就可以直接代入求解。
6、两个重要极限 （1）limx→0sin x x =1 （2）lim x→∞(1+1x)x =e 或lim x→0(1+x)1x =e例题1、limx→1x 3−5x+2x 2−2例题2、lim x→0x+22x 2+3例题3、lim x→1x 2+x−2x−1例题4、lim x→0sin x2x例题5、lim x→01−cos xx 2例题6、limx→0e x +e −x −2sin 2x例题7、lim x→∞(1−2x )x知识点二、连续性函数f(x)在某一点x 0上连续的必要条件：（1）f(x)在x 0有定义；（2）f(x)在x 0点左右极限存在且相等（3）f(x)极限等于f(x 0)例题：函数⎩⎨⎧<+≥+=1,1,1ln )(2x x ax x x x f 在x=1处连续，则a=______知识点三、导数★★1、常见的求导公式（1）、(c )′=0 （2）、(x a )′=ax a−1 （3）、(log a x )′=1xlna （4）、(lnx )′=1x （5）、(a x )′=a x lna （6）、(e x )′=e x （7）、(sin x )′=cos x （8）、(cos x )′=−sin x ★★2、导数的运算法则 （1）(u ±v )′=u ′+v′ （2）(u ∙v )′=u ′v +uv′ （3）(cu )′=cu ′ （4）(uv)′=u ′v−uv ′v 2★3、复合函数求导如果函数u =φ(x)在点x 处可导，函数y =f(u)在对应点u 处也可导，则复合函数y =f[φ(x )]在点x 处可导，且有dy dx=dy du ∙du dx。
2020成人高考专升本数学复习(高数一)复习题及答案
2020成人高考专升本数学复习(高数一)复习题及答案2020年成人高考专升本高等数学一复试卷构成分析一、题型分布：本试卷分为选择题、填空题和解答题三部分，分别占总分的40%、40%和70%。
二、内容分布本试卷内容包括极限函数、求导、微分、积分、空间几何、多元函数、无穷级数和常微分方程。
难点在于隐函数求导、全微分、多元函数极值和常微分方程。
复方法：1、结合自身情况制定研究目标；2、分章节重点突破，多做题，做真题。
第一部分极限与连续题型一：求极限方法一：直接代入法（当代入后分母不为零时可用）练1.lim (2x-1)/sinx = _______练2.lim sinx/x (x→π) = _______方法二：约去为零公因子法练1.lim (x²+x-2)/(x-1) (x→1) = _______练2.lim (x⁴-1)/(x³-1) (x→1) = _______方法三：分子分母同时除以最高次项（当极限为∞或-∞时）练1.lim (3x²+1)/(x-1) = _______练2.lim (2x⁵-x+1)/(x⁵-1) (x→∞) = _______练3.lim (√(5x-4)-√x)/(x-1) = _______方法四：等价代换法（当x→0时，sinx~x，tanx~x，arcsinx~x，arctanx~x，ln(1+x)~x，cosx~1-x²/2）等价代换只能用于乘除，不能用于加减）练1.lim sin(x-1)/(x²-1) (x→1) = _______练2.lim (1-cosx)/(xsinx) = _______练3.lim arcsin(x-1)/(x-1) = _______方法五：洛必达法则（分子分母求导）当极限为1-∞型或0/0型或其他变形形式时练1.lim (2n²-n+1)/(3x+5) (2n→∞) = _______练2.lim ln(x)+ex-eⁿx/(x-1) (x→1) = _______两个重要极限（背2个重要极限）lim (1+x)ⁿ/x = eⁿ (x→0)lim (aⁿ-1)/n = ln a (n→∞)练1.对函数f(x)=x^3-3x^2+2x求出其前三阶导数。
成人高考高升专数学必考知识点汇总
成人高考高升专数学必考知识点汇总成人高考高升专数学知识点汇总【篇一】1、知识范围（1）向量的概念向量的定义、向量的模、单位向量、向量在坐标轴上的投影、向量的坐标表示法、向量的方向余弦（2）向量的线性运算向量的加法、向量的减法、向量的数乘（3）向量的数量积二向量的夹角、二向量垂直的充分必要条件（4）二向量的向量积、二向量平行的充分必要条件2、要求（1）理解向量的概念，掌握向量的坐标表示法，会求单位向量、方向余弦、向量在坐标轴上的投影。
（2）熟练掌握向量的线性运算、向量的数量积与向量积的计算方法。
（3）熟练掌握二向量平行、垂直的充分必要条件。
【篇二】1、知识范围（1）不定积分、原函数与不定积分的定义、原函数存在定理不定积分的性质（2）基本积分公式（3）换元积分法、第一换元法（凑微分法）、第二换元法（4）分部积分法（5）一些简单有理函数的积分2、要求（1）理解原函数与不定积分的概念及其关系，掌握不定积分的性质，了解原函数存在定理。
（2）熟练掌握不定积分的基本公式。
（3）熟练掌握不定积分第一换元法，掌握第二换元法（限于三角代换与简单的根式代换）。
（4）熟练掌握不定积分的分部积分法。
（5）会求简单有理函数的不定积分。
【篇三】1、知识范围（1）导数概念导数的定义、左导数与右导数、函数在一点处可导的充分必要条件导数的几何意义与物理意义、可导与连续的关系（2）求导法则与导数的基本公式导数的四则运算、反函数的导数、导数的基本公式（3）求导方法复合函数的求导法、隐函数的求导法、对数求导法由参数方程确定的函数的求导法、求分段函数的导数（4）高阶导数高阶导数的定义、高阶导数的计算（5）微分微分的定义、微分与导数的关系、微分法则一阶微分形式不变性2、要求（1）理解导数的概念及其几何意义，了解可导性与连续性的关系，掌握用定义求函数在一点处的导数的方法。
（2）会求曲线上一点处的切线方程与法线方程。
（3）熟练掌握导数的基本公式、四则运算法则及复合函数的求导方法，会求反函数的导数。