运筹学例题
运筹学实例 含解析
案例1. 工程项目选择问题某承包企业在同一时期内有八项工程可供选择投标。
其中有五项住宅工程，三项工业车间。
由于这些工程要求同时施工，而企业又没有能力同时承担，企业应根据自身的能力，分析这两类工程的盈利水平，作出正确的投标方案。
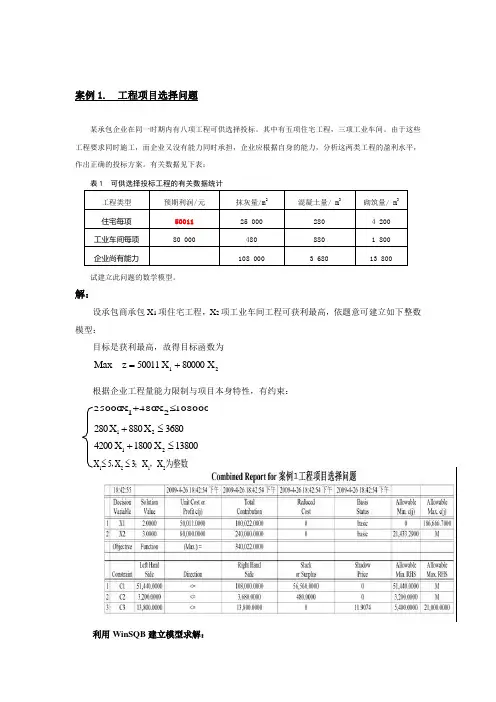
有关数据见下表：表1 可供选择投标工程的有关数据统计工程类型 预期利润/元 抹灰量/m 2混凝土量/ m 3砌筑量/ m 3住宅每项 50011 25 000 280 4 200 工业车间每项 80 000480 880 1 800 企业尚有能力108 0003 68013 800试建立此问题的数学模型。
解：设承包商承包X 1项住宅工程，X 2项工业车间工程可获利最高，依题意可建立如下整数模型：目标是获利最高，故得目标函数为21X 80000X 50011z Max +=根据企业工程量能力限制与项目本身特性，有约束：利用WinSQB 建立模型求解：1080002X 4801X 25000≤+3680X 880X 28021≤+13800X 1800X 420021≤+为整数，；，2121X X 3X 5X ≤≤综上，承包商对2项住宅工程，3项车间工程进行投标，可获利最大，目标函数Max z=340022 元。
案例2. 生产计划问题某厂生产四种产品。
每种产品要经过A，B两道工序加工。
设该厂有两种规格的设备能完成A工序，以A1 ，A2表示；有三种规格的设备能完成B工序，以B1 ，B2，B3 表示。
产品D可在A，B任何一种规格的设备上加工。
产品E可在任何规格的A设备上加工，但完成B工序时只能在B1设备上加工。
产品F可在A2及B2 ，B3上加工。
产品G可在任何一种规格的A设备上加工，但完成B工序时只能在B1 ，B2设备上加工。
已知生产单件产品的设备工时，原材料费，及产品单价，各种设备有效台时如下表，要求安排最优的生产计划，使该厂利润最大？设设产品设备有效台时1 2 3 4A1 A2 B1 B2 B357647109812111068108601110000400070004000原料费（元/件）单价（元/件）0.251.250.352.000.502.800.42.4解：设Xia(b)j为i产品在a(b)j设备上的加工数量,i=1,2,3,4;j=1,2,3，得变量列表设备产品设备有效台时Ta(b)j1 2 3 4A1 A2 B1 B2 B3X1a1X1a2X1b1X1b2X1b3X2a1X2a2X2b1X3b2X3b3X3a1X3a2X3b1X3b2X3b3X4a1X4a2X4b1X4b2X4b3601110000400070004000原料费Ci （元/件） 单价Pi （元/件） 0.25 1.25 0.352.00 0.50 2.80 0.4 2.4其中，令X 3a 1，X 3b 1，X 3b 2，X 3b 3，X 4b 3=0 可建立数学模型如下： 目标函数: ∑∑==-=4121)](*[Maxi j iaj Ci Pi X z=1.00*（X 1a 1+X 1a 2）+1.65*（X 2a 1+X 2a 2）+2.30* X 3a 2+2.00*（ X 4a 1+X 4a 2）约束条件：利用WinSQB 求解（X1~X4，X5~X8,X9~X12,X13~X17,X18~X20分别表示各行变量）：4,3,2,1X21j 31==∑∑==i X j ibjiaj2,1T X 41iaj=<=∑=j Taj i iaj 3,2,141=<=∑=j TbjT Xi ibj ibj2,1;4,3,2,10X iaj ==>=j i 且为整数32,1;4,3,2,10X ibj ，且为整数==>=j i 0X X X X X 4b33b33b23b13a1=====综上，最优生产计划如下：设备产品1 2 3 4A1 A2 B1 B2 B3774235004004008732875目标函数zMax=3495，即最大利润为3495案例3. 高校教职工聘任问题 （建摸）由校方确定的各级决策目标为：P 1 要求教师有一定的学术水平。
运筹学20道习题
1．已知线性规划（15分）123123123max 3452102351,2,3jZ x x x x x x x x x x j =++⎧+-≤⎪-+≤⎨⎪≥=⎩0，（1）求原问题和对偶问题的最优解；（2）求最优解不变时c j 的变化范围36.解：（1）化标准型 2分 （2）单纯形法 5分（3）最优解X=(0，7，4)；Z ＝48 （2分） （4）对偶问题的最优解Y ＝（3.4，2.8） (2分)（5）Δc 1≤6，Δc 2≥-17/2，Δc 3≥-6，则 1235(,9),,13c c c ∈-∞≥-≥-(4分)2．某公司要将一批货从三个产地运到四个销地，有关数据如下表所示。
现要求制定调运计划，且依次满足：（1）B 3的供应量不低于需要量； （2）其余销地的供应量不低于85%； （3）A 3给B 3的供应量不低于200； （4）A 2尽可能少给B 1；（5）销地B 2、B 3的供应量尽可能保持平衡。
（6）使总运费最小。
试建立该问题的目标规划数学模型。
3、请用表上作业法解下题，得到最优解,并计算此时总运费：现在有运价表如下:产地销地B1B2B3产量A1 5 1 6 12A2 2 4 0 14A3 3 6 7 4销量9 10 11 30 答案：根据上面运价表以及销量和产量的要求，使用表上作业法：5 1 62 4 03 6 79 10 11得到下面运输方案：检验空格：空格A检验：6 –(0+3) = 3 > 0空格B检验：7 – (3-2) = 6 > 0空格C检验：6 - (1-2) = 7 > 0空格D检验：4 – (1-3)= 6 > 0 故全部符合要求。
总运输费用：2×5 + 3× 2 + 4 × 3 + 10 × 1 + 11 × 0 = 38 答：上面的运输方案为最佳方案，总运费为38。
运筹学例题及解答
运筹学例题及解答一、市场对I、II两种产品的需求量为：产品I在1-4月每月需10000件，5-9月每月需30000件,10-12月每月需100000件；产品II在3-9月每月需15000件，其它月份每月需50000件。
某厂生产这两种产品成本为：产品I在1-5月内生产每件5元，6-12月内生产每件4.50元；产品II在1-5月内生产每件8元，6-12月内生产每件7元。
该厂每月生产两种产品能力总和应不超过120000件。
产品I容积每件0.2立方米，产品II容积每件0.4立方米，而该厂仓库容积为15000立方米，要求：(a)说明上述问题无可行解；(b)若该厂仓库不足时，可从外厂借。
若占用本厂每月每平方米库容需1元，而租用外厂仓库时上述费用增加为1.5元，试问在满足市场需求情况下，该厂应如何安排生产，使总的生产加库存费用为最少。
解： (a) 10-12月份需求总计：100000X3+50000X3=450000件，这三个月最多生产120000X3=360000件，所以10月初需要（450000-360000=90000件）的库存，超过该厂最大库存容量，所以无解。
••（b）考虑到生产成本，库存费用和生产费用和生产能力，该厂10-12月份需求的不足只需在7-9月份生产出来库存就行，则设xi第i个月生产的产品1的数量，yi第i个月生产的产品2的数量，zi，wi分别为第i个月末1，2的库存数s1i，s2i分别为用于第i+1个月库存的原有及租借的仓库容量m3，可建立模型：Lingo 程序为 MODEL: sets: row/1..16/:;!这里n 为控制参数; col/1..7/:; AZ(row,col):b,x; endsetsdata:12111277777787887898998910910109101110111110111211min (4.57)( 1.5)30000150003000015000300001500030000150003000015000.i i i i i i z x y s s x z y w x z z y w w x z z y w w x z z y w w x z z y w w st x z ===+++-=→-=+-=→+-=+-=→+-=+-=→+-=+-=→+-=+∑∑1211121100005000120000(712)0.20.415000(712)0i i i i i i iy w x z i z w s s s i ⎧⎪⎪⎪⎪⎪⎪⎪⎨=→+=⎪⎪+≤≤≤⎪+=+⎪⎪≤≤≤⎪⎪⎩变量都大于等于b=1.754167,1.737500,1.737500,1.770833,1.770833,1.762500,1.7 62500,1.667500,1.609167,1.609167,1.650833,1.650833,1.659167 ,1.659167,1.396667,1.380000,1.380000,1.438333,1.438333,1.41 3333,1.413333,1.658333,1.633333,1.633333,1.658333,1.658333, 1.658333,1.658333,1.546667,1.513333,1.513333,1.555000,1.555 000,1.546667,1.546667,1.538333,1.496667,1.496667,1.480000,1 .480000,1.505000,1.505000,1.562500,1.545833,1.545833,1.5791 67,1.579167,1.570833,1.570833,1.645833,1.604167,1.604167,1. 637500,1.637500,1.637500,1.637500,1.670833,1.645833,1.64583 3,1.645833,1.645833,1.654167,1.654167,1.454167,1.420833,1.4 20833,1.412500,1.412500,1.420833,1.420833,1.463333,1.480000 ,1.480000,1.421667,1.421667,1.430000,1.430000,1.682500,1.69 0833,1.690833,1.699167,1.699167,1.690833,1.690833,1.466667, 1.483333,1.483333,1.475000,1.475000,1.466667,1.466667,1.508 333,1.500000,1.500000,1.466667,1.466667,1.475000,1.475000,1 .552500,1.535833,1.535833,1.569167,1.569167,1.560833,1.5608 33,1.542500,1.509167,1.509167,1.550833,1.550833,1.542500, 1.542500;enddatamax=@sum(AZ(i,j): b(i,j)*x(i,j));@for(col(j): @sum(row(i):x(i,j))<=2);@for(col(j): @sum(row(i):x(i,j))>=1);@sum(AZ(i,j):x(i,j))=8;@for(row(i): @sum(col(j):x(i,j))=1);@for(AZ(i,j): @bin(x(i,j)));运行结果：Rows= 32 Vars= 112 No. integer vars= 112 ( all are linear)Nonzeros= 591 Constraint nonz= 448( 448 are +- 1) Density=0.163Smallest and largest elements in abs value= 1.00000 8.00000No. < : 7 No. =: 17 No. > : 7, Obj=MAX, GUBs <= 16Single cols= 0。
运筹学典型题型案例集
运筹学典型题型案例集第一章线性规划1 生产计划问题（（摘自王治祯环境应用数学309页））某企业为了搞好综合利用，用三种废品生产三种副产品，生产情况和利润见下表，求最佳利润。
解：设ABC三种产品的产量为X1X2X3Max Z =5X1+8X2+2X310X1+5X2+3 X3<=4006X1+10X2+2 X3<=4004X1+5X2+4X3<=200经过求解X1=34.23，X2=8.19X3=5.37最大利润为274.412 投资问题解：用Xij表示第i年初（i=1，2，3）给项目j（A，B，C，D）的投资金额。
第一年资金量：30万，可投项目：A、B；故：X1A+X1B＜=30。
第二年资金量：1.2*X1A，可投项目：A、C；故：X2A+X2C＜=1.2*X1A。
第三年资金量：1.2*X2A+1.5*X1B，可投项目：A、B、D；故：X3A+X3B+X3D＜=1.2*X2A+1.5*X1B。
其它条件：X1B＜=20；X2C＜=15；X3D＜=10。
目标：第三年底收益最大。
因投资X3B在第3年底不能收回，故无收益。
则目标函数为：f(x)=0.2*（X1A+ X2A + X3A）+0.5*X1B+0.6* X2C+0.4* X3D LINGO Model如下：max =0.2*(X1A+ X2A + X3A)+0.5*X1B+0.6* X2C+0.4* X3D;X1A+X1B<=30;X2A+X2C<=1.2*X1A;X3A+X3B+X3D<=1.2*X2A+1.5*X1B;@bnd(0,X1B,20); @bnd(0,X3B,20); @bnd(0,X2C,15); @bnd(0,X3D,10);运行结果如下：Global optimal solution found.Objective value: 27.50000Total solver iterations: 2Variable Value Reduced CostX1A 12.50000 0.000000X2A 0.000000 0.6000000E-01X3A 16.25000 0.000000X1B 17.50000 0.000000X2C 15.00000 -0.1000000X3D 10.00000 -0.2000000X3B 0.000000 0.2000000Row Slack or Surplus Dual Price1 27.50000 1.0000002 0.000000 0.80000003 0.000000 0.50000004 0.000000 0.2000000投资计划解释：第一年年初投资A项目12.5万元，投资B项目17.5万元；第二年年初投资C项目15万元；第三年年初投资A项目16.25万元，投资D项目10万元；第三年年年末可获最大收益27.5万元。
(典型例题)《运筹学》运输问题
xj0，yij0，zij0，（i=1,┈,4；j=1,┈,5）
2008/11
--22--
--《Ⅵ 产量
新购 1 第一天 M 第二天 M 第三天 M
第四天 M
1 1 1 1 0 5200
0.2 0.1 0.1 0.1 0 1000
2008/11
--21--
建立模型：
--《运筹学》 运输问题--
设 xj—第j天使用新毛巾的数量；yij—第i天送第j天使用快洗 餐巾的数量；zij—第i天送第j天使用慢洗餐巾的数量；
Min z=∑xj+∑∑0.2yij+∑∑0.1zij
第一天：x1=1000
需 第二天：x2+y12=700
求 约
m1
xij b j (j 1,2,...,n)
i1
x 0 (i 1,...,m,m 1; j 1,...,n) ij
2008/11
--16--
--《运筹学》 运输问题--
销＞产问题单位运价表
产地销地 B1 B2 ┈
A1
C11 C12 ┈
A2
C21 C22 ┈
┊ ┆┊┈
Am Cm1 Cm2 ┈
2008/11
--8--
产销平衡表
--《运筹学》 运输问题--
单位运价表
B1 B2 B3 B4 产量
A1 (1) (2) 4 3 7 A2 3 (1) 1 (-1) 4 A3 (10) 6 (12) 3 9 销量 3 6 5 6
B1 B2 B3 B4 A1 3 11 3 10 A2 1 9 2 8 A3 7 4 10 5
Ⅰ Ⅱ
示。又如果生产出来的柴
Ⅲ
运筹学试题及答案
运筹学试题及答案一、线性规划试题一某工厂生产A、B两种产品，A产品每件利润为20元，B 产品每件利润为30元。
已知生产一个A产品需10小时，生产一个B产品需15小时。
某次生产过程中，工厂共有50个小时可用于生产，且设定A产品的最少需求量为20件，B产品的最少需求量为15件。
问应该生产多少件A产品和多少件B产品，才能使得工厂的利润最大化？答案一为了使工厂的利润最大化，我们需要建立一个数学模型来描述这个问题。
设工厂生产的A产品数量为x，B产品数量为x。
根据题目中的要求，可得以下条件：1.$10x+15y\\leq50$ （生产时间的限制）2.$x\\geq20$ （A产品的最少需求量）3.$y\\geq15$ （B产品的最少需求量）另外，我们还需要定义目标函数，即使工厂利润最大化：$max\\ Z = 20x+30y$根据以上条件和目标函数，可以得到如下线性规划模型：$max\\ Z = 20x+30y$$\\begin{cases} 10x+15y\\leq50\\\\ x\\geq20\\\\y\\geq15\\\\ x,y\\geq0 \\end{cases}$以上模型可以通过线性规划求解软件进行求解，得到最优解。
试题二某公司有甲、乙、丙三个工厂，每个工厂都可以制造产品A和产品B。
甲工厂每天制造产品A的数量最多为80件，产品B的数量最多为100件；乙工厂每天制造产品A的数量最多为60件，产品B的数量最多为40件；丙工厂每天制造产品A的数量最多为50件，产品B的数量最多为70件。
公司有订单，要求每天至少制造产品A的30件，产品B的50件。
甲工厂生产产品A的成本为5元，产品B的成本为4元；乙工厂生产产品A的成本为4元，产品B的成本为3元；丙工厂生产产品A的成本为3元，产品B的成本为2元。
问如何安排存货以使公司在利润最大化的前提下能够满足订单需求？答案二为了使公司在利润最大化的前提下满足订单需求，我们需要建立一个数学模型来描述这个问题。
运筹学例题——精选推荐
例1-20 （生产计划问题）某工厂明年根据合同，每个季度末向销售公司提供产品，有关信息如表1-45所示，若当季生产的产品过多，季末有积余，则一个季度每积压一吨产品需支付存储费0.2万元，现该厂考虑明年的最佳生产方案，使该厂在完成合同的情况下，全年的生产费用最低. 试建立线性规划模型.表1-45例1-21 （多阶段投资问题）某公司现有资金30万元可用于投资，5年内有下列方案可供采纳：1#方案：在年初投资1元，2年后可收回1.3元；2# 方案：在年初投资1元，3年后可收回1.45元；3#方案：仅在第1年年初有一次投资机会，每投资1元，4年后可收回1.65元；4#方案：仅在第2年年初有一次投资机会，每投资1元，4年后可收回1.7元；5# 方案：在年初贷给其他企业，年息为10%，第二年年初可收回.每年年初投资所得收益及贷款本金利息也可用作安排. 问该公司在5年内怎样使用资金，才能在第六年年初拥有最多资金？例1-22 （混料问题）某糖果厂用原料A，B和C按不同比率混合加工而成甲、乙、丙3种糖果（假设混合加工中不损耗原料）. 原料A，B，C在糖果甲、乙、丙中的含量、原料成本、加工成本、原料限量及糖果售价如表1-47所示.问该厂对这3种糖果各生产多少千克，使得到的利润最大？表 1-47例1-23（下料问题）造纸厂接到定单，所需卷纸的宽度和长度如表1-48所示.(表中具体的单位长度是多少，我们没有给出，视具体问题而定.本教材在一些应用举例中不打算对讨论对象都给出具体的量纲而仅给出数字.例如本题在讨论时，有时连“单位长度”4个字都省去，就说宽度5，长度3000. 以后类似情况，我们不再说明. 当然，在同一问题中，同一讨论对象省去的量纲单位应统一.) 工厂生长1#（宽度10）和2#（宽度20）两种标准卷纸，其长度未加规定.现按定单要求对标准卷纸进行切割，切割后有限长度的卷纸可连接起来达到所需卷纸的长度. 问如何安排切割计划以满足定单需求而使切割损失量最小？。
运筹学例题-打印版
一、绪论一个班级的学生共计选修A 、B 、C 、D 、E 、F 六门课程，其中一部分人同时选修D 、C 、A ，一部分人同时选修B 、C 、F ，一部分人同时选修B 、E ，还有一部分人同时选修A 、B ，期终考试要求每天考一门课，六天内考完，为了减轻学生负担，要求每人都不连续参加考试，试设计一个考试日程表。
二、图解法例1. 某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产，已知生产单位产品所需的设备台时及A 、B 两种原材料的消耗、资源的限制，如下表：工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多？ 3.1例2 某公司由于生产需要，共需要A ，B 两种原料至少350吨（A ，B 两种材料有一定替代性），其中A 原料至少购进125吨。
但由于A ，B 两种原料的规格不同，各自所需的加工时间也是不同的，加工每吨A 原料需要2个小时，加工每吨B 原料需要1小时，而公司总共有600个加工小时。
又知道每吨A 原料的价格为2万元，每吨B 原料的价格为3万元，试问在满足生产需要的前提下，在公司加工能力的范围内，如何购买A ，B 两种原料，使得购进成本最低？ 三、单纯形法例1. 某厂生产甲乙两种产品，各自的零部件分别在A 、B 车间生产，最后都需在C 车间装配，相关数据如表所示：问如何安排甲、乙两产品的产量，使利润为最大。
例2. 某名牌饮料在国内有三个生产厂，分布在城市A1、A2、A3,其一级承销商有4个，分布在城市B1、B2、B3、B4，已知各厂的产量、各承销商的销售量及从A i 到B j 的每吨饮料运费为C ij ，为发挥集团优势，公司要统一筹划运销问题，求运费最小的调运方案。
四、线性规划在工商管理中的应用 例1．某昼夜服务的公交线路每天各时间段内所需司机和乘务人员数如下： 设司机和乘务人员分别在各时间段一开始时上班，并连续工作八小时，问该公交线路怎样安排司机和乘务人员，既能满足工作需要，又配备最少司机和乘务人员?例2．一家中型的百货商场，它对售货员的需求经过统计分析如下表所示。
2.6-运筹学应用实例汇总
一、生产计划问题例：某工厂拥有A、B、C三种类型的设备，生产甲、乙、丙、丁四种产品。
每件产品在生产中需要占用的设备机时数，每件产品可以获得的利润以及三种设备每月可利用的时数如下表所示，求使总利润最大的月度生产计划。
建模思路■用线性规划制订使总利润最大的生产计划。
■设变量X1为第i种产品的生产件数(i=1, 2, 3, 4),目标函数z为相应的生产计划可以获得的总利润。
在加工时间以及利润与产品产量成线性关系的假设下，可以建立如下的线性规划模型：建模max z= 5.24X1 +7.30x2 +8.34x3 +4.18x4目标函数1.5Xj +1.0x2+2.4X3+1.0X4<2000LOX1 +5.0X2+1.0X3+3.5X4<8000 约束条件1・5X] +3.0X2+3.5X3+1.0X4<5000Xp X2, X3, X4 >0 变量非负约束练习：某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品，都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量。
数据如下表。
问：公司为了获得最大利润，甲、乙、丙三种产品各生产多少件？甲、乙两种产品的铸造中，由本公司铸造和由外包协作各应多少件？甲 .乙丙资源限制铸造工时（小时/件）51078000机加工工时（小时/件）64812000装配工时（小时/件）32210000自产铸件成本（兀/件）354外协铸件成本（兀/件）56一机加工成本（元/件）213装配成本（元/件）322产品售价（元/件）231816解：设孙孙寺分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数，同，幅分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。
求占的利润：利润二售价-各成本之和产品甲全部自制的利润产品甲铸造外协，其余自制的利润产品乙全部自制的利润产品乙铸造外协，其余自制的利润产品丙的利润可得到毛（i = 1,2, 3,4,5）的利润分别为15、10、7、13、9=23-（3+2+3）=15 =23-（5+2+3）=13 =18-（5+1+2）=10 =18-（6+1+2）=9 =16-（4+3+2）=7通过以上分析,可建立如下的数学模型：目标函数：Max 15百+ 10电+ 7两+ 13题+ 9不约束条件：5为+ 10西+ 7玛＜80006为+ 4出+ 8^ + 6々+ 4不3百+ 2X2 + 2均+ 3局+ 2不毛，演，传，演，与12000 10000二、混合配料问题例：某工厂要用四种合金T1, T2, T3和T4为原料，经熔炼成为一种新的不锈钢G。
(完整版)《运筹学》习题集
第一章线性规划1．1将下述线性规划问题化成标准形式1)min z＝－3x1＋4x2－2x3＋5 x4－x2＋2x3－x4＝－24xst. x1＋x2－x3＋2 x4 ≤14－2x1＋3x2＋x3－x4 ≥2x1，x2，x3≥0，x4无约束2)min z ＝2x1－2x2＋3x3＋x2＋x3＝4－xst. －2x1＋x2－x3≤6x1≤0 ，x2≥0，x3无约束1．2用图解法求解LP问题，并指出问题具有唯一最优解、无穷多最优解、无界解还是无可行解。
1)min z＝2x1＋3x24x1＋6x2≥6st2x1＋2x2≥4x1，x2≥02)max z＝3x1＋2x22x1＋x2≤2st3x1＋4x2≥12x1，x2≥03)max z＝3x1＋5x26x1＋10x2≤120st5≤x1≤103≤x2≤84)max z＝5x1＋6x22x1－x2≥2st－2x1＋3x2≤2x1，x2≥01．3找出下述LP问题所有基解，指出哪些是基可行解，并确定最优解（1）min z＝5x1－2x2＋3x3＋2x4x1＋2x2＋3x3＋4x4＝7st2x1＋2x2＋x3 ＋2x4＝3x1，x2，x3，x4≥01．4 分别用图解法与单纯形法求解下列LP 问题，并对照指出最优解所对应的顶点。
1) maxz ＝10x 1＋5x 23x 1＋4x 2≤9 st 5x 1＋2x 2≤8 x 1，x 2≥02) maxz ＝2x 1＋x 2 3x 1＋5x 2≤15 st 6x 1＋2x 2≤24 x 1，x 2≥01．5 分别用大M 法与两阶段法求解下列LP 问题。
1) minz ＝2x 1＋3x 2＋x 3 x 1＋4x 2＋2x 3≥8 st 3x 1＋2x 2 ≥6 x 1，x 2 ，x 3≥02) max z ＝4x 1＋5x 2＋ x 3. 3x 1＋2x 2＋ x 3≥18 St. 2x 1＋ x 2 ≤4x 1＋ x 2－ x 3＝53) maxz ＝ 5x 1＋3x 2 +6x 3 x 1＋2x 2 －x 3 ≤ 18 st 2x 1＋x 2 －3 x 3 ≤ 16 x 1＋x 2 －x 3＝10 x 1，x 2 ，x 3≥01231231231231234)max 101512539561515.25,,0z x x x x x x x x x st x x x x x x =++++≤⎧⎪-++≤⎪⎨++≥⎪⎪≥⎩1．61.7某班有男生30人，女生20人，周日去植树。
运筹学之习题
运筹学习题1.某商业集团公司在A1，A2，A3三地设有三个仓库，它们分别存40，20，40个单位产品，而其零售店分布在地区B i，i=1，┅，5，他们需要的产品数量分别是252.某饲养场所用混合饲料由n种配料组成，要求这种混合饲料必须含有m种不同的营养成分，并且每一份混合饲料中第i种营养成分的含量不能低于b j。
已知每单位的第j种配料中所含第i种营养成分的量为a ij，每单位的第j种配料的价格为c j。
在保证营养的条件下，应如何配方，使混合饲料的费用最省。
试建立这个营养问题的数学模型，然后将其化成标准形式的线性规划问题。
3.用图解法求解下列线性规划问题：(1)121212min3..206122x xs t x xxx+⎧⎪+≥⎪⎨≤≤⎪⎪≥⎩(2)12121212min2..25122843x xs t x xx xxx+⎧⎪+≥⎪⎪+≤⎨⎪≤≤⎪⎪≤≤⎩4.用单纯形法求解下列线性规划问题：(1)123123123123min2..360210200,1,2,3jz x x xs t x x xx x xx x xx j⎧=--+⎪++≤⎪⎪-+≤⎨⎪+-≤⎪⎪≥=⎩(2)1234123124min3..22460,1,2,3,4jz x x x xs t x x xx x xx j=+++⎧⎪-++=⎪⎨++=⎪⎪≥=⎩35.用两阶段法求解下列问题：(1)123123412342max342..3040,1,2,3,4jz x x xs t x x x xx x x xxx j⎧=++⎪+++≤⎪⎪++≤⎨⎪≥⎪⎪≥=⎩36 -2(2)12121212min24..2323,0z x xs t x xx xx x=+⎧⎪-≥⎪⎨+≥⎪⎪≥⎩-6.写出下面线性规划的对偶规划：(1)121212121212min1010..52533224,x xs t x xx xx xx xx x+⎧⎪+≥⎪⎪+≥⎪⎨+≥⎪⎪+≥⎪⎪⎩48为自由变量(2)123123123123123min24..2342263355,x x xs t x x xx x xx x xx x x++⎧⎪++≥⎪⎪++≥⎨⎪++≥⎪⎪≥⎩0，为自由变量7.用对偶单纯形法求解下面问题：123123123123min234..23234,,x x xs t x x xx x xx x x++⎧⎪++≥⎪⎨-+≥⎪⎪≥⎩08.某厂生产A，B两种产品，每件产品均要在甲，乙，丙各台设备上加工。
运筹学例题(完全答案)
1、课上讲过的练习和要求课下做过的练习1〕答案更正答案：更正答案：2〕答案：题：答案：更改〔4〕答案题：答案：更改〔5〕答案2、最后给的练习1〕紧前工作A — 3B A 3C A 4D A 6E B、C、D 6 答案：2〕紧前工作A — 4B — 3C A 8D A 7E B、C 9F B、C 12G D、E 2H D、E 5I G、F 6答案：3〕紧前工作A —7B — 5C A、B 10D C 7E C 3F D 2G D、E 5答案：二、决策分析1、最后给的练习1〕有一个公司方案买两种复印机，选好两种型号的复印机可以满足未来10年的需求，但第一种复印机购置价格2000元，每年耗材使用到达150元可以免费维修；第二种复印机购置价格3000元，维修费用不确定，估计40%的可能不用修理，40%的可能维修费100元，20%的可能性维修费200元。
问该公司应该选择哪种复印机？2〕一家大型轧钢厂考虑向一家新客户〔服装厂〕贷款，轧钢厂将客户还款情况分三类：严重拖欠、一般拖欠、按时还款；估计20%可能严重拖欠，50%可能一般拖欠，30%可能按时还款，如果制衣厂得到贷款后又严重拖欠，那么轧钢厂将损失25万，服装厂一般拖欠，轧钢厂获利10万，按时还款轧钢厂获利20万。
借款期1年，1年的存款基准利率为3.22%。
问轧钢厂是否给制衣厂贷款？结论是给企业贷款或再问：如果将获利合为一个，严重拖欠损失25万，而其他情况获利是14万，问A、无差概率B、EVPI三、线性规划线性规划的步骤：1〕确定决策变量；2〕列出约束条件；3〕写出目标函数。
图解线性规划：1〕决定线性规划问题的可行域；2〕求解线性和整数规划1、课堂练习1〕答案：极大化Z = 40 x1 + 50 x2约束x1 + 2x2 ≤40 小时(劳力限制) 4x1 + 3x2 ≤120 磅(粘土限制)x1 , x2 ≥0解x1 = 24个碗x2 = 8个杯收入= 1,360美元2〕答案：(包括量度单位(打数)和时间单位(周))X1 = 每周生产宇宙光的打数X2 = 每周生产射击手的打数MAX 8X1 + 5X2s.t.2X1 + 1X2 ≤1000 (塑料)3X1 + 4X2 ≤2400 (加工时间)X1 + X2 ≤700 (总产量)X1 –X2 ≤350 (混合限制)所有X ≥03〕某家工厂面临的生产问题是：♦生产4种男人领带♦使用3种材料(有限资源)决策:每月每种领带各生产多少?目标:极大化利润生产数据4〕邮局一周在不同天要求全日工作人数不同，如表1所列。
运筹学例题
DP1. 下列关于动态规划问题的说法不正确的是（ ）。
A ．应用推理或逆推法可能会得出不同的最优解 B ．状态变量应具有无后效性C ．动态规划模型中，阶段是按时间或空间划分的D ．问题的阶段数等于问题中的子问题的数目2. 用动态规划方法求解多阶段问题时，指标函数应满足（ ）。
A ．定义在全过程和后部子过程上的数量函数 B ．具有可分离性，满足递推关系 C ．严格单调D ．以上A 、B 、C 都是3. 下述的（ ）不能设为动态规划中的状态变量。
A ．生产企业某种产品的每月月初库存 B ．某种设备每年年末的可利用量 C ．送货车辆行驶过的路程 D ．送货车辆行驶时的速度4. 某求极大值的线性规划问题的单纯形表如下：其中d 、1a 、1c 为待定常数。
该线性规划问题无界的时候，满足下面（ ）。
A ．110,00d c a ≥<<且 B ．110,00d c a ≥=>且 C ．110,00d c a ≥><且 D ．110,00d c a <>>且一、某投资者有总数为40万元的固定资金，他可在三个不同的投资机会中投资（比如，股票、银行、土地），投资额分别为(1,2,3)i x i =。
假定他做过预测，知道从每项投资中可获得效益分别为111()g x x =，2222()g x x =，333()g x x =，问如何分配投资数额才能使从所有投资中获得的总效益最大？ 二、某公司现有资金5千万元，拟对3个分公司增加投资，已知投资所获年效益如下表所示，问公司如何应对分配资金，才能使公司总的年收益最大？（用动态规划方法求解）三、某农业种植基地有某种肥料共5单位，准备供给三块农田施用，每块农田至少需要一个单位的肥料，肥料必须按整数单位施用。
每块农田施肥数量与增产数量关系如下表所示。
试求对每块田施多少单位的肥料，才使总的增产量最多。
要求：用动态规划方法求解，有必要的求解过程。
运筹学典型考试试题及答案
运筹学典型考试试题及答案⼆、计算题（60分）1、已知线性规划（20分）MaxZ=3X1+4X2X1+X2≤52X1+4X2≤123X1+2X2≤8X1,X2≥0其最优解为：基变量X1X2X3X4X5X33/2 0 0 1 -1/8 -1/4X25/2 0 1 0 3/8 -1/4X1 1 1 0 0 -1/4 1/2σj 0 0 0 -3/4 -1/21）写出该线性规划的对偶问题。
2）若C2从4变成5，最优解是否会发⽣改变，为什么？3）若b2的量从12上升到15，最优解是否会发⽣变化，为什么？4）如果增加⼀种产品X6，其P6=(2,3,1)T，C6=4该产品是否应该投产？为什么？解：1)对偶问题为Minw=5y1+12y2+8y3y1+2y2+3y3≥3y1+4y2+2y3≥4y1,y2≥02)当C2从4变成5时，σ4=-9/8σ5=-1/4由于⾮基变量的检验数仍然都是⼩于0的，所以最优解不变。
3）当若b2的量从12上升到15X＝9/829/81/4由于基变量的值仍然都是⼤于0的，所以最优解的基变量不会发⽣变化。
4）如果增加⼀种新的产品，则P6’=(11/8,7/8，－1/4)Tσ6=3/8>0所以对最优解有影响,该种产品应该⽣产2、已知运输问题的调运和运价表如下，求最优调运⽅案和最⼩总费⽤。
（共15分）。
B1B2B3产量销地产地A1 5 9 2 15 A2 3 1 7 11 A3 6 2 8 20 销量18 12 16解：初始解为计算检验数由于存在⾮基变量的检验数⼩于0，所以不是最优解，需调整调整为：重新计算检验数所有的检验数都⼤于等于0，所以得到最优解3、某公司要把4个有关能源⼯程项⽬承包给4个互不相关的外商投标者，规定每个承包商只能且必须承包⼀个项⽬，试在总费⽤最⼩的条件下确定各个项⽬的承包者，总费⽤为多少？各承包商对⼯程的报价如表2所⽰：（15分）项⽬投标者 A B C D 甲 15 18 21 24 ⼄ 19 23 22 18 丙 26 17 16 19 丁 19212317答最优解为：X= 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 总费⽤为504. 考虑如下线性规划问题（24分）B 1 B 2 B 3 产量/t A 1 15 15 A 2 11 11 A 3181 1 20 销量/t 18 1216B 1 B 2 B 3 产量/t A 1 5 13 0 15 A 2 －2 0 0 11 A 30 0 20 销量/t 181216B 1 B 2 B 3 产量/t A 1 15 15 A 2 11 11 A 3 7 12 1 20 销量/t 18 12 16 B 1 B 2 B 3 产量/t A 1 5 13 0 15 A 2 0 2 2 11 A 3 0 0 0 20 销量/t 18 12 16Max z=-5x1+5x2+13x3s.t. -x1+x2+3x3≤2012x1+4x2+10x3≤90x1，x2，x3≥0回答以下问题：1）求最优解2）求对偶问题的最优解3）当b1由20变为45，最优解是否发⽣变化。
运筹学应用实例
A
B
C
D
E
F
陆地、河流及桥梁示意图
解：
将A，B，C，D，E，F分别用一种点表达，相互之间有桥相连 旳连一条弧；弧旳容量就是两点间旳桥梁数；设一种方向，得 到网络图如下：
A
例3.设备更新问题
某单位使用一台生产设备，在每年年底，单位领导都要决 策下年度是购置新设备还是继续使用旧设备。
若购置新设备，需要支付一笔购置费；假如继续使用旧旳， 则要支付一定旳维修费用。
一般说来，维修费随设备使用年限旳延长而增长。根据以 往旳统计资料，已经估算出设备在各年年初旳价格和不同 使用年限旳年维修费用，分别示于表1和表2。
相应旳开门方案如图所 示，共开10个门。
B C IJ
H
A
D GK
E
F
开门方案
例5：选址问题
有六个居民点v1，v2，v3，v4，v5，v6，拟定建一夜校，已知 各点参加学习旳人数为25、20、30、10、35、45人，其道路 如图所示，试拟定学校位于哪一种居民点，才干使学习者 所走旳总旅程至少？（图中边旁旳数字为路段长度）
用一条边把代表这两个项目
v2
旳顶点连接起来。这么得到
v3
下图
v1
为了处理这个问题，只需
找到一条包括全部顶点旳
v4
初等链。
v5
如：{v4，v1，v2，v3，v5}是一条初等链，相应旳比赛是： 100m自由泳，50m仰泳，50m蛙泳，100m碟泳，200m自由泳。
此问题旳方案不唯一。
例 2.线路铺设问题
0 50 150 175 200 275 40 0 80 100 120 180 180 120 0 30 60 150 D= 70 50 10 0 10 40 280 210 70 35 0 105 495 405 225 180 135 0
运筹学期末复习例题.doc
《运筹学》期末复习例题例1 ：用图解法求解下面的LP问题：max z — 6%1 —2x2厂2兀1 —兀2 W 22%1 — 3%2 三 6xi W 6J1 ,兀2 $ 0解，由图知，该问题因为没有可行解，因而也没有最优解。
例2:某饲料厂用含蛋白质、葡萄糖、氨基酸的四种原料，配制一种新营养保健品。
四种原料中1 2 3 4成分蛋白质（%）30 40 20 15葡萄糖（％）20 30 25 40氨基酸（％）40 25 55 30单价（元）30 40 35 50要求该保健品中含蛋白质不少于20%,葡萄糖不少于35%,氨基酸不少于30%。
由于技术上的原因，原料2的用量不能少于30%,原料4不能超过40%。
试建立一个线性规划模型，以便求得成本最低而又合乎要求的新营养保健品（建模不计算）。
解：设单位产品中需要第j种原料的比例为心则可建立线性规划模型: min z=30%i + 40%2 + 35%3 + 50%4r30xi + 40%2 + 20%3 + 15%4》2020xi + 30%2 + 25%3 + 40%4》3540xi + 25%2 + 55%3 + 30%4》30〈疋》0.3 %4 < 0.4 兀1 +兀2 +兀3 +兀4 = 1 匕1，兀2，兀3，兀4》0例3：某工厂计划期内要安排生产A、B两种产品。
已知生产单位产品的利润与所需的资源如要求：(列出线性规划模型；(2)用图解法求解该问题的最优解；(3)用单纯形法求解最优解，并指出单纯形法的迭代步骤解与图解法顶点的关系。
例4：某工厂计划期内要安排生产A、B两种产品。
已知生产单位产品的利润与所需的资源如要求：(列出线性规划模型；(2)用图解法求解该问题的最优解;(3)用单纯形法求解最优解，并指出单纯形法的迭代步骤解与图解法顶点的关系。
问：1.表中解是否为最优解？为什么？写出该解。
2.若X4、*5、X6分别是原问题的松驰变量，请写出在该表中相应的对偶问题的解。
运筹学题目
运筹学题目
1. 企业A和企业B分别生产A类产品和B类产品，A类产品
的利润为500元/件，B类产品的利润为800元/件。
企业A每
天能生产100件A类产品，而企业B每天能生产150件B类
产品。
如果市场需求每天为200件A类产品和300件B类产品，如何安排生产和销售，才能使总利润最大化？
2. 一家货运公司有两种运输方式：陆路运输和铁路运输。
陆路运输每次可以运输10吨货物，费用为500元，而铁路运输每
次可以运输20吨货物，费用为800元。
如果货物总量为100吨，如何安排运输方式，才能使运输费用最低？
3. 一家航空公司有两种航班：航班A和航班B。
航班A每天
起飞一次，起飞时间为早上8点，机票价格为800元/张；航
班B每天起飞两次，分别在上午10点和下午2点，机票价格
为600元/张。
每天的预订数据显示，航班A平均预订量为
200张，航班B平均预订量为150张。
航空公司想要制定一个
票价策略，使得每天的总票价收入最大化，应该如何制定票价？
4. 一家快递公司每天有500个包裹需要投递，每个包裹的重量和体积不同，投递距离也不同。
公司有多种车辆可以选择，每种车辆拥有不同的载重能力和油耗情况。
如何选择合适的车辆数量和类型，使得投递成本最低？
5. 一家零售商要在不同城市开设新的分店，目前有五个城市可以选择。
每个城市的市场容量和租金不同。
如何选择合适的城市开设分店，使得总利润最大化？。
运筹学经典题型
P1：每周总利润不低于10000元； P2：合同要求A型机每周至少生产10台，S型机至 少15台； P3：工序1每周生成时间最好恰为150h,工序2生成 时间可适当超过其能力； 试写出目标规划的模型。
图论
1，用避圈法或破圈法求下图的最小树
v2
7
7 v6
v3
6
v1
5
v5
5
4 4
9 3
6
v4
2
v7
8( 6)
6( 4)
vT
6( 6)
2( 0)
2( 2)
v2
5( 4)
v3
4，求下图中流值为6的最小费用流，其中弧旁边 的数字为(cij , d ij ) , c ij 表示容量， d ij 表示单位流 量费用。
v 1 (6,5)
v2
( 3,2)
vs
(4,3)
(7,1)
vT
(4,1)
v3
(5,4)
( 3,3)
8
6 16 24 4 4 10 4 12 16 8
无
1，2 2 3 4，5 6 6 6 7 8，9，10 3
13
14
引道混凝土保养
清理场地交工验收
24
4
12
11，13
请解答（1）该工程从施工开始道工程结束的最 短周期；（2）如果引道混凝土施工工期拖延10 天，对整个工程进度有何影响？（3）若装天花 板的施工时间从12天缩短为8天，对整个工程进 度有何影响？（4）为保证工期不拖延，装门这 项作业最晚应从哪一天开工？（5）如果要求该 工程必须在75天内完工，是否应采取措施，应 采取什么措施？
运 筹 帷 幄 之 中
决
作业
运筹学复习例题
1.某制药厂在计划期内要安排生产Ⅰ、Ⅱ两种药品，这些药品分别需要在D C B A 、、、四种不同的设备上加工．按工艺规定，每千克药品Ⅰ和Ⅱ在各台设备上所需要的加工台时数如表1．已知各设备在计划期内有效台时数（1台设备工作1小时称为1台时）分别是12、8、16和12．该制药厂每生产1千克药品Ⅰ可得利润200元，每生产1千克药品Ⅱ可得利润300元．表1 B A 、两种药品每千克在各台设备上所需的加工台时数 药品ABCDⅠ 2 1 4 0 Ⅱ224（1）问应如何安排生产计划，才能使制药厂利润最大？分别利用软件和最终单纯型表回答剩余问题。
解 设1x ，2x 分别表示在计划期内药品Ⅰ和Ⅱ的产量（千克），Z 表示这个期间的制药厂利润．则计划期内生产Ⅰ、Ⅱ两种药品的利润总额为21300200x x Z +=（元）．但是生产Ⅰ、Ⅱ两种药品在A 设备上的加工台时数必须满足122221≤+x x ；在B 设备上的加工台时数必须满足8221≤+x x ；在C 设备上的加工台时数必须满足1641≤x ；在D 设备上的加工台时数必须满足1242≤x ；生产Ⅰ、Ⅱ两种药品的数量应是非负的数，即0,21≥x x ．于是上述的问题归结为：目标函数 21300200Max x x Z += 122221≤+x x 8221≤+x x 约束条件 1641≤ x 1242≤x 0,21≥x x单纯型法求解：首先将线性规划问题标准化，即在约束条件中引入松弛变量3x 、4x 、5x 、6x ，则标准化后的线性规划模型为：21300200Max x x Z +=12 22321＝x x x ++ 8 2421＝x x x ++..t s 16 451＝x x + 12 462＝x x + 0,,,621≥x x x此时约束方程组已为典型方程组，根据上述线性规划模型可以列出初始单纯形表（表2-4）：表2-4 单纯形法求解例2-1（1）表2-4中：100040010004001021000122 为典型方程组中变量的系数，j x 为规划中出现的变量，j c 为变量j x 在目标函数中的系数，B X 为基本变量，B C 为基本变量在目标函数中的系数，b 为典型方程组右端常数项（非负值），θ为确定出基变量的商值，ikii b βθ=（0>ik β），j C 为变量j x 的检验数，j P C c C B j j ⋅-=，Z 为此时目标函数值，b C Z B ⋅=．根据初始单纯形表可以看出：初始基本可行解是01=x ，02=x ，123=x ，84=x ，165=x ，126=x此时目标函数值()⎪⎪⎪⎪⎪⎭⎫⎝⎛⋅=12168120000Z ＝0检验数111P C c C B ⋅-=＝200－()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⋅04120000＝200222P C c C B ⋅-=＝300－()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⋅40220000＝3003C =4C =5C ＝6C ＝0（基本变量的检验数总等于零）由于01>C ，02>C ，所以初始基本可行解非最优解．又由于12C C >，所以确定2x 为进基变量．进一步求最小θ值：{}{}33,4,6min 412,28,212min 0min min ==⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧>=ik ik i i b ββθ即从第4个方程中算出的商值最小，而第4个方程中的基本变量是6x ，于是6x 为出基变量．表中给第4个约束方程中2x 的系数4加上方括号以突出其为枢元．接下去的工作是将2x 取代6x ，表2-4中的约束方程化为以3x 、4x 、5x 和2x为基本变量，1x 和6x 为非基本变量的典型方程，以便求出新的基本可行解．从表2-4中可以看到，只需对方程组实行初等变换，使枢元位置变成1，而枢列中的其它元素变为零（即以枢元为中心的初等变换）就可以了．此处可先将第4个方程除以4，使枢元位置变成1；然后用新得到的第4个方程乘以（-2）后分别加到第1个和第2个方程上，使枢列中的第1个和第二个方程所在位变为零．这样我们可以得到新的单纯形表（表2-5）．表2-5给出的新的基本可行解是1x ＝0，2x ＝3，3x ＝6，4x ＝2，5x ＝16，6x ＝0此时目标函数值()⎪⎪⎪⎪⎪⎭⎫⎝⎛⋅=31626300000Z ＝900检验数111P C c C B ⋅-=＝200-()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⋅0412300000＝200666P C c C B ⋅-=＝0-()⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⋅4102121300000＝75-2C ＝3C =4C =5C ＝0（基本变量的检验数总等于零）由于01>C ，所以此时基本可行解非最优解，确定1x 为进基变量． 进一步计算最小θ值：{}{}24,2,3min 416,12,26min 0min min ==⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧>=ik ik i i b ββθ即从第2个方程中算出的商值最小，而第2个方程中的基本变量是4x ，于是4x 为出基变量．接着进行第二次迭代，将1x 取代4x ，表2-5中的约束方程化为以3x 、1x 、5x 和2x 为基本变量，4x 和6x 为非基本变量的典型方程，以便求出新的单纯形表．重复单纯形法计算第2 步～第5步，一直到没有新的非基本变量可以改善目标函数为止（见表2-6和表2-7）．表2-7 单纯形法求解例2-1（4）表2-7中：目标函数值()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⋅=244030002000Z =1400检验数444P C c C B ⋅-==0-()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⋅2120130002000=-150555P C c C B ⋅-==0-()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⋅8121414130002000=225- 1C =2C =3C =6C =0（基本变量的检验数总等于零）由于0≤j C ，6,,2,1 =j ，所以此基本可行解41=x ，22=x ，03=x ，04=x ，05=x ，46=x ，即为最优解，最优值为Z *＝1400．与前面图解法求解结果一致．为了加深对单纯形法基本思想的理解，不妨将表2-4、表2-5、表2-6、表2-7和图2-1进行对照，可以发现表2-4给出的基本可行解对应于图中可行域顶点0，表2-5给出的基本可行解对应于顶点A ，表2-6给出的基本可行解对应于顶点B ，表2-7给出的最优解对应于顶点C ．线性规划问题有无穷多个可行解，应用单纯形法可以高效率地求解此类问题．（2）药品Ⅱ的价格在什么范围内变动，不影响原来的生产计划安排，但制药厂收益变化了．设基本变量2x 在目标函数中的系数2c 变化了2c ∆；这时表2-7的最终计算表便成为表2-16所示．表2-16 基本变量利润系数变化的灵敏度分析这时要保持最优解不变，则必须满足下列不等式：-150-()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--∆212010002c =-150-221c ∆≤0-()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--∆-812141410002252c =-281225c ∆+≤01003002≤∆≤-c即2c 可在[0,400]间变动，不影响原来的生产计划安排，但制药厂收益变化了．（3）设备C 在计划期内有效台时数在什么范围内变动时，原来最优解的基本变量不变，但最优解的值发生变化．第三个约束条件3b 发生变化，变化量为3b ∆，为了使最后的解仍为可行解，3b ∆应满足下列不等式：=∆+'-b B b 1⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2440＋⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----081210121200410004111⎪⎪⎪⎪⎪⎭⎫⎝⎛∆0003b ＝⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2440＋⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∆-∆∆∆-333381214141b b b b ＝⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∆-∆+∆+∆-333381221441441b b b b 0≥03≤∆b163-≥∆b 83-≥∆b163≤∆b 083≤∆≤-b所以3b ∆在[－8,0]之间变动时（即3b 的变化范围在[8,16]时），原来最优解的基本变量不变，但最优解的值发生变化．例如，3b ∆为－2时（即3b ＝14），则b B b b ∆+'='-1＝⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2440＋⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----081210121200410004111⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∆0003b ＝⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∆-∆+∆+∆-333381221441441b b b b ＝⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛4932721 最优解X *＝T⎪⎭⎫⎝⎛300214927，最优值Z *＝1375，见表2-17． 表2-17 右端常数变化后的最优解如果3b ∆的变化超出了[－8,0]的范围，这时最优解的基本变量就发生变化．在这种情况下要用对偶单纯形法继续求出新的最优解．例如3b ∆为2时（即3b ＝18），则b B b b ∆+'='-1＝⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2440＋⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----081210121200410004111⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∆0003b ＝⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∆-∆+∆+∆-333381221441441b b b b ＝⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-4752921 则最终单纯形表变为表2-18．表2-18 右端常数变化后的对偶单纯形法求解新的最优解X *＝()T420024，最优值Z *＝1400．（4）若计划生产的药品Ⅰ的工艺结构有了改进，相应地生产单位药品Ⅰ所需设备D C B A 、、、的台时改为（3,2,5,2），它的利润也提高到每千克400元．试分析已求得的最优计划有何变化？解 当1x 的系数列向量变化后,原最终单纯形表（表2-7）中1x 的系数列向量变成:111P B P -='=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----081210121200410004111⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2523=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-83214541 原最终单纯形表变成表2-19：表2-19 决策变量系数改变对最优解的影响（1）由1x 的系数列向量可知，到此尚未完成行变换，所以需继续使1x 的系数列向量变成单位列向量，于是得到表2-20．表2-20 决策变量系数改变对最优解的影响（2）因为j C ≤0，所以新的最优解()TX 4.2008.08.02.3*=，最优值Z *＝1520元.（5）设该制药厂除生产药品Ⅰ、Ⅱ以外，还有第三种药品可供选择．生产药品Ⅲ每千克需要使用D C B A 、、、设备的台时分别为3，2，6，3；每千克可得利润500元．问该制药厂的计划中要不要安排这种药品的生产，若要安排，应当生产多少？解 设7x 表示计划期内生产药品Ⅲ的数量（单位为千克），则原最终单纯形表（表2-7）中增加了一列,这新的一列为：=='-717P B P ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----081210121200410004111⎪⎪⎪⎪⎪⎭⎫ ⎝⎛3623=⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-4122321 将新增一列列入原最终单纯形表中，计算检验数，见表2-21．由于此时7x 相应的检验数为正值，所以此单纯形表给出的基本可行解不是最优解，继续用单纯形法求解结果，最后得最优解()TX 200015.11*=，最优值Z *＝1650元，比原计划增加了利润250元．表2-21 增加变量的灵敏度分析（6）若制药厂为了提高药品质量，考虑给药品Ⅰ、Ⅱ增加一道精加工工序，并在设备E 上进行．Ⅰ、Ⅱ两种药品分别需要的加工台时数为（2，2.4）．已知设备E 的计划工作时间为12个台时，试问增加一道精加工工序后，对原计划有何影响？解 上述问题相当于在原问题的基础上增加了一个约束条件124.2221≤+x x设7x 为新增的松弛变量，则得到124.22721=++x x x原最终单纯形表（表2-7）新增一行和一列，见表2-22．此时原最终单纯形表中的1x 和2x 的系数列向量不再是单位向量了，所以继续进行行变换．在行变换后得到的新单纯形表中，检验数均小于等于零，但右端项出现负值，所以可用对偶单纯形法继续运算．最后得最优解()TX 24015.23*=，最优值Z *＝1350元．表2-22 增加约束条件的灵敏度分析2. 某医院有一批长度为15分米的胶皮管原料．为了作输液管、止血带和听诊器胶管，需要截成长度分别为5.7分米，4.2分米和3.1分米的短管各100根，100根和200根．试问应如何安排截法，所用的胶管原材的总根数最少，而且每根料头不能超过2分米？解 先分析一下截取短管的方法．如果先考虑尽输液管截，然后考虑尽止血带截，再考虑尽听诊器胶管截，则截取的方法如下表2-23：表2-23 短管截取方法截法 输液管止血带听诊器胶管总长（分米）料头（分米）5.7（分米） 4.2（分米） 3.1（分米） 1 2 0 1 14.5 0.5 2 1 2 0 14.1 0.9 3 1 1 1 13.0 2.0 4 1 0 3 15.0 0.0 5 0 2 2 14.6 0.4 61313.51.5为了得到短管5.7分米100根，4.2分米100根和3.1分米200根，需混合截取原料．令j x 表示第j 种截法所用原材的根数，得到如下线性规划模型：∑==61Min j j x Z10024321=+++ x x x x100226532=+++ x x x x200323 65431=++++x x x x x0≥j x ，且为整数)6,,2,1( =j在上述约束条件中添加人工变量7x 、8x 、9x ，得到其典型方程组：98761Min Mx Mx Mx x Z j j +++=∑=100 274321=++++x x x x x 1002286532=++++ x x x x x 200323965431=+++++x x x x x x.t .s0≥j x ，且为整数)9,,2,1( =j用大M 法求解，如表2-24．因为非基本变量1x 的检验数为0，所以有多重最优解，其中一个最优解为X*＝()T010600400，最优值为Z *=110．即按第2种方法截取40根原材，按第4种方法截取60根原材，按第5种方法截取10根原材，总共截取110根原材．表2-24 大M 法求解短管截取问题3. A 医院放射科目前可以开展X 线平片检查和CT 检查业务，现拟购买磁共振仪，以增设磁共振检查业务．为此A 医院收集了有关信息，以决策是否购买磁共振仪．经过资料收集，A 医院估计今后放射科如果开展此3项业务，在现有放射科医务人员力量和病人需求的情况下，每月此3项业务的最多提供量为1800人次．平均每人次检查时间、每月机器实际可使用时间、平均每人次检查利润如下表2．表2 放射科3项检查时间与利润及机器可使用时间放射科业务项 目X 线平片检查CT 检查磁共振检查平均每人次检查时间（小时/次） 0.1 0.25 0.5 每月机器实际可使用时间（小时） 300 120 120 平均每人次检查利润（元/次）206010设每月X 线平片检查、CT 检查和磁共振检查的业务量分别为1x ,2x 和3x 人次，则使A 医院放射科此3项业务收入最多的线性规划模型如下：321106020Max x x x Z ++=300 1.01≤x 120 25.0 2≤x..t s 1205.0 1≤x1800 321≤++x x x0,,321≥x x x利用单纯形法可得最终单纯形表（见表2-26）．表2-26 放射科业务安排最终单纯形表最优解X *＝()T0120016804801320，最优值Z *＝55200．从最终单纯形表上可读出如下信息：1．A 医院从放射科收益的角度考虑，不应购买磁共振机.2．在每月X 线平片检查和CT 检查业务量各为1320人次和480人次时，放射科利润最大，达55200元．3．在最优业务安排情况下，每月X 光机仍有168小时未实际利用，故它的影子价格为0元/小时；每月CT 机可使用的时间已完全利用，它的影子价格为160元/小时，如果市场上能租到CT 机的价格低于影子价格160元/小时，那么就应当租用CT 机，增加CT 检查业务，以求得更高的利润．如果医院购买了磁共振机，而在最优业务安排情况下，并无利用，所以其影子价格为0元/小时．4．在最优业务安排情况下，每月X 线平片检查和CT 检查的服务量已达到现有医务人员服务提供和病人需求的最大量．A 医院如果想通过从人才市场上聘用医务人员以增加放射科的服务能力，并通过宣传扩大病人对其医院医疗服务（包括放射科业务）的需求，则只有当增加一个病人的服务量所需额外增加的人员招聘费和宣传费低于20元时，才是适宜的，可使放射科的利润更高．4. 某省医疗队从A 1、 A 2 、A 3三所省级医院抽调骨干医护人员配备必要设备去B 1、B 2、B 3、B 4四个贫困县进行巡回医疗扶贫，各医院抽调的人数、各县需要人数、以及从医院到各县的人均（包括设备交通）费用如表3所示，问如何安排可使总费用最小？表3 运输问题的人均费用表B 1 B 2 B 3 B 4医院抽出人数人均费用（单位：百元）A 1 A 2 A 3 县需求人数2 9 10 7 9 134 25 8 4 2 5 7 3 8 4 6（1）西北角法 所谓西北角法就是从表3-4的左上角第一格开始安排运输计划． 方法是：取其对应医院抽出数与县城需要数的最小值作为初始基本可行解的第一个分量值（{}1111,m in b a x =）． 这样第一列的需求已经满足，用线划去第一列，再看第二列、第一行，由于抽出数还有9-3=6，与B 2的需求数8比较，取最小值6（{}211112,m in b x a x -=）填入该格． 依此次序进行，即可得到第一个基本可行解，见表3-4．表3-4 运输问题作业表——西北角法（2）最小费用法 西北角法的优点是简单、易实现，但没有考虑最小费用． 可能要经过许多次迭代才能得到最优解． 而最小费用法的基本思想是就近供应， 优先考虑最小单位运费对应的ij x ， 这样得到的方案会更接近最优方案．以例3-1来说明具体步骤．表3-5 运输问题作业表——最小费用法在运输表3-5中，单位运费ij c 最小的是211c =. 这个格子处于A 2行B 1列，因而最多可供5人，但需求量为3人，于是，在这个格子里填上尽可能大的数是{}{}2121min ,min 3,53x a b ===. 这个格子填上数后，B 1的要求满足了，可用线划去该列.于是只需考虑B 2、B 3、B 4的需求. 从表3-5看到，在未划线的格子中ij c 最小者是24332c c ==. 任选一个，比如考虑33c 所在的格子. 此处的供求情况是：最多可供7，但最多需要4. 于是应填入的数是{}{}3333min ,min 7,44x a b ===. 这样B 3的需求也满足了，用线划去该列.后面只需考虑B 2和B 4的需求. 这时最小的c ij （≠c 11，≠c 13）是c 24=2. 此处，最大可供量为5－3=2（c 21处已占用了），需求量为6，从而应令{}{}242214min ,min 53,62x a x b =-=-=. 这时A 2的供应量用完了，用线划去该行. 后面只需考虑A 1和A 3的供应、B 2和B 4需求了，……这样依次分析下去，便得到：{}{}323332min ,min 74,83x a x b =-=-={}{}141424min ,min 9,624x a b x =-=-= {}{}12114232min ,min 94,835x a x b x =--=--=将上述六个数填在运输表内（为了与其它数字相区别，用圈号标记），其余为非基变量取0值，就可作为初始调运方案（见表3-5）.从表3-5容易算出，这个初始方案的总运费是 5×9+4×7+3×1+2×2+3×4+4×2 =100（百元）， 即10000元.（3）以上两种方法在求初始基可行解时，均会遇到一些特殊情况，一般称为“退化”. 大致有两种情况：①当选定元素ij x 后，发现该元素所在行的供给量等于需求量时，此时只能划去一行或一列，不能同时划去. ②当选定元素ij x 后，发现对应供给量i a 和需求量j b 均为0，那么{}0,min ==j i ij b a x ，此时仍应把ij x 作为基变量，把0值填入相应格子中（即基变量取0，退化）.（二）最优性检验上面已经得到初始基可行解，那是否为最优解呢？需要验证. 依单纯形法原理，要求出各变量的检验数；由于基变量的检验数恒为0，所以只要求出非基变量的检验数. 另外运输问题是极小化的线性规划问题，只要检验数全部非负即达最优解. 在表上作业法中常有闭回路法和位势法.（1）闭回路法 我们试从定义出发计算检验数. 先看11x 的检验数11C ，分析一个闭回路（表3-6中虚线所示）. 由于供求条件的限制，当从0增加到1时，将引起连锁反应：21x 减少1，24x 增加1，14x 减少1. 于是根据检验数的定义得到11C =1c 11+（-1）c 21+1c 24+（-1）c 14= c 11-c 21+c 24-c 14=2-1+2-7= -4，即11x 每增加1个单位，将使运费减少4个单位，这说明初始解非最优. 类似地，我们可以求出其他非基变量的检验数，但是，一般说来这种求检验数的方法是比较繁琐的. 例如，求31x 的检验数时，必须考虑下面那样的复杂闭回路(表3-6中实线所示)．表3-6 运输问题作业表（2） 用位势法 位势法又叫U-V 法，它是由解运输问题的对偶问题引出来的. 平衡型运输问题的对偶问题为：11Max s.t.(1,,;1,,)mni i i ji j i j ijY a u b v u v c i m j n ===++≤==∑∑对偶模型里的变量i u 与m 个供应约束方程对应，j v 与n 个需求约束方程对应，分别称它们为原问题变量ij x 的行位势和列位势.定理3-2 运输问题的决策变量ij x 的检验数()ij ij i j C c u v =-+. (证明略) 由于基变量的检验数等于0，所以对于基变量ij x 有： ij j i c v u =+. 而平衡型运输问题中的基变量个数为1-+n m ，从而得到1-+n m 个类似ij j i c v u =+这样方程构成的方程组. 但它有n m +个未知量，要解出这个方程组，必须给其中一个自由未知量赋值，比如令01=u （这样不会影响结果），就可求出所有变量的位势，进而算出所有非基变量的检验数. 仍用例3-1来说明具体求法. 对于最小费用法得到的初始基本可行解（见表3-5），得到方程组⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+=+=+=+=+=+242179332342124121v u v u v u v u v u v u 令 01=u ，解得：⎪⎩⎪⎨⎧====-=-==7,7,9,6,5,5,04321321v v v v u u u计算非基变量的检验数：111111()2064C c u v =-+=--=-，与闭回路法结果一致，其它检验数可类似求出填入作业表中，用（ ）圈起来，见表3-7.表3-7 运输问题作业表——位势法求检验数从表3-7可以看出，x 11的检验数11C =-4（与前面用定义求得的结果是一致的）是所有检验数中负值最小者. 这说明应当让x 11进基，以改进表3-5中的初始方案.（三）用闭回路法调整运输方案——改进基本可行解如果经过检验所得的解不是最优的，就需要对基变量进行迭代. 前面已经有选取进基变量的规则，即在所有非基变量中取检验数是负值最小者为进基变量. 下面，用闭回路法选取出基变量及基变量取值的调整量，以实现解的改进. 步骤是：① 找出入基变量所在的闭回路，并以该变量所在格为起点，沿闭回路顶点依次交替把它们所取的值前面加“+”、“-”号. 如表3-8所示； ② 所有被标“-”号格子中变量ij x 取值最小者作为出基变量，即被标“-”号的圆圈中数字最小者：}"-"min{的取值号的闭回路顶点上所有标ij x =θ. 在表3-8中{}min 3,43θ==.表3-8 基变量迭代调整表表3-9 迭代后的运输方案表③ 进行基的迭代,出基变量当然取值为0，即将所有带“+” 号的格子原取值加θ，带“-”号的格子原取值减θ,就得到一个新的调运方案（闭回路不涉及的基变量取值不变动，见表3-9）. 再求检验数，重复上述步骤，直至最优.从表3-9中容易算出，这个方案的总运费是 3×2+5×9+1×7+5×2+3×4+4×2 =88（百元）， 即8800元. 比初始表的方案优秀了，但在表中求出各非基变量的检验数显示，它还不是最优的. 22x 要作为入基变量. 再经过迭代得到调运方案如表3-10所示.表3-10 再次迭代后的运输方案表从表3-10容易得出，,4,3,5,6,33332221411=====x x x x x 其它非基变量为0；这时的总费用为：3×2+6×7+5×3+3×4+4×2 =83（百元）， 即8300元. 这时算出非基变量的所有检验数均非负，从而是最优的运输方案.在计算过程中需要注意的是，可能会有非基变量（空格）的检验数为0的情况，这时，该供销平衡的运输问题存在无穷多最优解. 在已得到的一个最优解的表格中，从这样的空格出发做闭回路重新进行调整，可以得到另一个最优解.5. 某卫生防疫站准备选拔防疫科、食品科、总务科的三名科长. 几经筛选，仅剩下赵、钱、孙三名候选人. 根据民主评议的统计结果，他们主持各个科的工作能力（以得分多少来衡量）如表4所示. 试从工作能力出发，确定各科长的指定方案，使总体效能最大.表4 工作能力表分析： 用i =1,2,3 分别表示赵、钱、孙三人；用j =1,2,3 分别表示防疫、食品、总务三个科. 则可以设防疫 食品 总务 工 作 能 力（分）赵35 30 27 钱 37 35 29 孙382832⎩⎨⎧=, ,0,,1其他科的科长第担任人表示第j i x ij 于是数学模型为3311Max ij ij i j Y b x ===∑∑()()()()31311,123353027s.t.1,123:37352938283201123ij i ij ij j ij x j , , x i , , b x i, j , , ==⎧==⎪⎪⎛⎫⎪ ⎪===⎨ ⎪⎪ ⎪⎝⎭⎪==⎪⎩∑∑其中或实际上，只要找出效率矩阵()ij b 中的最大元素b ，用b 减去矩阵中的每个元素ij b ，得到的矩阵()ij c 我们称为原矩阵对应的缩减矩阵（ij ij b b c -=）. 易见ij c 越小表示原效率矩阵中第i 个人去作第j 项任务的收益越大，反之则收益越小. 因此求()ij b 的最大化问题解，等价于求它对应的缩减矩阵()ij c 最小化问题的解.解 由于()353027373529382832ij b ⎛⎫⎪= ⎪ ⎪⎝⎭中的最大元素为:38=b ,所以它对应的缩减矩阵为()()38111390106ij ij c b b ⎛⎫ ⎪=-= ⎪ ⎪⎝⎭. 用匈牙利法求()ij c 的最优解() 3 8 11 1 3 9 0 10 6ij c ⎛⎫ ⎪= ⎪ ⎪⎝⎭⎪⎪⎪⎭⎫ ⎝⎛7 10 08 2 0 8 5 0 ⎪⎪⎪⎭⎫ ⎝⎛0 8 01 0 01 3 0 ⎪⎪⎪⎭⎫ ⎝⎛//(0) 8 0 1 (0) 01 3)0( -2 -7可见最优解为()100010001ij x ⎛⎫⎪= ⎪ ⎪⎝⎭，这也是原最大化指派问题的最优解，即派赵、钱、孙分别担任防疫科、食品科和总务科的科长，这样可使总的工作能效达到最大值102分.2. 效率矩阵不是方阵 在实践中，往往出现人少任务多或人多任务少的情况. 对效率矩阵来说，表现为矩阵不是方阵. 甚至要求某人不能完成某项任务或某项工作不能由某人去作. 这都需要作适当改进，再应用匈牙利法去解决.对于效率矩阵不是方阵，可以虚设几行或几列，使其构成方阵，虚设的行（列）的元素要根据目标函数的具体情况确定. 对于后一问题，只要将效率矩阵相应的元素取得充分大（极小问题）或充分小（极大化问题），使得最优指派方案不可能取在该元素上.6. 某公司生产A 、B 两种药品，这两种药品每小时的产量均为1000盒，该公司每天采用两班制生产，每周最大工作时间为80小时，按预测每周市场最大销量分别为70000盒和45000盒．A 种药每盒的利润为2.5元，B 种为1．5元．试确定公司每周A 、B 两种药品生产量x 1和x 2（单位：千盒），使公司的下列目标得以实现：P 1：避免每周80小时生产能力的过少使用． P 2：加班的时间限制在10小时以内．P 3：A 、B 两种药品的每周产量尽量分别达到70,000盒和45,000盒，但不得超出，其权系数依它们每盒的利润为准． P 4：尽量减少加班时间．解 先建立这个问题的线性规划模型，依题意分别建立各项目标约束⎪⎪⎪⎩⎪⎪⎪⎨⎧321=0≥0≥45=+70=+10=-+80=-+++-21-32-21+11-11+1+1-121),,(,,,, i d d x x d x d x d d d d d x x i i 权系数是指它们在目标函数中的重要程度，由2.5∶1.5=5∶3，故：目标函数为：()1121132341Min 53Z Pd P d P d d P d -+--+=++++建立单纯形表运算如下：表4-5 单纯形表至此，由于P 1 »P 2» P 3»P 4 ，可知各检验数均非负，从而得最优解为：x 1=70，x 2=20，0=-1d , 10=+1d , 0=-2d , 25=-3d , 0=-11d ,0=+11d即生产A 种药品70 000盒，B 种药品20 000盒，P 1，P 2级目标可完全实现．因10=+1d ，故每周需加班10小时，每周利润为：70000×2．5+20000×1．5=205000（元）．7. 某高校有各类教职员工如下：助教、助研、讲师、教授助理、副教授、教授、兼职教师、专家及职工, 各类人员所承担的工作性质、工作量和工资各不相同，预计在下一学年要招收一定数量的本科生与研究生，现应用目标规划来确定聘用各类人员的人数，既要保持各类人员之间的适当比例，完成学校的各项工作，同时又要取得最好的经济效益．设聘用各类人员的人数如下：x1助研（可由研究生兼任）y1教授助理（有博士学位）x2助教（可由研究生兼任）y2副教授（有博士学位）x3讲师y3教授（有博士学位）x4教授助理（无博士学位）y4兼职教师（有博士学位）x5副教授（无博士学位）y5专家（有博士学位）x6教授（无博士学位）w1所有教职工的工资总基数x7兼职教师（无博士学位）w2所有教职工的工资比上一年的总增加数x8专家（无博士学位）x9职工现各类人员承担的工作量，工资及所占比例见表5．校方确定的各级决策目标为：P1：要求教师有一定的学术水平，即75%的教师是专职的，担任本科生教学工作的教师中，至少有40%的人具有博士学位．担任研究生教学的至少有75%的人具有博士学位．P2：要求各类人员增加工资的总额不得超过176000美元，其中x1，x2和x9增加的工资数为其原工资数的6%，而其它人员为8%．P3：要求能完成学校的各项教学工作，即学校计划招收本科生1820名、研究生100名．要求为本科生每周开课共910学时，研究生每周开课100学时，并要求本科生教师与学生人数比为1∶20，研究生教师与学生人数比为1∶10．表5 各类人员工作量，工资及所占比例表变量承担的教学工作量（学时/周）所占教师的百分比（%）年工资（美元）本科生研究生最大最小x10 0 -- -- 3000 x2 6 0 7 -- 3000 x312 0 7 -- 8000 x49 0 15 -- 13000x 5 9 0 5 -- 15000 x 6 6 0 2 -- 17000 x 7 3 0 1 -- 2000 x 8 0 3 -- 1 30000 x 9 -- -- -- -- 4000 y 1 6 3 -- 21 13000 y 2 6 3 -- 14 15000 y 3 3 3 -- 23 17000 y 4 0 3 2 -- 2000 y 5 0 3 -- 2 30000P 4：要求各类教学人员之间有适当的比例，即x 2所占全体教师比例不超过7%，x 3不超过7%，x 4不超过15%，x 5不超过5%，x 6不超过2%，x 7不超过1%，x 8不低于1%，y 1不低于21%，y 2不低于14%，y 3不低于23%，y 4不超过2%，y 5不低于2%．P 5：要求教师与行政管理职工x 9之比不超过4∶1 P 6：要求教师与助研x 1的比不超过5∶1． P 7：要求所有人员总工资基数尽可能地小．（1） 75%的的教师是专职的:0=-++750-++++1-151=81=531=63=8∑∑∑∑d d y x y y x xi i i i i i i i)(.本科生教学中至少40%有博士学位：0=-++400-+2-231=72=31=∑∑∑d d y x y i i i i i i )(. 研究生教学中至少75%有博士学位：0=-++750-+3-351=851=∑∑d d y x y i i i i )(.（2） 教学任务本科生：910=-+3+6+6+3+6+9+9+12+6+4-4321765432d d y y y x x x x x x 研究生：100=-+3+3+3+3+3+3+5-5543218d d y y y y y x 教师数：91=-+++6-631=72=∑∑d d y x i i i i ， 10=-+++7-751=8∑d d y x i i（3） 教学人员比例：令T =∑∑51=82=+i i i i y x=-+-0200=-+-0200=-+-2300=-+-1400=-+-2100=-+-0100=-+-0100=-+-0200=-+-0500=-+-1500=-+-0700=-+-070+19-195+18-184+17-173+16-162+15-151+14-148+13-137+12-126+11-115+10-104+9-93+8-82d d y T d d y T d d y T d d y T d d y T dd x T d d x T d d x T d d x T d d x T d d x T d d x T ............（4） 教师与职工（x 9）之比不超过4∶1 ： 0=-+4-+20-209d d x T （5） 教师与助研（x 1）之比不超过5∶1 ： 0=-+5-+21-211d d x T （6） 全体人员工资增加总额=-+-30000+2000+17000+15000+13000+30000+2000+17000+15000+13000+8000080+4000++3000060+22-22254321876543921d d y y y y y x x x x x x x x x ω)(.])([. 这里助研x 1,助教x 2和职工x 9的工资增长率为6%，其它人员的工资增长率为8%，176000=2ω为目标期望值．（7） 全体人员工资总基数约束=-+-30000+2000+17000+15000+13000+4000+30000+2000+17000+15000+13000+8000++3000+23-23154321987654321d d y y y y y x x x x x x x x x ω))(其中1850000=1ω为目标期望值．目标优先级别如前面要求，在P 3级中，校方认为有关研究生开设的课与师生之比的重要性是本科生的2倍，建立目标函数如下31222357461131741819520621723814Min (22)()i i i i i i Z P d P d P d d d d P d d d d P d P d P d ++----=--+++++===++++++++++++∑∑∑经计算可得这个问题的解为.,,,,,,,,,,,,,,,176000=2471000=3=0=34=20=42=38=1=1=0=7=22=10=10=32=2154321987654321ωωy y y y y x x x x x x x x x 各级目标实现情况：P 1级：（基本实现）教师的学术水平实现． P 2级：增加工资总额实现．P 3级：完成学校的各项教学工作目标实现，师生数比例实现． P 4级：各类教师之间的比例实现． P 5级：教师与行政人员之比目标实现． P 6级：教师与助研人员之比例目标实现．P 7级：全体人员工资总基数超过了预期目标． （未实现）这时，学校只要能争取到充分的经费，达到2 471 000美元，则以上7个目标都能实现．如校方无法得到比1 850 000美元多的经费． 则说明经费限制很重要，即不应当把工资总数目标放在最低的P 7级而应提升到P 2级，将原P 2~P 6级目标均降一级，再将无博士学位的教授占全体教师的百分比由最多2%改为至少2%，因为在前面求解中x 6 = 0．这样新的目标函数为：312233224574611117513181219620721814Min (22)()i i i i i i Z P d P d P d P d d d d P d d d d d d P d P d +++----=--++++++===++++++++++++++∑∑∑可计算出解为.,,,,,,,,,,,,,,,135000=1850000=0=0=30=18=28=0=0=1=1=7=20=20=9=0=2154321987654321ωωy y y y y x x x x x x x x x 各级目标实现情况P 1级：教师学术水平目标实现． P 2级：全体人员工资总基数目标实现． P 3级：全体人员工资增长总数目标实现．P 4级：学校各项工作任务完成及师生比例目标实现． P 5级：教师中各类人员的比例未实现． P 6级：没实现 （因x 9=0,即没有职工）． P 7级：没实现（因x 1=0，即没有助研）．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
某昼夜服务的公交线路
解：设x i 表示第i班次时开始上班的司机和乘务人员数,这样我们建立如下的数学模型。
目标函数：Min x1 + x2 + x3 + x4 + x5 + x6 s.t. x1 + x6≥60 x1 + x2≥70 x2 + x3≥60 x3 + x4≥50 x4 + x5≥20 x5 + x6≥30 x1,x2,x3,x4,x5,x6 ≥0 解得50,20,50,0,20,10（x1到x6）一共需要150人
一家中型的百货商场
解：设x i ( i = 1,2,…,7)表示星期一至日开始休息的人数,这样我们建立如下的数学模型。
目标函数：Min x1 + x2 + x3 + x4 + x5 + x6 + x7 s.t. x1 + x2 + x3 + x4 + x5 ≥28 x2 + x3 + x4 + x5 + x6≥15 x3 + x4 + x5 + x6 + x7≥24 x4 + x5 + x6 + x7 + x1≥25 x5 + x6 + x7 + x1 + x2≥19 x6 + x7 + x1 + x2 + x3≥31 x7 + x1 + x2 + x3 + x4≥28 x1,x2,x3,x4,x5,x6,x7 ≥0 解得12.0.11.5.0.8.0(x1到x7) 最小值36
某工厂要做100套钢架
设x1,x2,x3,x4,x5 分别为5 种方案下料的原材料根数。
这样我们建立如下的数学模型。
目标函数：Min x1 + x2 + x3 + x4 + x5 s.t. x1 + 2x2 +x4≥100 2x3+2x4 +x5≥100
3x1+x2+2x3+3x5≥100 x1,x2,x3,x4,x5≥0 解得30,10,0,50,0 只需要90根原料造100钢架某工厂要用三种原料1、2、3
设设x ij 表示第i 种（甲、乙、丙）产品中原料j 的含量。
目标函数：Max z = -15x11+25x12+15x13-30x21+10x22-40x31-10x33 s.t. 0.5 x11-0.5 x12 -0.5 x13≥0 -0.25x11+0.75x12 -0.25x13≤0 0.75x21-0.25x22 -0.25x23≥0 -0.5 x21+0.5 x22 -0.5 x23≤0 x11+x21 +x31≤100 x12+x22 +x32≤100 x13+x23+x33≤60 x ij≥0 , i = 1,2,3; j = 1,2,3 解得x11=100,x12=50,x13=50原料分别为第1种100 第2种50 第3种50
资源分配
解：将问题按工厂分为三个阶段，甲、乙、丙三个厂分别编号为1、2、3厂。
设sk= 分配给第k个厂至第3个厂的设备台数（k=1、2、3）。
xk=分配给第k个工厂的设备台数。
已知s1=5, 并有S2=T1(s1,x1)=s1-x1,S3=T2(s2,x2)=s2-x2从Sk与Xk的定义，可知s3=x3
以下我们从第三阶段开始计算。
Maxr3(s3,x3)=r3(s3,x3)即F3（s3）= Maxr3(s3,x3)=r3(s3,x3). 第二阶段F2（s2）=max[r2(s2,x2)+f3(s3)]第一阶段当s1=5时最大盈利为f1(5)=max[r1(5,x1)+f2(5-x1)] 得出2个方案⑴分配给甲0台乙0台丙3台⑵分配甲2台乙2台丙1台，他们的总盈利值都是21.
背包
设Sk＝分配给第k种咨询项目到第四种咨询项目的所有客户的总工作日Xk=在第k种咨询项目中处理客户的数量已知s1=10,有S2=T1(s1,x1)=s1-x1. S3=T2(s2,x2)=s2-3x2. S4=T3(s3,x3)=s3-4x3,第四阶段F4(s4)=maxr4(s4,x4)=r4(s4,[s4/7])第三阶段F3(s3)=max[r3(s3,x3)+f4(s3-4x3)]第二阶段F2(s2)=max[r2(s2,x2)+f3(s2-3x2)]第一阶段已知s1=10，又因s2=s1-x1有F1(10)=max[r1(10,x1)+f2(10-x1)]
综上当x1*=0,x2*=1,x3*=0,x4*=1,最大盈利为28
京城畜产品
解：设：0--1变量xi = 1 (Ai 点被选用）或0 (Ai 点没被选用）。
这样我们可建立如下的数学模型：Max z =36x1+40x2+50x3+22x4+20x5+30x6+25x7+48x8+58x9+61x10 s.t. 100x1+120x2+150x3+80x4+70x5+90x6+80x7+140x8+160x9+180x10 ≤720 x1 + x2 + x3 ≤2 x4 + x5 ≥1 x6 + x7 ≥1 x8 + x9 + x10 ≥2 xi≥0 且xi为0--1变量，i = 1,2,3,……,10 函数值245 最优解1,1,0,0,1,1,0,0,1,1（x1到x10的解）
高压容器公司
设x1，x2，x3 分别为小号容器、中号容器和大号容器的生产数量。
设y i = 1(当生产第i 种容器, 即x i ＞0 时) 或0（当不生产第i种容器即x i = 0 时）。
这样我们可建立如下的数学模型：Max z = 4x1 + 5x2 + 6x3 - 100y1 - 150y2 - 200y3 s.t. 2x1 + 4x2 + 8x3 ≤500
2x1 + 3x2 + 4x3 ≤300 x1 + 2x2 + 3x3 ≤100 x i ≤M y i ，i =1，2，3，M充分大x j ≥0 y j 为0--1变量，i = 1,2,3 函数值300 最优解x1=100,x2=0,x3=0
一工艺品厂商
采用简化模式，最终得到目标线性规划如下：Min P1(d1+)+ P1(d2－)+P2(d3-)+ P3(d4-)+ P3(2d5-)s.t. 2x1+3x2-d1++d1-=680 对应第1个目标2x1+3x2-d2++d2-=600 对应第2个目标250x1+125x2-d3-+d3+＝70000 对应第3个目标x1-d4++d4-=200 对应第4个目标
x2-d5++d5-=120 对应第5个目标x1,x2,d1+,d1-,d2+,d2-,d3+,d3-,d4+,d4-,d5+,d5-≥0先考虑P1 根据上式得出x1=0，x2=200，d1+ =0，d1- =80，d2+= d2−=0，d3+=0，d3−=45 000
P2 上式加一步d1+加d2-=0得可得，x1=270，x2=20，d1+=0，d1−=80，d2+= d2−=0，d3+=d3−=0，d4+=70，d4−=0，d5+=0，d5−=100，目标函数d3−=0
P3 从P2加一步d3-=0 得出x1=250；x2=60；d1+=0；d1-=0；d2+=80；d2-=0；d3+=0；d3-=0；d4+=50；d4-=0；d5+=0；d5-=60，目标函数d4-+2d5- =120。
课件目标1、目标3和目标4达到了，但目标2、目标5都有一些偏差。
某公司装配（统筹方法）
公式Ts=LS-ES=LS-EF即下面数字减上面数字
注：无第2章，第11章,第3章套裁下料问题。