平面几何问题与证明
平面几何的证明方法

平面几何的证明方法平面几何是数学中的一个重要分支,主要研究平面内的点、线、面及其相互关系。
在解决平面几何问题时,证明是一个关键步骤。
本文将介绍一些常用的平面几何证明方法,并说明它们的应用场景。
一、直接证明法直接证明法是一种常用的证明方法,即通过逐步推导和陈述使命题成立。
这种方法依赖于已知条件和平面几何定理,逻辑严谨、思路清晰。
例如,当要证明某两条线段相等时,可以通过给出这两条线段的定义,然后根据它们的属性,逐步推导得出结论。
二、间接证明法间接证明法是通过否定反证法来证明结论。
假设原命题不成立,然后逐步推导,得出矛盾,从而推出原命题成立。
这种方法常用于证明无理数、无法被二分等问题。
例如,当要证明某条直线平分了一个角时,可以假设这条直线没有平分该角,然后通过逻辑推导得出矛盾,证明了该直线实际上是平分了这个角。
三、反证法反证法是通过假设结论不成立,然后推出矛盾,证明原结论的一个方法。
这种方法常用于证明唯一性问题。
例如,当要证明两个圆只有一个公共切点时,可以先假设它们有两个或更多个公共切点,然后通过推导得出矛盾,从而证明了原结论。
四、归纳法归纳法适用于一系列问题的证明。
首先证明基本情况成立,然后假设某个特定的情况成立,通过归纳法推导得出所有情况都成立。
这种方法常用于证明几何图形的性质。
例如,当要证明一个多边形的内角和公式时,可以通过归纳法证明三角形和四边形的情况,然后推广到所有多边形。
五、共线法共线法是通过证明多个点共线来证明结论的方法。
在平面几何中,当需要证明某些点共线时,可以利用已知条件中的共线关系,或者通过构造辅助线,从而达到共线的目的。
例如,当要证明一个四边形的对角线交于一点时,可以通过构造这两条对角线,然后利用平行线的性质证明它们的交点存在。
六、相似性法相似性法是通过画出几何图形的相似部分来证明结论的方法。
当需要证明两个三角形相似时,可以通过观察它们的角度和边长关系,利用相似三角形的性质得出结论。
初中数学平面几何的证明题目

初中数学平面几何的证明题目平面几何是数学中非常重要的一个分支,它研究的是平面上的点、线、面及其之间的关系和性质。
证明题目是平面几何中常见的一种题型,它要求我们通过逻辑推理和几何知识的运用来验证或证明某个几何命题的正确性。
在初中数学学习中,我们会遇到一些基本的平面几何的证明题目,下面我将选取一些典型的例子进行阐述。
1. 证明等腰三角形底角相等等腰三角形是指两边长度相等的三角形。
我们要证明的是等腰三角形的底角相等。
证明:设等腰三角形ABC中,AB = AC,从点A作BD⊥AC于D,则BD = DC。
∵△ABD ≌△ACD(公共边AC, AB = AC,∠BDA = ∠CDA = 90°)∴∠BAD = ∠CAD2. 证明三角形内角和等于180°三角形是由三条线段构成的闭合图形,它有三个内角。
我们要证明的是任意三角形三个内角的和等于180°。
证明:设三角形ABC的三个内角分别为∠A、∠B、∠C。
∵直线AB,BC可延长,可得到直线AC。
∵在AB、BC同侧取点D、E∵∠ABD = ∠ECB(两边平行,对顶角相等)∵∠BAC + ∠ACB + ∠ABD + ∠ECB = 180°(直线AC上的内角和为180°)∵∠A + ∠B + ∠C = 180°3. 证明直角三角形斜边上的中线等于半斜边直角三角形是指一个内角为90°的三角形。
我们要证明的是直角三角形斜边上的中线等于半斜边。
证明:设△ABC为直角三角形,∠B = 90°,D为AC的中点。
则BD = DC(D为AC的中点)由△ABC的相似性可得:△BDA ∼△BAC∴ BD/BA = DA/AC∴ BD/BA = 1/2∴ BD = 1/2 BA4. 证明平行线的对应角相等平行线是在同一个平面内,方向相同或者相反且不相交的两条直线。
我们要证明的是平行线的对应角相等。
证明:设直线l1 ∥ l2,交直线m∵∠1 + ∠2 = 180°(同旁内角和为180°)∵∠1 + ∠3 = 180°(同旁内角和为180°)∴∠2 = ∠3通过以上几个例子,我们可以看出,平面几何的证明题目,需要运用基本的几何知识和推理方法,在观察、分析和运算等方面进行逻辑推理,严谨而准确地证明某个几何命题的正确性。
平面几何-五大定理及其证明

平面几何定理及其证明梅涅劳斯定理1 .梅涅劳斯定理及其证明 定理:一条直线与 ABC 的三边AB BC CA 所在直线分别交于点 D E 、F ,且D E 、F 均证明:如图,过点C 作AB 的平行线,交EF 于点G. 因为 CG // AB ,所以 CG CF --------------------- ( 1)AD FA因为 CG // AB ,所以 EC ( 2) DB BEC F ,即得 AD C FEC FA DB EC FA2.梅涅劳斯定理的逆定理及其证明定理:在 ABC 的边AB BC 上各有一点 D E ,在边 AC 的延长线上有一点 F ,若二、 塞瓦定理3 .塞瓦定理及其证明定理:在ABC 内一点P,该点与ABC 的三个顶点相连所在的 三条直线分别交 ABCE 边AB BC CA 于点D E 、F ,且D E 、F 三点均不是 ABC不是ABC 的顶点,则有AD BECF 1DB EC由(1)宁(2) DB可得兀AD BE CF DB EC FA1,那么,D E 、F 三点共线.证明:设直线EF 交AB 于点D ,则据梅涅劳斯定理有AD /BE CF 丽EC FA因为AD Bl CF DB EC FA1,所以有誥段AB 上,所以点D 与D 重合.即得D鴿.由于点D D 都在线 E 、F 三点共线.证明:运用面积比可得 ADDB S ADP S BDPS ADC S BDC根据等比定理有S ADP S ADCSADC S ADP S APCSSBDPBDCSBDCSBDPS的顶点,则有AD BE CF “1 DB EC FA .所以AD S A PC .同理可得BE SDB S BPCAPB, CFEC S APC FA SBPCS APB三式相乘得竺吏 DB EC CF i FA 4.塞瓦定理的逆定理及其证明 定理:在 ABC 三边AB BC CA 上各有一点 H 1,那么直线CD AE BF 三线共点. DE 、F ,且 D E 、 F 均不是 ABC 的顶点,AD BE若 DB EC证明:设直线AE 与直线BF 交于点P,直线CP 交AB 于点D ,则 据塞瓦定理有 AD Z DBBE EC CA1 -1,所以有 段AB 上,所以点D 与D 重合.即得 因为竺 DB EC CF FA AD DB D DDB •由于点D D 都在线 E 、F 三点共线.三、西姆松定理 5.西姆松定理及其证明 定理:从 ABC 外接圆上任意一点 F ,则D E 、F 三点共线. 证明:如图示,连接PC ,连接EF P 向BC CA AB 或其延长线引垂线, 垂足分别为DE、交BC 于点D ,连接P D• 因为PE 因为A 、 所以, 共圆. 所以, 即 PD BC 由于过点 F D E 、 四、 6 AE,PF AF,所以A 、F 、P 、E 四点共圆,可得B 、P 、C 四点共圆,所以 FEP = BCP 即 DEP = CDP + CEP = 180°。
平面几何100题及答案(前80题)
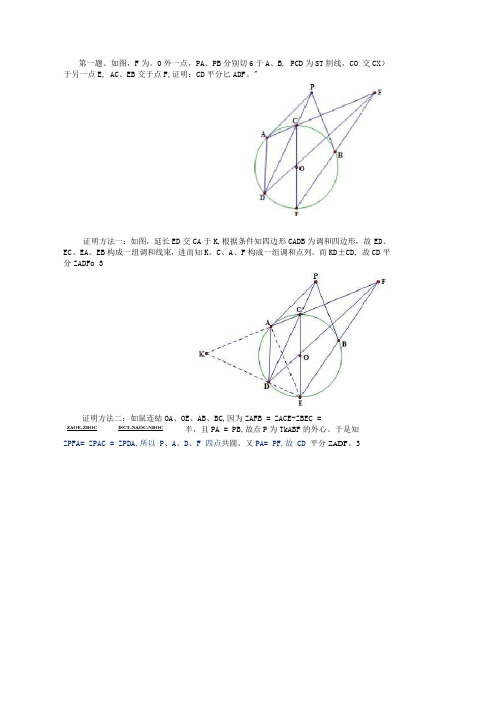
第一题、如图,F为。
0外一点,PA、PB分别切6于A、B, PCD为ST割线,CO 交CX)于另一点E, AC、EB交于点F,证明:CD平分匕ADF。
"证明方法一:如图,延长ED交CA于K,根据条件知四边形CADB为调和四边形,故ED、EC、EA、EB构成一组调和线束,进而知K、C、A、F构成一组调和点列。
而KD±CD, 故CD平分ZADFo 3证明方法二:如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半,且PA = PB,故点P为TkABF的外心。
于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。
又PA= PF,故CD 平分Z A DF。
3第二题、如图,AB为©0直径,C、D为O。
上两点,且在AB同侧,。
在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明:E、C、页、D四点共圆。
“证明:如图,延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。
又在圆内接六边形CCADDB中使用帕斯卡定理,知K、E、F三点共线,从而KM丄卽于価。
于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。
K第三题、如图,AB为。
直径,C、D为伽上两点'且在AB同侧,O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。
于点G,证明;ZCEF = 2/AGF。
“证明:如图,根据条件知匕CF D =典牌=(脸-®;(i对-命)=Z CAB + / DBA = ZECF + ZEDF;且EC = ED;故点E 为△CED 外心。
于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。
所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo,2 2第四題、如图,AB为直径,P为AB延长线上一点,PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点,AF交于K,求证:AP为ZXPCK外扬圆的切线。
初中平面几何解题技巧与证明方法

初中平面几何解题技巧与证明方法平面几何是初中数学课程中的一大重点内容,它涉及到图形的性质与关系、解题技巧等方面。
本文将介绍一些初中平面几何解题的技巧,并探讨一些常用的证明方法。
一、解题技巧1. 观察图形性质:在解题过程中,要善于观察图形的性质。
例如,对于平行四边形,我们可以利用对角线相等、同位角互补等性质来解题。
对于等腰三角形,我们可以利用底角相等、等腰三角形的高相等等性质来解题。
因此,在解题之前,仔细观察图形的性质对于解题是非常有帮助的。
2. 利用辅助线:辅助线是解决平面几何问题的常用方法。
通过引入辅助线,可以将原有的几何问题转化为更简单的几何问题。
例如,对于一个矩形,我们可以通过引入一条对角线将它分成两个等腰直角三角形,从而简化问题。
利用辅助线进行解题,可以帮助我们更好地理解图形,找到解题的关键。
3. 运用相似性质:相似是平面几何中一个非常重要的概念。
相似性质可以用来推导出一些未知的长度或角度。
在解题过程中,可以利用相似三角形的比例关系来求解未知量。
此外,相似性质还可以用来证明两个图形全等或相似。
二、证明方法1. 数学归纳法:数学归纳法是一种常用的证明方法,特别适用于证明一些与自然数有关的命题。
在平面几何中,数学归纳法可以用来证明一些与图形次数有关的命题,如证明正多边形的内角和公式。
数学归纳法的基本思想是,先证明命题在某个特定情况下成立,然后假设命题在某个情况下成立,证明它在下一个情况下也成立。
2. 反证法:反证法是证明一些命题的常用方法。
通过假设命题的否定,然后推导出一个矛盾的结论,从而证明了原命题的正确性。
在平面几何中,反证法可以用来证明一些关于垂直、平行关系的命题,如证明垂直平分线与角平分线互相垂直。
3. 作图法:在某些情况下,通过合理的作图可以帮助我们观察并找到证明的思路。
在平面几何中,作图法可以用来证明一些关于线段比例、角平分线等命题。
通过合理的构造和作图,可以帮助我们更好地理解几何问题,并找到证明的依据。
十大高中平面几何几何定理汇总及证明

高中平面几何定理汇总及证明1.共边比例定理有公共边AB的两个三角形的顶点分别是P、Q,AB与PQ的连线交于点M,则有以下比例式成立:△ PAB的面积:△ QAB的面积=PM:QM.证明:分如下四种情况,分别作三角形高,由相似三角形可证S△PAB=S△PAM-S△PMB=S△PAM/S△PMB-1×S△PMB=AM/BM-1×S△PMB等高底共线,面积比=底长比同理,S△QAB=AM/BM-1×S△QMB所以,S△PAB/S△QAB=S△PMB/S△QMB=PM/QM等高底共线,面积比=底长比定理得证特殊情况:当PB∥AQ时,易知△PAB与△QAB的高相等,从而S△PAB=S△QAB,反之,S△PAB=S△QAB,则PB∥AQ;2.正弦定理在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍”,即a/sinA = b/sinB =c/sinC = 2r=Rr为外接圆半径,R为直径证明:现将△ABC,做其外接圆,设圆心为O;我们考虑∠C及其对边AB;设AB长度为c;若∠C为直角,则AB就是⊙O的直径,即c= 2r;∵特殊角正弦函数值∴若∠C为锐角或钝角,过B作直径BC`交⊙O于C`,连接C'A,显然BC'= 2r=R; 若∠C为锐角,则C'与C落于AB的同侧,此时∠C'=∠C同弧所对的圆周角相等∴在Rt△ABC'中有若∠C为钝角,则C'与C落于AB的异侧,BC的对边为a,此时∠C'=∠A,亦可推出;考虑同一个三角形内的三个角及三条边,同理,分别列式可得;3.分角定理在△ABC中,D是边BC上异于B,C或其延长线上的一点,连结AD,则有BD/CD=sin∠BAD/sin∠CADAB/AC;证明:S△ABD/S△ACD=BD/CD………… 1.1S△ABD/S△ACD=1/2×AB×AD×sin∠BAD/1/2 ×AC×AD×sin∠CAD= sin∠BAD/sin∠CAD ×AB/AC…………1.2由1.1式和1.2式得BD/CD=sin∠BAD/sin∠CAD ×AB/A C4.张角定理在△ABC中,D是BC上的一点,连结AD;那么;证明:设∠1=∠BAD,∠2=∠CAD由分角定理,S△ABD/S△ABC=BD/BC=AD/ACsin∠1/sin∠BAC→ BD/BCsin∠BAC/AD=sin∠1/AC 1.1S△ACD/S△ABC=CD/BC=AD/ABsin∠2/sin∠BAC→ CD/BCsin∠BAC/AD=sin∠2/AB 1.21.1式+1.2式即得 sin∠1/AC+sin∠2/AB=sin∠BAC/AD5.帕普斯定理直线l1上依次有点A,B,C,直线l2上依次有点D,E,F,设AE,BD交于G,AF,DC交于I,BF,EC交于H,则G,I,H共线;6.蝴蝶定理设S为圆内弦AB的中点,过S作弦CF和DE;设CF和DE各相交AB于点M和N,则S 是MN的中点;证明:过O作OL⊥ED,OT⊥CF,垂足为L、T,连接ON,OM,OS,SL,ST,易明△ESD∽△CSF∴ES/CS=ED/FC根据垂径定理得:LD=ED/2,FT=FC/2∴ES/CS=EL/CT又∵∠E=∠C∴△ESL∽△CST∴∠SLN=∠STM∵S是AB的中点所以OS⊥AB∴∠OSN=∠OLN=90°∴O,S,N,L四点共圆,一中同长同理,O,T,M,S四点共圆∴∠STM=∠SOM,∠SLN=∠SON∴∠SON=∠SOM∵OS⊥AB∴MS=NS7.西姆松定理过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线,则三垂足共线;此线常称为西姆松线;证明:若L、M、N三点共线,连结BP,CP,则因PL⊥BC,PM⊥AC,PN⊥AB,有B、L、P、N和P、M、C、L分别四点共圆,有∠NBP = ∠NLP = ∠MLP= ∠MCP.故A、B、P、C四点共圆;若A、P、B、C四点共圆,则∠NBP= ∠MCP;因PL⊥BC,PM⊥AC,PN⊥AB,有B、L、P、N和P、M、C、L四点共圆,有∠NBP = ∠NLP= ∠MCP= ∠MLP.故L、M、N三点共线;西姆松逆定理:若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上;证明:PM⊥AC,PN⊥AB ,所以A,M,N,P共圆8.清宫定理设P、Q为△ABC的外接圆上异于A、B、C的两点,P关于三边BC、CA、AB的对称点分别是U、V、W,且QU、QV、QW分别交三边BC、CA、AB或其延长线于D、E、F,则D、E、F在同一直线上.证明:A、B、P、C四点共圆,因此∠PCE=∠ABP点P和V关于CA对称所以∠PCV=2∠PCE又因为P和W关于AB对称,所以∠PBW=2∠ABP从这三个式子,有∠PCV=∠PBW另一方面,因为∠PCQ和∠PBQ都是弦PQ所对的圆周角,所以∠PCQ=∠PBQ两式相加,有∠PCV+∠PCQ=∠PBW+∠PBQ即∠QCV=∠QBW即△QCV和△QBW有一个顶角相等,因此但是,,所以同理,于是根据梅涅劳斯定理的逆定理,D、E、F三点在同一直线上;9.密克定理三圆定理:设三个圆C1, C2, C3交于一点O,而M, N, P分别是C1 和C2, C2和C3, C3和C1的另一交点;设A为C1的点,直线MA交C2于B,直线PA交C3于C;那么B, N, C这三点共线;逆定理:如果是三角形,M, N, P三点分别在边AB, BC, CA上,那么△AMP、△BMN、△CPN 的外接圆交于一点O;完全四线形定理如果ABCDEF是完全四线形,那么三角形的外接圆交于一点O,称为密克点;四圆定理设C1, C2,C3, C4为四个圆,A1和B1是C1和C2的交点,A2和B2是C2 和C3的交点,A3和B3是C3和C4的交点,A4和B4是C1和C4的交点;那么A1, A2, A3, A4四点共圆当且仅当B1, B2, B3, B4四点共圆;证明:在△ABC的BC,AC,AB边上分别取点W,M,N,对AMN,△BWN和△CWM分别作其外接圆,则这三个外接圆共点;该定理的证明很简单,利用“圆内接四边形对角和为180度”及其逆定理;现在已知U是和的公共点;连接UM和UN,∵四边形BNUW和四边形CMUW分别是和的内接四边形,∴∠UWB+∠UNB=∠UNB+∠UNA=180度∴∠UWB=∠UNA;同理∠UWB+∠UWC=∠UWC+∠UMC=180度∴∠UWB=∠UMC;∵∠UMC+∠UMA=180度∴∠UNA+∠UMA=180度,这正说明四边形ANUM是一个圆内接四边形,而该圆必是,U必在上;10.婆罗摩笈多定理圆内接四边形ABCD的对角线AC⊥BD,垂足为M;EF⊥BC,且M在EF上;那么F是A D 的中点;证明:∵AC⊥BD,ME⊥BC∴∠CBD=∠CME∵∠CBD=∠CAD,∠CME=∠AMF∴∠CAD=∠AMF∴AF=MF∵∠AMD=90°,同时∠MAD+∠MDA=90°∴∠FMD=∠FDM∴MF=DF,即F是AD中点逆定理:若圆内接四边形的对角线相互垂直,则一边中点与对角线交点的连线垂直于对边;证明:∵MA⊥MD,F是AD中点∴AF=MF∴∠CAD=∠AMF∵∠CAD=∠CBD,∠AMF=∠CME∴∠CBD=∠CME∵∠CME+∠BME=∠BMC=90°∴∠CBD+∠BME=90°∴EF⊥BC11.托勒密定理圆内接四边形中,两条对角线的乘积两对角线所包矩形的面积等于两组对边乘积之和一组对边所包矩形的面积与另一组对边所包矩形的面积之和.圆内接四边形ABCD,求证:AC·BD=AB·CD+AD·BC.证明:过C作CP交BD于P,使∠1=∠2,又∠3=∠4,∴△ACD∽△BCP.得AC:BC=AD:BP,AC·BP=AD·BC ①;又∠ACB=∠DCP,∠5=∠6,∴△ACB∽△DCP.得AC:CD=AB:DP,AC·DP=AB·CD ②;①+②得ACBP+DP=AB·CD+AD·BC.即AC·BD=AB·CD+AD·BC.12.梅涅劳斯定理当直线交三边所在直线于点时,;证明:过点C作CP∥DF交AB于P,则两式相乘得梅涅劳斯逆定理:若有三点F、D、E分别在边三角形的三边AB、BC、CA或其延长线上,且满足AF/FB×BD/DC×CE/EA=1,则F、D、E三点共线;证明:先假设E、F、D三点不共线,直线DE与AB交于P;由梅涅劳斯定理的定理证明如利用平行线分线段成比例的证明方法得:AP/PBBD/DCCE/EA=1;∵ AF/FBBD/DCCE/EA=1;∴ AP/PB=AF/FB ;∴ AP+PB/PB=AF+FB/FB ;∴ AB/PB=AB/FB ;∴ PB=FB;即P与F重合;∴ D、E、F三点共线;13.塞瓦定理在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则BD/DC×CE/EA×AF/FB=1;∵△ADC被直线BOE所截,∴CB/BDDO/OAAE/EC=1①∵△ABD被直线COF所截,∴BC/CDDO/OAAF/FB=1②②/①约分得:DB/CD×CE/EA×AF/FB=114.圆幂定理相交弦定理:如图Ⅰ,AB、CD为圆O的两条任意弦;相交于点P,连接AD、BC,由于∠B与∠D同为弧AC所对的圆周角,因此由圆周角定理知:∠B=∠D,同理∠A=∠C,所以;所以有:,即:;割线定理:如图Ⅱ,连接AD、BC;可知∠B=∠D,又因为∠P为公共角,所以有,同上证得;切割线定理:如图Ⅲ,连接AC、AD;∠PAC为切线PA与弦AC组成的弦切角,因此有∠PBC=∠D,又因为∠P为公共角,所以有,易证图Ⅳ,PA、PC均为切线,则∠PAO=∠PCO=90°,在直角三角形中:OC=OA=R,PO为公共边,因此;所以PA=PC,所以;综上可知,是普遍成立的;弦切角定理:弦切角的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角度数;点对圆的幂P点对圆O的幂定义为点P在圆O内→P对圆O的幂为负数;点P在圆O外→P对圆O的幂为正数;点P在圆O上→P对圆O的幂为0;三角形五心:内心:三角形三条内角平分线的交点外心:三角形三条边的垂直平分线中垂线的相交点重心:三角形三边中线的交点垂心:三角形的三条高线的交点旁心:三角形的旁切圆与三角形的一边和其他两边的延长线相切的圆的圆心九点圆心:三角形三边的中点,三高的垂足和三个欧拉点〔连结三角形各顶点与垂心所得三线段的中点〕九点共圆的圆心15.根心定理三个两两不同心的圆,形成三条根轴,则必有下列三种情况之一:1 三根轴两两平行;2 三根轴完全重合;3 三根轴两两相交,此时三根轴必汇于一点,该点称为三圆的根心;平面上任意三个圆,若这三个圆圆心不共线,则三条根轴相交于一点,这个点叫它们的根心;若三圆圆心共线,则三条根轴互相平行;根轴定义:A与B的根轴L1:到A与B的切线相等的点;B与C的根轴L2:到B与C的切线相等的点;证明设A、B、C三个圆,圆心不重合也不共线;考察L1与L2的交点P;因为P在L1上,所以:P到A的切线距离=P到B的切线距离;因为P在L2上,所以:P到B的切线距离=P到C的切线距离;所以:P到A的切线距离=P到B的切线距离=P到C的切线距离;也就是:P到A的切线距离=P到C的切线距离;所以:P在A与C的根轴上; 所以:三个根轴交于一点;16.鸡爪定理设△ABC的内心为I,∠A内的旁心为J,AI的延长线交三角形外接圆于K,则KI=KJ=KB=KC;证明:由内心和旁心的定义可知∠IBC=∠ABC/2,∠JBC=180°-∠ABC/2∴∠IBC+∠JBC=∠ABC/2+90°-∠ABC/2=90°=∠IBJ同理,∠ICJ=90°∵∠IBJ+∠ICJ=180°∴IBJC四点共圆,且IJ为圆的直径∵AK平分∠BAC∴KB=KC相等的圆周角所对的弦相等又∵∠IBK=∠IBC+∠KBC=∠ABC/2+∠KAC=∠ABI+∠BAK=∠KIB∴KB=KI由直角三角形斜边中线定理逆定理可知K是IJ的中点∴KB=KI=KJ=KC逆定理:设△ABC中∠BAC的平分线交△ABC的外接圆于K;在AK及延长线上截取KI=KB=KJ,其中I在△ABC的内部,J在△ABC的外部;则I是△ABC的内心,J是△ABC 的旁心;证明:利用同一法可轻松证明该定理的逆定理;取△ABC的内心I'和旁心J’,根据定理有KB=KC=KI'=KJ'又∵KB=KI=KJ∴I和I'重合,J和J’重合即I和J分别是内心和旁心17.费尔巴哈定理三角形的九点圆与其内切圆以及三个旁切圆相切设△ABC的内心为I,九点圆的圆心为V;三边中点分别为L,M,N,内切圆与三边的切点分别是P,Q,R,三边上的垂足分别为D,E,F;不妨设AB>AC;假设⊙I与⊙V相切于点T,那么LT与⊙I相交,设另一个交点为S;过点S作⊙I的切线,分别交AB和BC于V,U,连接AU;又作两圆的公切线TX,使其与边AB位于LT的同侧;由假设知∠XTL=∠LDT而TX和SV都是⊙I的切线,且与弦ST所夹的圆弧相同,于是∠XTL=∠VST因此∠LDT=∠VST则∠UDT+∠UST=180°这就是说,S,T,D,U共圆;而这等价于:LU×LD=LS×LT又LP²=LS×LT故有LP²=LU×LD另一方面,T是公共的切点,自然在⊙V上,因此 L,D,T,N共圆,进而有∠LTD=∠LND由已导出的S,T,D,U共圆,得∠LTD=∠STD=180°-∠SUD=∠VUB=∠AVU-∠B而∠LND=∠NLB-∠NDB=∠ACB-∠NBD=∠C-∠B这里用了LN∥AC,以及直角三角形斜边上中线等于斜边的一半所以,就得到∠AVU=∠C注意到AV,AC,CU,UV均与⊙I相切,于是有∠AIR=∠AIQ∠UIS=∠UIP∠RIS=∠QIS三式相加,即知∠AIU=180°也即是说,A,I,U三点共线;另外,AV=AC,这可由△AIV≌△AIC得到;这说明,公切点T可如下得到:连接AI,并延长交BC于点U,过点U作⊙I的切线,切点为S,交AB于V,最后连接LS,其延长线与⊙I的交点即是所谓的公切点T;连接CV,与AU交于点K,则K是VC的中点;前面已得到:LP²=LU×LD而2LP=BL+LP-CL-LP=BP-CP=BR-CQ=BR+AR-CQ+AQ=AB-AC=AB-AV=BV即 LP=BV然而LK是△CBV的中位线于是 LK=BV因之 LP=LK故LK²=LU×LD由于以上推导均可逆转,因此我们只需证明:LK²=LU×LD;往证之这等价于:LK与圆KUD相切于是只需证:∠LKU=∠KDU再注意到 LK∥ABLK是△CBV的中位线,即有∠LKU=∠BAU又AU是角平分线,于是∠LKU=∠CAU=∠CAK于是又只需证:∠CAK=∠KDU即证:∠CAK+∠CDK=180°这即是证:A,C,D,K四点共圆由于 AK⊥KC易得,AD⊥DC所以 A,C,D,K确实共圆;这就证明了⊙I与⊙V内切;旁切圆的情形是类似的;证毕另略证:OI2=R2-2RrIH2=2r2-2Rr'OH2=R2-4Rr'其中r‘是垂心H的垂足三角形的内切圆半径,R、r是三角形ABC外接圆和内切圆半径FI2=1/2OI2+IH2-1/4OH2=1/2R-r2FI=1/2R-r这就证明了九点圆与内切圆内切九点圆半径为外接圆半径一半;F是九点圆圆心,I为内心18.莫利定理将三角形的三个内角三等分,靠近某边的两条三分角线相交得到一个交点,则这样的三个交点可以构成一个正三角形证明:设△ABC中,AQ,AR,BR,BP,CP,CQ为各角的三等分线,三边长为a,b,c,三内角为3α,3β,3γ,则α+β+γ=60°;在△ABC中,由正弦定理,得AF=csinβ/sinα+β;不失一般性,△ABC外接圆直径为1,则由正弦定理,知c=sin3γ,所以AF=sin3γsinβ/sin60°-γ= sinβsinγ3-4sin²γ/1/2√3cosγ-sinγ= 2sinβsinγ√3cosγ+sinγ= 4sinβsinγsin60°+γ.同理,AE=4sinβsinγsin60°+β∴AF:AE=4sinβsinγsin60°+γ:4sinβsinγsin60°+β=sin60°+γ:sin60°+β=sin∠AEF:sin∠AFE∴∠AEF=60°+γ,∠AFE=60°+β.同理得,∠CED=60°+α∠FED=180°-CED-AEF-α-γ=180°-60°-α-60°+α=60°∴△FED为正三角形19.拿破仑定理若以任意三角形的各边为底边向形外作底角为60°的等腰三角形,则它们的中心构成一个等边三角形;在△ABC的各边上向外各作等边△ABF,等边△ACD,等边△BCE;。
数学平面几何的推理和证明

数学平面几何的推理和证明数学平面几何是数学中的一个重要分支,研究平面上的图形和它们之间的关系。
推理和证明是数学平面几何中最基本的思维方式和方法,它们帮助我们发现几何图形之间的内在规律,解决各种几何问题。
本文将探讨数学平面几何中推理和证明的方法和技巧。
一、推理和证明的基本原理在数学平面几何中,推理和证明是建立在严格的逻辑基础之上的。
它们遵循一定的规则和原理,确保从已知事实推导出正确的结论。
以下是推理和证明中常用的基本原理:1. 公理和定义:数学平面几何的推理和证明是建立在一系列公理和定义之上的。
公理是不需要证明的基本事实,而定义是给出图形和概念的精确定义。
我们可以根据公理和定义来进行推理和证明。
2. 推理规则:在推理和证明过程中,我们需要运用一些基本的推理规则。
比如,反证法、数学归纳法、等价替代法等。
这些推理规则帮助我们从已知的条件中得出新的结论。
3. 推理链:推理和证明的过程是一个逐步推进的过程。
我们需要构建一个推理链,从已知条件开始,通过一系列推理步骤得出最终的结论。
二、推理和证明的方法和技巧推理和证明在数学平面几何中有许多不同的方法和技巧。
下面介绍几种常用的方法:1. 直接证明法:这是最常见的证明方法之一,也是最直接的方法。
它通过给出已知条件、构造推理链,最终得出所要证明的结论。
这个方法要求推理过程中每一步都是正确的,每一步都要给出充分的理由。
2. 反证法:反证法是推理和证明中常用的方法之一。
它假设所要证明的结论不成立,通过推理推导出矛盾的结论,从而证明原假设是错误的。
这个方法常用于证明某些定理的唯一性。
3. 数学归纳法:数学归纳法常用于证明一些关于自然数的结论。
它分为两个步骤:首先证明当n=1时结论成立,然后假设当n=k时结论成立,再证明当n=k+1时结论也成立。
通过这个过程可以推导出结论对于所有自然数成立。
4. 等价替代法:等价替代法是用于证明一个命题中的各个等价条件之间的关系。
通过证明这些等价条件的任意一个,就可以推导出其他等价条件的成立。
高中数学专题复习经典平面几何难题解析

AAB 经典平面几何题目解析经典难题(一)1、已知:如图,O 为半圆的圆心,C,E 是圆上的两点,CD AB ⊥,,EF AB EG CO ⊥⊥ 求证:CD=GF 。
证明:从已知条件,EF AB EG CO ⊥⊥G ,O,F,E 四点共圆,因为090EGO ∠=,所以 内接四边形的外接圆的直径为OE ,作出这个圆。
构造直角三角形,可以得到:sin sin GF NF GNF OE GNF =∠=∠又因为¼¼GOFGOF GNF GEF =⇒∠=∠ 又在RT DCO ∆中,得到sin GD OC COD =∠又圆内接四边形的性质可以得到COD GEF ∠=∠,又OE=OC 所以得到:CD=GF.2、已知,如图,P 为正方形ABCD 内点,015PAD PDA ∠=∠=. 求证:PBC ∆为等边三角形。
证明:将三角形PAD 绕点D 顺时针到DCE ,连接PE ,如图所示。
这样可以得到060PDE ∠=,因为PD=DE ,所以三角形 PDE 为等边三角形,因此PE=DE=CE(其实E 为三角形PDC 的内心)。
同时得到060PED ∠=.又0150APD DEC ∠=∠=所以有0150PEC ∠=.因此有D PEC CE ∆∆≌所以有 PC=CD.由PDC PD C P P AB ∆⇒=∆≌.所以PB=PC=BC.因此PBC ∆为等边三角形。
方法二:用三角法。
设正方形的边长为a 。
P在三角形PAD 中,用正弦定理有:00sin152sin15sin sin sin150AD PA a PA a APD ADP =⇒=⨯=∠∠ 在三角形BAD 中,依据余弦定理有:222202002cos (2sin15)22sin15cos 75AB PA AB PA BAP a a a a PB +-⋅∠=+-⨯=222022024sin 154sin 15a a a a =+-=所以PB a =这样得到PB PC BC a === 因此三角形PBC 为等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
演绎推理是根据已有的事实和正确的结论(包括定义、 公理、定理等),按照严格的逻辑法则得到新结论的推理 过程。 是一般到特殊的推理。 归纳推理是由特殊事理的成立来推出一般事理的成立。
证明通常包括逻辑证明和实验、实践证明。数学结论 的正确性必须通过逻辑证明来保证,是: A A 1
目录 上页 下页 返回 结束
例如:要证明 2 不是有理数,只要证明 2 是有理数 不真就可以了。
充足理由律是指在论证过程中,任何结论的得出,必 须有充分的理由,即不能凭借“直观”、“想当然”等 主观上的“臆想” 得出结公论式。是:A B. 它的涵义是:在一个论证中,要断定论题 B 真,必须满 足:第一,论据 A 真;第二,从论据 A 能推出论题 B 。 二、证明中的三种典型错误 1. 偷换论题 把命题的条件或结论中的某些涵义加以 扩大、缩小或改变,违反“同一律”。
A 1 [B¼EC B»D] 75, 2
命题的基本关系是指四种命题“原命题、逆命题、否 命题、逆否命题”之间的关系,其中原命题与逆否命题 等价,逆命题与否命题等价。
目录 上页 下页 返回 结束
一般情况下原命题与逆命题不等价,但有两种命题 除外。 即同一性命题和分断式命题 。 三、两种特殊命题 1. 同一性命题 命题的条件和结论所含事项都是唯一存在的命题。
目录 上页 下页 返回 结束
例1 设△ABC边BC的中垂线与 A 的平分线交于E点,
如图所示:
A
过E点分别向AB、AC作垂线EF、
EG,并连接EB、EC, 则由条件易得 △AEF≌△AEG , △BEF≌△CEG ,从而AB=AC,
F E
B
G C
即△ABC为等腰三角形。
上述过程是针对任意三角形,但结果却能得出 △ABC是等腰三角形,这是为什么?是什么地方存在问 题?
都把事物的可能性一一到尽,双方各自彼此互斥,那么
这样的命题 称为分断式命题。
例:设CM为△ABC的中线, 则
当C < 90 时, CM 1 AB ; 2
当C
=
90
时,
CM
1 2
AB ;
当C > 90 时,
CM 1 AB , 2
是分断式命题。
目录 上页 下页 返回 结束
分断式命题与它的逆命题是等价命题。
第七章
第七 章 平面几何问题与证明
§7.1几何逻辑 §7.2几何证题的推理方法 §7.3几何证题
目录 上页 下页 返回 结束
§7.1 几何逻辑 7.1.1 命题 一、命题 表达对某一事物的性质作出判断的词语。 命题有真假命题之分。符合客观实际的是真命题。 我们主要关注的是几何真命题。真命题称为定理。 包括:几何原始命题(公理或公设)和几何基本定理。 二、命题的基本关系
设一个分断式命题含有n个命题,其条件和结论各为 Ai 及 Bi (i 1,2,L ,n),并且 Ai Bi. 下证 Bi Ai. 证: 从这n个命题中,取出n-1个来, 不失一般性, 设为 Aj Bj ( j 2,L ,n). 由分断式命题的特性,这 n -1个命题联合起来实在无异议说 A1 B1, 由此得 B1 A1. 同理可得 Bk Ak (k 2,3,L ,n).
例如:两个数相等和不相等不能认为同时成立。 两条直线相交与不相交也不能认为同时成立。
注意:矛盾律只是指两个矛盾的判断不能同时为真,但 是两个矛盾的判断可能同假。例如“空间两直线必相交” 与“空间两直线必平行”。
排中律是指在论证过程中,一个判断与其互斥的判断 必有其一成立,即相互排斥的判断不能都不成立。 必有一真。
目录 上页 下页 返回 结束
2. 违反“充足理由律”:使用虚假或预期的理由。
例2 已知在ABCD中,AB>CD,BC>AD,
求证: D>B。
C
误证:
B
D
①连接A、C,并作AC的垂直
平分线l;
A
B/
②作ABC, 它与△ABC关于l对称;
③连接D、B′, 在四边形ADCB′中 ,因为 CDB CBD, ADB ABD,
目录 上页 下页 返回 结束
一、逻辑规律 同一律 矛盾律 排中律 充足理由律 同一律是指在同一个论证过程中,要求所涉及的任何要素 (概念,范围,性质等)保持同一性。 如在同一思维过程中,概念必须保持同一。 同一律的公式通常是:A=A。 违反这一要求的逻辑错误,称为“混淆概念”或“偷换概念 例如: 世间万物中,人是第一个可宝贵的。 我是人。因此,我是世间万物中第一个可宝贵的。
所以 CDB ADB CBD ABD, 所以 D B, 又 B B, 所以 D B. 上述过程错在哪里?
目录 上页 下页 返回 结束
循环论证:违反“充足理由律”,使用待证的结论。
例3 如图,设AD=2DC,C 45, ADB 60, 则AB为圆之切线。 误证:因为 C 45, 所以 B»D 90. 又ADB 60, 所以BDC 120,即 B¼EC 240.
所以 Bi Ai (i 1,2,L ,n).
目录 上页 下页 返回 结束
7.1.2 推理与证明 从已知的旧知识出发,通过实践、推想、验证,可
获得前所未有的新知识,这种推陈出新的思维过程, 叫做推理。
推理的过程一般为:三段论。
大前提(一般性) 三段论 小前提(特殊)
结论
推理一般包括:演绎推理和归纳推理。
在这个推理中,两个前提中的“人”不是同一概念。 第一个“人”是集合概念,第二个“人”是非集合概念, 因此,犯了“混淆概念”或“偷换概念”的错误。
目录 上页 下页 返回 结束
矛盾律是指在论证过程中,一个判断A与其相矛盾 的判断B不能同时成立,即相互矛盾的判断至多有一个 成立。其中至少有一个是假的。 矛盾律的公式通常是: A B 0
例:中国是世界上人口最多的国家。 世界上人口最多的国家是中国。
例:等腰三角形底边上的高是顶角的平分线。 (真命题) 对象“高”是唯一的,对象“平分线”也是唯一的。 逆命题:等腰三角形顶角的平分线也是底边上的高。
(也是真命题)
目录 上页 下页 返回 结束
2. 分断式命题
在一个命题中,若假设与结论有相同的款数,并且双方
