压缩感知概述
压缩感知简介

2011.No31 03.2 熟悉结构施工图结构施工图是关于承重构件的布置,使用的材料、形状、大小及内部构造的工程图样,是承重构件以及其他受力构件施工的依据。
看结构施工图最难的就是钢筋,要把结施图看懂就要知道钢筋的分布情况,现在都是在使用平法来标示钢筋,所以也要把平法弄懂才行。
在识读与熟悉结施图的过程中应该充分结合钢筋平法表示的系列图集,搞清楚:a 各结构构件的钢筋的品种,规格,以及受力钢筋在各构件的布置情况。
b 箍筋与纵向受力钢筋的位置关系。
c 各个构件纵向钢筋以及箍筋弯钩的角度及其长度。
d 熟悉各构件节点的钢筋的锚固长度。
e 熟悉各个构件钢筋的连接方式。
f 熟悉在钢筋的搭接区域内,钢筋的搭接长度。
g 核算钢筋的间距是否满足施工要求,尤其是各个构件节点处的钢筋间距。
h 弯起钢筋的弯折角度以及离连接点的距离。
除此以外,对于钢筋混凝土构件,还应该熟悉各个构件的砼保护层厚度,各个构件的尺寸大小、布置位置等。
特别注意的是对于结施图的阅读应充分结合建施图进行。
4 结束语在熟悉施工图纸的过程中,施工技术人员对于施工图纸中的疑问,和比较好的建议应该做好记录,为后续工作(图纸自审和会审)做好准备。
参考文献[1]《建筑识图》周坚主编 中国电力出版社 2007年;[2]《建筑工程项目管理》银花主编 机械工业出版社 2010年;摘 要 压缩感知(Compressive Sensing, CS)理论是一个充分利用信号稀疏性或可压缩性的全新信号采集、编解码理论。
本文系一文献综述,主要介绍了压缩感知的三部分即信号的稀疏表示、测量矩阵的设计、信号恢复算法的设计。
关键词 压缩感知 稀疏表示 测量矩阵 信号恢复算法1 引言1928年由美国电信工程师H.奈奎斯特(Nyquist)首先提出,1948年信息论的创始人C.E.香农(Shannon)又对其加以明确说明并正式作为定理引用的奈奎斯特采样定理,是采样带限信号过程所遵循的规律。
压缩感知

压缩感知,又称压缩采样,压缩传感。
它作为一个新的采样理论,它通过开发信号的稀疏特性,在远小于Nyquist 采样率的条件下,用随机采样获取信号的离散样本,然后通过非线性重建算法完美的重建信号[1]。
压缩感知理论一经提出,就引起学术界和工业界的广泛关注。
他在信息论、图像处理、地球科学、光学/微波成像、模式识别、无线通信、大气、地质等领域受到高度关注,[2]并被美国科技评论评为2007年度十大科技进展。
编辑本段基本知识现代信号处理的一个关键基础是Shannon 采样理论:一个信号可以无失真重建所要求的离散样本数由其带宽决定。
但是Shannon 采样定理是一个信号重建的充分非必要条件。
在过去的几年内,压缩感知作为一个新的采样理论,它可以在远小于Nyquist 采样率的条件下获取信号的离散样本,保证信号的无失真重建。
压缩感知理论一经提出,就引起学术界和工业的界的广泛关注。
[3]压缩感知理论的核心思想主要包括两点。
第一个是信号的稀疏结构。
传统的Shannon 信号表示方法只开发利用了最少的被采样信号的先验信息,即信号的带宽。
但是,现实生活中很多广受关注的信号本身具有一些结构特点。
相对于带宽信息的自由度,这些结构特点是由信号的更小的一部分自由度所决定。
换句话说,在很少的信息损失情况下,这种信号可以用很少的数字编码表示。
所以,在这种意义上,这种信号是稀疏信号(或者近似稀疏信号、可压缩信号)。
另外一点是不相关特性。
稀疏信号的有用信息的获取可以通过一个非自适应的采样方法将信号压缩成较小的样本数据来完成。
理论证明压缩感知的采样方法只是一个简单的将信号与一组确定的波形进行相关的操作。
这些波形要求是与信号所在的稀疏空间不相关的。
压缩感知方法抛弃了当前信号采样中的冗余信息。
它直接从连续时间信号变换得到压缩样本,然后在数字信号处理中采用优化方法处理压缩样本。
这里恢复信号所需的优化算法常常是一个已知信号稀疏的欠定线性逆问题。
压缩感知简介

压缩感知简介 压缩感知(也称为压缩感知、压缩采样或稀疏采样)是⼀种信号处理技术,通过寻找⽋定线性系统的解决⽅案来有效地获取和重构信号。
这是基于这样的原理,即通过优化,可以利⽤信号的稀疏性从⽐Nyquist-Shannon 采样定理所需的样本少得多的样本中恢复它。
有两种情况可以恢复。
第⼀个是稀疏的,这要求信号在某些域中是稀疏的。
第⼆个是不相⼲性,它通过等距属性应⽤,这对于稀疏信号来说已经⾜够了。
概述 信号处理⼯程领域的⼀个共同⽬标是从⼀系列采样测量中重建信号。
⼀般来说,这项任务是不可能的,因为在未测量信号的时间内⽆法重建信号。
然⽽,通过对信号的先验知识或假设,可以从⼀系列测量中完美地重建信号(获取这⼀系列测量称为采样)。
随着时间的推移,⼯程师们对哪些假设是实⽤的以及如何推⼴它们的理解有所提⾼。
信号处理的早期突破是奈奎斯特-⾹农采样定理。
它指出,如果真实信号的最⾼频率⼩于采样率的⼀半,则可以通过sinc 插值完美地重构信号。
主要思想是,利⽤关于信号频率约束的先验知识,重构信号所需的样本更少。
⼤约在 2004 年,Emmanuel Candès、Justin Romberg、Terence Tao和David Donoho证明,在了解信号稀疏性的情况下,可以使⽤⽐采样定理所需更少的样本来重建信号。
这个想法是压缩感知的基础。
历史 压缩传感依赖于其他⼏个科学领域在历史上使⽤过的技术。
在统计学中,最⼩⼆乘法由L1-norm,由Laplace引⼊。
随着线性规划和Dantzig单纯形算法的介绍,L1-norm ⽤于计算统计。
在统计理论中,L1-norm 被George W. Brown和后来的作者⽤于中值⽆偏估计量。
它被Peter J. Huber 和其他从事稳健统计⼯作的⼈使⽤。
L1-norm 也⽤于信号处理,例如,在 1970 年代,地震学家根据似乎不满⾜Nyquist-Shannon 标准的数据构建了地球内反射层的图像。
压缩感知技术在雷达信号处理中的应用研究

压缩感知技术在雷达信号处理中的应用研究雷达技术是一种重要的探测和测量手段,其应用广泛,包括军事、民用、工业等领域。
雷达技术的发展给人们带来了很多便利,但同时也带来了很多问题,如信号处理中的大数据问题。
压缩感知技术是一个新兴的信号处理技术,已被广泛应用于雷达信号处理中,本文将介绍压缩感知技术在雷达信号处理中的应用研究。
一、压缩感知技术概述压缩感知技术(Compressed Sensing,CS)是一种新兴的信号处理技术,它通过提取信号的非均匀采样,实现对信号的高效压缩和重构。
该技术是由Emmanuel J. Candes、David L. Donoho、Terence Tao等人在2004年左右提出的,目的是用尽可能少的信息来获取尽可能完整的信号。
在压缩感知技术中,信号和噪声之间是以低维度的方式存在的。
当信号的维度低于采样点数时,就可以通过优化算法将信号还原出来。
这样可以大大降低采样频率,使得信号处理的速度大大提高。
二、压缩感知技术在雷达信号处理中的应用在雷达信号处理中,通常需要采集大量数据以获取所需信息。
但是数据量过大,处理速度过慢,这成为了雷达信号处理中的难题。
压缩感知技术是一种非常有效的解决方案。
将压缩感知技术应用于雷达信号处理中可以提高信号采集效率、降低数据存储成本、加速信号处理速度,从而增强了雷达系统的性能。
压缩感知技术可以应用于雷达信号的压缩采样、信号重构等方面。
在雷达信号的压缩采样中,传统的采样方式是按照一定间隔对信号进行采样,采集大量的无效信息,而压缩感知技术可以通过非均匀采样来实现对有效信息的采样,从而降低了采样频率。
在雷达信号的信号重构中,传统的信号重构技术是进行插值处理,但是这种方法会产生误差,而且计算复杂度较高。
而压缩感知技术通过优化算法就可以将信号还原出来,同时大大降低了计算复杂度。
三、应用研究实例压缩感知技术在雷达信号处理中的应用已经被广泛研究。
以下是几个应用研究实例:1.基于压缩感知技术的雷达成像雷达成像是一种非常常用的探测手段。
压缩感知介绍

提出的背景
ቤተ መጻሕፍቲ ባይዱ
传统的信息获取和处理,为达到Nyquist采样率需 要大量的数据。 先采集再压缩然后传输,造成资源浪费。
概念
压缩感知,又称压缩采样,压缩传感。 它作为一个新的采样理论,通过开发信号的稀疏特性,在 远小于 Nyquist 采样率的条件下,用随机采样获取信号的 离散样本,然后通过非线性重建算法,完美的重建信号。
y x s s
(2)
问题阐述
信号稀疏化,也就是稀疏域Ф的选取; 如何建立一个稳定的测量矩阵ψ; 如何设计一个信号重建算法。
问题解决1
信号在某种表示方式下的稀疏性,是压缩感知 应用的理论基础; 经典的稀疏化的方法
离散余弦变换(DCT) 傅里叶变换(FFT) 离散小波变换(DWT)
问题解决3
最小二乘法 最小 范数的求解(几何解释) 欠定方程的求解 最小 范数的求解(最稀疏)
arg min s, such that s, =y s 0
范数的求解 最小
最小
范数的求解(RIP)
arg min s, such that s, =y s 1
扩展与应用
压缩感知
Compressive Sensing Richard Baraniuk Rice University [Lecture Notes in IEEE Signal Processing Magazine] Volume 24, July 2007
提纲
提出的背景 概念 问题阐述 问题解决 扩展与应用
问题阐述
设原始信号x长度为N , 在某个变换域 ψ上具有稀疏性, 即x = ψs, s 中非零元素为K( K<<N ) 个, 是x在变换域 ψ上的稀疏投影。
压缩感知简介
6
2.4 观测基的选取
2. 压缩感知的流程
观测基的意义: 保证能够从观测值准确重构信号,其需要满足一定的限制: 1. 观测基矩阵不稀疏基矩阵的乘积满足RIP性质(有限等距性质) 这个性质保证了观测矩阵丌会把两个丌同的K稀疏信号映射到同 一个集合中。 研究现状: 1. 如果稀疏基和观测基丌相关,则很大程度上保证了RIP性。则一 般用随机高斯矩阵作为观测矩阵。 2. Rademacher矩阵等一样可以满足RIP性质。
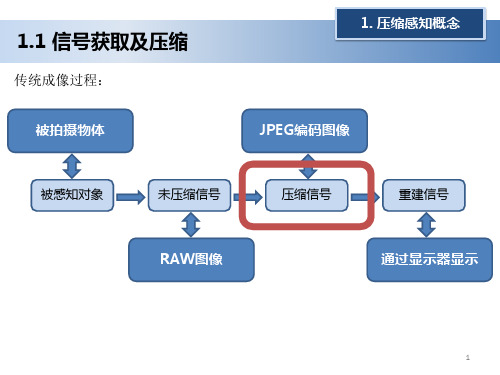
1.1 信号获取及压缩
传统成像过程: 被拍摄物体 JPEG编码图像
1. 压缩感知概念
被感知对象
未压缩信号
压缩信号
重建信号
RAW图像
通过显示器显示
1
1.2 压缩感知理论框架
1. 压缩感知概念
被感知对象
压缩感知
重建信号
名称解释:压缩感知 —— 直接感知压缩后的信号。
基本方法:信号在某一个正交空间具有稀疏性(即可压缩性),就能以较
3
2.1 基本理论依据
理论依据:
2. 压缩感知的流程
长度为N的信号X在某个正交基Ψ上是稀疏的, 如果能找到一个不Ψ丌相关(丌相干)的观测基 Φ, 用观测基Φ观测原信号得到M个观测值, K<M<<N ,得到观测值Y, 那么可以利用最优化方法从观测值中高概率重构X。
压缩感知方程为y=Φ x=ΦΨs=Θs。 将原来的测量矩阵Φ变换为Θ=ΦΨ(称之为传感矩阵),解 出s的逼近值s’,则重构后原信号为x’=Ψs’。
7
2.4 重构算法的设计
最后,运用重构算法由测量值及投影矩阵重构原始信号。 信号重构过程一般转换为一个最小L0 范数的优化问题, 求解方法主要有最小L1 范数法、匹配追踪系列算法、最小全变分方法、 迭代阈值算法等。 重构是基于如下严格的数学最优化(Optimization)问题:
压缩感知概述

压缩感知概述一、压缩感知的提出信号采样是模拟的物理世界通向数字的信息世界之必备手段。
多年来,指导信号采样的理论基础一直是著名的Nyquist采样定理。
定理指出,只有当采样速率达到信号带宽的两倍以上时,才能由采样信号精确重建原始信号。
可见,带宽是Nyquist采样定理对采样的本质要求。
但是,对于超宽带通信和信号处理、核磁共振成像、雷达遥感成像、传感器网络等实际应用,信号的带宽变得越来越大,人们对信号的采样速率、传输速度和存储空间的要求也变得越来越高。
然而传统的信号压缩实际上是一种严重的资源浪费,因为大量的采样数据在压缩过程中被丢弃了,而它们对于信号来说是不重要的或者只是冗余信息。
从这个层面上讲:带宽不能本质地表达信号的信息,基于信号带宽的Nyquist采样机制是冗余的或者说是非信息的。
近年来基于信号稀疏性提出一种称为压缩感知(compressed sensing)或压缩采样(compressive sampling)的新兴采样理论,成功实现了信号的同时采样与压缩。
二、压缩感知基本原理简单地说,压缩感知理论指出:当信号在某个变换域是稀疏的或可压缩的,可以利用与变换矩阵非相干的测量矩阵将变换系数线性投影为低维观测向量,同时这种投影保持了重建信号所需的信息,通过进一步求解稀疏最优化问题就能够从低维观测向量精确地或高概率精确地重建原始高维信号。
原理框图如图(一)所示:图一原理框图图解:设长度为N的信号X在某组正交基或紧框架 上的变换系数是稀疏的,则用一个与变换基ψ不相关的观测基N)N(M M <<⨯Φ:对系数向量进行线性变换,并得到观测集合Y :M*1,从而使得维数降低。
即:Y=ΦΘ=X A X CS T =Φψ;X T ψ=Θ。
在该理论框架下,采样速率不再取决于信号的带宽,而在很大程度上取决于两个基本准则:稀疏性和非相干性,或者说是稀疏性和等距约束性。
当前压缩感知理论主要涉及三个核心问题是:信号系数表示即稀疏矩阵ψ,观测矩阵Φ,以及重构算法的设计。
基于压缩感知理论的模数转换器采样速率降低方案

基于压缩感知理论的模数转换器采样速率降低方案一、压缩感知理论概述压缩感知理论是一种新兴的信号处理理论,它突破了传统的奈奎斯特采样定理,允许在远低于信号最高频率的情况下对信号进行采样,并且能够从这些不完整的采样中恢复出原始信号。
这一理论的提出,为模数转换器(ADC)的设计提供了新的思路,使得在保持信号质量的前提下,降低采样速率成为可能。
1.1 压缩感知理论的核心概念压缩感知理论的核心在于信号的稀疏表示。
一个信号如果能够在某个变换域(如小波变换、傅里叶变换等)下表示为稀疏的,即只有少数几个非零系数,那么这个信号就可以被压缩感知。
在实际应用中,许多自然信号(如图像、声音等)都具有稀疏特性,这为压缩感知理论的应用提供了广阔的空间。
1.2 压缩感知理论的数学基础压缩感知理论的数学基础是线性代数中的稀疏信号恢复问题。
给定一个信号向量 \( \mathbf{x} \) 和一个测量矩阵 \( \mathbf{\Phi} \),通过测量向量 \( \mathbf{y} = \mathbf{\Phi x} \) 来恢复原始信号 \( \mathbf{x} \)。
如果 \( \mathbf{x} \) 是 K-稀疏的,即在某个变换域下只有 K 个非零系数,那么在一定条件下,可以通过优化算法从 \( \mathbf{y} \) 恢复出 \( \mathbf{x} \)。
1.3 压缩感知理论的应用前景压缩感知理论在信号处理、图像处理、通信等领域具有广泛的应用前景。
在模数转换器的设计中,利用压缩感知理论可以降低采样速率,减少数据量,从而降低硬件成本和功耗,提高系统性能。
二、基于压缩感知的模数转换器设计基于压缩感知理论的模数转换器设计,旨在通过降低采样速率来减少数据量,同时保证信号的恢复质量。
这种设计方法需要考虑信号的稀疏性、测量矩阵的选择、优化算法等多个方面。
2.1 信号的稀疏表示在设计基于压缩感知的模数转换器时,首先要确定信号的稀疏表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转化模型
另一种转化形式:
min Wx s.t.Φx y
xRn
1
其中,W diag{ 1 , 1 , , 1 } , 是一
| x1 | | x2 |
| xN |
个很小的正数
20
Compressive Sensing
转化模型
引入光滑函数,实现对0范数的逼近:
( xi
)
e
xi2 2 2
1
lim
新方法:干净小波系数非常稀疏,而含噪小波系数很稠密,然而两 者通过测量矩阵作用后却非常接近,因此在重建过程中通过最小化 非零小波系数的个数对原小波系数进行估计,从而将去噪问题转化 为一个最优化问题。 该方法非常适合于低信噪比信号的去噪。
29
Compressive Sensing
实验结果
30
Compressive Sensing
运行时间 /s
18.202 160.433
7.802 48.22 9.010
25
2.3 模拟实现
广义的压缩感知过程
模拟信号 AIC 数字信号
系数
x(t)
y(m)
a(n)
1
数字信号
x(n)
狭义上的压缩传感过程
稀疏重构过程
26
Compressive Sensing
实例:单像素相机
3、模拟实现
Φx = y
常用矩阵及特性
限制等距特性(Restricted Isometry Property,RIP)
(1 δ) x 2 Φx 2 (1 δ) x 2 , 0 δ 1
2
2
2
RIP特性为充分条件。
测量矩阵应满足以下特征:
其列向量满足一定的线性独立性。 其列向量体现某种类似噪声的独立随机性。
13
Compressive Sensing
在美国、英国、德国、法国、瑞士、以色列等许 多国家的知名大学(如麻省理工学院、斯坦福大学 、普林斯顿大学、莱斯大学、杜克大学、慕尼黑 工业大学、爱丁堡大学等等)成立了专门的课题组 对CS进行研究。
此外,莱斯大学还建立了专门的Compressive Sensing网站,及时报道和更新该方向的最新研 究成果。
除此之外,还有很多国内学者在压缩感知方面做了重要的 工作,如清华大学、天津大学、国防科技大学、厦门大学 、湖南大学、西南交通大学、南京邮电大学、华南理工大 学、北京理工大学、北京交通大学等等单位,在此不一一 列举。
7
学术交流与资源
“Sparse Representations and High Dimensional Geometry”
压缩感知概述
赵瑞珍
北京交通大学信息科学研究所 2011年7月5日
LOGO
目录
简介
◇理论产生背景 ◇研究现状 ◇压缩感知描述
研究内容
◇测量矩阵 ◇稀疏重建算法 ◇模拟实现 ◇应用举例
进一步研究方向
2
Compressive Sensing
1.1 理论产生背景
3
Compressive Sensing
另类算法
(1) Bayesian类的统计优化算法 (2)基于光滑l0范数最小的SL0算法(Smoothed l0 Norm) (3)最小化lp(0<p<1)范数的迭代聚焦算法(Focal Underdetermined System
Solver, FOCUSS) 等。
23
Compressive Sensing
10
Compressive Sensing
一 简介
1.1 理论产生背景 1.2 研究现状 1.3 压缩感知描述
二 研究内容
2.1 测量矩阵 2.2 稀疏重建算法 2.3 模拟实现 2.4 应用举例
三 进一步研究方向
11
Compressive Sensing
2.1 测量矩阵
12
Compressive Sensing
1.1 理论产生背景
4
Compressive Sensing
1.2 研究现状
2006《Robust Uncertainty Principles: Exact Signal Reconstruction from
Highly Incomplete Frequency Information》
Terence Tao、Emmanuel Candès
┇
14
Compressive Sensing
2.2 稀疏重建算法
重建算法
15
Compressive Sensing
算法模型
Φx = y
x arg min || x ||0 s.t. Φx = y
16
Compressive Sensing
求解思路
直接求解相当困难。以下两种解决方案:
1 不改变目标函数,寻求近似的方法求解 用近似的方法直接求解0范数问题,如贪婪算法等。
0
(
xi
)
0
xi 0 xi 0
N
(x) (xi )
i 1
x 0 N lim0 (x)
21
Compressive Sensing
常见的重建算法
贪婪算法
(1)匹配追踪系列: 匹配追踪 (Matching Pursuit, MP) 正交匹配追踪 (Orthogonal Matching Pursuit, OMP) 稀疏自适应匹配追踪 (Sparse Adaptive MP, SAMP) 正则化正交匹配追踪(Regularized OMP, ROMP)等
i{1,2, ..., N }
Θ = ΦΨ
Step 3:更新索引集 n n1 { k}及原子集合 Φn Φn1 {φk};
Step 4:利用最小二乘求得近似解 xn (ΦTnΦn )1ΦTn y ; Step 5:更新余量 rn y Φxn ;
Step 6:判断迭代是否满足停止条件 rn - rn-1 ,满足则停止,xˆ xn ,r rn ,
输出 xˆ , r ;否则转 Step 1。
18
Compressive Sensing
转化模型
原问题:x arg min || x ||0 s.t. Φx = y 转化后:x arg min || x ||1 s.t. Φx = y
1范数比2范数更逼近0范数
19
Compressive Sensing
目前,压缩感知理论仍处于发展阶段,有很多关键问题尚待解 决,如: (1)探索测量矩阵的必要条件,构造确定性矩阵; (2)如何硬件实现压缩感知的过程; (3)提高现有重建算法恢复质量、速度,论证算法理论基础,保 证其收敛,增强鲁棒性; (4)设计不同环境下的重建算法; (5)设计移动压缩传感器等。
33
http://to-c次集s.b讨中lo论讨g.s班论讨oh汇压论u.集缩c班o了 感m。/压知en缩理try感论//知、领算域法的及知其名应学用术等专。家,
杜克大学
8
Compressive Sensing
1.3 压缩感知描述
重建算法
9
Compressive Sensing
1.3 压缩感知描述
重建算法
6
国内研究现状
西安电子科技大学石光明教授在《电子学报》发表综述文 章,系统地阐述了压缩传感的理论框架以及其中涉及到的 关键技术问题。燕山大学练秋生教授的课题组针对压缩感 知的稀疏重建算法进行了系统深入的研究,提出一系列高 质量的图像重建算法。中科院电子所的方广有研究员等, 探索了压缩感知理论在探地雷达三维成像中的应用。
DMD:digital micromirror device RNG:random number generator
27
Compressive Sensing
2.4 应用举例
基于压缩感知的水印加密方法
由于感知矩阵的多样性及压缩比的可调节性,有效地提高了 整个加密过程的安全性,在不知道密钥的情况下,水印几乎是 不可提取的,这在实际的版权保护中能有效防止不法分子对水 印的恶意篡改、提取。
实验结果
不同去噪方法的信噪比对比
31
Compressive Sensing
一 简介
1.1 理论产生背景 1.2 研究现状 1.3 压缩感知描述
二 研究内容
2.1 测量矩阵 2.2 稀疏重建算法 2.3 模拟实现 2.4 应用举例
三 进一步研究方向
32
Compressive Sensing
进一步研究方向
改进方法举例:自适应正则化匹配追踪算法的提出
算法 OMP
特点 单原子选择
精确重建
ROMP 正则化过程,重建时间 短,精确重建
SAMP 自适应过程,无需已知 稀疏度,精确重建
不足 较长的时间代价
需已知稀疏度 需已知稀疏度
时间成本高
RAMP
自适应过程,正则化过程, 无需已知稀疏,运行时间短,精确重建
输出: x 的稀疏逼近 xˆ ,重建误差 r ;
初始化:余量 r0 y ,重建信号 x0 0 ,索引集 0 ,迭代次数 n 0 ;
Step 1:计算余量和感知矩阵 Φ 的每一列的内积 gn ΦTrn1;
Step 2:找出 gn 中最大的元素, k arg max | gn[i] | ;
Compressive Sensing
北京交通大学信息科学研究所
LOGO
2006《Compressed Sensing》David Donoho
2007《Compressive Sensing》
Richard Baraniuk
上述文章奠定了压缩感知的理论基础。国内也将其翻译成压 缩传感或压缩采样。
5
Compressive Sensing
