人在雨中奔跑的速度与淋雨量的关系
数学模型--人在雨中奔跑速度及淋雨量的关系4

《数学模型与数学实验》课程设计任务书摘要本文在给定的降雨条件下,分别建立相应的数学模型,分析人体在雨中行走时淋雨多少与行走速度、降雨方向等因素的关系。
其中文中所涉及到的降雨量是指从天空降落到地面上的雨水,未经蒸发、渗透、流失而在水面上积聚的水层深度,它可以直观地表示降雨的多少。
淋雨量,是指人在雨中行走时全身所接收到得雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积。
针对问题一,设降雨淋遍全身不考虑雨的方向,经简化假设得人淋雨面积为前后左右及头顶面积之和。
针对问题二,雨迎面吹来,雨线方向与行走方向在同一平面,人淋雨面积为前方和头顶面积之和。
因各个方向上降雨速度分量不同,故分别计算头顶和前方的淋雨量后相加即为总的淋雨量。
据此可列出总淋雨量W与行走速度v之间的函数关系。
分析表明v时,淋雨量最少。
当行走速度为max针对问题三,雨从背面吹来,雨线与行走方向在同一平面内,人淋雨量与人和雨相对速度有关。
列出函数关系式分析并求解。
关键词淋雨量;降雨的大小;降雨的方向(风);路程的远近;行走的速度;雨滴下落的速度,角度;降雨强度;一、问题重述生活中的我们常常会遇到下雨而没带雨具的时刻,我们在那时会有很多选择,其中之一就是淋雨,往往好多人会在雨中快走或奔跑而使自己身体淋雨量最小化,但往往很多人会感觉到淋雨量并不会因为快走或奔跑而减少多少,反而有时候淋雨量倒有所增加,淋雨量和速度等有关参数的关系如何,是否人走得越快雨淋得越少,让我们假设一数学模型模拟计算真实情况。
当我们在雨中从一处沿直线跑到另一处时,如果雨速为常数,走的时候身体的动作的大小和暴露在雨中的面积大小影响着淋雨的多少,并且行走速度也同样影响着淋雨量Q,将人体简化成一个长方体,高a=1.5米,宽b=0.5米,厚c=0.2m,行走距离D,雨速u,降雨量I,行走速度为ν。
1、当我们不考虑风,即雨滴垂直下落时,淋雨量和人行走速度之间的关系?2、当雨滴从前方(斜的)下落时,即雨滴与人体的夹角为θ,建立总淋雨量与速度v及其它参数之间的关系,此时速度与淋雨量的关系?3、当雨从人的背面吹来,即雨滴与人体的夹角为θ,建立总淋雨量与速度v之间的关系?二、模型的假设与符号说明2.1 基本假设1、假设人行走的路线是直线;2、不考虑风的方向(即假定前后左右都淋雨),这是一种较为理想的假设,主要为了建模的方便,并且假设雨滴的速度为常数;3、为计算淋雨面积的方便,把人体表面积看成长方体,长用a表示,宽用b表示,厚度用c 表示,且abc都是定值。
雨中跑步数学模型(蒋伟)

雨中跑步的数学模型摘要:本模型建立了在雨中奔跑时淋雨最少与奔跑速度,雨量,降雨方向,路程远近的关系,从而得出在雨中如何奔跑才会淋雨最少的方法。
关键词:淋雨量,降雨的大小,降雨的方向,路程的远近,奔跑的速度问题重述:要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少。
模型假设及符号说明1)把人体视为长方体,身高h 米,宽度w 米,厚度d 米。
淋雨总量用C 升来记。
2)降雨大小用降雨强度I 厘米/时来描述,降雨强度指单位时间平面上的降下水的厚度。
在这里可视其为一常量。
3)降雨方向保持不变。
4)你以一定常的速度v 米/秒跑完全程D 米。
模型建立与计算1)不考虑雨的方向,此时,你的前后左右和上方都将淋雨。
淋雨的面积 )( 222米wd dh wh S ++=雨中行走的时间 )(秒vD t = 降雨强度 )/()3600/01.0()/(01.0)/(s m I I I ==时米时厘米(升)米S I v D S I t C ⨯⨯=⨯⨯⨯=3600/)/(10)(01.0)3600/(3 模型中为变量。
为参数,而v S I D ,, 结论:淋雨量与速度成反比。
这也验证了尽可能快跑能减少淋雨量。
米即米米米小时厘米米若取参数22.2,20.0,50.0,50.1,/2,1000======S d w h I D 秒。
分秒,即你在雨中行走了每秒,则计算得米度你在雨中行走的最大速472167/6=v从而可以计算被淋的雨水的总量为2.041(升)。
经仔细分析,可知你在雨中只跑了2分47 秒,但被淋了2 升的雨水。
这是不可思议的。
表明:用此模型描述雨中行走的淋雨量不符合实际。
原因:不考虑降雨的方向的假设, 使问题过于简化。
2)考虑降雨方向。
若记雨滴下落速度为r (米/秒)雨滴的密度为1 ,≤p p表示在一定的时刻在单位体积的空间内,由雨滴所占的空间的比例数,也称为降雨强度系数。
下雨天跑得快和跑得慢淋的雨物理题
下雨天跑得快和跑得慢淋的雨物理题
这个问题不但是一道物理问题,还是一道经典的数学建模问题,可以通过建立数学模型来对此进行求解。
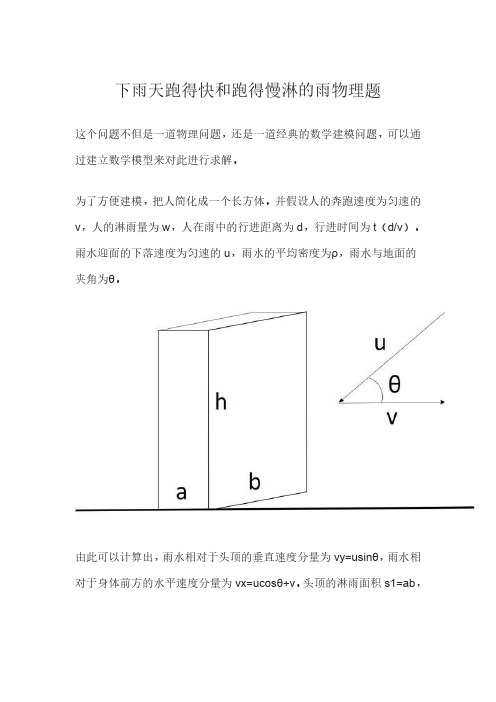
为了方便建模,把人简化成一个长方体。
并假设人的奔跑速度为匀速的v,人的淋雨量为w,人在雨中的行进距离为d,行进时间为t(d/v)。
雨水迎面的下落速度为匀速的u,雨水的平均密度为ρ,雨水与地面的夹角为θ。
由此可以计算出,雨水相对于头顶的垂直速度分量为vy=usinθ,雨水相对于身体前方的水平速度分量为vx=ucosθ+v。
头顶的淋雨面积s1=ab,
身体的淋雨面积s2=bh。
因此,人的总淋雨量就是头顶淋雨量和身体前方淋雨量之和。
头顶的淋雨量为:
身体前方的淋雨量为:
总的淋雨量为:
显然,w/v<0,这意味着随着速度v的增加,淋雨量w在逐渐减小。
并且如果人的身体与雨水平行,理论上只有头部会受到淋雨。
因此,在最为理想的情况下,对于没有带伞的人来说,在雨中奔跑的速度越快,并且身体的倾斜方向刚好跟雨水平行,那么,这个人所淋到的雨水是最少的。
为了便于计算,模型做了很多简化,最终得出的结论也是符合实际的。
关于在雨中是应该跑的慢还是跑的快,可以考虑两种极端的情况。
一种是在雨中以接近于零的速度运动,还有一种是在雨中以接近光速的速度运动。
显然,运动相同的距离,在雨中运动的时间越短,所淋到的雨水也会越少。
淋雨量与速度之间的关系

淋雨量与速度之间的关系的分析
下雨时,是慢点走还是快点走淋雨少?生活中,人们经常就这个问题进行讨论。
下面,我将对这个问题进行定量分析。
对于一个实际问题进行分析,首先应建立一个模型。
由质量m=ρV知,要求质量,必须先知道密度ρ。
在此就需引入雨水密度ρ,但要注意此密度并不是水的密度,而是把雨滴在空间中平均分布之后的密度。
有了密度之后,再必须知道体积。
在流体中,V=υtS.现在就可以求淋雨量了,这里的淋雨量其实就是质量。
设想有一个很小的面积元,在很短的时间内,则有
dQ=δρV dtd S ①
对其进行积分,就得到
Q=∫∫δρV dtd S ②
上面这个就是淋雨量的计算式子。
对于有些问题可以对此式进行简化求出。
下面就来具体解决下雨时,是慢点走还是快点走淋雨少这个问题。
先把问题进行简化,即令相对速度不随时间而变化,得到下面的式子
Q=∫δρV td S ③
有了上面的式子后,还可以进一步简化,设人的表面积为一竖着地面上的有限平面,得
Q=δρV t S ④
然后设雨的速度为V1,与水平面的夹角为θ,人的速度为V2,对上面的式子进行化简
V=V1-V2 ⑤
VS=-V1Ssinθ-V2S ⑥
将⑥代入④得
Q=-δρLS(V1/V2sinθ+1) ⑦
⑦就是下雨时,人的淋雨量计算式。
通过此式,可知速度越大淋雨越少。
当速度为零时,淋雨量为无穷。
这个好理解,当一直站在雨中时,只要雨一直下,人能够无限活下去,淋雨量自然为无穷。
但无论速度如何大,总会淋雨。
这个可以用一句话来说明“人在水中穿,怎能不湿衣”。
论雨中行走于跑步淋雨量不同的研究

论在雨中行走与跑步哪个方式淋雨更少的研究青岛滨海学院文理基础学院12文科4班刘维(20120500425)刘帅(20120500424)摘要:其实不论人在雨中是行走还是跑步,其实相当于在雨中这个坐标系中的一个斜面横扫面积的问题。
关键词:雨中;跑步;行走;淋雨总量1.问题的实际背景数学融于我们生活当中,我们在面对很多事情都会联想到,这个问题与数学有什么关系,例如下雨中,这个淋雨量与数学之间有联系吗?让我们来讨论下吧身边的数学吧。
2.问题的提出下雨仿佛是件很平常的事,但是很少有人会往这个方面想,但这是一个思维的好奇提问,于是,在雨中,我们是跑步淋雨多还是行走淋雨多的一个问题就被这样提出来了。
2.1数据分析要想要讨论在雨中我们的林雨量,就要认识到这里的常量与变量,先说下常量:如果把人比作一个长方体的容器(上下左右都可以承装的理想容器),那么有常量1、身高h2、身体厚度d3、身体宽度k4、可以得到一个恒常量C h d k=⨯⨯5、一个扫过雨的面积S h k=⨯6、其中常量分别还有人的行走速度11/v m s =7、跑步速度为25/v m s=7、雨的下落速度为重力常量g,这里省略理解为在地面速度约为V8、其中路程假设为l9、到达目的地的时间t ls=从这几个常量中我们可以看到,其实不论人在雨中是行走还是跑步,其实相当于在雨中这个坐标系中的一个斜面横扫面积的问题。
(注:这里由于能力问题,暂时假定风速为0,对任何量无影响,假定人体倾斜角刚好只有头部受到雨水的横扫面积,另对行走的肢体变化忽略,暂不记跑步时身体前与雨水相交的量,忽略雨的密度p 等相关变量)2.2问题重述当行走速度为11/v m s =时,当跑步速度为时25/v m s =,人所受到的淋雨量V 为多少?3.问题的求解3.1构建数学模型如果以下雨场景建立三维直角坐标系(),,x y z O =由xy 面可得水平淋雨面积行走时111S h k v t hkl =⨯⨯⨯=跑步时222S h k v t hkl =⨯⨯⨯=由xz 面可得垂直淋雨行走时面积31S V t Vl =⨯=跑步时面积4215S V t Vl =⨯= 由此可得,行走时淋雨量2113V S S Vhkl =⨯=跑步时淋雨量222415V S S Vhkl =⨯= 由此可得,淋雨量12V V <,跑步时淋雨量小.4.结论:由上述可知,在雨中跑步时,淋雨量较小。
淋雨量与人在雨中奔跑速度的关系

论文题目:淋雨量与人在雨中奔跑速度的关系目录一.摘要 ................................................................................二.问题的重述....................................................................三.问题分析 .........................................................................四.建模假设 .........................................................................五.模型的建立......................................................................六.模型的评价......................................................................七.参考文献 .........................................................................一.摘要本模型是研究人的淋雨量与人在雨中奔跑的速度的关系。
由于人在雨中行走的过程比较复杂,我们只能将人体简化为一个长方体建立模型,进行讨论。
本题中采用了优化模型,通过将人分为几个平面,分别求得各个平面所接受的淋雨量,然后求其加和的方法求解。
在问题一中,因为已经假设降雨淋遍全身,且人以最大的速度跑步。
所以根据已知条件,直接列出方程进行求解。
在问题二中,我们利用最优化原理,建立出一个动态规划模型。
雨迎面吹来,雨线方向与跑步方向在同一平面,人淋雨面积为前方和头顶面积之和。
ej淋雨量模型

雨中行走模型摘要:在实际的日常生活中,人在雨中移动,根据不同的雨速及风向等因素求出相应的移动速度,用数学分析的方法建立数学模型,使人在一定的移动距离下淋雨量最小。
关键词:人速雨速风向面积体积淋雨量1 问题的复述在雨中沿直线从一处跑到另一处,雨速为常数且方向不变,讨论人跑的速度与淋雨量的关系。
将人体简化成一个长方体,高a=1.5m(颈部以下),宽b=0.5m,厚,雨速u=4m/s,降雨量c=0.2m。
设跑步距离d=1000m,跑步最大速度=5m/sw=2cm/h,记跑步速度为v。
主要因素:淋雨量,降雨的大小,降雨的方向(风),路程的远近,行走的速度2问题的分析考虑到人(或物体)在雨中A地走到B地,其距离为L,为方便起见我们认为在雨中行走的这一段时间雨速不变的情况下,并且无其他因素的限制与影响下的移动,在此前提下建立数学模型找出最优的速度,才能使淋雨量最小。
3合理的假设3.1雨速在相当长的一段时间里是不变的,其中包括矢量速度的大小和方向3.2人(或物体)可以理想化为一个长方体。
3.3在一定的时间里降雨量是不变的,即为一个常值3.4可以建立空间直角坐标系使人的行走速度只在x方向有分量4符号的说明L :人从A地走到B地的距离V:雨的速度V X,V Y V Z :V在空间直角坐标系中x,y,z方向上的速度的分量t:时间变量v:人(或物体)的移动速度R(u)单位时间里的淋雨量K:比例系数5模型的建立人(或物体)的表面比较复杂,为简化模型我们设前侧,顶的面积之比为a:b:c,使在空间直角坐标系中人行走的v={u,0,0},V={V X,V Y,V Z},由此可以知道在雨中行走的时间为t=L/u。
在上述的假设下,我们容易有数学分析中的曲面积分的通量的概念和空间向量之间的关系知单位时间里的淋雨量是与(|u-V X|,|0-V Y|,|0-V Z|).(a,b,c)=a|u-V X|+b|0-V Y|+c|0-V Z|成正比的。
数学建模 雨中行走问题

数学模型论文学校:班级:姓名:学号:雨中行走问题摘要当我们在雨中冒雨行走时总会下意思的加快速度,似乎跑得越快淋雨量就会越小。
但事实上会是这种情况吗?在这里,我们将给予综合性的考虑,来解释不同情况下的淋雨量。
在不考虑风向的情况下,若人的全身都受到雨淋,理所当然人跑的越快所淋的雨就会越少。
那么模型也可算出淋雨量。
当雨线从正面和人的跑步方向在同一平面时,并且考虑风向的影响,雨线方向和竖直方向成θ角。
因为迎着雨的方向跑,所以全身都会淋到雨,由于有夹角,可以将雨分成竖直方向和水平方向两部分。
便可根据题的要求解出模型。
当雨线从后面和人的跑步方向在同一平面时,并且考虑风向的影响,雨线方向和竖直方向成α角。
因为背着雨的方向跑,所以全身不一定都会淋到雨。
可分几种情况分别来说。
关键词人速;雨速;风向;夹角1.问题的重述当人们在雨中行走时,是不是走的越快就会淋越少的雨呢?对于这个问题,建立合理的数学模型。
讨论一下,在不考虑风向时,人的淋雨量为多少;进而进一步讨论一下,在考虑雨线方向与人的跑步方向在同一平面内成不同角度时的淋雨量。
2.问题的分析当人在雨中行走时,是否跑的越快所淋的雨量就越少那,答案当然不是。
人在雨中所淋到的雨量和风向有关,因为风向的不同会导致雨线和人成不同的角度。
从而使人所淋到的雨量有所不同。
3.模型的假设与符号说明3.1模型的假设(1)把人体视为长方体,身高h米,身宽w米,身厚d米,淋雨总量C升。
(2)把降雨强度视为常量,记为:I(cm h)。
(3)风速保持不变。
v m s跑完全程D。
(4)以定速度()3.2符号说明h人体的身高(m)w 人体的宽度(m)d 人体的厚度(m)D 人跑步的全程(m)v 人跑步的速度(m/s)i 降雨强度(cm/h)c 人在跑步中的淋雨总量(L)s 人在雨中会被雨淋的面积 (㎡)t 人在雨中跑步的时间 (s)v 雨滴下落速度 (m/s)θ 雨滴反方向与人速度方向的夹角ρ 雨滴密度4.模型的建立与求解(1)不考虑雨的方向,此种情况,人的前后左右都会淋雨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人在雨中奔跑的速度与淋雨量的关系
摘要:本文通过分析人在雨中奔跑的速度与淋雨量之间存在的关联,针对不同的降雨方向,将人简化为长方体模型,建立了奔跑速度与总淋雨量的优化模型。
针对问题一,假设雨水淋遍全身且不考虑雨的方向,通过简单的模型分析得到跑完全程的总淋雨量。
针对问题二,考虑雨从迎面打来,雨线方向与奔跑方向在同一铅直平面,通过分析淋雨部位、竖直方向雨速和水平方向雨相对于人的速度,建立了总淋雨量的模型,又对模型进行了函数的单调性分析,得知总淋雨量最少时奔跑速度最大。
针对问题三,考虑雨从后面打来,雨线方向与奔跑方向在同一铅直平面,通过分析淋雨部位、竖直方向速度和水平方向上的相对速度,针对不同情况,建立了总淋雨量的模型,又对模型进行了函数单调性的分析讨论,得出了总淋雨量最少时的奔跑速度。
针对问题五,针对雨线方向与跑步方向不在同一平面内的情况,对雨速进行空间直角坐标分解,结合问题三,分析模型发生的变化。
关键词:跑步速度;总淋雨量;相对速度;单调性分析;矢量分解
一、问题重述
对于行人来说,下雨天最糟糕的情况莫过于出门在外雨伞没带。
在这种情况下,人们习惯用快跑来摆脱困境。
归根结底,“跑得越快淋雨就越少”的观点只是一种感性认识。
因此,考虑通过建模来科学分析两者之间的关系。
对于下列四个问题,分别给出奔跑速度与淋雨量之间的定性分析。
问题1:在不考虑雨线方向的情况下,计算以最大速度跑完全程的淋雨量。
问题2:考虑雨从迎面打来,且与跑步方向在同一铅直面上,雨线与人体的夹角为α。
建立总淋雨量与奔跑速度的模型,进而求总淋雨量最少时的速度。
问题3:考虑雨从背面打来,且与跑步方向在同一铅直面上,雨线与人体的夹角为β。
建立总淋雨量与奔跑速度的模型,进而求总淋雨量最少时的速度。
问题5:考虑雨线方向与跑步不在同一铅直面上时,模型的变化。
二、问题分析
问题1,将人简化为长方体模型,不考虑雨的方向,设降雨淋遍全身,分析人的淋雨面积共五个面分别为前面、背部、顶部、左侧面和右侧面。
在雨速为常数且方向不变情况下,可以根据人的最大奔跑速度和路程来求出时间;若测得单位时间,单位面积的降雨量,可以求出总淋雨量。
问题2,雨从迎面打来,雨线方向与奔跑方向在同一铅直面内,且与人体的夹角为θ,雨速为常数且方向不变,可以将雨速正交分解为水平方向和竖直方向,由此分析可知淋雨部位为前面和顶部。
另外,雨迎面打来,雨相对于人的速度会发生变化,查阅资料可以知道降雨强度与雨的空间密度以及雨速有关。
故通过关系式表示出雨的相对速度后,可以进一步表示出降雨强度(单位时间段内的降雨量),时间则可以用路程与人的速度相比得出。
将时间、淋雨面积、降雨强度与总淋雨量关系表示出来,即可建立总淋雨量与奔跑速度的模型,进而分析求解出总淋雨量最少时的奔跑速度。
问题3,雨从背面打来,雨线方向与跑步方向在同一铅直面内,且与人体的夹角为α,同问题2一样进行分析,忽略次要因素,分析得知淋雨面积为背部和顶部。
另外,由于雨线方向与问题2不同,以奔跑速度和雨速在水平方向上的分量大小分类讨论,时间仍由路程与奔跑速度之比表示,由此表示出时间、淋雨面积、降雨强度与淋雨量之间的关系,建立总淋雨量与奔跑速度的模型,进而讨论分析出总淋雨量最少时的奔跑速度。
问题5,若雨线方向与奔跑方向,不在同一平面内,可以建立空间直角坐标系,将雨速进行空间分解,分析可知淋雨部位,与问题3中的模型进行分析比较,可知模型变化。
三、模型假设
.1把人简化为一个长方体。
.2雨速对人的奔跑速度的影响忽略不计。
.3若长方体表面与雨速平行,假定不沾雨。
.4人的奔跑速度恒定。
.5降雨速度与强度不变。
.6风速始终不变。
四、符号表示
a 人体身高
b 人体宽度
c 人体厚度
d 跑步距离
m ax v 跑步最大速度
u 雨速
I 降雨强度 ω 降雨量 v 跑步速度
θ 同一平面内,雨从迎面吹来,雨线与人体夹角 α 同一平面内,雨从背面吹来,雨线与人体夹角 t 全过程所花费的时间 S 面积
Q 淋雨量
p 在一定时刻单位体积空间内雨滴所占的空间比例数
五、模型建立与求解
5.1 问题1的模型建立与求解 设长方体模型作为人的简化模型。
全身面积:
bc ac ab S ++=)(2
淋雨量:
[]
max
max
)(2v bc ac ab d v dS
Q ++=
=
ωω
5.2 问题2的模型建立与求解 图1为问题2的示意图。
迎面淋雨量:
v
v u abdp Q )
sin (1+=
θ
其中)sin (v u p I +=θ
顶部淋雨量:
v
bcdpu Q θ
cos 2=
其中θcos pu I =
淋雨量:
[]⎥⎦
⎤
⎢⎣⎡++=++=
+=a v c a u bdp v cu v u a bdp Q Q Q )cos sin (cos )sin (21θθθθ (1)
模型(1)连续变化,通过单调性分析,可知模型(1)是Q 关于v 的单调递减函数,故当人的奔跑速度达到最大时,总淋雨量最少。
5.3 问题3的模型建立与求解 图2为问题3的示意图。
背面淋雨量:
v
v
Q )
sin 3-=
α
其中)sin (v u p I -=α
顶部淋雨量:
v
bcdpu Q α
cos 2=
其中αcos pu I =
当v u ≥αsin 时 淋雨量:
u
α
[]
v v u a cu bdp Q Q Q )sin (cos 32-+=
+=αα (2)
模型(2)连续变化,通过单调性分析,模型(2)是Q 关于v 的单调递减函数,故当人的奔跑速度达到最大时,总淋雨量最少。
当v u ≤αsin 时 背面淋雨量:
v u v abdp Q )sin (`
3α-=
顶部淋雨量:
v bcdpu Q αcos `
2=
淋雨量:
[]⎥⎦
⎤
⎢⎣⎡+-=-+=
+=a v a c u bdp v u v a cu bdp Q Q Q )sin cos ()sin (cos `
3`2αααα (3)
当0sin cos >-ααa c 时,人奔跑的速度越大,总淋雨量越小。
人的奔跑速度最
大时,总淋雨量最少。
当0sin cos <-ααa c 时,人奔跑的速度越小,总淋雨量越小。
αsin u v =时,总淋雨量最少。
5.4 问题5的模型建立与求解 图3为问题5的示意图。
如图3所示,建立空间直角坐标系,将与跑步速度方向不在同一平面内的雨速分解,分析雨速u 在z y x ,,
轴上的分量,可知淋雨部位包括侧面,背面和顶部,
与模型)2(、)3(相比,多考虑了侧面,由此可知,若雨线方向与奔跑方向不在同一平面内,要多考虑侧面,另外雨相对于人的速度会发生变化,需要分类讨论,但问题的性质没有变。
六、模型结果的分析与检验
在不考虑雨的方向的情况下,奔跑速度越快,总淋雨量越小。
当雨从迎面打来时,奔跑速度越快,总淋雨量越小。
当雨从背面打来时,奔跑速度与总淋雨量的关系与参量的大小有关。
由以上结果可知,并不是奔跑速度越大淋雨量越小,淋雨量的大小与奔跑速度以及雨下落的方向有关。
查阅资料可以得到参数具体数值的一组数据如下:
4
1001039.142.05.07.16π
θ=
=⨯=====-m d p s
m u m c m b m a 通过MATLAB 进行简单数值运算和函数单调性分析,得到当
s m u v 828.2sin ==θ时,总淋雨量最小值为L 13.0,经检验符合实际情况。
七、模型评价与推广
优点:
.1模型结果的分析较易实现,不涉及复杂的编程运算。
.2模型简单易懂,便于计算和操作,实用性强。
缺点:
.1为了简化模型,忽略了一些影响因素。
.2降雨强度的测定会有误差。
该模型可以推广应用于估算总淋雨量(可以根据降雨强度等级划分标准找出降雨强度的估测值代入模型中),还可应用于确定火车、汽车、公交车等交通工具在雨中行驶的速度,以减少淋雨对车身的破坏。
该模型没有考虑人的奔跑速度是变化的情况,在改进模型的过程中可以假设雨速会适当延缓人的奔跑速度,奔跑速度为雨速和时间的函数,结合原模型的推导过程,得到改进后的模型。
参考文献
[]1姜启源, 数学模型(第三版)[M], 北京:高等教育出版社,1999。
