贪心法的编程实验
贪心算法 实验报告

贪心算法实验报告贪心算法实验报告引言:贪心算法是一种常用的算法设计策略,它通常用于求解最优化问题。
贪心算法的核心思想是在每一步选择中都选择当前最优的解,从而希望最终能够得到全局最优解。
本实验旨在通过实际案例的研究,探索贪心算法的应用和效果。
一、贪心算法的基本原理贪心算法的基本原理是每一步都选择当前最优解,而不考虑整体的最优解。
这种贪婪的选择策略通常是基于局部最优性的假设,即当前的选择对于后续步骤的选择没有影响。
贪心算法的优点是简单高效,但也存在一定的局限性。
二、实验案例:零钱兑换问题在本实验中,我们以零钱兑换问题为例,来说明贪心算法的应用。
问题描述:假设有不同面值的硬币,如1元、5元、10元、50元和100元,现在需要支付给客户x元,如何用最少的硬币数完成支付?解决思路:贪心算法可以通过每次选择当前面值最大的硬币来求解。
具体步骤如下:1. 初始化一个空的硬币集合,用于存放选出的硬币。
2. 从面值最大的硬币开始,如果当前硬币的面值小于等于待支付金额,则将该硬币放入集合中,并将待支付金额减去该硬币的面值。
3. 重复步骤2,直到待支付金额为0。
实验过程:以支付金额为36元为例,我们可以通过贪心算法求解最少硬币数。
首先,面值最大的硬币为100元,但36元不足以支付100元硬币,因此我们选择50元硬币。
此时,剩余待支付金额为36-50=-14元。
接下来,面值最大的硬币为50元,但待支付金额为负数,因此我们选择下一个面值最大的硬币,即10元硬币。
此时,剩余待支付金额为-14-10=-24元。
继续选择10元硬币,剩余待支付金额为-24-10=-34元。
再次选择10元硬币,剩余待支付金额为-34-10=-44元。
最后,选择5元硬币,剩余待支付金额为-44-5=-49元。
由于待支付金额已经为负数,我们无法继续选择硬币。
此时,集合中的硬币数为1个50元和3个10元,总共4个硬币。
实验结果:通过贪心算法,我们得到了36元支付所需的最少硬币数为4个。
贪心算法实验报告心得

贪心算法实验报告心得前言贪心算法是一种常见且重要的算法设计思想,通过每一步都选择当下最优的解决方案,以期望最终得到全局最优解。
在学习与实践贪心算法的过程中,我有了许多心得与体会。
什么是贪心算法?贪心算法是一种求解问题的算法思想,它的特点是每一步都选择当前最优的解决方案,而不考虑该选择对以后步骤的影响。
贪心算法通常适用于可以将问题分解为若干个子问题,并且通过每次选择当前最优解来得到整体最优解的情况。
贪心算法的基本步骤贪心算法的基本步骤可以总结为以下几个方面:1.确定问题的解空间,并找到问题的最优解。
贪心算法通常通过穷举法或者利用问题的特殊性质来确定解空间。
2.制定贪心策略。
贪心算法的核心是确定每一步选择的贪心策略,即选择当前最优解。
3.确定贪心策略的正确性。
贪心算法的一个关键问题是如何证明贪心策略的正确性。
可以通过数学证明、反证法或者举反例等方式来进行证明。
4.实现贪心算法。
将贪心策略转化为实际可执行的算法步骤,编写代码来求解问题。
贪心算法实验结果分析在本次实验中,我使用贪心算法解决了一个经典问题:找零钱问题(Change-Making Problem)。
给定一定面额的硬币和需找的金额,我们的目标是使用最少的硬币来完成找零钱。
贪心算法的思路是每次选择面额最大的硬币进行找零。
实验设计1.实验输入:我设计了多组输入来测试贪心算法的性能。
每组输入包括一个需找的金额和一个硬币集合。
2.实验输出:对于每组输入,贪心算法输出一个最优的硬币找零方案,以及使用的硬币数量。
3.实验评价:我使用了实际需找金额与贪心算法计算得到的找零金额的差值来评估算法的准确性,并统计了算法的时间复杂度。
实验结果从多组实验结果中可以观察到,贪心算法在大部分情况下给出了正确的找零金额,并且算法的时间复杂度较低。
结果分析贪心算法在找零钱问题中的应用是合理的。
每次选择面额最大的硬币进行找零,可以快速接近最优解,并且相对其他算法具有较低的时间复杂度。
贪心算法几个经典例子c语言

贪心算法几个经典例子c语言1. 零钱兑换问题题目描述:给定一些面额不同的硬币和一个总金额,编写一个函数来计算可以凑成总金额所需的最少的硬币个数。
如果没有任何一种硬币组合能够凑出总金额,返回 -1。
贪心策略:每次选择面额最大的硬币,直到凑出总金额或者无法再选择硬币为止。
C语言代码:int coinChange(int* coins, int coinsSize, int amount){int count = 0;for(int i = coinsSize - 1; i >= 0; i--){while(amount >= coins[i]){amount -= coins[i];count++;}}return amount == 0 ? count : -1;}2. 活动选择问题题目描述:有 n 个活动,每个活动都有一个开始时间和结束时间,选择一些活动使得它们不冲突,且能够参加的活动数最多。
贪心策略:每次选择结束时间最早的活动,直到所有活动都被选择或者无法再选择为止。
C语言代码:typedef struct{int start;int end;}Activity;int cmp(const void* a, const void* b){return ((Activity*)a)->end - ((Activity*)b)->end;}int maxActivities(Activity* activities, int n){qsort(activities, n, sizeof(Activity), cmp);int count = 1;int end = activities[0].end;for(int i = 1; i < n; i++){if(activities[i].start >= end){count++;end = activities[i].end;}}return count;}3. 跳跃游戏题目描述:给定一个非负整数数组,你最初位于数组的第一个位置。
单源最短路径(贪心法)实验报告
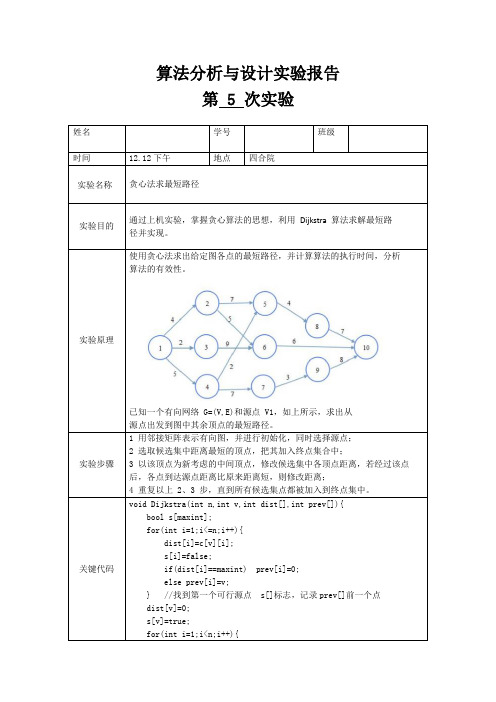
算法分析与设计实验报告第 5 次实验使用贪心法求出给定图各点的最短路径,并计算算法的执行时间,分析算法的有效性。
已知一个有向网络 G=(V,E)和源点 V1,如上所示,求出从源点出发到图中其余顶点的最短路径。
1 用邻接矩阵表示有向图,并进行初始化,同时选择源点;}手动输入实现实验所给图形:随机数产生图的权值:通过这次实验,我回顾了回溯法求解最短路径问题,在其中加入了舍伍德附录:完整代码#include<stdio.h>#include<stdlib.h>#include<time.h>#define maxint 1000int c[200][200]={0};void Dijkstra(int n,int v,int dist[],int prev[]){ bool s[maxint];for(int i=1;i<=n;i++){dist[i]=c[v][i];s[i]=false;if(dist[i]==maxint) prev[i]=0;else prev[i]=v;} //找到第一个可行源点 s[]标志,记录prev[]前一个点dist[v]=0;s[v]=true;for(int i=1;i<n;i++){int temp=maxint;int u=v;for(int j=1;j<=n;j++){if((!s[j])&&(dist[j]<temp)){u=j;temp=dist[j];}}s[u]=true;for(int j=1;j<=n;j++){int newdist=dist[u]+c[u][j];if(newdist<dist[j]){dist[j]=newdist;prev[j]=u;}}}}int main(){int n,v;printf("请输入顶点数: ");scanf("%d",&n);//printf("路径: ");srand(time(0));for(int i=1;i<n+1;i++){for(int j=1;j<n+1;j++){/* scanf("%d",&c[i][j]);*/ ///手动输入if(i!=j){if((c[j][i]==0)||(c[j][i]==1000))c[i][j]=rand()%100+1;else c[i][j]=1000;if(c[i][j]>50) c[i][j]=1000;}}}printf("请输入源点: ");scanf("%d",&v);int dist[n+1],prev[n+1];printf("\n路径:\n");for(int i=1;i<n+1;i++){for(int j=1;j<n+1;j++)printf("%5d ",c[i][j]);printf("\n");}Dijkstra(n,v,dist,prev);for(int i=1;i<n+1;i++){printf("\n%d到%d的最短路径为:%d",v,i,dist[i]);}}。
算法实验报告贪心

一、实验背景贪心算法是一种在每一步选择中都采取当前状态下最好或最优的选择,从而希望导致结果是全局最好或最优的算法策略。
贪心算法并不保证能获得最优解,但往往能获得较好的近似解。
在许多实际应用中,贪心算法因其简单、高效的特点而被广泛应用。
本实验旨在通过编写贪心算法程序,解决经典的最小生成树问题,并分析贪心算法的优缺点。
二、实验目的1. 理解贪心算法的基本原理和应用场景;2. 掌握贪心算法的编程实现方法;3. 分析贪心算法的优缺点,并尝试改进;4. 比较贪心算法与其他算法在解决最小生成树问题上的性能。
三、实验内容1. 最小生成树问题最小生成树问题是指:给定一个加权无向图,找到一棵树,使得这棵树包含所有顶点,且树的总权值最小。
2. 贪心算法求解最小生成树贪心算法求解最小生成树的方法是:从任意一个顶点开始,每次选择与当前已选顶点距离最近的顶点,将其加入生成树中,直到所有顶点都被包含在生成树中。
3. 算法实现(1)数据结构- 图的表示:邻接矩阵- 顶点集合:V- 边集合:E- 已选顶点集合:selected- 最小生成树集合:mst(2)贪心算法实现```def greedy_mst(graph):V = set(graph.keys()) # 顶点集合selected = set() # 已选顶点集合mst = set() # 最小生成树集合for i in V:selected.add(i)mst.add((i, graph[i]))while len(selected) < len(V):min_edge = Nonefor edge in mst:u, v = edgeif v not in selected and (min_edge is None or graph[u][v] < graph[min_edge[0]][min_edge[1]]):min_edge = edgeselected.add(min_edge[1])mst.add(min_edge)return mst```4. 性能分析为了比较贪心算法与其他算法在解决最小生成树问题上的性能,我们可以采用以下两种算法:(1)Prim算法:从任意一个顶点开始,逐步添加边,直到所有顶点都被包含在生成树中。
贪心算法-找零问题 实验报告

实验三课程名称:算法设计与实现实验名称:贪心算法-找零问题实验日期:2019年5月2日仪器编号:007班级:数媒0000班姓名:郝仁学号0000000000实验内容假设零钱系统的币值是{1,p,p^2,……,p^n},p>1,且每个钱币的重量都等于1,设计一个最坏情况下时间复杂度最低的算法,使得对任何钱数y,该算法得到的零钱个数最少,说明算法的主要设计思想,证明它的正确性,并给出最坏情况下的时间复杂度。
实验分析引理1(离散数学其及应用3.1.4):若n是正整数,则用25美分、10美分、5美分和1美分等尽可能少的硬币找出的n美分零钱中,至多有2个10美分、至多有1个5美分、至多有4个1美分硬币,而不能有2个10美分和1个5美分硬币。
用10美分、5美分和1美分硬币找出的零钱不能超过24美分。
证明如果有超过规定数目的各种类型的硬币,就可以用等值的数目更少的硬币来替换。
注意,如果有3个10美分硬币,就可以换成1个25美分和1个5美分硬币;如果有2个5美分硬币,就可以换成1个10美分硬币;如果有5个1美分硬币,就可以换成1个5美分硬币;如果有2个10美分和1个5美分硬币,就可以换成1个25美分硬币。
由于至多可以有2个10美分、1个5美分和4个1美分硬币,而不能有2个10美分和1个5美分硬币,所以当用尽可能少的硬币找n美分零钱时,24美分就是用10美分、5美分和1美分硬币能找出的最大值。
假设存在正整数n,使得有办法将25美分、10美分、5美分和1美分硬币用少于贪心算法所求出的硬币去找n美分零钱。
首先注意,在这种找n美分零钱的最优方式中使用25美分硬币的个数q′,一定等于贪心算法所用25美分硬币的个数。
为说明这一点,注意贪心算法使用尽可能多的25美分硬币,所以q′≤q。
但是q′也不能小于q。
假如q′小于q,需要在这种最优方式中用10美分、5美分和1美分硬币至少找出25美分零钱。
而根据引理1,这是不可能的。
算法分析与设计实验三贪心算法
实验三贪心算法实验目的1. 掌握贪心法的基本思想方法;2. 了解适用于用贪心法求解的问题类型,并能设计相应贪心法算法;3. 掌握贪心算法复杂性分析方法分析问题复杂性。
预习与实验要求1. 预习实验指导书及教材的有关内容,掌握贪心法的基本思想;2. 严格按照实验内容进行实验,培养良好的算法设计和编程的习惯;3. 认真听讲,服从安排,独立思考并完成实验。
实验设备与器材硬件:PC机软件:C++或Java等编程环境实验原理有一类问题是要从所有的允许解中求出最优解,其策略之一是“贪心法”,即逐次实施“贪心选择”:在每个选择步骤上做出的选择都是当前状态下最优的。
贪心选择依赖于在此之前所做出的选择,但不依赖于后续步骤所需要的选择,即不依赖于后续待求解子问题。
显然,这种选择方法是局部最优的,但不是从问题求解的整体考虑进行选择,因此不能保证最后所得一定是最优解。
贪心法是求解问题的一种有效方法,所得到的结果如果不是最优的,通常也是近似最优的。
实验内容以下几个问题选做一项:1. 用贪心法实现带有期限作业排序的快速算法应用贪心设计策略来解决操作系统中单机、无资源约束且每个作业可在等量时间内完成的作业调度问题。
假定只能在一台机器上处理N个作业,每个作业均可在单位时间内完成;又假定每个作业i都有一个截止期限di>0(它是整数),当且仅当作业i在它的期限截止以前被完成时,则获得pi的效益。
这个问题的一个可行解是这N个作业的一个子集合J,J中的每个作业都能在各自的截止期限之前完成。
可行解的效益值是J中这些作业的效益之和,即Σp。
具有最大效益值的可行解就是最优解。
2. 实现K元归并树贪心算法两个分别包含n个和m个记录的已分类文件可以在O(n+m)时间内归并在一起而得到一个分类文件。
当要把两个以上的已分类文件归并在一起时,可以通过成对地重复归并已分类的文件来完成。
例如:假定X1,X2,X3,X4是要归并的文件,则可以首先把X1和X2归并成文件Y1,然后将Y1和X3归并成Y2,最后将Y2和X4归并,从而得到想要的分类文件;也可以先把X1和X2归并成Y1,然后将X3和X4归并成Y2,最后归并Y1和Y2而得到想要的分类文件。
c++贪心算法经典例题
c++贪心算法经典例题和详解贪心算法(Greedy Algorithm)是一种优化问题解决方法,其基本思想是每一步都选择当前状态下的最优解,以期望达到全局最优解。
贪心算法的特点是每一步都要做出一个局部最优的选择,而这些局部最优选择最终构成了全局最优解。
下面是一个经典的贪心算法例题以及详解:例题:活动选择问题(Activity Selection Problem)假设有一个需要在同一时段使用同一个资源的活动集合,每个活动都有一个开始时间和结束时间。
设计一个算法,使得能够安排最多数量的互不相交的活动。
# 输入:-活动的开始时间数组`start[]`。
-活动的结束时间数组`end[]`。
# 输出:-选择的互不相交的活动的最大数量。
# 算法详解:1. 首先,将活动按照结束时间从小到大排序。
2. 选择第一个活动,并将其加入最终选择的集合中。
3. 对于剩下的活动,选择下一个结束时间最早且与前一个活动不冲突的活动。
4. 重复步骤3,直到所有活动都被选择。
```cpp#include <iostream>#include <algorithm>#include <vector>using namespace std;// 定义活动结构体struct Activity {int start, end;};// 比较函数,用于排序bool compareActivities(Activity a, Activity b) {return a.end < b.end;}// 贪心算法解决活动选择问题void activitySelection(vector<Activity>& activities) {// 按照结束时间排序sort(activities.begin(), activities.end(), compareActivities);// 第一个活动总是被选中cout << "Selected activity: (" << activities[0].start << ", " << activities[0].end << ")" << endl;// 选择其余活动int lastSelected = 0;for (int i = 1; i < activities.size(); i++) {// 如果当前活动的开始时间大于等于上一个选择的活动的结束时间,则选择该活动if (activities[i].start >= activities[lastSelected].end) {cout << "Selected activity: (" << activities[i].start << ", " << activities[i].end << ")" << endl;lastSelected = i;}}}int main() {vector<Activity> activities = {{1, 2}, {3, 4}, {0, 6}, {5, 7}, {8, 9}, {5, 9}};cout << "Activities before sorting:" << endl;for (const Activity& activity : activities) {cout << "(" << activity.start << ", " << activity.end << ") ";}cout << endl;activitySelection(activities);return 0;}```在这个例子中,我们首先定义了一个活动的结构体`Activity`,然后编写了一个比较函数`compareActivities` 用于排序。
实验3 贪心算法
淮海工学院计算机工程学院实验报告书课程名:《算法分析与设计》题目:实验3 贪心算法班级:学号:姓名:实验3 贪心算法实验目的和要求(1)了解前缀编码的概念,理解数据压缩的基本方法;(2)掌握最优子结构性质的证明方法;(3)掌握贪心法的设计思想并能熟练运用(4)证明哈夫曼树满足最优子结构性质;(5)设计贪心算法求解哈夫曼编码方案;(6)设计测试数据,写出程序文档。
实验内容设需要编码的字符集为{d 1, d 2, …, dn },它们出现的频率为{w 1, w 2, …, wn },应用哈夫曼树构造最短的不等长编码方案。
实验环境Turbo C 或VC++实验学时2学时,必做实验数据结构与算法//构造哈夫曼结构体struct huffman{double weight; //用来存放各个结点的权值int lchild,rchild,parent; //指向双亲、孩子结点的指针 };核心源代码#include<iostream>#include <string>using namespace std;#include <stdio.h>//构造哈夫曼结构体struct huffman{double weight;∑=j i k k aint lchild,rchild,parent;};static int i1=0,i2=0;//选择权值较小的节点int Select(huffman huff[],int i){int min=11000;int min1;for(int k=0;k<i;k++){if(huff[k].weight<min && huff[k].parent==-1){min=huff[k].weight;min1=k;}}huff[min1].parent=1;return min1;}//定义哈夫曼树,并对各个节点进行赋权值void HuffmanTree(huffman huff[],int weight[],int n) {for(int i=0;i<2*n-1;i++){huff[i].lchild=-1;huff[i].parent=-1;huff[i].rchild=-1;}for(int l=0;l<n;l++){huff[l].weight=weight[l];}for(int k=n;k<2*n-1;k++){int i1=Select(huff,k);int i2=Select(huff,k);huff[i1].parent=k;huff[i2].parent=k;huff[k].weight= huff[i1].weight+huff[i2].weight;huff[k].lchild=i1;huff[k].rchild=i2;}}//哈夫曼编码,左0右1void huffmancode(huffman huff[],int n){string s;int j;for(int i=0;i<n;i++){s="";j=i;while(huff[j].parent!=-1){if(huff[huff[j].parent].lchild==j)s=s+"0";else s=s+"1";j=huff[j].parent;}cout<<"第"<<i+1<<"个节点的哈夫曼编码为:";for(int j=s.length();j>=0;j--){cout<<s[j];}cout<<endl;}}void main(){huffman huff[20];int n,w[20];printf("请输入节点的个数:");scanf("%d",&n);for(int i=0;i<n;i++){printf("请输入第%d个节点的权值:",i+1);scanf("%d",&w[i]);}printf("\n");HuffmanTree(huff,w,n);huffmancode(huff,n);}实验结果实验体会本次实验是用贪心法求解哈夫曼编码,其实贪心法和哈夫曼树的原理是一样的,每次将集合中两个权值最小的二叉树合并成一棵新二叉树,每次选择两个权值最小的二叉树时,规定了较小的为左子树。
贪心算法实验报告
typedef struct node{
int id ,time;//作业所需时间
}jobnode;
typedef struct Node{
int id ,avail;//id机器编号、avail每次作业的初始时间
}manode;
manode machine[N];
jobnode job[N];
scanf("%d",&n);
printf("请输入加油站的个数:");
scanf("%d",&k);
for(i=0;i<=k;i++)
scanf("%d",&d[i]);
greedy(d,n,k);
}
实验结果截图:
(3)实验代码:设有n个正整数,将它们连接成一排,组成一个最大的多位整数
#include<stdio.h>
return;
}
}
for(i=0,s=0;i<=k;i++){
if(s<n)
s+=d[i];
else if(s>n){
n=s-d[i];
num++;
}
}
printf("%d\n",num);
}
void main(){
int i,n,k;
int d[1000];
printf("请输入汽车可行驶公里数:");
/*找出下一个作业执行机器*/
manode *Find_min(manode a[],int m){
manode *temp=&a[0];
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机器的最小数量k,以及当仅使用k台机器时, 所有的工作时间的最小总和。
• 输入
• 试题来源:ACM South America 2001 • 在线测试:ZOJ 1076,UVA 2387
• 随着大量的基因组DNA序列数据被获得,在这 些序列中寻找基因(基因组DNA中负责蛋白质 合成的部分)变得越来越重要。众所周知,对
于真核生物(相应于原核生物),这一过程更
为复杂,因为存在干扰基因组序列中基因编码
试题解析
• 本题要求计算FatMouse能够通过交易得到 的最大数量的Javabean。
• 首先,计算J[i]除以F[i],结果为a[i];然后, 对数组a按由大到小的顺序进行排序。在交 易 的 时 候 , FatMouse 为 了 获 得 最 多 的 Javabean,要先交易a[i]大的,这样就确保 了FatMouse能获得最多的Javabean。
求解任务调度的算法步骤
• 设n项任务组成的集合T,最少用的机器台数为m; • 对n项任务开始时间升序进行排序;m=0; • while (T) { • 从T中删除当前最小开始时间的任务i;//贪心策略:
每次选择当前最小开始时间的任务 • if(任务i和已经执行的任务不冲突) • 安排任务i在空闲的机器上完成; • else { • m++; //添加一台新机器 • 任务i在新机器m上完成; •} •}
• 输出
• 对于每个测试用例,您的程序通过枚举链 中的外显子,输出一行,给出具有可能最 多的外显子的链。如果有多个链具有相同 数量的外显子,输出其中的任何一个。
试题解析
• 本题是一道经典的采用贪心法求解区间调 度的试题,对于每个可能的外显子的区间, 按照区间的右端点从小到大排序。然后, 每次选取区间右端点小的外显子,同一个 位置只能放一个外显子。
– 产生最小生成树的Kruskal算法、求解单源最短 路径问题的Dijkstra算法、生成Huffman树的 Huffman算法等都是采用贪心算法的思想。
• 使用贪心法能否得到最优解,是必 须加以证明的。
– 采用贪心算法求解货郎担问题(Traveling SalesMan Problem)的最邻近方法,可以举出 反例说明该算法是一个近似算法,而货郎担问 题的最优算法还未找到。
背包中已经放置物品的总价值
• while (W<M) • {价取值当最前高v的i最物高品的放物入品背i;包//贪心策略:每次把当前单位
• if (M-W-wi0) { • W+= wi; P+= pi; //物品i放入背包 •} • else { • a=(M-W)/ wi; • W+= awi; P+= api; //物品i部分a放入背包 •} •}
• 输入的第一行给出整数t(1t100),表示 测试用例的个数。每个测试用例的第一行 给出一个整数n(0<n100000),接下来的 n行中的每一行给出两个整数si和ei (0si<ei1e9)。
• 输出
• 对于每个测试用例,输出两个整数,分别 表示最少用的机器台数和所有机器所用的 工作时间的总和。
体验贪心法内涵的实验范例
Pass-Muraille
• 在魔术表演中,穿墙术是非常受欢迎的,魔术师在 一个预先设计好的舞台上表演穿越若干面墙壁。在 每次穿越墙壁的表演中,穿墙魔术师有一个有限的 穿墙能量,通过至多k面墙。墙壁被放置在一个网 格状的区域中。下图给出俯视图。所有的墙的厚度 是一个单元,但长度不同。本题设定没有一个方格 会在2面墙或更多面墙中。观众选择一列方格。穿 墙魔术师从图的上方沿着一列方格向下走,穿过每 一面在他路上遇到的墙,到达图的下方。如果他试 图走的那一列要穿过的墙超过k面,他将无法完成 这个节目。例如,墙的结构如下图所示,一个穿墙 者在k=3的情况下,从上到下可以选择除了第6列以 外的任何一列。
任务调度问题
• 任务调度(Task Schedule)问题描述如下: 给定n项任务,每项任务的开始时间为si, 结束时间为ei(1in,0si<ei),且每项任 务只能在一台机器上完成,每台机器一次 只能完成一项任务。如果任务i和任务j满足 eisj或ejsi,则任务i和任务j是不冲突的, 可以在一台机器上完成。任务调度就是以 不冲突的方式,用尽可能少的机器完成n项 任务。
试题解析
• 本题是经典的任务调度问题。
• 首先,对于每个测试用例,输入n项加工任务 的开始时间和结束时间,一共有2n个时间点。 对这2n个时间点按升序进行排序,如果有相同 的时间点,则结束时间点排在前,开始时间点 排在后。每个时间点用pair<int, int>表示,其 中,前一个(first)表示时间点的时间值,后 一个(second)表示这个时间点是开始时间还 是结束时间,如果是某项任务的开始时间,则 second取值为1;否则,second取值-1。
• 本题要求,给出一组可能的外显子,找到具有 尽可能多的外显子的链,这些外显子可以组装 起来生成一个基因。
• 输入
• 输入给出若干测试用例。每个测试用例首 先给出序列中可能的外显子的个数 0<n<1000。然后,接下来的n行每行给出一 对整数,表示外显子在基因组序列中开始 位置和结束位置。本题设定基因组序列最 多有50000个碱基。输入以给出单个0的一 行结束。
– 对于Kruskal算法、Dijkstra算法、Huffman算 法等,我们都可以证明,最优解可以通过一系 列局部最优的选择即贪心选择来求解。
体验贪心法内涵的实验范例
• 贪心算法的核心是根据题意,选取 能产生问题最优解的贪心策略。然 后,在每一个阶段,贪心算法根据 贪心策略给出局部最优解。
– 例如,产生最小生成树的Kruskal算法,贪心策 略就是每一步从边集中选取一条权值最小的边, 若该条边的两个顶点分属不同的树,则将该边 加入,即把两棵树合成一棵树。
• 给出一个穿墙魔术师的能量以及一个表演 舞台,要求在舞台上拆除最少数量的墙, 使得穿墙魔术师可以沿任意观众选择的列 穿过所有的墙。
• 输入 • 输入的第一行给出一个整数t (1≤t≤10),表示测
试用例的个数,然后给出每个测试用例的数据。 每个测试用例的第一行给出两个整数n (1≤n≤100),表示墙的面数;和k (0≤k≤100),表示穿墙魔术师可以通过的墙 的最大面数。在这一行后,给出n行,每行包 含两个(x, y)对,表示一面墙的两个端点坐 标。坐标是小于等于100的非负整数。左上角 的方格的坐标为(0, 0)。下面给出的第二个 测试样例相应于上图。
• 输入
• 输入包含多个测试用例。每个测试用例的 第一行给出两个非负整数M和N,接下来的 N行每行给出两个非负整数J[i]和F[i],最后 一个测试用例是两个-1,所有整数的值不超 过1000。
• 输出
• 对于每个测试用例,在一行上输出一个3位 小数的实数,这个实数是FatMouse能够通 过交易得到的最大数量的Javabean。
• 然后,num表示当前运行的机器数量,ans表 示到当前开一共开过多少台机器。从前到后对 2n个时间点进行扫描:
• 如果当前时间点是某项任务的开始时间,则 num增加1,如果这台机器是新添加的机器, 则该时间点的时间值作为机器的开机时间;调 整到当前一共开过多少台机器的数量;
• 如果当前时间点是某项任务结束时间,则当前 时间点的时间值作为机器的关机时间,num减 少1。
Schedule
• 试题来源:2017 Multi-University Training Contest - Team 10
• 在线测试:HDOJ 6180
• 有n项加工任务,第i项加工任务的开始时间为 si,结束时间为ei(1in)。有若干台机器。 任何两个在完成加工的时间段上有交集的任务
不能在同一台机器上完成。每台机器的工作时
• 输出
• 对每个测试用例,输出一行,给出一整 数,表示最少拆除墙的面数,使得穿墙魔 术师能从上方任何一列开始穿越。
试题解析
• 由左而右扫描每一列,要使得拆墙数最少, 必须保证左方舞台可穿越的情况下被拆墙 最少,即本题具备了最优子结构的特点。 本题关键是怎样通过做局部最优(贪心) 选择来达到全局最优解。
FatMouse' Trade
• 试题来源:Zhejiang Provincial Programming Contest 2004
• 在线测试:ZOJ 2109
• FatMouse准备了M磅猫粮,它想和守卫仓库的 猫进行交易,因为仓库里有它最爱吃的食物 Javabean。
• 仓 库 里 有 N 个 房 间 , 在 第 i 间 房 间 里 有 J[i] 磅 Javabean , 需 要 用 F[i] 磅 猫 粮 来 进 行 交 换 。 FatMouse不必买在房间里的全部Javabean,他 可 以 给 猫 F[i]*a% 磅 猫 粮 , 来 换 取 J[i]*a% 磅 的 Javabean,其中a是一个实数。现在FatMouse 给您布置家庭作业,请您告诉他,他最多能够 获得多少磅Javabean。
背包问题和任务调度问题
• 两个采用贪心算法求解的经典问题: –背包问题 –任务调度问题
背包问题
求解背包问题的算法步骤
• for (i=1; i<=n; i++) • vi=pi/wi; //计算每个物品的单位价值 • 对物品的单位价值vi由高到低排序,1in; • W=0; P=0; //W:背包中已经放置物品的总重量;P:
• 若当前列的墙数D≤K,则不处理;若当前列的 墙数D>K,则需拆D-K面墙。对于拆除哪些墙, 采取这样一个贪心策略:在当前列所有的有墙 格中,选择右方最长的D-K面墙拆除。
