幻方与数表
四年级上册数学奥数试题 第三讲《排排数——数表与幻方》 人教新课标 含答案

一、幻方这个神奇的图案叫做“幻方”,由于它有3行3列,所以叫做“三阶幻方”,这个相等的和叫做“幻和”。
“洛书”就是幻和为15的三阶幻方。
如下图:我国北周时期的数学家甄鸾在《算数记遗》里有一段注解:“九宫者,二四为肩,六八为足,左三右七,戴九履一,五居中央。
”这段文字说明了九个数字的排列情况,可见幻方在我国历史悠久。
三阶幻方又叫做九宫图,九宫图的幻方民间歌谣是这样的:“四海三山八仙洞,九龙五子一枝连;二七六郎赏月半,周围十五月团圆。
”幻方的种类还很多,这节课我们将学习认识了解它们。
幻方是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的3⨯3的数阵称作三阶幻方,4⨯4的数阵称作四阶幻方,5⨯5的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样。
四年级奥数必考知识点:第三讲:排排数——数表与幻方【例 1】3 3的正方形中,在每个格子里分别填入1~9的9个数字,要求每行每列及对角线上的三个数的和相等(请给出至少一种填法)。
三阶幻方的主要性质:1.能组成三阶幻方的数必须为从小到大排列,首尾对应相加均相等且等于中间数两倍的九个数数列。
2.幻方的中心数为数列中的中间数。
3.幻方中所有相等的和称做幻和,幻方的幻和等于中心数的3倍。
中心数还等于所有所填数的平均数。
4.数列中最大与最小数的配对不能出现在幻方的四角,即只能出现在中间位置,依次可得知第二大与第二小数的配对只能出现在四角上。
【例 2】请你将2~10这九个自然数填入图中的空格内每行、每列、每条对角线上的三数之和相等。
例2图【例 3】在下面两幅图的每个空格中,填入7个自然数,使得每行、每列、每条对角线上的三个数之和等于21。
例3图【例 4】用1~16编制一个四阶幻方。
二、数表与周期性问题【例 5】如图,横、竖各有12个方格,每个方格内都有一个数。
已知横行上任意3个相邻数之和为20,竖列上任意3个相邻数之和为2l,并且其中4个方格内的数分别是3,5,8和x。
第七讲 幻方和数阵图

第七讲幻方和数阵图(一)(1)把1到9这9个数填到3行3列的格子里,使每一行,每一列,每条对角线上的三个数字的和都相等,这样的数学游戏叫做幻方,像这样的3行3列的幻方叫三阶幻方。
(2)在三阶幻方中任意行,任意列或任意一条对角线上的3个数字的和叫幻和,如:7+5+3=15 4+3+8=15 6+5+4=15 这个三阶幻方的幻和是15 (3)除三阶幻方以外,常见的幻方还有四阶幻方,五阶幻方,六阶幻方四阶幻方五阶幻方六阶幻方三阶幻方的口诀是:九子斜排上下对易左右相更四维挺出例1:用3、4、5、9、10、11、15、16、17这九个数,编制一个三阶幻方,它的幻和是多少?幻和为30总结:满足一下两个条件中任意一条的九个数,就可以做填三阶幻方的游戏:(1)把九个数从小到大排列,组成了等差数列;(2)把九个数从小到大排列后,每三个数分为一组,每一组都是等差数列,而且组与组之间也是等差数列。
幻和是中间这个数的三倍三阶幻方的幻和=正中间的数 3例2:在右边的方格里填入适当的数,使它成为一个三阶幻方。
三阶幻方的幻和=正中间的数⨯3 幻和:8⨯3=24 练习:1、用2、4、6、8、10、12、14、16、18这九个数编制三阶幻方,并求幻和。
2、用1、2、3、7、8、9、13、14、15这九个数编制三阶幻方,并求幻和。
3、在右边的三阶幻方的空格内填入适当的数,使幻和等于27.4、在右边的三阶幻方的空格内填入适当的数,使它成为一个三阶幻方。
数阵图:把一些数按照一定的要求排列成各种各样的图形。
例3:在下面的三角形数阵图的3个 内的数的和是12例4:在下面图中的内,填上适当的数,使每条线上三个于13。
例5:把10,20,30,40,50,这五个数填入图中的使每条线段的三个数的和相等。
例6:把1,2,3,4,5,6,7这七个数字填入图中的内,使每条线上的内的3个数的和相等。
练习:1、在正方形数阵图中的内填入适当的数使每条线上的3个数的和等于21.2、把10到20这11个数填在图中的内,使每条线段上三个数的和等于45.3、把3到7这五个数分别天入“T”2形和“十”字形的方格内,使横竖两行的3个数的和相等。
第八讲(幻方与数阵图)
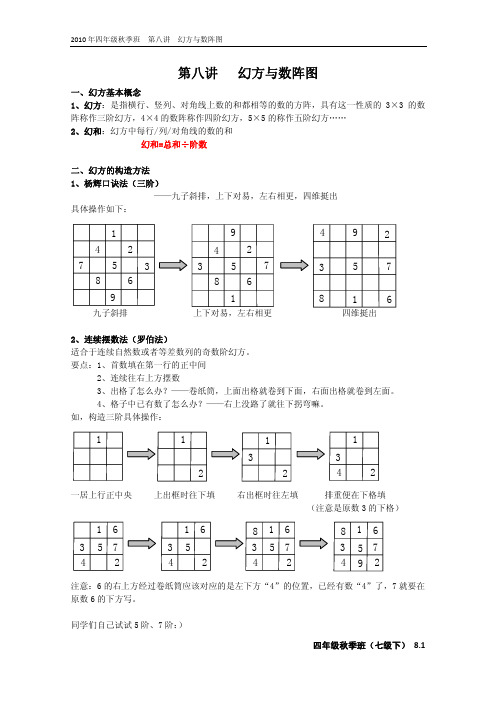
23
57
40
解析:告诉了幻和,先求中间数=90÷3=30
23 30
告诉了相邻 2 个棱块,一定能求对角角块=(23+57)÷2=40,得到右图
57
接下来就容易了吧?同学们自己计算吧!
(尖子)学案 1 按要求完成幻方
(1)只求 x
x
(2)如果中间格填入 100,请在(1)的基础上完成所有格的填数。
19
解析:想想窍门 2,95=(x+19)÷2,那么可算出 x=117
95
中间数是 100,可求出幻和是 300,其他的就好填了,同学们自己试试吧!
最后答案: 24 117 105 你填对了吗?
181 100 19
95 29 176
492 357
每个数加 3
7 12 5 6 8 10
816
11 4 9
先写出基本型
OK 啦
当然,本题并没有说用哪些数,所以答案很多,但是这种方法是不是更快呢?
拓展:请用 11.13.15.17.19.21.23.25.27 编制一个三阶幻方 解析:这是一个等差数列,将它与基本型中的 1-9 对应好
11 13 15 17 19 21 23 25 27 对应 1 2 3 4 5 6 7 8 9
2010 年四年级秋季班 第八讲 幻方与数阵图
第八讲 幻方与数阵图
一、幻方基本概念 1、幻方:是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的 3×3 的数 阵称作三阶幻方,4×4 的数阵称作四阶幻方,5×5 的称作五阶幻方…… 2、幻和:幻方中每行/列/对角线的数的和
四年级奥数幻方与数表

知识要点幻方与数表二、 如果一个n n ⨯的方阵中,每一横行、每一竖列以及两条对角线上数的和都相等,那么这个方阵称为n 阶幻方。
三、 在n 阶幻方中,其每一行、每一列、两条对角线上的数字之和都相等,这个和称为幻和。
对于n 行或者n 列,其和为幻和乘以n ,也等于所有2n 个数的和;所以,幻和2n S n=个数。
用1、2、……、2n 这2n 个数构造n 阶幻方,其幻和为2212(1)2n n n n ++++=……; 用1、2、3、4、5、6、7、8、9这9个数构造3阶幻方,其幻和为21234567893(13)1532++++++++⨯+==。
四、 对于n 阶幻方,当n 分别为奇数或偶数时,幻方有一个明显的不同,即奇数阶幻方有一个中心方格,而偶数阶幻方则没有;奇数阶幻方这个中心方格上的数称为中心数。
中心数等于幻方中所有2n 个数的平均数,也等于任意一行、一列、一条对角线中n 个数的平均数,也等于任意两个关于中心对称的空格中的数的平均数;中心数22n S n =个数n=幻和。
用1、2、……、2n 这2n 个数构造n 阶幻方,其中心数为212n +。
用1、2、3、4、5、6、7、8、9这9个数构造3阶幻方,其中心数为21352+=。
五、在3阶幻方中,2222a i b h c g d f e ++++====,2f h a +=、2d h c +=、2b f g +=、2b di +=。
ihgf e d c b a幻方【例1】 请将2009、2010、2011、2012、2013、2014、2015、2016、2017这9个自然数填入图中的空格内,使每行、每列、两条对角线上的3个数之和相等。
(只要构造出一种)一、 若一个n n ⨯的方阵1111n n nna a a a 是n 阶幻方,则方阵1111n n nn a b c a b ca b ca b c⨯+⨯+⨯+⨯+也是n 阶幻方。
数表中心数幻和三阶幻方的性质幻方的构造幻方幻方与数表(本讲)200920102011201220132014201520162017201620092014201520132011201220172010201420152010201720132009201620112012201020172012201120132015201420092016201620112012201720132009201420152010201020152014200920132017201220112016201420092016201120132015201020172012201220172010201520132011201620092014【分析】 (方法一)第一步——求幻和:幻和为(200920102011201220132014201520162017)36039++++++++÷=;第二步——求中心数:中心数为603932013÷=;第三步——确定4个角上的数:用尝试法,可推出4个角上的数只能为偶数; 第四步——求出幻方:根据幻和求出各边中点的数,求出1个基本解; 以基本解为基础,可通过旋转或镜像变换得到其它各解,共8解。
四年级计算幻方与数表教师版

知识要点幻方与数表一、 如果一个n n ⨯的方阵中,每一横行、每一竖列以及两条对角线上数的和都相等,那么这个方阵称为n 阶幻方。
二、 在n 阶幻方中,其每一行、每一列、两条对角线上的数字之和都相等,这个和称为幻和。
对于n 行或者n 列,其和为幻和乘以n ,也等于所有2n 个数的和;所以,幻和2n S n=个数。
用1、2、……、2n 这2n 个数构造n 阶幻方,其幻和为2212(1)2n n n n ++++=……; 用1、2、3、4、5、6、7、8、9这9个数构造3阶幻方, 其幻和为21234567893(13)1532++++++++⨯+==。
三、 对于n 阶幻方,当n 分别为奇数或偶数时,幻方有一个明显的不同,即奇数阶幻方有一个中心方格,而偶数阶幻方则没有;奇数阶幻方这个中心方格上的数称为中心数。
中心数等于幻方中所有2n 个数的平均数,也等于任意一行、一列、一条对角线中n 个数的平均数,也等于任意两个关于中心对称的空格中的数的平均数;中心数22n S n =个数n=幻和。
用1、2、……、2n 这2n 个数构造n 阶幻方,其中心数为212n +。
用1、2、3、4、5、6、7、8、9这9个数构造3阶幻方,其中心数为21352+=。
四、在3阶幻方中,2222a i b h c g d f e ++++====,2f h a +=、2d h c +=、2b f g +=、2b di +=。
ihgf e d c b a幻方【例1】 请将2009、2010、2011、2012、2013、2014、2015、2016、2017这9个自然数填入图中的空格内,使每行、每列、两条对角线上的3个数之和相等。
(只要构造出一种)200920102011201220132014201520162017201620092014201520132011201220172010201420152010201720132009201620112012201020172012201120132015201420092016201620112012201720132009201420152010201020152014200920132017201220112016201420092016201120132015201020172012201220172010201520132011201620092014【分析】 (方法一)第一步——求幻和:幻和为(200920102011201220132014201520162017)36039++++++++÷=;第二步——求中心数:中心数为603932013÷=;第三步——确定4个角上的数:用尝试法,可推出4个角上的数只能为偶数; 第四步——求出幻方:根据幻和求出各边中点的数,求出1个基本解; 以基本解为基础,可通过旋转或镜像变换得到其它各解,共8解。
幻方和数阵(精选)

幻方的起源
幻方的结构
杨辉(南宋)
中国研究幻方的第一人
载九履一,左三右七,二四为肩,六八为足, 以五居中,五方白圈皆阳数,四隅黑点为阴数
492 357 816
三阶幻方:在三行三列的正方形方格中,既不重 复又不遗漏地填上3×3个连续的自然数,使每一 行、每一列、每条对角线上的三个数的和均相等。 通常这样的图形叫做三阶幻方。 在三阶幻方中有: (1)幻和=九个数之和÷3, (2)中间数=幻和÷3. (3)C=(A+B)÷2 (如右图)
幻和=(1+2+3+…+8+9) ÷3=15
1 2 34 5 67 8 9
◆例1 将1、2、3、4、5、6、7、8、9九个数
填入下图的九个方格里,使每行、每列、每条 对角线上的三个数的和都相等。
1填首行正中央
依次斜上莫要忘。
罗
伯
上出下填右出左
法
若是重了填下方
◆例2 用2~10九个数填入下图的九个方格里,
九个连续的自然数中,第五个数是中间数,第二、 四、六、八个数是四角上的数。
1 2 34 5 67 8 9
◆例1 将1~9九个自然数填入下图的九个方 格里,使每行、每列、每条对角线上的三 个数的和都相等。
定中间数,填四角数,算其余数
把九个数最中间的一个填在方 格的正中央,第二、四、六、 八个数分别填在四个角上。
使每行、每列、每条对角线上的三个数的和都 相等。
4
3
7
添 耳
朵
2
6
10
法
5
9
8
◆例2 用5~20这16个数填入下图的16个方格里, 使每行、每列、每条对角线上的四个数的和都 相等。
小学数学《数表与幻方》练习题

数表与幻方幻方是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的3×3的数阵称作三阶幻方,4×4的数阵称作四阶幻方,5×5的称作五阶幻方…… 如图为三阶幻方、四阶幻方的标准式样,三阶幻方的中心位置上的数等于所有所填数的平均数,也等于横行、竖列、对角线上数和的三分之一.解决数表类问题中,首先要找出数填写的规律,再从规律中找到数表的数量关系,从而找出解决问题的关键.(一)幻方【例1】 3×3的正方形中,在每个格子里分别填入1~9的9个数字,要求每行每列对角线上的三个数的和相等,请给出至少一种填法【例2】 请你将1~25这二十五个自然数填入图中的空格内每行、每列、每条对角线上的五数之和相等.【例3】 用11,13,15,17,19,21,23,25,27编制成一个三阶幻方.987654321 14115106213169711548312【例4】 将九个数填入左下图的九个空格中,使得任一行、任一列以及两条对角线上的三个数之和都等于定数k ,则中心方格中的数必为k ÷3【例5】 在3×3的方格中,如果要求填入九个互不相同的质数,要求任一行、任一列以及两条对角线上的三个数之和都相等,那么这样填好的图称为三阶质数幻方.求任一列、任一行以及两条对角线上的三个数之和都等于267的三阶质数幻方.【例6】 在九宫图中,第一行第三列的位置上填5,第二行第一列位置上填6,如图.请你在其他方格中填上适当的数,使方阵横、纵、斜三个方向的三个数之和均为27.【例7】 将1、2、3、4、5、6、7、8、9这九个数字,分别填入3×3阵列中的九个方格,使第二行组成的三位数是第一行组成的三位数的2倍,第三行组成的三位数是第一行组成的三位数的3倍.【例8】 已知如图是一个四阶幻方,那么标有*的方格中所填的数是多少?3811165*49712(二)数表【例9】 如图,横、竖各有12个方格,每个方格内都有一个数.已知横行上任意3个相邻数之和为20,竖列上任意3个相邻数之和为2l ,并且其中4个方格内的数分别是3,5,8和x .那么x 所代表的数是多少?【例10】 请在4×8方格表的每个方格内填入数1,2或3,使得任何排列如图所示形状的4个方格中所填数的和都是7.【例11】 如图表中所示的顺序,将正整数1、2、3、4、5……按顺序依次填入,求2007在第几行第几列?第一列 第二列 第三列 第四列……第一行 1 2 5 10 17 第二行 4 3 6 11 第三行 9 8 7 12 第四行 16 15 14 13 ……【例12】 将1~8填入右图中的○内,要求按照自然数顺序相邻的两个数不能填入有直线段连接的相邻的两个○内.83x51.将九个连续自然数填入3行3列的九个空格中,使每一横行及每一竖列的三个数之和都等于60.2.用1,3,5,7,9,11,13,15,17编制成一个三阶幻方.3.在图中的每个空格内填入一个数,使得每行、每列及两条对角线上的3个方格中的各数之和都等于19.95.那么,标有*的格内所填的数是多少?4.在如左图6×6的方格网中填入1、2、3这三个数,使得用右图任意一种图形覆盖方格网,盖住的数和为12.5.将1~10这十个自然数分别填入下左图中的10个圆圈内,使五边形每条边上的三数之和都相等,并使值尽可能大.*8.804.33。
4年级-6-幻方和数阵图

传说在五千年前,大禹治水的时代,人们在黄河中发现一只大龟,龟背上有一些奇怪的图案,经过破译,人们将龟背上的神奇的图案译成了如下图这样的数阵图,也称做幻方。
幻方和数阵是我国文化遗产之一,早在公元前4世纪就有“河图”、“洛书”的传说与记载。
到了宋朝,杨辉对幻方已有较详细的记述,并探索出一些编制方法。
明朝程大位、清朝张潮等人,创制了绚丽多彩的幻方与数阵图式,其中九宫图是最简单的三阶幻方。
将三阶幻方推广,结合某些几何图形,把一些数字填入图形的某种位置上,并使数字满足一定的约束条件,这类问题,通常被称为“数阵图”。
幻方是特殊的数阵图。
大约在15世纪初,幻方传到国外,引起了欧洲很多数学家的兴趣,发现许多新成果。
人们发现幻方不仅仅是一种数字游戏,而且与实验方案的设计及一些高深数学分支有关,幻方已成为数阵图中最重要的课题,是数学研究中的一个重要分支。
数阵图大致分三种:封闭型数阵图、开放型数阵图和复合型数阵图。
幻方的特点:一个幻方每行、每列、每条对角线上的几个数的和都相等。
这个相等的和叫“幻和”。
要求在n 行n 列的方格里,既不重复又不遗漏地填上n ×n 个连续的自然数。
这些自然数所组成的一列数有极强的规律性,按顺序排列后,每一项都比它前面的一项大1,即它们构成了差相等的数列,是等差数列。
因此在解答这类问题时,常用的知识有: 1.等差数列的求和公式总和=(首项+末项)×项数÷2 2.数字的奇偶性 奇数±奇数=偶数偶数±偶数=偶数知识梳理奇数±偶数=奇数可简记为:同性为偶,异性为奇(注:同性是同奇或同偶,异性是指一奇一偶)。
数阵图【例1】★如图所示,在三个圆圈中各填入一个自然数,使每条线段两端的两个数之和均为奇数。
请问这样的填法存在吗?如不存在,请说明理由;如存在,请写出一种填法。
【例2】★小蜗牛不小心爬到一个三角形数阵图中,必须将1~6六个自然数分别填入下图的○内,使三角形每边上的三数之和都等于11才能通过这个数阵图,你能帮它吗?614532【小试牛刀】把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13.典型例题【例3】★把1~7这七个自然数,分别填在下图(1)的圆圈内,使每条直线上的三个数的和都相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幻方与数表
第六级上认识数阵图
⑴放射型数阵图;⑵掌握三种类型数阵图的填法。
第七级下幻方与数表
⑴认识幻方及其中心数,幻和等一些性质;⑵掌握准确构造或填补幻方的方法与技巧;⑶
掌握数表填补的方法和技巧。
第八级上数列与数表综合㈠
⑴系统巩固与数列数表有关的思路方法;⑵会求解综合性的数表问题;⑶熟练掌握周期法在数表问题中的运用;⑷初步掌握递推方法在数列与数表中的运用。
左边这个戴眼镜的男生叫铮铮,右边这个胖胖的男生叫昊昊。
他们两个是很好的朋友,但是两个人的性格可是大不相同。
铮铮学习好,喜欢看书,也因此早早就戴上了眼镜。
铮铮的绝招就是可以模仿柯南制造眼镜闪光纪录是连续眼镜闪光200次,闪晕同班17名同学!昊昊很喜欢吃东西,别看他胖胖的,却很喜欢运动。
昊昊也有一个很大的缺点,就是粗心大意。
昊昊也曾经创下出家门以后连续9次回家去取落下的东西的纪录!
他先后把铅笔盒、笔记本、作业、书包、饭盒…忘在家里。
看了这些介绍,同学们是不是很想知道在铮铮和昊昊身上都发生过什么事情呢?下一讲里,我们将继续介绍他们的一个好朋友。
关于他们的故事,以后还多着呢!
上面这个女孩名字叫做包包,至于为什么叫做包包不是因为她可爱,而是因为她的头上“长
了”两个包,虽然是一个非常聪明乖巧的女孩,偶尔也会做一些意义不明的事情,比如她曾经偷拿了老师的印章往自己身上狂盖…作为一名很有主见的女生,包包人生中的一大乐趣就是和铮铮斗嘴,和铮铮昊昊不同,包包是一个非常非常“正常”的人。
将20以内除数1以外的所有奇数编成一个3阶幻方。
请将2009,2010,2011,2012,2013,2014,2015,2016,2017这9个自然数填入图中的空格内,使每行、每列、两条对角线上的3个数之和相等。
(只要构造出一种)
(2007年春武汉明心奥数挑战赛五年级)在如图所示的魔方空格中填入5个数字,使魔方的每
一行、每一列、两 条对角线上的数字之和都相等。
请问这5个数字之和是_____。
(2007年12月第九届“中环杯”小学生思维能力训练活动四年级初赛)如图,要在下面的空格中填入适当的数,使每行、每列及对角线的3个数之和都相等,问号处应填入的数。
要求写出关键的解题推理过程。
例4
例3
例2
例1
例5
在下面3×3的表格中,填入7个不同自然数,使得对于表格中每行、每列、两条对角线上的3个数之和等于21。
例6
(2008年第十二届香港保良局小学数学世界邀请赛队际赛)如图,11个方格内分别各填入一个数,使得任何连续三个方格内所填的数之和为21。
已知第一个方格内所填的数为7,第九个方格内所填的数为6(方格由左向右数起)。
请问第2个方格内所填的数是什么?
测试题
1.将5,10,15,20,25,30,35,40,45这九个数分别填入下图,使每一行、每一列、两条对角线上三个数的和相等。
2.(2008年第十七届日本小学算术奥林匹克大赛初小组预赛)在55
⨯的方格表中放置16枚地雷,每个格子最多1枚地雷;使得在没有地雷的格子中标上数(这个数表示它周围格子中地雷的数量)时,恰好是0~8这九个数,例如图1就是满足要求;在图2中,已知其中一个格子填的数是3,请你将地雷和其它数都填出来。
3.(2008年3月第九届“中环杯”小学生思维能力训练活动六年级决赛)如图所示,9个小正方形内各填入一个有理数,使每行每列以及两条对角线上的三个有理数的和相等。
现在29和76两个数已给出,那么x=( )。
4.请编出一个三阶幻方,使其幻和为24。
答案
1.【解析】
答案如图所示。
2.【解析】
设i j R C 表示第i 行、第j 列方格中的数或地雷(,1i j =,2,3,4,5)25个格子中放入9
个数,16个地雷。
先考虑数0所在的位置。
数0周围都是数。
假设120R C =;1113212223R C R C R C R C R C =====数;所以,110R C =;矛盾;所以,假设120R C =不成立;所以,120R C ≠;同理,140R C ≠,210R C ≠,250R C ≠,410R C ≠,450R C ≠,520R C ≠,540
R C ≠。
假设220R C =;1112132123313233R C R C R C R C R C R C R C R C ========数; 所以,1112210R C R C R C ===;矛盾;所以,假设220R C =不成立;所以,220R C ≠;同理,240R C ≠,420R C ≠,440R C ≠。
假设230R C =;1213142224323334R C R C R C R C R C R C R C R C ========数;
所以,130R C =;矛盾;所以,假设230R C =不成立;所以,230R C ≠;同理,320R C ≠,340R C ≠,430R C ≠。
假设330R C =;2223243234424344R C R C R C R C R C R C R C R C ========数;所以,23R C ≤3,32R C ≤3,34R C ≤3,43R C ≤3;不存在4个小于等于3的正整数;矛盾;所以,22R C ≤5,23R C ≤3,24R C ≤5,32R C ≤3,34R C ≤3,42R C ≤5,43R C ≤3,44R C ≤5
;不存在8个小于等于5的正整数;矛盾;
所以,假设330R C =不成立;所以,330R C ≠。
假设130R C =;1214222324R C R C R C R C R C =====数;
所以,12R C ≤2,14R C ≤2,22R C ≤5,23R C ≤3,24R C ≤5;假设121R C =,则142R C =,
233R C =,245R C =,224R C =;当21R C =地雷时,111R C =,矛盾;当11R C =地雷时,
213R C =,矛盾;
所以,假设121R C =不成立;所以,121R C ≠;同理,521R C ≠;所以,130R C ≠;同理,310R C ≠,350R C ≠,530R C ≠。
所以,110R C =或150R C =或510R C =或550R C =。
令110R C =;12R C ≤2,21R C ≤2, 223R C =或4。
再考虑数8所在的位置。
数8周围都地
雷,且数8不能在角或边上。
假设448R C =;假设121R C =;则212R C =,224R C =;当427R C =时,414R C =或512R C =或524R C =;矛盾;所以,427R C ≠;
当247R C =时,426R C =;413R C =,523R C =或512R C =;矛盾;所以,247R C ≠; 所以,121R C ≠;同理,211R C ≠;所以,338R C ≠。
假设438R C =;则只能247R C =;数6没有填写的地方;所以,438R C ≠;同理,348R C ≠。
所以,428R C =或248R C =。
令428R C =。
假设23R C =地雷;13R C =数,133R C =;所以,15R C =地雷,55R C =地雷;所以,347R C =,446R C =或346R C =,447R C =;当347R C =,446R C =时,数5无法填写;当346R C =,447R C =时,数5无法填写;所以,假设假设23R C =地雷不成立;23R C ≠地雷。
所以,13R C =地雷;23R C ≤6。
此时各边的中间一个方格只剩下35R C 没有填写;所以353R C =。
所以,235R C =或6。
当236R C =时,数5无法填写。
所以,235R C =,246R C =。
综上所述,110R C =、121R C =、212R C =、353R C =、224R C =、235R C =、246R C =、447R C =、428R C =。
通过镜面反射(上下对称)可以得到510R C =、521R C =、
412
R C =、353R C =、424R C =、435R C =、446R C =、247R C =、228R C =。
答案如图
所示。
3.【解析】 中心数297610552.52
2
x +=
==
4.【解析】
根据题意,要求其三阶幻方的幻和为24,所以中心数为2438÷=。
既然8是中心数,那么与8在一条直线的各个组的其余两数的和为16,分别有
11516,21416,31316
41216,51116,610167916
+=+=+=+=+=+=+=,
按上述条件进行估算后填出,然后再进行调整即可正确的答案。
11
4
9
68107125。
