比例
比例怎么注写

比例怎么注写比例指的是两个事物之间的相对关系,通常用分数、百分数或者百分比来表示。
在数学和统计学中,比例是用于比较两个数量之间的相对大小。
在生活中,比例也常常用于描述事物的相对大小、比较不同事物的关系。
比例的表达方法有几种,以下是常见的几种表达方法:1. 分数形式:比例可以用一个分数表达,其中分子表示两个事物中的一个的数量,而分母表示另一个事物的数量。
例如,如果有3个苹果和5个橙子,比例可以用3/5来表示。
分数形式的比例可以简化,例如3/5可以约分为3:5。
2. 百分数形式:比例也可以用百分数来表示,其中数字表示一个事物占另一个事物的百分比。
例如,如果有40个男孩和60个女孩,比例可以用40%来表示。
百分数形式的比例可以换算成分数,例如40%可以换算成40/100。
3. 百分比形式:比例也可以用百分比符号(%)表示,例如比例可以写成2:3,表示两个事物之间的比例为2比3。
百分比形式通常在图表和统计数据中使用,以更直观地表示比例关系。
表示比例的方法取决于具体的使用场景和需求。
在解决实际问题时,根据不同问题的特点和要求,选择合适的比例表达方法能更好地描述事物的相对关系。
在实际生活和工作中,比例的应用非常广泛。
以下是一些常见的应用场景:1. 商业领域:比例可以用于分析销售额、市场份额、利润率等指标的占比关系,帮助企业了解业务运营情况,并作出相应的决策。
2. 统计学:比例在统计学中有很多应用,如调查问卷中的样本比例、概率比例、人口比例等。
通过研究和分析比例的变化,可以为决策制定提供重要参考。
3. 地理学:比例可以用于表示地图上的距离和面积的比例关系,例如1:100000的比例尺表示1厘米在地图上对应100000厘米的实际距离。
4. 工程领域:比例可以用于计算设计图纸上的缩放比例,以确保设计结果符合实际要求。
总之,比例作为描述事物相对关系的一种数学工具,在各个领域都有广泛的应用。
通过选择合适的比例表达方法,可以更好地理解和分析比例关系,为决策提供有力支持。
比例的公式及计算方法

比例的公式及计算方法
比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比。
公式为:比例尺
=图上距离与实际距离的比。
比例尺有三种表示方法:数值比例尺、图示比例尺和文字比
例尺。
地理比例尺分类:
压缩尺:
放大比例尺和地图比例尺的'计算方法相同。
但放大比例尺是指图上距离比实际距离
放大的倍数。
如:原长度为1cm的零件,画在图纸上为10cm,则这幅图的比例尺为10:1。
压缩比例尺的分母(后项)通常为1。
分子越大,比例尺就越大,内容也越详尽,精
度越高。
(备注:此为压缩比例尺,所以分母(后项)通常为1)
缩小尺:
增大比例尺的分子(前项)通常为1。
例如:1:(1/)
扩大比例比号(后项)通常为1.如:1(/1)
计算方法:
如果将原比例尺放大到n倍;那么原比例×n。
如果将原比例尺增大至1/n;那么原比例×1/n。
比例尺缩放后,原面积之比会变为缩放倍数的平方。
三个数算比例的公式

三个数算比例的公式
三个数之间的比例可以通过以下公式来计算:
比例=第二个数/第一个数=第三个数/第二个数=第三个数/第一个数在数学中,比例是指两个量之间的相对大小关系。
比例可以表示为分数形式,也可以表示为百分比形式。
1.分数形式的比例:对于三个数a、b和c,比例可以用以下分数形式表示:
比例=b/a=c/b=c/a
2.百分比形式的比例:如果要将比例转化为百分比形式,则将比例乘以100,得到的结果即为百分比形式的比例。
以下是一些示例来说明如何使用上述公式计算三个数之间的比例。
示例1:
假设有三个数:a=2,b=4,c=8、计算这三个数之间的比例。
比例=b/a=4/2=2
比例=c/b=8/4=2
比例=c/a=8/2=4
因此,这三个数之间的比例为2:2:4
示例2:
假设有三个数:a=5,b=3,c=15、计算这三个数之间的比例。
比例=b/a=3/5≈0.6
比例=c/b=15/3=5
比例=c/a=15/5=3
因此,这三个数之间的比例为0.6:5:3
示例3:
假设有三个数:a=8,b=12,c=16、计算这三个数之间的比例,并将结果转化为百分比形式。
比例=b/a=12/8=1.5
比例=c/b=16/12≈1.33
比例=c/a=16/8=2
将比例转化为百分比形式:
比例=1.5*100≈150%
比例≈1.33*100≈133%
比例=2*100=200%
因此,这三个数之间的比例为150%:133%:200%。
比例的知识点总结

比例的知识点总结一、比例的意义。
1. 定义。
- 表示两个比相等的式子叫做比例。
例如:2∶3 = 4∶6,这里2∶3和4∶6是两个比,因为它们的比值相等(2∶3 = 2÷3=(2)/(3),4∶6 = 4÷6=(2)/(3)),所以这两个比可以组成比例。
2. 比例的各部分名称。
- 组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项,中间的两项叫做比例的内项。
例如在比例3∶4 = 9∶12中,3和12是外项,4和9是内项。
- 在比例里,两个外项的积等于两个内项的积,这是比例的基本性质。
如3×12 = 4×9 = 36。
二、解比例。
1. 定义。
- 求比例中的未知项,叫做解比例。
2. 方法。
- 根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。
例如:解比例x∶2 = 3∶4,根据比例的基本性质可得4x = 2×3,即4x = 6,解得x=(6)/(4)=(3)/(2)。
三、正比例和反比例。
1. 正比例。
- 定义。
- 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
例如:汽车行驶的速度一定时,路程和时间是成正比例的量。
因为速度=(路程)/(时间)(速度一定),如速度为60千米/小时,当时间是1小时,路程是60千米;当时间是2小时,路程是120千米,(60)/(1)=(120)/(2) = 60。
- 正比例关系的图像。
- 是一条经过原点的直线。
2. 反比例。
- 定义。
- 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
例如:当长方形的面积一定时,长和宽是成反比例的量。
因为面积 = 长×宽(面积一定),如面积是24平方厘米,当长是8厘米时,宽是3厘米;当长是6厘米时,宽是4厘米,8×3 = 6×4 = 24。
人体黄金比例

人体黄金比例
上身与下身的标准比例为0.69,黄金比例为0.618。
1、大部分人的上下身标准比例为0.69:上下身的分界点是耻骨联合处。
测量方式从臀线开始量,测量颈后骨即挺胸低头时后颈最突出的部位到尾龙骨即臀部正中间比较尖的那块小骨头的距离,这个是上半身长度。
测量臀部皱褶即直立时大腿后侧与臀部的折线到赤脚的地面距离,这个是下半身长度。
用下半身长度减去上半身长度后得出一数值,就是上下身比例。
2、上下身的黄金比例为0.618:上下身的黄金比例符合黄金分割定律,即肚脐以上的身体长度与肚脐以下的比值是0.618:1.符合此比例的身材即为人口中的“黄金身材”。
每个人的上下身比例都不同,与生长发育、营养状况、遗传等多种因素有关,只要比例不影响人体健康都是正常的。
第2讲.比和比例

第二讲比和比例教学目标1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化,有目的的转化;4、单位“1”变化的比例问题5、方程解比例应用题知识点拨比例与百分数作为一种数学工具在人们日常生活中处理多组数量关系非常有用,这一部分内容也是小升初考试的重要内容.通过本讲需要学生掌握的内容有:一、比和比例的性质性质1:若a: b=c:d,则(a + c):(b + d)= a:b=c:d;性质2:若a: b=c:d,则(a - c):(b - d)= a:b=c:d;性质3:若a: b=c:d,则(a +x c):(b +x d)=a:b=c:d;(x为常数)性质4:若a: b=c:d,则a×d = b×c;(即外项积等于内项积)正比例:如果a÷b=k(k为常数),则称a、b成正比;反比例:如果a×b=k(k为常数),则称a、b成反比.二、主要比例转化实例①x ay b=⇒y bx a=;x ya b=;a bx y=;②x ay b=⇒mx amy b=;x may mb=(其中0m≠);③x ay b=⇒x ax y a b=++;x y a bx a--=;x y a bx y a b++=--;④x ay b=,y cz d=⇒x acz bd=;::::x y z ac bc bd=;⑤x的ca等于y的db,则x是y的adbc,y是x的bcad.三、按比例分配与和差关系⑴按比例分配例如:将x个物体按照:a b的比例分配给甲、乙两个人,那么实际上甲、乙两个人各自分配到的物体数量与x的比分别为():a a b+和():b a b+,所以甲分配到axa b+个,乙分配到bxa b+个.⑵已知两组物体的数量比和数量差,求各个类别数量的问题例如:两个类别A、B,元素的数量比为:a b(这里a b>),数量差为x,那么A的元素数量为axa b-,B的元素数量为bxa b-,所以解题的关键是求出()a b-与a或b的比值.四、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“l”。
人体比例标准对照表
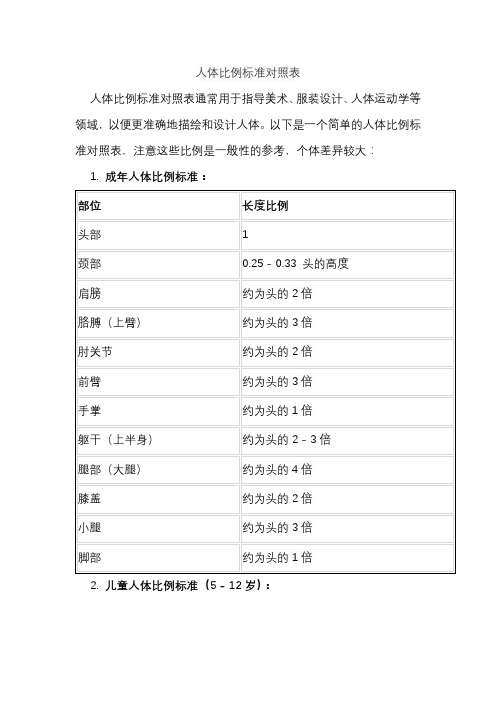
人体比例标准对照表通常用于指导美术、服装设计、人体运动学等领域,以便更准确地描绘和设计人体。以下是一个简单的人体比例标准对照表,注意这些比例是一般性的参考,个体差异较大:
1.成年人体比例标准:
部位
长度比例
头部
1
颈部
0.25 - 0.33 头的高度
肩膀
约为头的2倍
胳膊(上臂)
约为头的3倍
头部逐渐缩小,身体比例均衡
3.婴幼儿人体比例标准:
年龄阶段
头部与身高的比例
身体各部分相对比例
0 - 2岁
约为1:3.5 - 4
头部相对较大,身体较短
这些比例标准可以作为绘画、设计等领域的参考,但需要注意每个人的体型和比例有很大的个体差异,所以在实际应用时可以根据实际情况进行微调。
肘关节
约为头的2倍
前臂
约为头的3倍
手掌
约为头的1倍
躯干(上半身)
约为头的2 - 3倍
腿部(大腿)
约为头的4倍
膝盖
约为头的2倍
小腿
约为头的3倍
脚部
约为头的1倍
2.儿童人体比例标准(5 - 12岁):
年龄组
头部与身高的比例
身体各部分相对比例
5 - 岁
约为1:4.5
头部相对较大,躯干较短
9 - 12岁
约为1:4
1比多少的公式表格

1比多少的公式表格全文共四篇示例,供读者参考第一篇示例:1比多少的公式表格包括了数学中常见的比例关系公式,可以帮助我们解决各种实际问题中涉及到的比例计算。
在日常生活和工作中,我们经常会遇到各种比例关系的计算问题,比如商业中的成本与收益比例、物理中的速度与时间比例、化学中的溶液浓度比例等等。
掌握了这些比例关系公式,我们就能更方便地处理这些问题。
下面我为大家整理了一份关于1比多少的公式表格,希望对大家有所帮助:| 比例关系| 公式|| ------------------- | --------------------------------- || 1比2 | 1:2 = 1 / 2 = 0.5 || 1比3 | 1:3 = 1 / 3 ≈ 0.333 || 1比4 | 1:4 = 1 / 4 = 0.25 || 1比5 | 1:5 = 1 / 5 = 0.2 || 1比6 | 1:6 = 1 / 6 ≈ 0.166 || 1比7 | 1:7 = 1 / 7 ≈ 0.142 || 1比8 | 1:8 = 1 / 8 = 0.125 || 1比9 | 1:9 = 1 / 9 ≈ 0.111 || 1比10 | 1:10 = 1 / 10 = 0.1 || 1比20 | 1:20 = 1 / 20 = 0.05 || 1比50 | 1:50 = 1 / 50 = 0.02 || 1比100 | 1:100 = 1 / 100 = 0.01 || 1比1000 | 1:1000 = 1 / 1000 = 0.001|| 1比10000 | 1:10000 = 1 / 10000 = 0.0001 |比例关系公式的掌握对我们在解决实际问题中的比例计算至关重要,希望大家可以通过这份公式表格更好地理解和运用比例关系。
希望大家在学习和工作中都能够运用这些比例关系公式,更好地解决各种实际问题。
祝大家学习进步,工作顺利!第二篇示例:1比多少的公式表格是一种常见的数学工具,它可以帮助我们比较两个量之间的大小关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、判断题:1、圆的面积和圆的半径成正比例。
()2、圆的面积和圆的半径的平方成正比例。
()3、圆的面积和圆的周长的平方成正比例。
()4、正方形的面积和边长成正比例。
()5、正方形的周长和边长成正比例。
()6、长方形的面积一定时,长和宽成反比例。
()7、长方形的周长一定时,长和宽成反比例。
8、三角形的面积一定时,底和高成反比例。
()9、梯形的面积一定时,上底和下底的和与高成反比例。
()10、圆的周长和圆的半径成正比例。
()二、判断下面每题中的三个量成什么比例?(1)速度、路程和时间(2)工作总量、工作效率和工作时间(3)单价、总价和数量(4)平行四边形的面积、底和高(5)总千克数、每天吃的千克数和天数三、下列各题中的两种量是不是成比例,成什么比例,并说明理由。
(1)买相同的电脑,购买的电脑台数与总价(2)每捆练习本的本数相同,练习本的总本数与捆数(3)总路程一定,已行的路程与未行的路程(4)分数值一定,分数的分子与分母(5)长方形的长一定,它的面积和宽(6)长方体的体积一定,底面积和高(7)圆的周长和直径(8)一本书的总页数一定,看的天数与平均每天看的页数(9)订阅《扬子晚报》,订的份数与总价(10)图上距离一定,实际距离与比例尺(11)小麦的出粉率一定,小麦的质量与面粉的质量(12)六(1)班同学做操,每排站的人数与排数四、下面题里的数量成什么关系?你能列出式子表示数量之间的相等关系吗?(1小红看一本儿童小说,每天看12页,10天可以看完;如果每天看15页,8天可以看完。
(2)一种螺丝钉,20个重30克。
一盒这样的螺丝钉是600克,一共有400个。
五、填空1、速度一定,路程和时间()比例路程一定,速度和时间()比例时间一定,路程和速度()比例2、工作效率一定,工作总量和工作时间()比例工作时间一定,工作效率和工作总量()比例工作总量一定,工作效率和工作时间()比例3、总价一定,单价和数量()比例数量一定,单价和总价()比例单价一定,数量和总价()比例4、每公顷产量一定,总产量和公顷数()比例公顷数一定,每公顷产量和总产量()比例总产量一定,每公顷产量和公顷数()比例5、份数一定,每份数和总数()比例每份数一定,份数和总数()比例总数一定,每份数和份数()比例6、商一定,除数和被除数()比例除数一定,商和被除数()比例被除数一定,除数和商()比例7、积一定,两个因数()比例一个因数一定,另一个因数和积()比例8、和一定,两个加数()比例一个加数一定,另一个加数与和()比例9、差一定,减数和被减数()比例减数一定,被减数和差()比例被减数一定,减数和差()比例10、前项一定,比的后项和比值()比例比值一定,比的前项和后项()比例后项一定,比的前项和比值()比例11、分数值一定,分子和分母()比例分母一定,分数值和分子()比例分子一定,分数值和分母()比例12、在长方形中,长一定,面积和宽()比例宽一定,面积和长()比例面积一定,长和宽()比例周长一定,长和宽()比例长一定,周长和宽()比例宽一定,周长和长()比例13、在平行四边形里,底一定,面积和高()比例高一定,面积和底()比例面积一定,底和高()比例14、在三角形里,底一定,面积和高()比例高一定,面积和底()比例面积一定,底和高()比例15、在正方形中,边长和周长()比例面积和边长()比例16、在圆中,面积和半径()比例周长和半径()比例直径和半径()比例直径和面积()比例17、在长方体中,底面积一定,体积和高()比例体积一定,底面积和高()比例高一定,底面积和体积()比例18、在比例尺中,比例尺一定,图上距离和实际距离()比例图上距离一定,比例尺和实际距离()比例实际距离一定,比例尺和图上距离()比例19、用大豆榨油时,出油率一定时,油的重量和大豆的重量()比例大豆的重量一定,油的重量和出油率()比例油的重量一定时,大豆的重量和出油率()比例20、甲×乙=丙,当丙一定时,甲和乙()比例当甲一定时,丙和乙()比例当乙一定时,甲和丙()比例21、车轮的周长(或半径、直径)一定,车轮前进路程和转数()比例22、一堆煤的总重量一定,烧去的和剩下的()比例23、要行的总路程一定,已经走过的路程和剩下的路程()比例24、在规定的时间里,制造每个零件的时间和制造零件的个数()比例25、一批纸总页数一定,装订练习本本数和每本练习本的页数()比例26、每件上衣用布量一定,做上衣的件数和用布总米数()比例27、每块砖的面积一定,铺地总面积和用砖的总块数()比例28、铺地总面积一定,每块砖的面积和用砖的总块数()比例29、每立方厘米的铁的重量一定,铁的总重量和体积()比例30、购买各种货物的总价和数量()比例31、互相咬合的齿轮的齿数和转数()比例32、一个人的身高和体重()比例33、一个人的年龄和身高()比例35、总人数一定,每排人数和排数()比例36、一堆货物的总重量一定,每辆车的载重量和汽车辆数()比例37、正方体的棱长一定,它的体积和表面积()比例38、一条公路的全长一定,已经修好的和没修好的()比例39、同样的铁丝,每米长的重量一定一、口答.1.8是5的百分之几?2.5是8的百分之几?二、把下面各数化成百分数.0.25 1.0410.415三、求出下面的商,并且所得的商化成百分数.1.3÷82.20÷163.3.5÷74.22.4÷14四、应用题.1.一个田径队有男生20人,女生15人,男生人数是女生人数的百分之几?2.一个田径队有男生20人,女生15人,女生人数是男生人数的百分之几?3.李冰在一次测验中,做对的题数是11道,错了4道,李冰在这次测验中做对题数占总题数的百分之几?4.大米加工厂用2000千克的稻谷碾出1600千克大米,求稻谷的出米率.5.林场春季植树,成活了24570棵,死了630棵,求成活率.6.家具厂有职工1250人,有一天缺勤15人,求出勤率.百分数的应用(一)1、把下面各数化成百分数:0.25= 1.04=1=0.415=2、求出下面的商,并且所得的商化成百分数。
5÷6 24÷15 3.5÷722.4÷143、一个田径队有男生20人,女生15人,男生人数是女生人数的百分之几?4、李冰在一次测验中,做对的题数是11道,错了4道,李冰在这次测验中做对题数占总题数的百分之几?5、大米加工厂用2000千克的稻谷加工成大米时,共碾出大米1600千克,求大米的出米率。
6、林场春季植树,成活了24570棵,死了630棵,求成活率。
7、家具厂有职工1250人,有一天缺勤15人,求出勤率。
8、机床厂生产一批零件,合格品有385个,不合格品有17个,这批零件的合格率是多少?9. 小华和小明各集邮票45张,小华的邮票给小明5张,这时,小华的邮票是“小明”的百分之几?10、500千克小麦可以磨面粉425千克面粉,小麦的出粉率是多少?11、食堂为大米300千克,吃了40%,吃了多少千克?12、小明家养鸡60只,养鹅50只。
(1)鸡是鹅的百分之几?(2)鹅是鸡的百分之几?(3)鸡比鹅多百分之几?(4)鹅比鸡少百分之几?小学六年级数学毕业复习资料(一)整数小数分析填空:1、把下面的数位顺序表填完整:数位整数部分小数点小数部分……千亿位亿级千万位十万位百位个位十分位千分位…计数单位……十亿亿百万万千十个百分之一万分之一…数级……万级…………2、自然数的单位是(),78是由这样的()个单位组成。
3、在自然数中,最大的三位数是(),最小的二位数是(),它们相差()。
4、三个连续的自然数之和是60,这三个数是()。
5、用2、3、1、0、5、8、6这七个数组成一个最大的七位数是(),最小的七位数是()。
6、一个数,十位上是4,十分位是7,千分位上是2,其余各位上都是0,这个数写作()。
7、六亿零二十七万八千零一写作()。
8、把9460000000改写成用“亿”作单位的数是(),用四舍五入法去掉亿后面的尾数后是();把598400改写成用“万”作单位的数是(),将这个数四舍五入到万位后是()。
9、2003年世界人口是6179300000人,读作(),改写成用“亿”人用单位的数,是()亿人。
2004年底我国总人口为129988万人,读作()人,四舍五入到亿位约是()亿,如果每人都节约1分钱,全国就可以节约()万元。
10、一个数省略“万”后的尾数是9万,这个数在()~()之间。
11、敏敏在读一个小数时,把小数点丢了,结果读成了二万零四百零八。
原来的小数只读一个0,原来的小数是(或()。
12、一万里有()个十,0.012里有()个0.001。
0.628由()个0.1,2个()和()个()组成;它也是由()个0.001组成的。
1360890是由()个万和()个十组成的。
13、将9.52的小数点向()移动()位,这个数就扩大了100倍。
14、一个数由4个亿,78个万,34个十组成,这个数写作(),改写成用“万”作单位的数是()。
7.23亿中的2表示(),3表示()。
15、有一个小数,整数部分的万位上是自然数的单位,千位上是合数中的最小奇数,百位上是最小的质数,小数部分的百分位上是最小的合数,其余各位上都是0,这个数是()。
16、大于0.2而小于0.4的小数有()个。
17、小数点左边第四位是()位,小数点右边第三位是()位。
18、0.72里有()个千分之一,把它缩小100倍,得到的数是()。
19、一个数是由5个亿,64个万,27个十组成,这个数写作(),省略万后的尾数记作(),改写成用“亿”作单位的数是()。
20、一个数由3个1,4个0.1,5个0.01组成,这个数写作(),读作(),在这个数的未尾添上0,它的大小();如果把它的小数点去掉后,这个数就();如果把它的小数点向左移动一位,它就(),得到的小数叫做()小数。
21、一个八位数,最高数位上的数是2,千位上的数是8,十位上的数是最小的合数,其余各位上都是0,这个八位数写作()。
22、给一个自然数的末尾加上两个零,所得的数比原数多297,这个自然数是()。
23、用0、2、5、4、7、8组成不同的六位数,其中最大的比最小的数多()。
24、39个连续自然数,第一个是A,最后一个是()。
25、把一个三位小数精确到百分位后是 3.30,原来小数最小是(),最大是()。
26、一个小数的小数点向左移动三位后,再向右移动一位后是2.003,原数是( ).27、圆周率“л”是一个()。
小学六年级数学总复习资料(二)【数的整除】班级:姓名:一、填空:1、在自然数范围内,最小的质数是(),最小的合数是(),最小的奇数是(),最小的偶数是(),最小的自然数是()。
