第三章习题解答
第三章习题解答

第三章习题解答一、判断下列说法是否正确,凡对的在括号内打“√”,否则打“×”。
(1)现测得两个共射放大电路空载时的电压放大倍数均为-100,将它们连成两级放大电路,其电压放大倍数应为10000。
( )(2)阻容耦合多级放大电路各级的Q点相互独立,( )它只能放大交流信号。
( )(3)直接耦合多级放大电路各级的Q点相互影响,( )它只能放大直流信号。
( )(4)只有直接耦合放大电路中晶休管的参数才随温度而变化。
( )(5)互补输出级应采用共集或共漏接法。
( )二、现有基本放大电路:A.共射电路B.共集电路C.共基电路D.共源电路E.共漏电路根据要求选择合适电路组成两级放大电路。
(1)要求输入电阻为1kΩ至2kΩ,电压放大倍数大于3000,第一级应采用,第二级应采用。
(2)要求输入电阻大于10MΩ,电压放大倍数大于300,第一级应采用,第二级应采用。
(3)要求输入电阻为100kΩ~200kΩ,电压放大倍数数值大于100,第一级应采用,第二级应采用。
(4)要求电压放大倍数的数值大于10,输入电阻大于10MΩ,输出电阻小于100Ω,第一级应采用,第二级应采用。
(5)设信号源为内阻很大的电压源,要求将输入电流转换成输出电压,且,输出电阻R o<100,第一级应采用,第二级应采用。
三、选择合适答案填入空内。
(1)直接耦合放大电路存在零点漂移的原因是。
A.电阻阻值有误差B.晶体管参数的分散性C.晶体管参数受温度影响D.电源电压不稳定(2)集成放大电路采用直接耦合方式的原因是。
A.便于设计B.放大交流信号C.不易制作大容量电容(3)选用差分放大电路的原因是。
A.克服温漂B. 提高输入电阻C.稳定放入倍数(4)差分放大电路的差模信号是两个输入端信号的,共模信号是两个输入端信号的。
A.差B.和C.平均值(5)用恒流源取代长尾式差分放大电路中的发射极电阻R e,将使电路的。
A.差模放大倍数数值增大B.抑制共模信号能力增强C.差模输入电阻增大(6)互补输出级采用共集形式是为了使。
第三章 信道与信道容量 习题解答

,
,求
,
,
和
;
(2) 求该信道的信道容量及其达到信道容量时的输入概率分布。
解:
(1)先写出
:
根据公式
计算联合概率:
信宿端符号分布概率:
根据公式
计算:
3
求各熵: 信源熵:
比特/消息
信宿熵:
比特/消息
可疑度:
平均互信息量: 噪声熵: (2)二元对称离散信道的信道容量:
比特/消息 比特/消息
比特/秒
信源等概分布时(
解:设下标 1为原状况,下标 2为改变后状况。由
可得:
,
倍
如果功率节省一半则
倍 ,为 了 使 功 率 节 省 一 半 又 不 损 失 信 息 量 I,根 据
,可以: (1) 加大信道带宽 W,用带宽换取信噪比
,
,
7
缺点是对设备要求高。 (2) 加大传输时间 T,用传输时间换取信噪比,同理可得:
缺点是传输速度降低了。
噪声熵:
(5)平均互信息量:
2.有一个生产 A、B、C、D四种消息的信源其出现的概率相等,通过某一通信系统传输时,B和 C无误,A 以 1/4概率传为 A,以 1/4概率误传为 B、C、D,而 D以 1/2概率正确传输,以 1/2概率误传为 C,
(1)试求其可疑度?(2)收到的信号中哪一个最可靠?(3)散布度为多少? 解:(1)
,
将各数据代入: 解得:
如果
则
将各数据代入: 解得:
14.在理想系统中,若信道带宽与消息带宽的比为 10,当接收机输入端功率信噪比分别为 0.1和 10时,试
比较输出端功率信噪比的改善程度,并说明
与
之间是否存在阀值效应。
第三章存储系统(习题解答)

第三章存储系统(习题解答)————————————————————————————————作者:————————————————————————————————日期:第三章存储系统(习题参考答案)1.有一个具有20位地址和32位字长的存储器,问:(1)该存储器能存储多少个字节的信息?(2)如果存储器由512K×8位SRAM芯片组成,需要多少芯片?(3)需要多少位地址作芯片选择?解:(1)∵ 220= 1M,∴ 该存储器能存储的信息为:1M×32/8=4MB (2)(1024K/512K)×(32/8)= 8(片)(3)需要1位地址作为芯片选择。
(选择两个512K×32位的存储体)2. 已知某64位机主存采用半导体存储器,其地址码为26位,若使用256K×16位的DRAM芯片组成该机所允许的最大主存空间,并选用模块板结构形式,问:(1)每个模块板为1024K×64位,共需几个模块板?(2)每个模块板内共有多少DRAM芯片?(3)主存共需多少DRAM芯片? CPU如何选择各模块板?解:(1)最大主存空间为:226×64位,每个模块板容量为:1024K×64位=220×64位设:共需模块板数为m:则:m=(226×64位)/(220×64位)= 64 (块)(2). 设每个模块板内有DRAM芯片数为n:n=(/) ×(64/16)=16 (片)(3) 主存共需DRAM芯片为:m×n = 64×16=1024 (片)每个模块板有16片DRAM芯片,容量为1024K×64位,需20根地址线(A19~A0)完成模块板内存储单元寻址。
一共有64块模块板,采用6根高位地址线(A25~A20),通过6:64译码器译码,产生片选信号对各模块板进行选择。
3.用16K×8位的DRAM芯片组成64K×32位存储器,要求:(1) 画出该存储器的组成逻辑框图。
第3章习题答案

思考题:题3.1.1 组合逻辑电路在结构上不存在输出到输入的 ,因此 状态不影响 状态。
答:反馈回路、输出、输入。
题3.1.2 组合逻辑电路分析是根据给定的逻辑电路图,而确定 。
组合逻辑电路设计是根据给定组合电路的文字描述,设计最简单或者最合理的 。
答:逻辑功能、逻辑电路。
题3.2.1 一组合电路输入信号的变化顺序有以下三种情况,当 时,将可能出现竞争冒险。
(A )00→01→11→10 (B )00→01→10→11 (C )00→10→11→01 答:B题3.2.2 清除竞争冒险的常用方法有(1)电路输出端加 ;(2)输入加 ;(3)增加 。
答:电容,选通脉冲,冗余项。
题3.2.3 门电路的延时时间是产生组合逻辑电路竞争与冒险的唯一原因。
( ) 答:×题3.2.4 根据毛刺产生的方向,组合逻辑的冒险可分为 冒险和 冒险。
答:1型、0型。
题3.2.5 传统的判别方法可采用 和 法来判断组合电路是否存在冒险。
答:代数法、卡诺图。
题3.3.1 进程行为之间执行顺序为 ,进程行为内部执行顺序为 。
答:同时、依次。
题3.3.2 行为描述的基本单元是 ,结构描述的基本单元是 。
答:进程、调用元件语句。
题3.3.3 结构体中的每条VHDL 语句的执行顺序与排列顺序 。
答:无关题3.4.1串行加法器进位信号采用 传递,而并行加法器的进位信号采用 传递。
(A )超前,逐位 (B )逐位,超前 (C )逐位,逐位 (D )超前,超前 答:B题3.4.2 一个有使能端的译码器作数据分配器时,将数据输入端信号连接在 。
答:使能端题 3.4.3 优先编码器输入为70I I -(0I 优先级别最高),输出为2F 、1F 、0F (2F 为高位)。
当使能输入00,651====I I I S 时,输出012F F F 应为 。
答:110题3.4.4 用4位二进制比较器7485实现20位二进制数并行比较,需要 片。
第三章习题解答

第3章 力学基本定律与守恒律 习题及答案1.作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题.解: (1)若物体原来静止,则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理, 12v v ∆=∆,12I I=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理. (2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ,(s 20='t 舍去)2.一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3.如图所示,一质量为m 的球,在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。
第三章部分习题解答
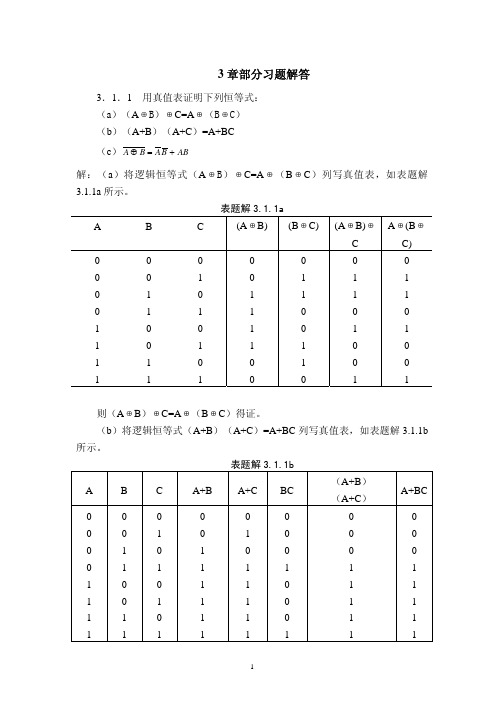
(b) ( A + B)(AB ) = AAB + BAB = AB
(c) ABC(B + C ) = ( A + B + C )(B + C ) = C + B( A + B ) = C + AB
(d) A + ABC + ABC + CB + CB = A(1 + BC + BC) + C(B + B ) = A + C
L3 = A3 ⊕ C
可分别用异或门、三态门设计逻辑电路,如图题解 3.4.4a、b 所示。
图题解 3.4.4
7
3.4.7 某雷达站有 3 部雷达 A、B、C,其中 A 和 B 功率消耗相等,C 的 功率是 A 的两倍。这些雷达由两台发电机 X 和 Y 供电,发电机 X 的最大输出功 率等于雷达 A 的功率消耗,发电机 Y 的最大输出功率是 X 的 3 倍。要求设计一 个逻辑电路,能够根据各雷达的启动和关闭信号,以最节约电能的方式启、停 发电机。
X = ABC + ABC + ABC + ABC = AB ⊕ C + B A ⊕ C
Y =AB+C 由逻辑表达式可设计出最节约电能的发电机启、停方式的逻辑电路,如图 题解 3.4.7b 所示。
表题解 3.4.7
A
B
C
X
Y
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
第三章 习题答案

第三章 消费者行为理论2. 假设某消费者的均衡如图3—1(即教材中第96页的图3—22)所示。
其中,横轴OX 1和纵轴OX 2分别表示商品1和商品2的数量,线段AB 为消费者的预算线,曲线图3—1 某消费者的均衡U 为消费者的无差异曲线,E 点为效用最大化的均衡点。
已知商品1的价格P 1=2元。
(1)求消费者的收入;(2)求商品2的价格P 2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E 点的MRS 12的值。
解答:(1)图中的横截距表示消费者的收入全部购买商品1的数量为30单位,且已知P 1=2元,所以,消费者的收入M =2元×30=60元。
(2)图中的纵截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入M =60元,所以,商品2的价格P 2=M 20=6020=3元。
(3)由于预算线方程的一般形式为 P 1X 1+P 2X 2=M 所以,由(1)、(2)可将预算线方程具体写为:2X 1+3X 2=60。
(4)将(3)中的预算线方程进一步整理为X 2=-23X 1+20。
很清楚,预算线的斜率为-23。
(5)在消费者效用最大化的均衡点E 上,有MRS 12=P 1P 2,即无差异曲线斜率的绝对值即MRS 等于预算线斜率的绝对值P 1P 2。
因此,MRS 12=P 1P 2=23。
5. 已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P 1=20元和P 2=30元,该消费者的效用函数为U =3X 1X 22,该消费者每年购买这两种商品的数量应各是多少?每年从中获得的总效用是多少?解答:根据消费者的效用最大化的均衡条件MU 1MU 2=P 1P 2其中,由U =3X 1X 22可得 MU 1=d TU d X 1=3X 22; MU 2=d TU d X 2=6X 1X 2 于是,有 3X 226X 1X 2=2030 整理得 X 2=43X 1 (1) 将式(1)代入预算约束条件20X 1+30X 2=540,得20X 1+30·43X 1=540 解得 X 1=9 将X 1=9代入式(1)得 X 2=12因此,该消费者每年购买这两种商品的数量应该为X 1=9 ;X 2=12。
第三章习题集答案

第三章习题集答案本章习题一、名词解释均衡产出或收入消费函数边际消费倾向平均消费倾向储蓄函数边际储蓄倾向平均储蓄倾向乘数投资乘数政府支出乘数税收乘数政府转移支出乘数平衡预算乘数对外贸易乘数相对收入消费理论生命周期消费理论永久收入消费理论二、判断题1.投资乘数起作用的关键因素是有确定的边际消费倾向值。
2.在一个没有政府的封闭经济中,经济均衡时一定是投资等于储蓄;在一个有政府的开放经济中情况仍是这样。
3.在均衡产出的情况下,企业的非意愿存货投资必然为零。
4.在045线上,消费支出和收入并不总是相等。
5.在经济学上,家庭储蓄是指可支配收入中未用于消费而放在银行的存款。
6.一般来说,高收入家庭消费倾向越高,低收入家庭消费倾向越低。
三、选择题1.收入超过支出,公司将减少生产,因为非计划存货量为( )A. 正;B. 负;C. 零;D.不确定。
2.消费函数为C=100+0.8(Y-T),政府支出乘数是( )A. 0.8B. 1.2C. 4D. 5。
3.消费函数的斜率取决于( )A. 边际消费倾向;B. 与可支配收入无关的消费总量;C. 平均消费倾向;D. 由于收入变化引起的投资量。
4.下列四种情况中,投资乘数最大的是( )A. 边际消费倾向为0.4 ; B . 边际储蓄倾向为0.1 ;C. 边际消费倾向为0.6 ;D. 边际储蓄倾向为0.35.在四部门经济中,其他条件不变,投资、储蓄、政府购买、税收、进口同时增加,则均衡收入( )A. 保持不变; B . 趋于增加; C. 趋于减少; D. 变化趋势不能确定。
6.在凯恩斯45°线图中,消费函数与45°线相交点的产出水平表示( )A. 净投资支出I大于零时的GNP水平;B. 均衡的GNP水平;C. 消费C和投资I相等;D. 没有任何意义,除非投资I恰好为零。
7.如果由于计划投资支出的减少而导致原来国民收入Y的均衡水平改变,可以预期( )A. Y将下降,但储蓄S不变;B. Y将下降,但储蓄S将上升;C. Y和储蓄S都将下降;D. Y不变,但储蓄S下降8.如果边际消费倾向为常数,那么消费函数将是( )A. 一条不通过原点的直线;B. 一条相对于横轴向上凸的曲线;C. 一条相对于横轴向下凹的曲线;D. 一条通过原点与横轴成45°的直线;E. 以上说法均不准确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
= 1 + e jωT + e − jωT + 1 = 2 + 2 cos(ωT )
SY (ω) = 2SX (ω)[1+cos(ω )] T
4
3.3 冲激响应为 h1 (t )和h2 (t )的两个系统并联 , 求用 h1 (t ), h2 (t )和X (t )的自相关函数表示的 Y1 (t )和 Y2 (t )的互相关函数 .
=∫
∞ −∞ −∞ −∞
∫ ∫
∞
∞
RX (t1 −λ ,t2 −λ2 −λ3)h (λ )h (λ2)h2(λ3)dλ dλ2dλ3 1 1 1 1 1
若 (t)平 ,则 : R 1Y2 (τ ) = RX (τ )∗h (τ)∗h (− )∗h2(τ ) X 稳 有 Y 1 1 τ
R1Y2 (t,t +τ) = R1Y2 (τ) Y Y =∫
1 dω ωL 2 2 [1 + ( ) ] R
W=
N0
π
∫
∞
0
[ +α2ω2]2 1
dω
N0 N0R W= = 4 α 4L
1 ∞ W= [ arctan(αω )]0 π 2α N0 1 π = ⋅ ⋅ π 2α 2
15
N0
3.6 当传输函数为H (ω ) = [1 + ( jωL )]−1的两个相同网络串 R 联时, 求输入白噪声的功率谱为N 0时的输出平均功率.
SY (ω) = 2SX (ω)[1+cos(ω )] T
3
3.2 若图示系统的输入X (t )为平稳随机过程, 求输出 的功率谱密度.
频域法
SY (ω) = SX (ω) H(ω)
2
Y(s) H(s) = =1+e−sT h(t) =δ(t) +δ(t −T) X(s) − jωT H(−ω) =1+ejωT H(ω) =1+e
−∞ −∞ ∞ ∞
= E[ ∫ =∫
∞
∞
−∞ −∞
∫
∞
X (t1 − λ1 ) X (t 2 − λ2 )h1 (λ1 )h2 (λ2 )dλ1dλ2 ]
5
−∞ −∞
∫
∞
E[ X (t1 − λ1 ) X (t 2 − λ2 )] ⋅ h1 (λ1 )h2 (λ2 )dλ1dλ2
3.3 冲激响应为 h1 (t )和h2 (t )的两个系统并联 , 求用 h1 (t ), h2 (t )和X (t )的自相关函数表 示的 Y1 (t ), Y2 (t )的互相关函数 .
∞
R 1Y2 (t1,t2) = R 1 (t1,t2 )∗h2(t2)= ∫− ∞ RY (t1 , t 2 − λ3 ) h2 (λ3 ) dλ3 Y Y
1
R1 (t1,t2) = RX (t1,t2)∗h (t1)∗h (t2) Y 1 1 =∫
∞ −∞ −∞
∫
∞
RX (t1 −λ ,t2 −λ2)h (λ )h (λ2)dλ dλ2 1 1 1 1 1
R 1Y2 (t1,t2) = RX (t1,t2)∗h (t1)∗h (t2)∗h2(t2) Y 1 1
=∫
∞ −∞ −∞ −∞
∫ ∫
∞
∞
RX (t1 −λ ,t2 −λ2 −λ3)h (λ )h (λ2)h2(λ3)dλ dλ2dλ3 1 1 1 1 1
9
R 1Y2 (t1,t2) = RX (t1,t2 )∗h (t1)∗h (t2)∗h2(t2) Y 1 1
14
3.6 当传输函数为H (ω ) = [1 + ( jωL )]−1的两个相同网络串 R 联时, 求输入白噪声的功率谱为N 0时的输出平均功率.
dx x 1 b ∫ (a2 +b2x2)2 = 2a2(a2 +b2x2) + 2a3b arctan( a x) +C
W=
N0
π
∫
∞
0
L α= R
1 W= 2π
∞
1 ∞ W= ∫−∞ SY (ω)dω 2π
N0 N0 ∫−∞ ωL 2 2 dω = π [1 + ( ) ] R
∫
∞
0
1 dω ωL 2 2 [1 + ( ) ] R
dx x 1 b ∫ (a2 +b2x2)2 = 2a2(a2 +b2x2) + 2a3b arctan( a x) +C
RY1Y2 (t1 , t 2 ) = ∫
∞
−∞ −∞ ∞
∫
∞
RX (t1 − λ1 , t 2 − λ2 )h1 (λ1 )h2 (λ2 )dλ1dλ2
∞ −∞
= ∫ h1 (λ1 )[ ∫ RX (t1 − λ1 , t 2 − λ2 )h2 (λ2 )dλ2 ]dλ1
−∞
= ∫ h1 (λ1 )[ RX (t1 − λ1 , t 2 ) ∗ h2 (t 2 )]dλ1
∞ −∞
−∞ −∞
= ∫ h (λ )[∫ RX (τ +λ −λ2 )h2(λ2)dλ2]dλ 1 1 1 1
−∞ ∞
∞
= ∫ h (Байду номын сангаас )[RX (τ +λ )∗h2(τ +λ )]dλ 1 1 1 1 1
−∞
7
3.4 随机过程 X (t )作用到脉冲响应为 h1 (t )和h2 (t )的串联系统 . 求用 h1 (t ), h2 (t )和X (t )的自相关函数表示的 Y1 (t )和Y2 (t )的 互相关函数 .
R (τ) = 2RX (τ) + RX (τ −T) + RX (τ +T) Y
1
3.2 若图示系统的输入X (t )为平稳随机过程, 求输出 的功率谱密度.
时域法和频域法 时域法一: 时域法一:定义
R (τ) = 2RX (τ) + RX (τ −T) + RX (τ +T) Y
SY (ω ) = FT [ RY (τ )] = FT [2 RX (τ ) + RX (τ − T ) + RX (τ + T )]
2
N0 SY (ω) = SN (ω) HS (ω) = ωL 2 2 [1+( ) ] R
2
13
3.6 当传输函数为H (ω ) = [1 + ( jωL )]−1的两个相同网络串 R 联时, 求输入白噪声的功率谱为N 0时的输出平均功率.
N0 SY (ω) = ωL 2 2 [1+( ) ] R
本题有两种解法
1 ∞ W = R (0) = R (τ)τ =0 = Y Y ∫−∞ SY (ω)dω 2π
低通网络的等效噪声带宽 ∆ ω e =
∫
∞
0
H s (ω ) dω H s (0)
2
N0 N0∆ωe 2 2 R (0) = 2∆ωe Hs (0) = Hs (0) Y 2π π
11
3.6 当传输函数为H (ω ) = [1 + ( jωL )]−1的两个相同网络串 R 联时, 求输入白噪声的功率谱为N 0时的输出平均功率.
∞ −∞ −∞
∫
∞
RX (t1 −λ ,t2 −λ2)h (λ )h2(λ2)dλ dλ2 1 1 1 1
R 1Y2 (τ ) = RX (τ )∗h2(τ )∗h (− ) Y 1 τ
∞
R1Y2 (t,t +τ) = ∫ Y
∫ =∫ ∫
∞
∞
−∞ −∞ ∞
RX (t −λ ,t +τ −λ2 )h (λ )h2(λ2)dλ dλ2 1 1 1 1 RX (τ +λ −λ2)h (λ )h2 (λ2)dλ dλ2 1 1 1 1
−∞
∞
R1Y2 (t1,t2) = RX (t1,t2)∗h2(t2)∗h (t1) Y 1 =∫
∞ −∞ −∞
∫
∞
RX (t1 −λ ,t2 −λ2)h (λ )h2(λ2)dλ dλ2 1 1 1 1
6
R1Y2 (t1,t2) = RX (t1,t2)∗h(t1)∗h(t2) Y =∫
若X (t )平稳, 则有 :
= ∫ h (λ ){∫ h (λ2)[RX (τ +λ −λ2)*h2(τ +λ −λ2)]dλ2}dλ 1 1 1 1 1 1
−∞ ∞ −∞
= ∫ h (λ ){RX (τ +λ )*h2(τ +λ )*h (τ +λ )}dλ 1 1 1 1 1 1 1
−∞
10
3.6 当传输函数为H (ω ) = [1 + ( jωL )]−1的两个相同网络串 R 联时, 求输入白噪声的功率谱为N 0时的输出平均功率.
∞ −∞ −∞ −∞ ∞
∫ ∫
∞
∞
RX (τ +λ −λ2 −λ3)h (λ )h (λ2)h2(λ3)dλ dλ2dλ3 1 1 1 1 1
∞ ∞ −∞ ∞ −∞
= ∫ h (λ ){∫ h (λ2)[∫ RX (τ +λ −λ2 −λ3)h2(λ3)dλ3]dλ2}dλ 1 1 1 1 1
−∞ ∞
R 1Y2 (t1,t2) = R 1 (t1,t2)∗h2(t2) Y Y
RY1Y2 (t1 , t 2 ) = E[Y1 (t1 )Y2 (t 2 )] = E[Y1 (t1 ) ⋅ ∫ Y1 (t 2 − λ3 )h2 (λ3 )dλ3 ]
−∞ ∞
= ∫ E[Y1 (t1 ) ⋅ Y1 (t 2 − λ3 )]h2 (λ3 )dλ3 = ∫ RY1 (t1 , t 2 − λ3 )h2 (λ3 )dλ3
