真空中静电场的基本方程
静电场分析

电位确定值(电位差)
两点间电位差有定值
选择电位参考点的原则: 应使电位表达式有意义 应使电位表达式最简单 同一个问题只能有一个参考点 电位参考点电位一般为0;
二、电位函数的求解
中国矿业大学
点电荷的电位
v E
q
40r 2
evr
vQ
Q v v P' Q v v
S
Ev(rv)g(4
r2
evr)0
Q
0
v E
Q
4 0 r 2
evr
r
Ñ 在球内区域:ra
Q 3Q
Ev(rv)gdSv
V 4 a3 S
Q
0
Ev(rv)g(4 r2
v E
Qr
4 0 a3
evr ) evr
4 r3
3
0
3.2 电位函数
中国矿业大学
一、电位函数与电位差
电位函数
v
E 0
中国矿业大学
补充内容:利用高斯定理求解静电场
Ñ Ev(rv)gdSv 1 (rv)dV Q
S
0 V
0
求解的关键:高斯面的选择。
高斯面的选择原则:
1)场点位于高斯面上;
2)高斯面为闭合面;
3)在整个或分段高斯面上,Ev
或
vv EgdS
为恒定值。
只有当电荷呈某种对称分布时才可能满足以上原则,因此用
中国矿业大学
真空中静电场性质小结:
微分形式
积分形式
gEv(rv) (rv)
Ev(rv)
0
0
ÑS Ev(rv)gdSv
ÑC
Ev(rv)
0
Q
0
静电场性质:是一种有源无旋场,是保守场。
第2讲 麦克斯韦方程组ppt课件

r E t
r )dS
C
S t
rr
Ñ S
B
dS
0
rr1
Ñ S
E
dS
0
V
ρdV
v v dq
ÑS JgdS dt
第二讲 麦克斯韦方程组
二、介质中的麦克斯韦方程
媒质对电磁场的响应可分为三种情况:极化、磁化和传导。 极化:媒质在电场作用下呈现宏观电荷(束缚电荷)分布 磁化:媒质在磁场作用下呈现宏观电流(磁化电流)分布 描述媒质电磁特性的参数为:介电常数、磁导率和电导率。
第二讲 麦克斯韦方程组
四、静态场与时变场的麦克斯韦方程
宏观电磁场的普遍规律是Maxwell方程组,而静态场是
时变场的特殊情况。
Maxwell方程组
H
E
J
D
t
B
t
B 0
D
0 t
静态场方程
静电场
E
0
( J = 0 ) D
J 0
恒定电场 (J≠0)
第二讲 麦克斯韦方程组
一、真空中的麦克斯韦方程
麦克斯韦方程组(Maxwell’s equations)
r B
r E r
微分形式
r 0(J
r B
t
0
r E t
)
B 0
r
E / 0
r gJ
t
Ñ
Ñ
C
r B r E
r dl
r dl
积分形式
r
0
(J
S
r
B
0 r
麦克斯韦第二方程,表明时变磁 场产生电场
麦克斯韦第三方程,表明磁场是 无源场,磁力线总是闭合曲线
电磁场理论基础试题集

电磁场理论基础习题集(说明:加重的符号和上标有箭头的符号都表示矢量)一、填空题1.矢量场的散度定理为(1),斯托克斯定理为(2)。
【知识点】:1.2 【难易度】:C 【参考分】:3【答案】:(1)()∫∫⋅=⋅∇SS d A d A v v v ττ (2)()S d A l d A SCvv v v ⋅×∇=⋅∫∫2.矢量场A v满足(1)时,可用一个标量场的梯度表示。
【知识点】:1.4 【难易度】:C 【参考分】:1.5【答案】:(1) 0=×∇A v 3.真空中静电场的基本方程的积分形式为(1),(2),微分形式为(3),(4)。
【知识点】:3.2 【难易度】:B【参考分】:6【答案】:(1) 0=⋅∫c l d E v v (2) ∑∫=⋅q S d D Sv v 0(3) 0=×∇E v (4)()r D vv ρ=⋅∇04.电位移矢量D v 、极化强度P v 和电场强度E v满足关系(1)。
【知识点】:3.6 【难易度】:B【参考分】:1.5【答案】:(1) P E P D D vv v v v +=+=00ε 5.有面电流s 的不同介质分界面上,恒定磁场的边界条件为(1),(2)。
【知识点】:3.8 【难易度】:B【参考分】:3【答案】:(1) ()021=−⋅B B n v v v (2) ()s J H H n v v vv =−×21 6.焦耳定律的微分形式为(1)。
【知识点】:3.8 【难易度】:B 【参考分】:1.5【答案】:(1) 2E E J p γ=⋅=v v 7.磁场能量密度=m w (1),区域V中的总磁场能量为=m W (2)。
【知识点】:5.9 【难易度】:B 【参考分】:3【答案】:(1) 221H μ (2) ∫Vd H τμ2218.理想导体中,时变电磁场的=(1),=(2) 。
【知识点】:6.1 【难易度】:A 【参考分】:3【答案】:(1)0 (2)0 9.理想介质中,电磁波的传播速度由(1)决定,速度=v (2)。
电磁场与波模拟题

电磁场与波模拟题一、填空题1.矢量分析中的散度定理(或高斯公式)是 ,斯托克斯定理(或斯托克斯公式)是 。
2.空间位场()+()()x y z R e x x e y y e z z '''=--+-,||R R =。
则R ∇= ,1R ⎛⎫∇= ⎪⎝⎭,R ∇⨯= 。
3.真空中静电场的基本方程的微分形式为 , ,静电场用静电位表示为 。
静电位满足的泊松微分方程为____________________。
4.导体中稳恒电流场的基本方程的微分形式为 , ,稳恒电流场用静电位表示为 。
静电位满足的拉普拉斯微分方程为____________________。
5.真空中恒定磁场的基本方程的微分形式为 , ,恒定磁场用矢量磁位表示为 。
若引入库伦规范条件___________,则矢量磁位满足的微分方程为__________。
6.在时变电磁场中,定义动态矢量位A 和标量位ϕ,则磁场B =__________,电场E =__________。
若引入洛仑兹规范条件___________,则动态位满足的微分方程为_____________、______________。
7.在理想介质分界面上磁场强度H 满足的关系是 ,磁感应矢量B 满足的关系 。
8.在理想介质分界面上电场强度E 满足的关系是 ,电位移矢量D 满足的关系 。
9.应用分离变量法在解矩形二维场的问题时,位函数所满足的拉普拉斯方程为_______,其第一步是令(,)x y ϕ=________,然后可将此偏微分方程分解为两个_____微分方程。
10.复数形式的麦克斯韦方程组是___________、______________、_____________、______________。
11.无源空间的电磁场波动方程为_____________、______________;时谐场的波动方程的复数形式即亥姆霍兹方程是_______________、________________。
高中物理-静电场

七静电场一、基本概念和规律1.库仑定律(1)内容:真空中两个静止点电荷之间的相互作用力,与它们的电荷量的乘积成正比,与它们之间距离的二次方成反比,作用力的方向在两点电荷的连线上。
(2)公式:F=k Q1Q2r2,式中的k=9×109 N·m2/C2,叫静电力常量。
(3)适用条件:点电荷且在真空中。
2.电场、电场强度(1)电场:电场是电荷周围存在的一种物质,电场对放入其中的电荷有力的作用。
静止电荷产生的电场称为静电场。
(2)电场强度①定义:放入电场中某点的电荷所受的电场力F与它的电荷量的比值。
②公式:E=F q。
(3)矢量性:规定正电荷在电场中某点所受电场力的方向为该点电场强度的方向。
(4)叠加性:如果有几个静止电荷在空间同时产生电场,那么空间某点的电场强度是各场源电荷单独存在时在该点所产生的电场强度的矢量和。
3.点电荷电场强度的计算式(1)设在场源点电荷Q形成的电场中,有一点P与Q相距r,则P点的电场强度E=k Qr2。
(2)适用条件:真空中的点电荷形成的电场。
4.电场线的用法(1)利用电场线可以判断电场强度的大小电场线的疏密程度表示电场强度的大小。
同一电场中,电场线越密集处电场强度越大。
(2)利用电场线可以判定电场强度的方向电场线的切线方向表示电场强度的方向。
(3)利用电场线可以判定场源电荷的电性及电荷量多少电场线起始于带正电的电荷或无限远,终止于无限远或带负电的电荷。
场源电荷所带电荷量越多,发出或终止的电场线条数越多。
(4)利用电场线可以判定电势的高低沿电场线方向电势是逐渐降低的。
(5)利用电场线可以判定自由电荷在电场中受力情况、移动方向等先由电场线大致判定电场强度的大小与方向,再结合自由电荷的电性确定其所受电场力方向,再分析自由电荷移动方向、形成电流的方向等。
5.电场的叠加(1)电场叠加:多个电荷在空间某处产生的电场强度为各电荷单独在该处所产生的电场强度的矢量和。
(2)运算法则:平行四边形定则。
第二章静电场恒定电场和恒定磁场

介质中的高斯定理表示为 式中电位移矢量为
在线性的各向同性的电介质中
例2.1在空气中放入一个带电量为Q、半径为a的球体,该球体的 相对介电常数为εr。求该球体内、外任意一点的电场强度。
解(1) 球内任意一点,设到球心距离为r,做高斯面为以r为半径的球面, 如图2.2所示。
由电场的对称性可知,E和D的方向为er,所以
大小、它们之间的距离和周围的电介质,即可以不用电容器。
例2.10同心金属球与球壳系统如图2.12所示,内导体球半径为a,外导体 球壳的内外半径分别为b和c,导体球与导体球壳带有等量异号电荷,它
们之间充满相对介电常数为 r 的电介质,球外为空气。求该导体系统
的电容。
解:根据高斯定理不难求出空间各点的电场强度,设导体球和导体球壳的 带电量分别是q和-q,则导体和导体球壳之间的电场强度的大小为
电场能为
WeΒιβλιοθήκη 1 2dVv
(2) 对于多导体系统
We
1 2
dV
v
例2.12半径分别为a和b的同轴线,外加电压为U,内圆柱体电荷量为正,外圆柱 面单位长度上的电荷量与内圆柱体等值异号。如图2.16(a)所示,两电极间在θ1的 角度内填充介电常数为ε的电介质,其余部分为空气,求同轴线单位长度上储存 的电场能量。
示,求在l长度上的外电感。
图2.25例2.20用图
例2.21一个半径为a的无限长直导线,在导线均匀流过的电流为I,求这个导线
在单位长度上的内电感,如图2.26所示(设导体内部的磁导率近似为μ0)。 解:截面上的磁通并没有与全部电流I交链,而只是与一部分电流交链,交链的总 磁链为
图2.26
2. 互 有两感个回路l1和l2,如图2.27所示。
真空中静电场(高斯定理)
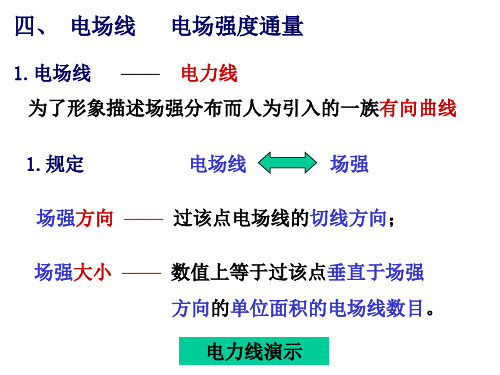
QR
电场方向、大小
Q P
o
r
E
S
dS
• 选取合适的高斯面(闭合面)
E dS EdS E dS E4 r 2
S
S
S
• 再根据高斯定理解方程
qi内
E4r 2 i 0
E 1
4 0
qi
i
r2
E 1
4 0
qi
ir2ຫໍສະໝຸດ ds E
ds
E ds
S
侧面
两底面
E2rl 0
利用高斯定理解出 E
ds r
l
Eds
E 2rl l 0
E 1 2 0 r
例三. 无限大均匀带电平面的电场分布
分析:无限大带电面两侧电场分布对称
作高斯面如图示:
e
E dS
例四. 金属导体静电平衡时,体内场强处处为0 求证: 体内处处不带电
证明:
在导体内任取体积元 dV
由高斯定理
E dS 0
qi内 内dV 0
S
i
V
体积元任取
内 0
证毕
作业
习题P321-322
7-15,7-17,7-18,7-21
讨论
Q P
Ro r
E
S
dS
r R qi 0
i
r R qi Q
i
rR E0
rR
E
1
4 0
Q r2
如何理解面内场强为0 ?
dE1 dE2
P
理工类专业课复习资料-电磁场与电磁波公式总结

电磁场与电磁波复习第一部分知识点归纳第一章矢量分析1、三种常用的坐标系(1)直角坐标系微分线元:dz a dy a dx a R d z y x →→→→++=面积元:⎪⎩⎪⎨⎧===dxdy dS dxdzdS dydzdS zyx ,体积元:dxdydzd =τ(2)柱坐标系长度元:⎪⎩⎪⎨⎧===dz dl rd dl drdl z r ϕϕ,面积元⎪⎩⎪⎨⎧======rdrdzdl dl dS drdz dl dl dS dz rd dl dl dS z zz r z r ϕϕϕϕ,体积元:dzrdrd d ϕτ=(3)球坐标系长度元:⎪⎩⎪⎨⎧===ϕθθϕθd r dl rd dl drdl r sin ,面积元:⎪⎩⎪⎨⎧======θϕθϕθθθϕϕθθϕrdrd dl dl dS drd r dl dl dS d d r dl dl dS r r r sin sin 2,体积元:ϕθθτd drd r d sin 2=2、三种坐标系的坐标变量之间的关系(1)直角坐标系与柱坐标系的关系⎪⎪⎩⎪⎪⎨⎧==+=⎪⎩⎪⎨⎧===z z x y yx r zz r y r x arctan,sin cos 22ϕϕϕ(2)直角坐标系与球坐标系的关系⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=⎪⎩⎪⎨⎧===z yz y x z z y x r r z r y r x arctan arccos ,cos sin sin cos sin 222222ϕθθϕθϕθ(3)柱坐标系与球坐标系的关系⎪⎪⎩⎪⎪⎨⎧=+=+=⎪⎩⎪⎨⎧===ϕϕθθϕϕθ22'22''arccos ,cos sin z r z zr r r z r r 3、梯度(1)直角坐标系中:za y a x a grad z y x∂∂+∂∂+∂∂=∇=→→→μμμμμ(2)柱坐标系中:za r a r a grad z r∂∂+∂∂+∂∂=∇=→→→μϕμμμμϕ1(3)球坐标系中:ϕμθθμμμμϕθ∂∂+∂∂+∂∂=∇=→→→sin 11r a r a r a grad r 4.散度(1)直角坐标系中:zA y A x A A div zy X ∂∂+∂∂+∂∂=→(2)柱坐标系中:z A A r rA r r A div zr ∂∂+∂∂+∂∂=→ϕϕ1)(1(3)球坐标系中:ϕθθθθϕθ∂∂+∂∂+∂∂=→A r A r A r rr A div r sin 1)(sin sin 1)(1225、高斯散度定理:⎰⎰⎰→→→→=⋅∇=⋅ττττd A div d A S d A S,意义为:任意矢量场→A 的散度在场中任意体积内的体积分等于矢量场→A 在限定该体积的闭合面上的通量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V=4r3/3 dv=4r2dr
r0
r 0
r2
r4 a2
4
r 2 dr
4r0
r3 3
r5
5a2
D内
r0
r 3
r3 5a2
r=a时 (连续)
D内
D外
2 15
r0a
解法二: 微分形式解 • Dvr r r 球坐标
∵对称性,D外仅有er 分量:
evr ev 0 evr ev 0
在球外 r r 0
1 r2 r
r 2 D外
0
D外
C2 r2
当 r ∞ 时可看成点电荷:
D外
1
4
q r2
1
4
8
15
r
0
a
3
1 r2
C2
2 15
r0a3
D外
2 15
r0
a3 r2
球内(r≤a):
1
r2
r
r 2D内
r0
1
r2 a2
r 2D内
2r 0
r0 1
r2 a2
r
2dr
q
4e 0 R
c
点
1
4e
0
1
rd c
R
sds c
4e
0
1
4e0
s l
R
rl dl
R
c
体 面 线
式子中: R r r为场与源的距离
电位——电场的表示式对比
f 1 rd c 3.7
4e 0 R
Er
1
4e
0
r r
1 R
d
2.6
可见f 的计算式简便得多 标量积分,
D0
dS
i
q
E dl 0
l
3.2.1 (高斯定理) 3.2.2 (静电守恒定理)
在半径为R的球面上取面元dS,与球 心构成的锥体。
定义立体角
d
ds R2
球面度
整个球面: 4 R2 4
R2
dS 在er
上的投
任意面对中心 点的立体角:
d
dS •
er
影 r
R2
与是否球 面无关
特性:d 与R无关
及D0 e0E 能解出E
{亥姆霍兹定理:场可由散度与旋度共同确定
F(r)=Fl (r)+FS(r) 无旋量+无散量}
当电荷对称分布时,适当选取坐标系,可使D
或E只有一个分量,且仅是坐标的函数,则
E自动满足
v E
0
,此时只要计算
D
即可
得场解。
例 3.2.1 电荷按 r r0
a 的球体,求球内外的D
静电守恒定理证明
vv E dl
q
evr
v dl
l
4 e0 l R2
Ñ
闭合
q
4 ev0 E
RB dR R RA 2
v dl
0
q
4 e0
1 RA
1 RB
由斯托克斯定理
vv
v v 任意回路
微分形式
Ñ E dl
l
S
E
dS
任意限定面
0
E 0 无旋场、保守场
理论上由
D0
r
E 0
静电场分析
第三章 静场分析
矢量分析
内容:以第一章
为基础
亥姆霍兹定律
静电场的解
1.电场基本方程 2.电位 3.泊松、拉普拉斯方程 4.格林函数 5.介质极化(微观宏观) 6.边界条件 7.电容 8.电场能量
§3.1 静电场分析的基本变量:
1.矢量场 场变量 E
体
2.标量源 恒定电荷 面
线
变量 r 有散场
三个基本量:1.源r rv
e13
e
23
e33
2.场
v D
v
E v D
Dx
Dy
Dz
rv
rv
v E
Ex Ey
Ez
§3.2 真空中静电场的基本
方程
▪ 场的求解一般有两种方法:
微分方程 但都要分析
积分方程
矢量在闭合面上的通量 矢量在闭合回路上的环流
真空中的基本方程
+++++++++ ||||||||
对带电物体产生力
导体电子运动 J
介质极化
D
电位移C/m2
法拉第定律:
v D
q
4 r2
evr
均匀介质点电荷周围
1840’s
麦克斯韦本构关系
v D
rv
e
v E
F m
e为材料特性参数
均匀—e常数 e e0 e r
e11 e12 非均匀—张量 e21 e22
e31 e32
dS
dl1
dl2
1R 2 R
d
dS R2
1 2
dl1 dl2
对闭合面
d
4( 在闭合面内)
0( 在闭合面外)
证明高斯通量定律
首先设仅有单个点电荷 q
蜒 s Ñ
v D0
q
4
ds SvevrRgd2sSv4qevrRq0( (2 gqqd在 在Sv 闭 闭合 合面 面内 外) )
N
(E矢量积分有3个分量), 而微分总是可 计算的,也简单(引入 f的原因)。
R
y : (,)
因为电荷密度均匀,故电通密度D0垂直与这个无限大平 面,且仅与距离有关取柱面垂直于S 作底面积为S
的小柱体,则由高斯定理有:
侧面D S, D dS侧 0
D
dS
D0S
ez
ez
D0S
(ez )
(ez )
s
2D0S S
v D0
2
evz
2
(evz
)
z0 z0
z 0处,
D0
z 0
D0
z 0
2
( )
2
对于均匀介质: Er Dr
e
e er e0
介质中电场
e
Er
r为相对介电系数(一至几千)
减少
§3.3
静电场
电 Ev位 0函, 数Ev 可用一标量梯度表示,
即电位函数f
Q
0,
等效得
v E
直角坐标
Ev=-evx
x
evy
y
evz
z
电场等于电位梯度的负值
电场沿任意方向l的变化: E在l v上的投v 影
El
l
d El dl E dl
电位差
Bv v
A B
E dl
A
A(x, y, z)相对参考点 P(xp , yp , zp ), p 0 的
电位为 (x, y, z)
(
x
p
,
y
p
,
z
p
)
E
dl
3.3.5
(x,y,z)
将电场(点、体、面、线)表达式代入上式, 即可得电位的相应表示式
再用叠加原理 D0 • dS D0i • dS
S
S i1
N N
D0i • dS qi
i1 S
i 1
可推广到体、面、线电荷情况(对源点积
分即可)
•
D0dV
D0 • dS q
r (rr)dV
s
对任意面(体积)均成立 ,我们可得到高斯
定理的微分形式: v
D0 r
体分布
c
D内
r0
r2
r3 3
r5 5a 2
c r2
r
0
r3 3
r5 5a2
c r2
r
0时,D有限,
c r2
0
*解题时,依照题作图、矢径、源、计算。
例 3.2.2 计算均匀面电荷密度为s 无限大平
面的电场。
解:显然如果用库仑定律的电场强度公式
计算较繁复;
E
1
4e 0 S
x : (,),
r 1 dS
1。 ar22
分布在半径为
显见:电场为球对称, D沿径向且仅为r的函数
总电量:Q rr d
a 0
r0
1
r2 a2
4r
2dr
8 15
r
0a3
球外场(r≥a):以球心中心到场点作球面(高斯面)
s
D外
dS
4r 2D外
Q
8 15
r
0a3
D外
2 15
r0
a3 r2
球内(r<av): v
Ñ D内 dS 4 r2D内
