卷积码编译码课设 (2)
卷积码的编码及解码Viterbi解码Word版
卷积码的编码及解码（Viterbi 解码）一、实验目的1、了解卷积码的基本原理；2、掌握卷积码编码的电路设计方法；2、掌握卷积码 Viterbi 译码的基本方法和电路设计方法。
二、实验仪器1、移动通信实验箱一台；2、台式计算机一台；三、实验原理1.卷积码编码原理卷积码是一个有限记忆系统，它也将信息序列切割成长度 k的一个个分组，与分组码不同的是在某一分组编码时，不仅参看本时刻的分组而且参看本时刻以前的 L 个分组。
我们把 L＋1 称为约束长度。
2.卷积码的译码算法（硬判决 Viterbi 译码）Viterbi译码算法是一种最大似然算法，它不是在网络图上依次比较所有可能的路径，而是接收一段，计算，比较一段，保留最有可能的路径，从而达到整个码序列是一个最大似然序列。
Viterbi解码算法的基本步骤如下：1、从某一时间单位j＝m开始，对进入每一状态的所有长为j段分支的部分路径，计算部分路径度量。
对每一状态，挑选并存储一条有最大度量的部分路径及其部分度量，称此部分路径为留选（幸存）路径。
2、j增加1，把此时刻进入每一状态的所有分支度量，和同这些分支相连的前一时刻的留选路径的度量相加，得到了此时刻进入每一状态的留选路径，加以存储并删去其他所有的路径。
因此留选路径延长了一个分支。
3、若j<L+m，则重复以上步骤，否则停止，译码器得到了有最大路径度量的路径。
上面的过程可以简单的总结为“加、比、选”（也称ACS）。
四、实验步骤1、将实验箱和计算机通过串行口连接好，为实验箱上电。
2、将与实验箱相连的电脑上的学生平台程序打开。
在“实验选择”栏中选择“卷积码”实验，点击确认键。
从而进入此实验界面。
3、在实验界面上点“生成数据”，让系统生成待编码的随机比特。
也可在界面上直接双击所显示的 bit，修改其值。
4、在界面上点击下发“原始数据”，该数据将被送入单片机（或 CPLD）进行卷积编码然后经过编码的数据被送回学生平台并显示在“编码数据”栏。
实验二 卷积码编码及译码实验
实验二卷积码编码及译码实验一、实验目的通过本实验掌握卷积编码的特性、产生原理及方法，卷积码的译码方法，尤其是维特比译码的原理、过程、特性及其实现方法。
二、实验内容1、观察NRZ基带信号及其卷积编码信号。
2、观察帧同步信号的生成及巴克码的特性。
3、观察卷积编码信号打孔及码速率匹配方法。
4、观察接收端帧同步过程及帧同步信号。
5、观察译码结果并深入理解维特比译码的过程。
6、观察随机差错及突发差错对卷积译码的影响。
三、基本原理1、卷积码编码卷积码是一种纠错编码，它将输入的k个信息比特编成n个比特输出，特别适合以串行形式进行传输，时延小。
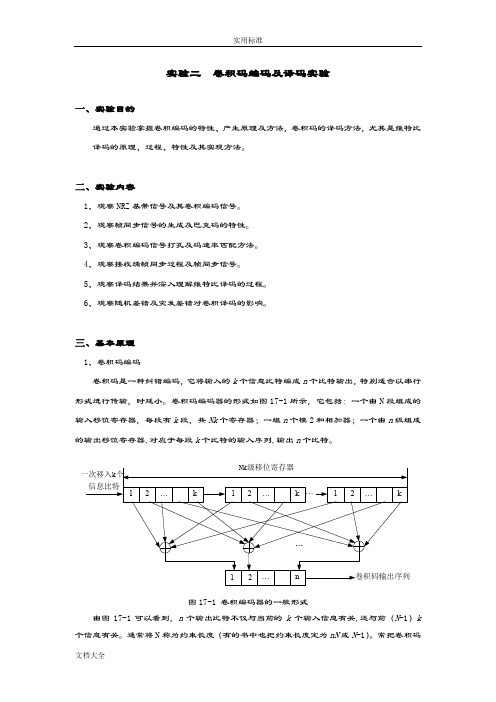
卷积码编码器的形式如图17-1所示，它包括：一个由N段组成的输入移位寄存器，每段有k段，共Nk个寄存器；一组n个模2和相加器；一个由n级组成的输出移位寄存器,对应于每段k个比特的输入序列,输出n个比特。
图17-1 卷积编码器的一般形式由图17-1可以看到，n个输出比特不仅与当前的k个输入信息有关,还与前（N-1）k 个信息有关。
通常将N称为约束长度（有的书中也把约束长度定为nN或N-1）。
常把卷积码记为：（n 、k 、N ），当k =1时，N -1就是寄存器的个数。
编码效率定义为：/c R k n =(17-1)卷积码的表示方法有图解表示法和解析表示法两种：解析法，它可以用数学公式直接表达，包括离散卷积法、生成矩阵法、码生成多项式法；图解表示法，包括树状图、网络图和状态图（最的图形表达形式）三种。
一般情况下，解析表示法比较适合于描述编码过程，而图形法比较适合于描述译码。
（1）图解表示法 （2）解析法下面以（2，1，3）卷积编码器为例详细讲述卷积码的产生原理和表示方法。
（2，1，3）卷积码的约束长度为3，编码速率为1/2，编码器的结构如图17-2所示。
jj图17-2 （2,1,3）卷积编码器这里我们主要介绍码多项式法。
我们可以用多项式来表示输入序列、输出序列、编码器中移位寄存器与模2和的连接关系。
卷积编码译码通信原理课程设计MATLAB
set(h,'color','y');
end
hold on
end
title('卷积编码译码');
legend('灾难编码器','1/2编码器','1/3编码器')
xlabel('信道信噪比');
ylabel('误码率');
六．实验结果及分析
编码器灾难性编码系统结果
对比三个仿真结果可知：灾难性编后果十分严重，在实际应用中必须编码，另外1/3编码器比1/2编码器性能要好。
d．网格图（研究卷积码最大似然译码维特比算法的工具）
纵坐标表状态，横坐标表时间。
从图中我们可看出编码过程中使用K-1个冲洗比特使得编码器恢复初始状态是有必要的。
三、卷积码的译码
Viterbi译码（最大似然译码）
先验概率条件下，后验概率最大者似然函数最大，最值MAP即最大似然(ML)译码。而最大对数似然函数即计算最小汉明距，如此，比较接受序列和发送序列汉明距，选出最小汉明距序列作为最佳译码即可。
如图：
状态表为：
ui
ui-1
si
0
0
a
1
0Байду номын сангаас
b
0
1
c
1
1
d
有如下状态图：
b．树图（将状态图按时间展开）
设初始状态s0=00为树根，对每个时刻的可能输入进行分支，分数级数L表示，L=0时，u0=0向上，u0=1向下，依次向后无限延伸，分支上数字表示相应输出，a，b，c，d表示状态。（优点：时序关系清晰）
四、卷积灾难性错误（Catastrophic error）
信道编码卷积码原理编码译码
（2）
m ' 0 0 1 1 0 0 . .. . . . 0 0 . .1 0 . .0 0 . .. .. . . . 0 0 . .1 0 . .0 0 . .. .. . . . m '( . . 1 ) m . .'( 2 . . )
000 000
.. ..
.... ....
000 000 000 000 000 000......
... ...
... ...
... ...
... ...
... ...
... ...
............
(11,011,100,000,139;''1 1
c(1,3) 10100.. ....
二. 卷积码-----有记忆的码-----有记忆编码电路
m（1）
c(1,1) 10000.. .... c(1)c(1,2)00000.. . .(.1.,0 01 0 ,00 ,0 01 0 ,00 0 ,.)0 ..,
(11， 11,11,11,...,)000 000 011 001 000 000 000 000 000 ......
000 000 000 101 000 001 000 000 000 ......
000 000 000 011 001 000 000 000 000 ......
000 000 001 000
000 000 000 000
000 000 000 000
000 000 000 000
000 000 000 000
000 000 000 000
实验九-(2-1-5)卷积码编码译码技术
实验九 (2,1,5）卷积码编码译码技术一、实验目的1、掌握(2,1,5）卷积码编码译码技术2、了解纠错编码原理。
二、实验内容1、(2,1,5）卷积码编码。
2、(2,1,5）卷积码译码。
三、预备知识1、纠错编码原理。
2、(2,1,5）卷积码的工作原理。
四、实验原理/卷积码是将发送的信息序列通过一个线性的，有限状态的移位寄存器而产生的编码。
通常卷积码的编码器由K级（每级K比特）的移位寄存器和n个线性代数函数发生器（这里是模2加法器）组成。
若以（n,k,m）来描述卷积码，其中k为每次输入到卷积编码器的bit数，n 为每个k元组码字对应的卷积码输出n元组码字，m为编码存储度，也就是卷积编码器的k元组的级数，称m+1= K为编码约束度m称为约束长度。
卷积码将k 元组输入码元编成n元组输出码元，但k和n通常很小，特别适合以串行形式进行传输，时延小。
与分组码不同，卷积码编码生成的n元组元不仅与当前输入的k元组有关，还与前面m-1个输入的k元组有关，编码过程中互相关联的码元个数为n*m。
卷积码的纠错性能随m的增加而增大，而差错率随N的增加而指数下降。
在编码器复杂性相同的情况下，卷积码的性能优于分组码。
编码器随着信息序列不断输入，编码器就不断从一个状态转移到另一个状态并同时输出相应的码序列，所以图3所示状态图可以简单直观的描述编码器的编码过程。
因此通过状态图很容易给出输入信息序列的编码结果，假定输入序列为110100，首先从零状态开始即图示a状态，由于输入信息为“1”，所以下一状态为b并输出“11”，继续输入信息“1”，由图知下一状态为d、输出“01”……其它输入信息依次类推，按照状态转移路径a->b->d->c->b->c->a输出其对应的编码结果“”。
译码方法⒈代数代数译码是将卷积码的一个编码约束长度的码段看作是[n0(m+1），k0(m+1)]线性分组码，每次根据（m+1）分支长接收数字，对相应的最早的那个分支上的信息数字进行估计，然后向前推进一个分支。
卷积码编译码课设 (2)
摘要卷积码是一种性能优越的信道编码。
它的编码器和译码器都比较容易实现，同时它具有较强的纠错能力。
随着纠错编码理论研究的不断深入，卷积码的实际应用越来越广泛。
本文对卷积码和卷积码的编译码有一个简单的介绍且给出了信道编码的发展历史及研究状况，然后详细讨论了（2，1，2）卷积码的编码过程和译码过程，通过状态转移方程和输出方程得出状态转移表和状态转移图，然后通过维特比译码器研究，总结出了维特比译码算法，最后通过Matlab软件进行设计与仿真，得到了编码程序和译码程序，其运行结果与理论分析一致。
关键字卷积码编码、信道编码、Viterbi译码、MATLAB仿真目录摘要........................................... 错误！未定义书签。
一、引言 (3)1.1发展历史及研究状况 (3)1.2设计目的和意义 (3)1.3设计方法 (4)二、卷积码编译码原理 (5)2.1 卷积码编码原理 (5)2.2编码器 (6)2.3 卷积码译码原理 (7)2.4 VITEBI 译码的关键步骤 (8)2.4.1 输入与同步单元 (8)2.4.2 支路量度计算 (8)2.4.3 路径量度的存储与更新 (8)2.4.4 信息序列的存储与更新 (8)2.4.5 判决与输出单元 (8)三、卷积码编码实现 (9)3.1 编码原理分析 (9)3.2 卷积码编码流程图 (10)四、卷积码译码实现 (11)4.1 译码编程思路 (11)4.2 卷积码译码流程图 (11)五、卷积码编译码程序的编译及仿真波形 (11)5.1 卷积码编码仿真 (12)5.2卷积码译码仿真 (13)5.3卷积码纠错码仿真 (14)六、总结 (15)七、参考文献 (16)附录 (17)一、引言1.1发展历史及研究状况1948年，Bell实验室的C.E.Shannon发表的《通信的数学理论》，是关于现代信息理论的奠基性论文，它的发表标志着信息与编码理论这一学科的创立。
卷积编译码
实验四：卷积编/译码一．实验目的1．学习卷积编码的方法与码字测量。
2．学习维特比译码方法及译码的测量。
3．观察卷积码的纠错能力。
二．实验仪器1．RZ8621D实验箱一台2．20MHZ双踪示波器一台三．实验电路连接及测量点说明图7-1 用单片机AT89C2051进行卷积编码电路图图7-2 用单片机AT89C2051进行维特比译码电路图差错控制编码的方法很多，卷积码是一种既能纠随机错，又能纠实发错的编码，在同样的传输速率和设备复杂的条件下，性能较优良的一种编码。
卷积码常采用维特比软判决译码，具有较好的纠错功能。
本实验为卷积码的编译码，它是由一片AT80C2051芯片用软件编程方法实现。
其编译码电路框图如下：图中各主要测量点说明如下：TP401—源码序列TP402—卷积码序列TP403—加错或不加错卷积码序列(模拟信道的传输)TP405—卷积码译码输出序列四．实验步骤及内容（一）卷积码编码1．拨线开关介绍。
用拨动开关SW401设置输入信息。
开关拨动至上面为1，下面为0。
拨动开关共9位，左起1-8位为信息位，第九位为状态位。
第九位为“1”表示无错误，第九位为“0”表示有错误。
2．信息码设置。
如上所述，信息码设置共8位，由SW401开关位置决定，例如设置信息为DCH则八位码为1101 1100。
3．信息码观察。
为了示波器上能看到周期性的信息码和编出的卷积码，本机规定在信息位第一位前加一个“1”，在末位加两个“0”。
因此信息码序列变成1 1101 110000，我们称它们为源码序列。
将示波器1通道探头接于TP401（DTAT3），便可看到该序列波形。
4．卷积编码序列手工编码。
根据源码序列和（2.1.3）卷积码编码规秩，写出卷积码编码序列。
上述源码序列的卷积码为1101 1001 0001 1001 110000。
5．无错卷积码编码序列观察。
将拨动开关第九位（状态位）置于“1”表示无错码。
示波器1通道探头接至TP402（DATA1），2通道探头接至TP403（DATA2），观察示波器上显示的波形，看看它是否与上述卷积编码的码型一致。
实验二--卷积码编码及译码实验
实验二--卷积码编码及译码实验实验二卷积码编码及译码实验一、实验目的通过本实验掌握卷积编码的特性、产生原理及方法，卷积码的译码方法，尤其是维特比译码的原理、过程、特性及其实现方法。
二、实验内容1、观察NRZ基带信号及其卷积编码信号。
2、观察帧同步信号的生成及巴克码的特性。
3、观察卷积编码信号打孔及码速率匹配方法。
4、观察接收端帧同步过程及帧同步信号。
5、观察译码结果并深入理解维特比译码的过程。
6、观察随机差错及突发差错对卷积译码的影响。
三、基本原理1、卷积码编码卷积码是一种纠错编码，它将输入的k个信息比特编成n个比特输出，特别适合以串行形式进行传输，时延小。
卷积码编码器的形式如图17-1所示，它包括：一个由N段组成的输入移位寄存器，每段有k 段，共Nk 个寄存器；一组n 个模2和相加器；一个由n 级组成的输出移位寄存器,对应于每段k 个比特的输入序列,输出n 个比特。
12…k 12…k …12…k12…n 卷积码输出序列信息比特一次移入k 个Nk 级移位寄存器…图17-1 卷积编码器的一般形式由图17-1可以看到，n 个输出比特不仅与当前的k 个输入信息有关,还与前（N -1）k 个信息有关。
通常将N 称为约束长度（有的书中也把约束长度定为nN 或N -1）。
常把卷积码记为：（n 、k 、N ），当k =1时，N -1就是寄存器的个数。
编码效率定义为：/c R k n (17-1)卷积码的表示方法有图解表示法和解析表示法两种：解析法，它可以用数学公式直接表达，包括离散卷积法、生成矩阵法、码生成多项式法；图解表示法，包括树状图、网络图和状态图（最的图形表达形式）三种。
一般情况下，解析表示法比较适合于描述编码过程，而图形法比较适合于描述译码。
（1）图解表示法（2）解析法下面以（2，1，3）卷积编码器为例详细讲述卷积码的产生原理和表示方法。
（2，1，3）卷积码的约束长度为3，编码速率为1/2，编码器的结构如图17-2所示。
开题报告-卷积码的编码译码的设计与实现
一、选题的依据及意义：（一）选题依据现代通讯技术正以其前所未有的速度发展着，信息传输对于信道的要求越来越高。
为了提高通信的可靠性，就需要对于信道状况进行控制。
增加发送信号功率的做法在实际中经常要受到条件的限制，而采用编程的方法则可以有效的对信道的差错进行控制，因而，在实际中编程控制差错的途径有着广泛的应用。
近年来，随着大规模集成电路的发展，电路实现技术水平获得较大程度的提高，卷积码在众多通信系统和计算机系统中得到了越来越广泛的应用。
对于卷积码的研究，编码器比较简单，模式也很统一。
主要是研究提高卷积码的译码速度和可靠性。
为实现通信的可靠性，基本有两种途径：一是增加输出信号的功率，增加接受端的信噪比；第二种是利用编码的方式对信道干扰误码进行控制。
前一种方法容易受到实际条件的限制，不是任何情况都能使用。
而这个问题可以利用编码来解决，使得实用性增加，成本下降。
译码算法中最重要的Viterbi算法问世以来，软件仿真和实现都得到了迅速的发展。
由于Viterbi 译码算法简单，易于实现，并且能够得到较大的编码增益，因此基于Viterbi 译码算法的卷积码得到了广泛应用。
事实上，Viterbi算法的过程可以看做是在状态机模型基础内逐渐减少概率路径的过程。
因为解码是编码的一个逆序过程，接受信息和初始信息是我们已知的信息，我们无法找到一个逆序的算法来计算所输入的信息。
Viterbi算法是利用重新编码的思想，计算每一条路径可能的概率的大小，用几率最大的那一条路径来模拟编码的过程。
从而译出输入信息比特。
而状态机模型的使用大幅度提升了解码过程中寻找正确路径的速度。
因此viterbi译码算法具有非常实用的意义。
（二）选题意义近年来，信息技术和通信技术的突出成就和急剧发展。
集中表现在个人通信，多媒体信息业务，互联网络应用三个方面。
把信息送给个人，使移动通信走向个人通信，在任何地方和任何状态都可打通电话的移动通信给人们带来了极大的方便。
卷积码译码器设计
卷积码译码器设计1 完成（2，1，4）卷积码编码器设计2 完成相应的维特比译码器设计卷积码编译码基本原理(n,k,m)卷积码中编码后的n个码元不仅与当前段的k个信息有关，而且也与前面段的信息有关，编码过程中相互关联的码元为n(m+1)个。
因此，这N时间内的码元数目n(m+1)通常被称为这种码的约束长度。
卷积码的纠错能力随着m的增加而增大。
因为任何一个发送序列对应于编码器网格图中的一条路径。
似然函数可以用接收序列与编码器网格图中的路径对应输出序列之间的距离来度量，译码的过程即是在网格图中寻找一条与接收序列距离最小的路径。
2个状态，若输入的信息序列的长度是(L+m)K 一般情况下，(n，k，m)卷积码编码器共有km(后mk个码元全为0)，则进入和离开每一状态各有k2条分支在网格图上共有kl2条不同的路径，相应于编码器输出的kl2个码序列。
具体理论见各种书籍介绍。
(2,1,4)卷积器结构及其性质本实验中所涉及的（2，1，4）卷积码编码器结构如图1所示：图1其对应的编码规则为:C[1]=input+D2+D3;C[0]=input+D0+D2+D3;该编码器的viterbi译码的篱笆图如图2所示：0 1 2 3 4 5……图2注：a) 0走实线，1走虚线；b) 在16个状态全部达到之后，状态图中间状态开始循环出现；viterbi卷积器的verilog实现一．设计和测试的总结构设计如图3所示：…图3Test_decode //to test the basic function of this project…….encode //to encode the original 01 code, and output the convoluted codes …….decode //input the codes which are generated by encoder and interfered by //random noise//to compute the length of the two paths linked to node x andx)//generated when a new code comes in (}15'1,0{,...,……..acs0……..acs1……..acs23……..acs_4_7……..acs_8_15……..mod2 //to computer the distance between this inputted code and 00//01 10 or 11, and the result is inputted into acs0,acs1 and//the like.//get the result of acs0, acs1 and the like, compare the//distance of the two paths linked to a single nod and choose//the shorter paths as the path value as the basic value of//the nod when a new code comes in……..path01……..path23……..path_4_7……..path_8_15Notation:1. 因为初始截断树的存在，各结点有着不同的特点，故分成acs0,acs1,acs23,acs_4_7,acs_8_15 5个不同的模块，其实他们功用相同;同样，path01,path23,path_4_7,path_8_15也由此原因得出；二．编码器设计利用上述(2，1,4)卷积编码器的结构生成相应的编码，见encode.v文件用R[3:0]寄存器寄存已输入的码，最多寄存之前输入的4位，所以为4位。
卷积码的编码和译码
卷积码是一种纠错编码技术，通常用于无线通信和数字通信系统中，以提高数据传输的可靠性。
卷积码的编码和译码是两个关键步骤，下面分别介绍这两个步骤：**编码：**1. **选择卷积码的参数：** 在编码之前，您需要确定卷积码的参数，包括约束长度（constraint length）、生成多项式（generator polynomial）和码率（code rate）。
这些参数将决定编码器的结构和性能。
2. **构建编码器：** 卷积码编码器通常是一个有限状态自动机（Finite State Machine，FSM）。
根据所选的生成多项式，配置编码器的状态转移图。
编码器的输入是要编码的数据位，输出是编码后的码字。
3. **编码操作：** 对每个输入位进行编码操作。
编码器的状态会根据输入位的不同而变化，从而生成不同的编码输出。
通常，每个输入位都会产生多个输出位，这是卷积码的特点之一。
4. **输出码字：** 编码器将生成的码字传送出来，以便传输或存储。
**译码：**1. **构建译码器：** 卷积码的译码器通常是使用一种称为Viterbi算法的最大似然译码方法来实现的。
译码器需要与编码器具有相同的约束长度和生成多项式。
2. **接收和测量：** 译码器接收传输的码字，并测量接收到的码字与每个可能的发送码字之间的距离或差异。
这些度量值用于决定哪个发送码字最有可能是原始数据。
3. **路径追踪：** Viterbi算法使用路径追踪技术来跟踪可能的状态序列，并根据度量值来选择最有可能的路径。
这个过程可以看作是在状态图上搜索最佳路径的过程。
4. **译码操作：** 根据最佳路径上的状态序列，译码器重建原始数据位。
这些数据位就是译码器的输出。
卷积码的译码是一种计算密集型的过程，通常需要高效的硬件支持，特别是在高速通信系统中。
Viterbi算法是一种复杂的算法，但它在纠错性能方面非常出色，可以大大提高数据传输的可靠性。
卷积码编译码原理课件
Viterbi算法具有较低的复杂度，适用于高速实时解码，且在信噪比较低的情况 下仍能保持较好的解码性能。
状态估计和路径选择
1 2 3
状态估计 在解码过程中，需要对每个状态进行估计，以确 定每个状态的转移概率和输出码字。
路径选择 在搜索所有可能的路径时，需要选择最可能的路 径作为解码结果，这涉及到路径选择和剪枝策略。
提高信号的纠错能力，保证数据的完整接收。
低误码率要求
02
在深空探测任务中，对数据的准确性和可靠性要求极高，卷积
码能够提供低误码率的保证。
自适应性能
03
卷积码可以根据信道状态自适应地调整编码参数，以适应不同
的传输环境。
在其他领域的应用
01
02
03
广播和多播通信
卷积码可以用于广播和多 播通信中，提高信号的覆 盖范围和接收质量。
04
仿真结果和分析
01
通过仿真实验，可以模拟卷积码 在实际通信系统中的性能表现。
03
仿真结果可以为实际应用提供参 考和指导，帮助选择合适的卷积
码参数和配置。
02
通过对比不同参数和配置下的仿 真结果，可以深入分析卷积码的
性能特点。
04
仿真结果还可以用于评估不同编 译码算法的性能优劣，为算法优
化提供依据。
性能优化 为了提高解码性能，可以采用一些优化措施，如 分支定界、路径剪枝和记忆算法等。
04 卷积码性能分析
误码率性能
误码率性能是衡量卷积码性能 的重要指标之一，它表示在传
输过程中发生错误的概率。
卷积码通过增加冗余位来纠正 错误，从而提高传输的可靠性。
随着信噪比的提高，卷积码的 误码率性能逐渐改善。
卷积码编码与译码
• 例： (n, k, N) = (3, 1, 3)卷积码编码器
– 方框图 输入bi
M1
M2
M3
bi
bi-1
bi-2
ei
di
编码输出
ci
– 设输入信息比特序列是bi-2 bi-1 bi bi+1，则当输入bi时，此编 码器输出3比特ci di ei，输入和输出的关系如下：
ci bi di bi bi2 ei bi bi`1 bi2
由于这是一个(n, k, N) = (3, 1, 3)卷积码，发送序列的 约束度N = 3，所以首先需考察nN ＝ 9比特。第1步 考察接收序列前9位“111 010 010”。由此码的网格 图可见，沿路径每一级有4种状态a, b, c和d。每种状 态只有两条路径可以到达。故4种状态共有8条到达 路径。
维特比译码算法使用最广泛，也是这次课程讨论的重点
输入bi
M1
M2
M3
bi
bi-1
bi-2
以前面介绍的(3,1,3)卷积码为例
移存器前一状态
M3 M2 a (00)
b (01)
c (10)
d (11)
当前输入信息位
bi 0 1
0 1
0 1
0 1
输出码元
cidiei 000 111
001 110
011 100
a 111
b
c 110
d
100 010
a
b 001
c
d
在上图中给出了输入信息位为11010时，在网格图中的编码路径。 图中示出这时的输出编码序列是：111 110 010 100 011…。由上述 可见，用网格图表示编码过程和输入输出关系比码树图更为简练。
卷积码编译码实验报告
厦门理工学院实验报告书课程名称：信息论与编码实验实验名称：卷积码编译码m•个有效的寄存器单元，而输出移位寄存器仅中输入移位寄存器最多只有k起一个并串转换作用。
因此称参量m为卷积吗的记忆长度（段）2、维比特译码原理它的基本思想是把接收到的矢量，和网格图上诸种可能的路径比较，删去距离大的路径，保留距离小的路径，以距离最小路径作为发码的估值五、实验内容在MATLAB环境下卷积码编/解码器的实现。
1、主函数main.mclear;clc;msg = randint(1,20,[0,1])word = encode_conv213(msg)word(1) =~word(1); %信道中存在污染，人为的模拟传输过word(10) =~word(10); %程中的出错码字word(15) =~word(15);word1=wordmsg_1 = decode_conv213(word1)msg-msg_12 、状态积state_machine.mfunction [output,nextState] = state_machine(input,current_state)output(1) = mod(current_state(1)+current_state(3),2);output(2) = mod(input+current_state(2)+current_state(1),2);nextState(1) = current_state(2);nextState(2) = current_state(3);nextState(3) = input;3、汉明距离hamming_distance.mfunction distance = hamming_distance(a,b)temp = a+b;temp = mod(temp,2);distance = sum(temp);4 、213编码程序encode_conv213.mfunction word = encode_conv213(msg)word = zeros(1,length(msg)*2);current = [0 0 0];for i = 1:length(msg)[out,next] = state_machine(msg(i),current);current = next;word(2*i-1) = out(1);word(2*i) = out(2);End5、213维比特译码decode_conv213.mfunction msg = decode_conv213(word)chip = 10; %初始状态选十个信息for i = 1:2^chipM(i,:) = de2bi(i-1,chip); %把所有可能性按二进制输出W(i,:) = encode_conv213(M(i,:));%得到相应的二进制编译后的码字D(i) = hamming_distance(W(i,:),word(1:chip*2));%与出错码字对比得到汉明距end[val,index] = sort(D);%val中存汉明距从小到大排列，index中存对应val数据所在位置ret_msg = zeros(1,length(word)/2); %开辟译出码字的存放空间for i = 1:6%1024种选择6种最小距离，并输出在ret_msg中，最小汉明距存于ret_dis ret_msg(i,1:chip) = M(index(i),:);ret_dis(i) = D(index(i));enditer = (length(word)-chip*2)/2; %剩余要译出的码字个数for i=1:iter %迭代过程for j=1:6msg_temp1 = [ret_msg(j,1:chip+i-1) 0]; %下一状态出“0”msg_temp2 = [ret_msg(j,1:chip+i-1) 1]; %下一状态出“1”word_temp1 = encode_conv213(msg_temp1);%下一状态为“0”时的编码word_temp2 = encode_conv213(msg_temp2);%下一状态为“1”时的编码dis_temp1 = hamming_distance(word_temp1,word(1:chip*2+2*i));dis_temp2 = hamming_distance(word_temp2,word(1:chip*2+2*i)); %算两种汉明距if (dis_temp1<dis_temp2)ret_msg(j,1:chip+i) = msg_temp1;ret_dis(j) = dis_temp1;elseret_msg(j,1:chip+i) = msg_temp2;ret_dis(j) = dis_temp2;%选择较小汉明距的状态储存并输出在ret_msg中，最小汉明距存于ret_disendendend[val,index] = sort(ret_dis); %把最终选择的6种最小汉明距按从小到大排列msg =ret_msg(index(1),:); %选出维特比译码最小的距离所译出的信息六、实验数据记录及分析（包括源程序清单及运行结果）：。
通信系统中的卷积码编码与译码技术研究
通信系统中的卷积码编码与译码技术研究近年来，随着通信技术的飞速发展，通信系统的规模逐渐扩大，通信速率不断提高，但通信信道却变得越来越复杂。
在这样的情况下，如何保证通信质量成为了一个亟待解决的问题。
卷积码编码与译码技术作为一种广泛应用于各种通信系统中的错误控制技术，为保障通信质量起到了至关重要的作用。
一、卷积码编码技术卷积码编码技术是一种线性分组码，利用移位寄存器和异或门可以实现。
它可以将输入信息序列编码成一个比特序列，以此达到纠错和误码检测的目的。
在卷积码编码中，输入信息序列经过“编码器”后生成的输出序列是由原输入信息序列和一些约束条件共同构成的。
卷积码编码通常采用生成矩阵或者状态图来进行描述。
其中生成矩阵是通过移位寄存器和异或门来描述卷积码的编码过程，由生成矩阵可以直接推导出卷积码的编码输出系数。
状态图是把卷积码的编码过程表示成有限状态机，从而实现对卷积码的解码。
基于状态图的解码技术可以应用于硬判决译码和软判决译码两种方式。
卷积码编码技术常用于数字通信、无线通信、卫星通信、有线通信等各种通信领域中，例如GSM、CDMA、WIMAX、LTE等通信系统中都采用了卷积码编码技术来实现传输数据的纠错。
二、卷积码译码技术卷积码译码技术是卷积码编码技术的逆过程，即将接收到的比特序列转换为原始比特序列。
前文提到的硬判决译码和软判决译码可以分别用于解码过程中。
硬判决译码是通过与预定义的码字比较，找到最接近接收序列的码字。
这种解码方式主要适用于信噪比较高的通信情况。
而在信噪比较低的情况下，就需要采用软判决译码技术。
软判决译码是通过概率计算得到最有可能的原始比特序列。
这种解码方式可以更好地处理信噪比较低的情况。
卷积码译码技术的速度、复杂度和电路成本等因素也是需要考虑的。
在实际通信中，具体选择哪种译码方式，还需要根据具体的通信场景情况和设计要求进行选择。
三、卷积码编码与译码的应用卷积码编码与译码技术广泛应用于现代通信系统中。
（2,1,2）卷积码的译码设计
（2,1,2）卷积码的译码设计前⾔卷积码是由伊莱亚斯(Elias)于1954 年⾸先提出来的。
它充分利⽤了各组之间的相关性，本组的信息元不但决定本组的监督元，⽽且也参与决定以后若⼲组的监督元。
同时在译码过程中，不但从该时刻所收到的码组中提取译码信息，⽽且还利⽤以后若⼲时刻内所收到的码组来提取有关信息。
⽆论从理论上还是实际上均已证明其性能优于线性分组码。
近年来众多有关卷积码研究结果表明，卷积码最有希望实现⾹农信道编码定理。
但卷积码在译码理论及实际应⽤较为复杂，这些缺点限制了其进⼀步发展和应⽤。
维特⽐译码算法由维特⽐（Viterbi）1964年提出，算法实质是最⼤似然译码，但它利⽤了编码⽹格图的特殊结构，在⽹格图中选择⼀条路径，使相应的译码序列与接收到的序列之间的汉明距(即量度)最⼩的⼀种最⼤似然译码⽅法，从⽽⼤⼤降低了计算的复杂性。
⽬前，第三代移动通信系统(3G) 在我国已经开始紧锣密⿎地实施，它带来的⾼速度、⾼品质的⽆线通信服务，将使我们领略到信息技术的⽆穷魅⼒。
信道纠错编码技术作为保证信息可靠传输的技术，在3G各系统中⼴泛采⽤，并且我们现在所使⽤的第⼆代移动通信系统，如GSM、 CDMA 通信系统，还有卫星与空间通信系统⼴泛采⽤了卷积码信道编、译码技术。
本次设计将以（2，1，2）卷积码为例，通过单⽚机，实现卷积码的译码，借助RS232完成单⽚机与单⽚机、单⽚机与计算机的串⼝通信，借助7279完成键盘扫描和数码管显⽰。
第⼀章系统组成及⼯作原理本次设计的（2，1，2）卷积码的译码由89C52单⽚机为⼯具，接收来⾃另⼀单⽚机或计算机的编码信息，通过7279的键盘扫描和数码管显⽰功能可以⽅便地观察到单⽚机接收的信息和译码结果。
其系统框图如下图1－1所⽰。
MAX232芯⽚能实现EIA-RS-232C的正负电压与TTL的⾼低电平之间的转换，通过它能够⽅便实现单⽚机与单⽚机、单⽚机与计算机间的串⼝通信。
HD7279是⼀⽚具有串⾏接⼝的, 可同时驱动8位共阴极数码管的智能显⽰驱动芯⽚, 该芯⽚同时还可连接多达64键的键盘矩阵,单⽚即可独⽴完成显⽰、键盘接⼝的全部功能。
卷积码的译码
有限状态编码的最大似然译码
当编码器的状态数有限时，不同编码路 径必然会有会合的情况。例：一个信息 长度为L的编码，所有可能路径数为2L个， 而对于一个4状态码而言，任一时刻路径 只能经过4个状态，因此大量的路径（当 用状态转移来描述时）是有重合的。 由于码的马氏特性，从某一时刻开始的 后续编码只与该时刻的状态有关，而与 之前如何到达该状态无关。
分段译码与残留路径
一个长度为L的码，在时刻k分为两段，之 前的称为A，之后的称为B。最大似然序列 必存在于从k时刻的M个状态出发（或在时 刻k经过M个状态的）的M*2L-k条路径之中。 而第k时刻到达每个状态都有2k/M条A路径， 显然，从第k时刻状态S出发的最佳路径的 前半段必然是到达该状态的2k/M条A路径中 的最佳A路径。称此最佳A路径为第k时刻 状态S的残留路径。
第八讲
卷积码的译码
回顾
卷积码是对信息流进行编码的一种有记 忆分组的编码方法 记忆有很多种，典型的为线性有限记忆 和线性无限记忆 当记忆为线性时，等效于输入信息流与 冲激响应之间的卷积 可分别用FIR和IIR滤波器来描述 矩阵描述、树图描述和网格图表示
卷积码的概率译码
概率译码：结合信道符号统计特性的译 码方法 一种简单的译码方法：逐分支译码 在码树图中每向前走一步，在决定走哪 一个分支时根据该分支子码与该时刻接 收子码之间的相似程度来判断
堆栈算法的本质
存贮一组可能路径 每次只有最可能的（度量最大的）路径 可以繁衍，同时删去父路径 繁衍出的子路径与其它未繁衍的路径一 起排序 堆栈满时最坏路径被丢弃
编码理论 第12章 卷积码的序列译码
北京邮电大学 信息工程学院
编码理论 第十二章 卷积码的序列译码
4、堆栈存储算法（3）
当算法终止时，存储器 中的领先路径就作为译 码路径。图 12.3 中示出堆栈 存储算法的一个完整流 程图。 在树的分叉部分，第一 步上有2 k 个新的量度要计算。在 树的尾部，只有 一个新的量度要计算。 注意：对于（ n,1, m）码，在树的分叉部分 每译一 步，存储器的容量就要 增加一，但当译码器处 于树的尾部时就跟本不 再 增加了。由于树的分叉 部分通常远远大于尾部 （L m） , 故存储器的容 量粗略等于算法终止时 的译码步数。
北京邮电大学 信息工程学院
编码理论 第十二章 卷积码的序列译码
2、费诺量度（2）
例12.1研究图 12.1 的码树，假定此码中的 一个码字经由 BSC 传送，且接受 序列为r (010,010,001 ,110,100,101 ,011 ). 对我BSC ，维特比算法中一条路 径V的量)度值由d(r, v)给定，他是最大似 然路径，即一条量度最 小的路径，现在比较两 条不同长度的路径。 [例如： 截短码字 [v]5 （ 111 ， 010 ， 001 ， 110 ， 100 ， 101 ）和[ v]0 （000 ） ]的部分路径量度。 部分路径量度是 d（[r ]5 , [ v]5） 2和d([r0 ],[ v]0 ) 1, 这表明 [ v]0 是两条路径 中“较好的”一个。然 而，直觉告诉我们，路 径[ v]5 要比[ v]更可能是部 分最大似然路径。因为 以[ v]0 开头来完成一条路径要 附加18 比特，而完 成以[ v 5 ]开头的整条路径只要求 加3比特。换句话说，以 [ v]0 作为开头的路 径远远比 [v5 ]开头的路径与 r之间的附加距离更可能 累积起来。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
摘要卷积码是一种性能优越的信道编码。
它的编码器和译码器都比较容易实现，同时它具有较强的纠错能力。
随着纠错编码理论研究的不断深入，卷积码的实际应用越来越广泛。
本文对卷积码和卷积码的编译码有一个简单的介绍且给出了信道编码的发展历史及研究状况，然后详细讨论了（2，1，2）卷积码的编码过程和译码过程，通过状态转移方程和输出方程得出状态转移表和状态转移图，然后通过维特比译码器研究，总结出了维特比译码算法，最后通过Matlab软件进行设计与仿真，得到了编码程序和译码程序，其运行结果与理论分析一致。
关键字卷积码编码、信道编码、Viterbi译码、MATLAB仿真目录摘要........................................... 错误！未定义书签。
一、引言 (3)1.1发展历史及研究状况 (3)1.2设计目的和意义 (3)1.3设计方法 (4)二、卷积码编译码原理 (5)2.1 卷积码编码原理 (5)2.2编码器 (6)2.3 卷积码译码原理 (7)2.4 VITEBI 译码的关键步骤 (8)2.4.1 输入与同步单元 (8)2.4.2 支路量度计算 (8)2.4.3 路径量度的存储与更新 (8)2.4.4 信息序列的存储与更新 (8)2.4.5 判决与输出单元 (8)三、卷积码编码实现 (9)3.1 编码原理分析 (9)3.2 卷积码编码流程图 (10)四、卷积码译码实现 (11)4.1 译码编程思路 (11)4.2 卷积码译码流程图 (11)五、卷积码编译码程序的编译及仿真波形 (11)5.1 卷积码编码仿真 (12)5.2卷积码译码仿真 (13)5.3卷积码纠错码仿真 (14)六、总结 (15)七、参考文献 (16)附录 (17)一、引言1.1发展历史及研究状况1948年，Bell实验室的C.E.Shannon发表的《通信的数学理论》，是关于现代信息理论的奠基性论文，它的发表标志着信息与编码理论这一学科的创立。
20世纪40年代，R.Hamming和M.Golay提出了第一个实用的差错控制编码方案，使编码理论这个应用数学分支的发展得到了极大的推动。
分组码所存在的固有缺点可以通过采用其他的编码方法来改善，这种编码方法就是卷积码。
卷积码是Elias等人在1955年提出的。
卷积码与分组码的不同在于：它充分利用了各个信息块之间的相关性。
通常卷积码记为(n，k，N)码。
卷积码的编码过程是连续进行的，依次连续将每k个信息元输入编码器，得到n个码元，得到的码元中的检验元不仅与本码的信息元有关，还与以前时刻输入到编码器的信息元(反映在编码寄存器的内容上)有关。
同样，在卷积码的译码过程中，不仅要从本码中提取译码信息，还要充分利用以前和以后时刻收到的码组．从这些码组中提取译码相关信息，而且译码也是可以连续进行的，这样可以保证卷积码的译码延时相对比较小。
通常，在系统条件相同的条件下，在达到相同译码性能时，卷积码的信息块长度和码字长度都要比分组码的信息块长度和码字长度小，相应译码复杂性也小一些。
由Wozencraft和Reiffen在1961年提出，Fano和Jelinek分别在1963年和1969年进行改进了的序贯译码算法。
该算法是基于码字树图结构的一种次最优概率译码算法。
由Massey在1963年提出的门限译码算法。
这个算法利用码字的代数结构进行代数译码。
由Viterbi在1967 年提出的Viterbi算法是基于码字格图结构的一种最大似然译码算法，是一种最优译码算法。
在Viterbi译码算法提出之后，卷积码在通信系统中得到了极为广泛的应用。
如GSM、3G、商业卫星通信系统等。
1.2设计目的和意义因为信道中信号不可避免会受到干扰而出错。
为实现可靠性通信，主要有两种途径:一种是增加发送信号的功率，提高接收端的信号噪声比;另一种是采用编码的方法对信道差错进行控制。
前者常常受条件限制，不是所有情况都能采用。
而编码理论可以解决这个问题，使得成本降低，实用性增强。
随着现代通信的发展，卷积码以其高速性和可靠性在实际应用中越来越广泛。
1967年Viterbi译码算法的提出，使卷积码成为信道编码中最重要的编码方式之一。
在卷积码中，因为Viterbi算法效率高，速度快，结构相对简单等特点，被广泛应用于各种数据传输系统。
特别是深空通信、卫星通信系统中。
因此采用Viterbi译码算法具有非常现实的意义。
1.3设计方法本文在分析卷积码编译码器原理的基础上，通过基于MATLAB对卷积编码，解码进行仿真。
通过仿真可以更清楚的认识到卷积码的编码，解码的各个环节，并对仿真结果进行了分析。
得出卷积码Viterbi译码的误比特性能和回溯长度，码率，约束长度的关系。
二、卷积码编译码原理2.1 卷积码编码原理2.1.1卷积码简介卷积码，又称连环码，是由伊莱亚斯(P.elias)于1955年提出来的一种非分组码。
卷积码编码的当前输出v(l)不仅与当前输入消息u(l)相关，还与此去前输入的m 个消息u(l-1),…,u(l-m) 相关，即v(l)=f(u(l),u(l-1),…,u(l-m)), l=0,1,2…卷积编码电路中移位寄存器初态可设定为全0，电路为按段工作方式，即对每段k 比特输出入，产生一段n 比特输出。
任意一输入段u(l-h)与输出v(l)的关系都是一个特殊的（n,k ）线性分组码的编码关系，即存在k*n 的二元矩阵h G ,使得h G h l u l v ∙-=)()(, h=0,1,2,…,m因此对于消息段序列u=(u(0),u(1),…，u(m),u(m+1),…),相应的输出端序列为v=(v(0),v(1),…,v(m)，v(m+1),…),并满足0)0()0(G u v =01)1()0()1(G u G u v +=011)()1()1()0()(G m u G m u G u G u m v m m +-+++=-011)1()()2()1()1(G m u G m u G u G u m v m m +++++=+-卷积编码电路在按段工作方式下只需存储或者记忆m 段的消息输入，电路中输入移位寄存器最多只有k m ∙个有效的寄存器单元，而输出移位寄存器仅起一个并串转换作用。
因此称参量m 为卷积码的记忆长度（段）。
二元（n ，k ，m ）卷积码共有M 2个不同的状态，记为1210,,,-M S S S 当状态为)(l δ（或δ）时,输入段)(l u （或u ）产生编码输出端)(l v （或v ） 并使该状态改变（或称为转移）到新的状态)1(+l δ(或'δ)。
δ到'δ的转移过程称为一个转移分支，记为（δ，'δ）或（)(l δ，)1(+l δ）并标记转移过程为)(/)(l u l v 或v/u 。
以状态δ为结点，转移分支为有向边描述卷积码的所有不同状态转移的有向图，称为卷积码的状态转移图。
2.2编码器2．2.1编码器的一般结构卷积码的编码器一般都比较简单。
输入图2-1 卷积码编码器框图图2-1是一般情况下的卷积码编码器框图。
它包括NK 级的输入移位器，一组n 个模2和加法器和n 级的输出移位寄存器 [6]。
对应于每段k 比特的输入序列，输出n 个比特。
由图可知，n 个输出比特不但与当前的k 个输入比特有关，而且与以前的(N-1)k 个输入信息比特有关。
整个编码过程可以看成是输入信息序列与由移位寄存器和模2加法器的连接方式所决定的另一个序列的卷积，卷积码由此得名。
本文采用的是冲击响应描述法编码思想。
2.2．2编码器的参数⑴ 有k 个输入信息端，n 个输出端（k<n ）,K-1节移位寄存器（共需k(K-1)个寄存器单元），称做（n,k,K ）卷积码。
⑵ 通常称K 为约束长度（一般来说，约束长度越大，则码字纠错性能越好）。
⑶ 码的效率：k/n⑷ 编码前，k(K-1)个寄存器单元全部复位清零。
⑸ 由于一段消息不仅影响当前段的编码输出，还影响其后m 段的编码输出，所以称参量为卷积吗的约束比特长度为n K n A ∙=注意进入卷积编码器的最后m 段消息仍是要编码输出的消息，对这最后m 段消息的编码处理，称作卷积编码的结尾处理。
一种常见的结尾处理方法是额外输入m段无效的0数据比特，一方面将存储的m 段消息编码全部推出，另一方面保证编码器回到全0的初态。
2.3 卷积码译码原理维特比算法的基本思想是把接收到的矢量，和网格图上诸种可能的路径比较，删去距离大的路径，保留距离小的路径，以距离最小路径作为发码的估值。
它的原理是将接收到的信号序列和所有可能的发送信号序列作比较,选择其中汉明距离最小的序列作为现在的发送信号序列。
为简便起见,讨论(n,k,N)卷积码当k=1的情形,从全0状态起始点开始讨论。
由卷积码网格图的前N-1级中支路构成的路径互不相交,即最初的2N-r条路径各不相同;当到达第N级时,每条路径都有2N-1条支路延伸到第N级上;而第N级上的每2条支路又都汇聚在一个节点上。
第N级以后的网格图图形完全是重复第N级的图形。
在维特比算法中,把汇聚在每个节点上的2条路径的对数似然函数累加值进行比较;然后把具有较大对数似然函数累加值的路径保存下来,称此部分路径为幸存路径,而丢弃另一条路径;经挑选后,第N级只留下2N-r条幸存路径,选出的路径连同它们的对数似然函数累加值一起被存储起来。
因每个节点引出2N-1条支路,因此以后各级中路径的延伸都增大一倍;但比较它们的似然函数累加值后,丢弃一半,结果留存下来的路径总数保持常数(等于其状态数)。
由此可见,上述译码过程中的基本操作是“加→比→选”。
即每级求出对数似然函数累加值,然后两两比较并做出选择。
有时会出现2条路径的对数似然函数累加值相等的情形,此时可任意选择其中一条作为“幸存路径”。
每一级都有21-N条幸存路径,则当序列发送完毕后，为判断其最后结果,通常要在网格图的终结处加上一些结束信息。
通常结束信息为N-1个已知信息,当然结束信息大于N-1也可以。
在此信息到来时,因每一个状态只有与已知发送信息相符的那条支路被延伸,因而在每级比较后,幸存路径减少一半。
因此,在接收到N-1个已知信息后,整个网格图中只有惟一的一条幸存路径保留下来。
这就是译码所得到的路径,这条译码路径和发送序列是最相似的。
从上述卷积码的译码过程可以看出:约束长度为N时,需要存储和计算21-N条路径的参量。
由此可见,维特比算法的复杂度随约束长度N按指数形式增长2N。
故维特比算法适合约束长度较小(N≤10)的编码。
当编码约束度不太大(≤10)或者误码率要求不太高(>105 )时,它的设备比较简单,用硬件译码计算速度快。
Viterbi译码的缺点是随着约束长度的增加算法的复杂度增加很快。