11.1.3函数的图象(2)
11.1.3函数的图像(1)vb
x y
画出函数 y=x+0.5的图象。 自变量怎样取值比较合理? … -2.5 -1.5 -0.5 0 0.5 1.5 2.5 … … -2 -1 0 0.5 1 2 3 … y 3 2 1
画出函数 y= 6 的图象. x
(4)(0,0.5) ;
1 (6)( 2 ,12)
(5)(1,6);
6 画出函数 y=x+0.5和y= 的图象. x
再观察图象Байду номын сангаас看看还能获取哪些 信息.
谈谈你的收获
作业:
11.1.3函数的图象(1)
y
o
x
根据图象你能获得哪些信息?
1.最大、最小值2.哪一段下降哪一段上升 3.哪一段温度不变4.每个时刻的温度
正方形的面积s与边长x的函数关 s=x2 ,其中自变量x的取 系为 值范围是 x>0 .
为了直观、清晰的看出两个变量s、x之间 的关系,我们如何画出函数s=x2的图象呢?
两个变量
有序实数对
图象
. (x,s)
s、x
(x,s)
2的图象呢? 如何画出函数s=x
计算并填写下表:
x s 0
0
0.5
0.25
1
1
1.5
2.25
2
4
2.5
6.25
3
9
3.5
12.25
4
16
这个点如何表示呢?
s 5 4 3
●
2 1
●
●
●
○
o
1 2
高中函数的总结归纳图像

高中函数的总结归纳图像函数是数学中一种重要的概念,它描述了数值之间的关系。
在高中数学学习过程中,函数是一个重要的内容,而函数的图像可以直观地展示函数的性质和特点。
本文将对高中函数的图像进行总结和归纳,以帮助读者更好地理解和掌握函数的概念。
一、一次函数的图像一次函数又称为线性函数,其图像是一条直线。
直线的基本特点是斜率和截距,因此一次函数的图像可以通过斜率和截距来确定。
1. 斜率为正数的一次函数:当一次函数的斜率为正数时,图像呈现上升的趋势。
斜率越大,图像越陡峭;斜率越小,图像越平缓。
此外,截距决定了图像与纵轴的交点位置。
2. 斜率为负数的一次函数:当一次函数的斜率为负数时,图像呈现下降的趋势。
与斜率为正数的情况类似,斜率的绝对值越大,图像越陡峭;斜率的绝对值越小,图像越平缓。
截距同样决定了图像与纵轴的交点位置。
3. 斜率为零的一次函数:当一次函数的斜率为零时,图像呈现平行于横轴的特点。
此时,函数的图像是一条水平线,截距决定了图像与纵轴的交点位置。
二、二次函数的图像二次函数的图像是一条抛物线,其形状取决于二次项的系数。
二次函数的图像可以分为三种不同情况进行讨论。
1. 二次函数的导数为正数的情况:当二次函数的导数为正数时,图像在极值点处取得最小值,图像开口朝上。
极值点的横坐标可以通过二次项系数的倒数来确定。
2. 二次函数的导数为负数的情况:当二次函数的导数为负数时,图像在极值点处取得最大值,图像开口朝下。
同样地,极值点的横坐标可以通过二次项系数的倒数来确定。
3. 二次函数没有极值点的情况:当二次函数没有极值点时,图像是一个开口朝上或者开口朝下的抛物线。
开口的方向取决于二次项的系数的正负。
三、指数函数和对数函数的图像指数函数和对数函数是高中数学中常见的函数类型,其图像具有以下特点。
1. 指数函数的图像:指数函数的图像呈现逐渐增长或逐渐减小的特点。
当指数为正数时,图像逐渐上升;当指数为负数时,图像逐渐下降。
11.1.3函数的图象(3)vb

X (小时)
如图表示一艘轮船和一艘快艇沿相 同路线从甲港出发到乙港行驶过程中路 程随时间变化的图像(分别是正比例函 数图象和一次函数图象).根据图像解答 S(千米) 下列问题:
160
0
2
6
x 8 (时)
从图中可以获得哪些信息呢?
小结
作业
一水库的水位在最近5小时内持续 上涨,下表记录了这5小时的水位高度.
t/时 y/米 0 10.00 1 10.05 2 10.10 3 10.15 4 10.20 5 10.25
(1)由记录表推出这5小时中水位高度y(米) 随时间t(时)变化的函数解析式,并画出函数图 象; (2)据估计这种上涨的情况还会持续2小时,预 测通过2小时水位高度将达到多少米?
11.1.3函数的图象(3)
y
o
x
已知大米的单价是2元/千克,试 用尽可能多的方法表示大米的总价y(元) 与所买数量x(千克)之间的函数关系.
x y
… …
0
0
1
2
2
4
y
3
6
…
…
y=2x
0
x
已知大米的单价是2元/千克,试 用尽可能多的方法表示大米的总价y(元) 与所买数量x(千克)之间的函数关系.
C
120
120 80 40
(A)
2 4
s(千米)
80
40
(B)
2 4
s(千米)
O
120 80 40
6 t(时)
O
120
6 t(时)
(C)
2 4 6 t(时)
80
40
(D)
2 4 6 t(时)
O
O
函数图像总结

函数图像总结函数图像是指函数在直角坐标系中的图形表示。
通过观察函数图像,可以了解函数的基本特征和性质。
下面我将对常见的函数图像进行总结。
一、一次函数图像:一次函数的一般形式为y = kx + b,其中k为斜率,b为截距。
当k>0时,函数图像呈现正斜率,向右上方倾斜;当k<0时,函数图像呈现负斜率,向右下方倾斜;当k=0时,函数图像为水平直线;当b>0时,函数图像在y轴上方截距b的位置;当b<0时,函数图像在y轴下方截距-b的位置。
二、二次函数图像:二次函数的一般形式为y = ax^2 + bx + c,其中a决定了函数的开口方向和开口大小,b决定了函数图像的对称轴位置,c决定了函数图像与y轴的交点。
当a>0时,函数图像向上开口;当a<0时,函数图像向下开口;当b=0时,函数图像的对称轴为y轴;当b>0时,函数图像的对称轴在原点的右侧;当b<0时,函数图像的对称轴在原点的左侧。
三、指数函数图像:指数函数的一般形式为y = a^x,其中a为底数。
当底数a>1时,函数图像呈现增长趋势,向上凸起;当0<a<1时,函数图像呈现递减趋势,向下凹陷;当a=1时,函数图像为水平直线。
四、对数函数图像:对数函数的一般形式为y = loga(x),其中a为底数。
当底数a>1时,函数图像呈现增长趋势,向右上方倾斜;当0<a<1时,函数图像呈现递减趋势,向右下方倾斜;当a=1时,函数图像为y轴。
五、三角函数图像:常见的三角函数包括正弦函数、余弦函数、正切函数等。
正弦函数的图像呈现周期性的波形,振动范围在[-1,1]之间;余弦函数的图像也呈现周期性的波形,振动范围也在[-1,1]之间;正切函数的图像在某些点上发生突变,振动范围在整个坐标轴上。
总结以上几种函数图像,可以根据函数的数学表达式和特点来推测图像的形状和性质,进而帮助解决与函数相关的问题。
函数的图像特征

函数图像的参 数影响
参数对函数图像形状的影响
斜率:斜率越大, 函数图像越陡峭
截距:截距越大, 函数图像越远离 原点
正负号:正负号 决定函数图像的 上升或下降趋势
幂指数:幂指数 越大,函数图像
越接近原点
常数项:常数项 影响函数图像的
起始位置
导数:导数决定 函数图像的凹凸
性
参数对函数图像位置的影响
翻转变换
翻转变换的定义:将 函数图像沿x轴或y轴 进行翻转
翻转变换的类型:包 括x轴翻转、y轴翻转 和原点翻转
翻转变换的应用:在 解决实际问题中,如 物理、工程等领域, 经常需要对函数图像 进行翻转变换
翻转变换的性质:翻 转变换不改变函数的 单调性、奇偶性、周 期性等性质
函数图像的对称性
轴对称:函数图像关于x轴、y轴或原点对称 旋转对称:函数图像关于某一点旋转一定角度后与原图像重合 反射对称:函数图像关于某一点或直线反射后与原图像重合 平移对称:函数图像关于某一点或直线平移一定距离后与原图像重合
圆函数:y=f(x)=x^2
开口方向:向上
形状:对称的抛物线
渐近线:y=x和y=-x
顶点:(0,0)
极值:(0,0)是最大值和最小值
函数图像的坐 标轴关系
截距
截距的定义:函数图像与x轴或y轴的交点 截距的作用:确定函数图像的位置和形状 截距的计算:通过函数解析式求解 截距的应用:解决实际问题,如物理、工程等领域
双曲线函数:y=a/x^2,其中a>0
形状:开口向上或向下,取决于a的 正负
顶点:(0,a)或(0,-a),取决于a的正 负
渐近线:y=x和y=-x,与x轴相交于 (0,a)和(0,-a)
焦点:(0,±a/2),取决于a的正负
初中知识点归纳——函数图像篇

初中知识点归纳——函数图像篇函数图像是初中数学中的重要内容之一。
通过函数图像的形状、特点以及变化规律,可以深入理解函数的性质和作用。
本文将从函数图像的基本形状与分类、常见函数图像的特点及其变化规律等方面进行归纳与总结。
一、函数图像的基本形状与分类函数图像的形状可以分为线性函数、二次函数、指数函数和对数函数等几种常见类型。
1. 线性函数图像线性函数的特点是图像为一条直线。
直线的斜率表示了函数的增减趋势,当斜率为正时,函数图像呈上升趋势;当斜率为负时,函数图像呈下降趋势;斜率为0时,函数图像为水平直线。
2. 二次函数图像二次函数的图像通常为抛物线形状。
抛物线的开口方向由二次项的系数决定,当二次项的系数为正时,抛物线开口向上;当二次项的系数为负时,抛物线开口向下。
二次函数的图像还受到常数项的影响,常数项决定了抛物线的位置。
3. 指数函数图像指数函数的图像为指数曲线,呈现上升或下降的趋势。
指数函数的底数决定了曲线在坐标系中的位置和形状。
当底数大于1时,指数曲线呈现上升趋势;当底数小于1但大于0时,指数曲线呈现下降趋势。
4. 对数函数图像对数函数的图像为对数曲线,也呈现上升或下降的趋势。
对数函数的底数决定了曲线在坐标系中的位置和形状。
当底数大于1时,对数曲线呈现上升趋势;当底数小于1但大于0时,对数曲线呈现下降趋势。
二、常见函数图像的特点与变化规律1. 线性函数的特点与变化规律线性函数的图像为一条直线,具有以下特点和变化规律:(1)斜率决定了线性函数图像的倾斜程度和方向,斜率越大图像越陡峭,斜率为正表示函数图像上升,斜率为负表示函数图像下降。
(2)截距决定了线性函数图像与纵轴的交点位置,截距为正表示交点在纵轴上方,截距为负表示交点在纵轴下方。
2. 二次函数的特点与变化规律二次函数的图像为抛物线,具有以下特点和变化规律:(1)开口方向由二次项的系数决定,正系数表示抛物线开口向上,负系数表示抛物线开口向下。
(2)顶点是抛物线的最高点或最低点,在坐标系中的横坐标为顶点的x坐标,纵坐标为顶点的y坐标。
人教新课标八年级上第11章一次函数_指导与训练_2
例 2.某市的公费医疗是这样规定的:挂号费 5 元由病人支付,药费(不包括挂号费)在 50 元 以内的部分(包括 50 元),其中一部分费用由病人支付,若超过 50 元。则超过部分全部由病 人支付.当 0≤x≤50 时,请根据下表提供的信息写出病人看病需支付的全部费用 y(元)与 药费 x(元)之间的函数关系式,并画出函数图象. 医药费用 x(元) 病人支付费用 y(元) 0 5 … … 30 11 35 12 40 13 45 14 50 15
2
x2 2 x 1 的图象上。那么 m=
.
4.已知函数 y=ax +bx 的图象经过点 A(-1.2)、B(2,2),则 a= ,b= . 5.如图 11-1-12 所示是某个函数的全部图象,根据图 象填空: (1)自变量的取值范围是 ; (2)函数 y 的变化范围是 ; (3)函数的最大值是 。 二、选择题 6.某非典疑似病人夜里开始发烧,早晨烧得厉害,医 院及时 抢救后体温开始下降,到中午时体温基本正常,但是 下午他 的体温又开始上升, 直到夜里他才感觉身上不那么发烫. 下面能较好地刻画出这位非典疑似 病人体温变化的图象是( )
7.张大伯出去散步.从家出发走了 20 分钟,到一个离家 900m 的阅报亭,看了 10 分钟报纸 后,用了 15 分钟返回家.下面图象中能表示张大伯离家时间与距离之间关系的是 ( )
8.函数 y=3x+1 的图 象一定通过( ) A. (3, 5) B. (-2, 3) C . (2 , 7) D.(4,10) 9.点 A(2,3)在函数 y=ax -x+1 的图象上,则 a 等于( ) A.1 B.-1 C.2 D.-2 2 10.函数 y=x 的图象与函数 y=2x 的图象交点是( ) A.(0,0) B.(2,4) C.(4,2) D.(0,0)和(2,4) 11.画出下列函数的图象,并判断括号内各点是否在该函数的图象上.
三角、反三角函数图像
六个三角函数值在每个象限的符号:
sinα·cscα cosα·secα tanα·cotα
三角函数的图像和性质:
函数
y=sinx
y=cosx
y=tanx
y=cotx
定义域
R
R
{x|x∈R且x≠kπ+ ,k∈Z}
{x|x∈R且x≠kπ,k∈Z}
值域
[-1,1]x=2kπ+ 时ymax=1
奇偶性
arcsin(-x)=-arcsinx
arccos(-x)=π-arccosx
arctan(-x)=-arctanx
arccotห้องสมุดไป่ตู้-x)=π-arccotx
周期性
都不是同期函数
恒等式
sin(arcsinx)=x(x∈[-1,1])arcsin(sinx)=x(x∈[- , ])
cos(arccosx)=x(x∈[-1,1]) arccos(cosx)=x(x∈[0,π])
y=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosy
y=tanx(x∈(- , )的反函数,叫做反正切函数,记作x=arctany
y=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty
理解
arcsinx表示属于[- , ]
且正弦值等于x的角
arccosx表示属于[0,π],且余弦值等于x的角
在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)
在(kπ- ,kπ+ )内都是增函数(k∈Z)
在(kπ,kπ+π)内都是减函数(k∈Z)
.反三角函数:
函数的图象
函数的图象[要点再现]1.一样地,关于一个函数,如果把自变量与函数的每对对应值分不作为点的横、纵坐标,那么在坐标平面内由这些点组成的图形,确实是 。
2.描点法画函数图象的一样步骤是:(1) ;(2) ;(3) 。
3.函数的表示方法共有 种。
分不是 法、 法和法。
4.你认为表示函数的几种方法各有什么优点?[基础闯关]下图是北京春季某一天的气温随时刻变化的图象:按照图象回答,在这一天:(1)8时、12时、20(2)(3)请你认真观看以下甲、乙两图,图中分不有几个变量?你能将其中的变量y 看成另一个变量x的函数吗?什么缘故?(甲) (乙)3.如图:向放在水槽底部的烧杯注水(流量一定),注满烧杯后,连续注水,直至注满水槽,水槽中水面上升高度h 与注水时刻t 之间的函数关系大致是下列图象中的( )ABCD4.一种豆子每千克售2元,即单价是2元/千克。
豆子的总的售价y(元)与所售豆子的数量x(千克)之间的函数关系能够表示成。
(1)按照上面的函数解析式,给出x一个值,就能算出y的一个相应的值,如此请你完成下表:(2)把x与y作为一对有序实数对,请你在坐标平面内描出上表中所得到的每一对有序实数(x,y)对相应的点。
(3)用线把上述的点连起来看看是什么图形?[能力提升]1.张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿,返回途中在读报栏前看了一会儿报,下图是据此情形画出的图象,请你回答下面的咨询题:(1)张爷爷在什么地点碰到老邻居的,交谈了多长时刻?(2)读报栏大约离家多少路程?(3)张爷爷在哪一段路程走得最快?(4)图中反映了哪些变量之间的关系?其中哪个是自变量?你能将其中某个变量看成另一个变量的函数吗?2.一慢车和一快车沿相同路线从A 地到相距120千米的B 地,所行地路程与时刻的函数图像如图所示.试按照图像,回答下列咨询题: ⑴慢车比快车早动身 小时,快车比慢车少用 小时到达B 地;⑵快车用 小时追上慢车;现在相距A 地 千米.3.水管是圆柱形的物体,在施工中,常常如下图那样堆放,随着的增加,水管的总数是如何变化的?如果假设层数为n ,物体总数为y ,t(min)s(m)O1020304050100200300400500600(2)请你写出y与n的函数解析式并画出函数图象。
高中数学函数图像大全
高中数学函数图像大全1. 常用数学函数1.1. 直线函数直线函数是数学中最简单的函数之一。
它的特点是图像为一条直线,表达式为y=kx+b,其中k和b是常数。
直线函数的图像与直线的斜率和截距有关。
1.2. 平方函数平方函数的图像为抛物线,表达式为y=x2。
平方函数的特点是对称于y轴,并且开口向上。
1.3. 立方函数立方函数的图像为一条类似于S字形的曲线,表达式为y=x3。
立方函数的特点是对称于原点,并且开口向上。
1.4. 平方根函数平方根函数的图像为一条向右开口的抛物线,表达式为 $y = \\sqrt{x}$。
平方根函数的特点是定义域为非负实数集。
1.5. 绝对值函数绝对值函数的图像为一条折线,表达式为y=|x|。
绝对值函数的特点是对称于y轴,并且在原点处转折。
2. 复合函数复合函数是由两个或多个函数相互组合而成的函数。
其图像可以通过将各个函数的图像进行组合来得到。
3. 反函数反函数是与给定函数互为反函数的函数。
其图像可以通过将给定函数的图像关于直线y=x进行对称得到。
4. 常见函数图像的变换常见函数图像可以通过平移、伸缩、翻转等操作进行变换,从而得到新的函数图像。
4.1. 平移变换平移变换是将函数图像沿x轴或y轴方向移动的操作。
对于函数y=f(x),平移变换的一般形式为y=f(x−a)或y=f(x)+b。
4.2. 伸缩变换伸缩变换是将函数图像在水平或垂直方向进行拉伸或压缩的操作。
对于函数y=f(x),伸缩变换的一般形式为 $y = a \\cdot f(bx)$。
4.3. 翻转变换翻转变换是将函数图像关于x轴或y轴进行翻转的操作。
对于函数y=f(x),翻转变换的一般形式为y=−f(x)或y=f(−x)。
5. 实际应用数学函数图像在实际应用中起到了重要的作用。
例如,在物理学中,函数图像可以用来描述物体的运动轨迹;在经济学中,函数图像可以用来描述经济变量之间的关系;在计算机科学中,函数图像可以用来进行数据的可视化等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)画出函数y=2x-1的图象; )画出函数 的图象; 的图象 (2)判断点 (-2.5,-4), )判断点A( , ), B(1,3), (2.5,4)是否 ),C( , ) ( , ), 在函数y=2x-1的图象上。 的图象上。 在函数 的图象上
6 的图象。 例2 画出函数 y = 的图象。 x
… 1 6 y= … 6 x x 2 3
3
4 5 2 1.5 1.2
6 … 1 …
从函数图象可以 看出, 看出,曲线从左 向右下降, 向右下降,即当 x由小变大时,y 由小变大时, 由小变大时 的值随之减小。
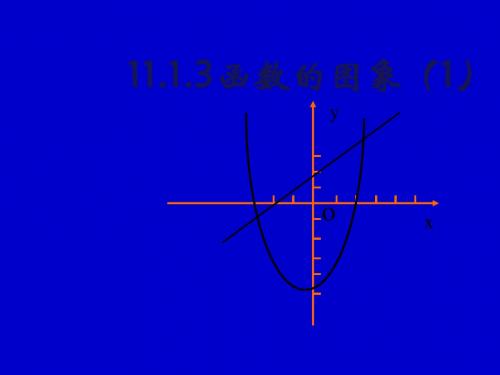
练习2 练习
的图象。 (1)画出函数 )画出函数y=X2的图象。 (2)从图象中观察,当x<0时, )从图象中观察, < 时 y随x的增大而增大,还是 随x的 的增大而增大, 随 的增大而增大 还是y随 的 增大而减小? 时呢? 增大而减小?当x >0时呢? 时呢
1、函数图象的画法: 、函数图象的画法: 画函数图象的方法为列表、描点、 画函数图象的方法为列表、描点、 连线,通常称为描点法。 连线,通常称为描点法。
2、通过观察函数的图象,理解 、通过观察函数的图象, 函数的两个变量的关系, 函数的两个变量的关系,能够从所给的 图象中获取信息从而解决简单问题
作业: 作业:P20页 10、12题 页 、 题
1、在某高速公路上,一辆轿车和一辆货车 、在某高速公路上, 沿相同路线从A地到 地到B地 沿相同路线从 地到 地 , 所经过的路程 y(千米 与时间x(小时 的函数关系图像如图 千米)与时间 小时)的函数关系图像如图 千米 与时间 小时 所示,试根据图像,回答下列问题: 所示,试根据图像,回答下列问题: 小时, (1)货车比轿车早出发 1 _小时,轿车追上货车 )货车比轿车早出发__ 小时 时行驶了_______千米 千米。 地到 地的距离为__ 地到B地的距离为 千米。 时行驶了 150 千米。A地到 地的距离为 300 _千米。 千米 (2) 货车的速度是 60 千米 时。 千米/时
如何在坐标系中表示S=x2? S=x (1) 列表 列表:
x S 0
0
0.5
0.25
1 1.5
1 2.25
2
4
2.5
3 3.5
4
6.25 9 12.25 16
(2)描点:表示与的对应的点有无数个,但是 描点:表示与的对应的点有无数个, 描点 实际上我们只能描出其中有限个点, 实际上我们只能描出其中有限个点,同时想 象出其他点的位置. 象出其他点的位置.
y
描点: ②描点: 连线: ③连线:
你能从所 画的图象 中获取哪 些信息? 些信息?
x
-3 -2 -1
3 2 1
o
-1 -2 -3
1
2
3
x
作函数图象的一 般步骤:列表、 般步骤:列表、 描点、连线. 描点、连线.
-3
-2
-1 0
1
2
3
y=x+0.5 -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5
画函数图象的一般分为哪几步? 画函数图象的一般分为哪几步?
1、列表 、 2、描点 、 3、连线 、
例1 画出函数y=x+0.5的图象 画出函数y=x+0.5的图象
解: x -3
列表: ①列表:
-2 -1 0 1 2 3
y=x+0.5 -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5
试一试
(2) )
问题: 、你能写出正方形的边长x与面积 与面积S的 问题:1、你能写出正方形的边长 与面积 的 函数关系式,并确定自变量x的取值范围吗 的取值范围吗? 函数关系式,并确定自变量 的取值范围吗?
S=x2 S=x
自变量x的取值范围是 > 自变量 的取值范围是x>0
2、能利用坐标系中画图的方法来表示S 、能利用坐标系中画图的方法来表示 与x的关系吗? 的关系吗? 的关系吗 提示:自变量 的一个确定值与它对应的函 提示 自变量x的一个确定值与它对应的函 自变量 数值S,就确定一个点(x,S) 数值 就确定一个点 就确定一个
的曲线去连接画出的点. (3)连线:用平滑的曲线去连接画出的点. )连线: 平滑的曲线去连接画出的点
函数图象 的定义
一般地, 一般地,对 于一个函数, 于一个函数,如 果把自变量与函 果把自变量与函 数的每对对应值 分别作为点的横、 分别作为点的横、 纵坐标, 纵坐标,那么坐 标平面内由这些 标平面内由这些 点组成的图形, 点组成的图形, 就叫做这个函数 就叫做这个函数 的图象。 的图象。
