第二讲 Matlab基础知识
合集下载
第二讲 MATLAB基本运算

2010-12-25 20
矩阵下标的用途
访问超出矩阵范围时,产生 Index exceeds matrix dimentions 存储超出矩阵范围时,矩阵自动调节 大小,将指定位置元素置入,其他没 指定数的位置默认为零。
2010-12-25
21
矩阵下标的用途
(2)矩阵连接 例:a=[1 2;3 4] b=[a a+5; a-5 zeros(size(a)] 将小矩阵嵌套入大矩阵,实现矩阵连接。
将矩阵按创建原则写入一个M文件, 在MATLAB的命令窗口或程序中直接执 行该M文件,即将矩阵调入工组空间。
2010-12-25
15
利用MATLAB函数创建矩阵 利用MATLAB函数创建矩阵 MATLAB
ones( m, n) - m行n列的1阵产生 zeros(m, n) -产生m行n列的全0阵 rand(m, n) -产生m行n列均匀分布全列的在 [0,1]区间的随机阵 randn(m, n) -产生m行n列的正态分布矩阵 eye(n) -产生n维单位阵
2010-12-25 18
2.2.3 矩阵的下标 .2.3
子矩阵提取A(v1, v2)
v1表示子矩阵包含的行标构成的向量 v2表示子矩阵包含的列标构成的向量 B1=A(:, [1, 3]) 为:时表示要提取所有行(列) B2=A(1:2:end, :) end表示最后一行(列) B3=A([3,2,1],[2,3,4]) 例: B4=A(:, end:-1:1) 提取A矩阵所有行、1,3列 提取A矩阵 3,2,1 行、2,3,4 列构成子矩阵 提取A矩阵全部奇数行,所有列 将A矩阵左右翻转
2010-12-25
13
直接输入法创建矩阵
例:创建矩阵
矩阵下标的用途
访问超出矩阵范围时,产生 Index exceeds matrix dimentions 存储超出矩阵范围时,矩阵自动调节 大小,将指定位置元素置入,其他没 指定数的位置默认为零。
2010-12-25
21
矩阵下标的用途
(2)矩阵连接 例:a=[1 2;3 4] b=[a a+5; a-5 zeros(size(a)] 将小矩阵嵌套入大矩阵,实现矩阵连接。
将矩阵按创建原则写入一个M文件, 在MATLAB的命令窗口或程序中直接执 行该M文件,即将矩阵调入工组空间。
2010-12-25
15
利用MATLAB函数创建矩阵 利用MATLAB函数创建矩阵 MATLAB
ones( m, n) - m行n列的1阵产生 zeros(m, n) -产生m行n列的全0阵 rand(m, n) -产生m行n列均匀分布全列的在 [0,1]区间的随机阵 randn(m, n) -产生m行n列的正态分布矩阵 eye(n) -产生n维单位阵
2010-12-25 18
2.2.3 矩阵的下标 .2.3
子矩阵提取A(v1, v2)
v1表示子矩阵包含的行标构成的向量 v2表示子矩阵包含的列标构成的向量 B1=A(:, [1, 3]) 为:时表示要提取所有行(列) B2=A(1:2:end, :) end表示最后一行(列) B3=A([3,2,1],[2,3,4]) 例: B4=A(:, end:-1:1) 提取A矩阵所有行、1,3列 提取A矩阵 3,2,1 行、2,3,4 列构成子矩阵 提取A矩阵全部奇数行,所有列 将A矩阵左右翻转
2010-12-25
13
直接输入法创建矩阵
例:创建矩阵
MATLAB课件-第二讲
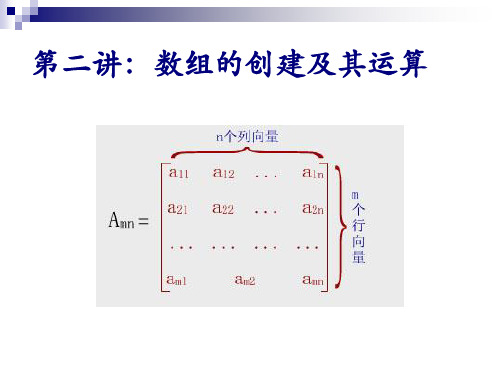
A(r,c)
访问A的由r指定行和c指定列上元素构 成的子数组;r,c可取多行或列
A(r, :)
访问A的r指定行上全部元素构成的子 数组;此处冒号表示全部列
A(:,c)
访问A的c指定列上全部元素的子数 组;此处冒号表示全部行
【例1】单下标的使用 >>a=zeros(2, 5); >>a(:)=-1:8
【例4】>> diag (diag(D)) %外面diag含义为利用一维数组生 成对角阵
ans= 100 010 001
【例5】>>命令栏输入:magic(3) ans =
816 357 492 说明:magic(3)生成一3x3魔方矩阵,即该矩阵横、竖、斜 各列元素总和相等
2.4 数组操作
常见的数组操作函数
命令 permute repmat
reshape
flipud
fliplr
rot90
含义
重排数组的维度次序
按指定的“行数、列数”铺放模块数组,以形成更大 的数组
在总元素数不变的前提下,改变数组的“行数、列 数” 以数组“水平中线”为对称轴,交换上下对称位置上 的数组元素
以数组“垂直中线”为对称轴,交换左右对称位置上 的数组元素
>>a([1 3 5 5 3 1])
ans = 0 5 10 10 5 0
>>a(6)
??? Index exceeds matrix dimensions. 索引超出矩阵维度。 下标值超出了数组的维数,导致错误
>>a(2.1)
??? Subscript indices must either be real positive integers or logicals.
MATLAB-2基础入门

format 只改变变量的输出格式, 但不会影响变量的值!
数值显示格式设置
缺省显示格式:简洁的短(short g)格式 窗口命令及语法格式:format 显示格式 关键字 如:format long %15位数字显示
21
各种 format 格式
格式
format
format short format long
为便于学习,以算例方式叙述,并通过 算例归纳一些MATLAB最基本的规则和语法结 构。
【例】
求 [12 2 (7 4)] 32 的算术运算结果。 本例演示:最初步的命令输入形式和必需的 操作步骤。
(1)用键盘在MATLAB命令窗中输入以下内容
>> (12+2*(7-4))/3^2
(2)在上述表达式输入完成后,按 [Enter] 键,该命令被执行,并显示如下结果。
29
Matalab7.1的workspace窗口
Matalab6.5的workspace窗口
32
工作空间浏览器主要功能及其操作方法
四、历史指令窗(Command History)
历史窗口:
首先记录每次启动时间;并记录在命令窗口输入 命令,此次运行期间,输入的所有命令被记录为 一组,并以此次启动时间为标志。
>>radius=5.2; %圆的半径 >>area=pi*5.2^2, circle_len=2*pi*5.2 area = 84.9487 circle_len = 32.6726
以上两例,命令行中用到了等号“=” 。 计算结果不再赋给“ans”,而是赋给 用户指定的变量y、area、circle_len 。 无论是预定义变量还是用户自定义变量 都被存储在系统的工作空间内,即系统 定义的一个存储窗口变量的内存空间。 Who、whos命令用来显示工作空间的 变量 clear命令用来清除工作空间的变量。
数值显示格式设置
缺省显示格式:简洁的短(short g)格式 窗口命令及语法格式:format 显示格式 关键字 如:format long %15位数字显示
21
各种 format 格式
格式
format
format short format long
为便于学习,以算例方式叙述,并通过 算例归纳一些MATLAB最基本的规则和语法结 构。
【例】
求 [12 2 (7 4)] 32 的算术运算结果。 本例演示:最初步的命令输入形式和必需的 操作步骤。
(1)用键盘在MATLAB命令窗中输入以下内容
>> (12+2*(7-4))/3^2
(2)在上述表达式输入完成后,按 [Enter] 键,该命令被执行,并显示如下结果。
29
Matalab7.1的workspace窗口
Matalab6.5的workspace窗口
32
工作空间浏览器主要功能及其操作方法
四、历史指令窗(Command History)
历史窗口:
首先记录每次启动时间;并记录在命令窗口输入 命令,此次运行期间,输入的所有命令被记录为 一组,并以此次启动时间为标志。
>>radius=5.2; %圆的半径 >>area=pi*5.2^2, circle_len=2*pi*5.2 area = 84.9487 circle_len = 32.6726
以上两例,命令行中用到了等号“=” 。 计算结果不再赋给“ans”,而是赋给 用户指定的变量y、area、circle_len 。 无论是预定义变量还是用户自定义变量 都被存储在系统的工作空间内,即系统 定义的一个存储窗口变量的内存空间。 Who、whos命令用来显示工作空间的 变量 clear命令用来清除工作空间的变量。
第二讲 Matlab的基本计算

>>a3=mat2str( a,2 ) %一行字符
字符串的应用:作出函数图形,并标注最大值点。 字符串的应用:作出函数图形,并标注最大值点。
y = e 2t sin(3t ) 0 ≤ t ≤ 10
clear %清除内存变量 t = 0 : 0.01 : 10; %时间 t 从 0 到 10 每隔 0.01 均匀采样 y = exp( -2*t ) .* sin( 3*t ); %对应每一个 t 求 y 值 %求最大值 y_max 及其下标 i_max [ y_max, i_max ] = max( y ); %横坐标字符串 t_text = [ 't = ', num2str( t(i_max) ) ]; %纵坐标字符串 y_text = [ 'y = ', num2str( y_max ) ]; %三行字符来标识最大值点 max_text = char( 'Maxium', t_text, y_text ); %图名称字符串 Title = [ 'y = exp( -2*t ) .* sin( 3*t )' ]; %新建一个图形窗 figure %画一条黑色的水平线 plot( t,zeros( size(t) ), 'k' ) %保持图形不被清除 hold on %蓝色实线画曲线 y(t) plot( t, y, 'b' ) %大小为 20 的红圆点标记最大值点 plot( t(i_max), y_max, 'r.', 'MarkerSize', 20 ) %在最大值点附近显示注释字符 text( t(i_max)+0.3, y_max+0.05, max_text ) %显示图名、横坐标名、纵坐标名 title( Title ); %取消图形保持 xlabel( 't' ) ylabel( 'y' ) hold off
第二讲 MATLAB基础PPT课件
3、MATLAB常用用户文件格式
• M文件:程序文件。文件扩展名为.m。可在File 菜单中创建或打开。也可从历史命令窗口生成。
• MAT文件:数据文件。文件扩展名为.mat。用 于保存工作空间中(内存中)的数据变量。可 用“save”命令生成。
• FIGURE文件:图形文件。文件扩展名为.fig。 可由MATLAB的绘图命令生成,也可在File菜 单中创建或打开。
save — 将全部变量保存到数据文件中 save a b— 将变量a,b保存到数据文件中 save a b-append— 将变量a,b添加到中 clear —— 从内存中删除变量 clear a b —— 从内存中删除变量a,b (clc —— 清屏 ) who —— 显示内存中的变量(只显示变量名) load —— 将变量从 .mat 数据文件中装入内存
Current Directory Browser 窗口
• Workspace Browser(工作空间浏览器窗口)
也是在左上方,可与目录浏览器窗口切换。又称内存浏 览器窗口。用于显示MATLAB工作空间中所有变量的变量名、 数据结构、数据类型、大小和字节数。并可以对变量进行观 察、编辑、提取、保存和图形显示等操作。
Clear Command History % 清除历史命令窗口中的内容
Clear Workspace
% 清除工作空间中的内容
• Desktop: Undock Workspace % 将工作空间窗口从主界面中分离
…ቤተ መጻሕፍቲ ባይዱ
Desktop Layout
% 主界面布局
Command Window % 打开(或关闭)命令窗口
在左上方。可显示当前目录下的M(程序)、 FIG(图形)、 MAT(数据)等文件信息,如文件 类型、文件名、最后修改时间等,并可复制、编辑 和运行M文件以及装载MAT数据文件。选中窗口中 列出的某个文件,单击鼠标右键,即可对其进行打 开、运行、装载等处理和创建、重命名、删除、复 制等常规操作。
MATLAB第二讲__数值计算和符号计算

(4)数值运算中必须先对变量赋值;符号运算无须事先对变 量赋值,但必须先定义,运算结果以标准的符号表达 式形式给出。
Matlab基础应用 21
2.2.2 符号运算中的运算符
(1)基本运算符 符号矩阵:‚+”,‚-”,‚*‛,‚\”, ‚/”, ‚^”, ‚ ’ ” 符号数组:‚.*”,‚./”,‚.\‛,‚.^”, ‚.’ ” (2)关系运算符 运算符只有‚==”,‚~=”。
Matlab基础应用 7
1.3.4 多项式乘除运算(续)
例4: a(x)=x2+2x+3; b(x)=4x2+5x;求c=a(x)*b(x)。 解: >>a=[1 2 3];b=[4 5 0]; >>c=conv(a,b) c= 4 13 22 15 0 >>[d,r]=deconv(c,a) d= 4 5 0 r= 0 0 0 0 0
注意: 方法一只创建了符号表达式,没有创建符号变量; 而方法二既创建了符号表达式,又创建符号变量.
Matlab基础应用 19
2.1.3 创建符号矩阵
使用sym和syms命令创建
例4: A=sym(‘[a,b;c,d]’) A= [ a, b] [ c, d] syms f g h k B=[f,g;h,k] B=
%方法二
Name Size Bytes Class a 1x1 126 sym object b 1x1 126 sym object c 1x1 126 sym object f2 1x1 146 sym object x 1x1 126 sym object Grand total is 20 elements using 650 bytes
Matlab 第二讲:Matlab中的函数

15
MATLAB is column dominant, so when sort is used with a 2-D matrix, each column is sorted in ascending order
16
查看矩阵的大小
查看矩阵的大小:size、length
size(A) size(A,1) size(A,2)
Matlab中的函数
1
函数取值
函数作用在矩阵上的取值
设 x 是变量, f 是一个函数
当 x = a 是标量时,f(x) = f(a) 也是一个标量 当 x = [x1, x2, … , xn ] 是向量时,则 f(x) = [ f(x1), f(x2), … , f(xn)] 是一个与 x 长度相同的向量
f 作用在 x 的每个分量上!
若 A 是矩阵,则 f (A) 是一个与 A 同形状的矩阵
2
函数取值
f ( a11 ) f (a ) 21 f ( A) f ( am1 ) f ( a12 ) f ( a22 ) f ( am 2 ) f ( a1n ) f ( a2 n ) f ( amn )
若参数 x 是矩阵, 则作用在其各列上
6
Function Input can be either scalars or matrices
7
内置函数的使用
Functions consist of
Name Input argument(s) Output In MATLAB sqrt (x)= result sqrt(4) ans = 2
log(x) % ln(x) 自然对数 (以 e 为底) log2(x) % 以 2 为底的对数 log10(x) % 以 10 为底的对数 sqrt(x) abs(x) % 平方根 % 绝对值
第2讲 MATLAB初步

(2) 范得蒙矩阵 范得蒙(Vandermonde)矩阵最后一列全为1, 倒数第二列为一个指定的向量,其他各列 是其后列与倒数第二列的点乘积。可以用 一个指定向量生成一个范得蒙矩阵。在 MATLAB中,函数vander(V)生成以向量V 为基础向量的范得蒙矩阵。例如, A=vander([1;2;3;5])即可得到上述范得蒙矩 阵。
各种 format 格式
格式 解释 例
format
format short format long
短格式(缺省显示格式),同short
短格式(缺省显示格式),只显示5位 长格式,双精度数15位,单精度数7位
3.1416
3.1416 3.14159265358979
format short e
format long e format short g format long g format compact format loose
(5) 伴随矩阵 MATLAB生成伴随矩阵的函数是 compan(p),其中p是一个多项式的系数向 量,高次幂系数排在前,低次幂排在后。 例如,为了求多项式的x3-7x+6的伴随矩阵, 可使用命令: p=[1,0,-7,6]; compan(p)
(6) 帕斯卡矩阵 我们知道,二次项(x+y)n展开后的系数随n 的增大组成一个三角形表,称为杨辉三角 形。由杨辉三角形表组成的矩阵称为帕斯 卡(Pascal)矩阵。函数pascal(n)生成一个n阶 帕斯卡矩阵。
2.1.3 内存变量的管理 1.内存变量的删除与修改
clear命令用于删除MATLAB工作空间中的变 量。who和whos这两个命令用于显示在 MATLAB工作空间中已经驻留的变量名清 单。who命令只显示出驻留变量的名称, whos在给出变量名的同时,还给出它们的 大小、所占字节数及数据类型等信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五.字符串操作
3. 通用字符串操作
S = string(A) 将整数数组转换为字符串(转换为相应的ASCII码) S = char(A) 将ASCII码转换为字符串 A = double(S) 将字符串转换为相应的ASCII码 isstr(S) 确认是否为字符串
18 2013-7-25
B. / A B点除A,如果B和A都是矩阵,且维数相 同,则结果等价于B中的元素除以A中对 应的元素;如果其中一个为数,则结果 为此数与相应的矩阵中的每个元素作运算
5 2013-7-25
一.一般运算符及操作符
2.操作符
“:”
j : k j,j 1, ,k
j : i : k j,j 1, ,k A(:, i ) 取矩阵的第i列(列向量) A(i, :) 取矩阵的第i行(行向量) A(:, :) 以A的所有元素构成二维矩阵 A( j : k ) A( j ), A( j 1), A(k ) A(:) 将A的元素作为一个列向量
26 2013-7-25
六.M文件与M函数
编写简单的M命令文件exam1.m
a = [ 1 2 3 4 5 ;2 3 4 5 6; 3 4 5 6 7;4 5 6 7 8]; b = a(:,2); a b 分析运行结果:
27 2013-7-25
六.M文件与M函数
2.M函数文件 注意到M命令文件只能“机械”的执 行,不能和用户产生互动,为此定义M 函数文件。 为了产生互动,M函数文件一般都要 带参数,都要有返回值,而且函数文件 要定义函数名。注意:函数文件中的变 量是局部变量,函数运行结束后被清除。
23 2013-7-25
五.字符串操作
常用矩阵函数
sqrtm() expm() funm() logm() size() 求矩阵的平方根 求矩阵的指数值 求矩阵计算的函数值 求矩阵的对数值 求矩阵的维数
24 2013-7-25
六.M文件与M函数
Matlab输入命令的方式大体有两种,一 种就是在工作空间(命令窗口)中直接输入 简单命令,这种命令只适合于比较简单、问 题比较特殊、没有一定的重复性和普遍性的 简单场合。 Matlab还提供了一种功能强大的工作方 式,这就是M文件的编程工作方式。M文件 的语法类似于一般高级语言,但更简单易学。 M文件的两种形式:命令文件(脚本文件), 函数文件。扩展名都是.m。
33 2013-7-25
六.M文件与M函数
3.函数的调用
函数的嵌套调用 在M函数中调用任意其他的函数
函数的递归调用 在M函数中直接或间接地调用本身
(看例程fac.m)
34 2013-7-25
七.程序结构与控制
程序结构一般分为顺序结构、循环结 构、分支结构,和其他高级语言一样, Matlab也包含以上3中基本结构。 1.顺序结构 依次顺序执行程序的各条语句 2.循环结构 根据一定的条件,重复执行
五.字符串操作
7. 常用函数
三角函数
sin(), asin(), cos(), acos(), tan(), atan(), sec(), asec(), cot(), acot(), sinh(), asinh()
常用计算函数
fix() 朝零方向取整 (相关函数floor(), ceil()) log() 自然对数 log10() 常用对数 sort() 求数值的平方根 conj() 求复数的共轭 real() 求复数的实部 imag() 求复数的虚部 abs() 求绝对值 exp() 求指数函数 roud() 四舍五入到最近的整数 rem() 求两整数相除的余数
25 2013-7-25
六.M文件与M函数
1.M命令文件 如果要输入较多的命令,而且要经常 对这些命令进行重复输入,则可以将这 些命令放到一个扩展名为“.m”的文本 文件中,每次运行时只要输入M文件的 文件名即可。注意:此M文件要放在系 统的搜索路径下,而且文件名不要与内 置函数和工具箱中的函数重名。从这点 看,M文件与Dos下的批处理命令或其 他语言的脚本文件有相似之处。
28 2013-7-25
六.M文件与M函数
a)
M函数文件fun.m的两种格式
带返回值的函数文件 function y = fun(a,b…) … y=… 不带返回值的函数文件 function fun(a,b…) …
29 2013-7-25
b)
六.M文件与M函数
编写函数文件exam2.m function y = exam2(n) %这是一个M函数的例子,y = exam2(n)中的n可以为任 %意数或矩阵 a1 = n ; a2 = n + 1 ; a3 = n + 2 ; y = a1 + a2 + a3;
主要用来对数与矩阵,矩阵与矩 阵进行比较,并返回二者之间大小关 系的0、1矩阵。 (equal) “==” eq(a, b) 比较两个对象是否相等(同)
“~=” ne(a, b) (not equal) 比较两个对象是否不等(同)
10 2013-7-25
三.关系运算
“>”
gt (a, b)
Isinf(A) 与finite(A)相反,用法相同
15 2013-7-25
四.逻辑运算(函数)
Isempty(A) 确定矩阵是否为空(区别零矩阵, 空间矩,矩阵不存在) Isequal(A,B…) 判断几个对象是否相等(和eq() 相区别) Isnumeric(A) 判断矩阵是否是数据矩阵
6 2013-7-25
一.一般运算符及操作符
“%” 在M文件和命令行中表注释 “…” 换行时的继续符 “ ‘” 矩阵的转置 “;” 在[]中表示矩阵行的结尾;在命令行中,则命 令不回显
7 2013-7-25
二.数据格式显示
Matlab软件中默认所有数值为双精度 显示(double型) Format 默认值,与short格式相同 Format short 短格式,只显示5位数值 Format long 长格式,显示15位数 Format short e 短格式e方式 Format long e 长格式e方式 Format hex 十六进制格式
16 2013-7-25
五.字符串操作
1. 建立字符串变量
S = „字符串’
2. 建立字符串矩阵
SA = [„string11‟ „string12‟ „string 13‟ … ; … „stringn1‟ „stringn2‟ „stringn3‟ …] 注:每行字符串元素的个数总数必须相等
17 2013-7-25
矩阵的数组乘法
X .*Y
(两个矩阵的相应元素相乘,特别:
其中一个为数时变为数与矩阵相乘)
矩阵的乘方运算
X^ y
(若X为方阵,y是一个大于1的整数,
则结果等价于线性代数中X y;若y不是 整数,则计算各特征值和特征向量的乘方)
3 2013-7-25
一.一般运算符及操作符
x^ Y 由各特征值和特征向量计算
12 2013-7-25
四.逻辑运算(函数)
2.逻辑函数 All(a) a为向量,若a中所有元素为非零, 则返回“1”,否则返回“0” All(A) 作用于列向量上,返回一个向量 (与A的列数相同维) All(A,dim) 将指定dim维作为向量运算
13 2013-7-25
四.逻辑运算(函数)
在将计算结果按某种格式进行输出,或对 图形对象进行标注和说明时必须将数值转换为 字符串。 S = int2str(A) 将整数转换为字符串 S = num2str(A) 将浮点数转换为字符串 A = str2num(S) 将字符串转换为浮点数
21 2013-7-25
五.字符串操作
6. 数的进制间的转换
31 2013-7-25
六.M文件与M函数
修改exam2.m如下: function y = exam2(n) %这是一个M函数的例子,y = exam2(n)中的n可以为任 %意数或矩阵,此函数用来验证M函数变量的局部性 a1 = n ; a2 = n + 1 ; a3 = n + 2 ; whos a1 a2 a3 y = a1 + a2 + a3; 分析运行exam2(2)结果:
矩阵的除运算
A\ B A左除B,其结果与inv( A) * B相同,X A \ B是方程AX B的解
4 2013-7-25
一.一般运算符及操作符
A/ B A右除B,其结果与B * inv( A)相同,可以 由左除得到: B / A ( A'\ B' )' X B / A是方程XA B的解
32 2013-7-25
六.M文件与M函数
ቤተ መጻሕፍቲ ባይዱ
带多个返回值的M函数文件exam3.m
function [x,y,z] = exam3( n ) %这是一个M 函数的例子,此函数返回3个值 x=n; y = n + 1; z = n + 2; 运行如下: a = [1 3; 2 3]; [x,y,z] = exam3(a)
8 2013-7-25
二.数据格式显示
Format bank 显示两位小数 Format rat 有理格式 Format + 紧密格式(正——“+”; 负——“-”);零——“ ”) Format compact 紧凑格式 Format loose 疏松格式
9 2013-7-25
三.关系运算
(great than)
“<”
lt(a, b)
(less than)
(great than or
“>=” ge(a, b) equal) “<=”
