高三数学算法和程序框图试题
高三数学算法和程序框图试题

高三数学算法和程序框图试题1.执行下图所示的程序框图,若输入A=2014,B=125,输出的A的值是____ .【答案】1【解析】:第一次循环:,,第二次循环:,,第三次循环:,,第四次循环:,,否,所以输出【考点】程序框图的循环结构2.某流程图如图所示,现输入如下四个函数,则可以输出的函数是()A.B.C.D.【答案】C【解析】根据程序框图知输出的函数为奇函数,并且此函数存在零点.经验证:不存在零点;不存在零点;为偶函数,且的定义域为全体实数,且,故此函数为奇函数,且令,得,函数存在零点,答案C 【考点】程序框图、函数的奇偶性、函数零点.3.(5分)(2011•陕西)如图框图,当x1=6,x2=9,p=8.5时,x3等于()A.7B.8C.10D.11【答案】B的值.【解析】从程序框图中得到求p的解析式;列出方程,求出x3解:∵∴=8解得x3故选B点评:本题考查通过程序框图能判断出框图的功能.4.执行如图所描述的算法程序,记输出的一列的值依次为,其中且.(1)若输入,写出全部输出结果.(2)若输入,记,求与的关系().【答案】(1)输出结果共4个,依次是:.(2).【解析】(1)这是一个循环结构,依次写出每次循环的结果即可.(2)由框图中可得当时,.再由可得.将代入即可得与的关系.(1)这是一个循环结构,前4次输出的为:,第5次循环的结果为,与相等,故结束循环.所以输出的为:.(2)当时,..【考点】1、程序框图;2、递推数列.5.已知一个算法的程序框图如图所示,当输出的结果为0时,输入的值为()A.或B.或C.或D.或【答案】C【解析】当时,,即;当时,,即,所以输入的x的值为1或-2.【考点】程序框图.6.按照下图的程序图计算,若开始输入的值为3,则最后输出的结果是()A.6B.21C.5050D.231【答案】D【解析】由程序框图,输入,第次进入循环体,,第次进入循环体,,第次进入循环体,,成立,输出结果,故选.【考点】程序框图.7.给出30个数:1,2,4,7,……其规律是:第1个数是1;第2个数比第1个数大1;第3个数比第2个数大2;第4个数比第3个数大3;……以此类推,要计算这30个数的和,现已给出了该问题的程序框图如图所示,那么框图中判断框①处和执行框②处应分别填入()A.B.C.D.【答案】【解析】由于要计算30个数的和,故循环要执行30次,由于循环变量的初值为1,步长为1,故终值应为30,即①中应填写;又由第1个数是1;第2个数比第1个数大1;第3个数比第2个数大2;第4个数比第3个数大3;…故②中应填写故选【考点】循环结构.8.阅读如下程序框图,如果输出,那么空白的判断框中应填入的条件是A.B.C.D.【答案】B【解析】由程序框图知前3次运算结果:因此终止条件为,故选B.【考点】本题主要考查算法的基本思想、算法的结构和功能,考查抽象思维能力和逻辑推理能力.9.图中,,,为某次考试三个评阅人对同一道题的独立评分,为该题的最终得分,当,,时,等于()A.11B.10C.8D.7【答案】C【解析】先读懂右图的逻辑顺序,然后进行计算判断,其中判断条件是否成立是解答本题的关键.,,不成立,即为“否”,所以再输入;由绝对值的意义(一个点到另一个点的距离)和不等式知,点到点的距离小于点到的距离,所以当时,成立,即为“是”,此时,所以,即,解得,不合题意;当时,不成立,即为“否”,此时,所以,即,解得,符合题意,故选C.10.如图所示的程序框图,输出的S的值为()A.B.2C.-1D.-【答案】A【解析】k=1时,S=2,k=2时,S=,k=3时,S=-1,k=4,S=2,……所以S是以3为周期的循环.故当k=2 012时,S=.11.程序框图(即算法流程图)如下图所示,其输出结果是.【答案】127【解析】运行该程序框图如下故填127【考点】程序框图12.右图是计算值的一个程序框图,其中判断框内应填入的条件是A.B.C.D.【答案】A【解析】判断框内应该填循环终止条件,∵要加到,一共加4次∴k>5.【考点】程序框图.13.执行如图所示的程序框图,输出的S=________.【答案】【解析】执行第一次循环时S=,i=1;第二次循环S=,i=2,此时退出循环.故输出S=.14.定义某种运算S=a⊗b,运算原理如图所示,则式子: +的值是.【答案】4【解析】2tan ="2,ln" e=1,∵2>1,∴⊗ln e==3;lg 100=2,=3,∵2<3,∴lg 100⊗==1.∴+=4.15.程序框图如图所示,该程序运行后输出的的值是()A.B.C.D.【解析】由程序框图知:…,可知S出现周期为4,当时,结束循环输出S,,即输出的,故选D.【考点】程序框图.16.执行如图所示的程序框图,若输入,则输出的值为 .【答案】.【解析】满足条件,执行第一次循环,,;满足条件,执行第二次循环,,;满足条件,执行第三次循环,,;不满足条件,跳出循环体,输出的值为.【考点】算法与程序框图17.一个算法的程序框图如图,则其输出结果是()A.0B.C.D.【解析】由题意可知:.【考点】1.程序框图;2.三角函数的周期性.18.阅读下边的程序框图,如果输出的函数值在区间内,则输入的实数的取值范围是.【答案】【解析】本题程序框图所反映的数学问题就是当函数的值域为时,求定义域.,,.【考点】程序框图与函数的定义域.19.阅读如图所示的程序框图,运行相应的程序.若输入某个正整数n后,输出的S∈(31,72),则n的值为( )A.5B.6C.7D.8【答案】A【解析】由程序框图可知:运行第一次:运行第二次:运行第三次:运行第四次:运行第五次:运行第六次:因为,所以运行第五次后应结束,则判断框中的条件应为,所以答案应选B.【考点】循环结构.20.执行如图所示的框图,若输出结果为3,则可输入的实数值的个数为()A.1B.2C.3D.4【答案】C【解析】若输入的时,则,当输出结果是,即,解得;若输入的时,则,当输出结果为,即,解得.则可输入的实数值的个数为3.故选C.【考点】1.程序框图的应用;2.指数与对数的运算.21.某算法的程序框图如图所示,如果输出的结果是26,则判断框内应为A.K>1B.K>2C.K>3D.K>4【答案】C【解析】第一次循环,否,;第二次循环,否,;第三次循环,否,;第四次循环,是,输出,运行结束,故判断框内应为K>3,选C.【考点】算法与程序框图22.已知函数f(x)=ax3+x2在x=-1处取得极大值,记g(x)=。
高中数学选修1-2同步练习题库:流程图(简答题:一般)

流程图(简答题:一般)1、执行如图所示的程序框图.(1)若输入的,,求输出的的值;(2)若输入的,输出的,求输入的()的值.2、已知函数,对每输入的一个值,都得到相应的函数值,画出程序框图并写出程序.3、已知数列的递推公式,且,请画出求其前5项的流程图.4、已知某算法的算法框图如图所示.(1)求函数的解析式;(2)求的值.5、的取值范围为[0,10],给出如图所示的程序框图,输入一个数.(1)请写出程序框图所表示的函数表达式;(2)求输出的()的概率;(3)求输出的的概率.6、已知数列的各项均为正数,观察程序框图,当,时,.(1)求数列的通项;(2)令,求的值.7、某药厂生产某种产品的过程如下:(1)备料、前处理、提取、制粒、压片、包衣、颗粒分装包装;(2)提取环节经检验,合格,进入下一工序,否则返回前处理;(3)包衣、颗粒分装两环节分别检验合格进入下一工序,否则为废品,画出生产该产品的工序流程图.8、根据下面的要求,求┅值.(Ⅰ)请将程序框图补充完整;(Ⅱ)求出(I)中输出S的值.9、求满足的最小正整数,写出算法的程序并画出程序框图.10、执行如下程序框图:(1)如果在判断框内填入“”,请写出输出的所有数值;(2)如果在判断框内填入“”,试求出所有输出数字的和。
11、根据下面的程序,画出其对应的程序框图.12、读下列程序,写出此程序表示的函数,并求当输出的时,输入的的值.13、执行如图所示的程序框图.(1)若输入的,,求输出的的值;(2)若输入的,输出的,求输入的()的值.14、某算法的程序框图如图所示,其中输入的变量在1,2,3,…30这30个整数中等可能随机产生. (1)分别求出(按程序框图正确编程运行时)输出的值为的概率;(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行次后,统计记录了输出的值为的频数,下面是甲、乙所作频数统计表的部分数据:甲的频数统计表(部分)乙的频数统计表(部分)当时,根据表中的数据,分别写出甲、乙所编程序各自输出的值为的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.15、(2015秋•宁德期末)阅读如图所示程序框图,根据框图的算法功能回答下列问题:(Ⅰ)当输入的x∈[﹣1,3]时,求输出y的值组成的集合;(Ⅱ)已知输入的x∈[a,b]时,输出y的最大值为8,最小值为3,求实数a,b的值.16、的取值范围为[0,10],给出如图所示程序框图,输入一个数.(1)请写出程序框图所表示的函数表达式;(2)求输出的()的概率;(3)求输出的的概率.17、(本题满分16分)对任意函数f(x),x∈D,可按如图构造一个数列发生器,记由数列发生器产生数列{x n}.(1)若定义函数,且输入,请写出数列{x n}的所有项;(2)若定义函数f(x)=xsinx(0≤x≤2π),且要产生一个无穷的常数列{x n},试求输入的初始数据x0的值及相应数列{x n}的通项公式x n;(3)若定义函数f(x)=2x+3,且输入x0=﹣1,求数列{x n}的通项公式x n.18、在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有6人.(1)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现从中随机抽取2人上台抽奖,求a和b至少有一人上台抽奖的概率;(2)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖",则该代表中奖;若电脑显示“谢谢”,则不中奖.求该代表中奖的概率.19、(本小题满分12分)如图所示程序框图中,有这样一个执行框=f()其中的函数关系式为,程序框图中的D为函数f(x)的定义域.,(1)若输入,请写出输出的所有;(2)若输出的所有xi都相等,试求输入的初始值.20、(本小题满分12分)已知数列的各项均为正数,观察流程图,当时,;当时,,(1)写出时,的表达式(用等来表示);(2)求的通项公式;(3)令,求.21、(本小题满分12分)如下图,给出了一个程序框图,其作用是输入的值,输出相应的的值,(I)请指出该程序框图所使用的逻辑结构;(Ⅱ)若视为自变量,为函数值,试写出函数的解析式;(Ⅲ)若要使输入的的值与输出的的值相等,则输入的值的集合为多少?22、(本小题满分13分)从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图的频率分布直方图,从左到右各组的频数依次记为,,,,.(1)求图中的值;(2)下图是统计图中各组频数的一个算法流程图,求输出的结果;(3)从质量指标值分布在、的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率.23、对任意函数,,可按如图构造一个数列发生器,记由数列发生器产生数列{}.(1)若定义函数,且输入,请写出数列{}的所有项;(2)若定义函数(0≤x≤2π),且要产生一个无穷的常数列{},试求输入的初始数据的值及相应数列{}的通项公式;(3)若定义函数,且输入,求数列{}的通项公式.参考答案1、(1);(2).2、见解析3、见解析4、(1);(2)5、(1)(2)(3)6、(1)(2)7、见解析8、(I);(II).9、程序见解析,程序框图见解析.10、(1)(2)11、程序框图见解析.12、,.13、(1);(2).14、(1),,;(2)乙.15、(Ⅰ)输入x∈[﹣1,3],输出y的值组成的集合为[0,8];(Ⅱ)所求实数a,b的值为或16、(1);(2);(3).17、(1);(2)故当,;当;(3)18、(1);(2)19、(1)(2)或20、(1);(2);(3).21、(I)条件结构和顺序结构(Ⅱ)(Ⅲ)22、(1)0.005;(2)18;(3)23、(1),,;(2)当时,;当时,;(3).【解析】1、试题分析:(1)根据程序框图的循环结构,根据判断框的条件,即可求解;(2)根据第一次运算,第二次运算,即可得出,即可求解的值.试题解析:(1)第一次运算:,,;第二次运算:,,;第三次运算:,,;第四次运算:,,;第五次运算:,,,输出.(2)第一次运算:,,,此时不成立,则.第二次运算:,,,此时成立,则,∴,又,∴.考点:程序框图的运算.2、试题分析:利用条件结构和条件语句可实现分段函数求值的算法,进而可得程序框图并编写相应的程序。
算法初步与框图 统计、统计案例专题试卷

《金版新学案》高三一轮总复习[B 师大]数学文科高效测评卷(九)算法初步与框图 统计、统计案例 概率—————————————————————————————————【说明】 本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入答题格内,第Ⅱ卷可在各题后直接作答,共150分,考试时间120分钟.第Ⅰ卷 (选择题 共60分)只有一项是符合题目要求的)1.下列有关线性回归的说法,不正确的是( ) A .相关关系的两个变量不一定是因果关系 B .散点图能直观地反映数据的相关程度C .回归直线最能代表线性相关的两个变量之间的关系D .任一组数据都有回归直线方程2.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( )A .4B .5C .6D .73.在一底面半径和高都是2 m 的圆柱形容器中盛满小麦种子,但有一粒带麦锈病的种子混入了其中.现从中随机取出2 m 3的种子,则取出带麦锈病的种子的概率是( )A.14B.18πC.14πD .1-14π4.如图表示甲、乙两名篮球运动员每场比赛得分情况的茎叶图,则甲和乙得分的中位数的和是( )A .56分B .57分C .58分D .59分5.阅读下边的程序框图,若输入的a 、b 、c 分别是1、2、3,则输出的a 、b 、c 分别是()A .3、1、2B .1、2、3C .2、1、3D .3、2、16.某外资企业人员及工资构成如表:A .200与220B .220与220C .220与200D .210与2007.(2010·陕西卷)如图,样本A 和B 分别取自两个不同的总体,它们的样本平均数分别为x A 和x B ,样本标准差分别为s A 和s B ,则( )A.x A >x B ,s A >s BB.x A <x B ,s A >s BC.x A >x B ,s A <s BD.x A <x B ,s A <s B8.一个算法的程序框图如图所示,若该程序输出的结果为56,则判断框中应填入的条件是( )A .i ≥5B .i ≥6C .i <5D .i <69.已知集合M ={(x ,y )|x +y ≤8,x ≥0,y ≥0},N ={(x ,y )|x -3y ≥0,x ≤6,y ≥0},若向区域M 内随机投一点,则点P 落入区域N 的概率为( )A.13B.12C.38D.31610.(2011·东北三校三模)如图,若依次输入的x 分别为56π、π6,相应输出的y 分别为y 1、y 2,则y 1、y 2的大小关系是( )A .y 1=y 2cosB .y 1>y 2C .y 1<y 2D .无法确定11.已知平面区域Ω=⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫(x ,y )⎪⎪⎪⎩⎪⎨⎪⎧ y ≤x +1y ≥0x ≤1, M =⎩⎨⎧⎭⎬⎫(x ,y )⎪⎪⎪⎩⎪⎨⎪⎧ y ≤-|x |+1y ≥0,向区域Ω内随机投一点P ,点P 落在区域M 内的概率为( )A.14 B.13C.12D.2312.设a ∈[1,2,3,4],b ∈[2,4,8,12],则函数f (x )=x 3+ax -b 在区间[1,2]上有零点的概率为( )A.12B.58C.1116D.34第Ⅱ卷 (非选择题 共90分)13.将容量为n 的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n 等于________.14.甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则这10天甲、乙两人日加工零件的平均数分别为________和________.15.在如图所示的程序框图中,当程序被执行后,输出s 的结果是________.16.如图,正方形OABC 的边长为2.(1)在其四边或内部取点P (x ,y ),且x ,y ∈Z ,则事件“|OP |>1”的概率是________;(2)在其内部取点P (x ,y ),且x ,y ∈R ,则事件“△POA ,△P AB ,△PBC ,△PCO 的面积均大于23”的概率是________.三、解答题(本大题共6小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(12分)在一个盒中装有6枝圆珠笔,其中3枝一等品,2枝二等品和1枝三等品,求:(1)从中任取1枝,得到一等品或二等品的概率; (2)从中任取2枝,没有三等品的概率.18.(12分)某高级中学共有学生3 000名,各年级男、女生人数如表:(1)问高二年级有多少名女生?(2)现对各年级用分层抽样的方法在全校抽取300名学生,问应在高三年级抽取多少名学生? 【解析方法代码108001137】19.(12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:(1)(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率. 【解析方法代码108001138】20.(12分)在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲.(1)根据以上数据建立一个2×2列联表;(2)若认为“性别与患色盲有关系”,则出错的概率会是多少?附临界值参考表:21.(12分)某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[120,130)内的频率,并补全这个频率分布直方图;(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.22.(14分)已知复数z =x +y i(x ,y ∈R )在复平面上对应的点为M .(1)设集合P ={-4,-3,-2,0},Q ={0,1,2},从集合P 中随机取一个数作为x ,从集合Q 中随机取一个数作为y ,求复数z 为纯虚数的概率;(2)设x ∈[0,3],y ∈[0,4],求点M 落在不等式组:⎩⎪⎨⎪⎧x +2y -3≤0,x ≥0,y ≥0所表示的平面区域内的概率. 【解析方法代码108001139】卷(九)一、选择题1.D 根据两个变量属相关关系的概念,可知A 正确,散点图能直观地描述呈相关关系的两个变量的相关程度,且回归直线最能代表它们之间的相关关系,所以B 、C 正确.只有线性相关的数据才有回归直线方程,所以D 不正确.2.C 共有食品100种,抽取容量为20,所以各抽取15,故抽取植物油类与果蔬类食品种数之和为10×15+20×15=6,所以选C.3.C 可用体积作为几何度量,易知取出带有麦锈病的种子的概率为P =2π·22·2=14π.4.B 由图可知甲的中位数为32,乙的中位数为25,故和为57.故选B.5.A 开始a =1,b =2,c =3→x =1,a =3,c =2,b =1→结束,输出a =3,b =1,c =2,故选A.6.A 由表知:周工资200的人数最多,故众数为200,周工资从小到大排列第12个数为220,故中位数为220.7.B A 中的数据都不大于B 中的数据,所以x A <x B ,但A 中的数据比B 中的数据波动幅度大,所以s A >s B .8.D 由框图知S =0+1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫1i -1i +1=1-1i +1=56.∴i =5,∴应填入i <6.9.D 在平面直角坐标系中分别画出区域M 和N ,可计算得区域M 和N 的面积分别等于S =12×8×8=32,S ′=12×6×2=6,所以点P 落入区域N 的概率P =632=316.10.C 由程序框图可知,当输入的x 为5π6时,sin 5π6>cos 5π6成立,所以输出的y 1=sin 5π6=12;当输入的x 为π6时,sin π6>cos π6不成立,所以输出的y 2=cos π6=32,所以y 1<y 2,故选C.11.C 如图,平面区域Ω表示△ABC 及其内部区域,区域M 表示△ABD 及其内部区域,设A 表示“P 落在区域M 内”,则由几何概型知识得:P (A )=S △ABD S △ABC =12,故选C.12.C 由已知f ′(x )=3x 2+a >0,所以f (x )在R 上递增,若f (x )在[1,2]上有零点,则需⎩⎪⎨⎪⎧f (1)=1+a -b ≤0,f (2)=8+2a -b ≥0,经验证有(1,2)、(1,4)、(1,8)、(2,4)、(2,8)、(2,12)、(3,4)、(3,8)、(3,12)、(4,8)、(4,12)共11对满足条件,而总的情况有C 14C 14=16种,故所求概率为1116,故选C.二、填空题13.解析: ∵第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1, ∴前三组频数为2+3+420·n =27,故n =60.答案: 6014.解析: x 甲=110(10×2+20×5+30×3+17+6+7)=24,x 乙=110(10×3+20×4+30×3+17+11+2)=23.答案: 24 2315.解析: 依题意i 的取值构成等差数列,设为{a n },a 1=1,d =3,则s =a 2+a 3+a 4+…+a 14=(a 2+a 14)×132=13a 8=13×(1+21)=22×13=286.答案: 28616.解析: (1)在正方形的四边和内部取点P (x ,y )且x ,y ∈Z ,所有可能的事件是(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),其中满足|OP |>1的事件是(0,2),(1,1),(1,2),(2,0),(2,1),(2,2),所以满足|OP |>1的概率为23.(2)在正方形内部取点,其总的事件的包含的区域面积为4,由于各边长为2,所以要使△POA ,△P AB ,△PBC ,△PCO 的面积均大于23,应该三角形的高大于23,所以这个区域为每个边长从两端各去掉23后剩余的正方形,其面积为23×23=49,所以满足条件的概率为494=19.答案: (1)23 (2)19三、解答题17.解析: (1)从6枝笔中任取1枝得一等品或二等品共有3+2=5种不同的取法, 任取一枝笔共有6种取法,∴任取1枝,得到一等品或二等品的概率为56.(2)从中任取2枝,有三等品的取法有5种,而任取2枝共有C 26=15种取法. ∴任取2枝,有三等品的概率为515=13,∴任取2枝,没有三等品的概率为1-13=23.18.解析: (1)由题设可知x 3 000=0.17, 所以x =510. (2)高三年级人数为y +z =3 000-(523+487+490+510)=990,现用分层抽样的方法在全校抽取300名学生,应在高三年级抽取的人数为:3003 000×990=99.故(1)高二年级有510名女生; (2)应在高三年级抽取99名学生.19.解析: (1)因为在20至40岁的58名观众中有18名观众收看新闻节目,而大于40岁的42名观众中有27名观众收看新闻节目,所以,经直观分析,收看新闻节目的观众与年龄是有关的.(2)从题中所给条件可以看出收看新闻节目的共45人,随机抽取5人,则抽样比为545=19,故大于40岁的观众应抽取27×19=3(人). (3)抽取的5名观众中大于40岁的有3人,在20至40岁的有2人,记大于40岁的人为a 1,a 2,a 3,20至40岁的人为b 1,b 2,则从5人中抽取2人的基本事件有(a 1,a 2),(a 1,a 3),(a 2,a 3),(b 1,b 2),(a 1,b 1),(a 1,b 2),(a 2,b 1),(a 2,b 2),(a 3,b 1),(a 3,b 2),共10个,其中恰有1人为20至40岁的有6个,故所求概率为610=35.20.解析: (1)(2)假设H 0:“根据(1)中2×2列联表中数据,可求得 χ2=1 000×(38×514-6×442)2480×520×44×956≈27.14,又P (χ2≥10.828)=0.001,即H 0成立的概率不超过0.001, 故若认为“性别与患色盲有关系”,则出错的概率为0.001.21.解析: (1)分数在[120,130)内的频率为1-(0.1+0.15+0.15+0.25+0.05)=1-0.7=0.3,频率组距=0.310=0.03,补全后的直方图如下.(2)平均分为x =95×0.1+105×0.15+115×0.15+125×0.3+135×0.25+145×0.05=121.(3)由题意,[110,120)分数段的人数为60×0.15=9人,[120,130)分数段的人数为60×0.3=18人.∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本, ∴需在[110,120)分数段内抽取2人,并分别记为m ,n ;在[120,130)分数段内抽取4人,并分别记为a ,b ,c ,d .设“从样本中任取2人,至多有1人在分数段[120,130)内”为事件A ,则基本事件共有:(m ,n )、(m ,a )、…、(m ,d )、(n ,a )、…、(n ,d )、(a ,b )、…、(c ,d )共15种,则事件A 包含的基本事件有:(m ,n )、(m ,a )、(m ,b )、(m ,c )、(m ,d )、(n ,a )、(n ,b )、(n ,c )、(n ,d )共9种.∴P (A )=915=35.22.解析: (1)记“复数z 为纯虚数”为事件A .∵组成复数z 的所有情况共有12个:-4,-4+i ,-4+2i ,-3,-3+i ,-3+2i ,-2,-2+i ,-2+2i,0,i,2i ,且每种情况出现的可能性相等,属于古典概型,其中事件A 包含的基本事件共2个:i,2i.∴所求事件的概率为P (A )=212=16.(2)依条件可知,点M 均匀地分布在平面区域⎩⎨⎧⎭⎬⎫(x ,y )⎪⎪⎪⎩⎪⎨⎪⎧ 0≤x ≤30≤y ≤4内, 属于几何概型.该平面区域的图形为右图中矩形OABC 围成的区域,面积为S =3×4=12.而所求事件构成的平面区域为{(x ,y )|⎩⎪⎨⎪⎧x +2y -3≤0x ≥0y ≥0},其图形如图中的△OAD (阴影部分).又直线x +2y -3=0与x轴、y 轴的交点分别为A (3,0)、D ⎝⎛⎭⎫0,32, ∴△OAD 的面积为S 1=12×3×32=94.∴所求事件的概率为P =S 1S =9412=316.。
高三数学框图试题

高三数学框图试题1.执行如图所示的程序框图,则输出的结果是()A.14B.15C.16D.17【答案】C【解析】根据程序框图,从到得到,因此将输出. 故选C.【考点】程序框图.2.右图是计算某年级500名学生期末考试(满分为100分)及格率的程序框图,则图中空白框内应填入()A.B.C.D.【答案】D.【解析】通过程序的判断语句可知,表示的是及格的人数,表示的是不及格的人数,∴.【考点】程序框图.3.执行如图所示的程序框图,若输入n的值为4,则输出S的值为 ( )A.5B.6C.7D.8【答案】C【解析】第一次循环后:S=1,i=2第二次循环后:S=2,i=3第三次循环后:S=4,i=4第四次循环后:S=7,i=5,故输出74.定义某种运算,运算原理如右图所示,则式子的值为【答案】13【解析】由算法知:,而【考点】新定义5.阅读右面的程序框图,运行相应的程序,输出的结果为()A.B.C.D.【答案】C【解析】第一次循环,第二次循环,第三次循环,第四次循环,,因此当时,【考点】循环体流程图6.执行如图所示的程序框图,则输出的k值是.【答案】3.【解析】由程序框图知,输出.【考点】程序框图.7.执行如图所示的程序框图.若输出,则框图中①处可以填入()A.B.C.D.【答案】B【解析】依次循环的结果为:;;;.因为输出,所以可满足,故选.【考点】程序框图.8.执行右面的程序框图,如果输入的t∈[-1,3],则输出的s属于( )A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]【答案】A;【解析】若,则;若,;综上所述.【考点】本题考查算法框图,考查学生的逻辑推理能力.9.如图,运行该程序后输出的值为()A.66B.55C.11D.10【答案】A【解析】由程序框图可以看出,本框图的作用就是计算的值,所以输出的.【考点】程序框图及其应用.10.如果执行框图,输入,则输出的数等于()A.B.C.D.【答案】D【解析】第一次循环,;第二次循环,;第三次循环,;第四次循环,;第五次循环,;此时不满足条件,输出,选D.【考点】算法与框图.11.程序框图如图所示,其输出结果是,则判断框中所填的条件是()A.B.C.D.【答案】B【解析】由题意可知第一次运行后,第二次运行后,第三次运行后,第四次运行后,第五次运行后,此时停止运算,又判断框下方是“是”,故应填.故选B.【考点】算法流程图.12.执行如图所示程序框图.若输入,则输出的值是()A.B.C.D.【答案】C【解析】通过程序循环计算,知道得到的x大于23就结束,即.【考点】考查程序框图.13.执行如图所示的程序框图,输出的S值为()A.1B.C.D.【答案】C【解析】第一次执行循环:,;第二次执行循环:,,满足≥2,结束循环,输出.【考点】本小题考查了对算法程序框图的三种逻辑结构的理解,考查了数据处理能力和算法思想的应用.14.如图所示,程序据图(算法流程图)的输出结果为()A.B.C.D.【答案】C【解析】;;,输出所以答案选择C【考点】本题考查算法框图的识别,逻辑思维,属于中等难题.15.随机抽取某产品件,测得其长度分别为,如图所示的程序框图输出样本的平均值,则在处理框①中应填入的式子是(注:框图中的赋值符号“=”也可以写成“←”“:=”)A.B.C.D.【答案】D,i=2时,s=,i=3【解析】如图所示的程序框图输出样本的平均值,当i=1时,s=a1时,…,因此,处理框①应填入的式子是,故选D。
高中数学算法与框图练习题练习题(含解析)

所以输出的 的最大值为 .
故选:D.
8.C
【分析】根据程序流程图,代入 ,计算出结果即可.
【详解】① , , , ,此时 ;
② , , ,此时 ;
③ , , ,此时 ;
④ , , ,此时 ;
⑤ , , ,此时 ;
⑥ , , ,此时 ,
结束程序,输出结果为44,
故选:C
第四步:判断 是否成立?若是,则 之间的任意值均为满足条件的近似根;若不是,则返回第二步.
【点睛】本题考查了求方程近似根的算法,意在考查学生对于算法的理解和应用.
【详解】(1) ,所以98的二进制数是 .
(2) , ,所以 与 的最大公约数为 .
(3) .
【点睛】本题考查二进制,辗转相除法,秦九昭算法等知识,属于基础题.
16.见解析
【分析】根据题目中的条件,找出各要素之间的关系,校长只负责两名副校长和校长办公室,所以校长下只有两名副校长和校长办公室,依次类推,两名副校长又各自管理教务处、教科室和保卫科、政教处、总务处;班级由所有的科室负责.
A.35B.56C.84D.120
二、填空题
11.运行如图所示的伪代码,输出的T的值为________.
12.用秦九韶算法求函数 ,当 时的值时, ___________.
13.执行如图所示的程序框图,若输1455的最大公约数为 ,则 化为三进制为__________.
根据程序框图可知,输出的 ,
又 , , , , , ,
所以 .
故选:B.
11.16
【分析】模拟程序的运行过程,即可得出程序运行后的输出结果.
【详解】当 时, ;
当 时, ;
当 时, ;
高三数学程序框图3

S=S+1/i
i=i+1 Y
i≤n N 输入S的值
结束
步骤A 步骤B
能
例3 设计一算法,求和:1+2+3+…+100
开始
开始
否 说 说
i=0,Sum=0
i=0,Sum=0
这 个
否 i<100?
流
i=i+1
程
是 i=i+1
Sum=Sum + i
图 的
Sum=Sum + i
否
异
i>=100?
同
是
点
输出Sum
高端外围 高端外围
i=i+1 Sum=Sum + i
当型结构
i<100? 是
否
i=i+1
Sum=Sum + i
i=i+1 Sum=Sum + i
解决方法就是加上一个判断,判断
是否已经加到了100,如果加到了则 退出,否则继续加。
否
请填上判断的条件。
i>=100?
是ቤተ መጻሕፍቲ ባይዱ
直到型结构
算法初步
§1.1.2 程序框图
习题课
1城区一中学生数学模块学
分认定由模块成绩决定,模
块成绩由模块考试成绩和平
时成绩构成,各占50%,若 模块成绩大于或等于60分, 获得2学分,否则不能获得学 分(为0分),设计一算法, 通过考试成绩和平时成绩计
算学分,并画出程序框图
开始
输入a,b
S=(a+b)*0.5
输出Sum
高三数学框图试题
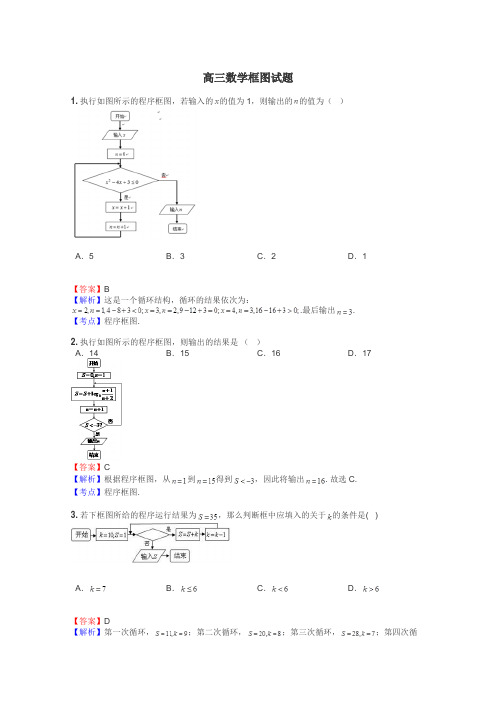
高三数学框图试题1.执行如图所示的程序框图,若输入的的值为1,则输出的的值为()A.5B.3C.2D.1【答案】B【解析】这是一个循环结构,循环的结果依次为:.最后输出.【考点】程序框图.2.执行如图所示的程序框图,则输出的结果是()A.14B.15C.16D.17【答案】C【解析】根据程序框图,从到得到,因此将输出. 故选C.【考点】程序框图.3.若下框图所给的程序运行结果为,那么判断框中应填入的关于的条件是( )A.B.C.D.【答案】D【解析】第一次循环,;第二次循环,;第三次循环,;第四次循环,,结束循环,输出,因此【考点】循环结构流程图4.阅读右图的程序框图,则输出S=( )A.14B.20C.30D.55【答案】C【解析】运行程序框图如下:故选C【考点】程序框图5.李强用流程图把早上上班前需要做的事情做了如下几种方案,则所用时间最少的方案是_______【答案】方案三【解析】方案一:所用时间为.方案二:所用时间为.方案三:所用时间为.所以所用时间最少的方案是方案三.【考点】流程图6.阅读右面的程序框图,运行相应的程序,输出的结果为()A.B.C.D.【答案】C【解析】第一次循环,第二次循环,第三次循环,第四次循环,,因此当时,【考点】循环体流程图7.某程序框图如图所示,现在输入下列四个函数,则可以输出函数是()A.B.C.D.【答案】B【解析】本题要从程序框图中发现函数的性质,第一个判断框说明是奇函数,第二个判断框说明方程有实解,即函数的图象与轴有交点,因此我们首先判断四个函数的奇偶性,可利用等式来判断,三个函数是奇函数,又,即或,从而,同样,因此两个函数图象与都无交点,只有中,,此函数图象与轴是相交的,因此选B.【考点】函数的奇偶性与函数的值域.8.下图是某算法的流程图,其输出值是 .【答案】.【解析】第一次循环,,不成立,执行第二次循环;,不成立,执行第三次循环;第三次循环,,不成立,执行第四次循环;第四次循环,,成立,跳出循环体,输出的值为.【考点】算法与程序框图9.阅读如图的程序框图,若输出的的值等于,那么在程序框图中判断框内应填写的条件是()A.?B.?C.?D.?【答案】A【解析】读懂框图可知求满足的值,易得所以.【考点】考查算法与框图.10.阅读程序框图(如图所示),若输入,,,则输出的数是.【答案】【解析】程序框图的功能是:输出中最大的数,∵,,,所以输出的数为.【考点】程序框图.11.某程序框图如图所示,该程序运行后输出的的值是()A.B.C.D.【答案】A【解析】第一步 ;第二步 ;第三步,第四步【考点】程序框图12.给出下面的程序框图,则输出的结果为_________.【答案】【解析】解:k=1,S=0+=,满足条件k≤5,执行循环,k=2,S=+,满足条件k≤5,执行循环,k=3,S=,满足条件k≤5,执行循环,k=4,S=,满足条件k≤5,执行循环,k=5,S=,满足条件k≤5,执行循环,k=6,S=,不满足条件k≤5,退出循环,输出S=故答案为:【考点】当型循环点评:本题主要考查了循环结构中的当型循环,以及程序框图,解题的关键是弄清循环次数,属于基础题13.如果右边程序框图的输出结果是10,那么在判断框中①表示的“条件”应该是()A.i≥3B.i≥4C.i≥5D.i≥6【答案】C【解析】第一执行,,第二执行,,第三次执行,,第四次执行,,因为输出结果为10,所以应填.选C.【考点】循环结构点评:本题考查循环结构,已知运算规则与最后运算结果,求运算次数的一个题,是算法中一种常见的题型.14.已知,由如右程序框图输出的为A.B.C.D. 0【答案】B【解析】因为,由程序框图,M<N,S=M=ln2,故选B。
考点1 算法与程序框图

温馨提示:检测题库为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,点击右上角的关闭按钮可返回目录。
考点1 算法与程序框图1. (2010上海高一检测)图中所示的算法流程图,表达式为()A.112399++++. B.1123100++++C.199D.1100【解析】选A。
2.(2010喀左高一检测)下面的程序框图,求输出的 y=0 那么输入的x为()A.-3 、0 B.-3、-5 C.0、-5 D.-3、0、-5【解析】选A。
上面的程序框图表示的函数为3,05,00,0x xy x xx+<⎧⎪=+>⎨⎪=⎩,故若输出的 y=0 那么输入的x为-3。
3.(2010济南高一检测)如图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图,其中判断框内应填入的条件是( )A. i>10B. i<10C. i>20D. i<20【解析】选A 。
因为循环体对应“否”分支,因此填10i >。
4.(2010个旧高一检测)给出以下一个算法的程序框图,该程序框图的功能是( )A .求出a, b, c 三数中的最大数B .求出a, b, c 三数中的最小数C .将a, b, c 按从小到大排列D .将a, b, c 按从大到小排列 【解析】选B 。
5.(2010济南高一检测)如图(1)、(2),它们都表示的是输出所有立方小于729的正整数的程序框图,那么判断框中应分别补充的条件为 ( )A.⑴3n ≥729 ? ⑵3n <729? B . ⑴3n ≤729 ? ⑵3n >729 ?C. ⑴3n <729 ? ⑵3n ≥729?D. ⑴3n <729 ? ⑵3n <729 ?【解析】选C 。
6. (2010银川高一检测)按如图所示的程序框图,在运行后输出的结果为( ) A .36 B .45 C .55 D .56【解析】选C 。
上面程序表示求12310++++ 的算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学算法和程序框图试题1.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是.【答案】5【解析】由图知运算规则是对S=2S+1,故第一次进入循环体后S=2×1+1=3,第二次进入循环体后S=2×3+1=7,第三次进入循环体后S=2×7+1=15,第四次进入循环体后S=2×15+1=31,第五次进入循环体后S=2×31+1=63,由于A的初值为1,每进入一次循环体其值增大1,第五次进入循环体后A=5,故判断框中H的值应为5,这样就可保证循环体只能被运行五次,答案为5.【考点】算法与程序框图2.如图给出的是计算1+++…+的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句分别是()A.n=n+2,i=15?B.n=n+2,i>15?C.n=n+1,i=15?D.n=n+1,i>15?【答案】B【解析】①的意图为表示各项的分母,而分母相差2,∴n=n+2.②的意图是为直到型循环结构构造满足跳出循环的条件,而分母从1到29共15项,∴i>15,故选B.3.执行右侧的程序框图,若输入,则输出 .【答案】C【解析】第一次运行后y=5,第二次运行后y=,第三次运行后,此时,满足条件,故输出.【考点】程序框图.4.执行如图所描述的算法程序,记输出的一列的值依次为,其中且.(1)若输入,写出全部输出结果.(2)若输入,记,求与的关系().【答案】(1)输出结果共4个,依次是:.(2).【解析】(1)这是一个循环结构,依次写出每次循环的结果即可.(2)由框图中可得当时,.再由可得.将代入即可得与的关系.(1)这是一个循环结构,前4次输出的为:,第5次循环的结果为,与相等,故结束循环.所以输出的为:.(2)当时,..【考点】1、程序框图;2、递推数列.5.执行如图所示的程序框图,输出结果S= .【答案】-2013【解析】根据程序框图,,故输出的S为.【考点】程序框图.6.已知某程序框图如图所示,则该程序运行后输出的结果为( )A.B.C.D.【答案】A【解析】运行第一次:成立;运行第二次:成立;运行第三次:成立;运行第四次成立;运行第五次:成立;运行第2007次:成立;运行第2008次:不成立;输出A的值:故选A.【考点】循环结构.7.执行如图所示的程序框图,则输出的的值是______.【答案】【解析】程序在执行过程中,的值依次为:;;;;;故的值依次周期性的出现,而且周期为4,当时,,故输出的.【考点】程序框图.8.执行如图所示的程序框图,如果输入,,那么输出的a值为()A.B.C.D.【答案】C【解析】不成立,执行第一次循环,;不成立,执行第二次循环,;不成立,执行第三次循环,;成立,跳出循环体,输出的值为,故选C.【考点】算法与程序框图9.运行如图所示的程序框图,若输出的是,则①应为()A.n≤5B.n≤6C.n≤7D.n≤8【答案】C【解析】由程序框图算法可知,,由于输出,即,解得,故①应为“”,故选【考点】算法程序框图。
10.已知实数x∈[1,9],执行如右图所示的流程图,则输出的x不小于55的概率为________.【答案】【解析】由流程图知,当输入x时,各次循环输出的结果分别是2x+1,2(2x+1)+1=4x+3,2(4x+3)+1=8x+7,此时退出循环.由解得6≤x≤9,故输出的x不小于55的概率为P=.11.如图,Ni 表示第i个学生的学号,Gi表示第i个学生的成绩,已知学号在1~10的学生的成绩依次为401、392、385、359、372、327、354、361、345、337,则打印出的第5组数据是________.【答案】8,361【解析】本题流程图表示的算法功能是筛选成绩大于等于360分的学生,打印出他们的学号和成绩,所以打印出的第5组数据是8,361.12.执行如图所示的程序框图,输出的S值为()A.2B.4C.8D.16【答案】C【解析】程序在执行过程中,的值依次为;;;,程序结束,输出的值为.【考点】程序框图.13.下图给出了一个程序框图,其作用是输入的值,输出相应的值.若要使输入的值与输出的值相等,则这样的值有__________个.【答案】3【解析】由题意得该程序的功能是:计算并输出分段函数的值,又∵输入的值与输出的值相等,当时,,解得,或,当时,,解得,当时,,解得(舍去),故满足条件的值共有3个,故答案为:3.【考点】程序框图.14.若某程序框图如图所示,则该程序运行后输出的值等于_______.【答案】49【解析】执行程序框图如下:所以程序输出,故填49.【考点】程序框图15.执行如图所示的程序框图,输出的S值为()A.2B.4C.8D.16【答案】C【解析】第一步:k=0<3,S=1·20=1,k=0+1=1;第二步:k=1<3,S=1·21=2,k=1+1=2;第三步:k=2<3,S=2·22=8,k=2+1=3;第四步:k=3不满足k<3,执行否,输出S=8.故选C.16.某程序框图如图所示,则该程序运行后输出的k的值是.【答案】5【解析】k=k+1=3,a=43,b=34,a<b.执行否;k=4,a=44,b=44,a=b,执行否;k=5,a=45,b=54,a>b,执行是,输出k=5.17.如图是某算法的程序框图,则程序运行后输出的结果是.【答案】3【解析】本题考查程序框图及递推数列等知识,考查枚举的数学思想方法及运算求解的数学能力. 此框图依次执行如下循环:第一次:T=0,k=1,sin>sin0成立,a=1,T=T+a=1,k=2,2<6,继续循环;第二次:sinπ>sin不成立,a=0,T=T+a=1,k=3,3<6,继续循环;第三次:sin>sinπ不成立,a=0,T=T+a=1,k=4,4<6,继续循环;第四次:sin2π>sin成立,a=1,T=T+a=2,k=5,继续循环;第五次:sin>sin2π成立,a=1,T=T+a=3,k=6,6<6不成立,跳出循环,输出T的值3.18.执行如右图所示的程序框图.则输出的所有点都在函数()的图象上.A.B.C.D.【答案】C【解析】根据框图的循环结构,依次输出的点为,,,,跳出循环,结束。
分析可知这些点均落在函数的图像上。
【考点】1算法程序框图;2函数解析式。
19.执行如图所示的程序框图,若输入的x值为2,则输出的x值为()A.3B.126C.127D.128【答案】C【解析】若输入的x=2,则x=22-1=3,而3<126,故x=23-1=7,而7<126,故x=27-1=127.因为127>126,所以输出的x值为127.20.执行如图所示的程序框图,若输出的的值为,则图中判断框内①处应填()A.B.C.D.【答案】B【解析】因为,选项中最小值是3,故从此验证起.如果,则共运行四次结束,输出的满足,不符合题意,再运行一次结束,输出的满足,故图中判断框内①处应填,选B.【考点】算法与程序框图21.运行如图所示的程序框图,输出的S值为________.【答案】【解析】S=0,n=1;S=,n=2;S=,n=3;S=,n=4;S=,n=5;S=0,n=6;S=,n=7;…,所以2 013÷5=402×5+3,∴S=.22.执行如图所示的程序框图,则输出的S值为 ( )A.3B.6C.7D.10【答案】D【解析】通过循环,可知该循环的作用是求数列的和,循环到结束循环,所以.故选:D.【考点】算法框图。
23.某程序框图如图所示,若输入的=10,则输出的结果是.【答案】5【解析】由程序框图的循环过程可知:第一步:;第二步:第三步:;第四步:第五步:;第六步:输出.【考点】程序框图的识别及应用24.右图是一个算法流程图,则输出的值是.【答案】25【解析】循环过程中有序数对的值依次为,,,,,所以输出的值为25,实质上.【考点】流程图和循环结构.25.某程序框图如图所示,该程序运行后输出的的值是()A.4B.5C.6D.7【答案】B【解析】所以输出.【考点】程序框图.26.阅读图的程序框图, 该程序运行后输出的的值为 __.【答案】【解析】,所以输出的的值为.【考点】程序框图和循环赋值.27.定义运算为执行如图所示的程序框图输出的s值,则的值为()A.4B.3C.2D.―1【答案】A【解析】由程序框图可知,,,,,所以.【考点】1.程序框图;2.特殊角的三角函数值28.若某程序框图如图所示,则该程序运行后输出的值等于.【答案】.【解析】由程序框图得当;.【考点】程序框图.29.某程序框图如图所示,若输出的S=57,则判断框内应________(请用k的不等关系填写,如k>10等)【答案】【解析】程序在运行过程中各变量值变化如下表:K S 是否继续循环循环前 1 1/第一圈 2 4 是第二圈 3 11 是第三圈 4 26 是第四圈 5 57 否故退出循环的条件应为k>4故答案为:k>4.【考点】算法框图,循环结构.30.阅读右边的程序框图,则输出的()A.B.C.D.【答案】A【解析】由程序框图可知,S=0,k=0S=1,k=1S=1+2=3,k=2S=3+23=11,k=3S=11+211>100,k=4,故选A.【考点】程序框图31.阅读如图所示的程序框图,运行相应的程序. 若输入的值为,则输出的结果__________.【答案】.【解析】第一次循环,,,,不成立;第二次循环,,,,不成立;第三次循环,,,,不成立;第四次循环,,,,成立,跳出循环体,输出.【考点】算法与程序框图32.在如程序框图中,若,则输出的是()A.B.C.D.【答案】C【解析】框图首先输入,给循环变量赋值0,执行,;判断不成立,执行,;判断不成立,执行,;…判断不成立,执行,;判断成立,输出的值为,故答案为.【考点】算法框图.33.执行如图所示的程序框图,则输出的值为( )A.91B.55C.54D.30【答案】B【解析】所给的程序的作用是计算:.【考点】程序框图及其应用34.阅读右边的程序框图,若输入,则输出的结果为()A.B.C.D.【答案】A【解析】当时,,走“是”一步,此时,所以.【考点】1.算法程序;2.等差数列求和.35.执行如图所示的程序框图,若输入的值为3,则输出的值是( )A.1B.2C.4D.7【答案】C【解析】【考点】程序框图36.左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是A.B.C.D.【答案】D【解析】根据流程图可知该算法表示统计14次考试成绩中大于等于90的人数,结合茎叶图可得答案.解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加14次考试成绩超过90分的人数;根据茎叶图的含义可得超过90分的人数为10个,故答案为D【考点】循环结构,以及茎叶图点评:本题主要考查了循环结构,以及茎叶图的认识,解题的关键是弄清算法流程图的含义,属于基础题.37.已知实数,执行如右图所示的程序框图,则输出的不小于55的概率为【】A.B.C.D.【答案】A【解析】本试题主要考查了解决程序框图中的循环结构时,一般采用先根据框图的流程写出前几次循环的结果,根据结果找规律.设实数x∈[0,8],经过第一次循环得到x=2x+1,n=2经过第二循环得到x=2(2x+1)+1,n=3经过第三次循环得到x=2[2(2x+1)+1]+1,n=3此时输出x输出的值为8x+7,令8x+7≥55,得x≥6由几何概型得到输出的x不小于55的概率为=故选A.解决该试题的关键是由程序框图的流程,写出前三项循环得到的结果,得到输出的值与输入的值的关系,令输出值大于等于54得到输入值的范围,利用几何概型的概率公式求出输出的x不小于55的概率。
