上海初三数学期末考试卷
上海初三初中数学期末考试带答案解析
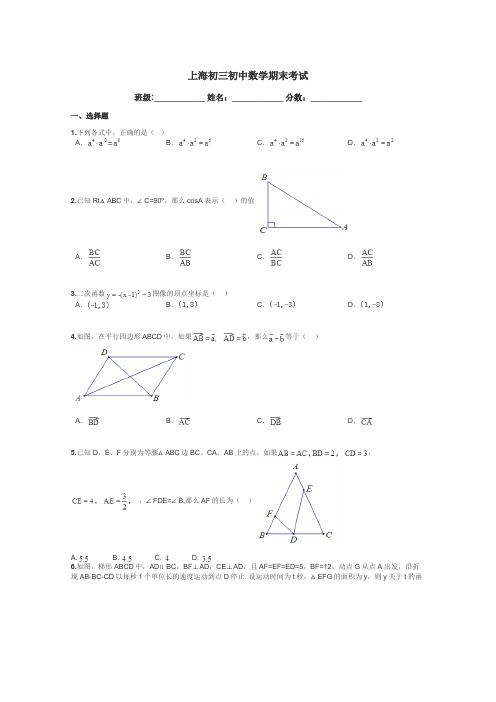
上海初三初中数学期末考试班级:___________ 姓名:___________ 分数:___________一、选择题1.下列各式中,正确的是()A.B.C.D.2.已知Rt△ABC中,∠C=90º,那么cosA表示()的值A.B.C.D.3.二次函数图像的顶点坐标是()A.B.C.D.4.如图,在平行四边形ABCD中,如果,那么等于()A.B.C.D.5.已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果,,∠FDE=∠B,那么AF的长为()A. B. C. D.6.如图,梯形ABCD中,AD∥BC,BF⊥AD,CE⊥AD,且AF=EF=ED=5,BF=12,动点G从点A出发,沿折现AB-BC-CD以每秒1个单位长的速度运动到点D停止. 设运动时间为t秒,△EFG的面积为y,则y关于t的函数图像大致是()二、填空题1.计算的结果是______________.2.不等式组的解集是______________.3.一元二次方程的根的判别式是_________________.4.二次函数的图像开口方向__________________.5.如图,二次函数的图像开口向上,对称轴为直线,图像经过(3,0),则的值是___________.6.抛物线可以由抛物线向__________________(平移)得到.7.若与的方向相反,且,则的方向与的方向_____________.8.如图已知△ABC中,D为边AC上一点,P为边AB上一点,,当AP的长度为__________时△ADP和△ABC相似.9.在△ABC中,∠A,∠B都是锐角,若,则△ABC的形状为_______三角形.10.某坡面的坡度为1:,某车沿该坡面爬坡行进了__________米后,该车起始位置和终止位置两地所处的海拔高度上升了5米11.在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示),已知立杆AB的高度是6米,从侧面D测到路况警示牌顶端C点和低端B点的仰角分别是60°和45°,则路况警示牌宽BC的值为_____________.12.如图,在平面直角坐标系中,Rt△OAB的顶点A的坐标为(9,0),,点C的坐标为(2,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_______________.三、解答题1.化简并求值:,其中.2.已知一个二次函数的顶点A的坐标为(1,0),且图像经过点B(2,3).(1)求这个二次函数的解析式.(2)设图像与y轴的交点为C,记,试用表示(直接写出答案)3.如图已知:,求证:.4.通过锐角三角比的学习,我们已经知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长比与角的大小之间可以相互转化. 类似的我们可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad). 如下图在△ABC中,AB=AC,顶角A的正对记作sadA,这时. 我们容易知道一个角的大小与这个角的正对值也是互相唯一确定的.根据上述角的正对定义,解下列问题:(1)sad60º=_____________;sad90º=________________。
2023-2024学年上海市长宁区九年级上学期期末考数学试卷(中考一模)含详解

2023学年第一学期初三数学教学质量调研试卷(考试时间:100分钟满分:150分)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本调研卷上答题一律无效2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸相应位置上写出证明或计算的主要步骤一、选择题(本大题共6题,每题4分,满分24分)【每小题只有一个正确选项,在答题纸相应题号的选项上用2B 铅笔正确填涂】1.在Rt ABC △中,90C ∠=︒,如果,A BC a α∠==,那么AC 等于()A.tan a α⋅ B.cot a α⋅ C.sin aαD.cos a α2.下列关于抛物线223y x x =+-的描述正确的是()A.该抛物线是上升的B.该抛物线是下降的C.在对称轴的左侧该抛物线是上升的D.在对称轴的右侧该抛物线是上升的3.已知点C 在线段AB 上,且满足2AC BC AB =⋅,那么下列式子成立的是()A.512AC BC -= B.12AC AB -= C.512BC AB -= D.352BC AC =4.已知a为非零向量,且3a b =-,那么下列说法错误的是()A.13a b=-B.3b a = C.30b a += D.b a∥5.如果点D 、E 分别在△ABC 的两边AB 、AC 上,下列条件中可以推出DE ∥BC 的是()A.23AD BD =,23CE AE = B.23AD AB =,23DE BC =C.32AB AD =,12EC AE = D.43AB AD =,43AE EC =6.已知在ABC 与A B C ''' 中,点D D '、分别在边BC B C ''、上,(点D 不与点B C 、重合,点D ¢不与点B C ''、重合).如果ADC △与'''A D C △相似,点A D 、分别对应点A ''、D ,那么添加下列条件可以证明ABC 与A B C ''' 相似的是()①AD A D ''、分别是ABC 与A B C ''' 的角平分线;②AD A D ''、分别是ABC 与A B C ''' 的中线;③AD A D ''、分别是ABC 与A B C ''' 的高.A.①②B.②③C.①③D.①②③二、填空题(本大题共12题,每题4分,满分48分)【在答题纸相应题号后的空格内直接填写答案】7.如果53(,x y x y =均不为零),那么():x x y +的值是____________.8.式子2cos30tan45︒-︒的值是______.9.已知线段a=3cm ,b=4cm ,那么线段a 、b 的比例中项等于_______cm .10.若两个相似三角形的周长比为2:3,则它们的面积比是_________.11.如图,////AB CD EF ,如果:2:3,10AC CE BF ==,那么线段DF 的长是__________.12.二次函数()2f x ax bx c =++图像上部分点的坐标满足下表:那么()5f -=____________.x⋯3-2-1-01⋯()f x ⋯3-2-3-6-11-⋯13.已知向量a 与单位向量e 方向相反,且3a = ,那么a =____________________(用向量e 的式子表示)14.已知一条斜坡的长度为13米,高度为5米,那么该斜坡的坡度为____________.15.如图,在ABC 中,AD 是BC 上的高,且5,3BC AD ==,矩形EFGH 的顶点F G 、在边BC 上,顶点E H 、分别在边AB 和AC 上,如果2EH EF =,那么EH =____________.16.如图,在ABC 中,90BAC ∠=︒,点G 是ABC 的重心,联结GA GC 、,如果533AC AG ==,,那么GCA ∠的余切值为____________.17.我们把顶角互补的两个等腰三角形叫做友好三角形.在ABC 中,10AB AC ==,点D E 、都在边BC 上,5AD AE ==,如果ABC 与ADE V 是友好三角形,那么BC 的长为____________.18.如图,在矩形ABCD 中,8,4,AD AB AC ==是对角线,点P 在边BC 上,联结DP ,将DPC △沿着直线DP 翻折,点C 的对应点Q 恰好落在ADC △内,那么线段BP 的取值范围是____________.三、解答题(本大题共7题,满分78分)【将下列各题的解答过程,做在答题纸的相应位置上】19.已知抛物线2241y x x =++.(1)用配方法把2241y x x =++化为2()y a x m k =++的形式,并写出该抛物线的开口方向、对称轴和顶点坐标;(2)如果将该抛物线上下平移,得到新的抛物线经过点()1,4,求平移后的抛物线的顶点坐标.20.在平行四边形ABCD 中,点E 是AD 的中点,BE AC 、相交于点F .(1)设,AB a AD b == ,试用a b 、表示EF ;(2)先化简,再求作:()()3222a b a b +-+(直接作在图中).21.如图,在四边形ABCD 中,90BAD AC BC DE AC ∠=⊥︒⊥,,,垂足为点43E AC DE ==,,.(1)求:AD AB 的值;(2)BD 交AC 于点F ,如果1tan 2BAC ∠=,求CF 的长.22.小明为测量河对岸大楼的高度,利用量角器和铅锤自制了一个简易测角仪,如图1所示.测量方法:如图2,人眼在P 点观察所测物体最高点C ,量角器零刻度线上A B 、两点均在视线PC 上,将铅锤悬挂在量角器的中心点O .当铅锤静止时,测得视线PC 与铅垂线OD 所夹的角为α,且此时的仰角为β.实践操作:如图3,小明利用上述工具测量河对岸垂直于水平地面的大楼EF 的高度.他先站在水平地面的点H 处,视线为GE ,此时测角仪上视线与铅垂线的夹角为60︒;然后他向前走10米靠近大楼站在水平地面的点R 处,视线为QE ,此时测角仪上视线与铅垂线的夹角为45︒.问题解决:(1)请用含α的代数式表示仰角β;(2)如果GH QR EF 、、在同一平面内,小明的眼晴到水平地面的距离为1.6米,求大楼EF 的高度.(结果保留根号)23.如图,在ABC 中,点,D E 分别是,BC AD 的中点,且AD AC =,连接CE 并延长交AB 于点F .(1)证明:ABC ECD ∽;(2)证明:4BF EF =.24.已知抛物线212y x bx c =++与x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点C ,直线6y x =--经过点A 与点C .(1)求抛物线的表达式;(2)点P 在线段AC 下方的抛物线上,过点P 作BC 的平行线交线段AC 于点D ,交y 轴于点E .①如果C F 、两点关于抛物线的对称轴对称,联结DF ,当DF CF ⊥时,求PDF ∠的正切值;②如果:3:5PD DE =,求点P 的坐标.25.已知ABC 中,2ABC C ∠=∠,BG 平分ABC ∠,8AB =,163AG =,点D ,E 分别是边BC ,AC 上的点(点D 不与点B ,C 重合),且ADE ABC =∠∠,AD ,BG 相交于点F .(1)求BC 的长;(2)如图1,如果2BF CE =,求:BF GF 的值;(3)如果ADE V 是以AD 为腰的等腰三角形,求BD 长.2023学年第一学期初三数学教学质量调研试卷一、选择题(本大题共6题,每题4分,满分24分)【每小题只有一个正确选项,在答题纸相应题号的选项上用2B 铅笔正确填涂】1.在Rt ABC △中,90C ∠=︒,如果,A BC a α∠==,那么AC 等于()A.tan a α⋅ B.cot a α⋅ C.sin aαD.cos a α【答案】B【分析】本题考查了锐角三角函数的定义的应用,主要考查学生的理解能力和计算能力.画出图形,根据锐角三角函数的定义求出即可.【详解】解:cot ACBCα=,∴cot cot AC BC a αα=⋅=⋅,故选:B .2.下列关于抛物线223y x x =+-的描述正确的是()A.该抛物线是上升的B.该抛物线是下降的C.在对称轴的左侧该抛物线是上升的D.在对称轴的右侧该抛物线是上升的【答案】D【分析】本题考查二次函数的性质、二次函数图象上点的坐标特征,根据抛物线的解析式和二次函数的性质,可以判断各个选项中的说法是否正确.【详解】解:∵抛物线223y x x =+-,∴20a =>,在对称轴左侧,该抛物线下降,在对称轴右侧上升,故选项A 、B 、C 均错误,不符合题意,选项D 正确,符合题意;故选:D .3.已知点C 在线段AB 上,且满足2AC BC AB =⋅,那么下列式子成立的是()A.12AC BC -= B.12AC AB -= C.12BC AB -= D.32BC AC =【答案】B【分析】本题考查黄金分割、解一元二次方程,把AB 当作已知数求出AC ,求出BC ,再分别求出各个比值,根据结果判断即可.【详解】解:令AC x =,()0AB a a =>,则BC a x =-,2AC BC AB =⋅可变形为()2x a x a =-⋅,整理,得220x ax a +-=,()2224150a a a ∆=-⨯⨯-=>,解得22a a x -±-±==,边长为正数,∴)122a a x --+==,)(1322a a a x a -=-=,即512AC AB -=⋅,352BC AB =⋅,∴23525112A ABC BC -⋅=+==,故A选项错误;122ABACABAB -==,故B选项正确;3322BC B B ABA A -==⋅,故C选项错误;251B ABC AC =-==,故D 选项错误;故选B .4.已知a 为非零向量,且3a b =- ,那么下列说法错误的是()A.13a b=-B.3b a= C.30b a += D.b a∥【答案】C【分析】本题考查了实数与向量相乘,向量的相关定义,根据其运算法则进行计算即可求解.【详解】解:A .∵a 为非零向量,且3a b =- ,∴13a b =- ,正确,故本选项不符合题意;B .∵a 为非零向量,且3a b =-,∴3b a = ,正确,故本选项不符合题意;C .∵a 为非零向量,且3a b =- ,∴30b a += ,原说法错误,故本选项符合题意;D .∵a 为非零向量,且3a b =-,∴b a ∥,故本选项不符合题意;故选:C .5.如果点D 、E 分别在△ABC 的两边AB 、AC 上,下列条件中可以推出DE ∥BC 的是()A.23AD BD =,23CE AE = B.23AD AB =,23DE BC =C.32AB AD =,12EC AE = D.43AB AD =,43AE EC =【答案】C【分析】根据各个选项的条件只要能推出AD AE AB AC =或AB ACAD AE=,即可得出△ADE ∽△ABC ,推出∠ADE=∠B ,根据平行线的判定推出即可.【详解】解:A 、根据23AD BD =和23CE AE =,不能推出DE ∥BC ,故本选项错误;B 、根据23AD AB =和23DE BC =,不能推出DE ∥BC ,故本选项错误;C 、∵12EC AE =,∴32AC AE =,∵32AB AD =,∴AB AD =ACAE∵∠A=∠A ,∴△ABC ∽△ADE ,∴∠ADE=∠B ,∴DE ∥BC ,故本选项正确;D 、根据AB AD =43和AE EC =43,不能推出DE ∥BC ,故本选项错误;故选C .【点睛】本题考查了相似三角形的性质和判定,平行线的判定的应用,解题的关键是推出△ABC ∽△ADE .6.已知在ABC 与A B C ''' 中,点D D '、分别在边BC B C ''、上,(点D 不与点B C 、重合,点D ¢不与点B C ''、重合).如果ADC △与'''A D C △相似,点A D 、分别对应点A ''、D ,那么添加下列条件可以证明ABC 与A B C ''' 相似的是()①AD A D ''、分别是ABC 与A B C ''' 的角平分线;②AD A D ''、分别是ABC 与A B C ''' 的中线;③AD A D ''、分别是ABC 与A B C ''' 的高.A.①② B.②③C.①③D.①②③【答案】A【分析】本题考查添加条件证明三角形相似,根据ADC △与'''A D C △相似,可得C C '∠=∠,DAC D A C '''∠=∠,AC DCA C D C ='''',再根据相似三角形的判定方法逐项判断即可.【详解】解: ADC △与'''A D C △相似,点A D 、分别对应点A ''、D ,∴C C '∠=∠,DAC D A C '''∠=∠,AC DCA C D C ='''',①AD A D ''、分别是ABC 与A B C ''' 的角平分线时:2BAC DAC ∠=∠,2B A C D A C ''''''∠=∠,∴BAC B A C '''∠=∠,又∴C C '∠=∠,∴ABC A B C '''∽ ;故①正确;②AD A D ''、分别是ABC 与A B C ''' 的中线时,2BC DC =,2B C D C ''''=,∴BC DCB C D C='''',∴AC BCA CBC ='''',又∴C C '∠=∠,∴ABC A B C '''∽ ;故②正确;③AD A D ''、分别是ABC 与A B C ''' 的高时,现有条件不足以证明ABC A B C '''∽ ,故③错误;综上可知,添加①或②时,可以证明ABC 与A B C ''' 相似故选A .二、填空题(本大题共12题,每题4分,满分48分)【在答题纸相应题号后的空格内直接填写答案】7.如果53(,x y x y =均不为零),那么():x x y +的值是____________.【答案】38【分析】本题考查的是比例的基本性质,令3x a =,则5y a =,然后化简整理即可求得.令3x a =,则5y a =,,()():33538x x y +=+=::,即可作答.【详解】解:根据题意,可令3x a =,则5y a =,因此,()():3353838x x y a a a a a +=+==:::.故答案为:38.8.式子2cos30tan45︒-︒的值是______.【答案】1-##1-【分析】直接将特殊角的三角函数值代入计算即可解答.【详解】解:32cos30tan452112︒-︒=⨯-=.1.【点睛】本题主要考查了三角函数的混合运算,牢记特殊角的三角函数值成为解答本题的关键.9.已知线段a=3cm ,b=4cm ,那么线段a 、b 的比例中项等于_______cm .【答案】【详解】试卷分析:根据线段的比例中项的定义列式计算即可得解.∵线段a=3cm ,b=4cm ,∴线段a 、b 的比例中项=cm .故答案为考点:比例线段.10.若两个相似三角形的周长比为2:3,则它们的面积比是_________.【答案】4∶9【详解】解:∵两个相似三角形的周长比为2:3,∴这两个相似三角形的相似比为2:3,∴它们的面积比是4:9.故答案为:4:9.考点:相似三角形的性质.11.如图,////AB CD EF ,如果:2:3,10AC CE BF ==,那么线段DF 的长是__________.【答案】6【分析】根据平行线分线段成比例定理结合比例解答即可.【详解】解:∵////AB CD EF ,:2:3,AC CE =∴23BD AC DF CE ==∵10BF =∴31065DF =⨯=.故答案为6.【点睛】本题考查平行线分线段成比例定理,灵活应用平行线分线段成比例定理列出比例式是解答本题的关键.12.二次函数()2f x ax bx c =++图像上部分点的坐标满足下表:那么()5f -=____________.x ⋯3-2-1-01⋯()f x ⋯3-2-3-6-11-⋯【答案】11-【分析】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了抛物线的对称性.利用表中数据确定抛物线的对称轴,然后根据抛物线的对称性求解.【详解】解:利用表中数据得抛物线的对称轴为直线2x =-,所以5x =-和1x =时的函数值相等,即当5x =-时,y 的值为11-.故答案为:11-.13.已知向量a 与单位向量e 方向相反,且3a = ,那么a = ____________________(用向量e 的式子表示)【答案】3e- 【分析】此题考查了平面向量的知识,由向量a 与单位向量e 方向相反,且3a = ,根据单位向量与相反向量的知识,即可求得答案.【详解】解:∵向量a 与单位向量e 方向相反,且3a = ,∴3a e =- .故答案为:3e - .14.已知一条斜坡的长度为13米,高度为5米,那么该斜坡的坡度为____________.【答案】1:2.4【分析】本题考查坡度,先利用勾勾股定理求出水平距离,然后利用公式计算是解题的关键.【详解】解:如图,13AB =,5AE =,∴12BE ===,∴斜坡的坡度为i :5:121:2.4AE BE ===,故答案为:1:2.4.15.如图,在ABC 中,AD 是BC 上的高,且5,3BC AD ==,矩形EFGH 的顶点F G 、在边BC 上,顶点E H 、分别在边AB 和AC 上,如果2EH EF =,那么EH =____________.【答案】3011【分析】本题考查了相似三角形的判定和性质及矩形的性质,通过四边形EFGH 为矩形推出EH BC ,因此AEH 与ABC 两个三角形相似,将AM 视为AEH 的高,可得出::AM AD EH BC =,再将数据代入计算是本题的关键.【详解】解:设AD 与EH 交于点M .∵四边形EFGH 是矩形,∴EH BC ,∴AEH ABC ∽,∵AM 和AD 分别是AEH 和ABC 的高,∴::AM AD EH BC =,DM EF =,∴3AM AD DM AD EF EF =-=-=-,∵2EH EF =,代入可得:3235EF EF -=,解得1511EF =,∴153021111EH =⨯=,故答案为:3011.16.如图,在ABC 中,90BAC ∠=︒,点G 是ABC 的重心,联结GA GC 、,如果533AC AG ==,,那么GCA ∠的余切值为____________.【答案】23【分析】延长CG 交AB 于F ,过G 作GD AC ⊥于G ,直线DG 交BC 于E ,证明DCE ACB ∽V V ,得CD DE AC AB =,同理可得DG CD CG GE AF AC CF BF ===,即有DE CG AB CF=,根据G 为ABC 的重心,3AC =,得2DE =,设tan ACG x ∠=,根据勾股定理列式计算53AG ===可得答案.【详解】解:过G 作GD AC ⊥于G ,延长CF 交AB 于点F ,如图:∵90GD AC BAC ⊥∠=︒,,∴DE AB ∥,90CDE BAC ==︒∠∠,∵DCE ACB ∠=∠,∴DCG ACF ∽,∴CD DG CG AC AF CF==,∵G 为ABC 的重心,∴23CD DG CG AC AF CF ===,∵3AC =,∴21CD AD ==,,∴2243DG AG AD =-=,则在直角三角形CDG 中,423tan 23DG ACG CD ∠===,故答案为:23【点睛】本题考查三角形的重心,涉及相似三角形的判定与性质,勾股定理,解直角三角形,难度较大,综合性较强,解题的关键是作辅助线,构造相似三角形.17.我们把顶角互补的两个等腰三角形叫做友好三角形.在ABC 中,10AB AC ==,点D E 、都在边BC 上,5AD AE ==,如果ABC 与ADE V 是友好三角形,那么BC 的长为____________.【答案】5【分析】本题考查相似三角形的判定和性质,等腰三角形的性质,勾股定理等知识,解题的关键是正确寻找相似三角形解决问题,学会利用参数构建方程.如图,过过点A 作AF BC ⊥于点F .证明FAD FBA ∽,推出51102AD AF DF AB FB AF ====,设DF EF x ==,这24AF x BF x ==,,构建方程求解.【详解】解:如图,过点A 作AF BC ⊥于点F .∵AB AC AD AE AF BC ==⊥,,,∴DF EF BF FC BAF CAF DAF EAF ==∠=∠∠=∠,,,,∵180BAC DAE ∠+∠=︒,∴22180BAF DAF ∠+∠=︒,∴90BAF DAF ∠+∠=︒,∵90BAF B ∠+∠=︒,∴∠=∠DAF B ,∵90AFD AFB ∠=∠=︒,∴FAD FBA ∽,∴51102AD AF DF AB FB AF ====,设DF EF x ==,这24AF x BF x ==,,∵222AB AF BF =+,∴()()2221024x x =+,∴5x =,∴285BC BF x ===故答案为:85.18.如图,在矩形ABCD 中,8,4,AD AB AC ==是对角线,点P 在边BC 上,联结DP ,将DPC △沿着直线DP 翻折,点C 的对应点Q 恰好落在ADC △内,那么线段BP 的取值范围是____________.【答案】46BP <<【分析】本题考查矩形的折叠问题,相似三角形的判定和性质等,计算出点Q 恰好落在AD 边上,以及点Q 恰好落在AC 边上时BP 的值,即可得出线段BP 的取值范围.【详解】解:当点C 的对应点Q 恰好落在AD 边上时,如图:由折叠的性质知CD QD =,CP QP =,90PQD PCD ∠=∠=︒,又 矩形ABCD 中,90ADC ∠=︒,∴四边形QDCP 是正方形,∴4CP CD AB ===,∴844BP BC CP AD CP =-=-=-=;当点C 的对应点Q 恰好落在AC 边上时,如图,由折叠的性质知PD CQ ⊥,∴90PDC ACD ∠+∠=︒,又 矩形ABCD 中,90ADC ∠=︒,∴90CAD ACD ∠+∠=︒,∴PDC CAD ∠=∠,又 90PCD CDA ∠=∠=︒,∴PDC CAD ∽,∴PC CD CD AD =,即448PC =,∴2PC =,∴826BP BC PC =-=-=,∴线段BP 的取值范围是46BP <<.故答案为:46BP <<.三、解答题(本大题共7题,满分78分)【将下列各题的解答过程,做在答题纸的相应位置上】19.已知抛物线2241y x x =++.(1)用配方法把2241y x x =++化为2()y a x m k =++的形式,并写出该抛物线的开口方向、对称轴和顶点坐标;(2)如果将该抛物线上下平移,得到新的抛物线经过点()1,4,求平移后的抛物线的顶点坐标.【答案】(1)该抛物线的开口向上,对称轴是直线=1x -,顶点坐标为(1,1)--(2)(1,4)--【分析】本题考查了二次函数图象与几何变换,二次函数的性质,二次函数图象上点的坐标特征,掌握二次函数的性质是解题的关键.(1)利用配方法把一般式化为顶点式,根据二次函数的性质写出抛物线的开口方向、对称轴和顶点坐标.(2)设平移后的抛物线解析式为22(1)y x =+1k -+,代入点(1,4),求得k 的值即可求解.【小问1详解】解:2241y x x =++()222121x x =++-+22(1)1x =+-,∴该抛物线的开口向上,对称轴是直线=1x -,顶点坐标为(1,1)--;【小问2详解】设平移后的抛物线解析式为22(1)y x =+1k -+,∵新的抛物线经过点(1,4),∴24221k =⨯-+,解得3k =-,∴平移后的抛物线解析式为22(1)4y x =+-,∴平移后的抛物线的顶点坐标是(1,4)--.20.在平行四边形ABCD 中,点E 是AD 的中点,BE AC 、相交于点F .(1)设,AB a AD b == ,试用a b 、表示EF;(2)先化简,再求作:()()3222a b a b +-+ (直接作在图中).【答案】(1)1136a b - (2)12a b -- ,见详解【分析】本题主要考查平行四边形的性质、平行线分线段成比例定理和平面向量,()1根据题意得AD BC ∥和BC AD =,进一步得到AE EF BC FB =,则1132EF DA AB ⎛⎫=+ ⎪⎝⎭,代入向量即可.()2化解得12a b -- ,将对应线段代入得到()AB AE -+ ,过点E 作EG AB ∥,则AE BG = ,1=2a b GA -- ,连接GA 即可.【小问1详解】解:∵四边形ABCD 为平行四边形,∴AD BC ∥,BC AD =,∴AFE CFB ∽,则AE EF BC FB=,∵点E 是AD 的中点,∴12AE AD =,则12EF FB =,∴()1111123332EF FB EB EA AB DA AB ⎛⎫===+=+ ⎪⎝⎭ ,∵,AB a AD b == ,∴1111=3236EF b a a b ⎛⎫=-+- ⎪⎝⎭ .【小问2详解】()()3312223222a b a b a b a b a b +-+=+--=-- ,∵,AB a AD b == ,∴()1122a b AB AD AB AE AB AE --=--=--=-+ ,过点E 作EG AB ∥,则AE BG = ,∴()()1===2a b AB AE AB BG AG GA --=-+-+- ,如图,GA即为所求.21.如图,在四边形ABCD 中,90BAD AC BC DE AC ∠=⊥︒⊥,,,垂足为点43E AC DE ==,,.(1)求:AD AB 的值;(2)BD 交AC 于点F ,如果1tan 2BAC ∠=,求CF 的长.【答案】(1)3:4(2)1CF =【分析】本题考查了相似三角形的性质与判定、解直角三角形:(1)根据90BAD AC BC DE AC ∠=⊥︒⊥,,,得90AED ACB ∠=∠=︒,EAD ABC ∠=∠,证明AED BCA △∽△,结合相似三角形的性质,得:AD AB 的值;(2)根据相似三角形的性质且1tan 2BAC ∠=,得2BC =, 1.5AE =,再证明BCF DEF ∽,列式代数计算,即可作答.【小问1详解】解:∵90BAD AC BC DE AC∠=⊥︒⊥,,∴90AED ACB ∠=∠=︒,90BAC DAE BAC ABC∠+∠=︒=∠+∠∴EAD ABC ∠=∠,∴AED BCA△∽△则::3:4AD AB DE AC ==【小问2详解】解:如图:∵AED BCA △∽△,1tan 2BAC ∠=,∴11242BC BC BAC ADE AC ==∠=∠,,,∴2BC =,∴1tan 32AE AE ADE ED ∠===,得 1.5AE =,∴4 1.5 2.5EC AC AE =-=-=,∵AC BC DE AC ⊥⊥,,∴90BCF DEF ∠=∠=︒,∵BFC DFE ∠=∠,∴BCF DEF ∽,即BC CF DE EF=,∴23 2.5CF CF =-,解得1CF =.22.小明为测量河对岸大楼的高度,利用量角器和铅锤自制了一个简易测角仪,如图1所示.测量方法:如图2,人眼在P 点观察所测物体最高点C ,量角器零刻度线上A B 、两点均在视线PC 上,将铅锤悬挂在量角器的中心点O .当铅锤静止时,测得视线PC 与铅垂线OD 所夹的角为α,且此时的仰角为β.实践操作:如图3,小明利用上述工具测量河对岸垂直于水平地面的大楼EF 的高度.他先站在水平地面的点H 处,视线为GE ,此时测角仪上视线与铅垂线的夹角为60︒;然后他向前走10米靠近大楼站在水平地面的点R 处,视线为QE ,此时测角仪上视线与铅垂线的夹角为45︒.问题解决:(1)请用含α的代数式表示仰角β;(2)如果GH QR EF 、、在同一平面内,小明的眼晴到水平地面的距离为1.6米,求大楼EF 的高度.(结果保留根号)【答案】(1)90βα=︒-(2)()6.6米【分析】本题考查了解直角三角形−仰角俯角问题,列代数式,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.(1)延长OD 交PK 于L ,根据题意可得:OL PK ⊥,从而可得:90OLP ∠=︒,然后利用直角三角形的两个锐角互余进行计算,即可解答;(2)延长GQ 交EF 于点M ,根据题意可得: 1.6GM EF GH QR MF ⊥===,米,10GQ HR ==米,然后设EM x =米,分别在Rt EGM 和Rt EQM 中,利用锐角三角函数的定义求出GM 和QM 的长,从而列出关于x 的方程,进行计算即可解答.【小问1详解】解:如图:延长OD 交PK 于L ,由题意得:OL PK ⊥,∴90OLP ∠=︒,∵POD α∠=,∴9090OPL POD α∠=︒-∠=︒-,∴90βα=︒-;【小问2详解】解:延长GQ 交EF 于点M ,由题意得: 1.610GM EF GH QR MF GQ HR ⊥=====,m,m ,设EM x =米,在Rt EGM 中,60GEM ∠=︒,∴tan60GM EM =⋅︒=(米),在Rt EQM 中,45QEM ∠=︒,∴45QM EM tan x =⋅︒=(米),∵GM QM GQ -=,10x -=解得:5x =∴()5EM =米,∴()5 1.6 6.6EF EM FM =+=+=米,∴大楼EF 的高度为()6.6+米.23.如图,在ABC 中,点,D E 分别是,BC AD 的中点,且AD AC =,连接CE 并延长交AB 于点F .(1)证明:ABC ECD ∽;(2)证明:4BF EF =.【答案】(1)见解析(2)见解析【分析】本题主要考查相似三角形的判定和性质,等腰三角形的判定和性质:(1)根据等边对等角可得EDC ACB ∠=∠,再证这组夹角的两边成比例即可;(2)作DH CF ∥交AB 于点H ,可证BHD BFC ∽,AFE AHD ∽,推出12HD BD FC BC ==,12FE AE HD AD ==,进而可得4FC EF =,再根据ABC DCE ∽得出FBC FCB ∠=∠,推出CF BF =,等量代换可证4BF EF =.【小问1详解】证明: AD AC =,∴ADC ACD ∠=∠,即EDC ACB ∠=∠,又 点,D E 分别是,BC AD 的中点,∴12DC CB =,1122ED AD AC ==,∴12DC ED CB AC ==,∴AC ED CB DC=,∴ABC ECD ∽;【小问2详解】证明:如图,作DH CF ∥交AB 于点H ,DH CF ∥,∴BHD BFC ∠=∠,BDH BCF ∠=∠;AFE AHD ∠=∠,AEF ADH ∠=∠,∴BHD BFC ∽,AFE AHD ∽,又 点,D E 分别是,BC AD 的中点,∴12HD BD FC BC ==,12FE AE HD AD ==,∴2FC HD =,2HD FE =,∴4FC EF =,由(1)得ABC ECD ∽,∴ABC ECD ∠=∠,即FBC FCB ∠=∠,∴CF BF =,∴4BF EF =.24.已知抛物线212y x bx c =++与x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点C ,直线6y x =--经过点A 与点C .(1)求抛物线的表达式;(2)点P 在线段AC 下方的抛物线上,过点P 作BC 的平行线交线段AC 于点D ,交y 轴于点E .①如果C F 、两点关于抛物线的对称轴对称,联结DF ,当DF CF ⊥时,求PDF ∠的正切值;②如果:3:5PD DE =,求点P 的坐标.【答案】(1)21262y x x =+-(2)①13②1532⎛⎫- ⎪⎝⎭,【分析】(1)先由一次函数求出()()6060A C --,,,,再运用待定系数法求二次函数解析式,即可作答.(2)①依题意,得DF CF ⊥,PE BC PDF ACB ∠=∠ ,,根据角的等量代换,即PDF OCB ∠=∠,先求出点B 的坐标.PDF ∠的正切值等于21tan 63OB OCB OC ∠===;②先表达出21062E p p ⎛⎫-- ⎪⎝⎭,,22111168484D p p p p ⎛⎫-+-- ⎪⎝⎭,,21262P p p p ⎛⎫+- ⎪⎝⎭,,23438EN p p -=,3EM p =-再根据相似三角形的性质与判定,列式化简计算,即可作答.【小问1详解】解:∵直线6y x =--经过点A 与点C则当06x y ==-,;06y x ==-,∴()()6060A C --,,,∴60186c b c =-⎧⎨=-+⎩,,解得62c b =-⎧⎨=⎩21262y x x =+-;【小问2详解】解:①如图:∵()()6060A C --,,,,且C F 、两点关于抛物线21262y x x =+-的对称轴对称,∴6F c y y ==-,221222b x a =-=-=-⨯则4F x =-∵DF CF⊥∴DF y ∥轴则FDC OCA∠=∠∵过点P 作BC 的平行线交线段AC 于点D ,交y 轴于点E .∴PE BC PDF ACB∠=∠ ,则PDF OCB∠=∠∵21262y x x =+-x 轴交于A B 、两点(点A 在点B 的左侧),∴210262x x =+-∴6x =-,2x =∴()20B ,∵PDF OCB∠=∠则PDF ∠的正切值等于21tan 63OB OCB OC ∠===;②设21262P p p p ⎛⎫+- ⎪⎝⎭,,BC 的解析式为y mx n =+∴把()()0620C B -,,,代入y mx n =+得602n m n=-⎧⎨=+⎩解得63n m =-⎧⎨=⎩∵过点P 作BC 的平行线交线段AC 于点D ,交y 轴于点E∴设PE 的解析式为3y x b=+把21262P p p p ⎛⎫+- ⎪⎝⎭,代入3y x b =+得2162p p b =--∴21623y x p p =--+令0x =,2162p p y =--即21062E p p ⎛⎫-- ⎪⎝⎭,当261362y x y x p p =--⎧⎪⎨=+--⎪⎩解得21184x p p +=-则把21184x p p +=-代入21623y x p p =--+得211684y p p =--∴22111168484D p p p p ⎛⎫-+-- ⎪⎝⎭,∵过点P 作PM y ⊥轴,过点D 作DN y ⊥轴,∴EDN EPM∽∴EN DE EM EP=∵:3:5PD DE =∴58EN EM =∶∶∵21062E p p ⎛⎫-- ⎪⎝⎭,,22111168484D p p p p ⎛⎫-+-- ⎪⎝⎭,,21262P p p p ⎛⎫+- ⎪⎝⎭,∴222111336628484EN p p p p p p ⎛⎫=-----=- ⎪⎝⎭,2211626322EM p p p p p ⎛⎫=---+-=- ⎪⎝⎭∴23358348p p p --=∶∶解得1103p p ==-,∵点P 在线段AC 下方的抛物线上,∴10p =(舍去)∴3p =-.把3p =-代入21262y p p =+-∴19241592362222y =⨯-⨯-=-=∴点P 的坐标1532⎛⎫- ⎪⎝⎭,【点睛】本题考查了二次函数的几何综合,相似三角形的判定与性质,解直角三角形,勾股定理等,综合性强,难度较大,正确掌握相关性质内容是解题的关键.25.已知ABC 中,2ABC C ∠=∠,BG 平分ABC ∠,8AB =,163AG =,点D ,E 分别是边BC ,AC 上的点(点D 不与点B ,C 重合),且ADE ABC =∠∠,AD ,BG 相交于点F .(1)求BC 的长;(2)如图1,如果2BF CE =,求:BF GF 的值;(3)如果ADE V 是以AD 为腰的等腰三角形,求BD 长.【答案】(1)10(2)278(3)325【分析】(1)证明ABG CAB ∽ ,再根据相似三角形的性质,等腰三角形的判定与性质,即可得到答案;(2)过点F 作FM AB ⊥于点M ,FN BD ⊥于点N ,先证明ABF DCE ∽ ,进一步求得6BD =,接着利用面积法证明4=3AF DF ,设4AF x =,证明FAG EAD ∽ ,求得3221FG =,即可进一步求得答案;(3)先证明CDE CBG ∽ ,可得32CD CE =,再利用等腰三角形的判定与性质以及平行线的性质逐步求得43FG =,最后证明AFG ADE ∽ ,进一步求出125CE =,即可得到答案.【小问1详解】BG 平分ABC ∠,22ABC ABG GBC ∴∠=∠=∠,2ABC C ∠=∠ ,ABG C GBC ∴∠=∠=∠,BAG CAB ∠=∠ ,ABG ACB ∴∽ ,AB AG BG AC AB CB ∴==,16838BG AC CB ∴==,12AC ∴=,32BC BG =,16201233CG AC AG ∴=-=-=,C GBC ∠=∠ ,203BG CG ∴==,3102BC BG ∴==;【小问2详解】过点F 作FM AB ⊥于点M ,FN BD ⊥于点N ,ADE ABC ∠=∠ ,ADE CDE ABC FAB ∠+∠=∠+∠,FAB EDC ∴∠=∠,又ABG C ∠=∠ ,ABF DCE ∴∽ ,AB AF BF CD DE CE∴==,2BF CE = ,142CD AB ∴==,2AF DE =,1046BD BC CD ∴=-=-=,BG 平分ABC ∠,FM FN ∴=,142132ABF DBF AB FM S AF S DF BD FN ⋅∴===⋅ ,设4AF x =,则3DF x =,7AD x =,2DE x =,2AGF GBC C C ABC ∠=∠+∠=∠=∠ ,ADE ABC =∠∠,AGF ADE ∴∠=∠,又FAG EAD ∠=∠ ,FAG EAD ∴∽ ,AG FG AD ED ∴=,16372FG x x ∴=,3221FG ∴=,367BF BG FG ∴=-=,3627732821BF GF ∴==;【小问3详解】ADE 是以AD 为腰的等腰三角形,AD AE ∴=,ADE AED ∴∠=∠,AGF ADE ∠=∠ ,AGF AED ∴∠=∠,BG DE ∴∥,CDE CBG ∴∽ ,CE CD CG CB ∴=,20103CE CD ∴=,32CD CE ∴=,BG DE ∥ ,AFG ADE ∴∠=∠,GBC EDC ∠=∠,AFG AGF ∴∠=∠,163AF AG ∴==,FAB EDC ∠=∠ ,ABG GBC C ∠=∠=∠,FAB ABG ∴∠=∠,EDC C ∠=∠,163BF AF ∴==,CE DE =,43FG BG BF ∴=-=,BG DE ∥ ,AFG ADE ∴∽ ,AG FG AE DE ∴=,1643312CE CE ∴=-,解得125CE =,3321225BD BC CD CE ∴=-=-=.【点睛】本题考查了相似三角形的判定与性质,等腰三角形的判定与性质,平行线的判定与性质,利用面积比求线段比等知识与方法,灵活运用相关知识与方法是解答本题的关键.。
2023-2024学年上海市金山区九年级(上)期末数学试卷(一模)(含解析)

2023-2024学年上海市金山区九年级(上)期末数学试卷(一模)一、选择题:本题共6小题,每小题4分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.把抛物线y=2x2向左平移1个单位后得到的新抛物线的表达式是( )A. y=2x2−1B. y=2x2+1C. y=2(x−1)2D. y=2(x+1)22.已知点E是平行四边形ABCD的边AD上一点,联结CE和BD相交于点F,如果AE:ED=1:2,那么DF:FB为( )A. 1:2B. 1:3C. 2:3D. 2:53.在直角坐标平面的第一象限内有一点A(a,b),如果射线OA与x轴正半轴的夹角为α,那么下列各式正确的是( )A. b=a⋅tanαB. b=a⋅cotαC. b=a⋅sinαD. b=a⋅cosα4.抛物线y=ax2+bx+c的图象如图所示,下列判断中不正确的是( )A. a<0B. b<0C. c>0D. a+b+c<05.将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么原来矩形较长边和较短边的比是( )A. 2:1B. 2:1C. 3:1D. 3:16.如图在4×1的方格中,每一个小正方形的顶点叫做格点,以其中三个格点为顶点的三角形称为格点三角形,△ABC就是一个格点三角形,现从△ABC的三个顶点中选取两个格点,再从余下的格点中选取一个格点联结成格点三角形,其中与△ABC相似的有( )A. 1个B. 2个C. 3个D. 4个二、填空题:本题共12小题,每小题4分,共48分。
7.如果a5=b3(b≠0),那么a−bb=______ .8.化简:2(−a+3b)−6b=______ .9.已知两个相似三角形的相似比为2:3,那么这两个三角形的周长比为______ .10.点P是线段AB的黄金分割点(AP>BP),AB=2,那么线段AP的长是______ .11.抛物线y=2x2−3的顶点坐标是______ .312.如果点A(2,a)、B(3,b)在二次函数y=x2−3x的图象上,那么a______ b(填“>”“<”或“=”).13.如果α是直角三角形的一个锐角,sinα=4,那么tanα=______ .514.如图,已知D、E、F分别是△ABC的边AB、AC、BC上的点,DE//BC,EF//AB,△ADE、△EFC的面积分别为1、4,四边形BFED的面积为______ .15.如图,在山坡上种树,要求株距(相邻两树间的水平距离)是4米,斜坡的坡度i=1:2,那么相邻两树间的坡面距离为______ 米.16.如图,为了绕开岛礁区,一艘船从A处向北偏东60°的方向行驶8海里到B处,再从B处向南偏东45°方向行驶到发点A正东方向上的C处,此时这艘船距离出发点A处______ 海里.17.把矩形ABCD绕点C按顺时针旋转90°得到矩形A′B′CD′,其中点A的对应点A′在BD的延长线上,如果AB=1,那么BC=______ .18.在△ABC中,AC=6,P是AB边上的一点,Q为AC边上一点,直线PQ把△ABC分成面积相等的两部分,且△APQ和△ABC相似,如果这样的直线PQ有两条,那么边AB长度的取值范围是______ .三、解答题:本题共7小题,共78分。
上海市浦东新区2022—2023学年九年级上学期数学期末考试(详解版)

初三数学期末测试卷(时间100分钟)一、选择题:(本大题共6题)1. 下列图形,一定相似的是( )A. 两个直角三角形B. 两个等腰三角形C. 两个等边三角形D. 两个菱形【答案】C2. 已知抛物线()2213y x =−+,那么它的顶点坐标是( )A. (1,3)−B. (1,3)C. (2,1)D. (2,3) 【答案】B3. 在Rt ABC 中,90B,如果A α∠=,BC a =,那么AC 的长是( ) A. tan a αB. cot a αC. cos a aD. sin a a 【答案】D4. 小杰在一个高为h 的建筑物顶端,测得一根高出此建筑物的旗杆顶端的仰角为30︒,旗杆与地面接触点的俯角为60︒,那么该旗杆的高度是( ) A. 23h B. 45h C. 43h D. 54h 【答案】C5. 已知二次函数2y ax bx c =++的图像如图所示,那么点(,)P a b 在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】B 6. 如图,DF AC ∥,DE BC ∥,下列各式中正确的是( )A. BD AB CE AC =B. AD BF BD FC =C. AD CE DE BD =D. AE BF CE CF= 【答案】A二、填空题:(本大题共12题)7. 如果23a b =,那么b a a b −=+__________. 【答案】158. 如果两个相似三角形的面积比是4:9,那么它们对应高的比是________【答案】2:39. 已知点P 是线段MN 的黄金分割点,>MP PN ,如果8MN =,那么PM 的长是 _____. 【答案】454或445−+10. 如果在比例尺为1:1 000 000的地图上,A 、B 两地的图上距离是3.4厘米,那么A 、B 两地的实际距离是 _____千米.【答案】3411. 两个相似三角形的对应边上中线之比为2:3,周长之和为20cm ,则较小的三角形的周长为__________.【答案】8cm12. 将抛物线241y x x =+−向右平移3个单位后,所得抛物线的表达式是_______________.【答案】224y x x =−−13. 如图,已知AD ∥BE ∥CF .如果 4.8AB =, 3.6DE =, 1.2EF =,那么AC 的长是 _____.【答案】6.4或32514. 已知一条斜坡的长度是10米,高度是6米,那么坡角的角度约为_______.(备用数据tan31° = cot59°≈0.6, sin37° = cos 53°≈0.6)【答案】37°.15. 在Rt ABC △中,90A ∠=︒,已知1AB =,2AC =,AD 是BAC ∠的平分线,那么AD 的长是 _____. 【答案】22322316. 如图,点E 、F 分别在边长为1的正方形ABCD 的边AB 、AD 上,2BE AE =、2AF FD =,正方形A B C D ''''的四边分别经过正方形ABCD 的四个顶点,已知A D EF ''∥,那么正方形ABCD ''''的边长是 _____.【答案】35517. 在ABC 中,2A B ∠=∠,如果4AC =,5AB =,那么BC 的长是 _____.【答案】618. 如图,正方形ABCD 的边长为5,点E 是边CD 上的一点,将正方形ABCD 沿直线AE 翻折后,点D 的对应点是点D ,联结CD '交正方形ABCD 的边AD 于点F ,如果AF CE =,那么AF 的长是______________.【答案】535或553−+【解析】【详解】解:连接DD ',如图,四边形ABCD 是正方形,AD CD ∴=,90ADC ∠=︒,90AED DAE ∴∠+∠=︒,由折叠的性质得:DE D E '=,AE DD '⊥,90D DE AED '∴∠+∠=︒,D DE DAE '∴∠=∠,AF CE =,AD AF CD CE ∴−=−,即DF DE =,90ADE CDF ∠=∠=︒,AD CD =,(SAS)ADE CDF ∴△≌△,DCF DAE ∴∠=∠,D DE DCF '∴∠=∠,CD DD ''∴=,90DCF CFD ∠+∠=︒,90D DE D DF ''∠+∠=︒,CFD D DF '∴∠=∠,D D D F CD '''∴==,即点D 是CF 的中点,设DF x =,则12DD CF '=, 222225CF CD DF x =+=+,221(25)4DD x '∴=+, DE D E '=,CD DD ''=,D DE DCF DD E ''∴∠=∠=∠,D DE DCD ''∴∽,DD DE CD CD '∴=', CD DD ''=,2DD CD DE '∴=⋅, 即21(25)54x x += 解得:1103x =−21053x =+,5(1053)535AF AD DF ∴=−=−−=− 故答案为:535−.三、解答题:(本大题共7题)19. 计算:cot 454sin 452tan 30cos30cos60︒︒−︒︒+︒【答案】2+1 解:原式=4×22-2×33×32+112 2 2 1.20. 如图,在ABC 中,BE 平分ABC ∠,DE BC ∥,3AD =,2DE =.(1)求:AE AC 的值;(2)设AB a =,BC b =求向量BE (用向量a b 、表示).【答案】(1)35AE AC = (2)3255BE b a =− 【解析】【小问1详解】解:∵BE 平分ABC ∠,∴DBE CBE ∠=∠,∵DE BC ∥,∴DEB EBC ∠=∠,ADE ABC △△∽,∴DBE DEB ∠=∠,而2DE =,∴2DB DE ==,而3AD =,∴5AB AD BD =+=,∵ADE ABC △△∽, ∴35AE AD AC AB ==. 【小问2详解】∵AB a =,BC b =,∴AC AB BC a b =+=+, ∵35AE AC =, ∴25CE AC =, ∴222555EC AC a b ==+, ∴22325555BE BC EC b a b b a =−=−−=−. 21. 如图,在Rt EAC 中,90EAC ∠︒=,45E ∠︒=,点B 在边EC 上,BD AC ⊥,垂足为D ,点F 在BD 延长线上,5FAC EAB BF ∠∠=,=,tan AFB ∠=34.求:(1)AD 的长;(2)cot DCF ∠的值.【答案】(1)125(2)916【小问1详解】解:∵90EAC ∠=︒,∴90EAB BAC ∠∠+=︒,∵FAC EAB ∠∠=,∴90FAC BAC ∠∠+=︒,∴90BAF ∠=︒, ∵3tan 4AB AFB AF ∠==,令3AB x =,则4AF x =,∵222BF AB AF =+,∴()()22234BF x x =+,∴55BF x ==,∴1x =,∴3344AB x AF x ====,,∵··2ABF BF AD AB AF S ==,∴53412AD =⨯=, ∴125AD =;【小问2详解】在Rt ABF 中,AD BF ⊥,∴2·AB BD BF =,∴95BD =, ∴95BD =, ∴165DF BF BD =−=, ∵9045EAC E ∠∠=︒=︒,,∴45BCD ∠=︒,∴45DBC ∠=︒, ∴95DC BD ==, ∴9cot 16DC DCF DF ∠==. 22. 某地一段长为50米混泥土堤坝,堤坝的横断面ABCD 是等腰梯形(如图所示),坝顶AD 宽为8米,坝高为4米,斜坡AB 的坡度为1:1.5.(1)求横断面ABCD 的面积;(2)为了提高堤坝的防洪能力,现需将原堤坝按原堤坝要求和坡度加高1米,求加高堤坝需要多少立方米的混泥土?(堤坝的体积=横断面的面积×堤坝的长度)【答案】(1)横断面ABCD 的面积为256m .(2)加高堤坝需要的混泥土为:3325m .【小问1详解】解:如图,过A 作AE BC ⊥于E ,过D 作DF BC ⊥于F ,由等腰梯形是轴对称图形可得:4AE DF ==,BE CF =,四边形AEFD 是矩形, ∴8AD EF ==,∵斜坡AB 的坡度为1:1.5,的∴11.5AE BE =, ∴4 1.56BE CF =⨯==,∴20BC BE EF CF =++=,∴横断面ABCD 的面积为()()21820456m 2+⨯=. 【小问2详解】如图,过G 作GK AD ⊥于K ,过H 作HL AD ⊥于L ,结合题意可得:1KG HL ==,斜坡AG 的坡度是1:1.5,四边形GADH ,四边形GBCH 都是等腰梯形,同理可得:AK DL =,GH KL , 由斜坡AG 的坡度是1:1.5, ∴11.5GK AK =, ∴ 1.5AK DL ==,∴8 1.5 1.55KL AD AK DL GH =−−=−−==,∴四边形GADH 的面积为:()()21135+81m 22⨯=, ∴加高堤坝需要的混泥土为:()31350325m 2⨯=. 23. 如图,在ABC 中,点D 、F 分别是边BC 、AB 上的点,AD 和CF 交于点E .(1)如果BF AB BD BC =,求证:EF CE DE AE =;(2)如果2AE BF AF DE =,求证:AD 是ABC 的中线.【答案】(1)见解析 (2)见解析【解析】【小问1详解】证明:∵BF AB BD BC =, ∴ BF BC BD AB=, ∵B B ∠=∠,∴ABD CBF ∽△△,∴BAD BCF ∠=∠,又∵AEF CED ∠=∠,∴∽AEF CED △△, ∴ EF AE ED CE=, ∴EF CE DE AE =;【小问2详解】过D 作DG AB ∥交CF 于G ,则DEG AEF ∽,∴AE AF ED DG=, ∵2AE BF AF DE =, ∴2AE AF ED BF =, ∴ 2AF AF DG BF=, 即122DG AF FB AF ==, ∵CD DG BC FB=, ∴12CD BC =, ∴D 为BC 的中点,AD 是ABC 的中线.24. 如图,在平面直角坐标系xOy 中,抛物线23y ax bx =++与x 轴的正、负半轴分别交于点B 、A ,与y 轴交于点C ,已知5AB =,tan 3CAB ∠=,:3:4OC OB =.(1)求该抛物线的表达式;(2)设该抛物线的对称轴分别与x 轴、BC 交于点E 、F ,求EF 的长;(3)在(2)的条件下,联结CE ,如果点P 在该抛物线的对称轴上,当CEP △和CEB 相似时,求点P 的坐标【答案】(1)239344y x x =−++ (2)158EF = (3)P 的坐标为:3,52⎛⎫⎪⎝⎭或39,24⎛⎫ ⎪⎝⎭. 【解析】【小问1详解】解:∵抛物线23y ax bx =++,当0x =,则3y =,即()0,3C ,∵:3:4OC OB =,∴4OB =,即()4,0B ,∵5AB =,∴1OA =,即()1,0A −,设抛物线为()()14y a x x =+−,把()0,3C 代入得:43a −=,解得:34a =−, ∴抛物线的解析式为:()()2339143444y x x x x =−+−=−++. 【小问2详解】∵()1,0A −,()4,0B ,∴抛物线的对称轴为直线14322x −+==,∵()4,0B ,()0,3C ,设直线BC 为3y kx =+,∴430k +=,解得:34k =−, ∴直线BC 为334y x =−+, 当32x =时,33153428y =−⨯+=,即315,28F ⎛⎫ ⎪⎝⎭, ∴158EF =. 【小问3详解】如图,过E 作EH BC ⊥于H ,∵()4,0B ,()0,3C ,3,02E ⎛⎫ ⎪⎝⎭, ∴22345BC =+=,22335322CE ⎛⎫=+= ⎪⎝⎭,35422BE =−=,3sin 5ABC ∠=, ∴35EH BE =,则32EH =,∴32EO EH ==,而90COE CHE ∠=∠=︒, ∴OCE BCE ∠=∠,而OC EF ∥,∴OCE CEF ∠=∠,∴BCE CEF ∠=∠,当CEP △和CEB 相似时,显然CO 与对称轴没有交点,∴P 不在E 的下方,只能在E 的上方,且CEP ∠与BCE ∠是对应角, 当CEB ECP ∽时, ∴1BC CE EP CE==, ∴5EP BC ==, ∴3,52P ⎛⎫ ⎪⎝⎭,当CEB EPC ∽, ∴CE BC EP CE=, ∴352352PE =94PE =, ∴39,24P ⎛⎫ ⎪⎝⎭. 综上:P 的坐标为:3,52⎛⎫⎪⎝⎭或39,24⎛⎫ ⎪⎝⎭. 25. 如图,在Rt ABC △中,90ABC ∠=︒,10AC =,3tan 4C =,点D 是斜边AC 上的动点,连接BD ,EF 垂直平分BD 交射线BA 于点F ,交边BC 于点E .(1)如图,当点D 是斜边AC 上的中点时,求EF 的长;(2)连接DE ,如果DEC 和ABC 相似,求CE 的长;(3)当点F 在边BA 的延长线上,且2AF =时,求AD 的长.【答案】(1)12524EF =(2)327CE =或5CE = (3)16665AD =【解析】 【小问1详解】解:如图,记BD ,EF 的交点为K ,∵10AC =,点D 是斜边AC 上的中点,90ABC ∠=︒, ∴152BD CD AC ===, ∴∠=∠DBC C ,∵EF 垂直平分BD ∴52BK DK ==,90BKF BKE ABC ∠=∠=︒=∠, ∴90BFK BEK BEK EBK ∠+∠=︒=∠+∠,∴BFK DBC C ∠=∠=∠, ∵3tan 4C =, ∴3tan 4EK EBK BK ∠==,3tan 4BK BFK FK ∠==, ∴3515428EK =⨯=,5410233FK =⨯=, ∴151********EF EK FK =+=+=. 【小问2详解】∵90ABC ∠=︒,10AC =,3tan 4C =, ∴3tan 4AB C BC==,设3AB m =,则4BC m =, ∴510AC m ==,解得:2m =,∴6AB =,8BC =,∵DEC 和ABC 相似,如图,当DEC ABC △∽△时,∴DE CE AB CB=, 由垂直平分线的性质可得:8BE DE CE ==−, ∴868CE CE −=,解得:327CE =, 如图,当DEC BAC ∽△△时,∴DE CE AB AC=, ∴8610CE CE −=,解得:5CE =. 【小问3详解】如图,连接DF ,过F 作FT AD ⊥交DA 的延长线于T ,∵4tan tan 3CB FAT CAB AB ∠=∠==, ∴43FT AT =,而2AF =, 同理可得:85FT =,65AT =, 由垂直平分线的性质可得:8FD FB AF AB ==+=, ∴221665TD FD FT =−= ∴166********AD DT AT −=−=−=.。
2023-2024学年上海市闵行区九年级(上)期末数学试卷(一模)(含解析)

2023-2024学年上海市闵行区九年级(上)期末数学试卷(一模)一、选择题:本题共6小题,每小题4分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列命题中,真命题是( )A. 两个直角三角形一定相似B. 两个等腰三角形一定相似C. 两个钝角三角形一定相似D. 两个等边三角形一定相似2.在Rt △ABC 中,∠C =90°,AB =3,AC =2,那么cosA 的值是( )A. 13B. 23C. 53 D. 523.下列说法错误的是( )A. 如果a 与b 都是单位向量,那么|a |=|b |B. 如果ka =0,那么k =0或a =0C. 如果a =−3b (b 为非零向量),那么a +3b =0D. 如果a +b =2c ,a−b =3c (c 为非零向量),那么a 与b 平行4.如图,已知l 1//l 2//l 3,直线l 1,l 2,l 3分别交直线l 4于点A 、B 、C ,交直线l 5于点D 、E 、F ,那么下列比例式正确的是( )A. AC BC =DF EFB. AB DE =BE ADC. ABBC=DF EF D. DFEF =CFBE 5.已知二次函数的解析式为y =−x 2+2x ,下列关于函数图象的说法正确的是( )A. 对称轴是直线x =−1B. 图象经过原点C. 开口向上D. 图象有最低点6.如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的图象经过(1,0),(−3,0),如果实数P表示9a−3b+c的值,实数Q表示−a−b的值,那么P、Q的大小关系为( )A. P>QB. P=QC. P<QD. 无法确定二、填空题:本题共12小题,每小题4分,共48分。
7.计算:10×2−1=______ .8.已知ab =13,那么a+bb=______ .9.计算:(a+b)−(72a−2b)=______ .10.在Rt△ABC中,∠C=90°,如果tanB=2,BC=2,那么AC=______ .11.如图,在△ABC中,点D在边AC上,点E在边BC上,DE//AB,AD:AC=2:3,那么S△DECS梯形ABED的值为______ .12.将抛物线y=x2+4x向上平移2个单位,平移后的抛物线的顶点坐标是______ .13.抛物线y=x2+bx+c的对称轴是直线x=−4,如果点A(0,y1)、B(1,y2)在此抛物线上,那么y1______ y2.(填“>”、“=”或“<”)14.小明沿斜坡坡面向上前进了5米,垂直高度上升了1米,那么这个斜坡的坡比是______ .15.已知反比例函数y=kx(k≠0),如果x1<x2<0,0<y1<y2,那么k______ 0.(填“>”或“<”) 16.“二鸟饮泉”问题中记载:“两塔高分别为30步和20步.两塔之间有喷泉,两鸟从两塔顶同时出发,以相同速度沿直线飞往喷泉中心,同时抵达.喷泉与两塔在同一平面内,求两塔之间的距离.”如图,已知AC⊥AB,BD⊥AB,M是AB上一点,CM=DM,在C处测得点M的俯角为60°,AC=30,BD=20,那么AB=______ .17.新定义:如果等腰三角形腰上的中线与腰的比值为黄金分割数(黄金数),那么称这个等腰三角形为“精准三角形”.如图,△ABC是“精准三角形”,AB=AC=2,CD⊥AB,垂足为点D,那么BD的长度为______ .18.如图,在△ABC中,AB=AC,tanC=3,点D为边BC上的点,4联结AD,将△ABD沿AD翻折,点B落在平面内点E处,边AE交边BC于点F,联结CE,如果AF=3FE,那么tan∠BCE的值为______ .三、解答题:本题共7小题,共78分。
沪科版九年级上册数学期末考试试卷附答案

沪科版九年级上册数学期末考试试题一、选择题。
(每小题只有一个正确答案)1.关于二次函数22y x =--下列说法正确的是()A .有最大值-2B .有最小值-2C .对称轴是1x =D .对称轴是1x =-2.对抛物线y=-x 2+4x-3而言,下列结论正确的是()A .开口向上B .与y 轴的交点坐标是(0,3)C .与两坐标轴有两个交点D .顶点坐标是(2,1)3.点P 1(﹣1,1y ),P 2(3,2y ),P 3(5,3y )均在二次函数22y x x c =-++的图象上,则1y ,2y ,3y 的大小关系是()A .321y y y >>B .312y y y >=C .123y y y >>D .123y y y =>4.如图,在直角坐标系中,△OAB 的顶点为O(0,0),A(-6,4),B(-3,0).以点O 为位似中心,在第四象限内作与△OAB 的位似比为12的位似图形△OCD ,则点C 坐标为()A .(2,-1)B .(3,-2)C .33,22⎛⎫- ⎪⎝⎭D .3,12⎛⎫- ⎪⎝⎭5.如图,点A ,B 分别是反比例函数12y x=-(x <0)和4y x =-(x <0)图象上的点,且AB ∥x 轴,点C 在x 轴上,则△ABC 的面积是()A .4B .5C .6D .86.若ad=bc ,则下列不成立的是()A .a cb d=B .a c ab d b-=-C .a b c db d++=D .1 111a cb d ++=++7.如图,四边形OABC 是矩形,四边形ADEF 是边长为3的正方形,点A ,D 在x 轴的正半轴上,点C 在y 轴的正半轴上,点F 在边AB 上,点B 、E 在双曲线(0)ky x x=>上,且5BF =,则k 值为().A .15B .714C .725D .178.正方形ABCD 中,AB=4,P 为对角线BD 上一动点,F 为射线AD 上一点,若AP=PF ,则△APF 的面积最大值为()A .8B .6C .4D .9.二次函数2(0)y ax bx c a =++≠的图象如图所示,对称轴为1x =-,下列结论不正确的是A .0abc >B .0a b c -+<C .24b ac >D .0a c -<10.如图,在正方形ABCD 和正方形BEFG 中,连接,AG DF ,则DF AG的值为()A .1B .12C 2D .22二、填空题11.抛物线2(2)y x =-+的顶点坐标是_________.12.如图,若芭蕾舞者拍起的脚尖点C 分线段AB 近似于黄金分割(AC <BC),已知AB=160cm ,BC 的长约为_________cm .(结果精确到0.1cm)13.如图,在边长为1的小正方形网格中,点A 、B 、C 均在格点上,则tan ∠B 的值为_________.14.如图,矩形ABCD 中,AB=6,AD=8,点P 是AB 边上一动点,把△ADP 沿DP 折叠得△A DP ',射线DA '交直线AB 于点Q 点.(1)当Q 点和B 点重合时,PQ 长为___________;(2)当△A DC '为等腰三角形时,DQ 长为____________.15.如图,在直角坐标系中,点E (﹣4,2),F (﹣2,﹣2),以O 为位似中心,将△EFO 缩小为△E 'F 'O ,且△E 'F 'O 与△EFO 的相似比为12,则点E 的对应点E '的坐标为_________.16.如图所示,在平面直角坐标系中,正方形OABC 的顶点O 与原点重合,顶点A ,C 分别在x 轴、y 轴上,双曲线ky x(k ≠0,x >0)经过AB 、BC 的中点N 、F ,连接ON 、OF 、NF .若S △BFN =3,则k =__.三、解答题17.计算:2sin 245°-6cos30°+3tan45°+4sin60°18.如图,二次函数y=-212x +bx+c 的图象经过A(2,0)、B(0,-4)两点,(1)求二次函数的解析式;(2)设该二次函数的对称轴与x 轴交于点C ,连接BA 、BC ,求△ABC 的面积.19.一次函数y1=kx+b的图象与反比性函数y2=mx的图象交于A(2,1)、B(-1,n)两点.(1)利用图中的条件,求反比例函数和一次函数的解析式;(2)根据图象直接写出使y1 y2的自变量x取值范围.20.如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,﹣4),B(3,﹣3),C (1,﹣1).(每个小方格都是边长为一个单位长度的正方形)(1)将△ABC沿y轴方向向上平移5个单位,画出平移后得到的△A1B1C1;(2)将△ABC绕点O顺时针旋转90°,画出旋转后得到的△A2B2C2,并求出线段AA2的长度.21.2020年6月23日,我国第55颗北斗卫星,即北斗全球卫星导航系统最后一颗组网卫星发射成功北斗导航装备的不断更新,极大方便人们的出行,某中学从A 地出发.组织学生利用导航到C 地区进行研学活动,出发时发现C 地恰好在A 地正北方向,且距离A 地24千米,由于A 、C 两地间是一块湿地.所以导航显示的路线是沿北偏东60°方向走到B 地,再沿北编西37°方向走一段距离才能到达C 地,求A 、B 两地的距离(精确到1千米).(参考数据sin37°=0.6,cos37°=0.8,tan37°=0.722.已知:如图,在Rt ABC △中,90BAC ∠=︒,AD BC ⊥于D ,E 为直角边AC 的中点,射线ED 交AB 的延长线于点F .(1)若6AB =,8AC =,求BD 长;(2)求证:AB AF AC DF ⋅=⋅.23.如图,在四边形ABCD 中,90,45,3ABC C CD BD︒︒∠=∠===.(1)求sin CBD ∠的值;(2)若3AB =,求AD 的长.24.如图,在ABCD 中,E 是CD 的延长线上一点,BE 与AD 交于点F ,12DE CD =.(1)求证:ABF CEB V V ∽;(2)若DEF 的面积为2,求四边形BCDF 的面积.25.如图,已知抛物线1(1)(5)y a x x =--和直线2y ax a =--(其中0a >)相交于A ,B 两点,抛物线1y 与x 轴交于C ,D 两点,与y 轴交于点G ,直线2y 与坐标轴交点于E ,F 两点.(1)若G 的坐标为(0,5),求抛物线1y 的解析式和直线2y 的解析式;(2)求证:直线2y ax a =--始终经过该抛物线1y 的顶点;(3)求AB EFAF+的值.参考答案1.A 【分析】利用二次函数的性质即可判断各个选项中的结论是否正确.【详解】解:∵二次函数y =﹣x 2﹣2,∴a =﹣1,开口向下,有最大值y =﹣2,∴选项A 正确,选项B 错误;∵二次函数y =﹣x 2﹣2的对称轴为直线x =0,∴选项C 、D 错误,故选:A .【点睛】本题考查了二次函数的性质、二次函数的最值,解题的关键是明确题意,利用二次函数的性质解答.2.D 【分析】根据二次函数的解析式结合二次函数的性质,逐一分析四个选项的正误即可得出结论.【详解】A 、因为a=-1<0,故抛物线开口向下,故本选项不符合题意;B 、当x=0时,y=-3,抛物线与y 轴的交点坐标是(0,-3),故本选项不符合题意;C 、()()24413161240=-⨯-⨯-=-= >,抛物线与x 轴有两个交点,所以与两坐标轴有三个交点,故本选项不符合题意;D 、对抛物线()224321y x x x =-+-=--+,顶点坐标是(2,1),故本选项符合题意;故选:D 【点睛】本题考查了二次函数的性质以及二次函数图象与系数的关系,熟练掌握二次函数图象与系数之间的关系是解题的关键.3.D 【详解】试题分析:∵22y x x c =-++,∴对称轴为x=1,P 2(3,2y ),P 3(5,3y )在对称轴的右侧,y 随x 的增大而减小,∵3<5,∴23y y >,根据二次函数图象的对称性可知,P 1(﹣1,1y )与(3,2y )关于对称轴对称,故123y y y =>,故选D .考点:二次函数图象上点的坐标特征.4.B 【分析】根据关于以原点为位似中心的对应点的坐标关系,把点A 的横纵坐标乘以12-即可得到答案.【详解】∵△OAB 与 OCD 关于原点O 位似,位似比为12,设点C 坐标为(),a b ,点A 坐标为()6,4-,点A 与点C 是对应点,∴()1632a =-⨯-=,1422b =-⨯=-,∴C 点坐标为:(3,-2)故选:B .【点睛】本题考查了位似变换,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或-k .5.A 【分析】先将△ABC 的面积转化成△ABO 的面积,再通过辅助线得S △ABO =S △ADO −S △BDO .【详解】解:连接AO ,BO ,延长AB 交y 轴于点D ,∵AB //x 轴,∴S △ABO =S △ABC ,∴S △ABO =S △ADO −S △BDO =124422-=∴S △ABC =4.故选:A .【点睛】本题考查反比例函数系数k 的几何意义,解题关键是熟练掌握添加辅助线方法.6.D 【分析】根据比例和分式的基本性质,进行各种演变即可得到结论.【详解】A 由a cb d=可以得到ad=bc ,故本选项正确,不符合题意;B 、由a c ab d b-=-可得:(a-c )b=(b-d )a ,即ad=bc ,故本选项正确,不符合题意;C 、由a b c db d ++=可得(a+b )d=(c+d )b ,即ad=bc ,故本选项正确,不符合题意;D 、由1 111a cb d ++=++,可得(a+1)(d+1)=(b+1)(c+1),即ad+a+d=bc+c ,不能得到ad=bc ,故本选项错误,符合题意;故选:D .【点睛】本题考查了比例线段,根据比例的性质能够灵活对一个比例式进行变形.7.C【分析】设AO =a ,即可得出B (a ,8),E (a +3,3),依据点B 、E 在反比例函数(0)k y x x=>的图象上,即可得到a 的值,进而得出k 的值.【详解】解:设AO =a ,∵四边形ADEF 是边长为3的正方形,BF =5,∴AB =8,OD =a +3,∴B (a ,8),E (a +3,3),又∵点B 、E 在反比例函数(0)k y x x =>的图象上,∴8a =3(a +3),解得a =95,∴B (95,8),∴k =95×8=725,故选:C .【点睛】此题主要考查了反比例函数图象上点的坐标特点以及正方形和矩形的性质,反比例函数图象上的点(x ,y )的横纵坐标的积是定值k ,即xy =k .8.C【分析】根据AP=PF 得到点P 在AF 的垂直平分线上,过P 作PG ⊥AF ,G 为垂足,则AG=GF ,DG=PG ,设DF=x ,得到AG=42x +,GD=PG=42x -,利用三角形面积公式计算得到S △APF =2144x -+,根据函数性质即可得到答案.【详解】∵AP=PF ,∴点P 在AF 的垂直平分线上,过P 作PG ⊥AF ,G 为垂足,则AG=GF ,DG=PG ,设DF=x ,则AG=42x +,∴GD=PG=42x -,∴S △APF =2141(4)4224x x x -⨯+⨯=-+≤4,所以△APF 面积最大值为4;故选:C ..【点睛】此题考查正方形的性质,线段垂直平分线的判定及性质,二次函数的最值问题,正确引出辅助线并设定未知数解决问题是解题的关键.9.D【分析】根据二次函数的图象与性质得到a b c 、、的符号,再逐一进行判断.【详解】解:由图知,二次函数的图象开口向上,即0a >,与y 轴交于正半轴,即0c >,对称轴12b x a=-=-2b a∴=a b 、同号,即0b >0abc ∴>,故A 正确;由图知,当1x =-时,0y <,0a b c ∴-+<,故B 正确;由图知,二次函数图象与轴有两个不同的交点,即240b ac ->,故C 正确;无法判断0a c -<,故D 错误,故选:D .【点睛】本题考查二次函数的图象与性质,是基础考点,难度较易,掌握相关知识是解题关键.10.C【分析】连接BD ,BF ,先证明ABG DBF ∽,进而即可求解.【详解】解:连接BD ,BF ,∵在正方形ABCD 和正方形BEFG 中,∴BD AB =BF BG =,∠ABD =∠GBF =45°,∴BD AB =BF BG,∠ABG =∠DBF ,∴ABG DBF ∽,∴DFAG =BF BG =,故选C .【点睛】本题主要考查正方形的性质以及相似三角形的判定和性质,添加辅助线,构造旋转相似模型,是解题的关键.11.()2,0-【分析】已知解析式为顶点式,可直接根据顶点式的坐标特点,求顶点坐标.【详解】2(2)y x =-+是抛物线的顶点式,根据顶点式的坐标特点可知,顶点坐标为()2,0-,故答案为:()2,0-.【点睛】本题考查了二次函数的性质,解题的关键是熟记顶点式2()y a x h k =-+的顶点坐标是()h k ,.12.98.9【分析】由点C 是线段AB 的黄金分割点,可得AC BC BC AB ==可得,BC AB =计算后可得答案.【详解】解:∵C 分线段AB 近似于黄金分割,且AC <BC ,AC BC BC AB ∴==∴)11160801801.23698.9.22BC AB cm -==⨯=≈⨯≈故答案为:98.9.【点睛】本题考查的是黄金分割的含义,掌握“点C 是线段AB 的黄金分割点,可得12AC BC BC AB -==”是解题的关键.13.12【分析】根据在直角三角形中,正切为对边比邻边,可得答案.【详解】解:如图所示,2222222222420,125,3425BD DC BC =+==+==+= ,222BD DC BC ∴+=,90D ∠=︒,BD DC ===,1tan 2DC B BD ==故答案:12【点睛】本题考查了锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.14.103645555或2455【分析】(1)画出点Q 与B 重合时的图象,根据折叠的性质得到相等的边,设PQ x =,则6PA PA x '==-,在Rt PQA ' 中利用勾股定理列式求出结果;(2)分情况讨论,利用等腰三角形“三线合一”的性质,结合相似三角形的性质和判定,列式求出DQ 的长.【详解】解:(1)如图,当点Q 与B 重合时,∵6AB =,8AD =,90A ∠=︒,∴10QD =,∵折叠,∴8AD A D '==,∴1082A Q QD A D ''=-=-=,设PQ x =,∴6PA PA x '==-,∵222PA A Q PQ ''+=,∴()2264x x -+=,解得103x =,故答案是:103;(2)①如图,当A´D=A´C=8时,过点A '作A M DC '⊥于点M ,由等腰三角形“三线合一”的性质得DM=12DC=3,∴A M '=∵//AD A M ',∴ADQ MA D '∠=∠,∵90DAQ A MD '∠=∠=︒,∴AQD MDA ' ,∴QDADDA MA ='',则8QD=55QD =;②如图,当A´C=DC=6时,过点C 作CN DQ ⊥于点N ,由等腰三角形“三线合一”的性质得DN=12DA´=4,∴CN =∵90CDN ADQ ∠+∠=︒,90DQA ADQ ∠+∠=︒,∴DQA CDN ∠=∠,∵90DAQ CND ∠=∠=︒,∴AQD NDC ,∴QD ADDC NC =,则6QD =QD =;③∵8A D AD '==,6DC =,∴A D DC '≠,故答案是:55【点睛】本题考查折叠问题,解题的关键是掌握勾股定理,矩形的性质,折叠的性质,以及相似三角形的性质和判定.15.(﹣2,1)或(2,﹣1)【分析】根据位似变换的性质计算即可.【详解】解:∵以O 为位似中心,将△EFO 缩小为△E 'F 'O ,△E 'F 'O 与△EFO 的相似比为12,∵E (﹣4,2),∴点E '的坐标为:(﹣2,1)或(2,﹣1);故答案为:(﹣2,1)或(2,﹣1).【点睛】本题考查了位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或k -.16.12【分析】先求出点N 坐标,利用待定系数法即可解决问题;【详解】解:∵N 、F 是AB 、BC 的中点,∴BF =12BC ,BN =12AB ,S △BFN =3,∴12BF •BN =12•12BC •12AB =3,∴BC •AB =24,∵四边形ABCO 是正方形,∴OA =AB =BC =CO =,∵N 是AB 中点,∴AN =BN ,∴N (),把N ()代入k y x=,得到k =12,故答案为:12.【点睛】本题考查了反比例函数系数k 的几何意义,正方形的性质,求出点N 坐标是解题的关键.17.4【分析】直接代入特殊角的三角函数值求解即可.【详解】解:原式=22()63142⨯-⨯⨯+⨯13=-+4=-,故答案为:4.【点睛】本题考查了特殊角三角函数的计算,属于基础题,计算过程中细心即可求解.18.(1)21342y x x =-+-;(2)2【分析】(1)由待定系数法即可求出抛物线解析式;(2)由(1)中求出的抛物线的解析式求出该抛物线的对称轴,得到点C 的坐标,通过A 、B 、C 三个点的坐标即可求得ABC 的面积.【详解】(1)分别把点A(2,0)、B(0,-4)代入212y x bx c =-++得,2122024x c c ⎧-⨯++=⎪⎨⎪=-⎩,解得:34b c =⎧⎨=-⎩,∴这个二次函数的解析式为:21342y x x =-+-(2)由(1)中抛物线对称轴为直线,331222b x a =-=-=⎛⎫⨯- ⎪⎝⎭,∴点C 的坐标为:(30),,∴321AC =-=,∴ABC 的面积为:1141222OB AC ⋅⋅=⨯⨯=,【点睛】本题考查了用待定系数法求二次函数、二次函数图像的性质、三角形面积,解题的关键是理解题意,利用二次函数图像的性质求解三角形的面积.19.(1)2,1y y x x==-;(2)1x <-或02x <<【分析】(1)由A 的坐标易求反比例函数解析式,从而求B 点坐标,进而运用待定系数法求一次函数的解析式;(2)观察图象,找出一次函数的图象在反比例函数的图象下方时,x 的取值即可.【详解】(1)由题意得:212m =⨯=,()12n -⨯=,2n =-,∴反比例函数解析式为:2y x=,()1,2B --,再由题意得:212k b k b +=⎧⎨-+=-⎩;解得:11k b =⎧⎨=-⎩∴一次函数的解析式为:1y x =-;(2)由图像可知:当12y y <时,自变量x 取值范围是:1x <-或02x <<.【点睛】本题考查的是反比例函数和一次函数的综合题,掌握利用待定系数法求一次函数、反比例函数的解析式和根据图象求自变量的取值范围是解决此题的关键.20.(1)见解析;(2)见解析;AA2【分析】(1)分别将点A 、B 、C 向上平移5个单位得到对应点,再顺次连接可得;(2)分别将点A 、B 、C 绕点O 顺时针旋转90°得到对应点,再顺次连接可得,再利用勾股定理求得AA 2的长度即可.【详解】(1)如图,△A 1B 1C 1即为所求:(2)如图,△A 2B 2C 2即为所求:连接OA 2,OA 1,由旋转性质得,OA 1=OA 2,∵OA 122(40)(10)--+--17∴AA 22212OA OA +1717+34【点睛】本题主要考查作图-平移变换、旋转变换,解题的关键是熟练掌握平移作图和旋转90°作图.21.14千米【分析】过B 作BD ⊥AC ,由题意得到三角形ABD 为直角三角形,设AD=x 千米,表示出CD 和BD ,在直角三角形BCD 中,利用锐角三角函数定义求出x 的值,即可确定出AB 的长.【详解】解:如图,过点B 作BD ⊥AC 于点D ,设AD=x ,∵∠A=60°,∴3x ,CD=24-x ,AB=2x ;∵∠BCD=37°,∴tan ∠BCD=BD CD ,即324x解得x=7,即AB=2x=14(千米)【点睛】此题属于解直角三角形题型,熟练掌握锐角三角函数定义是解本题的关键.22.(1) 3.6BD =;(2)见解析【分析】(1)由勾股定理得10BC =,C ABD BA ∽△△,得 3.6BD =;(2)首先由直角三角形的性质可得:DE CE AE ==,可得FDB FAD ∽△△,得出DF BD AF AD=,再利用等角的正切相等可得出结论.【详解】解:(1)在Rt ABC △中,∵6AB =,8AC =,∴10BC ===,∵90BAC ∠=︒,AD BC ⊥,∴90BAC ADB ∠==︒∠,∵∠B=∠B ,∴C ABD BA ∽△△,∴BD AB BA CB =,∴236 3.610AB BD CB ===,∴ 3.6BD =;(2)∵DE 是Rt ADC 斜边AC 边上的中线,∴DE CE AE ==,∴∠EAD=∠EDA ,∠C=∠CDE ,∵∠CDA=∠CAF=90°,∴∠CDE=∠FAD=∠C ,∴∠FDB=∠FAD ,∵∠F=∠F ,∴FDB FAD ∽△△,∴DF BD AF AD=,又∵tan tan BD AB DAB C AD AC=∠=∠=,∴DF AB AF AC =,即AB AF AC DF ⋅=⋅.【点睛】此题考查了相似三角形的判定与性质,直角三角形的性质以及锐角三角函数的性质等知识,合性较强,解题时要注意数形结合思想的应用.23.(1)1sin3CBD ∠=;(2)AD =【分析】(1)过点D 作DE BC ⊥于点E ,由三角函数求出1CE DE ==,再根据三角函数即可求出答案;(2)过点D 作DF AB ⊥于点F ,则四边形BEDF 是矩形,根据矩形的性质和勾股定理,即可得到答案.【详解】解:(1)如图,过点D 作DE BC ⊥于点E ,在Rt CED ∆中,∵45,C CD ∠=︒=∴1CE DE ==,在Rt BDE ∆中,1sin 3DE CBD BD ∠==;(2)过点D 作DF AB ⊥于点F ,则90BFD BED ABC ∠=∠=∠=︒,∴四边形BEDF 是矩形,∴1DE BF ==,∵3BD =,∴DF =∵3AB =,∴2AF =,∴AD =【点睛】本题考查了解直角三角形,锐角三角函数,勾股定理,以及矩形的判定和性质,解题的关键是熟练掌握所学的知识,正确利用解直角三角形和锐角三角函数进行解题.24.(1)见解析;(2)16【分析】(1)根据平行四边形的性质,证明两角对应相等,两三角形相似即可.(2)首先证明ABF DEF ∆≅,再证明EFD EBC ∆∆∽,利用相似三角形的性质面积比等于相似比的平方,即可求出EBC ∆的面积,由此即可解决问题.【详解】解:(1) 四边形ABCD 是平行四边形A C ∴∠=∠,//AB CDABF CEB∴∠=∠ABF CEB∴∆∆∽(2)解: 四边形ABCD 是平行四边形,//AD BC ∴,AB 平行且等于CD ,DEF CEB ∴∆∆∽,DEF ABF ∆∆∽,12DE CD = ,∴21()9DEF CEB S DE S CE ∆∆==,2DEF S ∆= ,18CEB S ∆∴=,16BCE DEF BCDF S S S ∆∆∴=-=四边形.【点睛】本题主要考查了平行四边形的性质,相似三角形的判定和性质,熟悉相似三角形的性质和判定是解决问题的关键.25.(1)1(1)(5)y x x =--,21y x =--;(2)见解析;(3)1【分析】(1)根据题意将点(0,5)G 代入抛物线解得1a =由此即可得出答案;(2)根据题意,求出顶点坐标为(3,4)a -.根据顶点和直线解析式2y ax a =--的关系即可证明;(3)过A ,B 两点作x 轴的垂线,垂足分别为M ,N 两点,根据题意可求出(1,0)E -,(2,0)M ,(3,0)N ,由////OF AM BN ,可得::::EF FA AB EO OM MN =,即可得出结论;【详解】解:(1)∵点(0,5)G 在该抛物线上,∴5(1)(5)a =-⨯-,∴1a =,所以抛物线解析式为:1(1)(5)y x x =--直线解析式为21y x =--(2)证明:令1(1)(5)y a x x =--=0解得:x 1=1,x 2=5所以与x 轴交点为(1,0)和(5,0),所以其对称轴为直线3x =,顶点坐标为(3,4)a -.当x=3时,234y a a a =--=-,∴2y 经过点(3,4)a -,所以直线2y ax a =--始终经过该抛物线的顶点.(3)过A ,B 两点作x 轴的垂线,垂足分别为M ,N 两点,令2y ax a =--=0,解得1x =-,即(1,0)E -,联立两个解析式12(1)(5)y a x x y ax a=--⎧⎨=--⎩得(1)(5)a x x ax a --=--,解得12x =,23x =,所以(2,0)M ,(3,0)N ,∵////OF AM BN∴::::1:2:1EF FA AB EO OM MN ==,∴1EF AB AF+=【点睛】本题主要考查了抛物线与一次函数及平行线分线段成比例的综合运用,熟练掌握相关概念是解题关键.。
2022-2023学年沪教版(上海)九年级第一学期数学期末复习试卷 (含答案)

2022-2023学年沪教版九年级上册数学期末复习试卷一.选择题(共6小题,满分24分,每小题4分)1.在比例尺为1:1000000的地图上,相距3cm的两地,它们的实际距离为()A.3km B.30km C.300km D.3000km2.如果将抛物线向右平移2个单位后得到y=x2,那么原抛物线的表达式是()A.y=x2+2B.y=x2﹣2C.y=(x+2)2D.y=(x﹣2)2 3.已知非零向量和单位向量,那么下列结论中,正确的是()A.B.C.D.4.已知P,Q是线段AB的两个黄金分割点,且AB=10,则PQ长为()A.5(﹣1)B.5(+1)C.10(﹣2)D.5(3﹣)5.如图,在离铁塔100米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.4米,则铁塔的高BC为()米.A.1.4+B.1.4+100tanαC.1.4+D.1.4+100sinα6.如图,△ABC中,DE∥BC,则下列等式中不成立的是()A.=B.=C.=D.=二.填空题(共12小题,满分48分,每小题4分)7.如果向量、、满足(+)=﹣,那么=(用向量、表示).8.如图,在边长为1的正方形网格中,连接格点D、N和E、C,DN和EC相交于点P,tan ∠CPN为.9.如图,正方形ABCD的边长是10cm,E是AB上一点,F是AD延长线上的一点,BE=DF.四边形AEGF是矩形,矩形AEGF的面积y(cm2)与BE的长xcm(0<x≤10)的函数关系是.10.请任写一个二次函数解析式,使这个函数的图象具备以下两个特点:①开口向上;②对称轴为y轴.这个函数可以是.11.已知锐角α的终边经过点P(x,2),点P到坐标原点的距离r=,则sinα=,cosα=.12.如图,平行四边形ABCD中,F为BC中点,延长AD至E,使DE:AD=1:3,连结EF交DC于点G,若△DEG的面积是1,则五边形DABFG的面积是.13.关于二次函数y=3x²+1和y=3(x﹣1)²,以下说法:①它们的开口方向、大小相同;②它们的对称轴都是y轴,顶点坐标都是(0,1);③当x>2时,它们的函数值都是y随x的增大而增大;④它们与坐标轴都有一个交点,其中正确的有.(填序号)14.如图,已知在△ABC中,∠ACB=90°,点G是△ABC的重心,CG=2,BC=4,那么cos∠GCB=.15.如图,在平行四边形ABCD中,=,=,则向量为.(结果用和表示16.如图,在矩形ABCD中,点E在边BC上,BE=3EC,点F在边DC上,CF=2DF,EF与AC交于点G.如果△GEC的面积等于2cm2,那么矩形ABCD的面积等于cm2.17.如图,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4)和B(8,2),若无论x取何值,S总取y1,y2中的最大值,则S的最小值是.18.如图,点D是等边△ABC边BC上一点,将等边△ABC折叠,使点A与点D重合,折痕为EF(点E在边AB上).(1)当点D为BC的中点时,AE:EB=;(2)当点D为BC的三等分点时,AE:EB=.三.解答题(共7小题,满分78分)19.(10分)计算:(1)2sin30°﹣3cos60°;(2)cos245°+tan245°﹣tan260°.20.(10分)如图所示,在▱ABCD中,点M是AB的中点,CM与BD相交于点N,设,(1)试用向量、表示;(2)试用向量、表示.21.(10分)在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度,他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进60米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.(参考数据:sin37°≈,tan37°≈,sin21°≈,tan21°≈)22.(10分)如图,在△ABC中,∠ACB=90°,cos A=,BC=12,D是AB的中点,过点B作直线CD的垂线,垂足为点E.求:(1)线段CD的长;(2)cos∠ABE的值.23.(12分)已知:如图,在△ABC中,ED∥BC,EF∥BD,求证:AD2=AF•AC.24.(12分)如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=a(x+6)(x﹣4)(a>0)交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴的负半轴于点C,连接AC、BC,∠BAC=2∠BCO.(1)求a的值;(2)如图2,点P在第二象限的抛物线上,横坐标为t,连接BP交y于点D,连接AD,△ABD的面积为s,求s与t之间的函数关系式;(3)如图3,在(2)的条件下,点Q在第三象限的抛物线上,横坐标为m,点R在第一象限的抛物线上,横坐标为4﹣m,连接QR,交x轴于点E(2,0),过Q点作QG ⊥PB于点G.过点R作RH⊥PB于点H,且QG=GH+RH.求点D的坐标.25.(14分)如图,在矩形ABCD中,AB=8,BC=4,点P为AB边上一动点(不与点A,B重合),DP交AC于点E.(1)求证:△APE∽△CDE.(2)当PD⊥AC时,求线段PA的长度.(3)当点P在线段AC的垂直平分线上时,求的值.参考答案与试题解析一.选择题(共6小题,满分24分,每小题4分)1.解:3÷=3000000(cm),3000000cm=30km.故选:B.2.解:∵将抛物线向右平移2个单位后得到y=x2,∴抛物线y=x2向左移2个单位得原函数解析式y=(x+2)2,故选:C.3.解:A、,不符合题意;B、不一定成立,因为非零向量和单位向量的方向不一定相同,不符合题意;C、,符合题意;D、不一定成立,因为非零向量和单位向量的方向不一定相同,不符合题意.故选:C.4.解:如图根据黄金分割点的概念,可知==,∵AB=10,∴AQ=PB=×10=﹣5.又∵PQ=AQ+PB﹣AB,∴PQ=﹣10==10(﹣2).故选:C.5.解:过点A作AE⊥BC,E为垂足,如图所示:则四边形ADCE为矩形,AE=CD=100米,∴CE=AD=1.4米,在△ABE中,∵tanα==,∴BE=100tanα,∴BC=CE+BE=(1.4+100tanα)(米),故选:B.6.解:∵DE∥BC,∴△ADE∽△ABC,∴,∴选项A,C,D成立,故选:B.二.填空题(共12小题,满分48分,每小题4分)7.解:∵(+)=﹣,∴,∴,故答案为:.8.解:连接格点MN、DM,如图所示:则四边形MNCE是平行四边形,△DAM和△MBN都是等腰直角三角形,∴EC∥MN,∠DMA=∠NMB=45°,DM=AD=2,MN=BM=,∴∠CPN=∠DNM,∴tan∠CPN=tan∠DNM,∵∠DMN=180°﹣∠DMA﹣∠NMB=180°﹣45°﹣45°=90°,∴tan∠CPN=tan∠DNM===2,故答案为2.9.解:∵AB=AD=10cm,BE=DF=xcm,∴AE=AB﹣BE=(10﹣x)cm,AF=AD+DF=(10+x)cm,∴矩形AEGF的面积y=(10﹣x)(10+x)=100﹣x2,故答案为:y=100﹣x2.10.解:∵抛物线的对称轴为y轴,∴该抛武线的解析式为y=ax2+c,又∵二次函数的图象开口向上,∴a>0,∴这个二次函数的解析式可以是y=2x2﹣1,故答案为:y=2x2﹣1(答案不唯一).11.解:∵点P(x,2)到坐标原点的距离r=,∴x2+22=()2,解得x=3,∴sinα==,cosα==.故答案为:;.12.解:如图,连接BG,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠E=∠CFG,∵F为BC中点,∴FC=BC=AD,∵DE :AD =1:3,∴DE :BC =1:3,∴DE :CF =2:3,∵∠E =∠CFG ,∠DGE =∠CGF ,∴△DGE ∽CGF ,∴DG :CG =DE :CF =2:3,∴S △DEG :S △CFG =4:9=1:S △CFG ,∴S △CFG =,取AD 的中点Q ,连接FQ ,∴FQ ∥DG ,∴△EDG ∽△EQF ,∴DE :EQ =1:2.5=2:5,∴S △DEG :S △QEF =4:25=1:S △EQF ,∴S △EQF =,∴S 四边形DQFG =﹣1=,∴S 四边形ABFQ =S 四边形DQFG +S △CFG =+=, ∴S 五边形DABFG =+=. 故答案为:. 13.解:∵二次函数y =3x ²+1和y =3(x ﹣1)²,a =3,∴它们的开口方向、大小相同,故①正确;二次函数y =3x ²+1的对称轴是直线x =0,顶点坐标为(0,1),y =3(x ﹣1)²的对称轴是直线x =1,顶点坐标为(1,0),故②错误;当x >2时,它们的函数值都是y 随x 的增大而增大,故③正确;二次函数y =3x ²+1与坐标轴有一个交点(0,1),y =3(x ﹣1)²与坐标轴有两个交点,坐标为(0,3),(1,0),故④错误;故答案为:①③.14.解:延长CG交AB于D,如图,∵点G是△ABC的重心,∴DG=CG=1,AD=BD,∵∠ACB=90°,∴CD=BD=AD=2+1=3,∴AB=6,∠DCB=∠B,在Rt△ACB中,cos B===,∴cos∠GCB=.故答案为.15.解:在平行四边形ABCD中,AO=AC.∵=,=,∴=+=+,∴==.故答案是:.16.解:如图,过点F作FH∥AD,∵四边形ABCD是矩形,∴AD =BC ,AD ∥BC ,∴FH ∥BC ∥AD ,∴△CHF ∽△CAD ,△FHG ∽△ECG .∵BE =3EC ,∴设EC =x ,则BE =3x ,BC =AD =4x ,∵△CHF ∽△CAD ,CF =2DF , ∴==, ∴=,∴HF =, ∵△FHG ∽△ECG , ∴=, ∴==, ∴==,==,∵△GEC 的面积等于2cm 2,∴S △FHG =×2=(cm 2),S △FGC =×2=(cm 2), ∴S △CFH =+=(cm 2), ∵△CHF ∽△CAD ,==, ∴=,∴S △CAD =×=44(cm 2),∴矩形ABCD 的面积为:2S △CAD =2×44=88(cm 2).故答案为:88.17.解:当x ≤﹣2时,S =ax 2+bx +c ,S 最小值为4,当﹣2<x <8时,S =kx +m ,2<S <4,当x ≥8时,S =ax 2+bx +c ,S 最小值为2,∴S的最小值为2,故答案为:2.18.解:(1)如图,连接AD,∵D为BC的中点,△ABC为等边三角形,折叠,∴AD⊥BC,∠DAB=∠DAC=,∠B=60°,∴∠EDB=90°﹣30°=60°=∠B,∴△BED为等边三角形,∴AE=ED=BE,即AE:EB=1:1,故答案为:1:1;(2)当DC:BD=1:2时,设CD=k,BD=2k,∴AB=AC=3k,∵△ABC为等边三角形,∴∠EDF=∠A=60°,∴∠EDB+∠FDC=∠BED+∠EDB=120°,∴∠BED=∠FDC,∵∠B=∠C=60°,∴△BED∽△CDF,∴,∴,∴BE=,AE=3k﹣=,∴AE:BE=7:5,当DC:BD=2:1时,设CD=2k,BD=k,同上一种情况得:,∴,∴BE=,AE=3k﹣=,∴AE:BE=7:8,故答案为:7:5或7:8.三.解答题(共7小题,满分78分)19.解:(1)2sin30°﹣3cos60°=2×﹣3×=1﹣=﹣;(2)cos245°+tan245°﹣tan260°=()2+12﹣()2=+1﹣3=﹣.20.解:(1)∵,,∴=﹣=﹣.∵在▱ABCD中,AD=BC,AD∥BC,∴=.又点M是AB的中点,∴MB=AB=.∴==.∴=+=+.(2)∵在平行四边形ABCD中,DC∥AB,BM=AB=CD,∴==.∴DN=2BN.∴DN=BD.∴=﹣=(﹣).同理,=.∵=+=+,∴=(+)=+.21.解:由题意知CD⊥AD,EF∥AD,∴∠CEF=90°.设CE=x米,在Rt△CEF中,tan∠CFE=,∴EF==≈x(米),在Rt△CEG中,tan∠CGE=,∴GE==≈x(米),∵EF=FG+EG,∴x=60+x,解得:x=45,∴CD=CE+ED=45+1.5=46.5(米).答:古塔的高度约是46.5米.22.解:(1)在△ABC 中,∵∠ACB =90°,∴cos A ==,∴可以假设AC =3k ,AB =5k ,则BC =4k ,而BC =12,∴k =3,∴AB =15∵D 是AB 中点,∴CD =AB =.(2)在Rt △ABC 中,∵AB =15,BC =12,AC =9,∵D 是AB 中点,∴BD =,S △BDC =S △ADC , ∴S △BDC =S △ABC ,即CD •BE =•AC •BC ,∴BE ==,在Rt △BDE 中,cos ∠ABE ===,即cos ∠ABE 的值为.23.证明:∵ED ∥BC ,∴△AED ∽△ABC , ∴, ∵EF ∥BD ,∴△AEF ∽△ABD , ∴, ∴,∴AD2=AF•AC.24.解:(1)∵抛物线y=a(x+6)(x﹣4)(a>0),当y=0时,解得:x1=﹣6,x2=4,∴A(﹣6,0),B(4,0),∴OA=6,OB=4,∴AB=OA+OB=6+4=10,∵∠BAC=2∠BCO,设:∠BAC=2∠BCO=2α,∴∠OCA=90°﹣∠OAC=90°﹣2α,∠OBC=90°﹣∠OCB=90°﹣α,∴∠ACB=∠OCA+∠OCB=90°﹣2α+α=90°﹣α,∴∠ACB=∠OBC,∴AC=AB=10,∴由勾股定理得:,∴C(0,﹣8),∵将C(0,﹣8)代入y=a(x+6)(x﹣4)(a>0),∴﹣8=a(0+6)(0﹣4),解得.(2)解:如图2,过点P作PE⊥x轴于点E,∵∠PEB=∠DOB=90°,∠PBE=∠DBO,∴△PBE∽△DBO,∴,∵点P在第二象限的抛物线上,横坐标为t,∴点P的纵坐标,∴OE=|t|=﹣t,,∴BE=4﹣t,∴,解得,∴,∴;(3)解:抛物线解析式,作QS⊥x轴于S,横坐标为m,则,作RL⊥x轴于L,横坐标为4﹣m,E(2,0),则OL=4﹣m,OE=2,∴EL=OL﹣OE=2﹣m,ES=2﹣m,∴EL=ES,又∵∠QSE=∠RLE=90°,∠SEQ=∠REL(对顶角),∴△ERL≌△EQS(ASA),∴RL=QS,∴,解得m1=6(舍),m2=﹣2,∴Q(﹣2,﹣8),R(6,8),在GP上截取GK,使得GK=RH,又∵QG=GH+RH=GH+GK∴KH=QG,连接KR、KQ,∵QG⊥PB,RH⊥PB,∴∠KGQ=∠RHK=90°,∴△KGQ≌△RHK,∴QK=RK,∠QKG=∠KRH,又∵∠RKH+∠KRH=90°,∴∠QKR=∠QKG+∠RKG=90°,∴△KQR是等腰直角三角形,过点K作KN⊥QS于N,交RL于M,∴∠QNK=∠KMR=90°,∵∠RKM+∠KRM=90°,∠QKR=∠QKM+∠RKM=90°,∴∠QKM=∠KRM,∴△QKN≌△KRM(AAS),设:ML=q,则RM=8﹣q=KN,NM=SL=8,∴KM=KN+NM=16﹣q,QN=8+q,∵KM=QN,∴16﹣q=8+q,解得q=4,∴K(﹣6,4),∵K(﹣6,4),B(4,0)在直线BP上,设直线BP的解析式:y=kx+b∴,解得,∴直线BP的解析式为:,令x=0,得,∴.25.(1)证明:如图1,∵四边形ABCD是矩形,∴AB∥CD,∴∠PAE=∠DCE,∠APE=∠CDE,∴△APE∽△CDE;(2)解:如图1,∵PD⊥AC,∴∠ACD+∠EDC=90°,∵四边形ABCD是矩形,∴∠ADC=∠PAD=90°,DA=BC,BA=DC,∴∠EDA+∠EDC=90°,∴∠ACD=∠EDA,∴△ADC∽△PAD,∴=,即=,∴PA=2;(3)如图2,当点P在线段AC的垂直平分线上时,连接PC,则PA=PC,设PA为x,∵∠B=90°,∴PB2+BC2=PC2,∴(8﹣x)2+42=x2,解得:x=5,∴==.。
上海初三初中数学期末考试带答案解析

上海初三初中数学期末考试班级:___________ 姓名:___________ 分数:___________一、选择题1.对一个图形进行放缩时,下列说法中正确的是()A.图形中线段的长度与角的大小都会改变;B.图形中线段的长度与角的大小都保持不变;C.图形中线段的长度保持不变、角的大小可以改变;D.图形中线段的长度可以改变、角的大小保持不变.2.已知点C是线段AB上的一个点,且满足,则下列式子成立的是……()A.;B.;C.;D.3.下列关于抛物线和的关系说法中,正确的是()A.它们的形状相同,开口也相同;B.它们都关于轴对称;C.它们的顶点不相同;D.点(,)既在抛物线上也在上4.下列关于向量的说法中,不正确的是()A.;B.;C.若,则或;D..5.已知、都是锐角,如果,那么与之间满足的关系是()A.;B.°;C.°;D.°.6.如图,平行四边形ABCD中,F是CD上一点,BF交AD的延长线于G,则图中的相似三角形对数共有()A.8对;B.6对;C.4对;D.2对.二、填空题1.已知a:b=3:2,则(a-b):a= .2.如图,已知AD∥BE∥CF,它们依次交直线、于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC= .3.在Rt△ABC和Rt△DEF中,∠ C=∠ F=90°,当AC=3,AB=5,DE=10,EF=8时,Rt△ABC和Rt△DEF是的.(填“相似”或者“不相似”)4.如果两个相似三角形的对应边上的高之比是2:3,则它们的周长比是5.化简:.6.如图,某人在塔顶的P处观测地平面上点C处,经测量∠ P=35°,则他从P处观察C处的俯角是度.7.将二次函数的图像向下平移1个单位后,它的顶点恰好落在轴上,则.8.在Rt△ABC中,∠C=90°,CD⊥AB于点D,若AD=9,BD=4,则AC= .9.一个边长为3厘米的正方形,若它的边长增加厘米,面积随之增加平方厘米,则关于的函数解析式是.(不写定义域)10.如图,在平行四边形ABCD中,AB=12,AD=18,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=,则△CEF的周长是.11.如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠ B的正切值为.12.如图,已知等腰△ABC,AD是底边BC上的高,AD:DC=1:3,将△ADC绕着点D旋转,得△DEF,点A、C分别与点E、F对应,且EF与直线AB重合,设AC与DF相交于点O,则= .三、解答题1.已知:抛物线经过A(,0)、B(5,0)两点,顶点为P.求:(1)求b,c的值;(2)求△ABP的面积;(3)若点C(,)和点D(,)在该抛物线上,则当时,请写出与的大小关系.2.已知:如图7, EF是△ABC的中位线,设,.(1)求向量、(用向量、表示);(2)在图中求作向量在、方向上的分向量.(不要求写作法,但要指出所作图中表示结论的向量)3.如图,在夕阳西下的傍晚,某人看见高压电线的铁塔在阳光的照射下,铁塔的影子的一部分落在小山的斜坡上,为了测得铁塔的高度,他测得铁塔底部B到小山坡脚D的距离为2米,铁塔在小山斜坡上的影长DC为3.4米,斜坡的坡度,同时他测得自己的影长NH﹦336cm,而他的身长MN为168cm,求铁塔的高度.4.已知:如图9,在△ABC中,已知点D在BC上,联结AD,使得,DC=3且﹦1﹕2.(1)求AC的值;(2)若将△ADC沿着直线AD翻折,使点C落点E处,AE交边BC于点F,且AB∥DE,求的值.5.小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:(1)如图1,已知锐角△ABC.求证:;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时,?6.已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP//AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.(1)求证:△ADE∽△ACB;(2)设CD=x,BAE = y,求y关于x的函数解析式,并写出它的定义域;(3)如果△COD与△BEA相似,求CD的值.上海初三初中数学期末考试答案及解析一、选择题1.对一个图形进行放缩时,下列说法中正确的是()A.图形中线段的长度与角的大小都会改变;B.图形中线段的长度与角的大小都保持不变;C.图形中线段的长度保持不变、角的大小可以改变;D.图形中线段的长度可以改变、角的大小保持不变.【答案】D.【解析】根据相似图形的性质得出相似图形的对应边成比例,对应角相等,即可得出答案.根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,∴对一个图形进行收缩时,图形中线段的长度改变,角的大小不变,故选D.【考点】相似图形.2.已知点C是线段AB上的一个点,且满足,则下列式子成立的是……()A.;B.;C.;D.【答案】B.【解析】把AB当作已知数求出AC,求出BC,再分别求出各个比值,根据结果判断即可.AC2=BC•AB,AC2-BC•AB=0,AC2-(AB-AC)AB=0,AC2+AB•AC-AB2=0,AC=,∵边长为正值,∴AC=AB,BC=AB-AC=,∴,即选项A、C、D错误,只有选项B正确;故选B.【考点】黄金分割.3.下列关于抛物线和的关系说法中,正确的是()A.它们的形状相同,开口也相同;B.它们都关于轴对称;C.它们的顶点不相同;D.点(,)既在抛物线上也在上【答案】B.【解析】根据抛物线y=ax2的性质直接回答即可.根据两个函数知道其二次项系数a的绝对值相等,所以开口方向相反,都关于y轴对称,顶点都为原点,故A、C错误,B正确,故选B.【考点】二次函数的性质.4.下列关于向量的说法中,不正确的是()A.;B.;C.若,则或;D..【答案】C.【解析】由平面向量的定义与运算,可求得答案,注意掌握排除法在选择题中的应用.A、2( + )=2+2,故本选项正确;B、|2|=2||,故本选项正确;C、若||=2||,无法判定与的关系,因为向量有方向性;故本选项错误;D、m(n)=(mn),故本选项正确.故选C.【考点】平面向量.5.已知、都是锐角,如果,那么与之间满足的关系是()A.;B.°;C.°;D.°.【答案】B.【解析】根据α、β都是锐角,sinα=cosβ,可得α、β互为余角.∵α、β都是锐角,如果sinα=cosβ,sinα=cos(90°-α)=cosβ,∴α+β=90°,故选:B.【考点】互余两角三角函数的关系.6.如图,平行四边形ABCD中,F是CD上一点,BF交AD的延长线于G,则图中的相似三角形对数共有()A.8对;B.6对;C.4对;D.2对.【答案】B.【解析】根据平行四边形的性质,得到平行四边形的对边平行,即AD∥BC,AB∥CD;再根据相似三角形的判定方法:平行于三角形一边的直线与三角形另两边或另两边的延长线所构成的三角形相似,进而得出答案.∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴△BEC∽△GEA,△ABE∽△CEF,△GDF∽△GAB,△DGF∽△BCF,∴△GAB∽△BCF,还有△ABC≌△CDA(是特殊相似),∴共有6对.故选:C.【考点】1.相似三角形的判定;2.平行四边形的性质.二、填空题1.已知a:b=3:2,则(a-b):a= .【答案】.【解析】根据比例关系即可得到答案.∵a:b=3:2∴(a-b):a=(3-2):3=1:3【考点】比例关系.2.如图,已知AD∥BE∥CF,它们依次交直线、于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC= .【答案】15【解析】根据平行线分线段成比例定理得出AB:BC="DE:EF=3:5" ,再根据BC=AC×代入计算即可.解;∵AD∥BE∥CF,∴AB:BC="DE:EF=3:5" ,∵AC=24,∴BC=24×=15,故答案为:15.【考点】平行线分线段成比例.3.在Rt△ABC和Rt△DEF中,∠ C=∠ F=90°,当AC=3,AB=5,DE=10,EF=8时,Rt△ABC和Rt△DEF是的.(填“相似”或者“不相似”)【答案】相似.【解析】首先利用勾股定理得出BC,DF的长,进而利用相似三角形的判定得出即可.如图所示:∵AC=3,AB=5,DE=10,EF=8,∴BC==4,DF==6,∴AC:DF="CB:EF=1:2" ,∵∠C=∠F=90°,∴Rt△ABC∽Rt△DEF.故答案为:相似.【考点】相似三角形的判定.4.如果两个相似三角形的对应边上的高之比是2:3,则它们的周长比是【答案】2:3【解析】根据相似三角形周长的比等于相似比进行解答即可.∵两个相似三角形的相似比为2:3,∴它们对应周长的比为2:3.故答案为:2:3.【考点】相似三角形的性质.5.化简:.【答案】.【解析】直接利用三角形法则求解,即可求得答案.【考点】平面向量6.如图,某人在塔顶的P处观测地平面上点C处,经测量∠ P=35°,则他从P处观察C处的俯角是度.【答案】55.【解析】过P作平行于地平面的直线PO,根据∠P=35°,可得∠CPO=90°-∠P=55°,继而可得从P处观察C处的俯角为55°.过P作平行于地平面的直线PO,∵∠P=35°,∴∠CPO=90°-∠P=55°,∵从P处观察C处的俯角即为∠CPO,∴从P处观察C处的俯角为55°.故答案为:55.【考点】解直角三角形的应用-仰角俯角问题.7.将二次函数的图像向下平移1个单位后,它的顶点恰好落在轴上,则.【答案】2.【解析】把二次函数解析式整理成顶点式形式,再根据向下平移横坐标不变,纵坐标减写出平移后的解析式,然后根据顶点在x轴上,纵坐标为0列式计算即可得解.y=x2-2x+m=(x-1)2+m-1,∵图象向下平移1个单位,∴平移后的二次函数解析式为y=(x-1)2+m-2,∵顶点恰好落在x轴上,∴m-2=0,解得m=2.故答案为:2.【考点】二次函数图象与几何变换.8.在Rt△ABC中,∠C=90°,CD⊥AB于点D,若AD=9,BD=4,则AC= .【答案】.【解析】根据题意画出图形,先根据相似三角形的判定定理得出△ACD∽△CBD,再由相似三角形的对应边成比例求出CD的长,根据勾股定理即可得出AC的长如图所示:∵Rt△ABC中∠C=90°,CD⊥AB,∴∠A+∠B=90°,∠A+∠ACD=90°,∠B+∠BCD=90°,∴∠A=∠BCD,∴△ACD∽△CBD,∴CD:AD="BD:CD" ,即CD2=AD•BD=9×4=36,解得CD=6,在Rt△ACD中,∵AD=9,CD=4,∴AC===5.故答案为:5.【考点】相似三角形的判定与性质;射影定理.9.一个边长为3厘米的正方形,若它的边长增加厘米,面积随之增加平方厘米,则关于的函数解析式是.(不写定义域)【答案】.【解析】首先表示出原边长为3厘米的正方形面积,再表示出边长增加x厘米后正方形的面积,再根据面积随之增加y平方厘米可列出方程.原边长为3厘米的正方形面积为:3×3=9(平方厘米),边长增加x厘米后边长变为:x+3,则面积为:(x+3)2平方厘米,∴y=(x+3)2-9=x2+6x.故答案为:y=x2+6x.【考点】根据实际问题列二次函数关系式.10.如图,在平行四边形ABCD中,AB=12,AD=18,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=,则△CEF的周长是.【答案】16.【解析】先计算出△ABE的周长,然后根据相似比的知识进行解答即可.∵在▱ABCD中,AB=CD=12,AD=BC=18,∠BAD的平分线交BC于点E,∴△ADF是等腰三角形,AD=DF=18;∵AB=BE=12,∴CF=6;∴在△ABG中,BG⊥AE,AB=12,BG=,可得:AG=4,又∵BG⊥AE,∴AE=2AG=8,∴△ABE的周长等于32,又∵▱ABCD,∴△CEF∽△BEA,相似比为1:2,∴△CEF的周长为16.故答案为16.【考点】1.相似三角形的判定与性质;2.等腰三角形的判定与性质;3.平行四边形的性质.11.如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠ B的正切值为.【答案】.【解析】连接AG并延长交BC于点H,因为点G是Rt△ABC的重心,所以BH=CH,AG:AH=2:3,再由相似三角形的判定定理可知△AGE∽△AHC,故可得出GE:CH=AE:AC=2:3,设GE=2x,则CH=3x,再根据GF:GE=1:2可知,GF=HF=x,由于四边形GECF是矩形,故CE=GF=x,所以AC=2CE=3x,根据tan∠B=即可得出结论.连接AG并延长交BC于点H,∵点G是Rt△ABC的重心,∴BH=CH,AG:AH ="2:3" ,∵GE∥BC,∴△AGE∽△AHC,∴GE:CH="AE:AC=2:3" ,设GE=2x,则CH=3x,BC=6x,∵GF:GE=1:2,∴GF=HF=x,∵四边形GECF是矩形,∴CE=GF=x,∴AC=2CE=3x,∴tan∠B=.【考点】三角形的重心.12.如图,已知等腰△ABC,AD是底边BC上的高,AD:DC=1:3,将△ADC绕着点D旋转,得△DEF,点A、C分别与点E、F对应,且EF与直线AB重合,设AC与DF相交于点O,则= .【答案】.【解析】如图,作DG⊥AB于G,DH⊥AC与H,设AD=x,则BD=3x,由勾股定理就可以求出AB=x,由三角形的面积公式求出DG的值,由三角函数值求出AG,就可以表示出AE,从而求出AF,再由△AFO∽△DCO就可以求出结论.解答:解:作DG⊥AB于G,DH⊥AC与H,∵AB=AC,AD⊥BC,∴∠ADB=∠ADC=90°,∠BAD=∠CAD,∠B=∠C.∴DG=DH.设设AD=x,则BD=3x,由勾股定理,得AB=x,∴AC=x.∴,∴,∴GD=.∵ =tan∠C.∴tan∠B=.∵∠ADG+∠GAD=90°,∠B+∠GAD=90°,∴∠ADG=∠B.∴tan∠ADG=,∴,∴AG=x.∵△FDE是由△CDA旋转得来的,∴△FDE≌△CDA,∴DE=DA.∠F=∠C.∵DG⊥AB,∴AG=EG.∴AE=2AG,∴AE=.∴AF= .∵∠AOF=∠DOC,∠F=∠C,∴△AFO∽△DCO,∴S△AOF:S△DOC==.故答案为:.【考点】旋转的性质.三、解答题1.已知:抛物线经过A(,0)、B(5,0)两点,顶点为P.求:(1)求b,c的值;(2)求△ABP的面积;(3)若点C(,)和点D(,)在该抛物线上,则当时,请写出与的大小关系.【答案】(1)b=4,c=5;(2)△ABP的面积=27;(3)< .【解析】(1)利用交点式得到y=-(x+1)(x-5),然后展开即可得到b和c的值;(2)先把抛物线的解析式配成顶点式得到P点坐标为(2,9),然后根据三角形面积公式计算即可;(3)由于抛物线的对称轴为直线x=2,开口向下,则根据二次函数的性质可确定y1与y2的大小关系.试题解析:(1)把点A(,0)、B(5,0)分别代入,得解得.(2)由(1)得抛物线解析式∴∴P(2,9)∵A(,0)、B(5,0)∴AB=6∴.(3)∵抛物线开口向下∴在对称轴直线x=2的左侧y随着x的增大而增大∴<.【考点】1.待定系数法求二次函数解析式;2.二次函数图象上点的坐标特征.2.已知:如图7, EF是△ABC的中位线,设,.(1)求向量、(用向量、表示);(2)在图中求作向量在、方向上的分向量.(不要求写作法,但要指出所作图中表示结论的向量)【答案】(1) (2)略.【解析】(1)由EF是△ABC的中位线,设=,=,利用三角形的中位线的性质,即可求得,然后由三角形法则,求得;(2)利用平行四边形法则,即可求得向量在、方向上的分向量.试题解析:(1)∵EF是△ABC的中位线∴EF∥BC,EF=∵∴∵,∴.(2)所以、是在和方向上的分向量.【考点】平面向量.3.如图,在夕阳西下的傍晚,某人看见高压电线的铁塔在阳光的照射下,铁塔的影子的一部分落在小山的斜坡上,为了测得铁塔的高度,他测得铁塔底部B到小山坡脚D的距离为2米,铁塔在小山斜坡上的影长DC为3.4米,斜坡的坡度,同时他测得自己的影长NH﹦336cm,而他的身长MN为168cm,求铁塔的高度.【答案】AB=4.1米 .【解析】作AC的延长线交BD的延长线于E,作CF⊥DE,垂足为F.利用勾股定理和相似三角形的性质求出DF,FE,从而得到BE的长,再用相似三角形的性质求出AB即可.试题解析:过点C作CE⊥BD于点E,延长AC交BD延长线于点F在Rt△CDE中,∴设CE="8x" ,DE="15x" ,则CD=17x∵DC=3.4米∴CE=1.6米,DE=3米在Rt△MNH中,tan∠MHN∴在Rt△ABF中,tan∠F tan∠MHN∴EF=3.2米即BF=2+3+3.2=8.2米∴在Rt△CEF中,tan∠F∴AB=4.1米答:铁塔的高度是4.1米.【考点】1.解直角三角形的应用-坡度坡角问题;2.相似三角形的应用.4.已知:如图9,在△ABC中,已知点D在BC上,联结AD,使得,DC=3且﹦1﹕2.(1)求AC的值;(2)若将△ADC沿着直线AD翻折,使点C落点E处,AE交边BC于点F,且AB∥DE,求的值.【答案】(1);(2).【解析】(1)根据等高的三角形的面积的比等于底边的比求出BD=2CD,然后求出BC,再根据两组角对应相等两三角形相似求出△ABC和△DAC相似,然后根据相似三角形对应边成比例可得AC:CD="BC:AC" ,代入数据计算即可得解;(2)根据翻折的性质可得∠E=∠C,DE=CD,再根据两直线平行,内错角相等可得∠B=∠EDF,然后求出∠EDF=∠CAD,再根据两组角对应相等两三角形相似求出△EFD和△ADC相似,根据相似三角形面积的比等于相似比的平方求解即可.试题解析:(1)∵﹦1﹕2∴CD:BD=1:2∵DC="3" ∴BD="6"在△ACD和△BCA中,∠CAD=∠B,∠C=∠C∴△ACD∽△BCA∴即∴.(2)∵翻折∴∠C=∠E,∠1=∠2,DE="DC=3"∵AB∥DE∴∠3=∠B∵∠1=∠B∴∠1=∠3∴△ACD∽△DEF∴.【考点】1.相似三角形的判定与性质;2.翻折变换(折叠问题).5.小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:(1)如图1,已知锐角△ABC.求证:;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时,?【答案】(1) ; (2)当t=3秒时,.【解析】(1)首先过点C作CE⊥AB于点E,则sinA=,进而得出EC的长,即可得出答案;(2)首先表示出△APQ的面积,进而得出△ABC的面积,进而利用,求出t的值即可.试题解析:(1)如图1,过点C作CD⊥AB于点D在Rt△ADC中,sinA=∴CD=AC.sinA∵∴.(2)根据题意:AP=2t厘米,CQ=t厘米∴AQ=(12—t)厘米由(1)得:∴化简得:解得(舍),即当t=3秒时,.【考点】解直角三角形.6.已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP//AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.(1)求证:△ADE∽△ACB;(2)设CD=x,BAE = y,求y关于x的函数解析式,并写出它的定义域;(3)如果△COD与△BEA相似,求CD的值.【答案】(1)略;(2)y=,定义域0<x<2;(3)当CD=时,△COD与△BEA相似.【解析】(1)根据等腰三角形的性质,得出角相等,然后角的等量代换,得出其余角相等,即可证明三角形相似;由(1)的结论可以得到线段成比例,解直角三角形即可求出函数解析式,并确定定义域;先由相似得出线段比例关系,设未知数解方程即可.试题解析:(1)证明:∵△ACB是等腰直角三角形∴∠CAB=∠B=45°∵CP//AB∴∠DCA=∠CAB=45°∴∠DCA=∠B∵∠DAE=45°∴∠DAC+∠CAE=∠CAE+∠EAB∴∠DAC=∠EAB∴△DCA∽△EAB∴即且∠DAE=∠CAB=45°∴△ADE∽△ACB.(2)过点E作EH⊥AB于点H由(1)得△DCA∽△EAB∴∵△ACB是等腰直角三角形,且CD=x∴EB=x∴EH=BH=x∴AH=4—x在Rt△AEH中,BAE=即y=定义域0<x<2.(3)若△COD与△BEA相似,又△BEA与相似△DCA即△COD与△DCA相似∴只有△DCO∽△ACD∴∵∠DAO=∠CEO∴∠CEO=∠EAB∴tan∠CEO=y即∴∴解得,经检验都是原方程的实数根,不合题意舍去∴当CD=时,△COD与△BEA相似.【考点】1.相似三角形的判定和性质;2.等腰三角形的性质;3.三角函数的定义.。
