雷电回击电磁场近场计算公式
滚球半径法计算防雷公式

滚球半径法计算防雷公式
滚球半径法是一种用于计算防雷公式的方法,也称为滚球法。
它
基于远离雷电地点的大圆距离与雷电附近的小圆距离之间的比例关系。
防雷公式是指用于确定安装避雷设施(如避雷针等)的高度或长
度的公式。
这些设施旨在保护建筑物或设备免受雷击的损害。
在滚球半径法中,假设雷电垂直撞击地面的距离为A,地面上的建筑物或设备需要保护的范围为B。
通过测量一个标准大小的滚球A和B
之间的半径差(记为R),可以得出以下公式:
B = R * A
其中,B是需要保护的范围的半径,R是滚球与雷电撞击地面的半
径差,A是雷电撞击地面的距离。
这个公式的原理是假设雷电撞击地面点附近的雷电场是均匀的,
且雷电的半径与雷电场的半径差是相似的。
通过测量滚球与雷电撞击
地面点附近的雷电场的半径差,可以推测出需要保护的范围的半径。
需要注意的是,滚球半径法是一种经验公式,其准确性取决于实际测量和具体环境条件。
在实际使用中,还需要考虑其他因素,如建筑物的高度、材料、地形等,以确定最佳的防雷设施布置和尺寸。
另外,滚球半径法也可以拓展到其他应用领域,如检测地下管道的腐蚀情况、测量建筑物的倾斜度等。
通过测量滚球与某个特定点之间的半径差,可以推断出该点与滚球之间的距离或物理变化情况。
这种方法在工程测量和地质勘探中有着广泛的应用。
雷电的防护及数值计算

1.6雷电的防护GB50057-94中对雷防提出的总则(第1.0.1条)规定:“为使建筑物(含构筑物,下同)放雷设计因地制宜地采取放雷措施,防止或减少雷击建筑物所发生的人身伤亡和文物、财产损失,做到安全可靠、技术先进、经济合理,制定本规范。
”————注意,这里提的是“防止或减少”而不是一概要求“防止”,同时也提出考虑安全可靠、技术先进和经济的合理要同时考虑。
在标准的条文说明中指出:“有人认为,建筑物安装防雷装置后就万无一失了。
从经济的观点出发,要达到这点是太浪费了,因此特指出“或减少”,以示不是万无一失,因为按照本规范设计的防雷装置的安全度不是100% 。
1.6.1直击雷的防护防直击雷的外部装置包括接闪器(避雷针、避雷带、避雷线、避雷网)、引下线、接地装置,另外也包括屏蔽措施,通过这些装置迅速地将把雷电流泄放放入地。
1.6.2 电涌的防护为保护设备安全和抑制各种雷电感应引起的浪涌过电压,必须采取系统有效的保护措施,即在电源线信号线上加装浪涌抑制器。
1.6.3等电位连接为防护雷电流引起电磁感应和地电位反击的破坏作用,所有允许连接的设备金属外壳,接地的金属管线和导体间应进行的等电位连接。
是防雷电引起的电磁感应、地电位反击的重要措施(但不允许连接的导体之间防反击是以保持足够的距离实现——防闪络)。
从实质上讲电涌保护也是一种瞬间的等电位连接,是用SPD器件把不能连续与地连接的通电导体(电源线、信号线)与地连接起来。
1.6.4屏蔽用于防护雷电引起的电磁脉冲辐射的破坏作用。
1.6.5防闪络措施对于不能采取等电位连接和使用点涌保护器防护时,通过保持距离抑制雷电引起的地点位反击和电磁感应等的破坏作用。
(下图为基站防雷系统图)1.7 雷电流的特性● 每次雷击的电流波形是随机的,差别很大。
● 雷电流波形一般都是前沿陡而后沿时间相对较长的波形,一般前沿时间在几个微秒到几十个微秒,后沿的半值值时间一般在几十到几百微秒。
高中物理电磁场公式总结

高中物理电磁场公式总结电磁场是物理学中重要的研究对象之一,它描述了空间中电荷和电流产生的电场和磁场之间的相互作用。
在高中物理学习中,我们需要掌握一些关键的电磁场公式,这些公式可以帮助我们理解电磁现象并进行相关计算。
下面将总结一些高中物理电磁场常用的公式。
电场相关公式1.电场强度公式:$$\\vec{E} = \\frac{1}{4\\pi\\epsilon_0}\\frac{q}{r^2}\\hat{r}$$2.其中,$\\vec{E}$为电场强度,$\\epsilon_0$为真空介电常数,q为电荷量,r为距离,$\\hat{r}$为单位矢量。
3.电场中电势能公式:U=qV4.其中,U为电荷在电场中的电势能,q为电荷量,V为电场中的电势。
5.电场中电势公式:$$V = \\frac{1}{4\\pi\\epsilon_0}\\frac{q}{r}$$6.其中,V为电场中的电势。
磁场相关公式1.磁感应强度公式:$$\\vec{B} = \\mu_0 \\mu_r \\vec{H}$$2.其中,$\\vec{B}$为磁感应强度,$\\mu_0$为真空磁导率,$\\mu_r$为相对磁导率,$\\vec{H}$为磁场强度。
3.洛伦兹力公式:$$\\vec{F} = q(\\vec{v} \\times \\vec{B})$$4.其中,$\\vec{F}$为洛伦兹力,q为电荷量,$\\vec{v}$为电荷运动速度,$\\vec{B}$为磁感应强度。
5.安培环路定理:$$\\oint \\vec{H} \\cdot d\\vec{l} = I_{enc}$$6.其中,$\\vec{H}$为磁场强度,I enc为通过曲线围成的面积的电流。
以上是高中物理电磁场公式的部分总结,通过学习和掌握这些公式,我们可以更好地理解电磁现象,进行相关的计算和分析。
在实际应用中,也可以根据具体情况结合这些公式进行问题求解,进一步深化对电磁场的理解和应用。
雷电回击电磁场近场计算公式

雷电回击电磁场近场计算公式杨春山周璧华(解放军理工大学工程兵工程学院电磁脉冲室,南京 210007)摘要:基于大地的有限导电性,利用Collin提出的Sommerfeld积分近似结果,得到了一个适用于几百米范围内雷电回击电磁场的频域近似计算公式,并给出了相应的地面以下透射场的表达式。
由MTLL模型计算结果表明,考虑大地有限导电性计算出的垂直电场更符合实测结果。
关键词:雷电;雷电电磁脉冲;电磁场;一、引言由雷击造成的破坏可以有多种方式分类。
考虑落地雷的破坏,通常可以分为直接雷害和间接雷害。
直接雷害是由落地雷主放电通道接触而产生的破坏,可导致人员伤亡、物体燃烧、爆炸、腐蚀、变形和其他因强电流磁力、高气压冲击波引起的结构性破坏。
间接雷害主要是指由雷电的电磁效应而造成的有关电气系统的损害。
人们对直接雷害有深刻认识,但对间接雷害的认识还不多。
随着信息时代的到来,信息设备的微电子化、高度集成化使之对雷电电磁脉冲(LEMP)的干扰与毁伤效应越来越敏感。
由雷电放电的陡、短、瞬变等特点导致感应、辐射效应而蒙受损失事件日益增加。
因此,间接雷害的防护问题显得格外重要。
国外雷电研究者们在理论和实验上对雷电回击电磁场的特征进行了深入研究,并建立了许多比较成熟的雷电回击模型。
在各种雷电回击模型中,一般假设大地为理想导体,即电导率s1?¥,但事实上大地不是严格意义上的理想导体,其电参数和数值变化范围很宽[1],特别是对干旱或沙漠地区,大地电导率对雷电回击电磁场的影响不能忽略。
本文以有耗半空间中垂直偶极子的辐射场为基础,通过Collin 提出的Sommerfeld积分近似结果[2]导出雷电回击电磁场的一个近似计算公式,并指出其适应条件和范围。
二、有耗半空间中垂直偶极子的辐射场在地闪回击模型中一般认为雷电回击通道不分支且垂直于地面,通道周围为无穷空间。
如图1所示,设通道起点高度为H0,通道电流分布已知。
对通道中的某一小段电流元,在满足一定条件下可以看作是一垂直电偶极子。
避雷针的反击与电磁脉冲

避雷针的反击与电磁脉冲
一、反击
雷直击避雷针时,雷电流要通过避雷针向大地泄放,此时雷电流在避雷针的接地电阻和等值电感上产生电压升高U 。
设避雷针的等值电感为L ,冲击接地电阻为Rch ,雷电流为i ,则:
dt
di L i R U ch += 如果U 在空气中超过了避雷针与被保护物之间气隙的击穿电压,避雷
针就会向被保护物放电,如果U 在土壤中超过了避雷针的接地装置与被保
护物的接地装置之间隙的击穿电压,避雷针的接地装置就会向被保护物的
接地装置放电,这种现象称为反击。
反击被认为是避雷针的主要缺点之一。
在《建筑物防雷设计规范》(GB50057-1994)中给出了不同类建筑物与避雷
针之间为防反击所需的距离的求解公式。
在电力系统,空气中避雷针与被
保护物之间的距离要求不小于5m ,土壤中,避雷针的接地装置与被保护物
的接地装置之间的距离要求不小于3m 。
当受现场条件限制满足不了安全净
距的要求时,可以将避雷针的接地装置与被保护物的接地装置进行等电位联结。
二、电磁干扰
雷电流具有较高的陡度,当雷击避雷针,雷电流通过避雷针向大地泄放时剧烈的电磁场变化会在避雷针周围的物体上形成感应过电压,造成电磁脉冲。
这也是避雷针的一个缺点。
例如在对地绝缘的金属物体上进行电容性充电,在金属环路中感应出电压和电流等。
但电磁感应造成的只在陡度大的雷电流波头部分出现,而持续时间不会超过1~2us 。
感应在《建筑物防雷设计规范》(GB50057-1994)中介绍了电磁脉冲防护措施。
感应过电压的大小与环路的尺寸及距离避雷针的远近有关。
电磁场公式总结
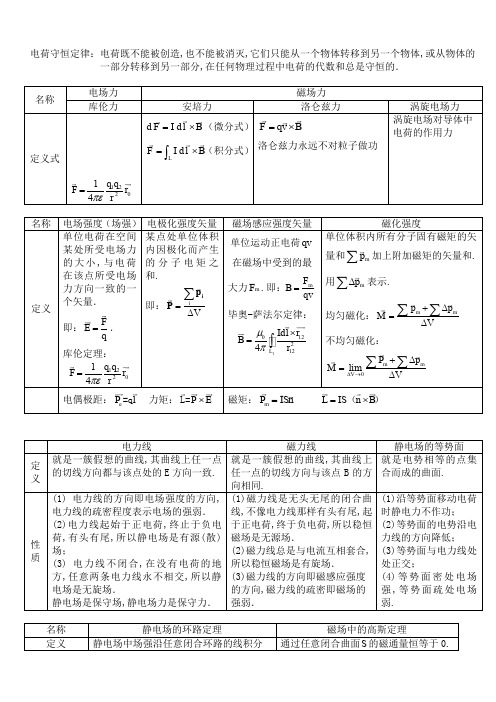
电荷守恒定律:电荷既不能被创造,也不能被消灭,它们只能从一个物体转移到另一个物体,或从物体的一部分转移到另一部分,在任何物理过程中电荷的代数和总是守恒的.名称电场力 磁场力库伦力 安培力 洛仑兹力 涡旋电场力定义式12021F 4q q r r πε=d d F I l B =⨯(微分式) d L F I l B =⨯⎰(积分式)F qv B =⨯洛仑兹力永远不对粒子做功 涡旋电场对导体中电荷的作用力名称 电场强度(场强)电极化强度矢量 磁场感应强度矢量 磁化强度定义单位电荷在空间某处所受电场力的大小,与电荷在该点所受电场力方向一致的一个矢量.即:FE q=.库伦定理:12021F 4q q r r πε=某点处单位体积内因极化而产生的分子电矩之和.即:i V =∆∑i p P单位运动正电荷qv在磁场中受到的最大力m F .即:mF B qv= 毕奥-萨法尔定律:112212L Idl r B 4r μπ⨯=⎰ 单位体积内所有分子固有磁矩的矢量和m p ∑加上附加磁矩的矢量和.用m p ∆∑表示. 均匀磁化:mmp pM V+∆=∆∑∑不均匀磁化:limmmV P p M V∆→+∆=∆∑∑电偶极距:e P l =q 力矩:P E ⨯L= 磁矩:m P ISn = L IS n B =⨯()电力线 磁力线 静电场的等势面定义就是一簇假想的曲线,其曲线上任一点的切线方向都与该点处的E 方向一致. 就是一簇假想的曲线,其曲线上任一点的切线方向与该点B 的方向相同.就是电势相等的点集合而成的曲面. 性质(1) 电力线的方向即电场强度的方向,电力线的疏密程度表示电场的强弱. (2)电力线起始于正电荷,终止于负电荷,有头有尾,所以静电场是有源(散)场; (3) 电力线不闭合,在没有电荷的地方,任意两条电力线永不相交,所以静电场是无旋场. 静电场是保守场,静电场力是保守力. (1)磁力线是无头无尾的闭合曲线,不像电力线那样有头有尾,起于正电荷,终于负电荷,所以稳恒磁场是无源场. (2)磁力线总是与电流互相套合,所以稳恒磁场是有旋场. (3)磁力线的方向即磁感应强度的方向,磁力线的疏密即磁场的强弱. (1)沿等势面移动电荷时静电力不作功; (2)等势面的电势沿电力线的方向降低; (3)等势面与电力线处处正交; (4)等势面密处电场强,等势面疏处电场弱.名称 静电场的环路定理 磁场中的高斯定理 定义 静电场中场强沿任意闭合环路的线积分通过任意闭合曲面S 的磁通量恒等于0.(称作环量)恒等于零.即:d 0LE l ⋅=⎰. 即:SB dS 0⋅=⎰⎰说明的问题电场的无旋性磁场的无源性电位差(电压):单位正电荷的电位能差.即:B AB ABABA W A U Edl q q===⎰.磁介质:在磁场中影响原磁场的物质称为磁介质.名称 电通量 磁通量定义 电通量就是垂直通过某一面积的电力线的条数,用 e Φ表示.即:SSe E dS EdScos θΦ==⎰⎰⎰⎰垂直通过某曲面磁力线的条数叫磁通量,用m Φ表示.即:SSm B dS BdScos θΦ==⎰⎰⎰⎰名称 静电感应 磁化定义 电场对电场中的物质的作用 磁场对磁场中的物质的作用在介质中求电(磁)场感应强度:方法 利用电介质时电场的高斯定理求电场感应强度利用磁介质中的安培环路定理求磁场感应强度 原理通过电介质中任一闭合曲面的电位移通量等于该面包围的自由电荷的代数和.0d SS q ⋅=∑⎰D S 内0ε=+D E PP n δ=⋅e 0P E χε=(各向同性介质)e 1r εχ=+ 0r εεε==D E E磁场强度沿任意闭合路径的线积分(环量)等于穿过以该路径为边界的面的所有传导电流的代数和,而与磁化电流无关.d H l I ⋅=∑⎰BH M μ=-M j n =⋅m M H χ=(各向同性介质)1r m μχ=+ 0H r B H μμμ==解题步骤(1)分析自由电荷分布的对称性,选择适当的高斯面,求出电位移矢量D .(2)根据电位移矢量D 与电场E 的关系,求出电场E . (3)根据电极化强度P 与电场E 的关系,求出(1)分析传导电流分布的对称性,选择适当的环路,求出磁场强度H .(2)根据磁场强度H 与磁场感应强度矢量B 的关系,求出磁场感应强度矢量B .(3)根据磁化强度M 与磁场感应强度矢量B 的电极化强度P . (4)根据束缚电荷e δ与电极化强度P 关系,求出束缚电荷e δ.关系,求出磁场强度M .(4)根据磁化电流0I 与磁化强度M 关系,求出磁化电流0I .电(磁)场能量: 电场 磁场 电磁波能量密度 e 1D E 2ω=⋅ m 1B H 2ω=⋅ 22221()2e m w w w E H E H εμεμ=+=+==能量 2e 11W D EdV=CU 22=⋅⎰⎰⎰ 2m 11W B HdV=LI 22=⋅⎰⎰⎰ m W D EdV=B HdV =⋅⋅⎰⎰⎰⎰⎰⎰位移电流与传导电流比较静电场 涡旋电场 传导电流 位移电流不同点电荷 变化的磁场 自由电荷运动 变化的电场电力线不闭和 电力线闭和 产生焦耳热 不产生焦耳热相同点 对电荷都有力的作用 产生等效的磁效应四种电动势的比较: 电动势 产生原因 计算公式 动生 洛仑兹力:q F v B =⨯d i Lv B l ε=⨯⋅⎰感生涡旋电场力:F qE =涡i d d d d L SB E l S t ε=⋅=-⋅⎰⎰⎰自感自身电流变化:m N LI Φ= i d d ILt ε=- 互感 相互电流变化:211MI φ= 122MI φ= 121d d I M t ε=- 212d d IM tε=- 关系:12L L M k = 楞次定律:闭合回路中感应电流的方向,总是使得它所激发的磁场来阻止引起感应电流的磁通量的变化。
感应雷过电压计算公式

感应雷过电压计算公式感应雷过电压是指当雷电击中地面或者物体时,由于电磁感应作用产生的电压。
雷电是一种自然现象,在大气中形成的云层之间产生的高压放电现象。
当云层中的电荷量积累到一定程度时,就会形成雷电,并通过大气中的电离层传播到地面或物体上。
雷电击中地面或物体时,会产生极强的电磁场,根据法拉第电磁感应定律,当磁通量发生变化时,就会产生感应电动势。
而感应电动势的大小与磁通量的变化速度成正比。
在雷电击中地面或物体的瞬间,磁通量的变化非常快速而剧烈,因此感应电动势也非常大。
根据感应电动势的计算公式,我们可以计算感应雷过电压的大小。
公式如下:U = -N * (∆Φ/∆t)其中,U表示感应电动势的大小,N为线圈匝数,∆Φ表示磁通量变化量,∆t表示磁通量变化的时间。
根据这个公式,我们可以看出,感应雷过电压的大小与线圈匝数、磁通量变化量以及磁通量变化的时间有关。
线圈匝数越大,感应电动势就越大;磁通量变化量越大,感应电动势也越大;磁通量变化的时间越短,感应电动势越大。
另外,雷电的能量也与感应电动势有关。
由于雷电的电能在瞬间转化为磁能,再由磁能转化为电能,所以感应雷过电压非常高。
为了防止感应雷过电压对设备和人身安全造成损害,我们需要采取相应的防护措施。
常见的防护手段有引雷线、接地线、避雷针等。
引雷线通过接地将雷电引导到地下,减少了雷电对建筑物和设备的影响;接地线是将雷电引到地下,避免了感应雷过电压的产生;避雷针则通过形成尖锐的尖端将雷电引到地下。
这些防护措施可以减少雷电对设备和人身所产生的危害。
在设计电气系统时,我们也需要考虑感应雷过电压的影响。
为了减少感应雷过电压对电气设备的影响,可以采用屏蔽线路、增加接地电阻、选择合适的电缆等措施。
屏蔽线路可以将感应雷过电压引导到地下,减少对电气设备的干扰;增加接地电阻能够降低感应雷过电压的大小;选择合适的电缆能够减少感应电动势的产生。
总之,感应雷过电压是雷电击中地面或物体时产生的电压。
电磁场的公式

电磁场的公式电磁场是物理学中一个相当重要的概念,而其中涉及到的公式更是理解和解决相关问题的关键钥匙。
咱先来说说电场强度的公式 E = F / q 。
这其中,E 表示电场强度,F 是电荷所受到的电场力,q 则是电荷量。
想象一下,就好像在操场上,老师吹哨子让同学们集合,老师的哨声就相当于电场力 F ,而同学们的数量 q 就像是电荷的量,哨声的强度除以同学的数量,就得出了老师哨声在每个同学那里产生的“影响力”,也就是电场强度 E 。
再看看电势的公式φ = Ep / q 。
这里的φ 是电势,Ep 是电荷在电场中某点的电势能,q 还是电荷量。
打个比方,电势就像是一个山坡的高度,电势能就是你爬山所需要的能量,而电荷量就像是你的体重。
山坡越高,你需要的能量就越多,但如果你的体重很轻,那么相对来说你感受到的“高度压力”就会小一些。
还有电场力做功的公式 W = qU 。
W 代表电场力做功,q 是电荷量,U 是电势差。
想象一下,你在坐电梯,电荷量 q 就是你的体重,电势差 U 就是电梯上升或者下降的高度差,体重乘以电梯的高度差,就是电梯对你做的功,反过来就是你在电场中移动电荷时电场力做的功。
磁场强度的公式 B = F / (IL) 也很有趣。
B 是磁场强度,F 是磁场对通电导线的作用力,I 是电流强度,L 是导线在磁场中的有效长度。
这就好比你在游乐场坐过山车,磁场强度 B 就是过山车轨道的“刺激程度”,磁场对通电导线的作用力 F 就是过山车给你的“推背感”,电流强度 I 就是车上乘客的“兴奋度”,导线的有效长度 L 就是过山车轨道的长度。
乘客越兴奋,轨道越长,“推背感”就越强,也就反映出轨道的“刺激程度”越高。
电磁感应中的公式E = nΔΦ / Δt 也不能忽视。
E 是感应电动势,n是线圈匝数,ΔΦ 是磁通量的变化量,Δt 是时间的变化量。
好比你在骑自行车,车轮上的辐条就像线圈匝数 n ,你骑车速度的变化导致周围风景变化的快慢就是磁通量的变化量ΔΦ 除以时间的变化量Δt ,而你感受到的那种“向前冲的动力”就是感应电动势 E 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
雷电回击电磁场近场计算公式
杨春山周璧华
(解放军理工大学工程兵工程学院电磁脉冲室,南京 210007)
摘要:基于大地的有限导电性,利用Collin提出的Sommerfeld积分近似结果,得到了一个适用于几百米范围内雷电回击电磁场的频域近似计算公式,并给出了相应的地面以下透射场的表达式。
由MTLL模型计算结果表明,考虑大地有限导电性计算出的垂直电场更符合实测结果。
关键词:雷电;雷电电磁脉冲;电磁场;
一、引言
由雷击造成的破坏可以有多种方式分类。
考虑落地雷的破坏,通常可以分为直接雷害和间接雷害。
直接雷害是由落地雷主放电通道接触而产生的破坏,可导致人员伤亡、物体燃烧、爆炸、腐蚀、变形和其他因强电流磁力、高气压冲击波引起的结构性破坏。
间接雷害主要是指由雷电的电磁效应而造成的有关电气系统的损害。
人们对直接雷害有深刻认识,但对间接雷害的认识还不多。
随着信息时代的到来,信息设备的微电子化、高度集成化使之对雷电电磁脉冲(LEMP)的干扰与毁伤效应越来越敏感。
由雷电放电的陡、短、瞬变等特点导致感应、辐射效应而蒙受损失事件日益增加。
因此,间接雷害的防护问题显得格外重要。
国外雷电研究者们在理论和实验上对雷电回击电磁场的特征进行了深入研究,并建立了许多比较成熟的雷电回击模型。
在各种雷电回击模型中,一般假设大地为理想导体,即电导率s1?¥,但事实上大地不是严格意义上的理想导体,其电参数和数值变化范围很宽[1],特别是对干旱或沙漠地区,大地电导率对雷电回击电磁场的影响不能忽略。
本文以有耗半空间中垂直偶极子的辐射场为基础,通过Collin 提出的Sommerfeld积分近似结果[2]导出雷电回击电磁场的一个近似计算公式,并指出其适应条件和范围。
二、有耗半空间中垂直偶极子的辐射场
在地闪回击模型中一般认为雷电回击通道不分支且垂直于地面,通道周围为无穷空间。
如图1所示,设通道起点高度为H0,通道电流分布已知。
对通道中
的某一小段电流元,在满足一定条件下可以看作是一垂直电偶极子。
设观察点在(z,r)处,距电偶极子及其镜像偶极子的距离分别为R0、R1;大地为良导体,电导率和电容率分别为和。
则有耗半空间上垂直电偶极子的电矢位Az0为
其中
式(2.1)中第三项就是著名的Sommerfeld积分,由于积分中存在极点且收敛速度很慢,很难用数值计算得出精确结果,必须进行近似处理。
Collin采用最速下降法对Sommerfeld积分进行近似处理,得出上半空间电偶极子的矢势为:其中
Q是R1与z轴正方向的夹角。
式(2.2)的物理意义是十分明显的,它由初级源直接辐射的球波和由初级源的镜像源的球波构成,式中第二项球波前面的系数刚好是以入射角投射到介质平面上的平面波的Fresnel反射系数,因此这一项就是被地面反射的波。
当大地变为理想导体时,这时s1?¥,k?¥,Fresnel反射系数为-1,此时式(2.2)可化为:
在Sommerfeld积分近似过程中采用了Hankel函数的近似条件,即|lr|<<1。
实际上式(2.2)也不适用于Q接近于n/2的情况。
但由于自然雷击一般都发生在高层建筑物、塔尖上,离地平面有一定距离(约几米到上百米),雷电回击电流通道起点高度大于零。
因此,对几十到几百米范围内地面以上(z30)的近场,式(2.2)是适用的。
对色散大地,在雷电主频谱范围内有|k|>>sin2Q。
因此,式(2.2)可以进一步近似为:
则垂直偶极子在有耗半空间的辐射场可表示为:
对地面以下的透射场,可由大地表面场及透射深度s给出,即
利用式(2.6)、(2.7)对雷电回击通道内所以偶极子进行求和然后进行Fourier 逆变换,即可得到雷电回击通道几十到几百米范围内的电磁场。
三、数值结果
在各种闪电模型中,工程模型最常用。
常用的工程模型有BG模型、TL模型、MTLL模型、MTLE模型、DU模型、TCS模型等。
其中BG、MTLL、DU、TCS模型与实测近场相符合[3]。
本文采用MTLL模型,通道基底电流取所谓的Heidler函数:
其参数同文献[4],通过数值计算,得到地面上距回击通道50m、500m处回击电磁场分别如图2~5所示。
图2、图4中虚线为垂直电场,实线为把大地看作是理想导体情形下得出的结果。
图3、图5中实线为σ1=1′10-4s/m,时的水平磁场,虚线为σ131′10-2s/m时的结果。
从图中可以看出,大地电导率对几十米范围内垂直电场的影响比较大,对水平磁场的影响比较小。
当σ131′10-2s/m时,对于水平磁场而言,在几百米范围内,把大地看作是理想导体可以得到相当高的精度。
与50米处实测垂直电场波形相比较[5],考虑大地电参数情形下得出结果更符合实测波形。
四、结论
利用Collin提出的Sommerfeld积分近似结果,导出了考虑大地有限导电性情形下雷电回击电磁场近场的频域计算公式,适用于计算距雷击通道几十到几百米范围内的地面上的垂直电场和水平磁场。
同时也给出了地面以下透射场的频域计算公式。
MTLL模型的计算结果表明,考虑了大地有限导电性情形下得出的垂直电场更符合实测波形。
对水平磁场而言,在距回击通道几百米范围内,当大地电导率σ131′10-2s/m时,把大地看作是理想导体得出的结果能达到很高的精度。
由于缺乏水平电场的实测波形及数据,本文没有对水平电场的计算公式进行验证。
参考文献
[1]L. B. Felsen, etc. . Transient Electromagnetic Fields [M]. New York, 1976, 238-245
[2] 龚中麟, 徐承和. 近代电磁理论[M]. 北京:北京大学出版社, 1990
[2]V. A. Rakov, M. A. Uman, Review and Evaluation of Lightning Return Stroke Models Including Some Aspects of Their Application [J]. IEEE Trans. On EMC, 1998,40(4): 403-426.
[3]C. A. Nucci, M. A. Uman, etc. Lightning Return Stroke Current Models With Specified Channel-Base Current: A Review and Comparison [J]. Geophys. Res., 1990,95(D12):20395-20408
[4]V. A. Rakov, M. A. Uman. New insights into lightning processes gained from triggered-lightning experiments in Florida and Alabama [J]. Geophys. Res. 1998,103(D12):14117-14130。
